Output Feedback Control of Discrete-Time T-S Fuzzy Affine Systems Using Quantized Measurements
1 Introduction
Last two decades have witnessed that the networked control systems (NCSs) have drawn a great deal of attention from industrial engineering to control community because of their considerably productive applications in broad fields, for instance, power grids, water distribution networks, transportation networks, mobile sensor networks, unmanned aerial vehicles[1-3]. Nevertheless, new challenges appear when the networks are exploited in feedback loops as a communication medium continuously because of their limited transmission capacity. Specifically, in synthesis of networked control systems, quantization issue is of great importance to be addressed because signals are always needed to be quantized before communicated in a network environment[4-5].
On another fruitful frontier, the T-S fuzzy-model-based method is characterized to be a considerably efficient strategy to control many nonlinear systems[6-8]. The underlying fuzzy model is composed by a set of local plants, that are blended via fuzzy rules smoothly[9-13]. Thus it possesses competence to approximate a complicated nonlinear system via choosing appropriate fuzzy rules to arbitrary degrees of accuracy. See the references[14-16] for the latest developments on this topic. Recently, some results on nonlinear NCSs control were reported in the open literature via fuzzy-model-based approach[17-22]. For instance, in Ref.[20], both fault detection filter and state-feedback controller were designed for time-delay fuzzy NCSs with considering of quantized output and packet dropouts phenomena.
Nevertheless, the aforementioned results for NCSs were mainly derived in the framework of CQLF. Aiming to reduce the conservatism, there have also been some results on control of nonlinear NCSs on the basis of PQLFs[15, 23-25]. Via a stochastic approach, the data-loss phenomenon of the network system existed in both uplink and downlink channels can be represented accurately. The authors in Ref.[23] proposed an asynchronous SOF controller for fuzzy discrete-time NCSs. Utilizing quantized measurements, Ref.[24] was concerned with the observer-based output-feedback control problem for fuzzy NCSs. Nevertheless, few results have been reported for fixed-order piecewise-affine (PWA) DOF controller design for fuzzy networked systems in framework of PQLFs.
Motivated by the above-mentioned statements, we propose a robust H∞ fixed-order piecewise-affine (PWA) DOF controller design approach for discrete-time fuzzy networked control systems with quantized measurements. Via a state-input augmentation method, one attains the closed-loop system to be a descriptor form, such that couplings between the piecewise affine controller gains and system matrices are eliminated. Through using S-procedure and some convexification techniques, sufficient conditions can be presented in terms of LMIs. Finally, two simulation studies will be conducted to verify the feasibility of the aforementioned control scheme.
2 Preliminaries
2.1 T-S Fuzzy Affine Models
Consider the discrete-time fuzzy-affine model which is characterized by IF-THEN rules as follows:
Plant Rule Rl : IF ζ1(t) is F1l and ζ2(t) is F2l and...and ζφ(t) is Fφl, THEN
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{x}}\left( {t + 1} \right) = {A_l}\mathit{\boldsymbol{x}}\left( t \right) + {a_l} + {B_l}\mathit{\boldsymbol{u}}\left( t \right) + {D_{l1}}\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{y}}\left( t \right) = {C_l}\mathit{\boldsymbol{x}}\left( t \right) + {D_{l2}}\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{z}}\left( t \right) = {L_l}\mathit{\boldsymbol{x}}\left( t \right) + {N_l}\mathit{\boldsymbol{u}}\left( t \right)
\end{array} \right.
$
|
(1) |
where l:= {1, 2, …, r}, Rl refers to the l-th fuzzy inference rule; r is the number of inference rules; Fφl is fuzzy sets; ζ(t) stand for the premise variables; x(t)∈Rnx is the state; y(t)∈Rny is the output; u(t)∈Rnu is the control input; w(t)∈Rnw is external disturbance assumed to be norm-bounded; z(t)∈Rnz is the measurement output; (Al, al, Bl, Dl1, Cl, Dl2, Ll, Nl) stands for the l-th local model.
Remark 2.1 It can be seen that the systems in Eq.(1) are in affine models. These models are with more powerful competence to approximate nonlinear systems.
Then denote μl[ζ(t)] the normalized membership function (MF) of the fuzzy set
|
$
{F^l}: = \prod\limits_{\phi = 1}^\phi {F_\phi ^l}
$
|
and
|
$
{\mu _l}\left[ {\zeta \left( t \right)} \right]: = \frac{{\prod\limits_{\phi = 1}^\phi {{\mu _{l\phi }}\left[ {{\zeta _\phi }\left( t \right)} \right]} }}{{\sum\limits_{g = 1}^r {\prod\limits_{\phi = 1}^\phi {{\mu _{g\phi }}\left[ {{\zeta _\phi }\left( t \right)} \right]} } }} \ge 0
$
|
|
$
\sum\limits_{l = 1}^r {{\mu _l}\left[ {{\zeta _\phi }\left( t \right)} \right]} = 1
$
|
Based upon Eq.(2), then one has,
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{x}}\left( {t + 1} \right) = A\left( \mu \right)\mathit{\boldsymbol{x}}\left( t \right) + a\left( \mu \right) + \\
\;\;\;\;\;\;\;\;\;B\left( \mu \right)\mathit{\boldsymbol{u}}\left( t \right) + {D_1}\left( \mu \right)\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{y}}\left( t \right) = C\left( \mu \right)\mathit{\boldsymbol{x}}\left( t \right) + {D_2}\left( \mu \right)\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{z}}\left( t \right) = L\left( \mu \right)\mathit{\boldsymbol{x}}\left( t \right) + N\left( \mu \right)\mathit{\boldsymbol{u}}\left( t \right)
\end{array} \right.
$
|
(2) |
where
|
$
\left\{ \begin{array}{l}
A\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{A_l}} ,a\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{a_l}} \\
B\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{B_l}} ,{D_1}\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{D_{l1}}} \\
L\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{L_l}} ,N\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{N_l}} \\
C\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{C_l}} ,{D_2}\left( \mu \right) = \sum\limits_{l = 1}^r {{\mu _l}{D_{l2}}}
\end{array} \right.
$
|
Following a similar process to Ref.[22], one can decompose the premise-variable space into crisp regions and fuzzy regions with
|
$
\begin{array}{l}
M\left( i \right): = \left\{ {m\left| {{\mu _m}\left[ {\zeta \left( t \right)} \right] > 0,m \in \left\{ {1,2, \cdots ,r} \right\},} \right.} \right.\\
\;\;\;\;\;\;\;\;\;\;\;\;\left. {\zeta \left( t \right) \in {S_i},i \in I} \right\}
\end{array}
$
|
Consequently, one can reformulate the system(2) as follows:
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{x}}\left( {t + 1} \right) = {A_i}\mathit{\boldsymbol{x}}\left( t \right) + {a_i} + {B_i}\mathit{\boldsymbol{u}}\left( t \right) + {D_{i1}}\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{y}}\left( t \right) = {C_i}\mathit{\boldsymbol{x}}\left( t \right) + {D_{i2}}\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{z}}\left( t \right) = {L_i}\mathit{\boldsymbol{x}}\left( t \right) + {N_i}\mathit{\boldsymbol{u}}\left( t \right)
\end{array} \right.
$
|
(3) |
where
|
$
\left\{ \begin{array}{l}
{A_i} = \sum\limits_{m \in M,\left( i \right)} {{\mu _m}{A_m}} ,{a_i} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{a_m}} \\
{B_i} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{B_m}} ,{D_{i1}} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{D_{m1}}} \\
{L_i} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{L_m}} ,{N_i} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{N_m}} \\
{C_i} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{C_m}} ,{D_{i2}} = \sum\limits_{m \in M\left( i \right)} {{\mu _m}{D_{m2}}}
\end{array} \right.
$
|
For each subspace Si, i∈I the indices utilized in the interpolation within that region are included in the set n(i). It is noted that for a crisp region, only one element is contained in n(i). Let the decomposed regions be divided into two classes I=I0∪I1 where I1 stands for the index set of regions that do not contain the origin, while I0 stands for the corresponding ones which contain the origin. Thus, for all, i∈I0, ai=0.
The boundaries partition S⊂Rg as:
|
$
\begin{array}{l}
\partial S_l^v: = \left\{ {\zeta \left( t \right)\left| {{\mu _l}\left[ {\zeta \left( t \right)} \right] = 1,} \right.} \right.\\
\;\;\;\;\;\;\;\;\;0 \le {\mu _1}\left[ {\zeta \left( t \right) + \delta } \right] < 1,\forall 0 < \left| \delta \right| \ll 1,\\
\;\;\;\;\;\;\;\;\;\left. {l \in \left\{ {1,2, \cdots ,r} \right\}} \right\}
\end{array}
$
|
where v satisfies əSl:= ∪vəSlv.
We introduce a set Γ to describe region transitions with all possibilities
|
$
\mathit{\Gamma }: = \left\{ {\left( {i,j} \right)\left| {\zeta \left( t \right) \in {S_i}} \right.,\zeta \left( {t + 1} \right) \in {S_j},i,j \in I} \right\}
$
|
For (i, j)∈Γ and in the context of i=j, the system states evolve in the same subspace Si at the time t. Otherwise, the states are to jump from the subspace Si to Sj at that time.
Specifically, we assume that there exist matrices Fi and fi such that
|
$
{S_i} \subseteq {R_i},{R_i}: = \left\{ {\mathit{\boldsymbol{x}}\left| {\left\| {{F_i}\mathit{\boldsymbol{x}} + {f_i}} \right\| \le 1} \right.} \right\}
$
|
This outer approximation is considerably useful especially when Si are slab regions.
Particularly, once Si are slabs with
|
$
{S_i} = \left\{ {\mathit{\boldsymbol{x}}\left| {{\alpha _i} \le \mathit{\boldsymbol{\theta }}_i^{\rm{T}}\mathit{\boldsymbol{x}} \le {\beta _i}} \right.} \right\},i \in I
$
|
where αi, βi∈R, θi∈Rnx, and then one can precisely describe each region via a degenerate ellipsoid with
|
$
{F_i} = \frac{{2\mathit{\boldsymbol{\theta }}_i^{\rm{T}}}}{{{\beta _i} - {\alpha _i}}},{f_i} = - \frac{{{\beta _i} + {\alpha _i}}}{{{\beta _i} - {\alpha _i}}}
$
|
Then one has the following relationship,
|
$
{\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{x}}\left( t \right)}\\
1
\end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{F}}_i^{\rm{T}}{\mathit{\boldsymbol{F}}_i}}&{\mathit{\boldsymbol{F}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i}}\\
* &{\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{x}}\left( t \right)}\\
1
\end{array}} \right] \le 0
$
|
(4) |
where i∈I.
2.2 Measurements Quantization
Here, the quantized measurements can be considered as:
|
$
{\mathit{\boldsymbol{y}}_q}\left( t \right) = \vartheta \left[ {\mathit{\boldsymbol{y}}\left( t \right)} \right] = {\left[ {\vartheta \left[ {{y_1}\left( t \right)} \right], \cdots ,\vartheta \left[ {{y_{{n_y}}}\left( t \right)} \right]} \right]^{\rm{T}}}
$
|
(5) |
where ϑ[.] stands for a logarithmic time-invariant and symmetric quantizer satisfying ϑ[-y(t)]=-ϑ[y(t)]. In addition, one has the following relationships for each output channel,
|
$
\begin{array}{l}
{U_j} = \left\{ { \pm {v_{ij}}\left| {{v_{ij}} = \rho _j^i{v_{0j}}} \right.,i = \pm 1, \pm 2, \cdots } \right\} \cup \\
\;\;\;\;\left\{ {{v_{0j}}} \right\} \cup \left\{ 0 \right\},0 < {\rho _i} < 1,{v_{0j}} > 0,1 \le j \le {n_y}
\end{array}
$
|
(6) |
where ρi is the quantization density. vij stands for the quantization level. With σi=(1+ρi)/(1-ρi) the associated quantizer ϑ[.] for the logarithmic quantizer can be denoted as follows:
|
$
\vartheta \left[ {{y_j}\left( t \right)} \right] = \left\{ \begin{array}{l}
\rho _j^i{v_{0j}},\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\rho _j^i{v_{0j}}}}{{1 + {\sigma _j}}} < {y_j}\left( t \right) \le \frac{{\rho _j^i{v_{0j}}}}{{1 - {\sigma _j}}}\\
0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_j}\left( t \right) = 0\\
- \vartheta \left[ { - {y_j}\left( t \right)} \right],\;\;\;{y_j}\left( t \right) < 0
\end{array} \right.
$
|
(7) |
Noticing Eqs.(5)-(7) and utilizing a sector bound method shown in Ref.[24], one has:
|
$
- {\sigma _j}{y_j}\left( t \right) \le \vartheta \left[ {{y_j}\left( t \right)} \right] - {y_j}\left( t \right) \le {\sigma _j}{y_j}\left( t \right)
$
|
(8) |
where 1≤j≤ny.
On the basis of Eq.(8), it can be obtained that:
|
$
{y_q}\left( t \right) = \vartheta \left[ {y\left( t \right)} \right] = \left( {{\mathit{\boldsymbol{I}}_{{n_y}}} + \mathit{\Lambda \bar \Delta }\left( t \right)} \right)y\left( t \right)
$
|
(9) |
where Λ:= diag{σ1, …, σny}, and ΔT(t) Δ(t)≤Iny.
2.3 Fixed-Order DOF Controller
For system (3) with measurements quantization, we have the DOF controller as,
|
$
\left\{ \begin{array}{l}
{\mathit{\boldsymbol{x}}_c}\left( {t + 1} \right) = {\mathit{\boldsymbol{A}}_{ci}}{x_c}\left( t \right) + {\mathit{\boldsymbol{a}}_{ci}} + {\mathit{\boldsymbol{B}}_{ci}}{\mathit{\boldsymbol{y}}_q}\left( t \right)\\
\mathit{\boldsymbol{u}}\left( t \right) = {\mathit{\boldsymbol{K}}_{ci}}{\mathit{\boldsymbol{x}}_c}\left( t \right) + {\mathit{\boldsymbol{k}}_{ci}} + {\mathit{\boldsymbol{D}}_{ci}}{\mathit{\boldsymbol{y}}_q}\left( t \right),i \in I
\end{array} \right.
$
|
(10) |
where xc(t)∈Rnc, 0≤nc≤nx is the controller states, Aci∈Rnc×nc, Bci∈Rnc×ny, Kci∈Rnu×nc, Dci∈Rnc×ny, aci∈Rnc, kci∈Rnu are controller gains to be determined. One can easily conclude that aci=0 and kci=0 for i∈I0. It is also worth mentioning that when nc=nx, Eq.(10) is characterized as a full-order DOF controller. While nc < nx, controller Eq.(10) refers to a educed-order one. Particularly, Eq.(5) reduces to a SOF controller if nc=0.
With consideration of quantized measurements Eq.(9), combine the controller Eq.(5) with Eq.(3), and then one has that,
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{x}}\left( {t + 1} \right) = {\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{a}}_i} + {\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{u}}\left( t \right) + {\mathit{\boldsymbol{D}}_{i1}}\mathit{\boldsymbol{w}}\left( t \right)\\
{\mathit{\boldsymbol{x}}_c}\left( {t + 1} \right) = {\mathit{\boldsymbol{A}}_{ci}}{\mathit{\boldsymbol{x}}_c}\left( t \right) + {\mathit{\boldsymbol{a}}_{ci}} + {\mathit{\boldsymbol{B}}_{ci}}\left( {{\mathit{\boldsymbol{C}}_i} + \mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{C}}_i}} \right)\mathit{\boldsymbol{x}}\left( t \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{B}}_{ci}}\left( {{\mathit{\boldsymbol{D}}_{i2}} + \mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{D}}_{i2}}} \right)\mathit{\boldsymbol{w}}\left( t \right)\\
0 \cdot u\left( {t + 1} \right) = {\mathit{\boldsymbol{K}}_{ci}}{\mathit{\boldsymbol{x}}_c}\left( t \right) + {\mathit{\boldsymbol{k}}_{ci}} - \mathit{\boldsymbol{u}}\left( t \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{D}}_{ci}}\left( {{\mathit{\boldsymbol{C}}_i} + \mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{C}}_i}} \right)\mathit{\boldsymbol{x}}\left( t \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{D}}_{ci}}\left( {{\mathit{\boldsymbol{D}}_{i2}} + \mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{D}}_{i2}}} \right)\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{z}}\left( t \right) = {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{N}}_i}\mathit{\boldsymbol{u}}\left( t \right),\zeta \left( t \right) \in {S_i},i \in I
\end{array} \right.
$
|
(11) |
Define $\mathit{\boldsymbol{\tilde x}}\left( t \right)$=[xT(t) xcT(t) u(t)]T and reformulate system (11) into the following descriptor form,
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{E\tilde x}}\left( {t + 1} \right) = \left( {{{\mathit{\boldsymbol{\tilde A}}}_i} + \Delta {{\mathit{\boldsymbol{\tilde A}}}_i}} \right)\mathit{\boldsymbol{\tilde x}}\left( t \right) + {{\mathit{\boldsymbol{\tilde a}}}_i} + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{{\mathit{\boldsymbol{\tilde D}}}_i} + \Delta {{\mathit{\boldsymbol{\tilde D}}}_i}} \right)\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{z}}\left( t \right) = {{\mathit{\boldsymbol{\tilde L}}}_i}\mathit{\boldsymbol{\tilde x}}\left( t \right),\zeta \left( t \right) \in {S_i},i \in I
\end{array} \right.
$
|
(12) |
where
|
$
\mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{c}}
\mathit{\boldsymbol{I}}&0&0\\
0&\mathit{\boldsymbol{I}}&0\\
0&0&0
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde A}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_i}}&0&{{\mathit{\boldsymbol{B}}_i}}\\
{{\mathit{\boldsymbol{B}}_{ci}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{i}}}}&{{\mathit{\boldsymbol{A}}_{ci}}}&0\\
{{\mathit{\boldsymbol{D}}_{ci}}{\mathit{\boldsymbol{C}}_i}}&{{K_{ci}}}&{ - \mathit{\boldsymbol{I}}}
\end{array}} \right]
$
|
|
$
\Delta {{\mathit{\boldsymbol{\tilde A}}}_i} = \left[ {\begin{array}{*{20}{c}}
0&0&0\\
{{B_{ci}}\Lambda \bar \Delta \left( t \right){C_i}}&0&0\\
{{D_{ci}}\Lambda \bar \Delta \left( t \right){C_i}}&0&0
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\bar a}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{a_i}}\\
{{\mathit{\boldsymbol{a}}_{ci}}}\\
{{k_{ci}}}
\end{array}} \right],{{\mathit{\boldsymbol{\bar D}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{D_{i1}}}\\
{{B_{ci}}{D_{i2}}}\\
{{D_{ci}}{D_{i2}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde L}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{L_i}}&0&{{N_i}}
\end{array}} \right]
$
|
Via the state-input augmentation scheme, one can decouple the controller gains from the system matrices. This feature makes it easier to develop the proposed DOF controller (10) according to a convex optimization framework on the basis of LMI techniques.
Thus, we aim to synthesize a DOF controller such that the closed-loop system is asymptotically stable with robust performance γ as
|
$
{\left\| \mathit{\boldsymbol{z}} \right\|_2} < \gamma {\left\| \mathit{\boldsymbol{w}} \right\|_2}
$
|
where
|
$
{\left\| \mathit{\boldsymbol{z}} \right\|_2} = \sqrt {\sum\limits_{t = 0}^\infty {{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right)} }
$
|
|
$
{\left\| \mathit{\boldsymbol{w}} \right\|_2} = \sqrt {\sum\limits_{t = 0}^\infty {{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right)} }
$
|
3 Main Results
We will present several novel results on the robust H∞ fixed-order DOF controller synthesis for system (1) in this section.
3.1 Analysis and Synthesis of Fixed-Order DOF Controller
Theorem 3.1 The closed-loop system in Eq.(12) is asymptotically stable with performance γ, if there exist matrices 0 < Pi1=Pi1T∈R(nx+nc)×(nx+nc), Pi2∈R(nx+nc)×nu, Pi3∈Rnu×nu, Gi1(1), Gi2(1)∈Rnx×nx, Gi1(2), Gi2(2)∈Rnc×nx, Gi1(3), Gi2(3)∈Rnu×nx, Gi1(4)∈Rnc×nc, Gi1(5)∈Rnu×nu, Gi4(1)∈Rnω×nx, Âci∈Rnc×nc, ${{\mathit{\boldsymbol{\hat B}}}_{ci}}$∈Rnc×ny, ${{\mathit{\boldsymbol{\hat K}}}_{ci}}$ci∈Rnu×nc, ${{\mathit{\boldsymbol{\hat D}}}_{ci}}$∈Rnu×ny, for i∈I0, Gi3(1)∈R1×nx, âci∈Rnc, ${{\hat k}_i}$∈Rnu, for i∈I1, scalars εi>0, i∈I, and λij < 0, i∈I1, j∈I, such that the subsequent LMIs hold,
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{ijm}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i}}&{{\varepsilon _i}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m}}\\
* &{ - {\varepsilon _i}}&0\\
*&* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}
\end{array}} \right] < 0
$
|
where m∈M(i), i∈I0, (i, j)∈Γ,
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_{ijm}}}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_i}}&{{\varepsilon _i}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m}}\\
* &{ - {\varepsilon _i}}&0\\
*&* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}
\end{array}} \right] < 0
$
|
(13) |
where m∈M(i), i∈I1, (i, j)∈Γ, and
|
$
{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{ijm}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j} - {\mathit{\boldsymbol{G}}_{i1}} - \mathit{\boldsymbol{G}}_{i1}^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {12} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {13} \right)}}\\
* &{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {22} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {23} \right)}}\\
*&* &{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {33} \right)}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}_{ijm}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j} - {\mathit{\boldsymbol{G}}_{i1}} - \mathit{\boldsymbol{G}}_{i1}^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {12} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {13} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {14} \right)}}\\
* &{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {22} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {23} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {24} \right)}}\\
*&* &{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {33} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {34} \right)}}\\
*&*&* &{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {44} \right)}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{P}}_j} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_{j1}}}&{{\mathit{\boldsymbol{P}}_{j2}}}\\
0&{{\mathit{\boldsymbol{P}}_{j3}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i1}} = \left[ {\begin{array}{*{20}{c}}
{{G_{i1\left( 1 \right)}}}&{{{\hat H}_1}{G_{i1\left( 4 \right)}}}&{{{\hat H}_2}{G_{i1\left( 5 \right)}}}\\
{{G_{i1\left( 2 \right)}}}&{{\delta _1}{G_{i1\left( 4 \right)}}}&0\\
{{G_{i1\left( 3 \right)}}}&0&{{\rho _1}{G_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i2}} = \left[ {\begin{array}{*{20}{c}}
{{G_{i3\left( 1 \right)}}}&{{\delta _2}{{\hat H}_1}{G_{i1\left( 4 \right)}}}&{{\rho _2}{{\hat H}_2}{G_{i1\left( 5 \right)}}}\\
{{G_{i2\left( 2 \right)}}}&{{\delta _3}{G_{i1\left( 4 \right)}}}&0\\
{{G_{i2\left( 3 \right)}}}&0&{{\rho _3}{G_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i3}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}}&0&0
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i4}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}}&0&0
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\hat H}}}_1} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{I}}_{{n_c}}}}\\
{{0_{\left( {{n_x} - {n_c}} \right){n_c}}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\hat H}}}_2} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{I}}_{{n_u}}}}\\
{{0_{\left( {{n_x} - {n_u}} \right){n_u}}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{ijm}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j} - {\mathit{\boldsymbol{G}}_{i1}} - \mathit{\boldsymbol{G}}_{i1}^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {12} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {13} \right)}}\\
* &{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {22} \right)}}&{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {23} \right)}}\\
*&* &{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {33} \right)}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {12} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {121} \right)} - \mathit{\boldsymbol{G}}_{i2}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {121} \right)} = \left[ {\begin{array}{*{20}{c}}
{{G_{i1\left( 1 \right)}}{A_m} + {{\hat H}_1}{{\hat B}_{ci}}{C_m} + {{\hat H}_2}{{\hat D}_{ci}}{C_m}}&{{{\hat H}_1}{{\hat A}_{ci}} + {{\hat H}_2}{{\hat K}_{ci}}}&{{G_{i1\left( 1 \right)}}{B_m} - {{\hat H}_2}{G_{i1\left( 5 \right)}}}\\
{{G_{i1\left( 2 \right)}}{A_m} + {\delta _1}{{\hat B}_{ci}}{C_m}}&{{\delta _1}{{\hat A}_{ci}}}&{{G_{i1\left( 2 \right)}}{B_m}}\\
{{G_{i1\left( 3 \right)}}{A_m} + {\rho _1}{{\hat D}_{ci}}{C_m}}&{{\rho _1}{{\hat K}_{ci}}}&{{G_{i1\left( 3 \right)}}{B_m} - {\rho _1}{G_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {13} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {131} \right)} - G_{i4}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {131} \right)} = \left[ {\begin{array}{*{20}{c}}
{{G_{i1\left( 1 \right)}}{D_{m1}} + {{\hat H}_1}{{\hat B}_{ci}}{D_{m2}} + {{\hat H}_2}{{\hat D}_{ci}}{D_{m2}}}\\
{{G_{i1\left( 2 \right)}}{D_{m1}} + {\delta _1}{{\hat B}_{ci}}{D_{m2}}}\\
{{G_{i1\left( 3 \right)}}{D_{m1}} + {\rho _1}{{\hat D}_{ci}}{D_{m2}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {22} \right)} = - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_m^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_m} + Sym\left\{ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {221} \right)}} \right\}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {221} \right)} = \\
\left[ {\begin{array}{*{20}{c}}
{{G_{i2\left( 1 \right)}}{A_m} + {\delta _2}{{\hat H}_1}{{\hat B}_{ci}}{C_m} + {\rho _2}{{\hat H}_2}{{\hat D}_{ci}}{C_m}}&{{\delta _2}{{\hat H}_1}{{\hat A}_{ci}} + {\rho _2}{{\hat H}_2}{{\hat K}_{ci}}}&{{G_{i2\left( 1 \right)}}{B_m} - {\rho _2}{{\hat H}_2}{G_{i1\left( 5 \right)}}}\\
{{G_{i2\left( 2 \right)}}{A_m} + {\delta _3}{{\hat B}_{ci}}{C_m}}&{{\delta _3}{{\hat A}_{ci}}}&{{G_{i2\left( 2 \right)}}{B_m}}\\
{{G_{i2\left( 3 \right)}}{A_m} + {\rho _3}{{\hat D}_{ci}}{C_m}}&{{\rho _3}{{\hat K}_{ci}}}&{{G_{i2\left( 3 \right)}}{B_m} - {\rho _3}{G_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {23} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {231} \right)} + {\left\{ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {232} \right)}} \right\}^{\rm{T}}}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {231} \right)} = \left[ {\begin{array}{*{20}{c}}
{{G_{i2\left( 1 \right)}}{D_{m1}} + {\delta _2}{{\hat H}_1}{{\hat B}_{ci}}{D_{m2}} + {\rho _2}{{\hat H}_2}{{\hat D}_{ci}}{D_{m2}}}\\
{{G_{i2\left( 2 \right)}}{D_{m1}} + {\delta _3}{{\hat B}_{ci}}{D_{m2}}}\\
{{G_{i2\left( 3 \right)}}{D_{m1}} + {\rho _3}{{\hat D}_{ci}}{D_{m2}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {232} \right)}{\rm{ = }}\left[ {\begin{array}{*{20}{c}}
{{G_{i\left( 4 \right)1}}{A_m}}&0&{{G_{i\left( 4 \right)1}}{B_m}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {33} \right)} = - {\gamma ^3}\mathit{\boldsymbol{I}} + Sym\left\{ {{G_{i\left( 4 \right)1}}{D_{m1}}} \right\}
$
|
|
$
\sum\nolimits_i { = \left[ {\begin{array}{*{20}{c}}
{\sum\nolimits_i^{\left( 1 \right)} {} }\\
{\sum\nolimits_i^{\left( 2 \right)} {} }\\
0
\end{array}} \right]} ,\sum\nolimits_i^{\left( 1 \right)} { = \left[ {\begin{array}{*{20}{c}}
{{{\hat H}_1}{{\hat B}_{ci}}\mathit{\Lambda + }{{\hat H}_2}{{\hat D}_{ci}}\mathit{\Lambda }}\\
{{\delta _1}{{\hat B}_{ci}}\mathit{\Lambda }}\\
{{\rho _1}{{\hat D}_{ci}}\mathit{\Lambda }}
\end{array}} \right]}
$
|
|
$
\sum\nolimits_i^{\left( 2 \right)} { = \left[ {\begin{array}{*{20}{c}}
{{\delta _2}{{\hat H}_1}{{\hat B}_{ci}}\mathit{\Lambda + }{\rho _2}{{\hat H}_2}{{\hat D}_{ci}}\mathit{\Lambda }}\\
{{\delta _3}{{\hat B}_{ci}}\mathit{\Lambda }}\\
{{\rho _3}{{\hat D}_{ci}}\mathit{\Lambda }}
\end{array}} \right]}
$
|
|
$
{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m} = \left[ {\begin{array}{*{20}{c}}
0\\
{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m^{\left( 1 \right)}}\\
{\mathit{\boldsymbol{D}}_{{m_2}}^{\rm{T}}}
\end{array}} \right],\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m^{\left( 1 \right)} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{C}}_m^{\rm{T}}}\\
0\\
0
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde L}}}_m} = \left[ {\begin{array}{*{20}{c}}
{{L_m}}&0&{{N_m}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {12} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {12} \right)}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {13} \right)} = \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {131} \right)} - \mathit{\boldsymbol{G}}_{i3}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {131} \right)} = \left[ {\begin{array}{*{20}{c}}
{{G_{i1\left( 1 \right){a_m}}} + {{\hat H}_2}{{\hat k}_{ci}} + {{\hat H}_1}{{\hat a}_{ci}}}\\
{{G_{i1\left( 2 \right){a_m}}} + {\delta _1}{{\hat a}_{ci}}}\\
{{G_{i1\left( 3 \right){a_m}}} + {\rho _1}{{\hat k}_{ci}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {14} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {13} \right)}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {22} \right)} = - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_m^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_m} + {\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + Sym\left\{ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {221} \right)}} \right\}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {23} \right)} = {\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} + \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {231} \right)} + {\left\{ {\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {232} \right)}} \right\}^{\rm{T}}}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {231} \right)} = \left[ {\begin{array}{*{20}{c}}
{{G_{i2\left( 1 \right){a_m}}} + {\delta _2}{{\hat H}_2}{{\hat k}_{ci}} + {\rho _2}{{\hat H}_1}{{\hat a}_{ci}}}\\
{{G_{i2\left( 2 \right){a_m}}} + {\delta _3}{{\hat a}_{ci}}}\\
{{G_{i2\left( 3 \right){a_m}}} + {\rho _3}{{\hat k}_{ci}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {232} \right)} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{A}}_m}}&0&{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{B}}_m}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {24} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{im}^{\left( {23} \right)}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {33} \right)} = {\lambda _{ij}}\left( {\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1} \right) + Sym\left\{ {{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{a}}_m}} \right\}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {34} \right)} = {\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{m1}} + \mathit{\boldsymbol{a}}_{im}^{\rm{T}}\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}_{im}^{\left( {44} \right)} = - {\gamma ^2}\mathit{\boldsymbol{I}} + Sym\left\{ {{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{m1}}} \right\}
$
|
|
$
{{\bar \Sigma }_i} = \left[ {\begin{array}{*{20}{c}}
{\sum\nolimits_i^{\left( 1 \right)} {} }\\
{\sum\nolimits_i^{\left( 2 \right)} {} }\\
0\\
0
\end{array}} \right],{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m} = \left[ {\begin{array}{*{20}{c}}
0\\
{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m^{\left( 1 \right)}}\\
0\\
{\mathit{\boldsymbol{D}}_{m2}^{\rm{T}}}
\end{array}} \right]
$
|
Moreover, we can attain the controller gains as:
|
$
\left\{ \begin{array}{l}
{A_{ci}} = G_{i1\left( 4 \right)}^{ - 1}{{\hat A}_{ci}},{B_{ci}} = G_{i1\left( 4 \right)}^{ - 1}{{\hat B}_{ci}}\\
{a_{ci}} = G_{i1\left( 4 \right)}^{ - 1}{{\hat a}_{ci}},{K_{ci}} = G_{i1\left( 5 \right)}^{ - 1}{{\hat K}_{ci}}\\
{D_{ci}} = G_{i1\left( 5 \right)}^{ - 1}{{\hat D}_{ci}},{k_{ci}} = G_{i1\left( 5 \right)}^{ - 1}{{\hat k}_{ci}}
\end{array} \right.
$
|
(14) |
Proof Without loss of generality, we only prove the more complicated situation when i∈I1 in the following. Take the PQLF as follows:
|
$
\mathit{\boldsymbol{V}}\left( t \right) = {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right){\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E\tilde x}}\left( t \right)
$
|
(15) |
where ${\mathit{\boldsymbol{P}}_i} = \left[{\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_{i1}}}&{{\mathit{\boldsymbol{P}}_{i2}}}\\
*&{{\mathit{\boldsymbol{P}}_{i3}}}
\end{array}} \right]$ is symmetric Lyapunov matrix, and 0 < Pi1=Pi1T∈R(nx+nc)×(nx+nc), Pi2∈R(nx+nc)×nu, Pi3∈Rnu×nu, i∈I.
On the basis of Eq.(15), if inequality Eq.(15) holds for (i, j)∈Γ, i∈I1,
|
$
\begin{array}{l}
{{\mathit{\boldsymbol{\bar x}}}^{\rm{T}}}\left( {t + 1} \right){\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_j}\mathit{\boldsymbol{E\bar x}}\left( {t + 1} \right) - {{\mathit{\boldsymbol{\bar x}}}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E\bar x}}\left( t \right) + \\
\;\;\;{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right) - {\gamma ^2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{\omega }}\left( t \right) < 0
\end{array}
$
|
(16) |
closed-loop system in Eq.(12) is asymptotically stable with robust H∞ performance γ.
Define an augmented vector as,
|
$
\mathit{\boldsymbol{\xi }}\left( t \right) = {\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( {t + 1} \right){\mathit{\boldsymbol{E}}^{\rm{T}}}}&{{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)}&1&{{\mathit{\boldsymbol{\omega }}^{\rm T}}\left( t \right)}
\end{array}} \right]^{\rm{T}}}
$
|
(17) |
and then with (i, j)∈Γ, Eq.(18) implies (17),
|
$
{\mathit{\boldsymbol{\xi }}^{\rm{T}}}\left( t \right)\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j}}&0&0&0\\
* &{ - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_i}}&0&0\\
*&* &0&0\\
*&*&* &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}
\end{array}} \right]\mathit{\boldsymbol{\xi }}\left( t \right) < 0
$
|
(18) |
Noticing the space partition (4) and using S-procedure, then it yields:
|
$
\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{\xi }}^{\rm{T}}}\left( t \right)\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j}}&0&0&0\\
* &{ - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_i}}&0&0\\
*&* &0&0\\
*&*&* &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}
\end{array}} \right]\mathit{\boldsymbol{\xi }}\left( t \right) + }\\
{{\lambda _{ij}}{{\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{x}}\left( t \right)}\\
1
\end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{F}}_i^{\rm{T}}{\mathit{\boldsymbol{F}}_i}}&{\mathit{\boldsymbol{F}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i}}\\
* &{\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{x}}\left( t \right)}\\
1
\end{array}} \right] < 0}
\end{array}
$
|
where λij < 0, i∈I1. It is noted that x(t)=J·$\mathit{\boldsymbol{\tilde x}}\left( t \right)$, J=[Inx 0nx×nc 0nx×nu]T, and then one has,
|
$
{\mathit{\boldsymbol{\xi }}^{\rm{T}}}\left( t \right){{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{ij}}\mathit{\boldsymbol{\xi }}\left( t \right) < 0,\left( {i,j} \right) \in \mathit{\Gamma },i \in {\mathit{\boldsymbol{I}}_1}
$
|
(19) |
where
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{ij}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j}}&0&0&0\\
* &{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}_{ij}^{\left( 1 \right)}}&{{\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i}}&0\\
*&* &{{\lambda _{ij}}\left( {\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1} \right)}&0\\
*&*&* &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}
\end{array}} \right]
$
|
and $\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}_{ij}^{\left( 1 \right)} =-{\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_i} + {\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{J}}^{\rm{T}}}$.
On the basis of Eq.(12), then for any matrices Gi the following equality holds:
|
$
\begin{array}{*{20}{c}}
{0 = {\mathit{\boldsymbol{\xi }}^{\rm{T}}}{{\mathit{\boldsymbol{\bar G}}}_{\rm{i}}}\left\{ { - \mathit{\boldsymbol{E\tilde x}}\left( {t + 1} \right) + \left( {{{\mathit{\boldsymbol{\tilde A}}}_i} + \Delta {{\mathit{\boldsymbol{\tilde A}}}_i}} \right)\mathit{\boldsymbol{\tilde x}}\left( t \right) + {{\mathit{\boldsymbol{\tilde a}}}_i} + } \right.}\\
{\left. {\left( {{\mathit{\boldsymbol{D}}_i} + \Delta {\mathit{\boldsymbol{D}}_i}} \right)\mathit{\boldsymbol{\omega }}\left( t \right)} \right\} = {\mathit{\boldsymbol{\xi }}^{\rm{T}}}\left( t \right){{\mathit{\boldsymbol{\bar G}}}_i}{{\mathit{\boldsymbol{\tilde A}}}_i}\mathit{\boldsymbol{\xi }}\left( t \right)}
\end{array}
$
|
(20) |
where
|
$
{{\mathit{\boldsymbol{\bar G}}}_i} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{G}}_{i1}^{\rm{T}}}&{\mathit{\boldsymbol{G}}_{i2}^{\rm{T}}}&{\mathit{\boldsymbol{G}}_{i3}^{\rm{T}}}&{\mathit{\boldsymbol{G}}_{i4}^{\rm{T}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\bar A}}}_i} = \left[ {\begin{array}{*{20}{c}}
{ - \mathit{\boldsymbol{I}}}&{{{\mathit{\boldsymbol{\tilde A}}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde A}}}_i}}&{{{\mathit{\boldsymbol{\tilde a}}}_i}}&{{{\mathit{\boldsymbol{\tilde D}}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde D}}}_i}}
\end{array}} \right]
$
|
Combining Eq.(20) and Eq.(19), then one has,
|
$
{\mathit{\boldsymbol{\xi }}^{\rm{T}}}\left( t \right)\left\{ {{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}}_{ij}} + Sym\left\{ {{{\mathit{\boldsymbol{\bar G}}}_i}{{\mathit{\boldsymbol{\bar A}}}_i}} \right\}} \right\}\mathit{\boldsymbol{\xi }}\left( t \right) < 0
$
|
where
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}}_{ij}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j}}&0&0&0\\
* &{\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{ij}^{\left( 1 \right)}}&{{\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i}}&0\\
*&* &{{\lambda _{ij}}\left( {\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1} \right)}&0\\
*&*&* &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}
\end{array}} \right]
\\
{\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{ij}^{\left( 1 \right)} = - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_i^{\rm{T}}{\mathit{\boldsymbol{\tilde L}}_i} + {\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{J}}^{\rm{T}}}}
$
|
Extracting the fuzzy membership functions, the following inequality implies,
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}}_{ijm}} + Sym\left\{ {{{\mathit{\boldsymbol{\bar G}}}_i}{{\mathit{\boldsymbol{\bar A}}}_{im}} + {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPsi} }}}_{im}}} \right\} < 0
$
|
where
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}}_{ijm}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j}}&0&0&0\\
* &{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}_{ijm}^{\left( 1 \right)}}&{{\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i}}&0\\
*&* &{{\lambda _{ij}}\left( {\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1} \right)}&0\\
*&*&* &{ - {\gamma ^2}\mathit{\boldsymbol{I}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}_{ijm}^{\left( 1 \right)} = - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_m^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_m} + {\lambda _{ij}}\mathit{\boldsymbol{JF}}_i^{\rm{T}}{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{J}}^{\rm{T}}}
$
|
|
$
{{\mathit{\boldsymbol{\bar A}}}_{im}} = \left[ {\begin{array}{*{20}{c}}
{ - \mathit{\boldsymbol{I}}}&{{{\mathit{\boldsymbol{\tilde A}}}_{im}}}&{{{\mathit{\boldsymbol{\tilde a}}}_{im}}}&{{{\mathit{\boldsymbol{\tilde D}}}_{im}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde A}}}_{im}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_m}}&0&{{\mathit{\boldsymbol{B}}_m}}\\
{{\mathit{\boldsymbol{B}}_{ci}}{\mathit{\boldsymbol{C}}_m}}&{{\mathit{\boldsymbol{A}}_{ci}}}&0\\
{{D_{ci}}{C_m}}&{{K_{ci}}}&{ - \mathit{\boldsymbol{I}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde a}}}_{im}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{a}}_m}}\\
{{\mathit{\boldsymbol{a}}_{ci}}}\\
{{\mathit{\boldsymbol{k}}_{ci}}}
\end{array}} \right],{{\mathit{\boldsymbol{\tilde D}}}_{im}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{D}}_{m1}}}\\
{{\mathit{\boldsymbol{B}}_{ci}}{\mathit{\boldsymbol{D}}_{m2}}}\\
{{\mathit{\boldsymbol{D}}_{ci}}{\mathit{\boldsymbol{D}}_{m2}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde L}}}_m} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{L}}_m}}&0&{{\mathit{\boldsymbol{N}}_m}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPsi} }}}_{im}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_i}\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right)\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}_m^{\rm{T}}
$
|
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPsi} }}}_{im}} = \left[ {\begin{array}{*{20}{c}}
0&{{\mathit{\boldsymbol{G}}_{i1}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde A}}}_{im}}}&0&{{\mathit{\boldsymbol{G}}_{i1}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde D}}}_{im}}}\\
0&{{\mathit{\boldsymbol{G}}_{i2}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde A}}}_{im}}}&0&{{\mathit{\boldsymbol{G}}_{i2}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde D}}}_{im}}}\\
0&0&0&0\\
0&0&0&0
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde A}}}_{im}} = \left[ {\begin{array}{*{20}{c}}
0&0&0\\
{{\mathit{\boldsymbol{B}}_{ci}}\mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{C}}_m}}&0&0\\
{{\mathit{\boldsymbol{D}}_{ci}}\mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{C}}_m}}&0&0
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\mathit{\boldsymbol{\tilde D}}}_{im}} = \left[ {\begin{array}{*{20}{c}}
0\\
{{\mathit{\boldsymbol{B}}_{ci}}\mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{D}}_{m2}}}\\
{{\mathit{\boldsymbol{D}}_{ci}}\mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{D}}_{m2}}}
\end{array}} \right]
$
|
Based on Lemma 1, for εi>0, one has:
|
$
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}}_{ijm}} + Sym\left\{ {{{\mathit{\boldsymbol{\bar G}}}_i}{{\mathit{\boldsymbol{\bar A}}}_{im}}} \right\} + \varepsilon _i^{ - 1}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_i}\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}_i^{\rm{T}} + {\varepsilon _i}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m}\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}_m^{\rm{T}} < 0
$
|
(21) |
where ${{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_i}$ and ${{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m}$ are defined in Theorem 3.1.
Applying Schur complement, and then Eq.(21) can be reformulated as,
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}}_{ijm}} + Sym\left\{ {{{\mathit{\boldsymbol{\bar G}}}_i}{{\mathit{\boldsymbol{\bar A}}}_{im}}} \right\}}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_i}}&{{\varepsilon _i}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m}}\\
* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}&0\\
*&* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}
\end{array}} \right] < 0
$
|
(22) |
For the numerical tractability, the slack variable matrices Gi1, Gi2, Gi3, Gi4, are with the following structure,
|
$
\left\{ \begin{array}{l}
{\mathit{\boldsymbol{G}}_{i1}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i1\left( 1 \right)}}}&{{{\mathit{\boldsymbol{\hat H}}}_1}{\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}}&{{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i1\left( 2 \right)}}}&{{\delta _1}{\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}}&0\\
{{\mathit{\boldsymbol{G}}_{i1\left( 3 \right)}}}&0&{{\rho _1}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]\\
{\mathit{\boldsymbol{G}}_{i2}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i2\left( 1 \right)}}}&{{\delta _2}{{\mathit{\boldsymbol{\hat H}}}_1}{\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}}&{{\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i2\left( 2 \right)}}}&{{\delta _3}{\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}}&0\\
{{\mathit{\boldsymbol{G}}_{i2\left( 3 \right)}}}&0&{{\rho _3}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]\\
{\mathit{\boldsymbol{G}}_{i3}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}}&0&0
\end{array}} \right],\;\;{\mathit{\boldsymbol{G}}_{i4}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}}&0&0
\end{array}} \right]\\
{{\mathit{\boldsymbol{\hat H}}}_1} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{I}}_{{n_c}}}}\\
{{0_{\left( {{n_x} - {n_c}} \right) \times {n_c}}}}
\end{array}} \right],{{\mathit{\boldsymbol{\hat H}}}_2} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{I}}_{{n_u}}}}\\
{{0_{\left( {{n_x} - {n_u}} \right) \times {n_u}}}}
\end{array}} \right]
\end{array} \right.
$
|
(23) |
where δ1, δ2, δ3, ρ1, ρ2, ρ3 are scalar parameters.
Define
|
$
\left\{ \begin{array}{l}
{{\mathit{\boldsymbol{\hat A}}}_{ci}} = {\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}{\mathit{\boldsymbol{A}}_{ci}},{{\mathit{\boldsymbol{\hat B}}}_{ci}} = {\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}{\mathit{\boldsymbol{B}}_{ci}}\\
{{\mathit{\boldsymbol{\hat a}}}_{ci}} = {\mathit{\boldsymbol{G}}_{i1\left( 4 \right)}}{{\mathit{\boldsymbol{\hat a}}}_{ci}},{{\mathit{\boldsymbol{\hat K}}}_{ci}} = {\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}{\mathit{\boldsymbol{K}}_{ci}}\\
{{\mathit{\boldsymbol{\hat D}}}_{ci}} = {\mathit{\boldsymbol{D}}_{i1\left( 5 \right)}}{\mathit{\boldsymbol{D}}_{ci}},{{\mathit{\boldsymbol{\hat k}}}_{ci}} = {\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}{\mathit{\boldsymbol{k}}_{ci}}
\end{array} \right.
$
|
(24) |
With consideration of Eq.(24), substituting the matrices defined in Eq.(23) into Eq.(22), it leads to Eq.(13).
Furthermore, the conditions in Eq.(13) indicates that Gi1(4) and Gi1(5) are invertible. Consequently, one can attain the controller gains via Eq.(14).
Thus the proof is completed.
Remark 3.1 It is worth pointing out that the results shown in Theorem 3.1 are deduced based upon a PWA DOF controller as in Eq.(10). However the proposed control method can be further synthesized as a fuzzy PWA controller with quantization measurements as follows:
|
$
\begin{array}{*{20}{c}}
{{x_c}\left( {t + 1} \right) = \sum\limits_{m \in M\left( i \right)} {{\mu _{im}}{A_{cim}}{x_c}\left( t \right)} + \sum\limits_{m \in M\left( i \right)} {{\mu _{im}}{a_{cim}}} + }\\
{\sum\limits_{m \in M\left( i \right)} {{\mu _{im}}{B_{cim}}{y_q}\left( t \right)} }
\end{array}
$
|
|
$
\begin{array}{*{20}{c}}
{u\left( t \right) = \sum\limits_{m \in M\left( i \right)} {{\mu _{im}}{K_{cim}}{x_c}\left( t \right)} + \sum\limits_{m \in M\left( i \right)} {{\mu _{im}}{k_{cim}}} + }\\
{\sum\limits_{m \in M\left( i \right)} {{\mu _{im}}{D_{cim}}{y_q}\left( t \right)} ,i \in \mathit{\boldsymbol{I}}}
\end{array}
$
|
3.2 A Special Case for Static Output Feedback (SOF) Control Method Synthesis with Measurements Quantization
If nc=0, the proposed DOF controller (10) declines to a SOF one as,
|
$
\mathit{\boldsymbol{u}}\left( t \right) = {\mathit{\boldsymbol{D}}_{ci}}{\mathit{\boldsymbol{y}}_q}\left( t \right) + {\mathit{\boldsymbol{k}}_{ci}},i \in \mathit{\boldsymbol{I}}
$
|
(25) |
where Dci∈Rnu×ny and kci∈Rnu are controller gains. It is easy to see that kci=0 for i∈I0.
Denote $\mathit{\boldsymbol{\tilde x}}\left( t \right)$=[xT(t) uT(t)]T, then
|
$
\begin{array}{l}
{\rm{Denote}}\;\mathit{\boldsymbol{\tilde x}}\left( t \right) = {\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( t \right)}&{{\mathit{\boldsymbol{u}}^{\rm{T}}}\left( t \right)}
\end{array}} \right]^{\rm{T}}},{\rm{then}}\\
\;\;\;\mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{\tilde x}}\left( {t + 1} \right) = \left( {{{\mathit{\boldsymbol{\tilde A}}}_i} + \Delta {{\mathit{\boldsymbol{\tilde A}}}_i}} \right)\mathit{\boldsymbol{\tilde x}}\left( t \right) + {{\mathit{\boldsymbol{\tilde a}}}_i} + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{{\mathit{\boldsymbol{\tilde D}}}_i} + \Delta {{\mathit{\boldsymbol{\tilde D}}}_i}} \right)\mathit{\boldsymbol{w}}\left( t \right)
\end{array}
$
|
|
$
\mathit{\boldsymbol{z}}\left( t \right) = {{\mathit{\boldsymbol{\tilde L}}}_i}\mathit{\boldsymbol{\tilde x}}\left( t \right),\zeta \left( t \right) \in {S_i},\;\;i \in \mathit{\boldsymbol{I}}
$
|
where
|
$
\mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}}
\mathit{\boldsymbol{I}}&0\\
0&0
\end{array}} \right],{{\mathit{\boldsymbol{\tilde A}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_i}}&{{\mathit{\boldsymbol{B}}_i}}\\
{{\mathit{\boldsymbol{D}}_{ci}}{\mathit{\boldsymbol{C}}_i}}&{ - \mathit{\boldsymbol{I}}}
\end{array}} \right]
$
|
|
$
\Delta {{\mathit{\boldsymbol{\tilde A}}}_i} = \left[ {\begin{array}{*{20}{c}}
0&0\\
{{\mathit{\boldsymbol{D}}_{ci}}\mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{C}}_i}}&0
\end{array}} \right]
$
|
|
$
{{\tilde {\boldsymbol{a}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{a}}_i}}\\
{{k_{ci}}}
\end{array}} \right],{{\mathit{\boldsymbol{\tilde D}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{D}}_{i1}}}\\
{{\mathit{\boldsymbol{D}}_{ci}}{\mathit{\boldsymbol{D}}_{i2}}}
\end{array}} \right]
$
|
|
$
\mathit{\Delta }{{\mathit{\boldsymbol{\tilde D}}}_i} = \left[ {\begin{array}{*{20}{c}}
0\\
{{\mathit{\boldsymbol{D}}_{ci}}\mathit{\Lambda }\mathit{\boldsymbol{ \boldsymbol{\bar \varDelta} }}\left( t \right){\mathit{\boldsymbol{D}}_{i2}}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde L}}}_i} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{L}}_i}}&{{\mathit{\boldsymbol{N}}_i}}
\end{array}} \right]
$
|
Specifically, x(t)=J1·$\mathit{\boldsymbol{\tilde x}}\left( t \right)$ where J1=[Inx 0nx×nu]T.
Based upon Theorem 3.1, one has the synthesis conditions of the aforementioned SOF controller (25).
Corollary 3.1 Considering fuzzy system (1), closed-loop system (23) is asymptotically stable with robust performance γ, if there exist matrices 0 < Pi1=Pi1T∈Rnx×nx, Pi2∈Rnx×nu, Pi3=Rnu×nu, Gi1(1), Gi2(1)∈Rnx×nx, Gi1(3), Gi2(3)∈Rnu×nx, Gi1(5)∈Rnu× nu, Gi4(1)∈Rnω×nx, ${{\mathit{\boldsymbol{\hat D}}}_{ci}}$∈Rnu×ny, for i∈I, Gi3(1)∈R1×nx, ${{\mathit{\boldsymbol{\hat k}}}_i}$∈Rnu, for i∈I1, scalars εi>0, i∈I, and λij < 0, i∈Ii, (i, j)∈ Γ such that the subsequent LMIs hold,
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{\Upsilon}}_{ijm}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i}}&{{\varepsilon _i}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m}}\\
* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}&0\\
*&* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}
\end{array}} \right] < 0
$
|
where m∈M(i), i∈I0, (i, j)∈ Γ.
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\boldsymbol{\bar \Upsilon}}}_{ijm}}}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_i}}&{{\varepsilon _i}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m}}\\
* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}&0\\
*&* &{ - {\varepsilon _i}\mathit{\boldsymbol{I}}}
\end{array}} \right] < 0
$
|
(26) |
where m∈M(i), i∈I1, (i, j)∈ Γ, and
|
$
{\mathit{\boldsymbol{\Upsilon}}_{ijm}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j} - {\mathit{\boldsymbol{G}}_{i1}} - \mathit{\boldsymbol{G}}_{i1}^{\rm{T}}}&{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {12} \right)}}&{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {13} \right)}}\\
* &{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {22} \right)}}&{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {23} \right)}}\\
*&* &{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {33} \right)}}
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\bar \Upsilon}}}_{ijm}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_j} - {\mathit{\boldsymbol{G}}_{i1}} - \mathit{\boldsymbol{G}}_{i1}^{\rm{T}}}&{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {12} \right)}}&{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {13} \right)}}&{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {14} \right)}}\\
* &{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {22} \right)}}&{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {23} \right)}}&{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {24} \right)}}\\
*&* &{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {33} \right)}}&{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {34} \right)}}\\
*&*&* &{\mathit{\boldsymbol{\bar \Upsilon}}_{im}^{\left( {44} \right)}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{P}}_j} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_{j1}}}&{{\mathit{\boldsymbol{P}}_{j2}}}\\
* &{{\mathit{\boldsymbol{P}}_{j3}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i1}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i1\left( 1 \right)}}}&{{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i1\left( 3 \right)}}}&{{\rho _1}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i2}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i2\left( 1 \right)}}}&{{\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i2\left( 3 \right)}}}&{{\rho _3}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i3}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}}&0
\end{array}} \right],\;\;{\mathit{\boldsymbol{G}}_{i4}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}}&0
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\hat H}}}_2} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{I}}_{{n_u}}}}\\
{{0_{\left( {{n_x} - {n_u}} \right) \times {n_u}}}}
\end{array}} \right],\mathit{\boldsymbol{ \Upsilon}}_{im}^{\left( {12} \right)} = \mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {121} \right)} - \mathit{\boldsymbol{G}}_{i2}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {121} \right)} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i1\left( 1 \right)}}{\mathit{\boldsymbol{A}}_m} + {{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{C}}_m}}&{{\mathit{\boldsymbol{G}}_{i1\left( 1 \right)}}{\mathit{\boldsymbol{B}}_m} - {{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i1\left( 3 \right)}}{\mathit{\boldsymbol{A}}_m} + {\rho _1}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{C}}_m}}&{{\mathit{\boldsymbol{G}}_{i1\left( 3 \right)}}{\mathit{\boldsymbol{B}}_m} - {\rho _1}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {13} \right)} = \mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {131} \right)} - \mathit{\boldsymbol{G}}_{i4}^{\rm{T}},\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {131} \right)} = \left[ \begin{array}{l}
{\mathit{\boldsymbol{G}}_{i1\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{ml}} + {{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{D}}_{m2}}\\
{\mathit{\boldsymbol{G}}_{i1\left( 3 \right)}}{\mathit{\boldsymbol{D}}_{ml}} + {\rho _1}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{D}}_{m2}}
\end{array} \right]
$
|
|
$
\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {22} \right)} = - {E^{\rm{T}}}{P_i}E + \tilde L_m^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_m} + Sym\left\{ {\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {221} \right)}} \right\}
$
|
|
$
\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {221} \right)} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i2\left( 1 \right)}}{\mathit{\boldsymbol{A}}_m} + {\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{C}}_m}}&{{\mathit{\boldsymbol{G}}_{i2\left( 1 \right)}}{\mathit{\boldsymbol{B}}_m} - {\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i2\left( 3 \right)}}{\mathit{\boldsymbol{A}}_m} + {\rho _3}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{C}}_m}}&{{\mathit{\boldsymbol{G}}_{i2\left( 3 \right)}}{\mathit{\boldsymbol{B}}_m} - {\rho _3}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]
}\\
{\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {23} \right)} = \mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {231} \right)} + {\left\{ {\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {232} \right)}} \right\}^{\rm{T}}}}
\end{array}
$
|
|
$
\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {231} \right)} = \left[ \begin{array}{l}
{\mathit{\boldsymbol{G}}_{i2\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{m1}} + {\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{D}}_{m2}}\\
{\mathit{\boldsymbol{G}}_{i2\left( 3 \right)}}{\mathit{\boldsymbol{D}}_{ml}} + {\rho _3}{{\mathit{\boldsymbol{\hat D}}}_{ci}}{\mathit{\boldsymbol{D}}_{m2}}
\end{array} \right]
$
|
|
$
\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {232} \right)} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}{\mathit{\boldsymbol{A}}_m}}&{{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}{\mathit{\boldsymbol{B}}_m}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{\Upsilon}}_{im}^{\left( {33} \right)} = - {\gamma ^2}\mathit{\boldsymbol{I}} + Sym\left\{ {{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{m1}}} \right\}
$
|
|
$
\sum\nolimits_i { = \left[ {\begin{array}{*{20}{c}}
{\sum\nolimits_i^{\left( 1 \right)} {} }\\
{\sum\nolimits_i^{\left( 2 \right)} {} }\\
0
\end{array}} \right]} ,\;\;\sum\nolimits_i^{\left( 1 \right)} { = \left[ {\begin{array}{*{20}{c}}
{{{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat D}}}_{ci}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}\\
{{\rho _1}{{\mathit{\boldsymbol{\hat D}}}_{ci}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}
\end{array}} \right]}
$
|
|
$
\sum\nolimits_i^{\left( 2 \right)} { = \left[ {\begin{array}{*{20}{c}}
{{\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat D}}}_{ci}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}\\
{{\rho _3}{{\mathit{\boldsymbol{\hat D}}}_{ci}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}
\end{array}} \right]}
$
|
|
$
{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m} = \left[ {\begin{array}{*{20}{c}}
0\\
{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m^{\left( 1 \right)}}\\
{\mathit{\boldsymbol{D}}_{m2}^{\rm{T}}}
\end{array}} \right],\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m^{\left( 1 \right)} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{C}}_m^{\rm{T}}}\\
0
\end{array}} \right]
$
|
|
$
{{\mathit{\boldsymbol{\tilde L}}}_m} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{L}}_m}}&{{\mathit{\boldsymbol{N}}_m}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {12} \right)} = \mathit{\boldsymbol{\gamma }}_{im}^{\left( {12} \right)},\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {13} \right)} = \mathit{\boldsymbol{\tilde \gamma }}_{im}^{\left( {131} \right)} - \mathit{\boldsymbol{G}}_{i3}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{\tilde \gamma }}_{im}^{\left( {131} \right)} = \left[ \begin{array}{l}
{\mathit{\boldsymbol{G}}_{i1\left( 1 \right){\mathit{\boldsymbol{a}}_m}}} + {{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat k}}}_{ci}}\\
{\mathit{\boldsymbol{G}}_{i1\left( 3 \right){\mathit{\boldsymbol{a}}_m}}} + {\rho _1}{{\mathit{\boldsymbol{\hat k}}}_{ci}}
\end{array} \right]
$
|
|
$
\mathit{\boldsymbol{\tilde \gamma }}_{im}^{\left( {14} \right)} = \mathit{\boldsymbol{\gamma }}_{im}^{\left( {13} \right)}
$
|
|
$
\mathit{\boldsymbol{\tilde \gamma }}_{im}^{\left( {22} \right)} = - {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{\tilde L}}_m^{\rm{T}}{{\mathit{\boldsymbol{\tilde L}}}_m} + {\lambda _{ij}}{\mathit{\boldsymbol{J}}_1}\mathit{\boldsymbol{F}}_i^{\rm{T}}\mathit{\boldsymbol{FJ}}_1^{\rm{T}} + Sym\left\{ {\mathit{\boldsymbol{\gamma }}_{im}^{\left( {221} \right)}} \right\}
$
|
|
$
\mathit{\boldsymbol{\tilde \gamma }}_{im}^{\left( {23} \right)} = {\lambda _{ij}}{\mathit{\boldsymbol{J}}_1}\mathit{\boldsymbol{F}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} + \mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {231} \right)} + {\left\{ {\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {232} \right)}} \right\}^{\rm{T}}}
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {231} \right)} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i2\left( 1 \right){a_m}}} + {\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{{\mathit{\boldsymbol{\hat a}}}_{ci}}}\\
{{\mathit{\boldsymbol{G}}_{i2\left( 3 \right){\mathit{\boldsymbol{a}}_m}}} + {\rho _3}{{\mathit{\boldsymbol{\hat k}}}_{ci}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {232} \right)} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{A}}_{im}}}&{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{B}}_{im}}}
\end{array}} \right]
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {24} \right)} = \mathit{\boldsymbol{\gamma }}_{im}^{\left( {23} \right)}
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {33} \right)} = {\lambda _{ij}}\left( {\mathit{\boldsymbol{f}}_i^{\rm{T}}{\mathit{\boldsymbol{f}}_i} - 1} \right) + Sym\left\{ {{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{a}}_m}} \right\}
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {34} \right)} = {\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{m1}} + \mathit{\boldsymbol{a}}_m^{\rm{T}}\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}^{\rm{T}}
$
|
|
$
\mathit{\boldsymbol{\bar \gamma }}_{im}^{\left( {44} \right)} = - {\gamma ^2}\mathit{\boldsymbol{I}} + Sym\left\{ {{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}{\mathit{\boldsymbol{D}}_{m1}}} \right\}
$
|
|
$
{{\bar \Sigma }_i} = \left[ {\begin{array}{*{20}{c}}
{\sum\nolimits_i^{\left( 1 \right)} {} }\\
{\sum\nolimits_i^{\left( 2 \right)} {} }\\
0\\
0
\end{array}} \right],{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_m} = \left[ {\begin{array}{*{20}{c}}
0\\
{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_m^{\left( 1 \right)}}\\
0\\
{\mathit{\boldsymbol{D}}_{m2}^{\rm{T}}}
\end{array}} \right]
$
|
Moreover, one can attain the controller gains via
|
$
{\mathit{\boldsymbol{D}}_{ci}} = \mathit{\boldsymbol{G}}_{i5}^{ - 1}{{\mathit{\boldsymbol{\hat D}}}_{ci}},{\mathit{\boldsymbol{k}}_{ci}} = \mathit{\boldsymbol{G}}_{i5}^{ - 1}{{\mathit{\boldsymbol{\hat k}}}_{ci}}
$
|
Proof Similar to Theorem 3.1, the more complicated case (26) i∈I1, is to be presented. It is noted that nc=0, and specify the matrix Gi=[Gi1T, Gi2T, Gi3T, Gi4T]T with
|
$
{\mathit{\boldsymbol{G}}_{i1}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i1\left( 1 \right)}}}&{{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i1\left( 3 \right)}}}&{{\rho _1}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i2}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i2\left( 1 \right)}}}&{{\rho _2}{{\mathit{\boldsymbol{\hat H}}}_2}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}\\
{{\mathit{\boldsymbol{G}}_{i2\left( 3 \right)}}}&{{\rho _3}{\mathit{\boldsymbol{G}}_{i1\left( 5 \right)}}}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{G}}_{i3}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i3\left( 1 \right)}}}&0
\end{array}} \right],\;\;\;{\mathit{\boldsymbol{G}}_{i4}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{G}}_{i4\left( 1 \right)}}}&0
\end{array}} \right]
$
|
where ${{\mathit{\boldsymbol{\hat H}}}_2} = {\left[{{\mathit{\boldsymbol{I}}_{{n_u}}}\;\;{0_{\left( {{n_x}-{n_u}} \right) \times {n_u}}}} \right]^{\rm{T}}}$, and ρ1, ρ2, ρ3 are tuning parameters.
The rest derivation procedures are omitted for it is similar to Theorem 3.1.
4 Simulations
Example 4.1 Considering a discrete-time fuzzy-affine system as follows,
Plant Rule Rl: IF x2(t) is Fll, THEN
|
$
\mathit{\boldsymbol{x}}\left( {t + 1} \right) = {\mathit{\boldsymbol{A}}_l}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{a}}_l} + {\mathit{\boldsymbol{B}}_l}\mathit{\boldsymbol{u}}\left( t \right) + {\mathit{\boldsymbol{D}}_{l1}}\mathit{\boldsymbol{w}}\left( t \right)
$
|
|
$
\mathit{\boldsymbol{y}}\left( t \right) = {\mathit{\boldsymbol{C}}_l}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{D}}_{l2}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right)
$
|
|
$
\mathit{\boldsymbol{z}}\left( t \right) = {\mathit{\boldsymbol{L}}_l}\mathit{\boldsymbol{x}}\left( t \right) + {N_l}\mathit{\boldsymbol{u}}\left( t \right),l = \left\{ {1,2,3} \right\}
$
|
and the system matrices are given as,
|
$
\left[ {{\mathit{\boldsymbol{A}}_1}\left| {{\mathit{\boldsymbol{a}}_1}} \right.} \right] = \left[ {\begin{array}{*{20}{c}}
{1.001}&{ - 0.009}\\
{0.121}&{ - 0.7}
\end{array}\left| {\begin{array}{*{20}{c}}
0\\
{0.080}
\end{array}} \right.} \right]
$
|
|
$
\left[ {{\mathit{\boldsymbol{A}}_2}\left| {{\mathit{\boldsymbol{a}}_2}} \right.} \right] = \left[ {\begin{array}{*{20}{c}}
{1.003}&{ - 0.01}\\
{0.179}&{0.5}
\end{array}\left| {\begin{array}{*{20}{c}}
0\\
0
\end{array}} \right.} \right]
$
|
|
$
\left[ {{\mathit{\boldsymbol{A}}_3}\left| {{\mathit{\boldsymbol{a}}_3}} \right.} \right] = \left[ {\begin{array}{*{20}{c}}
{1.000}&{0.01}\\
{0.1729}&{0.6}
\end{array}\left| {\begin{array}{*{20}{c}}
{0.1}\\
{ - 0.08}
\end{array}} \right.} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{B}}_1}}&{\left| {{\mathit{\boldsymbol{B}}_2}} \right.}&{\left| {{\mathit{\boldsymbol{B}}_3}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.15}\\
{0.10}
\end{array}}&{\left| {\begin{array}{*{20}{c}}
{0.1}\\
{0.1}
\end{array}} \right.}&{\left| {\begin{array}{*{20}{c}}
{0.1}\\
{0.2}
\end{array}} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{D}}_{11}}}&{\left| {{\mathit{\boldsymbol{D}}_{21}}} \right.}&{\left| {{\mathit{\boldsymbol{D}}_{31}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.01}\\
{0.011}
\end{array}}&{\left| {\begin{array}{*{20}{c}}
{0.02}\\
{0.01}
\end{array}} \right.}&{\left| {\begin{array}{*{20}{c}}
{0.01}\\
{0.02}
\end{array}} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{C}}_1^{\rm{T}}}&{\left| {\mathit{\boldsymbol{C}}_2^{\rm{T}}} \right.}&{\left| {\mathit{\boldsymbol{C}}_3^{\rm{T}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.965}\\
{0.10}
\end{array}}&{\left| {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right.}&{\left| {\begin{array}{*{20}{c}}
{0.5}\\
0
\end{array}} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{D}}_{12}}}&{\left| {{\mathit{\boldsymbol{D}}_{22}}} \right.}&{\left| {{\mathit{\boldsymbol{D}}_{32}}} \right.}
\end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}}
{0.02}&{\left| {0.02} \right.}&{\left| {0.02} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{L}}_1}}&{\left| {{\mathit{\boldsymbol{L}}_2}} \right.}&{\left| {{\mathit{\boldsymbol{L}}_3}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.898}\\
0
\end{array}}&{\left| {\begin{array}{*{20}{c}}
{0.898}\\
0
\end{array}} \right.}&{\left| {\begin{array}{*{20}{c}}
{0.891}\\
0
\end{array}} \right.}
\end{array}} \right]
$
|
|
$
{N_l} = 0.5,l = \left\{ {1,2,3} \right\}
$
|
where d1=50, d2=300. The normalized MFs and regions Si, i=1, 2, 3 are presented in Fig. 1.
One can see that region S2 is crisp, and region S1 and S3 are fuzzy. Noticing that θi=[0 1]T, for i∈I, and the parameters can be seen as,
|
$
{\mathit{\boldsymbol{F}}_1} = \frac{{2\mathit{\boldsymbol{\theta }}_i^{\rm{T}}}}{{{d_2} - {d_1}}},\;\;\;\;{\mathit{\boldsymbol{f}}_1} = \frac{{{d_2} + {d_1}}}{{{d_2} - {d_1}}}
$
|
|
$
{\mathit{\boldsymbol{F}}_2} = \frac{1}{{{d_1}}},\;\;\;\;{\mathit{\boldsymbol{f}}_2} = 0
$
|
|
$
{\mathit{\boldsymbol{F}}_3} = \frac{{2\mathit{\boldsymbol{\theta }}_i^{\rm{T}}}}{{{d_2} - {d_1}}},\;\;\;\;{\mathit{\boldsymbol{f}}_3} = - \frac{{{d_2} + {d_1}}}{{{d_2} - {d_1}}}
$
|
Quantization dense ρ=0.8 is selected for the quantizer, and utilizing Theorem 3.1 with ρ1=ρ3=1, ρ2=3, δ1=10, δ2=1, and δ3=-1, for the full-order (2-order) case, one can attain the feasible solutions with γmin= 0.970 9. Consequently, the DOF controller gains are:
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_{c1}}}&{\left| {{\mathit{\boldsymbol{a}}_{c1}}} \right.}&{\left| {{\mathit{\boldsymbol{B}}_{c1}}} \right.}
\end{array}} \right] = \\
\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.0965}\\
{ - 0.1259}
\end{array}}&{\begin{array}{*{20}{c}}
{0.0139}\\
{0.1228}
\end{array}\left| {\begin{array}{*{20}{c}}
{7.7575}\\
{2.8217}
\end{array}} \right.\left| {\begin{array}{*{20}{c}}
{ - 0.1647}\\
{ - 0.0578}
\end{array}} \right.}
\end{array}} \right]
\end{array}
$
|
|
$
{\mathit{\boldsymbol{K}}_{c1}} = \left[ {\begin{array}{*{20}{c}}
{3.2565}&{ - 0.5801}
\end{array}} \right]
$
|
|
$
{k_{c1}} = 0.7439,{D_{c1}} = - 1.2509
$
|
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_{c2}}}&{\left| {{\mathit{\boldsymbol{a}}_{c2}}} \right.}&{\left| {{\mathit{\boldsymbol{B}}_{c2}}} \right.}
\end{array}} \right] = \\
\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.3972}\\
{ - 0.1756}
\end{array}}&{\begin{array}{*{20}{c}}
{ - 0.1934}\\
{0.2940}
\end{array}\left| {\begin{array}{*{20}{c}}
0\\
0
\end{array}} \right.\left| {\begin{array}{*{20}{c}}
{ - 0.1799}\\
{ - 0.0725}
\end{array}} \right.}
\end{array}} \right]
\end{array}
$
|
|
$
{\mathit{\boldsymbol{K}}_{c2}} = \left[ {\begin{array}{*{20}{c}}
{2.5603}&{0.4576}
\end{array}} \right]
$
|
|
$
{k_{c1}} = 0,{D_{c2}} = - 1.4254
$
|
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_{c3}}}&{\left| {{\mathit{\boldsymbol{a}}_{c3}}} \right.}&{\left| {{\mathit{\boldsymbol{B}}_{c3}}} \right.}
\end{array}} \right] = \\
\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.3692}\\
{ - 0.0947}
\end{array}}&{\begin{array}{*{20}{c}}
{ - 0.0696}\\
{0.0388}
\end{array}\left| {\begin{array}{*{20}{c}}
{ - 1.3453}\\
{ - 8.0866}
\end{array}} \right.\left| {\begin{array}{*{20}{c}}
{ - 0.1016}\\
{ - 0.0380}
\end{array}} \right.}
\end{array}} \right]
\end{array}
$
|
|
$
{\mathit{\boldsymbol{K}}_{c3}} = \left[ {\begin{array}{*{20}{c}}
{3.0959}&{ - 0.5770}
\end{array}} \right]
$
|
|
$
{k_{c3}} = - 60.2217,{D_{c3}} = - 0.9004
$
|
For the reduced-order (1-order) case, the H∞ performance is γmin= 0.975 3 with controller gains,
|
$
\left[ {\begin{array}{*{20}{c}}
{{A_{c1}}}&{\left| {{a_{c1}}} \right.}&{\left| {{B_{c1}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{0.1315}&{\left| {7.4528} \right.}&{\left| { - 0.1625} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{K_{c1}}}&{\left| {{k_{c1}}} \right.}&{\left| {{D_{c1}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{3.0472}&{\left| {1.5828} \right.}&{\left| { - 1.2432} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{A_{c2}}}&{\left| {{a_{c2}}} \right.}&{\left| {{B_{c2}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{0.2856}&{\left| {0.0000} \right.}&{\left| { - 0.1738} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{K_{c2}}}&{\left| {{k_{c2}}} \right.}&{\left| {{D_{c2}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2.4267}&{\left| {0.0000} \right.}&{\left| { - 1.4226} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{A_{c3}}}&{\left| {{a_{c3}}} \right.}&{\left| {{B_{c3}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{0.3470}&{\left| { - 0.3930} \right.}&{\left| { - 0.0991} \right.}
\end{array}} \right]
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{K_{c1}}}&{\left| {{k_{c1}}} \right.}&{\left| {{D_{c1}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2.8384}&{\left| { - 65.6408} \right.}&{\left| { - 0.8826} \right.}
\end{array}} \right]
$
|
In addition, by using Corollary 3.1, for the SOF controller case, we can attain feasible solution with γmin=1.185 9, and the controller gains are:
|
$
\left\{ \begin{array}{l}
\left[ {{k_{c1}}\left| {{D_{c1}}} \right.} \right] = \left[ {17.9352\left| { - 1.8444} \right.} \right]\\
\left[ {{k_{c2}}\left| {{D_{c2}}} \right.} \right] = \left[ {0.00000\left| { - 1.9455} \right.} \right]\\
\left[ {{k_{c3}}\left| {{D_{c3}}} \right.} \right] = \left[ { - 62.0612\left| { - 1.1697} \right.} \right]
\end{array} \right.
$
|
It is worth mentioning that when ki≡0, the piecewise-affine controller (10) reduces to a piecewise-linear one. Table 1 compares the robust performance between piecewise-affine (PWA) controllers with piecewise-linear (PWL) controllers.
表 1

Table 1 Comparison of robust H∞ performance for piecewise-affine/piecewise-linear controllers
| Controllers | Full-order | Reduced-order | 0-order |
| PWA controllers | 0.970 9 | 0.975 3 | 1.185 9 |
| PWL controllers | 1.113 8 | 1.167 8 | 2.352 2 |
|
Table 1 Comparison of robust H∞ performance for piecewise-affine/piecewise-linear controllers
|
One can attain a better robust H∞ performance with a higher order controller in piecewise-affine form.
With the initial conditions x0=[1.5 -1]T, and the external disturbances w=270e-2t·sin(2t), the state trajectories are presented in Fig. 2.
The H∞ performance can be verified in Fig. 3 with zero initial conditions. The ratio
|
$
\sqrt {\sum\limits_{t = 0}^\kappa {{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right)} } /\sqrt {\sum\limits_{t = 0}^\kappa {{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right)} }
$
|
is about 0.168, that is lower than γmin=0.970 9.
In view of the practical industrial application, another simulation study is to be considered.
Example 4.2 Considering a nonlinear networked continuous stirred tank reactor (CSTR) system as follows,
|
$
\left\{ \begin{array}{l}
{{\dot x}_1} = {b_0}\left( {{T_{fs}} - {x_1}} \right) + {b_1}{k_0}\exp \left( { - \frac{{{b_2}}}{{{x_1}}}} \right){x_2} - \\
\;\;\;\;\;\;\;{b_3}{x_1} + {b_3}u + {b_0}w\\
{{\dot x}_2} = {b_0}\left( {{C_{a0}} - {x_2}} \right) - {k_0}\exp \left( { - \frac{{{b_2}}}{{{x_1}}}} \right){x_2}
\end{array} \right.
$
|
where the system states x1 and x2 stand for the reactor temperature and the concentration, respectively.u refers to the coolant stream's temperature, which is also the system control input and w stands for the external disturbance. In this simulation example, Table 2 presents the nominal plant parameters, and
|
$
{b_0} = F/V,{b_1} = - \Delta H\left( {\rho {C_p}} \right),{b_2} = E/R,{b_3} = \left( {UA} \right)/\left( {V\rho {C_p}} \right)
$
|
表 2

Table 2 Nominal parameters of CSTR system in Example 4.2
| F(L/min) | Cao(mol/L) | Tfs (K) | V (L) | ρ (g/L) |
| 100 | 1 | 350 | 100 | 1 000 |
| Cp (J/gk) | -ΔH (J/mol) | E/R (K) | k0 (l/min) | UA (J/min·k) |
| 0.239 | 5×104 | 8 750 | 7.2×1010 | 5×104 |
|
Table 2 Nominal parameters of CSTR system in Example 4.2
|
The CSTR system contains one equilibrium state that x0=[300 0.5]T, at steady input u0= 300 K. Select three operating points, xo1=[324.4 0.875]T, xo2=[350 0.5]T, xo3=[370.65 0.2]T, and then the system can be linearized based upon transformation of coordinates $\tilde x = x-{x_o}$, ũ=u-uo. With sampling period T= 0.01 s, the nonlinear system is reformulated as,
Plant Rule Rl: IF x1(t) is F1l, THEN
|
$
\begin{array}{l}
\left\{ \begin{array}{l}
\mathit{\boldsymbol{\tilde x}}\left( {t + 1} \right) = {\mathit{\boldsymbol{A}}_l}\mathit{\boldsymbol{\tilde x}}\left( t \right) + {\mathit{\boldsymbol{a}}_l} + {\mathit{\boldsymbol{B}}_l}\mathit{\boldsymbol{\tilde x}}\left( t \right) + {\mathit{\boldsymbol{D}}_{l1}}\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{y}}\left( t \right) = {\mathit{\boldsymbol{C}}_L}\mathit{\boldsymbol{\tilde x}}\left( t \right) + {\mathit{\boldsymbol{D}}_{l2}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right)\\
\mathit{\boldsymbol{z}}\left( t \right) = {\mathit{\boldsymbol{L}}_l}\mathit{\boldsymbol{\tilde x}}\left( t \right) + {\mathit{\boldsymbol{N}}_l}\mathit{\boldsymbol{\tilde x}}\left( t \right),\;\;l = \left\{ {1,2,3} \right\}
\end{array} \right.
\end{array}
$
|
where
|
$
\left[ {{\mathit{\boldsymbol{A}}_1}\left| {{\mathit{\boldsymbol{a}}_1}} \right.} \right] = \left[ {\begin{array}{*{20}{c}}
{0.9902}&{0.2909}\\
{ - 0.0001}&{0.9886}
\end{array}\left| {\begin{array}{*{20}{c}}
{ - 0.3589}\\
{0.0017}
\end{array}} \right.} \right]
$
|
|
$
\left[ {{\mathit{\boldsymbol{A}}_2}\left| {{\mathit{\boldsymbol{a}}_2}} \right.} \right] = \left[ {\begin{array}{*{20}{c}}
{1.0438}&{2.0919}\\
{ - 0.0004}&{0.9800}
\end{array}\left| {\begin{array}{*{20}{c}}
0\\
0
\end{array}} \right.} \right]
$
|
|
$
\left[ {{\mathit{\boldsymbol{A}}_3}\left| {{\mathit{\boldsymbol{a}}_3}} \right.} \right] = \left[ {\begin{array}{*{20}{c}}
{1.0764}&{8.4224}\\
{ - 0.0005}&{0.9497}
\end{array}\left| {\begin{array}{*{20}{c}}
{0.9498}\\
{ - 0.0045}
\end{array}} \right.} \right]
$
|
|
$
{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}}
{0.0209}\\
0
\end{array}} \right],{\mathit{\boldsymbol{D}}_{l1}} = \left[ {\begin{array}{*{20}{c}}
{0.01}\\
0
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{C}}_l} = \left[ {\begin{array}{*{20}{c}}
{1.0}&0
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{L}}_l} = \left[ {\begin{array}{*{20}{c}}
{1.0}&0
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{D}}_{l2}} = 0.02
$
|
|
$
{\mathit{\boldsymbol{N}}_l} = 0.5
$
|
|
$
l \in \left\{ {1,2,3} \right\}
$
|
Fig. 4 shows the normalized MFs with d1=-50, d2=-25.6, d3=-20.65, and d4= 50.
Based on Fig. 4, one can divide the premise-variable space into three subspaces,
|
$
\left\{ \begin{array}{l}
{S_1} = \left\{ {x\left( t \right)\left| {{d_1} < {x_1}\left( t \right) \le {d_2}} \right.} \right\}\\
{S_2} = \left\{ {x\left( t \right)\left| {{d_2} < {x_1}\left( t \right) \le {d_3}} \right.} \right\}\\
{S_3} = \left\{ {x\left( t \right)\left| {{d_3} < {x_1}\left( t \right) \le {d_4}} \right.} \right\}
\end{array} \right.
$
|
One has that regions S1 and S3 are crisp while region S2 is fuzzy.
For brevity, based on Theorem 3.1, only the full-order DOF controller will be calculated in this example.
With the quantization dense ρ=0.64 for the quantizer, consequently, one can attain the controller gains:
|
$
\begin{array}{l}
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_{c1}}}&{\left| {{\mathit{\boldsymbol{a}}_{c1}}} \right.}&{\left| {{\mathit{\boldsymbol{B}}_{c1}}} \right.}
\end{array}} \right] = \\
\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.5487}\\
{ - 0.0010}
\end{array}}&{\begin{array}{*{20}{c}}
{ - 2.6501}\\
{0.9590}
\end{array}\left| {\begin{array}{*{20}{c}}
{4.1694}\\
{ - 0.0004}
\end{array}} \right.\left| {\begin{array}{*{20}{c}}
{ - 0.0194}\\
{ - 0.0001}
\end{array}} \right.}
\end{array}} \right]
\end{array}
$
|
|
$
{\mathit{\boldsymbol{K}}_{c1}} = \left[ {\begin{array}{*{20}{c}}
{15.6103}&{368.0173}
\end{array}} \right]
$
|
|
$
{k_{c1}} = 174.6103,{D_{c1}} = - 0.9783
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_{c2}}}&{\left| {{\mathit{\boldsymbol{a}}_{c2}}} \right.}&{\left| {{\mathit{\boldsymbol{B}}_{c2}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.0402}\\
{ - 0.0007}
\end{array}}&{\begin{array}{*{20}{c}}
{ - 9.0590}\\
{0.9747}
\end{array}\left| {\begin{array}{*{20}{c}}
0\\
0
\end{array}} \right.\left| {\begin{array}{*{20}{c}}
{ - 0.0517}\\
{ - 0.0001}
\end{array}} \right.}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{K}}_{c2}} = \left[ {\begin{array}{*{20}{c}}
{22.3939}&{507.8564}
\end{array}} \right]
$
|
|
$
{k_{c1}} = 0,{D_{c2}} = - 4.8164
$
|
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_{c3}}}&{\left| {{\mathit{\boldsymbol{a}}_{c3}}} \right.}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{0.0213}\\
{ - 0.0008}
\end{array}}&{\begin{array}{*{20}{c}}
{ - 8.3427}\\
{0.9884}
\end{array}\left| {\begin{array}{*{20}{c}}
{ - 1.5337}\\
{0.0007}
\end{array}} \right.}
\end{array}} \right]
$
|
|
$
{\mathit{\boldsymbol{B}}_{c3}} = \left[ {\begin{array}{*{20}{c}}
{ - 0.5042}\\
{0.0007}
\end{array}} \right] \times {10^{ - 3}}
$
|
|
$
{\mathit{\boldsymbol{K}}_{c3}} = \left[ {\begin{array}{*{20}{c}}
{18.4785}&{560.4158}
\end{array}} \right]
$
|
|
$
{k_{c3}} = - 189.8622,{D_{c3}} = - 0.0706
$
|
with performance index γmin=0.684 8.
With initial condition ${{\mathit{\boldsymbol{\tilde x}}}_0} = {\left[{15\;\;0.5} \right]^{\rm{T}}}$, and disturbance w(t)=135e-2tsin(3t), the state responses are presented in Fig. 5. Under zero initial conditions, the response of ratio $\sqrt {\sum\limits_{t = 0}^\mathit{\boldsymbol{\kappa }} {{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right)} /\sqrt {\sum\limits_{t = 0}^\mathit{\boldsymbol{\kappa }} {{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{w}}\left( t \right)} } } $ is shown in Fig. 6, which is about 0.306, and lower than γmin= 0.684 8.
5 Conclusions
This paper develops a new robust H∞ fixed-order DOF controller for discrete-time fuzzy NCSs utilizing quantized measurements. Via a descriptor system transformation method and several convexification procedures, it is easy to see that one can attain the PWA fixed-order DOF controller gains via solving a set of LMIs. Two simulation studies have been conducted to illustrate the feasibility of the aforementioned strategy.
Appendix
Lemma 1[15] For two real matrices M and N with appropriate dimensions, the inequality
|
$
{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\left( t \right)\mathit{\boldsymbol{N + }}{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\left( t \right)\mathit{\boldsymbol{M}} \le \varepsilon {\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{M + }}{\varepsilon ^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}
$
|
holds for a scalar ε>0.
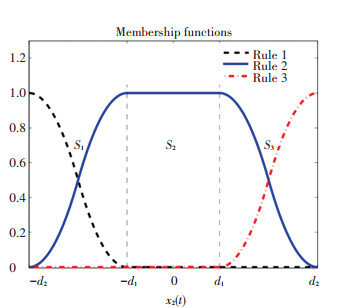
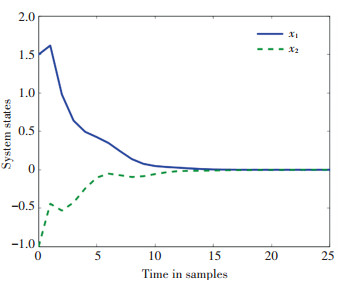
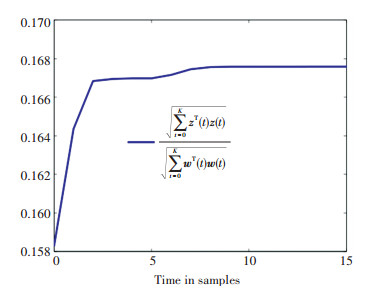
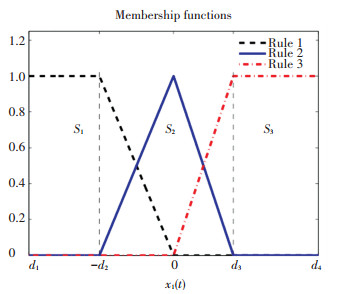
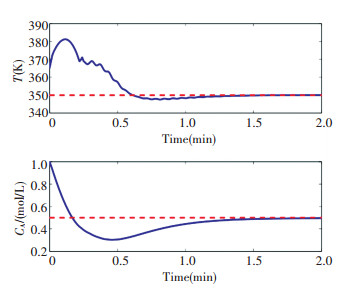
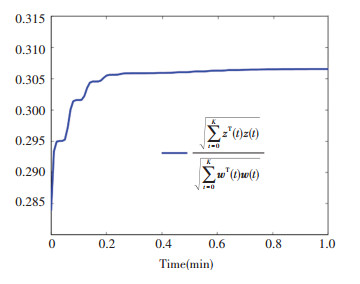
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2018, Vol. 25
2018, Vol. 25


