2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China;
3. School of Computer and Science Technology, Tianjin University, Tianjin 300072, China
Recent years have witnessed a growing number of application areas involving high-dimension data, such as machine learning, data mining, bio-informatics and computer vision[1-2].In practice, the learning task is not relevant to all the features, whereas lots of them are usually irrelevant and redundant.This not only dramatically increases the computation and storage cost, but also induces over-fitting and incomprehensible models.To overcome these issues, feature selection technique has been considered as an effective tool for dimensionality reduction by removing irrelevant and redundant features.The aim of feature selection is to obtain a subset of features by removing the noise and redundancy in original features, so that the more intrinsic representation of data and the better performance is achieved[3].
A great amount of feature selection methods have been proposed and categorized into supervised methods[4-6] and unsupervised methods[7-9]. Supervised feature selection methods increase the performance of learning tasks by utilizing label information.However, label information is usually costly in reality, so unsupervised feature selection holds great potential in real-world applications.
The early unsupervised feature selection algorithms use feature ranking techniques as the principle criteria for feature selection[8, 10-12].One of the main limitations of these methods is that they treat features independently without considering possible correlation among features.To address this problem, a series of algorithms[9, 13-15] have been proposed.A typical method is spectral clustering based algorithms, which can select a feature subset to best preserve the underlying structure between clusters.Spectral clustering based methods explore the cluster structure of data using matrix factorization for spectral analysis, and then select features via sparsity regularization models.Nevertheless, they heavily rely on the learned graph Laplacian.Noises in features may lead to their unreliability.Recently, the self-representation technique has shown significant potential in many tasks, such as subspace clustering[16-19] and active learning[20-21].Motivated by this, some researchers consider the feature selection from the perspective of self-representation property among features[22], i.e., each feature can be well expressed by the linear combination of other relevant features.However, considering the local geometrical structure of feature, it is more reasonable to constrain the representation coefficients of two features to be close when the features are close to each other.
In this paper, we propose a novel method, called Structured Self-Representation (SSR) for unsupervised feature selection.SSR can accurately select the most representative features by exploring the local geometrical structure of features.Specifically, based on self-representation property, each feature can be commendably approximated by the linear combination of other similar features.Meanwhile, the representation coefficients of the features are constrained by their local geometrical structure.In the objective function, two important regularization terms are employed to incorporate the locality information and enforce the sparsity of the coefficients for feature reconstruction, respectively.Furthermore, an efficient algorithm is presented to optimize the problem.Experiments on the synthetic dataset and six real-world datasets demonstrate that our proposed SSR has a better performance than other state-of-the-art algorithms.
Notations: In the following paper, boldface uppercase letters indicate matrices and boldface lowercase letters indicate vectors.Let pi, pj denote the ith row, j-column for a matrix P ={ pij }. For a vector v, its ℓ2 norm is given as || v ||2=
In this section, we mainly review most existing unsupervised feature selection methods.These methods can be roughly divided into three main categories:filter, wrapper and embedded methods.
Filter methods use feature ranking techniques as the principle criteria for feature selection due to their simplicity and good success reported for practical applications.They usually employ a ranking criterion to score the features and use a threshold to remove features below it.The typical methods include:Maximum Variance[10], Laplacian Score (LS)[8], Spectral Feature Selection (SPEC)[11], Trace Ratio[12], and Eigenvalue Sensitive Feature Selection[23].However, the main limitation of these methods is that they treat features independently without considering possible correlation among features and thus the selected subset might not be optimal in that a redundant subset might be obtained.
Wrapper methods commonly use the clustering as the mining algorithm[24-27].These methods consider feature selection and clustering simultaneously and search for features better suited to clustering with the aim of improving clustering performance.However, the optimization program of these methods is known to be NP-hard[28] and the searching becomes quickly computationally intractable.
Embedded methods are developed to perform feature selection and fit a learning model simultaneously.The basic principle behind these methods is to use sparsity regularization for all features indicating which ones are selected.To enforce the sparsity of the feature weights, various sparsity inducing norms has been explored, such as sparse logistic regression[29-30] and group sparsity[13-14, 31-34].The typical methods include:Multi-Cluster Feature Selection (MCFS)[9], joint Feature Selection and Subspace Learning (FSSL)[35], Unsupervised Discriminative Feature Selection (UDFS)[14], and Unsupervised Feature Selection using Feature Similarity (FSFS)[36].Recently, an unsupervised feature selection method based on the regularized self-representation is proposed to choose the most representative features and shows state-of-the-art results[22].However, this method only considers the representativeness of selected features and neglects the local geometric structure among them.
3 BackgroundThe recent work most related to our proposed method is the regularized self-representation (RSR)[22] for unsupervised feature selection.The key of RSR is to select the most representative features based on self-representation property.The objective function can be formulated as follows:
| $ \mathop {{\rm{min}}}\limits_A {\left| {\left| {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{XA}}} \right|} \right|_{2, 1}} + \lambda {\left| {\left| \mathit{\boldsymbol{A}} \right|} \right|_{2, 1}} $ | (1) |
where X =[f1, f2, …, fm]∈ Rn×m is the data matrix with n samples and m dimensional features, and f1, f2, …, fm ∈ Rn are the corresponding feature vectors.The parameter λ>0 sets the trade-off between the two terms. A is the coefficient matrix.Note that, ℓ2, 1-norm minimization term is firstly adopted into the loss function, which enforces robustness to outlier samples; meanwhile, ℓ2, 1 norm is also applied to the feature selection coefficient matrix to ensure the matrix sparse in rows.
With the obtained coefficient matrix A, rows of matrix A are sorted by its row-sum values in the decreasing order and the feature selection task is carried out by choosing the k features corresponding to the top k row-sum of A.
4 Unsupervised Feature Selection Using Structured Self-representationFrom the objective function (1), it can be observed that RSR reconstructs each feature via a linear combination of all the selected features.Geometrically speaking, it is more reasonable to reconstruct coefficient matrix A by the linear combination to preserve the local geometrical information of features.For any two selected features fi, fj, we denote || fi-fj ||2 to be the Euclidean distance between them.Intuitively, the smaller || fi-fj ||2 is (fi is closer to fj), the smaller || ai-aj ||2 should be (ai is also closer to aj).Therefore, when the features are similar to each other their representation coefficients should be also similar to each other.Motivated by this, we introduce the local geometrical structure formulated by minimizing the following[37]:
| $ \begin{array}{l} \frac{1}{2}\sum\limits_{i, j = 1}^m {{w_{ij}}||{\mathit{\boldsymbol{a}}_i}-{\mathit{\boldsymbol{a}}_j}||_2^2} = \\ \sum\limits_{j = 1}^m {\mathit{\boldsymbol{a}}_j^{\rm{T}}{\mathit{\boldsymbol{a}}_j}{\mathit{\boldsymbol{b}}_{jj}}}-\sum\limits_{i, j = 1}^m {\mathit{\boldsymbol{a}}_j^{\rm{T}}{\mathit{\boldsymbol{a}}_i}{\mathit{\boldsymbol{w}}_{jj}}} = \\ Tr(\mathit{\boldsymbol{AB}}{\mathit{\boldsymbol{A}}^{\rm{T}}})-Tr(\mathit{\boldsymbol{AW}}{\mathit{\boldsymbol{A}}^{\rm{T}}}) = Tr{\rm{ }}(\mathit{\boldsymbol{ALA}}{^{\rm{T}}}) \end{array} $ | (2) |
where L = B-W is the Laplacian matrix, in which B is the diagonal degree matrix with
| $ {w_{ij}} = e{^{\frac{{-{{\left| {\left| {{\mathit{\boldsymbol{f}}_i}-{\mathit{\boldsymbol{f}}_j}} \right|} \right|}^2}}}{{{\sigma ^2}}}}} $ | (3) |
Putting Eq.(1) and Eq.(2) together, the proposed method SSR is to solve the following optimization problem:
| $ \mathop {{\rm{min}}}\limits_A {\left| {\left| {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{XA}}} \right|} \right|_{2, 1}} + \alpha {\left| {\left| \mathit{\boldsymbol{A}} \right|} \right|_{2, 1}} + \beta Tr(\mathit{\boldsymbol{ALA}}{^{\rm{T}}}) $ | (4) |
where α and β are two positive trade-off parameters to adjust the degree of penalty.
5 OptimizationAlthough the Eq.(4) is convex, it is not easy to be settled because two non-smooth terms are contained.In the following section, an iterative algorithm is presented to settle this optimization problem.
5.1 Optimization AlgorithmTake the derivative of Eq.(4) with regard to A and set the derivative to zero, we get:
| $ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{GXA}}-{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{GX}} + \alpha \mathit{\boldsymbol{HA}} + \beta \mathit{\boldsymbol{AL}} = 0 $ | (5) |
where G denotes a diagonal matrix with its ith diagonal entry as gii=(2|| xi-xiA||2)-1, and H denotes a diagonal matrix with its ith diagonal entry as hii=(2||ai ||2)-1.Note that the derivation of || A||2, 1 with regard to A is computed to 2 HA.Then the Eq.(5) can be rewritten as:
| $ ({\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{GX}} + \alpha \mathit{\boldsymbol{H}})\mathit{\boldsymbol{A}} + \beta \mathit{\boldsymbol{AL}} = \mathit{\boldsymbol{X}}{^{\rm{T}}}\mathit{\boldsymbol{GX}} $ | (6) |
which is a standard Sylvester equation[38] and has a unique solution as given in Proposition 1.
Proposition 1 There is a unique solution for the Sylvester Eq.(6).
Proof Matrices G, XTX and H are all positive semi-definite, hence term (XTGX +αH) is positive semi-definite and its eigenvalues are all less than or equal to zero:ξj≤0, ∀j.Meanwhile, matrix L is also positive definite, hence its eigenvalues are all greater than zero:φi>0, ∀i.Therefore, we get φi+ξj>0 for all the eigenvalues of (XTGX +αH) and L.According to Ref.[39], there is a unique solution for the Sylvester Eq.(6).
The Bartels-Stewart algorithm[38]can be used to solve the Sylvester equation.This algorithm transforms coefficient matrices into Schur forms using QR decomposition, and then settle the resulting triangular system by back substitution.
In summary, the objective function in Eq.(3) is solved through an iterative way as illustrated in Algorithm 1.The most time-consuming part of Algorithm 1 is solving Sylvester equation in Step 2.Let m denote the dimension size.The Bartels-Stewart algorithm has a computational complexity of O(m3) for solving the Sylvester equation.If Algorithm 1 has t iterations, its overall time complexity turns into O(tm3).
| Algorithm 1:Unsupervised feature selection using structured self-representation (SSR) |
| Input:The data matrix X∈Rn×m. |
| Initialization:A∈Rm×m, ξ=10-6. |
| While not converged do |
| 1) Solve matrix G, in which the i-th diagonal element of G is: |
| |
| Solve matrix H, in which the i-th diagonal element of H is: |
| |
| 2)Solving the Sylvester Eq.(6) by the Bartels-Stewart algorithm to get the coefficient matrix A. |
| 3)Check the convergence condition by: |
| |
| end while |
| Output:according to ||ai||2(i=1, …, m) in descending order, all m features are sorted and the top k ranked features can be selected. |
5.2 Convergence Analysis
The following section shows that the objective function in Eq.(4) decreases in each iteration and it is guaranteed to convergence.
Lemma 1 The following inequality holds if
| $ {\left| {\left| {\mathit{\boldsymbol{\tilde a}}} \right|} \right|_2}-\frac{{\left| {\left| {\mathit{\boldsymbol{\tilde a}}} \right|} \right|_2^2}}{{2{{\left| {\left| \mathit{\boldsymbol{a}} \right|} \right|}_2}}} \le {\left| {\left| \mathit{\boldsymbol{a}} \right|} \right|_2}-\frac{{\left| {\left| \mathit{\boldsymbol{a}} \right|} \right|_2^2}}{{2{{\left| {\left| \mathit{\boldsymbol{a}} \right|} \right|}_2}}} $ | (7) |
Next, we give a simple proof of convergence of our algorithm in the Theorem 1.
Theorem 1 Algorithm 1 decreases the objective value of Eq.(4).
Proof Suppose the updated A is
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_A Tr\left[{\left( {\mathit{\boldsymbol{X}}\mathit{-}\mathit{\boldsymbol{XA}}\mathit{ }} \right){^{\rm{T}}}\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{XA}}{\rm{ }}} \right)} \right] + \\ \;\;\;\;\;\;\;\alpha Tr{\rm{ }}(\mathit{\boldsymbol{A}}{^{\rm{T}}}\mathit{\boldsymbol{HA}}) + \beta Tr(\mathit{\boldsymbol{AL}}{\mathit{\boldsymbol{A}}^{\rm{T}}}) \end{array} $ | (8) |
Therefore, the following inequality holds:
| $ \begin{array}{l} Tr\left[{{{\left( {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{X\tilde A}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{X\tilde A}}} \right)} \right] + \alpha Tr\left( {{{\mathit{\boldsymbol{\tilde A}}}^{\rm{T}}}\mathit{\boldsymbol{H\tilde A}}} \right) + \\ \;\;\;\beta Tr\left( {\mathit{\boldsymbol{\tilde AL\tilde A}}{^{\rm{T}}}} \right) \le Tr\left[{{{\left( {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{XA}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{XA}}} \right)} \right] + \\ \;\;\;\alpha Tr{\rm{ }}({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{HA}}) + \beta Tr(\mathit{\boldsymbol{AL}}{\mathit{\boldsymbol{A}}^{\rm{T}}}) \end{array} $ | (9) |
which is further equivalent to:
| $ \begin{array}{l} {\left| {\left| {{\rm{ }}\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{X\tilde A}}{\rm{ }}} \right|} \right|_{2, 1}} + \alpha {\left| {\left| {{\rm{ }}\mathit{\boldsymbol{\tilde A}}{\rm{ }}} \right|} \right|_{2, 1}}-({\left| {\left| {{\rm{ }}\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{X\tilde A}}{\rm{ }}} \right|} \right|_{2, 1}} - \\ \;\;\;\;\;\sum\limits_i {\frac{{||{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{\tilde A}}||_2^2}}{{2||{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{A}}|{|_2}}}} ) - \alpha({\left| {\left| {\mathit{\boldsymbol{\tilde A}}} \right|} \right|_{2, 1}} - \\ \sum\limits_i {\frac{{||{{\mathit{\boldsymbol{\tilde a}}}^i}||_2^2}}{{2||{\mathit{\boldsymbol{a}}^i}|{|_2}}}} ) + \beta Tr(\mathit{\boldsymbol{\tilde AL\tilde A}}{^{\rm{T}}}) \le \\ {\left| {\left| {{\rm{ }}\mathit{\boldsymbol{X}}\mathit{ - }\mathit{\boldsymbol{XA}}{\rm{ }}} \right|} \right|_{2, 1}} + \alpha {\left| {\left| \mathit{\boldsymbol{A}} \right|} \right|_{2, 1}} - ({\left| {\left| {\mathit{\boldsymbol{X}}\mathit{ - }\mathit{\boldsymbol{XA}}} \right|} \right|_{2, 1}} - \\ \sum\limits_i {\frac{{||{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{A}}||_2^2}}{{2||{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{A}}|{|_2}}}} ) - \alpha ({\left| {\left| \mathit{\boldsymbol{A}} \right|} \right|_{2, 1}} - \sum\limits_i {\frac{{||{\rm{ }}\mathit{\boldsymbol{\tilde a}}{^i}||_2^2}}{{2||\mathit{\boldsymbol{a}}{^i}|{|_2}}}} )\\ + \beta Tr(\mathit{\boldsymbol{AL}}{\mathit{\boldsymbol{A}}^{\rm{T}}}) \end{array} $ | (10) |
According to the Lemma 1, we have the following two inequalities:
| $ \begin{array}{l} \alpha \left( {{{\left| {\left| {{\rm{ }}\mathit{\boldsymbol{\tilde A}}{\rm{ }}} \right|} \right|}_{2, 1}}-\sum\limits_i {\frac{{\left| {\left| {{\rm{ }}{{\mathit{\boldsymbol{\tilde a}}}^i}} \right|} \right|_2^2}}{{2{{\left| {\left| {{\mathit{\boldsymbol{a}}^i}} \right|} \right|}_2}}}} } \right) \le \alpha ({\left| {\left| \mathit{\boldsymbol{A}} \right|} \right|_{2, 1}}-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_i {\frac{{||{\mathit{\boldsymbol{a}}^i}||_2^2}}{{2||{\mathit{\boldsymbol{a}}^i}|{|_2}}}} ) \end{array} $ | (11) |
| $ \begin{array}{l} {\left| {\left| {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{X\tilde A}}} \right|} \right|_{2, 1}}-\sum\limits_i {\frac{{\left| {\left| {{\mathit{\boldsymbol{x}}^i}-{\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{\tilde A}}{\rm{ }}} \right|} \right|_2^2}}{{2{{\left| {\left| {{\rm{ }}{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{A}}{\rm{ }}} \right|} \right|}_2}}}} \le ||\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{XA}}|{|_{2, 1}} - \\ \sum\limits_i {\frac{{||{\rm{ }}{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{A }}||_2^2}}{{2||{\rm{ }}{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}^i}\mathit{\boldsymbol{A }}|{|_2}}}} \end{array} $ | (12) |
Summing Eqs.(10)-(12) in the two sides, we obtain:
| $ \begin{array}{l} {\left| {\left| {{\rm{ }}\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{X\tilde A}}{\rm{ }}} \right|} \right|_{2, 1}} + \alpha {\left| {\left| {{\rm{ }}\mathit{\boldsymbol{\tilde A}}{\rm{ }}} \right|} \right|_{2, 1}} + \beta Tr{\rm{ }}\left( {\mathit{\boldsymbol{\tilde AL\tilde A}}{^{\rm{T}}}} \right) \le \\ {\left| {\left| {{\rm{ }}\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{XA}}{\rm{ }}} \right|} \right|_{2, 1}} + \alpha \left| {\left| \mathit{\boldsymbol{A}} \right|} \right|{_{2, 1}} + \beta Tr{\rm{ }}(\mathit{\boldsymbol{ALA}}{^{\rm{T}}}) \end{array} $ | (13) |
Therefore, Theorem 1 can be proved.Note that the derivative of Eq.(4) with regard to A is exactly the Eq.(5), thus A, G, H will satisfy the Eq.(5) in the convergence.Because closed form solution can be obtained in each iteration, the proposed algorithm converges fast.
6 ExperimentsIn this section, we conduct experiments to evaluate the effectiveness of SSR.Following Refs.[9, 13], performances of the proposed algorithm are evaluated in terms of clustering.
6.1 Experimental Settings1) Datasets.
In the experiments, six public datasets are used to compare the performance of different unsupervised feature selection algorithms.These datasets include two face image datasets (ORL[9] and COIL20[9]), one hand written digit image dataset (USPS[40]), one spoken letter recognition dataset (Isolet[9]) and two biological datasets (Colon[41] and Lung[42]).The detailed information of these datasets is listed in Table 1.Example images of three datasets among all datasets are shown in Fig. 1.
| Table 1 Summary of datasets |

|
Figure 1 Example images of three datasets used in this paper |
2) Compared algorithms.
The proposed method SSR is compared with the following representative unsupervised feature selection methods:
·AllFea: The method selects all the features as a baseline method.
·Laplacian score (LS) [8]: The method selects the features according to their capacity of locality preserving of the data manifold structure.
·MCFS [9]: The method evaluates the features by using spectral regression with ℓ1 norm regularization.
·UDFS [14]: The method exploits feature correlations and local discriminative information simultaneously to select features.
·NDFS [13]: The method selects features by a joint framework of nonnegative spectral analysis and ℓ2, 1 regularized regression.
·RSR [22]: The method choosess the most representative features by using the self-representation property with ℓ2, 1 norm regularization.
There are some parameters to be set in advance.Following Refs.[15, 43], for LS, MCFS, UDFS and NDFS, the neighborhood size is fixed to be 5 for all the datasets.To fairly compare all the unsupervised feature selection methods, the parameters are tuned by a "grid-search" strategy from{10-4, 10-3, …, 103, 104} for all the compared algorithms.The number of chosen features is set as {50, 100, 150, 200, 250, 300} for all the datasets except USPS.Since the total feature number of USPS is 256, we set the number of chosen features as {50, 100, 150, 200, 250} for this dataset.After choosing the features, both the clustering and classification are performed based on the selected features.Then the average results are reported over different number of features.
3) Evaluation metrics.
Following Refs.[11, 14], all the unsupervised feature selection algorithms are evaluated on the clustering task.To better estimate the clustering performance, we adopt two metrics, i.e., Accuracy (ACC) and Normalized Mutual Information (NMI).Suppose li be the cluster label obtained by all the different algorithms and pi be the ground truth collected by the dataset.The ACC is given as follows:
| $ ACC = \frac{{\sum\limits_{i = 1}^n {\delta ({p_i}, map({l_i}))} }}{n} $ | (14) |
where δ(x, y) denotes the delta function, where δ(x, y)=1 if x=y and δ(x, y)=0 otherwise.map(li) denotes the mapping function, which transforms each cluster label li to the equivalent label in the dataset.ACC is used to measure the percentage of correct clustering labels against the ground truth class labels.The larger ACC is, the better performance has.Given two variables P and Q, NMI is given as follows:
| $ NMI = \frac{{R\left( {\mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{P}}{\rm{ }}} \right)}}{{\sqrt {H\left( \mathit{\boldsymbol{Q}} \right)H\left( \mathit{\boldsymbol{P}} \right)} }} $ | (15) |
where P is the clustering result and Q is the true label.H(P) and H(Q) are the entropies of P and Q, respectively.R(P, Q) is the mutual information between Q and P.NMI shows the consistency between clustering results and ground truth labels.Meanwhile, a larger NMI indicates a better clustering result.
6.2 Experiments on Synthetic DataThe experiment on synthetic data is first conducted to demonstrate that the proposed SSR can effectively select representative features using local structure information.The synthetic data has 135 samples and 225 features.There are 6 independent types for the features.The features in the same type can be represented each other whereas the features between different types are orthogonal.The numbers of data produced from the six types of features are 10, 15, 20, 25, 30 and 35, respectively.The numbers of the six types of features are 25, 30, 35, 40, 45 and 50, respectively, which are relatively large to the data.The features within each type are randomly generated in the range of 0 and 1.Furthermore, to enhance difficulty in feature selection, the noise data randomly generated in the range of 0 and 0.5 is added to synthetic features.
Fig. 2(a) exhibits the learned matrix A in Eq.(1) by algorithm RSR, and Fig. 2(b) exhibits the learned matrix A in Eq.(1) by algorithm SSR.Fig. 2(c) is the original similarity matrix of features.Compared with RSR, the learned matrix A can reveal the underlying feature structure more clearly.The results clearly indicate that our method could effectively select representative features by exploring the local structure of features.

|
Figure 2 The learned A by RSR and DISR on the synthetic data.Obviously, SSR can reveal the underlying feature structure more clearly |
6.3 Experiments on Real-world Data
To better estimate the performances of unsupervised feature selection algorithms (except for AllFea), the averaged clustering results are reported over different number of chosen features since the optimal number of chosen features is unpredictable in advance.In the experiment, we compare the clustering performances of various feature selection algorithms in terms of ACC and NMI.The best results are marked in bold.The K-means clustering algorithm is carried out with the selected features of all the competing algorithms.Because the clustering results vary with different initializations, we repeatedly run the experiment with different random initializations for 20 times and report the average results for all the competing algorithms.
The experimental results are shown in Table 2 and Table 3.From two tables, it can be observed that the performance of the proposed method SSR is superior to the rest of the algorithms on most of the datasets in terms of ACC and NMI. In particular, compared with the clustering results using all features (AllFea), SSR achieves the best performance on all the datasets, which implies that it cannot only reduce the number of features, but also improve the clustering performance.Moreover, SSR outperforms other methods on most of six datasets in terms of ACC and NMI, further demonstrating the effectiveness of SSR.AS shown in two tables, for LS, UDFS and MCFS, both of them select the features that try preserving the data similarity of the original feature space.UDFS and MCFS utilize the regression model while LS uses the feature ranking model.The results of UDFS and MCFS are better than LS, which demonstrates the superiority of the regression manner.For NDFS, and RSR, they both consider the relationship between features.NDFS explores the relationship between two features and adopts clustering technique to choose the representative features, while RSR utilizes the self-representation property of features to consider their relationship jointly and achieves a promising result.However, the proposed SSR considers the representation property and the local structure information of features simultaneously to select representative features and achieves better performances.
| Table 2 Clustering results (ACC % ± std) on different datasets for different feature selection algorithms(The best performances are highlighted in bold) |
| Table 3 Clustering results (NMI % ± std) on different datasets for different feature selection algorithms(The best performances are highlighted in bold) |
For further evaluating the performance of SSR, performances of various feature selection algorithms are compared in terms of classification accuracy.In classification task, for each dataset, we randomly select 50% of all the data as the training data and the rest as the testing data.This process is repeated for 50 times with random data selection.The nearest neighbor classifier[44] is adopted for the classifi cation.The average results are reported in Table 4.Similarly, bold values in the table indicate the best results.From Table 5, it can be observed that SSR also produces superior classifi cation performance compared with other algorithms.
| Table 4 Classification accuracy (ACC% ± std) on different datasets for different feature selection algorithms(The best performances are highlighted in bold) |
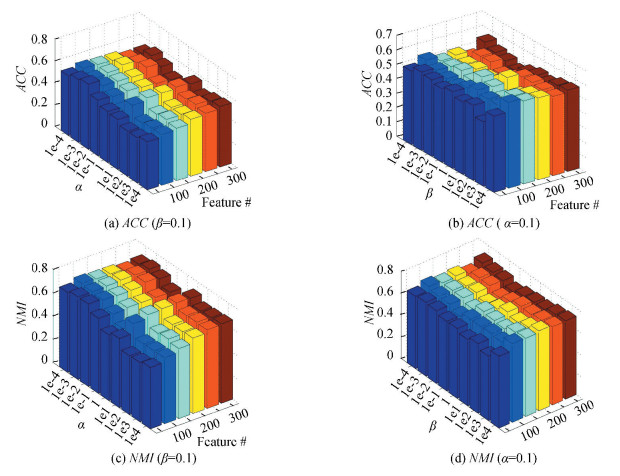
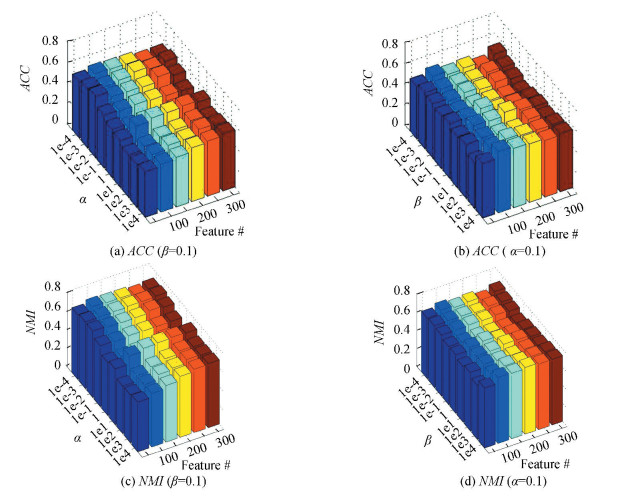
Next, a study of parameter sensitivity in SSR is provided as follows.There are two important parameters α and β, in our method SSR, where α is used to control the sparsity of selected features and β controls the degree of low-dimensional latent semantics reserving the local geometry structure in the original space.In this subsection, we study how the clustering ACC and NMI of SSR vary with the two parameters.Due to the space limit, we only show the results on datasets COIL20 and Lung.The experimental results are shown in Fig. 3 and Fig. 4.It can be observed that the proposed algorithm is not sensitive to α and β with wide ranges.Furthermore, experiments are conducted to compare the results with well-chosen parameters to ones with the default parameters.In the proposed experimental results, α=0.1 and β=0.1 are set as our default parameter values.The comparative results are given in Fig. 5.It can be seen that, with the default parameter, the proposed algorithm gains relatively good results on all the datasets.That is, without tuning parameters, our method can work well on the given datasets in most cases.However, the performance of algorithm is more sensitive to the number of chosen features, which is still an open issue.
|
Figure 3 The ACC and NMI of SSR with respect to the parameters α, β and feature numbers on the dataset COIL20 |
|
Figure 4 The ACC and NMI of SSR with respect to the parameters α, β and feature numbers on the dataset Lung |

|
Figure 5 Performance comparison between the cases with the default (i.e., α=0.1 and β=0.1) and the best parameters |
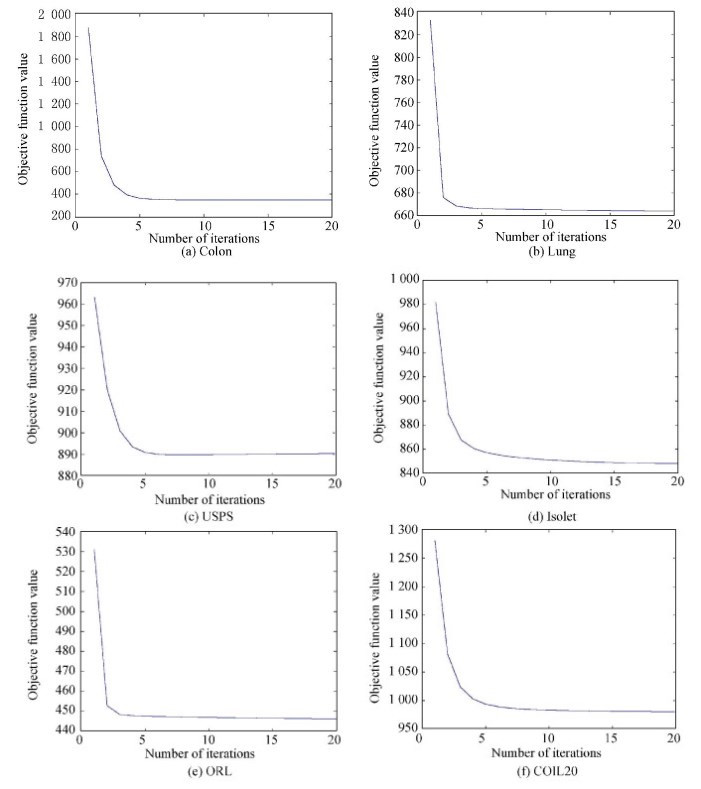
Finally, an experimental study of the speed of convergence of the proposed Algorithm 1 is given.The convergence curves of the objective function value over all the datasets are given in Fig. 6.It can be observed that the proposed Algorithm 1 converges very fast and almost within 10 iterations.So, the proposed optimization algorithm is effective and it converges quickly.
|
Figure 6 Convergence curves of the objective function value over all the datasets |
7 Conclusions
In this paper, we propose a novel Structured Self-Representation (SSR) model for an unsupervised feature selection by integrating local geometrical structure and self-representation property of features simultaneously.Two important regularization terms are utilized to incorporate the locality information and enforce the sparsity of the coefficients for feature reconstruction, respectively.To solve the proposed objective function, a simple but efficient algorithm is presented by an iterative manner.In the experiments, the proposed algorithm is applied in both clustering and classification task.Experiments on the synthetic dataset and six real-world datasets have validated the effectiveness of our proposed method.
| [1] |
Wang M, Hua X S, Hong R, et al. Unified video annotation via multi-graph learning. IEEE Transactions on Circuits and Systems for Video Technology, 2009, 19(5): 733-746. DOI:10.1109/TCSVT.2009.2017400 ( 0) 0)
|
| [2] |
Gupta M D, Xiao J. Non-negative matrix factorization as a feature selection tool for maximum margin classifierss. Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2011, 2841-2848. DOI:10.1109/CVPR.2011.5995492
( 0) 0)
|
| [3] |
Guyon I, Elisseeff A. An introduction to variable and feature selection. Journal of Machine Learning Research, 2003, 3(3): 1157-1182. ( 0) 0)
|
| [4] |
Zhao Z, Wang L, Liu H, et al. On similarity preserving feature selection. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(3): 619-632. DOI:10.1109/TKDE.2011.222 ( 0) 0)
|
| [5] |
Nie F, Huang H, Cai X, et al. Efficient and robust feature selection via joint ℓ2, 1 -norms minimization. Advances in Neural Information Processing Systems (NIPS), 2010, 1813-1821. ( 0) 0)
|
| [6] |
Peng H, Long F, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238. DOI:10.1109/TPAMI.2005.159 ( 0) 0)
|
| [7] |
Liang D, Shen Z, Xuan L, et al. Local and global discriminative learning for unsupervised feature selection. Proceedings of the 2013 IEEE 13th International Conference on Data Mining (ICDM). Piscataway: IEEE, 2013, 131-140. DOI:10.1109/ICDM.2013.23
( 0) 0)
|
| [8] |
He X, Cai D, Niyogi P. Laplacian score for feature selection. Proceedings of the Advances in Neural Information Processing Systems (NIPS). Vancouver, 2005. http://papers.nips.cc/paper/2909-laplacian-score-for-feature-selection.pdf. [2017-05-19]
( 0) 0)
|
| [9] |
Cai D, Zhang C, He X. Unsupervised feature selection for multi-cluster data. Proceedings of the International Conference on Knowledge Discovery and Data Mining (KDD). New York: ACM, 2010, 333-342. DOI:10.1145/1835804.1835848
( 0) 0)
|
| [10] |
Krzanowski W J. Series C (Applied Statistics). Selection of variables to preserve multivariate data structure, using principal components. Journal of the Royal Statistical Society, 1987, 36(1): 22-33. DOI:10.2307/2347842 ( 0) 0)
|
| [11] |
Zhao Z, Liu H. Spectral feature selection for supervised and unsupervised learning. Proceedings of the 24th Annual International Conference on Machine Learning (ICML). New York: ACM, 2007, 1151-1157. DOI:10.1145/1273496.1273641
( 0) 0)
|
| [12] |
Nie F, Xiang S, Jia Y, et al. Trace ratio criterion for feature selection. Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2008, 671-676.
( 0) 0)
|
| [13] |
Li Z, Yang Y, Liu J, et al. Unsupervised feature selection using nonnegative spectral analysis. Proceedings of the Twenty-sixth AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2012, 1026-1032.
( 0) 0)
|
| [14] |
Yang Y, Shen H T, Ma Z, et al. ℓ2, 1-norm regularized discriminative feature selection for unsupervised learning.Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence (IJCAI). Palo Alto: AAAI, 2011, 1589-1597.
( 0) 0)
|
| [15] |
Qian M, Zhai C. Robust unsupervised feature selection. Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (IJCAI). Palo Alto: AAAI, 2013, 1621-1627.
( 0) 0)
|
| [16] |
Elhamifar E, Vidal R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2765-2781. DOI:10.1109/TPAMI.2013.57 ( 0) 0)
|
| [17] |
Lu C, Feng J, Lin Z, et al. Correlation adaptive subspace segmentation by trace lasso. Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV). Piscataway: IEEE, 2013, 1345-1352. DOI:10.1109/ICCV.2013.170
( 0) 0)
|
| [18] |
Wang S, Yuan X, Yao T, et al. Efficient subspace segmentation via quadratic programming. Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence (AAAI). Palo Alto: AAAI, 2011, 519-524.
( 0) 0)
|
| [19] |
Lu C Y, Min H, Zhao Z Q, et al. Robust and efficient subspace segmentation via least squares regression. European Conference on Computer Vision (ECCV). Berlin: Springer, 2012, 47-360. DOI:10.1007/978-3-642-33786-4_26
( 0) 0)
|
| [20] |
Nie F, Wang H, Huang H, et al. Early Active Learning via Robust Representation and Structured Sparsity. Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (IJCAI). Palo Alto: AAAI, 2013, 1572-1578.
( 0) 0)
|
| [21] |
Hu Y, Zhang D, Jin Z, et al. Active learning via neighborhood reconstruction. Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (IJCAI). Palo Alto: AAAI, 2013, 1415-1421.
( 0) 0)
|
| [22] |
Zhu P, Zuo W, Zhang L, et al. Unsupervised feature selection by regularized self-representation. Pattern Recognition, 2015, 48(2): 438-446. DOI:10.1016/j.patcog.2014.08.006 ( 0) 0)
|
| [23] |
Jiang Y, Ren J. Eigenvalue sensitive feature selection. Proceedings of the 28th International Conference on Machine Learning. Washington, 2011, 89-96. ( 0) 0)
|
| [24] |
Constantinopoulos C, Titsias M K, Likas A. Bayesian feature and model selection for Gaussian mixture models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(6): 1013-1023. DOI:10.1109/TPAMI.2006.111 ( 0) 0)
|
| [25] |
Dy J G, Brodley C E, Wrobel S. Feature selection for unsupervised learning. Journal of Machine Learning Research, 2004, 5(8): 845-889. ( 0) 0)
|
| [26] |
Law M H C, Figueiredo M A T, Jain A K. Simultaneous feature selection and clustering using mixture models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(9): 1154-1166. DOI:10.1109/TPAMI.2004.71 ( 0) 0)
|
| [27] |
Roth V, Lange T. Feature selection in clustering problems. Advances in Neural Information Processing Systems (NIPS). Massachusetts : MIT, 2003. http://papers.nips.cc/paper/2486-feature-selection-in-clustering-problems.pdf.
( 0) 0)
|
| [28] |
Amaldi E, Kann V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theoretical Computer Science, 1998, 209(1/2): 237-260. DOI:10.1016/S0304-3975(97)00115-1 ( 0) 0)
|
| [29] |
Ng A Y. Feature selection, ℓ1 vs. ℓ2regularization, and rotational invariance. Proceedings of the Twenty-First International Conference on Machine Learning. New York: ACM, 2004, 78-86. DOI:10.1145/1015330.1015435
( 0) 0)
|
| [30] |
Cawley G C, Talbot N L C, Girolami M. Sparse multinomial logistic regression via Bayesian ℓ1 regularization. Advances in Neural Information Processing Systems (NIPS). Neural Information Processing Systems Foundation, Inc, 2007, 209-217.
( 0) 0)
|
| [31] |
Zhao Z, Wang L, Liu H. Efficient Spectral Feature Selection with Minimum Redundancy. Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence (AAAI). Palo Alto: AAAI, 2010, 673-678.
( 0) 0)
|
| [32] |
Hou C, Nie F, Yi D, et al. Feature selection via joint embedding learning and sparse regression. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence (IJCAI). Palo Alto: AAAI, 2011, 1324-1330.
( 0) 0)
|
| [33] |
Liu X, Wang L, Zhang J, et al. Global and local structure preservation for feature selection. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(6): 1083-1095. DOI:10.1109/TNNLS.2013.2287275 ( 0) 0)
|
| [34] |
Li Z, Liu J, Yang Y, et al. Clustering-guided sparse structural learning for unsupervised feature selection. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(9): 2138-2150. DOI:10.1109/TKDE.2013.65 ( 0) 0)
|
| [35] |
Gu Q, Li Z, Han J. Joint feature selection and subspace learning. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence. Palo Alto: AAAI, 2011, 1294-1302. DOI:10.5591/978-1-57735-516-8/IJCAI11-219
( 0) 0)
|
| [36] |
Mitra P, Murthy C A, Pal S K. Unsupervised feature selection using feature similarity. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(3): 301-312. DOI:10.1109/34.990133 ( 0) 0)
|
| [37] |
Hu H, Lin Z, Feng J, et al. Smooth representation clustering. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Picataway: IEEE, 2014, 3834-3841.
( 0) 0)
|
| [38] |
Bartels R H, Stewart G W. Solution of the matrix equation AX+XB=C[F4]. Communications of the ACM, 1972, 15(9): 820-826. DOI:10.1145/361573.361582 ( 0) 0)
|
| [39] |
Lancaster P. Explicit solutions of linear matrix equations. Siam Review, 1970, 12(4): 544-566. DOI:10.1137/1012104 ( 0) 0)
|
| [40] |
Hull J J. A database for handwritten text recognition research. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 550-554. DOI:10.1109/34.291440 ( 0) 0)
|
| [41] |
Alon U, Barkai N, Notterman D A, et al. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. The National Academy of Sciences, 1999, 96(12): 6745-6750. DOI:10.1073/pnas.96.12.6745 ( 0) 0)
|
| [42] |
Bhattacharjee A, Richards W G, Staunton J, et al. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. The National Academy of Sciences, 2001, 98(24): 13790-13795. DOI:10.1073/pnas.191502998 ( 0) 0)
|
| [43] |
Wang S, Tang J, Liu H. Embedded unsupervised feature selection. Proceedings of the National Conference on Artificial Intelligence. Palo Alto: AAAI, 2015, 470-476.
( 0) 0)
|
| [44] |
Lindenbaum M, Markovitch S, Rusakov D. Selective sampling for nearest neighbor classifiers. Machine Learning, 2004, 54(2): 125-152. DOI:10.1023/B:MACH.0000011805.60520.fe ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25


