Composite materials have been used extensively as primary structures in various industrial applications due to their outstanding properties including higher strength to weight ratios, greater resistances to corrosion and lower maintanance cost[1-2]. The major factor driving an impressive growth rate for the usage of composites is the development of next generation structure of composite materials, which promotes the pursuit of resin systems and new types of reinforcement with better performances such as carbon-based and ceramic nanoparticles[3-4]. Nanofillers have become an important pathway to increase technological potential of composite materials, and produce new nanocomposites with unique mechanical properties that can be applied into large-scale commercialization[5].
Silica, which is an inorganic additives, has been used to enhance the toughness of epoxies without sacrificing their fundamental properties. Micro-and nano-scale silica fillers are the essential ceramic materials that improve the modulus of elasticity, mechanical properties at high temperatures, and the fracture tenacity of the composites[6-8]. However, the reinforced performance of micro-silica is less satisfied due to higher percentage of filler loading requirement which may increase the risk of agglomeration in composite materials. Contrarily, nano-silica filler (less than 100 nm) with higher specific surface area requires less filler content as the homogeneous filler dispersion in matrix can be achieved by strengthened chemical bonding between fillers and matrix interfaces. The epoxy/SiO2 nanocomposites improved the elastic modulus which means the decrease of material elongation compared to neat epoxy matrix[9]. Besides, impact strength, tensile strength, modulus value, and specific heat capacity with the increase of temperature were all increased by the effect of SiO2 nanofiller in sisal fibre reinforced polyester composites[10]. The addition of SiO2 nanoparticles enhanced the interlaminar fracture toughness on glass fibre epoxy composites[11]. The maximum fatigue stress rised by 39% due to the combining of 3 Vol% SiO2 with epoxy/glass fibre, because the small size of nanosilica had the ability to occupy itself into small voids or porosity of the epoxy resins. It also acted as a bridge to create more molecular interconnectivity, resulting in reduction in total free volume as well as an increase in cross-linking density[12].
However, the quality of filler dispersion state and filler loading of silica particles could be enhanced or deteriorated by stress concentration of filler agglomerations, filler-matrix compatibility, and interfacial interaction[13]. While the numerous amount of silica increase the viscosity and result in poor dispersion and fabricating difficulty[14]. Here graphene oxide (GO) was proposed to improve the dispersion of SiO2 nanofillers and the interfacial interaction between fillers and matrix.
As graphene is mentioned to be the thinnest and strongest known material in the universe[15] with extraordinary mechanical and thermal properties, graphene and graphene derivatives are good candidates for nanoreinforcement. Intrinsic graphene is not compatible with organic polymers, and tends to agglomerate due to the high Van der Waals intermolecular forces, but through modified Hummer and Offeman's method, graphene oxide heavily oxygenated with carbonyl, hydroxyl and epoxide groups on the basal plane can be obtained. The aforementioned chemical groups of GO reduced Van der Waal interactions and led to an improved graphene's solubility and interfacial bonding[16-17], so GO is much more compatible with organic polymer matrices. The incorporation of GO in PVA resulted in 76% and 62% increase in tensile strength and young's modulus, respectively[18]. Adding 6% GO in rubbery epoxy matrix could enhance the Young's modulus, impact strength, and micro hardness of the rubber[19]. The influence of GO on epoxy matrices was investigated in the range of 1.5 Vol% to 6 Vol%, results in the increasement of tensile strength, Young's modulus, hardness, and also impact strength compared to the neat epoxy matrix[20].
In this work, 0.1wt% GO filler loading is chosen as the optimum loading for carbon fiber/epoxy (CF/E) composite[21]. The GO and SiO2 nanoreinforcements were filled into CF/E composites to investigate the influence of GO and SiO2 nanofillers on the flexural properties, hardness, impact, moisture absorption, and temperature effect.
2 ExperimentsGraphene oxide (GO) powders (average diameter: 2.6 μm, thickness: between 0.8 and 1.2 nm) were prepared by optimization of Hummers method by using potassium permanganate (KMnO4), sulfuric acid (H2SO4) and nitric acid (HNO3)[22]. Silica (SiO2) nanoparticles have an average diameter of 15 nm, a bulk density of 0.05 g/cm3 and a specific surface area of 600 m2/g. Both GO and SiO2 nanofillers were supplied by JCNANO Technology (China). Epoxy resins were a diglycidyl ether of bisphenol-A (DGEBA) based epoxy resin E51 cured with amine-based curing agent hardener, was purchased by Hongxing Composite Material (China). The epoxy resin to hardener ratio was recommended to be 4 to 1 by mass. Epoxy resin, E51 has an epoxide equivalent weight from 180 to 190 g/eq and viscosity at 25 ℃ from 8 000-11 000 mPa·s as provided by the vendor. In this study, all of the materials were directly used without any further synthesis or purification. The plain weave 3K carbon fiber (CF) was used for fiber reinforcements, supplied by Yixing Yitai Carbon Fibre Weaving (China). The thickness and density were 0.22 mm and 220 g/m2, respectively.
For epoxy/GO/SiO2 pre-polymer composites preparation, the desired amount of GO and SiO2 powders were dispersed into 2 mg/mL in DI water by sonication for 2 h and then mixed with predetermined amount of epoxy resin at 100 ℃ under magnetic hotplate stirrer for 3 h. Next, the mixture was further degassed overnight in a vacuum oven and then cooled down to room temperature. Subsequently, the amine-based curing agent hardener was added to the resin at an epoxy: amine stoichiometric ratio of 4:1 and mixed by mechanical stirrer for 5 min. The mixture was degassed prior to laminate fabrication to eliminate trapped solvent or air bubbles. Laminates comprising of 8 plies carbon fiber (with and without nanofillers) were fabricated by VARTM method and left to cure at ambient conditions for 24 h as shown in Fig. 1. The material designation and composition of CF/E are presented in Table 1.

|
Figure 1 Composite materials fabrication by VARTM process |
| Table 1 Types of material designations and composition of CF/E composites |
Three-point bending tests were determined according to ASTM D7264-15[23] using an Instron 5982 machanical testing system with 100 kN load cell. The geometry of rectangular specimens are 80 mm ×13 mm ×2 mm. The support span length and testing speed were set at 50 mm and 2 mm/min, respectively. The Charpy flatwise impact test was performed using pendulum hammer to investigate the impact energy of un-notched specimens. According to the ASTM6110-10, it is low energy testing of composite specimens with impact energy variable up to 50 J and 3.8 m/s of impact velocity[24]. The dimension of specimens is 80 mm×12.7 mm×2 mm. The HRS-150 Digital Rockwell Hardness tester was used to conduct Rockwell hardness tests according to the ASTM D785-08[25]. The test apparatus consists of a steel ball indenter, mounted under a 100 kg force sensor on a motor driven controlling vertical positioning carriage. At least five replicate specimens were examined in each testing series for reproducibility. The minimum of three replicate specimens from each condition (56 mm×12.7 mm×2 mm) were conducted according to ASTM D7028-07[26] and subjected to DMA from TA Instruments DMA Q800 using three-point bending mode. The samples were oscillated to 5 μm amplitude at frequency of 1 Hz, the pre-load force was set at 1 N. The specimens were heated from 30 ℃ to 150 ℃ with 5 ℃/min heating rate.
The moisture absorption tests were carried out according to ASTM D5229-14[27]. Specimens as flexural and impact bars were dried in a vacuum oven at 70 ℃ until a constant weight was attained. Specimens were placed in two different containers of DI water and salt water at temperature of 90 ℃ for 14 days. The weight gain of the specimens was measured as a function of time after removing the solvents on their surfaces. Wet specimens (wet) were tested straight away, while re-dried specimens (re-dried) had dried in the oven at 70 ℃ for 24 h after immersion process. The flexural and impact properties of hybrid composites at 90 ℃ in DI and salt water were investigated by the effect of wet and re-dried set of spcimens. The morphological properties of impact bar specimens were investigated by HITACHI SU8010 FESEM (Field Emission Scanning Electron Macrograph) equipped with a resolution of 1.3 nm at 1 kV and 1.0 nm at 1.5 kV. The used of acceleration voltage was 5 kV. The surface of specimens was coated by gold (Au) to improve the image quality.
3 Results and Discussion 3.1 Investigation of Mechanical PropertiesFlexural properties, Charpy impact strength, and hardness of CF/E as a function of GO and nano-SiO2 loading were measured by three-point bending system, pendulum hammer and Rockwell hardness tester to investigate the mechanical properties of CF/E composites with GO and nano-SiO2 fillers. Measurement data was summarized in Table 2 to compare the mechanical properties with different nanofillers.
| Table 2 Mechanical properties of the effects of GO and SiO2 fillers on CF/E composites |
The flexural strength of the CF/E/0.1GO was 698 MPa, approximately 5.23% higher than CF/E composites. CF/E/0.1GO/2SiO2 had the highest flexural strength of 784 MPa by approximately 18.17 % higher than CF/E composites. The flexural modulus of CF/E showed similar trend with flexural strength upon the addition of filler into CF/E, 0.1 GO enhanced the flexural modulus of CF/E by approximately 9.13% (48 GPa). CF/E/0.1GO/2SiO2 composites indicated the highest result in flexural modulus (55 GPa) increased up to 26.69%. Besides, CF/E/0.1GO/2SiO2 composites also presented the highest result in impact strength and hardness. Impact strength of CF/E increased from 6.30 J/cm2 to 6.67 J/cm2 when 0.1% GO was added, further addition of 2% SiO2 enhanced the impact strength to 7.04 J/cm2. Hardness of CF/E increased from 53.6 HRBS to 58.3 HRBS when 0.1% GO was added, further addition of 2%SiO2 aised the hardness to 69.8 HRBS.
It can be seen that the increment in mechanical properties of the CF/E composites were attributed to the reinforcing ability of the GO and SiO2 fillers. The addition of GO and SiO2 had successfully enhanced the aforementioned properties due to the reinforced ability of fillers that was associated to the higher modulus and rigidity of composites[28-29]. Fillers had filled in the free volume in the epoxy matrix, which restricted the polymer chain movement, decreased the polymer chain mobility, and increased hardness and stiffness[30]. The enhancement of mechanical properties could also attributed to the mechanical interlocking between polymer chains. When the fillers were added in the CF/E composites system, the polymer chain movement was restricted, which increased the resistance of composites toward deformation.
Furthermore, the small size of SiO2 nanofiller facilitated the process of composite fabrication with better dispersion of fillers due to less possibility of agglomeration. The great quality of fillers distribution in the matrix can increase the surface area availability of fillers, which indicated higher degree cross linking, homogeneous dispersion, and potential interfacial interaction of fillers-matrix via covalent bonding. The better interfacial interaction facilitated the effective stress transfer across matrix and fillers interface[31-32] and led to a higher flexural, stiffness, toughness, and hardness in the matrix system. The nanofillers can fill the voids between bigger fillers, minimize the accumulation of stress concentration, and reduce distance between neighboring filler[33-35]. They necessitated a postponement of the composite material damages such as interfacial de-bonding between fiber and matrix, extended crack propagation route, and durable larger deformation. It can be observed that the CF/E/0.1GO/2SiO2 with the most optimum fillers loading improved three different aspects of mechanical properties.
3.2 Dynamic Mechanical Analysis (DMA)DMA study was used to derive the information of storage modulus (E') and tanδ of these composites. The E' as a function of temperature is an indication of degree of interaction between fillers and matrix phase[36], as shown in Fig. 2(a). CF/E showed the minimum storage modulus of 38.03 GPa, while that of CF/E/0.1GO/2SiO2 increased by approximately 26% and reached the maximum level at 47.90 GPa. Both GO and SiO2 fillers had filled free voids volume of matrix which restricted the molecular chain motion as a result of high compatibility[37-38]. The increment of E' was further attributed to the better interfacial interaction between matrix and fillers improved the efficiency of stress transfer from matrix to fillers[39-40]. Storage modulus started to decrease with higher temperature due to the increase of polymer molecules mobility, which might cause deformations and matrix breakup because of low interfacial interaction between fillers and composite materials[37-41].
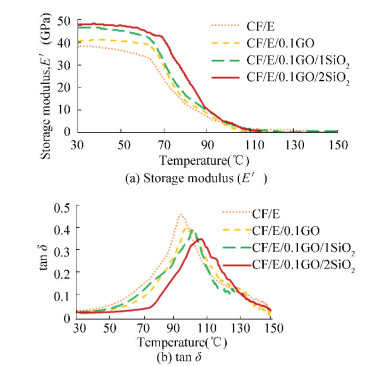
|
Figure 2 Dynamic mechanical properties of the effects of GO and SiO2 loading on CF/E composites |
It can be seen that the intensity of tanδ moderately declined with the addition of GO and SiO2 fillers. The tanδ of CF/E presented the highest peak at the value of 0.467, while CF/E/0.1GO/2SiO2 indicated the lowest peak value of tanδ at 0.357. GO and SiO2 fillers can restrict the chain mobility of polymer materials, result in higher E' and lower tanδ value, and reduce viscoelasticity[40]. The peak intensity of tanδ reflects the stiffness of composites while the lower tanδ peak intensity represents the higher stiffness[39-42]. The addition of GO and SiO2 fillers were capable of enhancing the stiffness of CF/E, so CF/E/0.1GO/2SiO2 indicated the stronger and stiffer composites compared to other specimens. CF/E/0.1GO/2SiO2 with lower peak intensity of tanδ showed better filler-matrix interaction. The better stress transfer in filler-matrix interface result in the increase of E' and damping properties[43].
The maximum glass transition temperature (Tg) of the composites increased as the fillers loading increase, which can be determined from the peak position of tanδ(Table 3). Fig. 2(b) shows the Tg shifted to the right with increasing filler loading, the enlargement of Tg can be observed. Tg of CF/E was at 94.35 ℃, while Tg of CF/E/0.1GO/2SiO2 increased up to 106.85 ℃, approximately 12.5 ℃ higher than that of CF/E. The addition of GO and SiO2 into composites had reduced the free volume of the epoxy matrix that can increase the chain interlocking. It also shifted tanδ of polymer composites to the higher temperature due to the reinforcing effect of fillers that restricted polymer molecular chain motion[44]. Hence, the higher Tg represented great compatibility and the better fillers-matrix interfacial interaction was. Moreover, the shifting of tanδ to the higher temperature was asociated with the lower free volume of the composites due to the addition of fillers. Therefore, it minimizes free volume restricts of polymer chain mobility due to the higher cross linking and better dispersion, and results in strengthened polymer compact structural material required much more energy to activate the segmental motion of the chain mobility[45]. The study shows that the limitation of chain mobility can cause the changes in mechanical and thermal properties.
| Table 3 Dynamic mechanical properties properties as effect of different GO and SiO2 loading of CF/E composites |
3.3 Analysis of Hygroscopic Aspect
The hygroscopic properties of GO/SiO2 filled CF/E composite were investigated by immersing in DI water and salt water for 2 weeks. As shown in Fig. 3, The maximum moisture absorption (Mm) of specimens reached their saturation state between 0.51% and 0.81% for DI water and between 0.47% and 0.73% for salt water after 14 days of immersion. Due to water absorption and loss in specimen's weight caused by leaching of the monomer, specimens' weight is increased[46]. The Mm of polymer composite materials can be governed by several factors due to the free and reactive hydroxyl groups of the fillers particles which exhibit great solubility in polar solvents such as water molecules. Moreover, the different chemical nature of fillers and matrix also exhibit the micro-sized free voids volume which formes weak bonding area, reduce the interfacial strength of fibre-matrix, and damage interfacial interaction between both hydrophilic GO and SiO2 fillers and hydrophobic epoxy matrix. Hence, the weak-link provides diffused route for water molecules, so water can penetrate into the micro-sized voids or accumulate at the filler-matrix interfaces. Excessive water absorption can degrade laminates because the nanocomposite structure breaks down and causes filler-matrix debonding in the ubiquity of porosity and filler particle aggregates. This chemical degradation at the interface between fillers and matrix may cause non-Fickian diffusion[47]. Even though water diffusion initially based on Fick's law, the excessive moisture uptake has an ability to diffuse into free volumes along the fillers-matrix interface, as bulk resin causes the changes in the internal stress-state of interphase areas and debonding of porosity and filler particle aggregates can break down the structural materials.
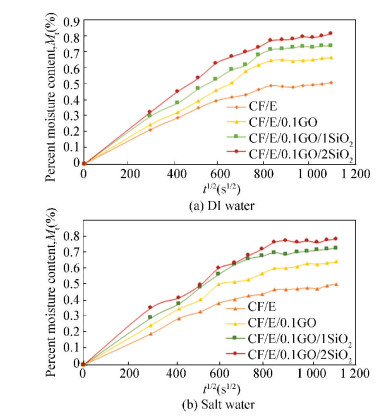
|
Figure 3 Moisture absorption curves of the effects of GO and SiO2 loading on CF/E composites |
Due to the hydrophilic properties of GO and SiO2 fillers, the percentage moisture absorption (Mm) of CF/E/0.1GO/2SiO2 was higher than those of other conditions in both of two different solvents. Fig. 3(b) shows the moisture absorption behavior of the specimens in salt water, illustrating a similar trend as in DI water (Fig. 3(a)). However, the absorption rate of specimens under salt water was slightly lower than those specimens immersed in DI water. The effect of moisture within the polymer composite systems changed both chemical and physical characteristics due to the plasticizing effect in the interphase of epoxy matrix, which led to reducing the efficiency of fibre-matrix adhesion, propagating of micro-cracks, and degradation of the whole material structure performances[48].
The Fickian diffusion of all types of specimens in both DI water and salt water was used to determine the diffusion coefficient (D) and the average percentages mass loss (Ml), as shown in Table 4. In both cases of DI water and salt water, CF/E presented the lowest diffusivity because of hydrophobic behavior of epoxy matrix, while the maximum D was shown in CF/E/0.1GO/2SiO2. Due to the effect of hydrophilicity of the GO and SiO2 fillers, the water had diffused into the free micro-voids and fillers themselves that were controlled by the available hydrogen bonding. Based on Fickian's law, the changing of Ml is caused by moisture penetration along the fiber polymer interface, porosity in the resin matrices, and crack or delamination of materials. The maximum Ml was 0.51% in DI water and 0.49% in salt water for CF/E, while CF/E/0.1GO/2SiO2 showed the minimum Ml of 0.28% in DI water and 0.33% in salt water of their initial mass. Even though the addition of fillers GO and SiO2 into CF/E had increased the Mm, the results of dry mass loss was lower than that of CF/E due to the effect of hydrophilic properties of both GO and SiO2 nanofillers. It indicated that GO and SiO2 fillers had an ability to prevent the material structural delamination much better than conventional CF/E composites.
| Table 4 The maximum moisture absorption (Mm), diffusivity (D), and mass loss (Ml) of the effects of GO and SiO2 loading on CF/E composites immersed in DI water and saturated solution of salt water at 90 ℃ |
3.4 Effects of Water Absorption on the Flexural and Impact Properties
After being subjected to moisture absorption for 14 days, the CF/E composites with and without nanofiller showd varying degrees of gradual deterioration in flexural and impact properties, which was determined in two different solvents (DI water and salt water) in wet and redried states, the obtained data was collected in Table 5.
| Table 5 Flexural and impact properties of the effects of GO and SiO2 loading on CF/E composites in wet and re-dried states after being subjected to moisture absorption for 2 weeks |
The percentage of retention indicates the degradation of flexural and impact properties of wet specimens. The water molecule can lead to plasticizing effect in the composites and diminish fillers-matrix interfacial bonding because of mismatch of the mositure induced by volume expansion within both phases. Thus, the water molecules can be accommodated at the interface between the filler and matrix through a weak link that provide paths of active water molecule diffusion, resulting in mismatch of the moisture between matrix and fillers[49]. The filler agglomeration and entanglement in the polymer chains, which significantly affect to the relaxation of molecular chains of polymers and influence the water molecules absorption, could generate greater micro-voids.
As shown in percentage of recovery, it can be observed that the effect of moisture on mechanical properties of composites was almost fully recovered after redrying process due to the continuous polymerization of polymers[50]. The leaching of residual monomer that may act as plasticizer after water storage would contribute to flexural and impact properties recovering[51]. On the other hand, the elevated temperature during drying process also produces irreversible effect because of the chemical degradation of matrix and partially breaking down of the component in the polymer composites. The cooling down process of polymer composites can minimize the efficiency of mechanical interlocking between fibre and matrix interface induced by the differences in thermal expansion coefficients between two different components.
The moisture-induction also caused the interfacial damage due to the presence of the internal stress state or residual stresses in the interphase region. Promoting chain expansion and reducing fibre-matrix adhesion or failure of fibre-matrix interphase, these effects had much more chances to produce internal voids of the entangled polymer chains, which causes the formation and propagation of micro-cracks, mechanisms damages and polymer composite performance degradations. Therefore, debonding of the interphase region due to aforementioned moisture and thermal effects on the polymer composites results in an irreversible damage. Compared with DI water, the salt water showed less effects on flexural and impact properties. Even though an irreversible loss of the composites mechanical properties caused by the moisture absorption effects, CF/E/0.1GO/2SiO2 still indicated the best mechanical performances.
3.5 Morphological AnalysisTo understand themechanical properties of CF/E hybrid composites with GO and SiO2 nanofillers in an visible way, FESEM was employed to take micrographes from the fracture surfaces of CF/E based composites, predominantly to characterize the pregression of interfacial debonding with the noticeable gap between fibre and epoxy resin that resultes in impact fracture toughness degradation. Fig. 4 illustrates the simultaneous breakage of fibres and debonding of fibre-matrix with better composite interfaces. It can be seen that GO and SiO2 fillers were embedded into the epoxy matrix with homogenous distribution and strengthened chemical bonding of hydrogen and covalent bonding, resulting in the stronger bonding at the interfacial adhesion region[52].

|
Figure 4 Impact fracture surface of the effects of GO and SiO2 loading on CF/E composites |
Upon the failure of hybrid carbon fiber epoxy composites, fibers were still tightly bonded together with less voids and cracks in the interfaces, which was the reason for the increase in surface roughness, hence the resin still firmly attached with the fibres after impact test, so that the synergy between GO and SiO2 particles had enhanced durability, interfacial impact fracture interaction and strengthened interfacial bonding area to hold carbon fibre and epoxy matrix together. Moreover, these nanofillers had also induced the deflection of propagating crack route, slowed down the advancing of crack front, and effectively promoted better toughening effect[38]. These aforementioned reasons are in good agreement with the improvement of flexural and toughness properties.
As a result, the physiomechanical properties of the agglomerates such as the size, surface roughness, porosity as well as flexural and impact behaviours were evaluated for different hybrid carbon fibre epoxy composites. The size, surface roughness, and porosity of agglomerates increased with the presence of polymer matrix reinforced by fillers owing to their changes in material behavior. Therefore, the random and agglomerated GO filler in the interfacial interaction and non-homogeneous epoxy distribution on the surface of carbon fibre could act as a type of stress concentration. It caused the damage in fiber and matrix, failure of filler-matrix bonding and elements breaking down. This extent damages can have a negative effect on the repeated load life, residual strength, and damage tolerance, resulting in the interfacial bonding strength reduction and mechanical properties degradation including flexural and impact properties. Hence, the optimum of GO filler loading was 0.1%, SiO2 was added as a second fillers that can further enhance the mechanical properties without GO agglomertion.
4 ConclusionsGraphene oxide and silica nanoparticles were added into carbon fiber epoxy composites by VARTM method with the objective of improving the potential of mechanical properties. The incorporation of 0.1 wt% GO showed noteworthy enhancement of mechanical properties including 5.23% in flexural strength, 9.13% in flexural modulus, 5.74% in impact strength, and 8.77% in hardness over unmodified CF/E composites. By continuing to add 2 wt% SiO2 in the composite system, flexural strength, flexural modulus, impact strength and hardness further heightened by approximately 18.17%, 26.69%, 11.69%, and 30.22%. Meanwhile, DMA showed a 12.5 ℃ increase of Tg for CF/E/0.1GO/2SiO2. The inclusion of SiO2 had boosted the mechanical properties (with/without temperature effect) over CF/E/GO composites, while GO had comforted SiO2 nanofillers distribution in the epoxy. The moisture absorption behavior of CF/E reinforced with GO and SiO2 nanofillers presented the degradation in flexural and impact properties; however, CF/E/0.1GO/2SiO2 exhibited the strongest resistance to this degradation compared to other batches.
The good performance of CF/E composite with bi-hybrid nanofillers originated from the synergistic GO and SiO2 nanofillers, which enabled better chemical bonding formation in the epoxy matrix and replenished porosities and voids fraction value. Due to the high degree cross-linking structure and homogeneous dispersion, they had also improved fillers-matrix interfacial interaction and strengthened polymer structural materials. Both GO and SiO2 nanofillers had the capacity to limit the motion of epoxy polymer molecular chain, resulting in remarkable compatibility and preferable stiffness of the matrix system due to the sufficient stress transfer in the composite system. These aforementioned reasons could attribute to the significant retention and recovery of GO and SiO2 in CF/E composites on mechanical properties.
In summary, the synergy of GO and SiO2 nanoparticles had established the possibility of new CF/E laminates which could be considered as potential additive nanofillers to promote the development in different advanced performance composite materials. This study will contribute to the great knowledge in development of hybrid composite materials with essentially enhanced mechanical properties including function of temperature and moisture for various industrial applications.
AcknowledgmentsThe authors would like to thank Kelvin Ng for the useful revision of English.
| [1] |
Sguvajynar Gouda P S, Kulkarni R, Kurbet S N, et al. Effects of multi walled carbon nanotubes and graphene on the mechanical properties of hybrid polymer composites. Advanced Materials Letters, 2013, 4(4): 261-270. DOI:10.5185/amlett.2012.9419 (  0) 0) |
| [2] |
Dinca I, Ban C, Stefan A, et al. Nanocomposites as advanced materials for aerospace industry. Incas Bulletin, 2012, 4(4): 57-72. DOI:10.13111/2066-8201.2012.4.4.6 (  0) 0) |
| [3] |
Masuelli M A. Introduction of fibre-reinforced polymers-polymers and composites: Concepts, properties and processes. Fiber Reinforced Polymers-The Technology Applied for Concrete Repair, 2013, 3-40. DOI:10.5772/54629 (  0) 0) |
| [4] |
Di Sante R. Fibre optic sensors for structural health monitoring of aircraft composite structures: Recent advances and applications. Sensors, 2015, 15(8): 18666-18713. DOI:10.3390/s150818666 (  0) 0) |
| [5] |
Masoodi R, El-Hajjar R F, Pillai K M, et al. Mechanical characterization of cellulose nanofiber and bio-based epoxy composite. Materials & Design, 2012, 36: 570-576. DOI:10.1016/j.matdes.2011.11.042 (  0) 0) |
| [6] |
Chen C, Justice R S, Schaefer D W, et al. Highly dispersed nanosilica-epoxy resins with enhanced mechanical properties. Polymer, 2008, 49(17): 3805-3815. DOI:10.1016/j.polymer.2008.06.023 (  0) 0) |
| [7] |
Preghenella M, Pegoretti A, Migliaresi C. Thermo-mechanical characterization of fumed silica-epoxy nanocomposites. Polymer, 2005, 46(26): 12065-12072. DOI:10.1016/j.polymer.2005.10.098 (  0) 0) |
| [8] |
Silva L J D, Panzera T H, Velloso V R, et al. Hybrid polymeric composites reinforced with sisal fibres and silica microparticles. Composites Part B:Engineering, 2012, 43(8): 3436-3444. DOI:10.1016/j.compositesb.2012.01.026 (  0) 0) |
| [9] |
Zhao R, Luo W. Fracture surface analysis on nano-SiO2/epoxy composite. Materials Science & Engineering A, 2008, 483-484(1): 313-315. DOI:10.1016/j.msea.2006.08.151 (  0) 0) |
| [10] |
Gowthami A, Ramanaiah K, Ratna Prasad A V, et al. Effect of silica on thermal and mechanical properties of sisal fiber reinforced polyester composites. Journal of Materials & Environmental Science, 2013, 4(2): 199-204. (  0) 0) |
| [11] |
Tsai J L, Huang B H, Cheng Y L. Enhancing fracture toughness of glass/epoxy composites by using rubber particles together with silica nanoparticles. Journal of Composite Materials, 2009, 43(25): 3107-3123. DOI:10.1177/0021998309345299 (  0) 0) |
| [12] |
Ajaj E A, Jubier N J, Majeed K J. Fatigue behavior of epoxy/SiO2 nanocomposites reinforced with e-glass fiber. International Journal of Application or Innovation in Engineering and Management (IJAIEM), 2013, 2(9): 62-69. (  0) 0) |
| [13] |
Ahmad F N, Jaafar M, Palaniandy S, et al. Effect of particle shape of silica mineral on the properties of epoxy composites. Composites Science & Technology, 2008, 68(2): 346-353. DOI:10.1016/j.compscitech.2007.07.015 (  0) 0) |
| [14] |
Balakrishnan S, Start P R, Raghavan D, et al. The influence of clay and elastomer concentration on the morphology and fracture energy of preformed acrylic rubber dispersed clay filled epoxy nanocomposites. Polymer, 2005, 46(25): 11255-11262. DOI:10.1016/j.polymer.2005.10.053 (  0) 0) |
| [15] |
Geim A K. Science, Graphene: Status and Prospects. Science, 2009, 324(5934): 1530-1534. DOI:10.1126/science.1158877 (  0) 0) |
| [16] |
Kuilla T, Bhadra S, Yao D, et al. Recent advances in graphene based polymer composites. Progress in Polymer Science, 2010, 35(11): 1350-1375. DOI:10.1016/j.progpolymsci.2010.07.005 (  0) 0) |
| [17] |
Gao W. The Chemistry of Graphene Oxide. In: Gao W. (eds)Graphene Oxide. Cham: Springer, Cham, 2015. DOI: 10.1007/978-3-319-15500-5_3.
(  0) 0) |
| [18] |
Du J, Cheng H M. The Fabrication, properties, and uses of graphene/polymer composites. Macromolecular Chemistry & Physics, 2012, 213(10-11): 1060-1077. DOI:10.1002/macp.201200029 (  0) 0) |
| [19] |
Allaoui A, Bai S, Cheng H M, et al. Mechanical and electrical properties of a MWNT/epoxy composite. Composites Science & Technology, 2002, 62(15): 1993-1998. DOI:10.1016/s0266-3538(02)00129-x (  0) 0) |
| [20] |
Abdullah S I, Ansari M N M. Mechanical properties of graphene oxide (GO)/epoxy composites. Hbrc Journal, 2015, 11(2): 151-156. DOI:10.1016/j.hbrcj.2014.06.001 (  0) 0) |
| [21] |
Norhakim N, Hj Ahmad S, Chia C H, et al. Mechanical and thermal properties of graphene oxide filled epoxy nanocomposites. Sains Malaysiana, 2014, 43(4): 603-609. (  0) 0) |
| [22] |
Jr Hummers W S, Offeman R E. Preparation of graphitic oxide. Journal of the American Chemical Society, 1958, 80(6): 1339. DOI:10.1021/ja01539a017 (  0) 0) |
| [23] |
ASTM International. ASTM D7264/D7264M -15, Standard test method for flexural properties of polymer matrix composite materials. West Conshohocken, PA: ASTM International, 2015. DOI: 10.1520/d7264_d7264m-06.
(  0) 0) |
| [24] |
ASTM International. ASTM D6110-10, Standard Test Method for Determining the Charpy Impact Resistance of Notched Specimens of Plastics. West Conshohocken, PA: ASTM International, 2010. DOI: 10.1520/d6110-10.
(  0) 0) |
| [25] |
ASTM International. ASTM D785-08, Standard Test Method for Rockwell Hardness of Plastics and Electrical Insulating Materials. West Conshohocken, PA: ASTM International, 2015. DOI: 10.1520/d0785-08.
(  0) 0) |
| [26] |
ASTM International. ASTM D7028-07, Standard test method for glass transition temperature (DMA Tg) of polymer matrix composites by dynamic mechanical analysis (DMA). West Conshohocken, PA: ASTM International, 2008. DOI: 10.1520/d7028-07e01.
(  0) 0) |
| [27] |
ASTM International. ASTM D5229/D5229M - 14, Standard test method for moisture absorption properties and equilibrium conditioning of polymer matrix composite materials. West Conshohocken, PA: ASTM International, 2014. DOI: 10.1520/d5229_d5229m-92r04.
(  0) 0) |
| [28] |
Medhekar N V, Ramasubramaniam A, Ruoff R S, et al. Hydrogen bond networks in graphene oxide composite paper: Structure and mechanical properties. ACS Nano, 2010, 4(4): 2300-2306. DOI:10.1021/nn901934u (  0) 0) |
| [29] |
Ajaj E A, Jubier N J, Majeed K J. Fatigue behavior of epoxy/SiO2 nanocomposites reinforced with e-glass fiber. International Journal of Application or Innovation in Engineering & Management (IJAIEM), 2013, 2: 62-69. (  0) 0) |
| [30] |
Essabir H, Raji M, Bouhfid R, et al. Nanoclay and Natural Fibers Based Hybrid Composites: Mechanical, Morphological, Thermal and Rheological Properties. In: Jawaid M, Qaiss A, Bouhfid R. (eds) Nanoclay Reinforced Polymer Composites. Engineering Materials. Singapore: Springer, Singapore, 2016. 29-49. DOI: 10.1007/978-981-10-0950-1_2.
(  0) 0) |
| [31] |
Norhakim N, Hj Ahmad S, Chia C H, et al. Mechanical and thermal properties of graphene oxide filled epoxy nanocomposites. Sains Malaysiana, 2014, 43(4): 603-609. (  0) 0) |
| [32] |
Glaskova T, Zarrelli M, Aniskevich A, et al. Quantitative optical analysis of filler dispersion degree in MWCNT-epoxy nanocomposite. Composites Science & Technology, 2012, 72(4): 477-481. DOI:10.1016/j.compscitech.2011.11.029 (  0) 0) |
| [33] |
Izzati W A, Arief Y Z, Adzis Z, et al. Partial discharge characteristics of polymer nanocomposite materials in electrical insulation: a review of sample preparation techniques, analysis methods, potential applications, and future trends. The Scientific World Journal, 2014, 2014(21): Article ID 735070. DOI:10.1155/2014/735070 (  0) 0) |
| [34] |
Marghalani H Y. Effect of filler particles on surface roughness of experimental composite series. Journal of Applied Oral Science, 2010, 18(1): 59-67. DOI:10.1590/s1678-77572010000100011 (  0) 0) |
| [35] |
Mollo M, Bernal C. Polymer Nanocomposites for Structural Applications. In: Mohanty S, Nayak S K, Kaith B S, et al. (eds. ) Polymer Nanocomposites Based on Inorganic and Organic Nanomaterials. Hoboken: John Wiley & Sons, Inc. 2015. 505-518. DOI: 10.1002/9781119179108.ch14.
(  0) 0) |
| [36] |
Ganguli S, Roy A K, Anderson D P. Improved thermal conductivity for chemically functionalized exfoliated graphite/epoxy composites. Carbon, 2008, 46(5): 806-817. DOI:10.1016/j.carbon.2008.02.008 (  0) 0) |
| [37] |
Martí-Ferrer F, Vilaplana F, Ribes-Greus A, et al. Flour rice husk as filler in block copolymer polypropylene: Effect of different coupling agents. Journal of Applied Polymer Science, 2010, 99(4): 1823-1831. DOI:10.1002/app.22717 (  0) 0) |
| [38] |
Chen L, Chai S, Liu K, et al. Enhanced epoxy/silica composites mechanical properties by introducing graphene oxide to the interface. ACS Applied Materials & Interfaces, 2012, 4(8): 4398-4404. DOI:10.1021/am3010576 (  0) 0) |
| [39] |
Rana A K, Mitra B C, Banerjee A N. Short jute fiber-reinforced polypropylene composites: Dynamic mechanical study. Journal of Applied Polymer Science, 2015, 71(4): 531-539. DOI:10.1002/(sici)1097-4628(19990124)71:4<531::aid-app2>3.0.co;2-i (  0) 0) |
| [40] |
Ray D, Sarkar B K, Das S, et al. Dynamic mechanical and thermal analysis of vinylester-resin-matrix composites reinforced with untreated and alkali-treated jute fibres. Composites Science & Technology, 2002, 62(7-8): 911-917. DOI:10.1016/s0266-3538(02)00005-2 (  0) 0) |
| [41] |
Sperling L H. Introduction to Physical Polymer Science, 4th Edition. Hoboken: Wiley, 1986.
(  0) 0) |
| [42] |
Ratna D, Divekar S, Samui A B, et al. Poly(ethylene oxide)/clay nanocomposite: Thermomechanical properties and morphology. Polymer, 2006, 47(11): 4068-4074. DOI:10.1016/j.polymer.2006.02.040 (  0) 0) |
| [43] |
Martínez-Hernández A L, Velasco-Santos C, De-Icaza M, et al. Dynamical-mechanical and thermal analysis of polymeric composites reinforced with keratin biofibers from chicken feathers. Composites Part B: Engineering, 2007, 38(3): 405-410. DOI:10.1016/j.compositesb.2006.06.013 (  0) 0) |
| [44] |
Alexandre M, Dubois P. Polymer-layered silicate nanocomposites: preparation, properties and uses of a new class of materials. Materials Science & Engineering:R: Reports, 2000, 28(1-2): 1-63. DOI:10.1016/s0927-796x(00)00012-7 (  0) 0) |
| [45] |
Dixit M, Gupta S, Mathur V, et al. Study of glass transition temperature of PMMA and CdS-PMMA composite. Chalcogenide Letters, 2009, 6(3): 131-136. (  0) 0) |
| [46] |
Harper E J, Braden M, Bonfield W. Mechanical properties of hydroxyapatite reinforced poly (ethylmethacrylate) bone cement after immersion in a physiological solution: influence of a silane coupling agent. Journal of Materials Science Materials in Medicine, 2000, 11(8): 491-497. DOI:10.1023/A:1013057724268 (  0) 0) |
| [47] |
Shirangi M H, Michel B. Mechanism of Moisture Diffusion, Hygroscopic Swelling, and Adhesion Degradation in Epoxy Molding Compounds. In: Fan X., Suhir E. (eds) Moisture Sensitivity of Plastic Packages of IC Devices. Micro-and Opto-Electronic Materials, Structures, and Systems. Boston: Springer, Boston, MA, 2010. 29-69. DOI: 10.1007/978-1-4419-5719-1_2.
(  0) 0) |
| [48] |
Söderholm K J M, Roberts M J. Influence of water exposure on the tensile strength of composites. Journal of Dental Research, 1990, 69(12): 1812. DOI:10.1177/00220345900690120501 (  0) 0) |
| [49] |
Sabbagh J, Vreven J, Leloup G. Dynamic and static moduli of elasticity of resin-based materials. Dental Materials, 2002, 18(1): 64-71. DOI:10.1016/s0109-5641(01)00021-5 (  0) 0) |
| [50] |
Söderholm K J, Roberts M J. Influence of water exposure on the tensile strength of composites. Journal of Dental Research, 1990, 69(12): 1812. DOI:10.1177/00220345900690120501 (  0) 0) |
| [51] |
Rui L R, Román J S. Biodegradable Systems in Tissue Engineering and Regenerative Medicine. Boca Raton: CRC Press, 2014.
(  0) 0) |
| [52] |
Saleem H, Edathil A, Ncube T, et al. Mechanical and Thermal Properties of Thermoset-Graphene Nanocomposites. Macromolecular Materials & Engineering, 2016, 301(3): 231-259. DOI:10.1002/mame.201500335 (  0) 0) |
 2018, Vol. 25
2018, Vol. 25


