2. Aerospace System Engineering Shanghai, Shanghai 201108, China
Control Moment Gyroscope is a kind of spacecraft attitude control actuator[1-2]. It has the absolute advantage of powerful torque amplification capacity over Reaction Wheel (RW), thruster, magnetic torquer, etc.CMG, owing to its efficiency, plays a significant role in large spacecraft attitude control[2-7]. Besides, large-angle maneuver, multi-target acquisition and pointing of agile satellite also rely on great output torque of CMG.Both Skylab and Salyut Space Station employed CMG system, and the International Space Station (ISS) took benefit on double gimbal control moment gyroscope[8-9].The World View series satellites launched by the Digital Globe and Ball Aerospace and Technology Corporation could capture High Resolution (HR) images for their agility. World View 4 (Fig. 1, launched in 2016/11/11) is the most advanced agile satellite and World View 1 (Fig. 2, launched in 2001) is the first commercial HR satellite actuated by CMG[10]. Table 1 illustrates some properties of Pléiades-HR imaging satellites, Pléiades-1 and Pléiades-2[11-13].What we can find is that their rapid maneuver capability is beyond tradition satellites′. Tiangong 1 and Tiangong 2 were also equipped with several single gimbal control moment gyros.

|
Fig.1 World View 4 satellite |

|
Fig.2 World View 1 satellite |
| Table 1 Pléiades-HR imaging satellite property |
Bong Wie[14] predicted that the future space mission would have a slew rate requirement of 6 °/s for the next generation earth observation and imaging satellite to get HR image. It is obvious that CMG would draw the attention of researchers in the future[8, 15].
Generally, CMGs are mounted into particular group, known as CMG configuration, with a certain number and structure according to different task requirements[16-17].The configuration varies to satisfy different conditions. The pyramid configuration, more practically, with four CMGs mounted as a rectangular pyramid for 3-axis control is the mini-redundant group. Most scientific theoretical studies and practical experiments adopt this configuration due to its functional integrity, theoretic maturity and structural simplicity and symmetry. Other configurations with more than 4 CMG units or less than 3 units (non-redundant configuration) are also studied.
The most serious situation, however, in using CMG is the inherent geometric singularity problem in which there is no torque output in particular direction, meaning an uncontrollable sate[4, 8, 16].Based on the consideration above, it urges investigators to make clear and distinguish the singularity problem and steer CMG with an excellent performance somehow. Theories and strategies change and vary for CMG singularity analysis. Different approaches can give a unique insight into singularity description and depiction. Meanwhile corresponding CMG steering logic/law would emerge consequently. Some new modern methods, rather than the classical techniques like Null Motion[3, 6, 18-21] and Singularity Value Decomposition (SVD)[22-23], are employed to CMG such as game theory[24] and differential geometry[19, 21, 25]. All of those techniques and strategies establish the comprehensive CMG theoretical framework.
Many literatures are studied to setup an integrated system for SGCMG in this work and their core ideas are reorganized by certain principles. The rest of this paper is briefly outlined as follows. In Section 2, different CMG configurations are presented after the discussion of CMG fundamentals, as well as the CMG configuration evaluation methods. Section 3 summarizes four different CMG modeling methods, examined by some CMG clusters in Section 2. Section 4 presents the visualization tools to form and depict the intuitional impression of the CMG singular moment surface. Based on this surface, different approaches are used for singularity analysis. In Section 5, different CMG steering logics/laws are compared and analyzed in terms of their errors and singularity escaping ability. Section 6 summarizes the entire work with some proposals for future research.
2 CMG ConfigurationThis section will focus on the configuration and evaluation of CMG, while some fundamentals will also be presented to provide comprehensive and systematic CMG basic knowledge for CMG dynamic modeling in next section.
2.1 CMG FundamentalsActive attitude control actuators of modern spacecraft can be categorized into 3 main groups, including moment exchanging actuator, mass expulsion actuator and environment interactive actuator.Thruster categorized into the 2nd type depends on propellant or fuel consumption to generate control torque. However, propellant can not be replenished on orbit. In spite of considerable torque, the short-term operating life prevents its implementation in agile spacecraft. The magnetic torquer and reaction wheel, the representative of the 3rd and 1st type respectively, are energy-efficient without the requirement of chemical propellant consumption, making they can work in long-term space missions. However, their output torque is relatively small and does not meet the spacecraft rapid maneuver requirements, even without consideration of reaction wheel dead zone and saturation problems[15].
While the CMG, especially the SGCMG, a kind of moment exchanging actuator, performs well to improve the agility of spacecraft.Although the singularity is serious and intractable, it can be escaped by certain logics.
A CMG consists of 3 main parts as presented in Fig. 3.

|
Fig.3 Single gimbal control moment gyroscope |
1) A Flywheel which holds on a constant angular momentum magnitude;
2) A Gimbal which supports the flywheel;
3) A Gimbal Motor which changes the gimbal direction (the direction of flywheel momentum) to generate the desired torque according to the control torque command.
CMG tracks the control signal by exchanging the momentum with the spacecraft, the same way as RW.What distinguishes CMG and RW is the way of momentum changing, direction or magnitude.
According to the mechanical characteristics, CMG can be characterized into 3 types as presented in Fig. 4.

|
Fig.4 Different types of control moment gyroscope |
1) Single Gimbal Control Moment Gyroscope, only one degree of freedom (DOF)exists for momentum direction.
2) Double Gimbal Control Moment Gyroscope, (DGCMG), two gimbals (inner and outer)are mounted so that the output torque would be generated for two DOFs.
3) Variable Speed Control Moment Gyroscope, (VSCMG), both the magnitude and direction of flywheel momentum vector could bechanged.
It is extremely clear that DGCMG and VSCMG have 2 DOFs, with thus more mechanical and dynamical complexity.SGCMG has been studied more frequently and comprehensively because of the structural simplicity, light mass and in particular the powerful output capacity. In following text, unless otherwise mentioned, CMG refers to SGCMG.
The CMG operation mechanism is illustrated in Eq.(1):
| $ \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{\dot \delta }} \times \mathit{\boldsymbol{h}} $ | (1) |
where
To achieve 2-axis or 3-axis attitude maneuver and stabilization control of spacecraft, CMGs should be mounted into specific arrays or configurations.
Three-axis attitude control requires at least 3 CMGs. When taking system reliability into consideration, we could find only redundant arrays are practicable. The same concern will be involved in this paper and more texts will be occupied by redundant CMG. That does not mean we will pay no attention to non-redundant arrays, since the redundant clusters is the extension and expansions of non-redundant arrays.
2.2.1 Non-redundant CMG configurationThe choice of redundant or non-redundant configurationis are determined by specific space requirements and the cost. Most agile imaging satellites, such as the earth observing satellite, only have a large torque requirement along the roll and pitch axes. So the advisable strategy is to employ 2 or 3 CMGs with the parallel gimbal axis for roll and pitch axes control, while RW can be mounted to track the yaw axis command with a relatively smaller torque[21].
Fig. 5 shows a 3-parallel CMG system, where the gimbal axes are parallel. It can generate 2 dimensional output torque lying in a plane perpendicular to the gimbal axis. Once the flywheel momentum direction of each CMG changes as commanded, the system will generate the desired torque.
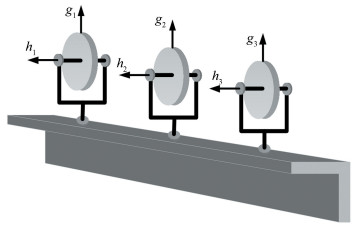
|
Fig.5 3-Parallel configuration CMG cluster |
2.2.2 Redundant CMG configuration
In general cases, large-angle maneuver, multi-target acquisition and reorientation are basic capacities of modern spacecraft. Obviously, non-redundant system may not be qualified for this kind of full axis maneuver missions[16-17].This requires some special and appropriate CMG clusters, especially the redundant clusters. We can not deny that some redundant CMG systems are upgrades of non-redundant arrays.
Most CMG researchers focus on the pyramid configuration(the min-redundant cluster). The regular pyramid is the main type, while other specific ones for the need of theoretical research are summarized as well, though they may never sever in any orbiting spacecraft.
A) Pyramid configuration.
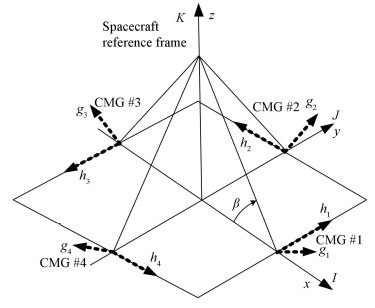
Pyramid configuration, as a representative of redundant type, also known as rectangular pyramid has been studied from the 1960s[26-29], which has a min-redundancy of one. In other words there are 4 CMGs, as illustrated in Fig. 6.
|
Fig.6 Pyramid configuration CMG cluster |
Fig. 6 depicts the pyramid or rectangular pyramid configuration, in which there are 4 SGCMG units mounted in an orthogonal relationship along the X and Y axis of Spacecraft Reference Frame(SRF).The four gimbal axes are normal to the pyramid side surfaces, respectively. And the angle β denotes the skew angle. Skew angle β varies in different cases, 53.13°, 54.73° and 60° are most common values.The Pléiades-HR satellites have employed pyramid cluster as attitude control actuator to get HR images.
It's obvious that pyramid configuration is symmetrical. Once unexpected disturbances acts on one CMG, the other 3 can track control command through reconstitution without loss of full axes control ability because of the redundancy.
Crenshaw[30] argued a special case of pyramid configuration (as illustrated in Fig. 7), β=90 °, named Two-Scisored-Pair-Ensemble, Explicit-Distribution, 2-SPEED. The gimbal axes lie along the SRF X and Y axes, resulting into two orthogonal pairs of two parallel CMG arrays.

|
Fig.7 2-SPEED cluster |
B) Tetrahedron configuration.
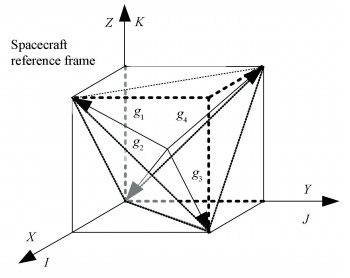
In Ref.[9], tetrahedron mount CMG clusters is given and is compared with the classical pyramid CMG array, as shown in Fig. 8.
|
Fig.8 Tetrahedron configuration CMG cluster |
The tetrahedron configuration, like the pyramid clusters, is a redundant 4-CMGs system. In this configuration, each gimbal axis is perpendicular to one surface of the tetrahedron. In Fig. 8, we may find that 4 CMGs shape like a methane. Each CMG is equivalent to each other in three dimensional space in terms of structure and function. Analysis implies that the momentum envelope of this configuration is much larger than the pyramid cluster's[9], owing to the symmetry. A larger momentum envelope indicates larger momentum storage capability.
C) 5-CMGs configuration.
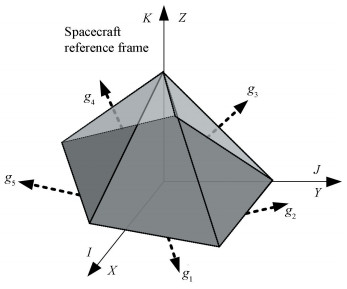
Apart from the 4-CMGs arrays, various 5/6-CMGs[4-5, 9]serve as a great part in theoretical and practical research.There is no doubt that the Five Pyramid Configuration (FPC)is the main role of 5-CMGs system expanded from pyramid cluster. Mounting a CMG with its gimbal axis lying along the Z axis of SRF in a pyramid cluster, we would get another 5-CMGs system (named as'Pyramid-Z' configuration). Fig. 9 and Fig. 10 represent the two clusters respectively.
|
Fig.9 Five pyramid configuration CMG cluster |

|
Fig.10 Pyramid-Z configuration CMG cluster |
The FPC shares similar properties, such as redundancy and mounting symmetry, with the pyramid configuration.
D) 6-CMGs configuration.
Inspired by extension of 4-CMGs system, one can derive some specific 6-CMGs configuration from 5-CMGs cluster. Definitely, hexagonal pyramid cannot be ignored.And, the FPC-Z configuration(with one CMG added in the FPC whose gimbal axis is parallel to the Z axis of the SRF)is the main part.
Other non-redundant arrays such as 2/3 parallel clusters can inspire us to obtain several very unique configurations. By adding 2 CMGs in the SPEED cluster with their gimbal axes parallel to the Z axis of SRF, we can obtain the cube configuration[9], as shown in Fig. 11.
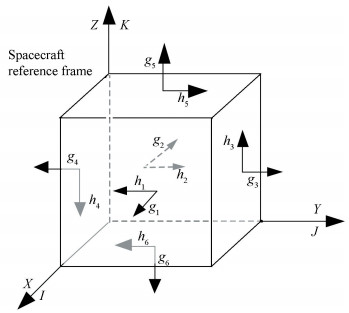
|
Fig.11 Cube configuration CMG cluster |
Double 3-parallel cluster, another example of the improvement of non-redundant arrays, can also serve as full axes control actuator[4-5], shown in Fig. 12.
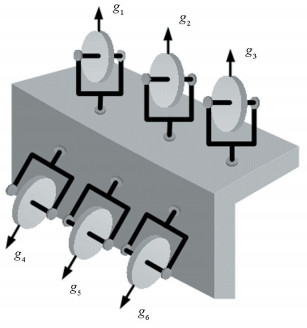
|
Fig.12 Double 3-parallel configuration CMG cluster |
Although one can argue that there are some More-Than-6-CMGs, more redundancy means more complexity in control algorithm and steering logic, larger payload and cost, which may counteract the agility of the spacecraft.The sphere configuration with infinite CMGs whose gimbal axes lie along the radius vector direction acquires greatest redundancy.
2.3 Evaluation of CMG ConfigurationThe CMG configuration efficiency and evaluation are essential for designing and evaluating an optimal configuration for a specific space mission.The evaluation system consists of static and dynamic indexes.The static indexes are determined by the configuration, while dynamic indexes characterize the performance of CMG cluster in mission phase. Configuration efficiency, controllable efficiency and failure efficiency are the three traditional static indexes[31-33]. However, the configuration efficiency is not normalized, and the controllable efficiency depends on the magnitude of the angular momentum envelope.The normalized indexes, capacity ratio and no-singular ratio, were proposed as a supplement[32].
2.3.1 Static indexIn this subsection we will discuss the static index without consideration of the CMG dynamic performance.All those evaluation criteria could help setup or select a kind of cluster for specific space mission.
A) Configuration efficiency.
Configuration efficiency denotes the ratio of the minimum momentum of the CMG cluster's momentum envelope or the radius of the inscribed sphere of the momentum envelope over the sum of angular momentum of each CMG, and is described as:
| $ \gamma = \frac{{\mathop {\min }\limits_\mathit{\boldsymbol{u}} \left[ {\mathop {\max }\limits_\mathit{\boldsymbol{\delta }} \left| {{\mathit{\boldsymbol{H}}_{{\rm{cmg}}}}\left( \mathit{\boldsymbol{\delta }} \right)} \right|} \right]}}{{\sum\limits_{i = 1}^n {{h_i}} }} $ | (2) |
where δ = (δ1, δ2, …, δn) is the gimbal angle of each CMG in the n-CMGs system. Hcmg is angular momentum of the CMG system represented in SRF, and its norm is | Hcmg (δ) | =(HcmgT Hcmg) 1/2. u ∈ R 3×1 is the unit vector of the angular momentum space and hi is the angular momentum magnitude of the ith flywheel.
A greater γ indicates larger space of system angular momentum and output torque for control.
B) Controllable efficiency.
The controllable efficiency refers to the ratio of the inscribed sphere of the nearest elliptic singular point (which cannot be treated by null motion) within the system angular momentum envelope over the sum of angular momentum of each CMG, and is described as:
| $ \chi = \frac{{\mathop {\min }\limits_{{\mathit{\boldsymbol{\delta }}_{ES}}} \left| {{\mathit{\boldsymbol{H}}_{{\rm{cmg}}}}\left( {{\mathit{\boldsymbol{\delta }}_{ES}}} \right)} \right|}}{{\sum\limits_{i = 1}^n {{h_i}} }} $ | (3) |
where δES is the elliptic singular gimbal angle set.
The controllable efficiency describes the maximum ideal CMG momentum motion space without any significant singular points, in which the singularity can be avoided through basic null motion to achieve high efficiency for CMG steering.
C) Failure efficiency.
It is hard to guarantee the reliability of each CMG in the cluster during the entire lifespan.The failure efficiency is the configuration efficiency of the new configuration with failure of one CMG.
| $ \lambda = \frac{{\mathop {\min }\limits_\mathit{\boldsymbol{u}} \left[ {\mathop {\max }\limits_{{\mathit{\boldsymbol{\delta }}^ * }} \left| {\mathit{\boldsymbol{H}}_{{\rm{cmg}}}^ * \left( {{\mathit{\boldsymbol{\delta }}^ * }} \right)} \right|} \right]}}{{\sum\limits_{i = 1}^{n - 1} {h_i^ * } }} $ | (4) |
where, the superscript (*) denotes the corresponding quantities in failure situation.
D) Singular loss ratio.
The difference between the configuration efficiency and the controllable efficiency is defined as the singular loss ratio, and is written as:
| $ \Delta = \gamma - \chi $ | (5) |
It characterizes the area where elliptic singular points appear intensively and restricts the non-singular motion of CMG. A lager Δ space raises greater challenge for CMG control.
E) Capacity ratio and no-singular ratio.
Using normalized method, Ref.[26] introduced other two static indexes.
Capacity ratio:
| $ {\eta _1} = \frac{\gamma }{{{\gamma _{\max }}}} = \frac{{\mathop {\min }\limits_\mathit{\boldsymbol{u}} \left[ {\mathop {\max }\limits_\mathit{\boldsymbol{\delta }} \left| {{\mathit{\boldsymbol{H}}_{{\rm{cmg}}}}\left( \mathit{\boldsymbol{\delta }} \right)} \right|} \right]}}{{\sum\limits_{i = 1}^n {{h_i}} }}\frac{4}{{\rm{ \mathit{ π} }}} $ | (6) |
No-singular ratio:
| $ {\eta _2} = \frac{\chi }{\gamma } $ | (7) |
where, γmax=π/4 corresponds to the sphere CMG configuration. Both capacity ratio and no-singular ratio are relative indexes and are more general.
2.3.2 Dynamic indexThe dynamic index refers to a measurement describing how singular the system is or how far the cluster will be in singularity[29]. And it is given by:
| $ \xi = \det \left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}}} \right) $ | (8) |
where, J ∈ R3×n is the Jacobian Matrix of the system with n CMGs.The index becomes zero only when the cluster encounters singularity. The index naturally is regarded as the measurement or ruler to describe the current state of CMG system.
2.4 Summary of ConfigurationFor different space mission requirements, researchers have studied various CMG clusters, among which no one can meet all control situation.So, it's significant to understand the unique characteristics of all the clusters.The advisable way is to make use of the evaluation method to choose the optimal array for specific requirements. Of all the clusters the pyramid cluster and FPC-Z cluster are most outstanding, in terms of the redundancy and efficiency. The future 3-axis scientific exploration should fully exploit these two arrays.Fig. 13 illustrates the relationship of extension, expansion and evolution among all the clusters, in which the same line style represents that the corresponding CMG configurations have similar characteristics.

|
Fig.13 CMG configuration relationship |
The efficiency of traditional configurations is summarized in Table 2.
| Table 2 Efficiency and evaluation for different CMG configurations |
As shown in Table 2, we can find that pyramid configurations (including the pyramid-Z cluster) have a lager configuration efficiency value meaning that these clusters have larger envelope for momentum movement in some degree.For the cube cluster, γ=χ, which implies that there is no internal elliptic singular point in the momentum and is a best case for CMG control. However, its failure efficiency is the least among 6-CMGs system as illustrated in Table 2, which means the reliability of the cube cluster is low. And the FPC-Z cluster system has the largest configuration efficiency as well as other indexes over the others.That's the reason why both Tiangong-1 and MIR space station adopted this kind of configuration.In general, the pyramid and FPC-Z clusters are two effective candidates for 3-axis control of agile spacecraft.
3 CMG Dynamic ModelingThe dynamic and mathematical model of the CMG cluster will be treated in this section. Several different CMG modeling methods are introduced for some unique CMG arrays.These methods or techniques will be examined by CMG clusters in Section 2.
3.1 CMG ModelThe so called dynamic model is used to determine the mathematical relationship between the input and output of a system.The gimbal rate and momentum or torque are two main quantities in CMG, corresponding to input and output respectively. In this paper the angular momentum of the gimbal frame is neglected, as the gimbal rate is much less than the speed of flywheel.
Hereafter, four modeling methods, including coordinate transformation method, configuration method, generalized constrain model and inverse kinematic model, will be introduced.
3.1.1 Coordinate transformation methodAccording to the relationship in Eq.(1) and the mechanical constraint (the orthogonality between gimbal axis and momentum of flywheel), a Gimbal Coordinate Frame (GCF)emerges logically, as illustrated in Fig. 3, where the { g, h, f } just lies along the unit vector {ig, jg, kg}.
Considering a cluster consists of n CMGs, there always exists a set of Euler Angles {φi, θi, ψi} to transfer current state of ith CMG state from its GCF to SRF, i=1, ..., n. The Direction Cosine Matrix (DCM) for this transformation is as follows:
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{J}}\\ \mathit{\boldsymbol{K}} \end{array}} \right] = \mathit{\boldsymbol{R}}\left( {{\varphi _i}} \right)\mathit{\boldsymbol{R}}\left( {{\theta _i}} \right)\mathit{\boldsymbol{R}}\left( {{\psi _i}} \right)\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{i}}_g}}\\ {{\mathit{\boldsymbol{j}}_g}}\\ {{\mathit{\boldsymbol{k}}_g}} \end{array}} \right] $ | (9) |
where, Ci = R (φi) R (θi) R (ψi), and { I, J, K } is the orthogonal unit vector of SRF.
Eq.(9) implies that all the quantities can be represented in SRF with certain transformation. And we have:
| $ {\mathit{\boldsymbol{H}}_{{\rm{cmg}}}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{h}}_{gi}}} $ | (10) |
where, hgi is the angular momentum vector of the ith CMG represented in its GCF, and has constant magnitude. The torque equation can be generated by applying differentiation to Eq.(10) or by vector sum of each CMG torque (Eq.(1)).
| $ {{\mathit{\boldsymbol{\dot H}}}_{{\rm{cmg}}}} = \frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{cmg}}}}}}{{\partial \mathit{\boldsymbol{\delta }}}}\mathit{\boldsymbol{\dot \delta }} = \mathit{\boldsymbol{J\dot \delta }} $ | (11) |
or
| $ {{\mathit{\boldsymbol{\dot H}}}_{{\rm{cmg}}}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{T}}_{gi}}} $ | (12) |
where,
Note that the two equations above are the same actually. This method has the benefits of universality and simplicity and its key is to determine the Euler angles in Eq.(9).
3.1.2 Configuration methodIn Ref.[9], the author introduced a novel modeling method for tetrahedron CMG cluster. First the system momentum is represented as:
| $ {\mathit{\boldsymbol{H}}_{{\rm{cmg}}}} = {h_0}\left( {\mathit{\boldsymbol{A}}\sin \mathit{\boldsymbol{\delta }} + \mathit{\boldsymbol{B}}\cos \mathit{\boldsymbol{\delta }}} \right)\mathit{\boldsymbol{E}} $ | (13) |
where, h0 is the momentum magnitude of CMG flywheel and is supposed to be the same without loss of generality and En×1=[1 … 1]T.A3×n and B3×n are matrix characterized by the CMG configuration, whose ith column vector denotes the ith flywheel momentum when gimbal angle equals 90° or 0°, respectively. And
| $ \left\{ \begin{array}{l} \sin \mathit{\boldsymbol{\delta }} = {\rm{diag}}\left( {\sin {\delta _i}} \right)\\ \cos \mathit{\boldsymbol{\delta }} = {\rm{diag}}\left( {\cos {\delta _i}} \right) \end{array} \right. $ | (14) |
Consequently the torque in SRF is written as:
| $ \mathit{\boldsymbol{T}} = {{\mathit{\boldsymbol{\dot H}}}_{{\rm{cmg}}}} = \mathit{\boldsymbol{J}}\left( \delta \right)\mathit{\boldsymbol{\dot \delta }}{h_0} $ | (15) |
where,
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{A}}\cos \mathit{\boldsymbol{\delta }} - \mathit{\boldsymbol{B}}\sin \mathit{\boldsymbol{\delta }} $ | (16) |
Eqs.(13) and (15) imply how the configuration influence the dynamic model, as the name configuration method suggests.
3.1.3 Generalized constrain modelTo avoid the computation of Jacobian matrix inversion, which is a tough and complicated problem, Refs.[4-5] introduced generalized constrain model to expand the dimension of the Jacobian matrix by adding constrain conditions. A Jacobian matrix of n CMGs cluster belongs to R3×n, so there should be m=n-3 constrains
| $ {\mathit{\boldsymbol{D}}^{m \times 1}} = {\mathit{\boldsymbol{C}}^{m \times n}}\mathit{\boldsymbol{\dot \delta }} $ | (17) |
then
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}^{3 \times 1}}}\\ {{\mathit{\boldsymbol{D}}^{m \times 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}^{3 \times n}}}\\ {{\mathit{\boldsymbol{C}}^{m \times n}}} \end{array}} \right]\mathit{\boldsymbol{\dot \delta }} = \mathit{\boldsymbol{J}}_E^{n \times n}\mathit{\boldsymbol{\dot \delta }} $ | (18) |
and JEn×n is the expanded Jacobian matrix.
The constrains should guarantee non-singularity, that's:
| $ {\rm{det}}\left( {\mathit{\boldsymbol{J}}_E^{\rm{T}}{\mathit{\boldsymbol{J}}_E}} \right) \ne 0 $ | (19) |
The key is to find constrains, which would really relieve the burden on inversion calculation and singularity avoidance.
3.1.4 Inverse kinematic modelContrary to the models above, the inverse kinematic model is bullied for singular avoidance by calculating the gimbal angle rather than gimbal rate in Ref.[28].
Supposing one gimbal angle of pyramid cluster is decided, the procedure adopts the dichotomy and newton iteration method to search the other three angles with the requirement of singularity avoidance. Using this logic, the author proposed Inverse Kinematics Computational Procedure (IKCP) and Inverse Kinematics Steering Logic (IKSL) and discussed optimized program for online control. The simulation and ground experiment showed that IKSL was capable of real-time implementation although there existed eighth-order polynomial equations.
3.2 Example of CMG Cluster ModelingIn this part, above modeling methods will be examined by several classical configurations, as illustrative examples.
3.2.1 Modeling for parallel clusterAlthough non-redundant CMG arrays are not qualified for three-axis control, they can still serve in Earth observing and imaging tasks, as mentioned in Section 1. With the gimbal axes parallel to each other (supposing gi = K shown in Fig. 4), 2 parallel cluster's dynamic formula is
| $ {\mathit{\boldsymbol{H}}_{{\rm{cmg}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\delta _1} + \cos {\delta _2}}\\ {\sin {\delta _1} + \sin {\delta _2}} \end{array}} \right] $ | (20) |
and the control torque is
| $ \mathit{\boldsymbol{T}} = {{\mathit{\boldsymbol{\dot H}}}_{{\rm{cmg}}}} = \left[ {\begin{array}{*{20}{c}} { - \sin {\delta _1}}&{ - \sin {\delta _2}}\\ {\cos {\delta _1}}&{\cos {\delta _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \delta }_1}}\\ {{{\dot \delta }_2}} \end{array}} \right] $ | (21) |
which is quite simple due to its configuration.
3.2.2 Pyramid cluster modelingAs the major CMG configuration, pyramid cluster (not only refers to rectangular pyramid)has been widely used and deeply studied. It is shown that the coordinate transformation method can suit all symmetric clusters, especially for the pyramid arrays or their variants.
By observing Fig. 3, the ith CMG gimbal axis of n- pyramid array can transform to SRF by a set of Euler angles with the sequence 'XYZ' as follows:
| $ {\mathit{\boldsymbol{R}}_i} = \left[ { - {\delta _i},{\rm{ \mathit{ π} }}/2 - \beta ,2{\rm{ \mathit{ π} }}\left( {i - 1} \right)/n} \right] $ | (22) |
where, β is the skew angle. The direction cosine matrix (DCM) is
| $ {C_i} = Angle2Dcm\left( {{\mathit{\boldsymbol{R}}_i},'XYZ'} \right) $ | (23) |
where, Angle2Dcm represents the transformation function from Euler angle to DCM with 'XYZ' sequence.
Consequently the momentum equation of pyramid cluster is
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_{{\rm{cmg}}}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{h}}_i}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{h}}_{gi}}} = \\ \;\;\;\;\;\;\;\;\;\;\left( {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{C}}_i}} } \right){\left[ {\begin{array}{*{20}{c}} 0&{{{\rm{h}}_0}}&0 \end{array}} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;{h_0}\sum\limits_{i = 1}^n {{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{i - 12}}}&{{\mathit{\boldsymbol{C}}_{i - 22}}}&{{\mathit{\boldsymbol{C}}_{i - 32}}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (24) |
where hi and hgi are ith CMG momentum in SRF and GCF respectively.Ci-xy denotes (x, y) element of ith DCM matrix.
The system output torque then is
| $ {{\mathit{\boldsymbol{\dot H}}}_{{\rm{cmg}}}} = {h_0}\sum\limits_{i = 1}^n {{{\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot C}}}_{i - 12}}}&{{{\mathit{\boldsymbol{\dot C}}}_{i - 22}}}&{{{\mathit{\boldsymbol{\dot C}}}_{i - 32}}} \end{array}} \right]}^{\rm{T}}}\mathit{\boldsymbol{\dot \delta }}} = \mathit{\boldsymbol{J\dot \delta }} $ | (25) |
We suppose h0=1 without losing of generality.The momentum and torque equations of pyramid cluster (PC)with 4 CMGs matrix form are
| $ {\mathit{\boldsymbol{H}}_{{\rm{PC}}}} = \left[ {\begin{array}{*{20}{c}} { - {\rm{c}}\beta {s_1}}&{ - {c_2}}&{{\rm{c}}\beta {s_3}}&{{c_4}}\\ {{c_1}}&{ - {\rm{c}}\beta {s_2}}&{ - {c_3}}&{{\rm{c}}\beta {s_4}}\\ {{\rm{s}}\beta {s_1}}&{{\rm{s}}\beta {s_2}}&{{\rm{s}}\beta {s_3}}&{s\beta {{\rm{s}}_4}} \end{array}} \right] $ | (26) |
and
| $ {{\mathit{\boldsymbol{\dot H}}}_{{\rm{PC}}}} = \mathit{\boldsymbol{J\dot \delta }} = \left[ {\begin{array}{*{20}{c}} { - {\rm{c}}\beta {c_1}}&{{\rm{s}}{\delta _2}}&{{\rm{c}}\beta {c_3}}&{ - {s_4}}\\ { - {s_1}}&{ - {\rm{c}}\beta {c_2}}&{{s_3}}&{{\rm{c}}\beta {c_4}}\\ {{\rm{s}}\beta {c_1}}&{{\rm{s}}\beta {c_2}}&{{\rm{s}}\beta {c_3}}&{{\rm{s}}\beta {c_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \delta }_1}}\\ {{{\dot \delta }_2}}\\ {{{\dot \delta }_3}}\\ {{{\dot \delta }_4}} \end{array}} \right] $ | (27) |
where, ci=cos δi, si=sin δi, cβ=cos β and sβ=sin β.
3.2.3 Tetrahedron cluster modelingApplying the configuration method to tetrahedron cluster, we can get the configuration matrixes:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \frac{{{h_0}}}{{\sqrt 6 }}\left[ {\begin{array}{*{20}{c}} 2&{ - 1}&{ - 1}&{ - 1}\\ { - 1}&{ - 1}&{ - 2}&{ - 1}\\ 1&2&{ - 1}&2 \end{array}} \right]\\ \mathit{\boldsymbol{B}} = \frac{{{h_0}}}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 0&{ - 1}&{ - 1}&1\\ { - 1}&{ - 1}&0&{ - 1}\\ 1&0&{ - 1}&0 \end{array}} \right] \end{array} \right. $ | (28) |
then the Jacobian Matrix can be derived by using Eq.(29)
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{A}}\cos \mathit{\boldsymbol{\delta }} - \mathit{\boldsymbol{B}}\sin \mathit{\boldsymbol{\delta }} $ | (29) |
By adding three independent constrains below, the cube cluster's dynamics formula can be written as the generalized constrain model.
| $ {\delta _1} - {\delta _2} = 0,\;\;\;{\delta _3} - {\delta _4} = 0,\;\;\;{\delta _5} - {\delta _6} = 0 $ | (30) |
and the constrain equation is
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{ - 1}&0&0&0&0\\ 0&0&1&{ - 1}&0&0\\ 0&0&0&0&1&{ - 1} \end{array}} \right]\mathit{\boldsymbol{\dot \delta }} = \mathit{\boldsymbol{C\dot \delta }} $ | (31) |
The constraints implying the CMGs mounted along X, Y or Z axis have the same magnitude of gimbal rate respectively in SRF[4].The generalized constrain model is illustrated by Eq.(33).
The dynamic index is
| $ \det \left( {{\mathit{\boldsymbol{J}}_E}} \right) = - 8\cos \left( {{\delta _1}} \right)\cos \left( {{\delta _3}} \right)\cos \left( {{\delta _5}} \right) $ | (32) |
which implies that the singular point is δ1, δ3, δ5=±π/2 and that's the saturation point where the momentum reaches the edge of envelope and is a trivia state. In other words, there are no internal singular points for JE. The detailed analysis can be found in Refs.[4] and [5].
| $ \left[ {\begin{array}{*{20}{c}} {{T_x}}\\ {{T_y}}\\ {{T_z}}\\ 0\\ 0\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \cos {\delta _1}}&{ - \cos {\delta _2}}&0&0&{ - \sin {\delta _5}}&{\sin {\delta _6}}\\ { - \sin {\delta _1}}&{\cos {\delta _2}}&{ - \cos {\delta _3}}&{\cos {\delta _4}}&0&0\\ 0&0&{ - \sin {\delta _3}}&{\sin {\delta _4}}&{ - \cos {\delta _5}}&{ - \cos {\delta _6}}\\ 1&{ - 1}&0&0&0&0\\ 0&0&1&{ - 1}&0&0\\ 0&0&0&0&1&{ - 1} \end{array}} \right]\mathit{\boldsymbol{\dot \delta }} = {\mathit{\boldsymbol{J}}_E}\mathit{\boldsymbol{\dot \delta }} $ | (33) |
Four different CMG modeling methods are introduced and examined by particular cluster. Exactly speaking, the former two are modeling methods while the latter two are special model types.The coordinate transformation modeling method has the absolute convenience especially when dealing with all kinds of pyramid and symmetric configurations.We advise that the generalized constrain model should be further studied to find the general constraint form for different clusters.Thus CMG singularity can be more easily handled.
4 CMG Singularity AnalysisThe significant challenge in CMG application is the inherent geometric singularity where the cluster is failed to track the command signal[4, 8, 16]. The steering logics designed to avoid/escape this situation involve comprehensive knowledge and theory. Null motion[3, 6, 18-21] generates zero net torque but helps increase the rank of Jacobian matrix at singular state.Focusing on CMG singular momentum surface structure, differential geometry and topology deal with manifold to distinguish singular problem. Singular value decomposition[22-23] can give a new insight into the Jocabian matrix, while inverse kinematics[28]focuses on the singular gimbal angles. The thorough singularity analysis is the first step for CMG steering and this section thus presents a diverse series of methods for singularity description.
4.1 Singularity MechanismAt first we would like to introduce the singularity concept or mechanism(how and why CMG cluster fall into singularity).
Definition 1 : The CMG cluster (whose gimbals are not parallel to each other) traps into singularity if and only if all units' output fi lie in a plane which the command vector τ is normal to, for some specific gimbal angel sets δs=(δ1, …, δn), represented in Fig. 14. Consequently the vector which is perpendicular to the torque plane is named as singular vector and the corresponding gimbal angel sets are called singular gimbal angles.
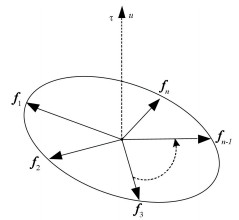
|
Fig.14 Singular torque |
The definition implies degeneration of torque space to 2-dimension and this is the explanations why CMG fails to operate. All CMGs can be singular but SGCMG suffers most severely[32].
Considering a cluster arranged with n CMGs:
| $ {\rm{d}}{\mathit{\boldsymbol{H}}_{{\rm{cmg}}}} = \sum\limits_{i = 1}^n {{\rm{d}}{\mathit{\boldsymbol{h}}_i}} = \sum\limits_{i = 1}^n {\frac{{{\rm{d}}{\mathit{\boldsymbol{h}}_i}}}{{{\rm{d}}{\delta _i}}}{\rm{d}}{\delta _i}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{f}}_i}{\rm{d}}{\delta _i}} $ | (34) |
where
| $ {\mathit{\boldsymbol{f}}_i} = \frac{{{\rm{d}}{\mathit{\boldsymbol{h}}_i}}}{{{\rm{d}}{\delta _i}}} = {\mathit{\boldsymbol{g}}_i} \times {\mathit{\boldsymbol{h}}_i} $ | (35) |
Note that fi is the ith column vector of the Jacobian matrix. And when the cluster is in singularity, we have:
| $ {\mathit{\boldsymbol{f}}_i} \cdot \mathit{\boldsymbol{u}} = 0\;\;\;\;{\rm{or}}\;\;\;\;{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{u}} = 0,i = 1, \cdots ,n $ | (36) |
Eq.(36)known as singular condition implies:
| $ {\rm{rank}}\left( \mathit{\boldsymbol{J}} \right) = 2 < 3 $ | (37) |
which means J is no longer full rank or det(JJT)=0, posing a tough problem for CMG control.
4.2 Singularity ClassificationThe dynamic function indicates the 1-to-1 or n-to-1 mapping from gimbal angle space to momentum space, which inversely may not be so simple. There are more gimbal angle solutions for given momentum and some angles could reduce the rank of Jacobian matrix and encounter a singularity unexpectedly.
Therefore, CMG singularity can be categorized into two types, elliptic singularity and hyperbolic singularity[21, 34]. The following analysis would demonstrate that the former is more severe.
4.2.1 Elliptic singularityOnce CMG moves into elliptic singularity, no other substitutable angle sets exist with a full rank Jacobian matrix, which in other words poses the 1-to-1 mapping relationship between gimbal rates and torque output.
The elliptic singularity, in terms of the singular momentum magnitude, has two parts, saturation/external or internal. As the name suggests the so-called saturation or external singular momentum reaches the maximum or edge of momentum envelope along the singular vector direction. It can no longer generate output torque (by increasing the size), the only path is the tangent of the envelope. On the contrary internal momentum is less than saturation value.
4.2.2 Hyperbolic singularityThe hyperbolic singularity emerges when another solution exists for the given momentum. Those angles can be traversed using null motion, with no effect on momentum. Hyperbolic singularity has two subsections degenerate and non-degenerate. The Jacobin matrix is full rank when in a non-degenerate singularity.
4.3 Singularity EvaluationThe momentum of CMG is a continuous function parameterized by gimbal angles, which means the cluster enters into singularity gradually. It is suggested that some active strategies should be carried out when in the neighborhood of singularity.
So the principal step is to evaluate or measure how far the cluster reaches the singularity. Some steering logics based on this idea have been designed. The frequently-used evaluation functions are summed up blow.
1) S1=det(JJT) or S1=
2) S2=
3) S3=min(1/|di|), where di is the ith row vector of JT (J JT)-1;
4) S4=min(σi), where σi is the singular value of J[23, 25];
5) S5=cond(J), where cond is the condition number function[36];
The function S1 is widely used due to its simplicity and correspondence to singular sate, in which S1=0 and rank(J)=2. The smaller S1 becomes, the worse CMG cluster state is.
An advisable strategy is to apply a different law when measurement function value passes through the threshold rather than when CMG encounters the singularity.These functions on other hand can examine the performance of steering law.
4.4 Singularity VisualizationNote that all the singularity evaluation functions are scalar functions whose value cannot reflect the singularity mechanism and geometric characteristics. Different configurations have different kind of singularities and even for a specific cluster it can be singular at different gimbal angle combinations.
It is urgent to depict the singular momentum surface that represents the geometric properties and describes the relationship between singularity and configurations. Hereafter, some classical ways are introduced to depict the physical graphs and refine the understanding of CMG singularity, known as singularity visualization.
4.4.1 Singularity visualizing methodSingularity visualizing methods can be categorized into three main parts, global search[36], Margulies-Auburn method[37]and the technique based on inverse kinematic model[28].
A) Global search.
The CMG would be singular along any direction in 3-dimensional space. We can consequently search all the singular momentum in a specific direction, and then extend to the whole space thoroughly[36]. The procedure is demonstrated below.
1) Set the singular vector which would travel around the space, for example u = cos θ cos φI + cos θ sin φJ +sin θK, where θ and φ are the latitude and longitude angle.
2) Search the singular angle for the given direction.
3) Calculate the momentum and identify the type of the singularity.
4) Move the singular vector and take the above steps until all singularities are found.
5) Depict the momentum.
The program above is clear and simple, but it is a tedious process.
B) Margulies-Auburn method.
The singular vector was also employed by Margulies-Auburn[37]to search the momentum. What however makes the difference is that no gimbal angle will be needed to execute the procedure.
The ith CMG output fi is norm to singular vector u and there exists the orthogonal relationship among {gi, hi, fi }. In other words, fi is perpendicular to both gi and u, and we consequently have:
| $ {\mathit{\boldsymbol{f}}_i} = \pm \frac{{{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}}}{{\left| {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right|}} $ | (38) |
Considering {gi, hi, fi } is a set of unit basis vector set, we have:
| $ {\mathit{\boldsymbol{h}}_i} = {\mathit{\boldsymbol{f}}_i} \times {\mathit{\boldsymbol{g}}_i} $ | (39) |
Substituting Eq.(38) into Eq.(39) we obtain:
| $ {\mathit{\boldsymbol{h}}_i} = {\mathit{\boldsymbol{f}}_i} \times {\mathit{\boldsymbol{g}}_i} = \pm \frac{{\left( {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right) \times {\mathit{\boldsymbol{g}}_i}}}{{\left| {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right|}} = {\varepsilon _i}\frac{{\left( {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right) \times {\mathit{\boldsymbol{g}}_i}}}{{\left| {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right|}} $ | (40) |
where εi=±1 and gi ≠ u.
So the singular momentum of the CMG system is:
| $ {\mathit{\boldsymbol{H}}_{\rm{s}}} = \sum\limits_{i = 1}^n {{\varepsilon _i}\frac{{\left( {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right) \times {\mathit{\boldsymbol{g}}_i}}}{{\left| {{\mathit{\boldsymbol{g}}_i} \times \mathit{\boldsymbol{u}}} \right|}}} $ | (41) |
where Hs =Hs (u)= Hs(θ, φ). The momentum is parameterized by two variables rather than n variables in Eq.(26). There are 2n combinations of {εi} for an n- CMGs cluster, which can reduces to 2n-1 due to symmetry(for example, all positive {εi} and all negative {εi} share the same momentum).
In Ref.[28], the author proposed the visualizing technique based on inverse kinematic model, which can give the local momentum surface while Margulies-Auburn method cannot.
4.4.2 Example of singularity visualizingThe Margulies-Auburn method in this part will be examined by several CMG clusters. Meanwhile the geometric properties will be analyzed.
A) Parallel configuration.
Moving momentum vector into (x, y) plane, we can get the gimbal axis gi=[0 0 1]T (i=1, 2, 3) for 3-parallel cluster. The Margulies-Auburn method denotes that {εi} has two types:
| $ \left\{ {{\varepsilon _i}} \right\} = \left\langle {\left\{ { + , + , + } \right\},\left\{ { + , + , - } \right\}} \right\rangle $ | (42) |
which corresponds to saturation and internal singularity or 3H and 1H singularity, as illustrated in Fig. 15. There simply are two concentric circles R=1, 3 respectively.
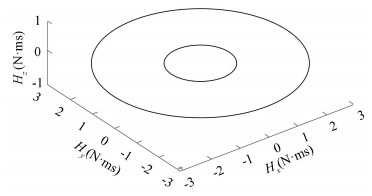
|
Fig.15 Singular momentum line of 3-parallel clusters |
B) Pyramid configuration.
The surface of pyramid cluster is much more complex. It is three- dimensional unlike the circular line of the parallel arrays.
The gimbal vectors represented in SRF are:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{g}}_1} = {\left[ {\begin{array}{*{20}{c}} {\sin \beta }&0&{\cos \beta } \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_2} = {\left[ {\begin{array}{*{20}{c}} 0&{\sin \beta }&{\cos \beta } \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_3} = {\left[ {\begin{array}{*{20}{c}} { - \sin \beta }&0&{\cos \beta } \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_4} = {\left[ {\begin{array}{*{20}{c}} 0&{ - \sin \beta }&{\cos \beta } \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (43) |
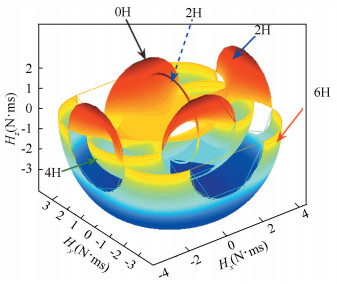
where, the skew angle β=54.73°.There are eight combinations for (εi), corresponding to three different kinds of singularity 4H, 2H and 0H, illustrated in Table 3. Fig. 16 depicts the singular surface of pyramid cluster.
| Table 3 Singularity type of pyramid cluster |

|
Fig.16 Singularity Visualization of pyramid CMG cluster |
Fig. 16(a), (c) and (e)show the 4H, 2H, 0H singular surface, respectively.Due to structural symmetry, the surfaces also appear symmetric.Fig. 16 (b) shows the largest momentum is about 3.3 rather than 4 as the name 4H suggests.What is more the largest momentum in different direction varies. Eight holes resulted from the condition gi ≠ u exist on the 4H surface (Fig. 16(a)) which can match the trumpet-shaped surface in 2H (Fig. 16(c)) smoothly and form whole momentum envelop, as illustrated in Fig. 16 (f).(In order to show the structure of the envelope, there is only half of 4H surface.)
C) Cube configuration.
More complexity comes along with more units in CMG cluster. The cube configuration with 6 CMGs would show some new findings about the singularity surface. The gimbal axis vectors are:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{g}}_1} = {\left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_2} = {\left[ {\begin{array}{*{20}{c}} 0&1&0 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_3} = {\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_4} = {\left[ {\begin{array}{*{20}{c}} { - 1}&0&0 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_5} = {\left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0 \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{g}}_6} = {\left[ {\begin{array}{*{20}{c}} 0&0&{ - 1} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (44) |
Definitely, there should be 6H, 4H, 2H and 0H surface. The visualization is shown in Fig. 17.

|
Fig.17 Singularity Visualization of cube CMG cluster |
Besides the similar properties with pyramid cluster, there is something unique and interesting. The projections of Fig. 17(a) in three different direction show that the 6H surface resembles a cube with edge length of 8 and circles (radius=2) on the surface. 4H surface is a combination of three same ellipsoids which are the same as the saturation surface of 2-SPEED configuration. The same circles can also be found on 2H and 0H surfaces. All singularity surfaces can be put together and are illustrated in Fig. 18.
|
Fig.18 Singular surface of cube cluster |
Fig. 18 depicts the multi-layers of cube cluster singular momentum surface, which means more energy will be consumed to pass through those layers from inner one to outer one. All 0H and 2H surfaces make up the first layer, 4H is the second layer, 6H together with 2H trumpet-shaped surface forms the third layer. Both the first and second layers are internal, while the third one is external, known as momentum envelop.
4.5 Binet-Cauchy IdentityThe Margulies-Auburn method above simplifies the visualization problem by reducing the variables to 2 but gives no concern about the gimbal angle. In some cases, however, we should know where the CMG could be singular to plan gimbal angle path. Here a new mathematical method, Binet-Cauchy Identity[38], will help to analyze the gimbal angle.
The evaluation function S1, when in singular sate implies:
| $ \det \left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right) = 0 $ | (45) |
Applying Binet-Cauchy identity to the above equation:
| $ \det \left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right) = \sum\limits_{i = 1}^n {M_i^2} = 0 $ | (46) |
where, Mi=det(Ji) and Ji is the matrix with ith column vector removed from the Jacobian matrix. Using Eq.(46), the singular condition of pyramid configuration can be rewritten as:
| $ \begin{array}{l} {M_i} = {\rm{s}}\beta \left[ {\left( {{s_{i + 1}}{s_{i + 2}}{c_{i + 3}} + {c_{i + 1}}{s_{i + 2}}{s_{i + 3}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;{\rm{c}}\beta \left( {{c_{i + 1}}{c_{i + 2}}{s_{i + 3}} - {s_{i + 1}}{c_{i + 2}}{c_{i + 3}}} \right) + \\ \;\;\;\;\;\;\;\;\left. {2{{\left( {{\rm{c}}\beta } \right)}^2}{c_{i + 1}}{c_{i + 2}}{c_{i + 3}}} \right] = 0 \end{array} $ | (47) |
where, i=1, 2, 3, 4.(Note that the subscript of each quantity in Eq.(47)cannot be larger than 4, otherwise it should subtract 4).
Eq.(47) implies that there are four conditions when in singularity. Dominguez and Wie[39] argued that only two conditions were independent because the minimum rank of Jacobian matrix was 2. Consequently we can figure out the singular angle set.
When ci≡cos δi≠0, four conditions can be simplified as:
| $ \begin{array}{l} \tan {\delta _{i + 2}}\left( {\tan {\delta _{i + 1}} + \tan {\delta _{i + 3}}} \right) + {\rm{c}}\beta \left( {\tan {\delta _{i + 3}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\tan {\delta _{i + 1}}} \right) = - 2{\left( {{\rm{c}}\beta } \right)^2} \end{array} $ | (48) |
Using any two of the above 4 equations (in Eq.(48)), one may get the angle solutions.
Case 1: For all δ1, δ2, we get:
| $ \begin{array}{l} {\delta _3} = {\tan ^{ - 1}}\left[ {\left( { - 2{{\left( {{\rm{c}}\beta } \right)}^2} - \tan {\delta _1}\left( {\tan {\delta _2} - {\rm{c}}\beta } \right)} \right)} \right./\\ \;\;\;\;\;\;\;\left. {\left( {\tan {\delta _2} + {\rm{c}}\beta } \right)} \right]\\ {\delta _4} = {\tan ^{ - 1}}\left[ {\left( { - 2{{\left( {{\rm{c}}\beta } \right)}^2} - \tan {\delta _2}\left( {\tan {\delta _1} + {\rm{c}}\beta } \right)} \right)} \right./\\ \;\;\;\;\;\;\;\left. {\left( {\tan {\delta _1} - {\rm{c}}\beta } \right)} \right] \end{array} $ | (49) |
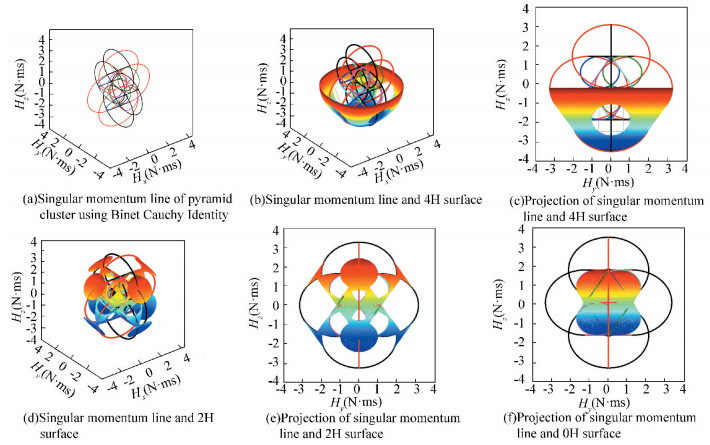
The other five cases (when ci≡cos δi≠0) and cases when ci≡cos δi=0 can be found by the same way.Corresponding singular surface can be defined by Eq.(26).
The graphs for all six cases (ci≡cos δi=0) are demonstrated in Fig. 19(a). And meanwhile we put momentum surface and Fig. 19(a) together (Figs. 19(b)-(f)). There are 6 kinds of color corresponding to 6 cases. Eight bigger ellipses (red and black line) in the projection figure (Figs. 19(b), (c)) determine the basic frame of CMG momentum roughly. What is more all lines just like skeleton support the surface which resembles covers.
|
Fig.19 Singularity Visualization of pyramid cluster using Binet-Cauchy Identity |
4.6 Null Motion
All fi are coplanar in singularity, and then the CMGs lose 3-axis control capacity. The hyperbolic singularity can be escaped by null motion as discussed above[3, 6, 18-21], while elliptic singularity cannot. The motion that generates zero net torque is named as null motion, its mathematical form is
| $ \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \delta }}}_N} = 0 $ | (50) |
where,
The changes of momentum (torque) for null motion represented in SRF is
| $ {\rm{d}}\mathit{\boldsymbol{H}} = \sum\limits_{i = 1}^n {{\rm{d}}{\mathit{\boldsymbol{h}}_i}} = 0 $ | (51) |
expanding Eq.(51) by Taylor series and we suppose that
| $ {\rm{d}}\mathit{\boldsymbol{H}} = \sum\limits_{i = 1}^n {\left[ {\frac{{{\rm{d}}{\mathit{\boldsymbol{h}}_i}}}{{{\rm{d}}{\delta _i}}}{{\dot \delta }_i} + \frac{1}{{2!}}\frac{{{{\rm{d}}^2}{\mathit{\boldsymbol{h}}_i}}}{{{\rm{d}}{\delta _i}^2}}\dot \delta _i^2 + \frac{1}{{3!}}\frac{{{d^3}{\mathit{\boldsymbol{h}}_i}}}{{{\rm{d}}{\delta _i}^3}}\dot \delta _i^3 + \cdots } \right]} $ | (52) |
given dhi/dδi =fi and d2hi/dδi2=-hi, then:
| $ {\rm{d}}\mathit{\boldsymbol{H}} = \sum\limits_{i = 1}^n {\left[ {{\mathit{\boldsymbol{f}}_i}{{\dot \delta }_i} - \frac{1}{{2!}}{\mathit{\boldsymbol{h}}_i}\dot \delta _i^2 + \frac{1}{{3!}}{\mathit{\boldsymbol{f}}_i}\dot \delta _i^3 + \cdots } \right]} = 0 $ | (53) |
Considering only first-order term:
| $ {\rm{d}}\mathit{\boldsymbol{H}} = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{f}}_i}{{\dot \delta }_i}} = \mathit{\boldsymbol{J\dot \delta }} = 0 $ | (54) |
Taking inner product of Eq.(36) with singular vector and applying the singular condition (54), we obtain:
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}^{\rm{T}}}{\rm{d}}\mathit{\boldsymbol{H = }}{\mathit{\boldsymbol{u}}^{\rm{T}}}\left\{ {\sum\limits_{i = 1}^n {\left[ {{\mathit{\boldsymbol{f}}_i}{{\dot \delta }_i} - \frac{1}{{2!}}{\mathit{\boldsymbol{h}}_i}\dot \delta _i^2 + \frac{1}{{3!}}{\mathit{\boldsymbol{f}}_i}\dot \delta _i^3 + \cdots } \right]} } \right\} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\left( {{\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{h}}_i}} \right)\left( { - \frac{1}{{2!}}\dot \delta _i^2 + \frac{1}{{4!}}\dot \delta _i^4 + \cdots } \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{e_i}\left( {\cos {{\dot \delta }_i} - 1} \right)} = 0 \end{array} $ | (55) |
where ei=uT hi.
Considering only second-order term:
| $ \sum\limits_{i = 1}^n {{e_i}\dot \delta _i^2} = 0 $ | (56) |
which can be rewritten as matrix form:
| $ {{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{E\dot \delta }} = 0 $ | (57) |
where, E = diag(ei).
Eq.(57) implies that no null motion solution exists for a sign-definite matrix E, which corresponds to an elliptic singularity point (the only solution is
In this part a new mathematical method, singular value decomposition, will be employed to analyze the characteristic of Jacobian matrix[22-23]. For a cluster consists of n CMGs, there exists orthonormal matrixes U and V satisfying:
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{US}}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (58) |
where
| $ {\mathit{\boldsymbol{U}}^{3 \times 3}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_1}}&{{\mathit{\boldsymbol{u}}_2}}&{{\mathit{\boldsymbol{u}}_3}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{V}}^{n \times n}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_1}}&{{\mathit{\boldsymbol{v}}_2}}& \cdots &{{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{n}}}} \end{array}} \right] $ |
and UUT= I3, VVT =In And S represents block matrix with the following form:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}^{3 \times n}} = \left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&0&0& \cdots &0\\ 0&{{\sigma _2}}&0& \cdots &0\\ 0&0&{{\sigma _3}}& \cdots &0 \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left( {\begin{array}{*{20}{c}} {{\sigma _1}}&{{\sigma _2}}&{{\sigma _3}} \end{array}} \right)}&0 \end{array}} \right]} \end{array} $ | (59) |
where σ1>σ2>σ3 is the singular value of J. So:
| $ \begin{array}{l} \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_1}}&{{\mathit{\boldsymbol{u}}_2}}&{{\mathit{\boldsymbol{u}}_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&0&0& \cdots &0\\ 0&{{\sigma _2}}&0& \cdots &0\\ 0&0&{{\sigma _3}}& \cdots &0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_1^{\rm{T}}}\\ {\mathit{\boldsymbol{v}}_2^{\rm{T}}}\\ \vdots \\ {\mathit{\boldsymbol{v}}_n^{\rm{T}}} \end{array}} \right] = \\ \;\;\;\;\;\;\sum\limits_{i = 1}^3 {{\sigma _i}{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} \end{array} $ | (60) |
And the singular index is rewritten as:
| $ \det \left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right) = \prod\limits_{i = 1}^3 {\sigma _i^2} $ | (61) |
When the CMG system traps into singularity, rank(J)=2 and σ3=0. What's more u3 is the singular vector (JT u3=0) and the null motion space is
| $ \mathit{\boldsymbol{N}} = {\rm{null}}\left( \mathit{\boldsymbol{J}} \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_3}}& \cdots &{{\mathit{\boldsymbol{v}}_n}} \end{array}} \right] $ | (62) |
Consequently the null motion gimbal rate is
| $ {\mathit{\boldsymbol{\delta }}_N} = \sum\limits_{i = 3}^n {{c_i}{\mathit{\boldsymbol{v}}_i}} $ | (63) |
where, ci is scalar parameter denoting the magnitude of null motion gimbal rate.
Above analysis indicates that the singular value σ3 denotes the singular degree of CMG system. Both singular vector and null motion space can be decided by SVD. Moreover, the SVD method will be further used in steering logic design.
4.8 Differential GeometryThe discussion above provided several classical methods for singularity analysis, which in some degrees still cannot identify CMG geometric characteristics. Some new viewpoints can be found by using differential geometry[19, 21, 25, 40], and the key conclusions about the CMG singularity are summarized here.
The three dimensional unit vector parameterized by θ1, θ2 is given by:
| $ \begin{array}{l} \mathit{\boldsymbol{u}} = {u_x}\mathit{\boldsymbol{I}} + {u_y}\mathit{\boldsymbol{J}} + {u_z}\mathit{\boldsymbol{K}} = \sin {\theta _2}\mathit{\boldsymbol{I}} - \sin {\theta _1}\cos {\theta _2}\mathit{\boldsymbol{J}} + \\ \;\;\;\;\;\;\cos {\theta _1}\cos {\theta _2}\mathit{\boldsymbol{K}} \end{array} $ | (64) |
and we can define u1 and u2 as:
| $ {\mathit{\boldsymbol{u}}_1} = \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {\theta _1}}},{\mathit{\boldsymbol{u}}_2} = \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {\theta _2}}} $ | (65) |
Similarly H1 and H2 for given singular momentum Hs(θ1, θ2) are
| $ {\mathit{\boldsymbol{H}}_i} = \frac{{\partial {\mathit{\boldsymbol{H}}_{\rm{s}}}}}{{\partial {\theta _i}}} = \frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{s}}x}}}}{{\partial {\theta _i}}}\mathit{\boldsymbol{I}} + \frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{s}}y}}}}{{\partial {\theta _i}}}\mathit{\boldsymbol{J + }}\frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{s}}z}}}}{{\partial {\theta _i}}}\mathit{\boldsymbol{K}} $ | (66) |
where i=1, 2. Then we have:
| $ \mathit{\boldsymbol{G}} = \left[ {{G_{ij}}} \right] = \left[ {{\mathit{\boldsymbol{H}}_i} \cdot {\mathit{\boldsymbol{H}}_j}} \right] $ |
| $ \mathit{\boldsymbol{B}} = \left[ {{B_{ij}}} \right] = \left[ { - {\mathit{\boldsymbol{H}}_i} \cdot {\mathit{\boldsymbol{u}}_j}} \right] $ |
| $ \mathit{\boldsymbol{C}} = \left[ {{C_{ij}}} \right] = \left[ {{\mathit{\boldsymbol{u}}_i} \cdot {\mathit{\boldsymbol{u}}_j}} \right] $ |
Given following mapping:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_1}}\\ {{\mathit{\boldsymbol{u}}_2}} \end{array}} \right] = - \mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_1}}\\ {{\mathit{\boldsymbol{H}}_2}} \end{array}} \right] $ | (67) |
consequently we have:
| $ \mathit{\boldsymbol{B}} = - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_1}}\\ {{\mathit{\boldsymbol{H}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_1}}&{{\mathit{\boldsymbol{u}}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_1}}\\ {{\mathit{\boldsymbol{H}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_1}}&{{\mathit{\boldsymbol{H}}_2}} \end{array}} \right]{\mathit{\boldsymbol{D}}^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}^{\rm{T}}} $ | (68) |
therefore, D=G-1 B=B G-1, and further C= DGDT = DB = G-1 B2= B2 G-1.
In the same way we assume:
| $ \left[ {\begin{array}{*{20}{c}} {{\rm{d}}{\theta _1}}\\ {{\rm{d}}{\theta _2}} \end{array}} \right] = \mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{c}} {{\omega _1}}\\ {{\omega _2}} \end{array}} \right] = \mathit{\boldsymbol{E\omega }} $ | (69) |
Then the first fundamental form of singular surface would be diagonalized as:
| $ \begin{array}{l} \mathit{\boldsymbol{I}} \equiv {\rm{d}}\mathit{\boldsymbol{H}} \cdot {\rm{d}}\mathit{\boldsymbol{H}} = {\rm{d}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{G}}{\rm{d}}\mathit{\boldsymbol{\theta }} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{BE\omega }} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{I\omega }} = {\omega _1}^2 + {\omega _2}^2 \end{array} $ | (70) |
And the 2nd and 3rd fundamental forms are:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{II}} \equiv - {\rm{d}}\mathit{\boldsymbol{H}} \cdot {\rm{d}}\mathit{\boldsymbol{u}} = {\rm{d}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{B}}{\rm{d}}\mathit{\boldsymbol{\theta }} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{BE\omega }} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{L\omega }}\\ \mathit{\boldsymbol{III}} \equiv {\rm{d}}\mathit{\boldsymbol{u}} \cdot {\rm{d}}\mathit{\boldsymbol{u}} = {\rm{d}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{C}}{\rm{d}}\mathit{\boldsymbol{\theta }} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{CE\omega }} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{L}}^2}\mathit{\boldsymbol{\omega }} \end{array} \right. $ | (71) |
So we can obtain the normal curvature kn, Gaussian curvature k and mean curvature
| $ \left\{ \begin{array}{l} {k_n} = \mathit{\boldsymbol{II/I}}\\ k = {k_1}{k_2}\det \mathit{\boldsymbol{L}}\\ \tilde k = \frac{1}{2}\left( {{k_1} + {k_2}} \right) = \frac{1}{2}{\rm{tr}}\mathit{\boldsymbol{L}} \end{array} \right. $ | (72) |
where k1, k2 are the eigenvalues of L and tr is to find the trace of a matrix. The relationship among them is
| $ k\mathit{\boldsymbol{I}} - 2\tilde k\mathit{\boldsymbol{II}} + \mathit{\boldsymbol{III}} = 0 $ | (73) |
Equivalently we have:
| $ k\mathit{\boldsymbol{G}} - 2\tilde k\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{C}} = 0 $ | (74) |
The sign of Gaussian curvature suggests an elliptic point if k>0, hyperbolic point if k < 0 and parabolic point or planar umbilic of the surface if k=0 for specific H*[21].
4.9 Summary of Singularity AnalysisIn this section, CMG singularity are analyzed and visualized by several classical and modern methods.Singular surface presents intuitive expression about CMG singularity, which can be evaluated and measured by certain functions. We analyzed the gimbal angels, null motion and the properties of Jacobian matrix from different angles of view.Different methods for singularity analysis would inspire some unique steering logics. The next section would concentrate on steering laws.
5 CMG Steering StrategyThe major concern for using CMG as spacecraft attitude control actuator is steering strategy design. On one hand it is expected to solve the inverse mapping problem, and on the other hand the accuracy should be guaranteed. What is more the CMG inherent geometric singularity is the main problem which deserve more attention. The pseudo-inverse solution is considered as an exact method without any torque error but fails to escape singularity. In order to escape the singularity null motion[3, 6] is added to the pseudo-inverse solution, which however can only deal with the hyperbolic singularity.When making a compromise between the accuracy and robust, researchers have proposed the singularity robust steering logic[8, 10], of which the generalized singular robust logic is most effective with singularity escape for all singularities. To minimize the torque error further, the singular direction steering logic[22-23]has been derived by the SVD method.Besides these, other techniques[1, 18-21] and theory are also applied to CMG control.This section will summarize different steering logics and finally form a comprehensive and integrated CMG theory framework.
5.1 Overview of CMG Steering StrategyThe so-called steering logic is designed to determine the gimbal angle rate
Definition 2: The steering strategy is an algorithm or a procedure that can determine the gimbal angle rate vector
| $ \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{J\dot \delta }}\;{\rm{or}}\;\mathit{\boldsymbol{\tau }} \approx \mathit{\boldsymbol{J\dot \delta }} $ | (75) |
The definition above implies:1)the torque command must be tracked precisely within error tolerance; 2)the system should be controllable which means singularity avoidance.
Many researchers have proposed various logics although the above requirements sometimes could not be guaranteed exactly.
5.2 Pseudo-inverse Steering LogicThe most classical and basic steering logic for CMG cluster is pseudo-inverse solution. Considering the equation about
| $ \mathit{\boldsymbol{J\dot \delta }} = \mathit{\boldsymbol{\tau }} $ | (76) |
whose solution is expected to minimize the index:
| $ \mathit{\Gamma } = \frac{1}{2}{{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{\dot \delta }} $ | (77) |
Consequently the pseudo-inverse solution is the mini-two norm solution[8, 10, 20].More generally, let's discuss the weighted minimum-two norm problem:
| $ \mathit{\Gamma } = \min \left[ {\frac{1}{2}{{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{Q\dot \delta }}} \right]\;\;\;\;{\rm{s}}.{\rm{t}}.\;\;\;\mathit{\boldsymbol{J\dot \delta }} = \mathit{\boldsymbol{\tau }} $ | (78) |
where Q=QT is a weighted matrix.
The Lagrange multiplier method will be used to find the solution and the Lagrange equation of this problem is
| $ L\mathit{\boldsymbol{ = }}\frac{1}{2}{{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{Q\dot \delta }} + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{J\dot \delta }}} \right) $ | (79) |
where λ is Lagrange multiplier. The partial derivative of L for the optimal problem should meet:
| $ \frac{{\partial \mathit{\boldsymbol{L}}}}{{\partial \mathit{\boldsymbol{\dot \delta }}}} = {{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{Q}} - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{J}} = 0 $ | (80) |
| $ \frac{{\partial \mathit{\boldsymbol{L}}}}{{\partial \mathit{\boldsymbol{\lambda }}}} = \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{J\dot \delta }} = 0 $ | (81) |
from Eq.(80) we have:
| $ {{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}} = {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{Q}}^{ - 1}}\;{\rm{or}}\;\mathit{\boldsymbol{\dot \delta }} = {\left( {{\mathit{\boldsymbol{Q}}^{ - 1}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }} $ | (82) |
substituting Eq.(82) into Eq.(81):
| $ \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{J\dot \delta }} = \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{J}}{\left( {{\mathit{\boldsymbol{Q}}^{ - 1}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = 0 $ | (83) |
So
| $ \mathit{\boldsymbol{\lambda }} = {\left[ {\mathit{\boldsymbol{J}}{{\left( {{\mathit{\boldsymbol{Q}}^{ - 1}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right]^{ - 1}}\mathit{\boldsymbol{\tau }} $ | (84) |
substituting Eq.(84) into Eq.(80):
| $ \mathit{\boldsymbol{\dot \delta }} = {\left( {{\mathit{\boldsymbol{Q}}^{ - 1}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = {\left( {{\mathit{\boldsymbol{Q}}^{ - 1}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{J}}{{\left( {{\mathit{\boldsymbol{Q}}^{ - 1}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right]^{ - 1}}\mathit{\boldsymbol{\tau }} $ | (85) |
considering Q=QT we have:
| $ \mathit{\boldsymbol{\dot \delta }} = {\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{J}}_Q^ + \mathit{\boldsymbol{\tau }} $ | (86) |
where, JQ+= Q-1JT (J Q-1JT)-1. When Q=I, J+=JT (J JT)-1 is the solution of Eq.(77).Note that no pseudo-inverse solution exists for rank(J)=2. That's why it cannot treat the singular problem.
5.3 Null Motion Steering StrategyThe null motion is added into steering logic to deal with the singular problem[3, 6, 30-31, 35]. The algebra implies the integrated form of solution for an equation contains: the particular solution and homogeneous solution. So gimbal rate for Eq.(76) is
| $ \mathit{\boldsymbol{\dot \delta }} = {{\mathit{\boldsymbol{\dot \delta }}}_P} + {{\mathit{\boldsymbol{\dot \delta }}}_H} = {\mathit{\boldsymbol{J}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{\tau }} + \rho \mathit{\boldsymbol{n}} $ | (87) |
where,
| $ \rho \mathit{\boldsymbol{ = }}\left\{ \begin{array}{l} {S^6},S \ge 1\\ {S^{ - 6}},S < 1 \end{array} \right. $ | (88) |
where:
Another way to determine the null motion vector is
| $ \mathit{\boldsymbol{n}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{J}}^ + }\mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{d}} $ | (89) |
where d is a nonzero vector and is usually chosen as:
| $ \mathit{\boldsymbol{d}} = {\rm{grad}}f = \nabla f = {\left[ {\begin{array}{*{20}{c}} {\partial f/\partial {\delta _1}}& \cdots &{\partial f/\partial {\delta _n}} \end{array}} \right]^{\rm{T}}} $ | (90) |
where
| $ f\left( \mathit{\boldsymbol{\delta }} \right) = \frac{1}{{\det \left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right)}} $ | (91) |
Above method is the gradient method[3]. Null motion however still fails to deal with elliptic singularity. Consequently Ref.[41] proposed the approach of state feedback along with null motion. Choosing Lyapunov energy function as:
| $ V = \frac{1}{2}{\left( {{\mathit{\boldsymbol{\delta }}_r} - \mathit{\boldsymbol{\delta }}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{\delta }}_r} - \mathit{\boldsymbol{\delta }}} \right) $ | (92) |
where δr is the reference sate. The performance index is
| $ \mathit{\Gamma } = \min \left( {{{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{\dot \delta }} + \rho {{\left( {{\mathit{\boldsymbol{\delta }}_r} - \mathit{\boldsymbol{\delta }}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\dot \delta }}} \right) $ | (93) |
The achieved solution is:
| $ \mathit{\boldsymbol{\dot \delta }} = {\mathit{\boldsymbol{J}}^ + }\mathit{\boldsymbol{\tau }} + \rho \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{J}}^ + }\mathit{\boldsymbol{J}}} \right)\left( {{\mathit{\boldsymbol{\delta }}_r} - \mathit{\boldsymbol{\delta }}} \right) $ | (94) |
The first term is pseudo-inverse solution and the second is null motion solution. Eq.(94) in ideal conditions can avoid singularity.
5.4 Steering Strategy with Torque ErrorIn large-angle attitude maneuver scenarios, the extreme accuracy will not be a major concern, which implies much tolerance for torque error. Some singularity avoidance/escape logics[3, 8, 10, 21]introduces torque error to treat the singular problem.
By adding some error into mini-two norm problem, we can find:
| $ \mathit{\Gamma } = \min \left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Pe}} + {{\mathit{\boldsymbol{\dot \delta }}}^{\rm{T}}}\mathit{\boldsymbol{Q\dot \delta }}} \right) $ | (95) |
where,
| $ \mathit{\boldsymbol{\dot \delta }} = {\mathit{\boldsymbol{J}}^{\# 1}}\mathit{\boldsymbol{\tau }} $ | (96) |
where:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}^{\# 1}} = {{\left[ {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{PJ}} + \mathit{\boldsymbol{Q}}} \right]}^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + } \right.}\\ {{{\left. {{\mathit{\boldsymbol{P}}^{ - 1}}} \right]}^{ - 1}} = \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{J}}^{\rm{T}}}{{\left[ {\mathit{\boldsymbol{JW}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + \mathit{\boldsymbol{V}}} \right]}^{ - 1}}} \end{array} $ | (97) |
where W=Q-1, V=P-1.[ JT PJ+Q]-1∈ Rn×n and [JW JT+ V]-1∈ R3×3 are always non-singular because of the positive definiteness of matrix Q and P. Generally weighted matrices are chosen as:
| $ {\mathit{\boldsymbol{P}}^{ - 1}} = \mathit{\boldsymbol{V}} = \lambda \left[ {\begin{array}{*{20}{c}} 1&{{ \in _3}}&{{ \in _2}}\\ {{ \in _3}}&1&{{ \in _1}}\\ {{ \in _2}}&{{ \in _1}}&1 \end{array}} \right] > 0 $ | (98) |
| $ {\mathit{\boldsymbol{Q}}^{ - 1}} = \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{W_1}}&\lambda &\lambda &\lambda \\ \lambda &{{W_2}}&\lambda &\lambda \\ \lambda &\lambda &{{W_3}}&\lambda \\ \lambda &\lambda &\lambda &{{W_4}} \end{array}} \right] > 0 $ | (99) |
Once P =0 it will become pseudo-inverse logic. And when Q = λ I4, we can get the generalized singular robust steering logic:
| $ \begin{array}{l} {\mathit{\boldsymbol{J}}^{\# 2}} = {\left[ {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{PJ}} + \lambda {\mathit{\boldsymbol{I}}_4}} \right]^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{J}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{PJ}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + \lambda {\mathit{\boldsymbol{I}}_3}} \right]^{ - 1}}\mathit{\boldsymbol{P}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{J}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + \lambda {\mathit{\boldsymbol{P}}^{ - 1}}} \right]^{ - 1}} = {\mathit{\boldsymbol{J}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + \lambda \mathit{\boldsymbol{E}}} \right]^{ - 1}} \end{array} $ | (100) |
where:
| $ {\mathit{\boldsymbol{P}}^{ - 1}} = \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} 1&{{ \in _3}}&{{ \in _2}}\\ {{ \in _3}}&1&{{ \in _1}}\\ {{ \in _2}}&{{ \in _1}}&1 \end{array}} \right] > 0 $ | (101) |
Further, when P=I3 and Q = λ I4, it will degenerate to the singular robust steering logic:
| $ {\mathit{\boldsymbol{J}}^{\# 3}} = {\left[ {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}} + \lambda {\mathit{\boldsymbol{I}}_4}} \right]^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} = {\mathit{\boldsymbol{J}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}} + \lambda {\mathit{\boldsymbol{I}}_3}} \right]^{ - 1}} $ | (102) |
The parameters λ, ∈i and Wi above should be properly chosen.Parameter λ decides whether it will introduce error or not. If λ=0, we can get the precise solution. Therefore an advisable way is to set a threshold value (Eq.(103)) to add the torque error:
| $ \lambda = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ {\lambda _0}\left( {1 - S/{S_0}} \right), \end{array}&\begin{array}{l} S \ge {S_0}\\ S < {S_0} \end{array} \end{array}} \right. $ | (103) |
where S=[det (J JT)]1/2 and S0 is the threshold.Another continuous function[9, 30, 32] is
| $ \lambda = {\lambda _0}\exp \left[ { - \mu \det \left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right)} \right] $ | (104) |
where, λ0 and μ are scalar parameters. The worse CMGs system is, the lager λ becomes and consequently the more errors are added.
For any non-zero torque command, generalized singular robust steering logicis should guarantee non-zero gimbal rate solution. The simple way is to modulate ∈i continuously:
| $ { \in _i} = { \in _0}\sin \left( {\omega t + {\phi _i}} \right) $ | (105) |
where, the amplitude ∈0, frequency ω and initial phase ϕi should be properly selected.
The singular robust steering logic J#3 cannot guarantee the singularity escape and even can constrain the available momentum workspace. The sensor noise would result in singularity when using J#3[3, 8, 21]. J#2 could deal with all internal singularities and exploit the momentum envelope fully.When W≠I, J#1 is expected to escape all kinds of singularities including the saturation singularity with a compromise between accuracy and robustness.
5.5 Singular Value Decomposition Analysis for Steering LogicHere the singular value decomposition will be used again to find some interesting factors of the logics discussed above.Pseudo-inverse steering logic can be decomposed as:
| $ {\mathit{\boldsymbol{J}}^ + } = \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{S}}^ + }{\mathit{\boldsymbol{U}}^{\rm{T}}} $ | (106) |
where:
| $ {\mathit{\boldsymbol{S}}^ + } = \left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left( {\begin{array}{*{20}{c}} {\frac{1}{{{\sigma _1}}}}&{\frac{1}{{{\sigma _2}}}}&{\frac{1}{{{\sigma _3}}}} \end{array}} \right)}\\ 0 \end{array}} \right] $ | (107) |
So
| $ {\mathit{\boldsymbol{J}}^ + } = \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{S}}^ + }{\mathit{\boldsymbol{U}}^{\rm{T}}} = \sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{u}}_i^{\rm{T}}/{\sigma _i}} $ | (108) |
and when σ3=0, it's advised:
| $ {\mathit{\boldsymbol{J}}^ + } = \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{S}}^ + }{\mathit{\boldsymbol{U}}^{\rm{T}}} = \sum\limits_{i = 1}^2 {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{u}}_i^{\rm{T}}/{\sigma _i}} $ | (109) |
similarly we have the form for J#3= VS#3UT, where:
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}^{\# 3}} = \\ \;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left( {\begin{array}{*{20}{c}} {\frac{{{\sigma _1}}}{{\sigma _1^2 + \lambda }}}&{\frac{{{\sigma _2}}}{{\sigma _2^2 + \lambda }}}&{\frac{{{\sigma _3}}}{{\sigma _3^2 + \lambda }}} \end{array}} \right)}\\ 0 \end{array}} \right] \end{array} $ | (110) |
SVD implies the orthogonality between { u1, u2, u3}, which can construct a set of three-dimensional basis unit vector. And torque command τ represented by this new basis can be rewritten as:
| $ \mathit{\boldsymbol{\tau }} = \sum\limits_{i = 1}^3 {{\tau _i}{u_i}} $ | (111) |
Substituting Eq.(111) into Pseudo-inverse logic:
| $ \begin{array}{l} {{\mathit{\boldsymbol{{\dot \delta }}}}^ + } = {\mathit{\boldsymbol{J}}^ + }\mathit{\boldsymbol{\tau }} = \left( {\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{u}}_i^{\rm{T}}/{\sigma _i}} } \right)\left( {\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{u}}_i}} } \right) = \\ \;\;\;\;\;\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{v}}_i} \cdot \mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_i}/{\sigma _i}} = \sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{v}}_i}/{\sigma _i}} \end{array} $ | (112) |
The output torque is:
| $ \begin{array}{l} \mathit{\boldsymbol{T}}_{\rm{o}}^ + = \mathit{\boldsymbol{J}}\;\;{{\mathit{\boldsymbol{\dot \delta }}}^ + } = \left( {\sum\limits_{i = 1}^3 {{\sigma _i}{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} } \right)\left( {\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{v}}_i}/{\sigma _i}} } \right) = \\ \;\;\;\;\;\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{u}}_i}} = \mathit{\boldsymbol{\tau }} \end{array} $ | (113) |
and the torque error is
| $ \Delta {\mathit{\boldsymbol{\tau }}^ + } = \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{T}}_{\rm{o}}^ + = 0 $ | (114) |
similarly the gimbal rate solution for J#3is
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \delta }}}^{\# 3}} = {\mathit{\boldsymbol{J}}^{\# 3}}\mathit{\boldsymbol{\tau }} = \\ \;\;\;\;\;\left( {\sum\limits_{i = 1}^3 {{\sigma _i}{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{u}}_i^{\rm{T}}} /\left( {\sigma _i^2 + \lambda } \right)\left( {\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{u}}_i}} } \right)} \right. = \\ \;\;\;\;\;\sum\limits_{i = 1}^3 {{\sigma _i}{\tau _i}{v_i}} /\left( {\sigma _i^2 + \lambda } \right) \end{array} $ | (115) |
The control torque is:
| $ \begin{array}{l} \mathit{\boldsymbol{T}}_{\rm{o}}^{\# 3} = \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \delta }}}^{\# 3}} = \\ \;\;\;\;\;\;\left( {\sum\limits_{i = 1}^3 {{\sigma _i}{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} } \right)\left( {\sum\limits_{i = 1}^3 {{\sigma _i}{\mathit{\boldsymbol{\tau }}_i}{\mathit{\boldsymbol{v}}_i}} /\left( {\sigma _i^2 + \lambda } \right)} \right) = \\ \;\;\;\;\;\;\sum\limits_{i = 1}^3 {\sigma _i^2{\tau _i}{\mathit{\boldsymbol{u}}_i}} /\left( {\sigma _i^2 + \lambda } \right) \end{array} $ | (116) |
and the torque error becomes:
| $ \Delta {\mathit{\boldsymbol{\tau }}^{\# 3}} = \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{T}}_o^{\# 3} = \sum\limits_{i = 1}^3 {\lambda {\mathit{\boldsymbol{u}}_i}/\left( {\sigma _i^2 + \lambda } \right)} $ | (117) |
We can find the torque error in J#3 is as designed.
Here we may have a more deeply understanding about the matrixes U and V. The gimbal rate is a linear combination of vi (i=1, 2, 3 when CMG cluster does not encounter singularity). What is more U is the torque space and the singular value σi plays an important role in the mapping between torque and gimbal rate. Once the system is singular, σ3=0 and the output torque space degenerates to 2-dimension expressed by u1 and u2.Meanwhile v3 degenerates to null motion solution and u3 becomes singular vector.
5.6 Singular Direction Steering StrategySingular value decomposition implies torque error in some logics. In order to reduce error further, singular direction avoidance is proposed[22-23]. It is:
| $ {{\mathit{\boldsymbol{\dot \delta }}}^{{\rm{SDA}}}} = {\mathit{\boldsymbol{J}}^{{\rm{SDA}}}}\mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{S}}^{{\rm{SDA}}}}{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{\tau }} $ | (118) |
where:
| $ {\mathit{\boldsymbol{S}}^{{\rm{SDA}}}} = \left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left( {\begin{array}{*{20}{c}} {{\sigma _1}}&{{\sigma _2}}&{\frac{{{\sigma _3}}}{{\sigma _3^2 + \lambda }}} \end{array}} \right)}\\ 0 \end{array}} \right] $ | (119) |
And torque error is
| $ \Delta {\mathit{\boldsymbol{\tau }}^{{\rm{SDA}}}} = \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{T}}_o^{{\rm{SDA}}} = \lambda {\tau _3}{\mathit{\boldsymbol{u}}_3}/\left( {\sigma _3^2 + \lambda } \right) $ | (120) |
when in singularity Δ τSDA=τ3 u3, which means no torque along the singular direction and is terrible situation. The modified singular direction avoidance successfully handled the singularity is proposed by Tao Meng[23] with an Euler rotation to { u1, u2, u3}.
SVD inspired people to complement the error along the singular direction by making use of hybrid actuators. The strategy argued by Jin Lei[42] is a good example and the CMG steering logic is
| $ \mathit{\boldsymbol{\dot \delta }} = - {\mathit{\boldsymbol{V}}_1}{\mathit{\boldsymbol{S}}_{\lambda 1}}{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{\tau }} $ | (121) |
where, V1=[v1 v2 v3].
| $ {\mathit{\boldsymbol{S}}_{\lambda 1}} = {\rm{diag}}\left( {\begin{array}{*{20}{c}} {\frac{1}{{{\sigma _1}}}}&{\frac{1}{{{\sigma _2}}}}&{\frac{1}{{{\sigma _3} + \lambda }}} \end{array}} \right) $ | (122) |
where, λ is determined by Eq.(104). The control law for momentum wheel is
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} = - {\mathit{\boldsymbol{D}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{D}}^{\rm{T}}}} \right)^{ - 1}}{\mathit{\boldsymbol{u}}_3}\mathit{\boldsymbol{u}}_3^{\rm{T}}\mathit{\boldsymbol{\tau }}/\left( {{{\rm{ \mathit{ σ} }}_3} + \lambda } \right) $ | (123) |
where
Based on generalized-inverse, Ref.[26] proposed steering law for pyramid CMG system (four CMGs in this configuration). Pseudo-inverse and singular robust are said to suffer internal singularity and cannot exploit the entire workspace. The generalized inverse law would solve this tough problem.
Defining a new set of angles ψ ∈ R3 and a mapping, we have:
| $ \mathit{\boldsymbol{\psi }} = g\left( \mathit{\boldsymbol{\delta }} \right) $ | (124) |
Considering a new matrix A(δ)
| $ \mathit{\boldsymbol{\dot \delta }} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\dot \psi }} $ | (125) |
and so
| $ \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{J\dot \delta }} = \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\dot \psi }} $ | (126) |
For a non-singular matrix J AT
| $ \mathit{\boldsymbol{\dot \psi }} = {\left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{\tau }} $ | (127) |
Consequently
| $ \mathit{\boldsymbol{\dot \delta }} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\dot \psi }} = {\mathit{\boldsymbol{A}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{\tau }} $ | (128) |
The matrix A(δ) is chosen as A=J+H, in which the column vectors of J are orthogonal to the column vectors of matrix H. Simulation results indicate the accuracy in attitude maneuvers and singularity avoidance. The great momentum capacity of CMG is fully exploited to track the command torque.Moreover, the proposed steering logic brings gimbal angle to zero at the end of maneuver serving as an initial condition for next time.
5.8 Generalized Constrained Steering StrategyThe generalized constrain model is designed to move the burden from steering logic designing to modeling. Now let's focus on a simple cluster of 3-parallel with following Jacobian Matrix
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} { - \sin {\delta _1}}&{ - \sin {\delta _2}}&{ - \sin {\delta _3}}\\ {\cos {\delta _1}}&{\cos {\delta _2}}&{\cos {\delta _3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{J_1}}\\ {{J_2}} \end{array}} \right] $ | (129) |
The constrained condition[4-5] is chosen artfully as:
| $ \mathit{\boldsymbol{D}} = \left[ {{\beta _1}{J_1} + {\beta _2}{J_2} + {\beta _3}\left( {{J_1} \times {J_3}} \right)} \right]\mathit{\boldsymbol{\dot \delta }} = \mathit{\boldsymbol{C\dot \delta }} $ | (130) |
where we can find the constrained matrix C is linear independent to J1 and J2. And the dynamic formula is
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\tau }}\\ \mathit{\boldsymbol{D}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\tau _x}}\\ {{\tau _y}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{J_1}}\\ {{J_2}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \delta }_1}}\\ {{{\dot \delta }_2}}\\ {{{\dot \delta }_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{J}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]\mathit{\boldsymbol{\dot \delta }} $ | (131) |
If J1×J2≠0, the system is non-singular and further study implies the above method can avoid singularity effectively. However it may not be easy to find those constrained equations just like the difficulty in steering logic designing.
5.9 Other Steering StrategiesMore theories have been introduced to design steering logics, such as cost function[1], inverse kinematics[28], constrained gimbal angle[18, 27], constrained energy and loads[43-44], game theory[24], and differential geometry[19, 21, 25]. Refs.[6] and[33] proposed hybrid steering logics against the single law used in CMG control. The mixed actuators based on CMG also were studied[45-49].
Cost function in Ref.[1] is proposed to denote how much sacrifice is needed to pass the singular surface. The function at the point (h,
| $ {\mathit{\boldsymbol{F}}_{S\mathit{\boldsymbol{h}},\mathit{\boldsymbol{\dot h}}}} = \sum\limits_{{\varepsilon _s} = 1}^7 {\left[ {{\gamma _{{\varepsilon _s}}}\left( {{\mathit{\boldsymbol{n}}_{{\mathit{\boldsymbol{h}}^s}}} \cdot \mathit{\boldsymbol{\dot h}}} \right)} \right]} $ | (132) |
where, γεs is the surface density and nhs is the normal vector of singular surface at singular momentum hs which is the nearest to h.By using momentum path planning and look-up table method, it adds some errors to help to change momentum route to pass the internal singular surface with least cost.
Another method for pyramid singularity is inverse kinematic steering logic, based on inverse kinematics computational procedure.Some improvements have been made, resulting in an online law.
When considering the practical case, Lapps[18]proposed the gimbal angel constrained logic. The constrained robust steering is
| $ {{\mathit{\boldsymbol{\dot \delta }}}_c} = \mathop {sat}\limits_{ \pm {{\dot \delta }_{\max }}} \left\{ {{\mathit{\boldsymbol{J}}^{\# 2}}\mathit{\boldsymbol{\tau }} + \gamma \left[ {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{J}}^{\# 2}}\mathit{\boldsymbol{J}}} \right]\left( {{\mathit{\boldsymbol{\delta }}^ * } - \mathit{\boldsymbol{\delta }}} \right)} \right\} $ | (133) |
where sat is saturation function, δ* is a set of desired gimbal angle and γ is a properly selected scalar.
Two kinds of steering logics were proposed in Ref.[24]using game theory analysis. One is the steering logic based on cooperative game theory, which treated the singularity avoidance as parameter optimization problem. And the other one was based on transfer utility multi-player game theory.
5.10 Summary of CMG Steering LogicIn order to determine the gimbal rate for given control torque command, several steering logics have been proposed based on different theories and are summarized in Fig. 20, where the arrow implies derivative relationship.

|
Fig.20 Diagram for CMG steering logic |
From the discussion above, it can be summarized that an optimal CMG steering logic should have the following characteristics:
1) Singularity avoidance/escape;
2) Error-free torque output;
3) Universality for different configurations;
4) Satisfaction for hardware restriction.
Two different research directions for CMG steering logic including hybrid logics and steering strategies based on modern theory should be intensively studied.It necessitates the modification of the classical laws to meet above requirements for space activities.
6 ConclusionsHigh-resolution image acquisition, rapid maneuvering for spacecraft imaging and other space observation missions depend on the powerful output of CMG. We have reviewed SGCMG control problems for agile spacecraft in the current literature. A theory framework about single gimbal control moment gyroscope, relating to configuration, evaluation and modeling, singularity visualization and singularity steering logics, are surveyed.The research presents comprehensive theories and knowledge. What's more, it's advised that the pyramid CMG cluster and FPC-Z cluster are two effective candidates for agile spacecraft for their static performance. The generalized singular steering logic is an efficient method to escape all kinds of singularities. What should be further dealt with is the practical form of this logic when considering the physical constrains.
Although the present work about CMG is quite comprehensive and well conducted, there still further work that should be done, including:
1) Refining the modeling method and finding universal and simple procedure for singularity avoidance;
2) Building the framework of configuration evaluation to select optimal clusters for specific space activities;
3) Designing more practical and efficient control logics for spacecraft in consideration of physical constrains with robustness and accuracy;
4) Studying mixed actuators based on CMG to pursue powerful torque amplification and free of singularity.
As many researches on this area are ongoing, this survey is by no means complete. The authors believe that the summarization of this work will provide new ideas for further investigation. References
| [1] |
Takada K, Kojima H, Matsuda N. Control moment gyro singularity-avoidance steering control based on singular-surface cost function. Journal of Guidance, Control, and Dynamics, 2010, 33(5): 1442-1450. DOI:10.2514/1.48381 (  0) 0) |
| [2] |
Kanzawa T, Haruki M, Yamanaka K. Steering law of control moment gyroscopes for agile attitude maneuvers. Journal of Guidance, Control, and Dynamics, 2016, 39(4): 952-962. DOI:10.2514/1.G001261 (  0) 0) |
| [3] |
Wie B, Bailey D, Heiberg C. Robust CMG steering logic for redundant single-gimbal control moment gyros. AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston: American Institute of Aeronautics and Astronautics, 2000.1-11.
(  0) 0) |
| [4] |
Laura, J, Mason P. A generalized framework for linearly-constrained singularity-free controlmoment gyro steering laws.AIAA Guidance, Navigation, and Control Conference.Reston: American Institute of Aeronautics and Astronautics, 2009.1-10.DOI: 10.2514/6.2009-5903. https://www.researchgate.net/publication/268557359_A_Generalized_Framework_for_Linearly-Constrained_Singularity-Free_Control_Moment_Gyro_Steering_Laws
(  0) 0) |
| [5] |
Jones L L, Zeledon R A, Peck M A. Generalized framework for linearly constrained control moment gyro steering. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1094-1103. DOI:10.2514/1.56207 (  0) 0) |
| [6] |
Leve F A, Fitz-Coy N G. Hybrid steering logic for single-gimbal control moment gyroscope. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1202-1212. DOI:10.2514/1.46853 (  0) 0) |
| [7] |
Wie B, Lu J. Feedback control logic for spacecraft eigenaxis rotations under slew rate and control constraints. Journal of Guidance, Control, and Dynamics, 1995, 18(6): 1372-1379. DOI:10.2514/3.21555 (  0) 0) |
| [8] |
Wie B. New singularity escape/avoidance steering logic for control moment gyro systems.AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston: American Institute of Aeronautics and Astronautics, 2003.1-11.
(  0) 0) |
| [9] |
Ozan T. Momentum envelopes and steering of control moment gyroscope clusters. AIAA/AAS Astrodynamics Specialist Conference.Reston: American Institute of Aeronautics and Astronautics, 2012.1-8. https://arc.aiaa.org/doi/10.2514/6.2012-4961
(  0) 0) |
| [10] |
Wie B. Singularity escape/avoidance steering logic for control moment gyro systems. Journal of Guidance, Control, and Dynamics, 2005, 28(5): 948-956. DOI:10.2514/1.10136 (  0) 0) |
| [11] |
Damilano P. Pleiades high resolution satellite: a solution for military and civilian needs in metric-class optical observation. Proceedings of the 15th Annual/USU Conference on Small Satellites.Reston: AIAA/USU, 2001.Paper No.SSC01-I-5. https://digitalcommons.usu.edu/cgi/viewcontent.cgi?referer=https://cn.bing.com/&httpsredir=1&article=1959&context=smallsat
(  0) 0) |
| [12] |
Girouart B, Sebbag I, Lachiver J M. Performance of Pleiades-HR agile attitude control system.Proceedings of the 5th International ESA Conference on Spacecraft Guidance, Navigation and Control System.Frascati, 2002.497-500.
(  0) 0) |
| [13] |
Defendini A, Faucheux P, Guay P, et al. A compact CMG products for agile satellites.Proceedings of 5th International ESA Conference on Spacecraft Guidance, Navigation and Control System. Frascati, 2002, 24-26. (  0) 0) |
| [14] |
Wie B, Barba P M. Quaternion feedback for spacecraft large angle maneuvers. Journal of Guidance, Control, and Dynamics, 1985, 8(3): 360-365. DOI:10.2514/3.19988 (  0) 0) |
| [15] |
Wie B, Bailey D, Heiberg C. Singularity robust steering logic for redundant single-gimbal control moment gyros. Journal of Guidance, Control, and Dynamics, 2001, 24(5): 865-872. DOI:10.2514/2.4799 (  0) 0) |
| [16] |
Wie B, Bailey D, Heiherg C. Rapid multi-target acquisition and pointing control of agile spacecraft. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 96-104. DOI:10.2514/2.4854 (  0) 0) |
| [17] |
Hans-Christian J, Rafal W. Quaternion feedback control for rigid-body spacecraft.AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston: American Institute of Aeronautics and Astronautics, 2001.1-6.
(  0) 0) |
| [18] |
Lappas V, Wie B. Robust CMG steering logic withgimbal angle constraints. Reston: AIAA, 2006: 2006.
(  0) 0) |
| [19] |
Kurokawa H. Survey of theory and steering laws of single-gimbal control moment gyros. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1331-1340. DOI:10.2514/1.27316 (  0) 0) |
| [20] |
Heiberg C J, Bailey D, Wie B. Precision spacecraft pointing using single-gimbal control moment gyroscopes with disturbance. Journal of Guidance, Control, and Dynamics, 2000, 23(1): 77-85. DOI:10.2514/2.4489 (  0) 0) |
| [21] |
Wie B. Space Vehicle Dynamics and Control. Second Edition.Reston:AIAA, 2008, 667-708. (  0) 0) |
| [22] |
Ford K A, Hall C D. Singular direction avoidance steering for control moment gyros. Journal of Guidance, Control, and Dynamics, 2000, 23(4): 648-656. DOI:10.2514/2.4610 (  0) 0) |
| [23] |
Meng T, Matunaga S. Modified singular-direction avoidance steering for control moment gyros. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1915-1920. DOI:10.2514/1.52640 (  0) 0) |
| [24] |
Jung Shin L, Hyo Choong B, Hyunjae L. Singularity avoidance by game theory for control moment gyros.AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: American Institute of Aeronautics and Astronautics, 2005: 1-20.
(  0) 0) |
| [25] |
Kurokawa H. A Geometric Study of Single Gimbal Control Moment Gyros-Singularity and Steering Logic.Report of Mechanical Engineering Laboratory, 1998.No 175. https://pdfs.semanticscholar.org/3de8/611270a0f70b04bdd60498e0632cd069b993.pdf.
(  0) 0) |
| [26] |
Sajjad A, Palmer P L, Roberts M. Exact steering law for pyramid-type four control moment gyro systems. AIAA/AAS Astrodynamics Specialist Conference and Exhibit: Keystone.Reston: American Institute of Aeronautics and Astronautics, 2006.1-10.
(  0) 0) |
| [27] |
Kurokawa H. Constrained steering law of pyramid-type control moment gyros and ground tests. Journal of Guidance, Control, and Dynamics, 1997, 20(3): 445-449. DOI:10.2514/2.4095 (  0) 0) |
| [28] |
Yamada K, Asai T, Jikuya I. Inverse kinematics in pyramid-type single-gimbal control moment gyro system. Journal of Guidance, Control, and Dynamics, 2016, 39(8): 1897-1907. DOI:10.2514/1.G001441 (  0) 0) |
| [29] |
Lappas J. A Control Moment Gyro Based Attitude Control System for Agile Small Satellite. Surrey: University of Surrey, 2002.
(  0) 0) |
| [30] |
Crenshaw J. 2-SPEED, a single-gimbal control moment gyro attitude control system.AIAA Guidance and Control Conference.Reston: American Institute of Aeronautics and Astronautics, 1973.No 73-895.
(  0) 0) |
| [31] |
Zhang Weitai, Xu Shiji. Singularity analyses of the five pyramid configuration with gyro failures. Journal of Tsinghua University(Science and Technology), 2008, 48(5): 888-891. (in Chinese) (  0) 0) |
| [32] |
Zhang Jinjiang. Research on configuration analysis and comparison of SGCMG system. Chinese Space Science and Technology, 2003, 23(3): 52-56. (in Chinese) (  0) 0) |
| [33] |
Wei Kongming, Wu Zhong, Liu Tao. Configuration analysis visualization of single gimbal control moment gyroscopes. Chinese Space Science and Technology, 2013, 1: 21-29. (in Chinese) (  0) 0) |
| [34] |
Jonathan W, Eric S, Frederick L, et al. Hardware testing of hybrid steering logic for single-gimbal control moment gyroscopes. AIAA Guidance, Navigation, and Control Conference.Reston: American Institute of Aeronautics and Astronautics, 2012.1-20.
(  0) 0) |
| [35] |
Wu Zhong, Wu Hongxin, Chou Wusheng. Kinematic singularity and its research progress in single gimbal control moment gyroscope system. Chinese Space Science and Technology, 2000, 3: 34-39. (in Chinese) (  0) 0) |
| [36] |
Cheng Guodong. Research on Attitude Maneuver Control of Agile Satellite Using Control Moment Gyroscopes. Harbin: Harbin Institute of Technology, 2014. (in Chinese)
(  0) 0) |
| [37] |
Margulies G, Aubrun J N. Geometric theory of single-gimbal control moment gyro systems. Journal of the Astronautical Sciences, 1978, 26(2): 159-191. (  0) 0) |
| [38] |
Shafarevich I R, Remizov A O. Linear Algebra and Geometry. Berlin: Springer, 2012: 67-69.
(  0) 0) |
| [39] |
Dominguez J, Wie B. Computation and visualization of control moment gyroscope singularity. Reston: AIAA, 2002: No 2002-4570.
(  0) 0) |
| [40] |
Kurokawa H. Exact singularity avoidance control of the pyramid type CMG system.AIAA Guidance, Navigation, and Control Conference.Reston: American Institute of Aeronautics and Astronautics, 1994.170-180. https://arc.aiaa.org/doi/abs/10.2514/6.1994-3559
(  0) 0) |
| [41] |
Takehiro H, Seiya U, Takuya O. Singularity avoidance steering logic for SGCMG systems using state feedback. AIAA/AAS Astrodynamics Specialist Conference.Reston: American Institute of Aeronautics and Astronautics, 2010. 1-11.
(  0) 0) |
| [42] |
Jin L, Xu S J. Attitude tracking control of a spacecraft using single gimbal control moment gyros and momentum wheels. Journal of Astronautics, 2008, 29(3): 916-921. (in Chinese) (  0) 0) |
| [43] |
Hyugjoo Y, Panagiotis T. Singularity analysis and avoidance of variable-speed control moment gyros-Part Ⅱ: Power constraint case. AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Reston: American Institute of Aeronautics and Astronautics, 2004.1-16. https://wenku.baidu.com/view/8497cb0e6c85ec3a87c2c5af.html
(  0) 0) |
| [44] |
Yasuyuki N, Masaki T. An integrated steering law considering Biased loads and singularity for control moment gyroscopes. AIAA Guidance, Navigation, and Control Conference.Reston: American Institute of Aeronautics and Astronautics, 2015.1-17. https://keio.pure.elsevier.com/en/publications/an-integrated-steering-law-considering-biased-loads-and-singulari-3
(  0) 0) |
| [45] |
Cole C D, Eric D S, Richard G C, et al. Optimal attitude control of agile spacecraft using combined reaction wheel and control moment gyroscope arrays. AIAA Modeling and Simulation Technologies Conference.Reston: American Institute of Aeronautics and Astronautics, 2016.1-23. https://arc.aiaa.org/doi/abs/10.2514/6.2016-0675
(  0) 0) |
| [46] |
Geng Miao, Lu Shan, Xia Yongjing. Fast maneuver by mixed control moment gyro and momentum wheel. Aerospace Shanghai, 2013, 30(1): 8-13. (in Chinese) (  0) 0) |
| [47] |
Geng Yunhai, Hou Zhili. Hybrid actuator control torque allocation algorithm for rapid maneuver satellite. Journal of Astronautics, 2013, 5: 611-616. (in Chinese) (  0) 0) |
| [48] |
Wang Huanjie, Jin Lei, Jia Yinghong. Agile satellite attitude maneuver. Aerospace Control and Application, 2015, 6: 19-24. (in Chinese) (  0) 0) |
| [49] |
Hu Yusang, Wang Dayi, Liu Chengrui. Reconfigurability research on satellite control system with mixed actuators. Aerospace Control, 2014, 32(3): 44-50. (in Chinese) (  0) 0) |
 2018, Vol. 25
2018, Vol. 25


