2. Department of Bridge Engineering, Tongji University, Shanghai 200092, China
Bridges represent essential parts of transportation network. Due to the existence of various risk factors, unavoidable damage may occur to bridge structures, which leads to huge economic loss and casualties. Thus, it is necessary to rigorously perform risk assessment to avert accidents. Risk assessment is the process of evaluating risks related to a specific case. The aim of risk assessment for bridges during construction is to help decision-makers propose 1) reasonable security arrangements and 2) appropriate organization plans[1]. Compared with other phases, the construction stage of bridges is more likely to be plagued by various risk factors related to construction technologies, natural hazards, and human factors, which often give rise to extra costs, schedule delays, and even total project failure[2]. Nevertheless, literature suggests that risk analysis of bridges during construction has not been taken into account as equally as that of bridges in design, operation, or maintenance stage[3].
Risk identification, the first step of risk assessment of bridges during construction, is an extremely complex issue and has important impact on the validity of the subsequent risk analysis and control. As a matter of fact, finding out more probable risk factors among the many risk factors can be regarded as a multi-criteria decision making (MCDM) problem, in which the criteria should meet various requirements. The analytical hierarchy process (AHP) method has become one of the most commonly used approaches to solve various decision-making problems over the past several decades. The principle behind this method is that by organizing the key factors of a MCDM problem into a hierarchical structure, the analysts are able to make the best decision on the basis of a set of simple comparisons and rankings instead of complex decisions. Therefore, the AHP method can be used for bridge risk identification. Since Saaty[4] proposed the AHP method in the mid-1970s, several efforts have been made to improve this method and enlarge its applicable range. So far, the AHP method has made rapid progress in a variety of fields such as optimization, best alternative selecting, planning, etc[5-14]. However, the AHP method is unable to handle the intrinsic inaccuracy and vagueness derived from the transformation of one's standpoint to a precise number. To tackle this problem, the FAHP method has been developed recently[15-16].
However, most approaches of the existing AHP and FAHP methods to solve MCDM problems are based on a 9-point scale of relative importance between Ci(i-th criterion) and Cj(j-th criterion), which can be referred to in Table 1. Although these methods have been widely used, the conventional AHP and FAHP methods have the following disadvantages: 1) fuzzy comparison matrices are hardly consistent in the course of risk identification by using the 9-point scale. Thus, pairwise comparisons process is required to be repeated, which may consume a large amount of time; 2) in practice, decision-makers usually find it extremely difficult to conduct exact pairwise comparison judgments by using a 9-point scale.
| Table 1 A 9-point scale of relative importance |
To circumvent the above disadvantages, a risk assessment method combining the FAHP method based on a 3-point scale (see Table 2), fuzzy set theory, and fuzzy logic was proposed in this paper. By using "logical checking", which only contains three cases: 1) "Ci" is equally important as "Cj"; 2) "Ci" is more important than "Cj", and 3) "Ci" is less important than "Cj", the process of constructing comparison matrix is greatly simplified. In the proposed method, fuzzy set theory and fuzzy logic can process inaccurate datasets consisting of non-numerical information. Aside from this feature, compared with other methods, the most valuable aspect of the fuzzy set theory is that it can be manipulated with linguistic variables since not every event can be represented numerically[17-19]. Literature indicates that in terms of risk assessment of bridges during construction, the application of this approach has not been studied before.
| Table 2 A 3-point scale of relative importance |
The organizational structure of this paper is as follows. Section 2 presents the framework of fuzzy logic-based theory for risk assessment. Section 3 demonstrates the proposed fuzzy logic-based method, where the FAHP method based on a 3-point scale is described and primary steps of the proposed fuzzy logic-based method are briefly presented. Section 4 investigates a numerical example which undergoes bridge risk assessment to prove the validity of the proposed method. Finally, main conclusions are drawn in Section 5.
2 Framework of Fuzzy Logic-Based Theory for Risk AssessmentAs depicted in Fig. 1, the hierarchically structured framework of the proposed fuzzy logic-based method to assess the risk of bridges during construction is based on the current codes in China[20]. The framework includes risk identification, risk ranking, risk analysis, and risk assessment. The first step of fuzzy logic-based method is risk identification, which is to identify all potential risks and their specifics that could undermine structural safety in construction stage. According to their order of importance, risk factors identified previously should be prioritized. Risk ranking plays a vital role in risk assessment and is implemented on the basis of experts′ subjective standpoints. The next step is risk analysis, which is to evaluate impacts of identified risks and is the pivotal step in the overall process of risk assessment. It consists of two parts: 1) probability of occurrence (probability analysis); 2) risk losses (loss analysis). The probability of risk occurrence during bridge construction can be obtained by probability analysis, and loss analysis is performed according to effects of risks on communities, environment, and people. In general, parameters of risk factors, including probability of occurrence and risk losses, can be obtained by quantitative and qualitative methods. Quantitative methods employ mathematical models to identify potential risks and their specifics that could influence the project. Qualitative methods such as Delphi technique estimate risks on the basis of experts′ subjective judgments depending on their experience and expertise[21]. Risk analysis was conducted by referring to experts′ subjective judgments and was calculated through the processes of fuzzification and aggregation in this study, as depicted in Fig. 1.
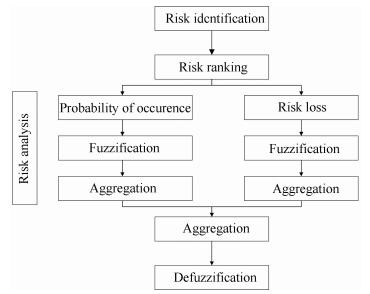
|
Fig.1 Framework of fuzzy logic-based theory for risk assessment |
Risk assessment including the process of aggregation and defuzzification is the last step of the framework. Mathematically, the final risk value of a bridge during construction can be derived by the following equation:
| $ R=PL $ | (1) |
where, P—probability of risk occurrence, L—risk losses.
3 Proposed Fuzzy Logic-Based Method for Risk Assessment of Bridges During ConstructionIn this study, the proposed fuzzy logic-based method integrated the FAHP method based on a 3-point scale, fuzzy logic, and fuzzy set theory and used the same basic concept of the aforementioned framework for risk assessment. In this approach, the FAHP method based on a 3-point scale was used to construct and rank diverse risk factors of a bridge during construction. Then the final risk level of this bridge was derived by using the proposed fuzzy logic-based theory.
3.1 FAHP Method Based on 3-Point Scale for Risk Identification and Risk RankingIn order to perform risk identification and figure out the priority weights of risk factors, an FAHP method based on a 3-point scale consisting of fuzzy consistent matrix (FCM) method and AHP was developed in Ref.[22]. The structured pairwise comparison matrix can be converted to an FCM C′ by FCM method. Since FCM is consistent, repeated consistency checking is not necessary. FAHP method based on a 3-point scale is not presented in this paper. Refer to Ref. [22] and [23] for more detailed introduction.
3.2 Fuzzy Logic-Based Theory for Risk Analysis and Risk AssessmentIn the proposed fuzzy logic-based method, risk analysis and risk assessment were conducted by utilizing fuzzy logic and fuzzy set theory, which can process inaccurate datasets consisting of non-numerical information. In this section, the procedure of risk analysis and risk assessment is outlined below, and more details can be found in Andric and Lu [1].
Step 1 Select the linguistic scale: Generally, we use linguistic variables to describe a specific issue. For example, to rank the probability of risk occurrence of a bridge, such a set of linguistic variables as very frequent (VF), frequent (F), moderate (M), rare (R), and very rare (VR) can be used. Similarly, to characterize the extent of risk losses, linguistic variables like very big (VB), big (B), moderate (M), small (S), and very small (VS) can be used. A set of linguistic variables like these is termed as linguistic scale. Mathematically, linguistic scale represents a group of fuzzy numbers. Trapezoidal and triangular fuzzy numbers are the most commonly used fuzzy numbers, and their membership functions are respectively defined as:
| $ {\mu _{{{\tilde A}_1}}}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {x - a} \right)/\left( {b - a} \right), }&{a \le x \le b}\\ {1, }&{b \le x \le c}\\ {\left( {d - x} \right)/\left( {d - c} \right), }&{c \le x \le d}\\ {0, }&{{\rm{otherwise}}} \end{array}} \right. $ | (2) |
| $ {\mu _{{{\tilde A}_2}}}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {x - a} \right)/\left( {b - a} \right), }&{a \le x \le b}\\ {\left( {d - x} \right)/\left( {d - b} \right), }&{b \le x \le d}\\ {0, }&{{\rm{otherwise}}} \end{array}} \right. $ | (3) |
For simplicity, trapezoidal and triangular fuzzy numbers are generally expressed as (a, b, c, d) and (a, b, d)[24]. The linguistic scale is selected based on the characteristic of the fuzzy numbers which is suited to represent specific linguistic variables for a specific issue.
Step 2 Collect linguistic data: In this step, subjective judgments of different experts are made in linguistic variables that have been selected in the previous step. The probability of risk occurrence and risk losses are assigned by experts in bridge engineering through questionnaire survey about every risk sub-factor.
Step 3 Fuzzify the collected data: The collected linguistic data of every risk sub-factor is transformed to matching fuzzy numbers which are selected in Step 1 in this step.
Step 4 Aggregate expert opinions: Every expert has his own judgments about every risk sub-factors. To integrate these judgments made by different experts, the process of fuzzy aggregation is needed.
This process can be expressed as the following equations, and expert judgments are weighted equally in this study.
| $ F{P_i} = \frac{1}{n}\mathop \sum \limits_{j = 1}^n F{P_{ij}} $ | (4) |
| $ F{L_i} = \frac{1}{n}\mathop \sum \limits_{j = 1}^n F{L_{ij}} $ | (5) |
where, n is the number of experts; j reprents the j-th expert; and i reprents the i-th risk factor; FLi is fuzzy risk loss of i-th risk factor; FPi is fuzzy probability of occurrence of i-th risk factor.
Step 5 Calculate fuzzy risk factor: The i-th fuzzy risk factor (FRFi) in accordance with i-th risk factor is obtained through multiplying FPi by FLi:
| $ FR{F_i} = F{P_i} \times F{L_i} $ | (6) |
Step 6 Calculate fuzzy risk index: The integral fuzzy risk index FR can be obtained by:
| $ FR = \mathop \sum \limits_{i = 1}^m {W_i} \times FR{F_i} $ | (7) |
where, m reprents the number of identified risk sub-factors, and Wi reprents the weight of i-th risk factor derived by using FAHP method presented in Section 3, FR is fuzzy risk.
Step 7 Defuzzify the aggregated fuzzy risk: Since the fuzzy risk index calculated in the previous step is a fuzzy number, it is necessary to conduct the defuzzification process to transform the fuzzy risk to a crisp risk value. In this step, the membership degree of fuzzy risk belonging to the fuzzy numbers selected in Step 1 are obtained first, and then the fuzzy risk is transformed to a crisp risk value by the following equation:
| $ R = \frac{{\mathop \sum \limits_{i = 1}^k {Y_i} \times \mu ({y_i})}}{{\mathop \sum \limits_{i = 1}^k \mu ({y_i})}} $ | (8) |
where, Yi reprents the center of i-th fuzzy set, μ(yi) reprents the membership function of i-th matching fuzzy set, and k reprents the total number of fuzzy sets in linguistic scale.
Step 8 Classify bridge risk: The bridge risk can be graded into several levels on the basis of different crisp risk values of fuzzy risk ratings calculated by using Eq. (8), and the final risk level of a bridge can thus be derived.
4 An Illustrative Example: A Bridge in Hunan, ChinaAizhai Suspension Bridge, with a central span length of 1 176 m in Hunan, China, was investigated as an example. Span arrangements of this bridge are (242+1 176+116) m. The deck cross-section is a steel truss girder which is 27 m in width and 7.5 m in height. The distance between two cables is 27 m and the hanger spacing is 14.5 m. The elevation view of this bridge is shown in Fig. 2.

|
Fig.2 Elevation of Aizhai Suspension Bridge (unit: cm) |
4.1 Risk Identification and Risk Ranking for Aizhai Suspension Bridge
The hierarchical structure for risk identification was established for Aizhai Suspension Bridge referring to the experts′ suggestions derived by using Delphi approach. The constructed hierarchical structure, as shown in Fig. 3, divides all identified criteria into four levels. The top and lowest level of the hierarchical structure denote the overall objective and the sub-risk factors, respectively. The construction sequence of Aizhai Suspension Bridge that consists of road excavation, slope protection construction, anchor construction, tower construction, cable construction, girder construction, deck pavement, and ancillary facilities construction was included at the second level. Four main criteria including quality, safety, schedule, and finance were in the third level. Further, the four main criteria were divided into several sub-criteria.

|
Note: A—Goal; B1—Road excavation and slope protection construction risk; B2—Anchor construction risk; B3—Tower construction risk; B4—Cable construction risk; B5—Girder construction risk; B6—Deck pavement and ancillary facilities construction risk; C1—Quality risk; C2—Safety risk; C3—Schedule risk; C4—Finance risk; D1—Drainage measures; D2—Foundation improvement; D3—Personnel security; D4—Severe weather; D5—Mechanical equipment; D6—Blasting work; D7—The quality of structural members; D8—Construction positioning; D9—Alignment quality; D10—Pushing of cable saddle; D11—Effect of temperature; D12—Design changes; D13—Structural material; D14—Hoisting procedure; D15—High altitude operation; D16—Electricity safety; D17—Construction organization management; D18—Construction load. Fig.3 Hierarchical structure for risk identification and ranking during construction of Aizhai Suspension Bridge |
Then the FAHP method on the basis of a 3-point scale described in Section 3 was used to perform risk identification and risk ranking of this bridge. The details are not displayed in this paper. The results shown in Tables 3-5 present the weight vectors and ranking of risk factors. It can be seen from Tables 3-5 that 1) anchor construction risk is the most important risk factor in risk group B, quality risk is the most important risk factor in risk group C, and drainage measures has the highest priority value in group D; 2) the 3-point scale in the adopted FAHP method is practical to complete the comprehensive risk identification and ranking of bridges during construction.
| Table 3 Weight vectors and ranking of pairwise comparison matrixes for risk group B based on the proposed method |
| Table 4 Weight vectors and ranking of pairwise comparison matrixes for risk group C based on the proposed method |
| Table 5 Weight vectors and ranking of pairwise comparison matrixes for risk group D based on the proposed method |
4.2 Risk Analysis and Risk Assessment for Aizhai Suspension Bridge
The analysis procedure which follows up the approach described in Section 3 is summed up as follows:
Step 1 Select the linguistic scale: A group of triangular fuzzy numbers were selected to characterize linguistic variables, as shown in Table 6.
| Table 6 Linguistic classification of grades of risk factors |
Step 2 Collect linguistic data: Two linguistic datasets with regard to risk losses and the probability of risk occurrence were gathered from five experienced experts (E1-E5) by questionnaires. Tables 7-8 indicate the collected data.
| Table 7 Probability of risk occurrence provided by experts in linguistic variables |
| Table 8 Risk losses provided by experts in linguistic variables |
Step 3 Fuzzify the collected data:The linguistic datasets in Tables 7-8 were transformed into fuzzy sets by utilizing linguistic scale in Table 6 and Fig. 4.

|
Fig.4 Linguistic scale of five members to evaluate probability of risk occurrence and risk losses |
Step 4 Aggregate expert opinions: The fuzzy sets obtained from the previous process were aggregated by Eqs. (4) and (5) in this step. The second and third columns in Table 9 show the results.
| Table 9 Aggregated parameters of fuzzy risk and fuzzy degree of risk factors |
Step 5 Calculate fuzzy risk factor: Fuzzy risk factor can be derived by Eq. (6) and the results are presented in the last column of Table 9.
Step 6 Calculate fuzzy risk index: The integral fuzzy risk of bridge was calculated using Eq. (7):
| $ FR = \mathop \sum \limits_{i = 1}^m {W_i} \times FR{F_i} = \left( {0.0330, 0.1232, 0.3479} \right) $ |
Step 7 Defuzzify the aggregated fuzzy risk: According to Fig. 5, the degree of membership of bridge fuzzy risk belonging to these fuzzy sets are:
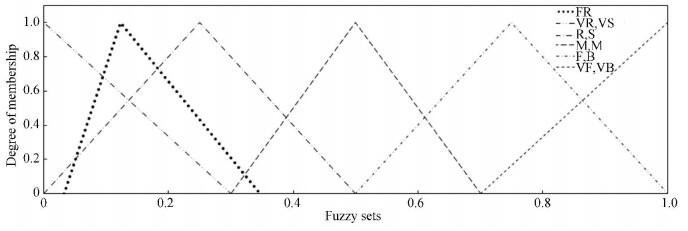
|
Fig.5 Corresponding fuzzy sets of fuzzy risk |
Moderate: μ=0.112 8;
Low: μ=0.732 9;
Very low: μ=0.684 3.
The bridge fuzzy risk was transformed to a crisp risk value by using Eq. (8):
| $ \begin{array}{l} \\ R = \frac{{0.1 \times 0.6843 + 0.25 \times 0.7329 + 0.5 \times 0.1128}}{{0.6843 + 0.7329 + 0.1128}} = 0.2013 \end{array} $ |
Step 8 Classify bridge risk: Five different crisp risk values were calculated by utilizing Eq. (8) (see Table 10) and four risk categories were defined corresponding to these crisp values (Risk Category 1-4), ranging from 0.13 to 0.80. The highest risk rating was 0.80. The minimum risk rating was 0.13. Then, risk categories represent four risk levels: low risk (LR), moderate risk (MR), high risk (HR), and very high risk (VHR), as is presented in Table 11.
| Table 10 Crisp risk levels |
| Table 11 Crisp risk ranges and categories |
It can be seen from Tables 6-11 that 1) the risk level of Aizhai Suspension Bridge obtained by the proposed method is moderate, which corresponds to the result estimated by Tongji University (2011)[25]; 2) fuzzy logic and fuzzy set theory can handle imprecise datasets and can be manipulated with linguistic variables. These advantages make the fuzzy logic-based method proposed in this study more practical since not all events can be represented numerically.
5 ConclusionsA new fuzzy logic-based method was developed in this paper for risk assessment of bridges during construction. The proposed method synthesized FAHP based on a 3-point scale, fuzzy logic, and fuzzy set theory into a single integrated approach. It can be reliably conducted by integrating both qualitative information based on the quantitative method and subjective judgments of experts. Firstly, FAHP based on a 3-point scale was applied to obtain weights of various risk factors and perform risk ranking. Moreover, the fuzzy logic and fuzzy set theory were utilized to compute the imprecise risk indicators with the linguistic variables.
On the basis of the risk assessment of Aizhai Suspension Bridge during construction, it can be concluded that:
1) The FAHP method on the basis of a 3-point scale is feasible for risk identification and risk ranking. A distinctive feature of this method is that it utilizes a 3-point scale to structure an FCM rather than a customary pairwise comparison matrix. Since the fuzzy comparison matrix is consistent, consistency checking is not required. Therefore, computation time of the whole process can be greatly saved. Another merit of this method is that only "1", "0.5", and "0" are used to describe the scale of significance in FCMM, thus overcoming the difficulties of making comparison and judgment caused by using a 9-point scale.
2) The example illustrated in Section 4 indicates that the proposed fuzzy logic-based method can be applied to risk assessment of bridges during construction. Further, it may be used for risk assessment in other engineering fields.
3) This paper provides an efficient method for risk assessment of bridges during construction. However, the results obtained from this study are restricted to special circumstances. Further study is needed to consider more alternatives of risk factors and establish more comprehensive hierarchical structure for a risk assessment problem.
| [1] |
Andric J M, Lu D G. Risk assessment of bridges under multiple hazards in operation period. Safety Science, 2016, 83: 80-92. DOI:10.1016/j.ssci.2015.11.001 (  0) 0) |
| [2] |
An M, Baker C, Zeng J. A fuzzy-logic-based approach to qualitative risk modeling in the construction process. World Journal of Engineering, 2005, 2(1): 1-12. (  0) 0) |
| [3] |
Hashemi H, Mousavi S M, Mojtahedi S M H. Bootstrap technique for risk analysis with interval numbers in bridge construction projects. Journal of Construction Engineering & Management, 2011, 137(8): 600-608. DOI:10.1061/(ASCE)CO.1943-7862.0000344 (  0) 0) |
| [4] |
Saaty T L. The Analytic Hierarchy Process. New York: McGraw-Hill, 1980.
(  0) 0) |
| [5] |
Vaidya O S, Kumar S. Analytic hierarchy process: An overview of applications. European Journal of Operational Research, 2006, 169(1): 1-29. DOI:10.1016/j.ejor.2004.04.028 (  0) 0) |
| [6] |
Mahdi I M, Alreshaid K. Decision support system for selecting the proper project delivery method using analytical hierarchy process (AHP). International Journal of Project Management, 2005, 23(7): 564-572. DOI:10.1016/j.ijproman.2005.05.007 (  0) 0) |
| [7] |
Bertolini M, Bevilacqua M. A combined goal programming-AHP approach to maintenance selection problem. Reliability Engineering & System Safety, 2006, 91(7): 839-848. DOI:10.1016/j.ress.2005.08.006 (  0) 0) |
| [8] |
Abudayyeh O, Zidan S J, Yehia S, et al. Hybrid prequalification-based, innovative contracting model using AHP. Journal of Management in Engineering, 2007, 23(2): 88-96. DOI:10.1061/(ASCE)0742-597X(2007)23:2(88) (  0) 0) |
| [9] |
Lin C C, Wang W C, Yu W D. Improving AHP for construction with an adaptive AHP approach (A3). Automation in Construction, 2008, 17(2): 180-187. DOI:10.1016/j.autcon.2007.03.004 (  0) 0) |
| [10] |
Al-Subhi Al-Harb A S. Application of the AHP in project management. International Journal of Project Management, 2001, 19(1): 19-27. DOI:10.1016/S0263-7863(99)00038-1 (  0) 0) |
| [11] |
Deng X Y, Hu Y, Deng Y, et al. Supplier selection using AHP methodology extended by D numbers. Expert Systems with Applications, 2014, 41(1): 156-167. DOI:10.1016/j.eswa.2013.07.018 (  0) 0) |
| [12] |
Yang J, Lee H. An AHP decision model for facility location selection. Facilities, 1997, 15(9/10): 241-254. DOI:10.1108/02632779710178785 (  0) 0) |
| [13] |
Liu H C, Liu L, Liu N. Risk evaluation approaches in failure mode and effects analysis: a literature review. Expert Systems with Applications, 2012, 40(2): 828-838. DOI:10.1016/j.eswa.2012.08.010 (  0) 0) |
| [14] |
Ghimire L P, Kim Y. An analysis on barriers to renewable energy development in the context of Nepal using AHP. Renewable Energy, 2018, 129(Part A): 446-456. DOI:10.1016/j.renene.2018.06.011 (  0) 0) |
| [15] |
Goyal R K, Kaushal S. Deriving crisp and consistent priorities for fuzzy AHP-based multicriteria systems using non-linear constrained optimization. Fuzzy Optimization and Decision Making, 2018, 17(2): 195-209. DOI:10.1007/s10700-017-9267-y (  0) 0) |
| [16] |
Chen J F, Hsieh H N, Do Q H. Evaluating teaching performance on the basis of fuzzy AHP and comprehensive evaluation approach. Applied Soft Computing, 2015, 8: 100-108. DOI:10.1016/j.asoc.2014.11.050 (  0) 0) |
| [17] |
Andric J M, Lu D G. Risk assessment of bridges using Fuzzy Logic Controller. EURODYN-International Conference on Structural Dynamics, 2014, 3073-3078. DOI:10.13140/RG.2.1.4218.2802 (  0) 0) |
| [18] |
Bede B. Fuzzy set-theoretic operations. Mathematics of Fuzzy Sets and Fuzzy Logic, 2013, 295: 13-31. DOI:10.1007/978-3-642-35221-8_2 (  0) 0) |
| [19] |
Petrović D V, Tanasijević M, Milic V, et al. Risk assessment model of mining equipment failure on the basis of fuzzy logic. Expert Systems with Applications, 2014, 41(18): 8157-8164. DOI:10.1016/j.eswa.2014.06.042 (  0) 0) |
| [20] |
Ministry of Transport of the People's Republic of China. Guidance on Safety Risk Assessment for Highway Bridge and Tunnel Construction (Trial). Beijing: China Communications Press, 2011.
(  0) 0) |
| [21] |
Linstone H A, Turoff M. The Delphi Method: Techniques and Applications. London: Addison-Wesley, 1975.
(  0) 0) |
| [22] |
Cheng J, Xiao R C. An efficient method for identification of risk factors. Science in China Series E: Technological Sciences, 2009, 52(12): 3626-3631. DOI:10.1007/s11431-009-0383-y (  0) 0) |
| [23] |
Yao M. A kind of adaptive fuzzy system. Control Theory and Applications, 1998, 15(3): 364-371. (  0) 0) |
| [24] |
Wang Y M, Elhag T M S. Fuzzy TOPSIS method on the basis of alpha level sets with an application to bridge risk assessment. Expert Systems with Applications, 2006, 31(2): 309-319. DOI:10.1016/j.eswa.2005.09.040 (  0) 0) |
| [25] |
Tongji University. Test Study on Risk Assessment During Construction of Aizhai Suspension Bridge. Shanghai: Tongji University, 2011.
(  0) 0) |
 2019, Vol. 26
2019, Vol. 26


