Since the realization of Bose-Einstein condensation in 1995[1-3], experimental and theoretical research related to Bose-Einstein condensation have been vigorously developed and research in the field of ultracold atom gas set off this boom. Specifically, the BHM[4-5] has been widely used to study the quantum phase transition process of the trapped ultracold atom system from the superconducting phase to the MI phase[6-7] as well as from the SF phase to MI phase[8-9]. BHM approximates the system of interacting bosons moving in a periodic potential at sufficiently low temperatures, in which long-range interactions among particles are ignored and only interactions between bosons in neighboring sites are considered. In second quantization notation, the Hamiltonian could be written as:
| $ H = - \mu \sum\limits_i {{n_i}} - t\sum\limits_{\left\langle {i,j} \right\rangle } {b_i^ + {b_j}} + \frac{U}{2}\sum\limits_i {{n_i}\left( {{n_i} - 1} \right)} $ | (1) |
where t is the hopping amplitude, μ is the chemical potential of the system, U is the repulsion interaction between on-site bosons, bi+ and bi are the creation and the annihilation operators of bosons. The symbol 〈i, j〉 denotes summation over all nearest-neighboring lattice sites i and j, while ni=bi+bi refers to the boson particle number operator on the lattice site i. The first term in the right-hand side of Eq. (1) represents the external potential of trapped atoms, the second term is the kinetic energy allowing for tunneling of particles between adjacent lattice sites, and the last contribution to the Hamiltonian is the potential term consisting of an on-site repulsive interaction when particles occupy the same lattice site.
The BHM provides a simple realization of the quantum phase transition. When t ≪ U, the on-site repulsion is dominant and the system is in a localized MI state. On the other hand, if t ≫ U, the hopping interactions play a more important role and the particle fluctuations are suppressed. In this situation, particles delocalize over the entire lattice, and the system will stay in the SF state.
The BHM has been studied using various methods, such as the coarse graining method[10], the strong-coupling expansion[11-12], the quantum Monte Carlo simulation[13], and the exact diagonalization algorithm[14]. Most of these methods are numerical calculations, which may mask useful physical information in the solutions. As a contrast, analytical methods can give more insight into the physical aspects of problems and can be easily used in further applications. At present, analytical and exact solutions for the BHM cannot be obtained, so scientists have to resort to approximation methods. The mean-field theory is one of the successful systematic methods to find analytical solutions, with which essential properties of the quantum phase diagram of the ground state for the 1-D BHM can be obtained analytically[15]. The key idea of the mean-field theory is that the fluctuation of particle interactions is ignored, and the influence of other particles on the given boson is approximated by a single effective mean "field" ψ. In this way, the many-body problem is reduced to a one-body problem which is easier to be solved.
The mean "field" ψ could be regarded as an order parameter of the system. As a consequence, free energy could be expressed as a Taylor expansion in the order parameter: E=α+γψ2+O(ψ4), where α and γ are expansion coefficients. According to the Landau theory, the phase transition boundary can be characterized by the order parameter. When ψ=0, the system is in the MI phase which has a relatively high symmetry, whereas ψ≠0 corresponds to a state in the SF phase which has a low symmetry. Then the phase transition boundary can be determined by the equation γ=0. Quantum phase transition phenomena could also be described by the particle-hole correlation function[16]. When the hopping energy t equals zero, the system is in a localized insulating state, and no particle-hole pairs exist. As t increases, quantum fluctuations will create correlated particle-hole pairs. This result implies the emergence of a non-local order in the system.
The double-chain BHM could be realized by loading ultracold Bose atoms into a double-well optical lattice potential[17-18]. The experiments have been studied via different theoretical methods, and offered new perspective on low-dimensional quantum liquids. It was found that novel quantum phases can emerge due to different inter- and intra-chain interactions[19]. Tschischik et al.[20] obtained the exact energy spectra of the system with a full diagonalization method. Pandey et al.[21] investigated various phases of hardcore bosons at zero temperature by using a time-dependent density-matrix renormalization group (t-DMRG) technique. Using quantum Monte Carlo simulations, Lv and Wang[22] identified the Haldane superfluid phase which has both nonlocal Haldane order and superfluidity. These methods are demonstrated to be powerful tools in dealing with the model, in the meantime they will require a huge amount of computational resources. In this paper, we apply the mean-field theory and the perturbation method to the double-chain BHM (as shown in Fig. 1), and obtain phase diagrams for systems with different parameters.In Fig. 1, the potential along the x axis is an asymmetric double-well potential, and potential along the z axis is a standing wave potential. The bosons can hop to nearest-neighbor sites between the chain a and the chain b with the energy -tab. ta (tb) is the hopping amplitude of the chain a (b), and U is the on-site repulsion interaction. The influence of tunneling and on-site repulsive interactions on the phase transition from SF to MI is discussed in detail. The quantum phase transition is also discussed using the correlation function of the associated particle-hole pairs, both for the inter-chain and the inner-chain cases.
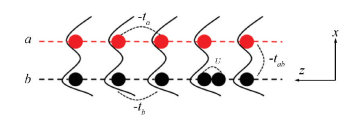
|
Fig.1 Schematic diagram of the double-chain BHM |
2 Model and Solution 2.1 Single-Chain Bose-Hubbard Model
Using the mean-field theory, the interaction effect of surroundings on the given boson could be approached by an effective "field" ψ. So that the Hamiltonian (1) in the single-chain system can be rewritten as:
| $ H = {H_{MF}} - t\sum\limits_{\left\langle {i,j} \right\rangle } {\left[ {\left( {b_i^ + - \frac{{{\psi ^ * }}}{{zt}}} \right){b_j} + b_j^ + \left( {{b_i} - \frac{\psi }{{zt}}} \right)} \right]} $ | (2) |
| $ {H_{MF}} = \sum\limits_i {\left[ { - \mu {n_i} + \frac{U}{2}{n_i}\left( {{n_i} - 1} \right)} \right]} - \sum\limits_i {\left( {\psi b_i^ + + {\psi ^ * }{b_i}} \right)} $ | (3) |
where z is the coordination number, ψ and ψ* refers to the order parameter and its complex conjugate. The order parameter could be determined by the self-consistent condition:
| $ \psi = zt\left\langle b \right\rangle $ | (4) |
and then the ground state energy of the Hamiltonian HMF can be expressed as:
| $ {E_n} = - \mu n + \frac{U}{2}n\left( {n - 1} \right) + F\left( {\mu ,U,n} \right){\left| \psi \right|^2} $ | (5a) |
| $ \begin{array}{l} F\left( {\mu ,U,n} \right) = \left( {n + 1} \right)/\left( {\mu - Un} \right) - n/\left[ {\mu - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {U\left( {n - 1} \right)} \right] \end{array} $ | (5b) |
Because t ≪ U in experiments, and the last term of Eq. (2) which describes the fluctuation of hopping interactions is very small compared to HMF, the system could be approached by the ground state wave function of HMF. Then the ground state energy of the total Hamiltonian Eq. (1) could be (approximately) obtained. According to the Ginzburg-Landau phase transition theory, near the phase transition boundary, the order parameter is small, so that the ground state energy can be expanded in powers of the order parameter ψ:
| $ {E_0} = {E_{00}} + \gamma {\left| \psi \right|^2} + O\left( {{{\left| \psi \right|}^4}} \right) $ | (6) |
where E00 is the zeroth-order approximation energy, O(|ψ|4) means higher-order corrections. Explicit calculations show that the second-order coefficient γ is proportional to
| $ 1 - ztF\left( {\mu ,U,n} \right) $ | (7) |
If γ is positive, the order parameter will vanish according to the self-consistence condition (4), as a consequence the system is in the MI phase. If γ is negative, we have ψ≠0, and the system is in the SF phase regime. The phase transition appears at the boundary determined by the equation γ=0.
2.2 Double-Chain Bose-Hubbard ModelFollowing the same idea as shown above, we apply the Ginzburg-Landau theory to the double-chain BHM which describes the system composed of two coupled chains a and b as illustrated in the Fig. 1. In addition to intra-chain hopping and on-site repulsive interactions, we include in the Hamiltonian the effect of inter-chain tunneling effects with which particles could hopping between corresponding sites in different chains, and the double-chain BHM could be defined by the Hamiltonian:
| $ H = {H_a} + {H_b} - {t_{ab}}\sum\limits_i {\left( {a_i^ + {b_i} + b_i^ + {a_i}} \right)} $ | (8) |
| $ {H_a} = - {t_a}\sum\limits_{\left\langle {i,j} \right\rangle } {a_i^ + {a_j}} - \mu \sum\limits_i {{n_{ai}}} + \frac{U}{2}\sum\limits_i {{n_{ai}}\left( {{n_{ai}} - 1} \right)} $ | (9) |
| $ {H_b} = - {t_b}\sum\limits_{\left\langle {i,j} \right\rangle } {b_i^ + {b_j}} - \mu \sum\limits_i {{n_{bi}}} + \frac{U}{2}\sum\limits_i {{n_{bi}}\left( {{n_{bi}} - 1} \right)} $ | (10) |
where Ha (Hb) is the single-chain Hamiltonian of the chain a (b), ta (tb) is the intra-chain hopping energy of the chain a (b), tab is the inter-chain hopping energy, ai+(bi+) and ai (bi) are the creation and the annihilation operators of the chain a (b), nai=ai+ai and nbi=bi+bi are the particle number operators at site i in the chain a and the chain b respectively. In parallel to the analysis of the single-chain model, we can rewrite the Hamiltonian (8) into the summation of mean-field Hamiltonians of two single chains and higher order corrections. Up to the quadratic terms of order parameters, the Hamiltonian Eq. (8) can be approximated as:
| $ \begin{array}{l} H = {H_{MFa}} - {t_a}\sum\limits_{\left\langle {i,j} \right\rangle } {\left\lfloor {\left( {a_i^ + - \frac{{\psi _a^ * }}{{z{t_a}}}} \right){a_j} + a_j^ + \left( {{a_i} - \frac{{{\psi _a}}}{{z{t_a}}}} \right)} \right\rfloor } + \\ \;\;\;\;\;\;{H_{MFb}} - {t_b}\sum\limits_{\left\langle {i,j} \right\rangle } {\left\lfloor {\left( {b_i^ + - \frac{{\psi _b^ * }}{{z{t_b}}}} \right){b_j} + b_j^ + \left( {{b_i} - \frac{{{\psi _b}}}{{z{t_b}}}} \right)} \right\rfloor } + \\ \;\;\;\;\;\;{t_{ab}}\sum\limits_{\left\langle {i,j} \right\rangle } {\left[ {\frac{{\psi _a^ * }}{{z{t_a}}}\frac{{{\psi _b}}}{{z{t_b}}}+\frac{{\psi _b^ * }}{{z{t_b}}}\frac{{{\psi _a}}}{{z{t_a}}}} \right]} \end{array} $ | (11) |
where HMFa (HMFb) is the mean-field Hamiltonian of the chain a (b) with the form as Eq.(3), ψa (ψb) and ψa* (ψb*) are order parameters and their complex conjugates for the chain a (b). These order parameters are determined by the self-consistence conditions:
| $ \psi _a^ * = zt\left\langle a \right\rangle ,\psi _b^ * = zt\left\langle b \right\rangle $ | (12) |
Suppose |ψa〉 and |ψb〉 are eigenstates of single-chain mean-field Hamiltonians HMFa and HMFb, the corresponding ground state energies are:
| $ {E_0} = {E_{00}} + {E_{{n_a}}} + {E_{{n_b}}} $ | (13) |
| $ {E_{00}} = \sum\limits_{k = a,b} {\left[ { - \mu {n_k} + \frac{U}{2}{n_k}\left( {{n_k} - 1} \right)} \right]} $ | (14) |
| $ \begin{array}{l} {E_{{n_a}}} = F\left( {\mu ,U,{n_a}} \right)\left[ {{{\left| {{\psi _a}} \right|}^2} + \frac{{{t_{ab}}}}{{z{t_b}}}\left( {\psi _a^ * {\psi _b} + \psi _b^ * {\psi _a}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\left( {\frac{{{t_{ab}}}}{{z{t_b}}}} \right)}^2}{{\left| {{\psi _b}} \right|}^2}} \right] \end{array} $ | (15) |
| $ \begin{array}{l} {E_{{n_b}}} = F\left( {\mu ,U,{n_b}} \right)\left[ {{{\left| {{\psi _b}} \right|}^2} + \frac{{{t_{ab}}}}{{z{t_a}}}\left( {\psi _b^ * {\psi _a} + \psi _a^ * {\psi _b}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\left( {\frac{{{t_{ab}}}}{{z{t_a}}}} \right)}^2}{{\left| {{\psi _a}} \right|}^2}} \right] \end{array} $ | (16) |
Obviously, in the limit of tab→0, the system will approach the one composed of two decoupled single chains with energies in the form of Eq. (5). In the mean-field theory, the system defined by Eq. (11) could be described by the product state |ψa〉⊗|ψb〉, therefore the expected value of the rest terms in Eq. (11) can be computed easily. Explicit calculations show that, near the MI-SF phase transition point, the ground state energy of the double-chain BHM in Eq.(8) can be described in the matrix form as:
| $ {E_0} = {E_{00}} + \left[ {\begin{array}{*{20}{c}} {\psi _a^ * }&{\psi _b^ * } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\gamma _a}}&{{\gamma _b}}\\ {{\gamma _{ba}}}&{{\gamma _b}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _a}}\\ {{\psi _b}} \end{array}} \right] + O\left( {{{\left| \psi \right|}^4}} \right) $ | (17) |
where
| $ {\gamma _k} = F\left( {\mu ,U,{n_k}} \right) + \frac{{t_{ab}^2}}{{z{t_k}}}F\left( {\mu ,U,{n_k}} \right) + \frac{1}{{z{t_k}}},k = a,b $ | (18) |
| $ {\gamma _{ab}} = {\gamma _{ba}} = F\left( {\mu ,U,{n_a}} \right) + \frac{{t_{ab}^2}}{{z{t_b}}}F\left( {\mu ,U,{n_b}} \right) + \frac{{{t_{ab}}}}{{{z^2}{t_a}{t_b}}} $ | (19) |
The ground state energy, which is a function of order parameters ψa and ψb, can be simplified to the following form via a unitary transformation:
| $ {E_0} = {E_{00}} + \left[ {\begin{array}{*{20}{c}} {\tilde \psi _a^ * }&{\tilde \psi _b^ * } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\lambda _a}}&0\\ 0&{{\lambda _b}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde \psi }_a}}\\ {{{\tilde \psi }_b}} \end{array}} \right] + O\left( {{{\left| \psi \right|}^4}} \right) $ | (20) |
where
| $ {\lambda _a} = \frac{{{\gamma _a} + {\gamma _b} - \sqrt {{{\left( {{\gamma _a} - {\gamma _b}} \right)}^2} + 4\gamma _{ab}^2} }}{2} $ | (21) |
| $ {\lambda _b} = \frac{{{\gamma _a} + {\gamma _b} + \sqrt {{{\left( {{\gamma _a} - {\gamma _b}} \right)}^2} + 4\gamma _{ab}^2} }}{2} $ | (22) |
and
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{{\gamma _a} - {\lambda _b}}}{{{\gamma _{ab}}}}}&{\frac{{{\gamma _a} - {\lambda _a}}}{{{\gamma _{ab}}}}}\\ 1&1 \end{array}} \right] $ | (23) |
One can find that, when λa or λb is negative, the minimal point of the ground state energy will be located at a non-zero point in the space expanded by
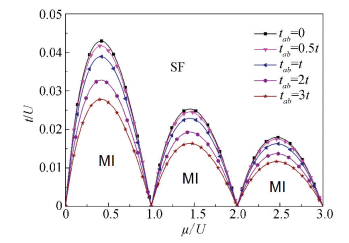
The analytical expressions of results for phase boundary conditions λa=0 or λb=0 with arbitrary tunneling and repulsive parameters are very lengthy and will not be presented here. In the following, we show some numerical results. In Fig. 2, the solid curves are real phase transition boundaries corresponding to tab=0, 0.5t, t, 2t and 3t respectively. we show phase diagrams for symmetric double-chain systems with ta=tb=t, where t is the parameter introduced for computational convenience. When the inter-chain hopping tab is vanishing, we obtain two coincide phase boundaries (the black-square-solid line in Fig. 2) because of ta=tb. The region above the boundary is the SF phase region, whereas below the boundary is the MI region. As the inter-chain hopping tab increases to 0.5t, two phase transition boundaries separate. One of them (the blue-up-triangle-solid line, determined by λb=0) moves toward the bottom of the phase diagram, and the other (the red-dot-dotted line, determined by λa=0) moves in the opposite direction. Obviously, the red-dot-dotted line is the false boundary, and the blue-up-triangle-solid line is the real phase boundary for the whole double-chain system, due to the fact that, in physics, the non-vanishing inter-chain hopping tab provides extra channels for bosons tunneling to other sites, which increases the correlation effects and narrows the scope of the MI phase.

|
Fig.2 Phase diagrams of the symmetric double-chain systems with ta=tb=t at zero temperature |
In Fig. 2, we also show phase diagrams for symmetric systems with different inter-chain hopping tab=0, 0.5t, t, 2t and 3t. As discussed above, there exist two boundary solutions for each system with the non-zero tab. In the figure, only solid lines (determined by the condition λb=0) below the boundary of tab =0 curve are real physical boundaries, and all dotted lines above are false boundaries. It could be found that the MI phase region shrinks as tab increases, and the phase boundary moves gradually toward the bottom of the figure. The additional inter-chain hopping effect makes the system easier to transit from the MI phase to the SF phase.
Now we consider an asymmetric system with ta≠tb. The optical lattice in asymmetric systems could be regarded as composed of two kinds of elements. As an example, Fig. 3 shows phase diagrams for systems with tb=2ta=2t, tab=0, 0.5t, t, 2t, and 3t. The curves are real phase transition boundaries corresponding to tab=0, 0.5t, t, 2t, and 3t respectively. Only real phase boundaries are plotted in the figure. In this paper, all real boundaries are determined by the phase boundary condition λb=0 due to the parameters given. When tab=0, particles cannot hop between chains, and the system consists of two independent single chains. When tab≠0, for example tab=0.5t, particles have more possibilities tunneling to neighboring sites compared to particles in the system with tab=0. Therefore, the phase boundary corresponding to the chain b with tb=2t (the black-square-solid line) has been pushed into the MI phase region. This means the inter-chain hopping effect enlarges the SF phase region for the asymmetric double-chain systems.
|
Fig.3 Phase diagrams of asymmetric double-chain systems with tb=2ta=2t at zero temperature |
In Fig. 3, we show more phase boundaries for asymmetric systems with tb=2ta=2t, and tab=0, 0.5t, 1t, 2t, and 3t. As tab increases, the kinetic energy rises and particle fluctuations increase. The localized MI states of systems near the phase boundary tend to transit to the delocalized states. Therefore, the MI region shrinks gradually. In the range of 4tatb < tab2 (tab < 2t), our method provides two MI-SF phase transition boundaries, and only curves below the black-square-solid line (tab=0) are actual ones. With the gradual increase of tab, the decreasing speed of MI phase space is slowed. When 4tatb > tab2(tab > 2t), only one solution corresponding to λa=0 is obtained by our method.
3 Correlation of Particle-Hole PairsThe correlation of particles is another physical quantity usually employed to characterize the quantum phase phenomena of strongly correlated many-body systems. In the optical lattice system, quantum fluctuations induced by tunneling effects produce correlated particle-hole pairs, which is fundamental to some important quantum properties. Recently, Endres et al.[15] observed correlated particle-hole pairs in the low-dimensional strongly correlated ultracold quantum gas using high-resolution images. They found that, in one-dimensional systems, the existence of correlated particle-hole pairs is closely related to a non-local order parameter, and could be used to explain some interesting properties near the MI-SF quantum phase transition point. When a particle is hopping from the kth to the (k+d)th site of the lattice, one particle-hole pair appears which indicates the correlation between particles at the kth and the (k+d)th sites. The two-site parity correlation function between neighboring lattice sites is then defined as[16, 23-24]:
| $ {C_d} = \left\langle {{{\hat s}_k}{{\hat s}_{k + d}}} \right\rangle - \left\langle {{{\hat s}_k}} \right\rangle \left\langle {{{\hat s}_{k + d}}} \right\rangle $ | (24) |
where d is the distance between lattice sites,
In order to demonstrate the reliability and the efficiency of our method, we plot in Fig. 4 the intra-chain nearest-neighbor correlation functions for the single-chain system with different chain length N=4, 20, 50, 100, 1 000, 3 000, 9 000, 10 000. From the plot, we can see that, for all chain length N, C1 increases with t/U monotonically. When t/U is small, each curve increases rapidly at first, and then approaches a flat asymptote. As N increases, the correlation function values tend to a saturation value. For example, the curves of N=9 000 and N=10 000 systems coincide in the plot. This indicates that our result is convergent if we increase the chain length N. Obviously, we can obtain results with arbitrarily high precision by including in the above calculations a large enough chain length N. The calculation needs less than 9×10-4 CPU seconds of a i5-2.50 GHz PC computer to obtain the correlation results for the N=10 000 system, which is good enough for our investigation.

|
Fig.4 Two-site parity correlation functions between nearest-neighboring sites for single-chain systems with chain length N=4, 20, 50, 100, 1 000, 3 000, 9 000, and 10 000 |
In Fig. 5, we plot two-site parity correlation functions versus t/U for N=10 000, ta=tb=t, and tab=t, 2t, 3t. Doted lines denote inter-chain correlation functions, whereas solid lines refer to intra-chain correlation functions. Within the limit of t→0, the quantum fluctuations are completely inhibited, and the nearest-neighbor correlations C1 vanish for all systems, which indicates that the systems are in the MI states. As the ratio of t/U increases, the tunneling effect becomes more important. It is easier for particles to transit from one site to nearby sites, and correlated particle-hole pairs gradually emerge. As a result, the correlation functions of particles increase correspondingly. It should be emphasized that the system will stay in the Mott insulating region if t/U is not large enough. In this case, repulsive interactions play a dominant role and correlated particle-hole pairs could be understood as virtual excitations[17]. As t/U is large enough, the tunneling effects achieve the dominant position instead, and the large number of particle-hole pairs appears. As a consequence, the correlation function C1 leads to a saturation value, which means the system has transited from MI phase to SF phase.
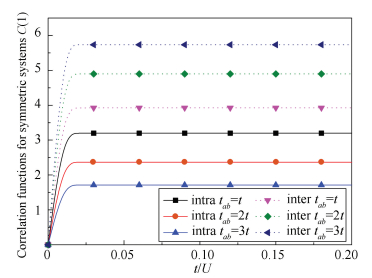
|
Fig.5 Two-site parity correlation functions between nearest-neighboring sites versus t/U for symmetric systems with ta=tb=t |
In Fig. 5, we also show the relationship between the two-site parity correlation functions and hopping effects t/U for the chain length N=10 000. As tab increases, the hopping effects between two chains are enhanced, which augment the inter-chain correlation function. Comparatively, the growth of the possibility that bosons tunneling between chains reduces the possibility of bosons hopping within the same chains. Therefore, the intra-chain correlation function decreases with tab in the mean time. Also, we can see in the plot 5 that the MI-SF phase transitions occur at almost the same value of t/U for different tab. This indicates that the ratio of tab to U determines the quantum phase transition point for symmetric double-chain systems.
4 ConclusionsIn this paper, we have investigated the MI-SF quantum phase transition properties of symmetric and asymmetric double-chain BHMs by using the Landau theory and the mean-field approximation. In the symmetric double-chain system, two identical chains coupled with each other through inter-chain hopping effects. The interactions of other particles on the given boson are approximated by an average effect, which is described by an order parameter ψ. Thus, the ground state energy can be obtained analytically as a function of ψ, and phase diagrams can be achieved according to Landau's quantum phase transition theory. We found the increasing of inter-chain hopping energy tab facilitates further hopping for bosons to neighboring sites, so that the scope of SF phase enlarges during the procedure. In the asymmetric double-chain BHM, the system is composed of two different optical lattice chains. Hence, we have to introduce two different order parameters for two single chains. Our results indicate that the growth of tab also increases the scope of SF phase. In this paper, two-site correlation functions are also employed to study properties of the system near the quantum phase transition point. It is found that the rising of tab leads to the enhancement of inter-chain hopping effects, but decreases the intra-chain hopping effects. For a symmetric system with given ta=tb=t, our results show that the quantum phase transition point is related to the ratio of ta/tab or tb/tab, but determined by the ratio of tab/U.
| [1] |
Anderson M H, Ensher J R, Matthews M R, et al. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science, 1995, 269: 198-201. DOI:10.1142/9789812813787_0062 (  0) 0) |
| [2] |
Davis K B, Mewes M O, Andrews M R, et al. Bose-Einstein condensation in a gas of sodium atoms. Physical Review Letters, 1995, 75: 3969-3973. DOI:10.1103/PhysRevLett.75.3969 (  0) 0) |
| [3] |
Bradley C C, Sackett C A, Tollett J J, et al. Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions. Phys. Rev. Lett., 1995, 75: 1687-1690. DOI:10.1103/PhysRevLett.75.1687 (  0) 0) |
| [4] |
Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases. Rev. Mod. Phys., 2008, 80: 885-964. DOI:10.1103/RevModPhys.80.885 (  0) 0) |
| [5] |
Bruder C, Fazio R, Schon G. Superconductor mott-insulator transition in Bose systems with finite-range interactions. Phys. Rev. B, 1993, 147: 342-347. DOI:10.1103/PhysRevB.47.342 (  0) 0) |
| [6] |
van Otterlo A, Wagenblast K-H, Baltin R, et al. Quantum phase transitions of interacting bosons and the supersolid phase. Phys. Rev. B, 1995, 52: 16176-16186. DOI:10.1103/PhysRevB.52.16176 (  0) 0) |
| [7] |
Jaksch D, Bruder C, Cirac J I, et al. Cold bosonic atoms in optical lattices. Phys. Rev. Lett., 1998, 81: 3108-3111. DOI:10.1103/PhysRevLett.81.3108 (  0) 0) |
| [8] |
Fisher M P A, Weichman P B, Grinstein G, et al. Boson localization and the superfluid-insulator transition. Phys. Rev. B, 1989, 40: 546-570. DOI:10.1063/1.38820 (  0) 0) |
| [9] |
Kampf A P, Zimanyi G T. Superconductor-insulator phase transition in the boson Hubbard model. Phys. Rev. B, 1993, 47: 279-286. DOI:10.1103/PhysRevB.47.279 (  0) 0) |
| [10] |
Freericks J K, Monien H. Strong-coupling expansions for the pure and disordered Bose-Hubbard model. Phys. Rev.B, 1996, 53: 2691-2700. DOI:10.1103/PhysRevB.53.2691 (  0) 0) |
| [11] |
Elstner N, Monien H. Dynamics and thermodynamics of the Bose-Hubbard model. Phys. Rev. B, 1999, 59: 12184-12187. DOI:10.1103/PhysRevB.59.12184 (  0) 0) |
| [12] |
Zhang J M, Dong R X. Exact diagonalization: the Bose-Hubbard model as an example. European Journal of Physics, 2010, 31: 591. DOI:10.1088/0143-0807/31/3/016 (  0) 0) |
| [13] |
Lewenstein M, Sanpera A, Ahufinger V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-Body Systems. Oxford: Oxford University Press, 2012.
(  0) 0) |
| [14] |
Sachdev S. Quantum Phase Transitions. Cambridge: Cambridge University Press, 2011.
(  0) 0) |
| [15] |
Endres M, Cheneau M, Fukuhara T, et al. Observation of correlated particle-hole pairs and string order in low-dimensional Mott insulators. Science, 2011, 334: 200-203. DOI:10.1126/science.1209284 (  0) 0) |
| [16] |
Cheneau M, Barmettler P, Poletti D, et al. Light-cone-like spreading of correlations in a quantum many-body system. Nature, 2011, 481: 484-487. DOI:10.1038/nature10748 (  0) 0) |
| [17] |
Chen Y A, Huber S D, Trotzky S, et al. Many-body Laudau-Zener dynamics in coupled one-dimensional Bose liquids. Nature Physics, 2011, 7: 61-67. DOI:10.1038/nphys1801 (  0) 0) |
| [18] |
Deng H M, Dai H, Huang J H, et al. Cluster Gutzwiller study of the Bose-Hubbard ladder: Ground-state phase diagram and many-body Laudar-Zener dynamics. Phys Rev A, 2015, 92(2): 023618. DOI:10.1103/PhysRevA.92.023618 (  0) 0) |
| [19] |
Lv J, Chen Q, Deng Y. Two-species hard-core bosons on the triangular lattice: A quantum Monte Carlo study. Phys Rev A, 2014, 89: 013628. DOI:10.1103/PhysRevA.89.013628 (  0) 0) |
| [20] |
Tschischik W, Haque M, Moessner R. Nonequilibrium dynamics in Bose-Hubbard ladders. Phys Rev A, 2012, 86: 063633. DOI:10.1103/PhysRevA.86.063633 (  0) 0) |
| [21] |
Pandey B, Sinha S, Pati S K. Quantum phases of hardcore bosons in two coupled chains: A density matrix renormalization group study. Phys. Rev. B, 2015, 91: 214432. DOI:10.1103/PhysRevB.91.214432 (  0) 0) |
| [22] |
Lv J P, Wang Z D. Exotic Haldane superfluid phase of soft-core bosons in optical lattices. Phys. Rev. B, 2016, 93: 174507. DOI:10.1103/PhysRevB.93.174507 (  0) 0) |
| [23] |
Kapit E, Mueller E. Even-odd correlation functions on an optical lattice. . Phys. Rev. A, 2011, 82: 013644. DOI:10.1103/PhysRevA.82.013644 (  0) 0) |
| [24] |
Lode P. A review of monte carlo simulations for the Bose-Hubbard model with diagonal disorder. Comptes Rendus Physique, 2013, 14(8): 712-724. DOI:10.1016/j.crhy.2013.08.005 (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


