An oscillating bubble subjected to acoustic radiation forces in ultrasound fields shows different kinds of stability status[1], among which the spherical and diffusional stabilities are the most important. In medical diagnostic fields, the spherical stability of maintaining spherical shape is key to the theoretical model buildings of encapsulated bubbles for ultrasound contrast agents[2-3]. Furthermore, for drug delivery, gene transfection within living cells[4], sonothrombolysis enhancement[5], central nervous system capillaries[6], and even the onset of the single bubble sonoluminescence[7-10] are related to the energy emitted by the collapse of bubbles which to a great extent is caused by the diffusional instability. Some engineering applications, e.g., the fouling removal system[11-12] and enhancement of the sonochemical reactors[13], are also determined by the shock waves or the localized hotspots of extremely high temperature from the instability of bubbles in liquids[9]. For the purposes above, it is essential to investigate the stability of the bubbles in liquids during the rectified diffusion process.
In previous literatures, the stability of bubbles has been the focus for years. Lauterborn[1] and Brennen [14] gave outstanding reviews of the linear and nonlinear process of the introductions of three different stability mechanisms: positional, spherical, and diffusional stabilities. The positional stability is related to the bubble motion determined by the Primary Bjerknes force [15], which is not discussed in the present paper.
For spherically stable bubbles, the dynamic relationship of bubble radical motion is the ordinary differential equation which is widely employed in model buildings[16]. The instable conditions are due to the surface distortion caused by the acoustic radiation force[17] and finally lead to shape oscillation[18]. A bubble during shape oscillation may become extremely violent until the collapse[19]. The spherical stability was also investigated under the excitation of the dual-frequency acoustic field[20] or external flow[21].
For an oscillating bubble during the rectified diffusional process, it exchanges the gas molecules between the surrounding liquids and the bubble content across its interface until the diffusional stability is reached. Diffusional stability is an equilibrium state that the inside gas content and the partial gas content in liquids achieve dynamic balance which can prevent the bubble from dissolution or collapse. Fyrillas and Szeri[22] considered the equilibrium condition of diffusional oscillation problem related to the gas concentration in liquids based on the Henry's Law as follows:
| $ \frac{{{{\left\langle {p\left( {R\left( t \right)} \right)} \right\rangle }_\tau }}}{{{p_0}}} = \frac{{{c_\infty }}}{{{c_0}}} $ |
where p(R(T)) denotes the pressure inside the bubble at the time t, depending on the instantaneous bubble radius R(t), and 〈〉τ abbreviates the indicated time averaging. The solutions of the problem were investigated by the thin-diffusion approximation approaches [23-25]. Zhang and Li [26] derived the full expression of the solution considering the influence of the term of thermal viscosity based on the Fick's Law which combinates the diffusion flux and the gas concentration in liquids. The bubble could be in diffusional stability when the acoustic pressure amplitude is higher than the threshold pressure amplitude. However, the motion boundary of the spherical stability counteracting the rectified diffusion of oscillating gas bubbles in liquids has not been well researched.
In the present paper, the spherical and diffusional stability mechanisms of the oscillating gas bubbles in liquids were analyzed in detail. The structure of the discussions is organized as follows: Section 2 gives the basic equations of the bubble motion, diffusional stability, and the spherical stability and the experimental verification of the numerical model; Section 3 presents the effects of concentration of partial gas in the liquids on the stability of oscillating gas bubbles; Section 4 shows the influences of acoustic parameters on the stability status; finally, Section 5 concludes the main findings of the whole research.
2 Theoretical AnalysisThis section introduces the basic equations of the theoretical models employed in the present paper. The problem of bubble stability should be separated into approaches of bubble wall, the diffusional and the spherical stability. The amplitude of bubble oscillation is limited considering the spherical cases.
2.1 Equations of Interface Motion of the BubblesIn this section, the expressions of interface motion of gas bubble are introduced. Based on the work of Rayleigh, Plesset [27] proposed the general equation of the interface motion for spherical oscillating bubbles, the well-known Rayleigh-Plesset equation, which is employed as below:
| $ R\ddot R + \frac{3}{2}{{\dot R}^2} = \frac{{{p_{{\rm{ext}}}}\left( {R,t} \right) - {p_s}\left( t \right)}}{{{\rho _l}}} $ | (1) |
with
| $ {p_{{\rm{ext}}}}\left( {R,t} \right) = \left( {{P_0} + \frac{{2\sigma }}{{{R_0}}}} \right){\left( {\frac{R}{{{R_0}}}} \right)^{3\kappa }} - \frac{{2\sigma }}{R} $ | (2) |
and
| $ {p_s}\left( t \right) = {P_0} + {P_{\rm{A}}}\cos \left( {\omega t} \right) $ | (3) |
where R is the instantaneous radius of the gas bubble; the overdot is the time derivation; t is the time; ρl is the density of the liquids; P0 is the ambient pressure; σ is the coefficient of surface tension; R0 is the bubble radius at equilibrium; κ is the polytropic exponent; PA is the amplitude of acoustic excitation; ω is the angular frequency of acoustic excitation.
Here, the linearization (by x(t)=R/R0-1) is employed to investigate the motion dynamics within a limited range of the bubble oscillation. Furthermore, the compressibility of the ambient liquid is neglected in the present paper. Therefore, the differential equation (Eq. (1)) and the solution[28] for small-amplitude oscillation could be
| $ \ddot x + \omega _0^2x = - \frac{{{P_{\rm{A}}}}}{{{\rho _l}R_0^2}}\cos \left( {\omega t} \right) $ | (4) |
and
| $ x\left( t \right) = \frac{{{P_{\rm{A}}}}}{{{\rho _l}R_0^2\left| {\omega _0^2 - {\omega ^2}} \right|}}\cos \left( {\omega t + \phi } \right) $ | (5) |
with
| $ \omega _0^2 = \frac{1}{{{\rho _l}R_0^2}}\left[ {3\kappa \left( {{P_0} + \frac{{2\sigma }}{{{R_0}}}} \right) - \frac{{2\sigma }}{{{R_0}}}} \right] $ | (6) |
where ω0 is the natural frequency during bubble's oscillation which is the function of equilibrium radius of the gas bubble; ϕ is the phase angle. It can be found that the natural frequency is the function of bubble radius at equilibrium.
2.2 Diffusional StabilityIn this section, the criterion of diffusional stability of gas bubbles is introduced in detail following the bubble motion equations. Based on the Fick's law, the relationship between the diffusional flux and the gas concentration is a combination as the mass transfer equation shows [24]:
| $ \frac{{\partial c}}{{\partial t}} + u \cdot \nabla c = D{\nabla ^2}c $ | (7) |
Boundary conditions are
| $ \begin{array}{*{20}{c}} {c\left( {r,0} \right) = {C_i},r > R}\\ {\mathop {\lim }\limits_{r \to \infty } c\left( {r,t} \right) = {C_i}}\\ {c\left( {R,t} \right) = {C_s},t > 0} \end{array} $ | (8) |
where c is the concentration of the dissolved gas in liquids; u is the velocity of the liquid; D is the diffusion constant; Ci is the initial uniform concentration of gas; Cs is the concentration of the gas in liquids at the bubble surface.
Some researches of mass transfer equation are analyzed, among which Crum and Zhang et al.[25, 28] gave the solution below:
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}{R_0}}}{{{\rm{d}}t}} = \frac{{Dd}}{{{R_0}}}\left[ {\left\langle {R/{R_0}} \right\rangle + {R_0}{{\left( {\frac{{\left\langle {{{\left( {R/{R_0}} \right)}^4}} \right\rangle }}{{{\rm{ \mathsf{ π} }}tD}}} \right)}^{1/2}}} \right] \times }\\ {{{\left( {1 + \frac{{4\sigma }}{{3{P_0}{R_0}}}} \right)}^{ - 1}}\left( {\frac{{{C_i}}}{{{C_0}}} - \frac{{\left\langle {\left( {{P_{{\rm{in}}}}/{P_0}} \right)} \right\rangle }}{{\left\langle {{{\left( {R/{R_0}} \right)}^4}} \right\rangle }}} \right)} \end{array} $ | (9) |
with
| $ d = {R_g}{T_\infty }{C_0}/{P_0} $ | (10) |
| $ \begin{array}{l} R/{R_0} = 1 + \alpha \left( {{P_A}/{P_0}} \right)\cos \left( {\omega t + \delta } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;{\alpha ^2}K{\left( {{P_A}/{P_0}} \right)^2} \end{array} $ | (11) |
| $ \alpha = - \frac{{{P_0}}}{{{\rho _l}R_0^2}}{\left[ {\frac{1}{{{{\left( {{\omega ^2} - \omega _0^2} \right)}^2} + {{\left( {{\delta _{{\rm{tot}}}}\omega _0^2} \right)}^2}}}} \right]^{1/2}} $ | (12) |
and
| $ \delta = {\tan ^{ - 1}}\left[ {\frac{{{\delta _{{\rm{tot}}}}\omega _0^2}}{{\left( {{\omega ^2} - \omega _0^2} \right)}}} \right] $ | (13) |
Here, angle brackets mean the time averages. The total damping constants (δtot) in Eq. (13) and the corresponding viscous, thermal, and acoustic ones in rectified diffusion can be solved as [29]:
| $ {\delta _{{\rm{tot}}}} = {\delta _{{\rm{vis}}}} + {\delta _{{\rm{th}}}} + {\delta _{{\rm{ac}}}} $ | (14) |
| $ {\delta _{{\rm{vis}}}} = 4\omega {\mu _l}/\left[ {3\kappa \left( {{P_0} + 2\sigma /{R_0}} \right) - 2\sigma /{R_0}} \right] $ | (15) |
| $ \begin{array}{l} {\delta _{{\rm{th}}}} = 3\left( {\gamma - 1} \right)\left[ {X\left( {\sinh X + \sin X} \right) - 2\left( {\cosh X - } \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. {\cos X} \right)} \right]/\left[ {{X^2}\left( {\cosh X - \cos X} \right) + 3\left( {\gamma - 1} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\left. {X\left( {\sinh X - \sin X} \right)} \right] \end{array} $ | (16) |
| $ {\delta _{{\rm{ac}}}} = {\rho _l}R_0^3{\omega ^3}/{c_l} \times \left[ {3\kappa \left( {{P_0} + 2\sigma /{R_0}} \right) - 2\sigma /{R_0}} \right] $ | (17) |
with
| $ X = {R_0}{\left( {2\omega /{D_l}} \right)^{1/2}} $ | (18) |
| $ \begin{array}{*{20}{c}} {K = \left[ {\left( {3\kappa + 1 - {\beta ^2}} \right)/4 + \left( {\sigma /2{R_0}{P_0}} \right)\left( {3\kappa + 1 - } \right.} \right.}\\ {\left. {\left. {2/3\kappa } \right)} \right]/\left[ {1 + \left( {2\sigma /{R_0}{P_0}} \right)\left( {1 - 1/3\kappa } \right)} \right]} \end{array} $ | (19) |
and
| $ {\beta ^2} = \rho {\omega ^2}R_0^2/3\kappa {P_0} $ | (20) |
where C0 is the saturation concentration of the gas in the liquid; Rg is the universal gas constant; T∞ is the temperature at infinity; μl is the viscosity of the liquid; γ is the ratio of specific heat of the gas; Dl is the thermal diffusivity of the gas; cl is the sound speed in the liquid.
The terms of the time average in Eq. (9) can be determined by[25]
| $ \left\langle {R/{R_0}} \right\rangle = 1 + K{\alpha ^2}{\left( {{P_A}/{P_0}} \right)^2} $ | (21) |
| $ \left\langle {{{\left( {R/{R_0}} \right)}^4}} \right\rangle = 1 + \left( {3 + 4K} \right){\alpha ^2}{\left( {{P_A}/{P_0}} \right)^2} $ | (22) |
and
| $ \begin{array}{l} \left\langle {{{\left( {R/{R_0}} \right)}^4}\left( {{P_{{\rm{in}}}}/{P_0}} \right)} \right\rangle = \\ \;\;\;\;\;\;\left[ {1 + \frac{{3\left( {\kappa - 1} \right)\left( {3\kappa - 4} \right)}}{4}{\alpha ^2}{{\left( {{P_A}/{P_0}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\left. {\left( {4 - 3\kappa } \right)K{\alpha ^2}{{\left( {{P_A}/{P_0}} \right)}^2}} \right]\left( {1 + \frac{{2\sigma }}{{{P_0}{R_0}}}} \right) \end{array} $ | (23) |
Hence, the threshold value of PA is given by dR0/dt=0:
| $ \begin{array}{l} P_{\rm{T}}^2 = \frac{{P_0^2}}{{{\alpha ^2}}}\left[ {1 + \frac{{2\sigma }}{{{R_0}{P_0}}} - \frac{{{C_i}}}{{{C_0}}}} \right]/\left[ {\frac{{\left( {3 + 4K} \right){C_i}}}{{{C_0}}} - } \right.\\ \;\;\;\;\;\;\;\;\left[ {\frac{{3\left( {\kappa - 1} \right) \cdot \left( {3\kappa - 4} \right)}}{4} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {\left( {4 - 3\kappa } \right)K} \right]\left( {1 + \frac{{2\sigma }}{{{P_0}{R_0}}}} \right)} \right] \end{array} $ | (24) |
where PT is defined as the critical pressure amplitude of acoustic fields.
2.3 Spherical StabilityIn this section, the criterion of spherical stability of gas bubbles is introduced in detail. Spherical stability is useful for the numerical models in many practical applications. The theoretical analysis is started with the distortion equation[30]
| $ {r_s} = R + \sum\limits_{n = 1}^\infty {{a_n}{Y_n}} $ | (25) |
| $ \frac{{{{\rm{d}}^2}{b_n}}}{{{\rm{d}}{t^2}}} + G{b_n} = 0 $ | (26) |
with
| $ {b_n} = {R^{3/2}}{a_n} $ | (27) |
and
| $ \begin{array}{*{20}{c}} {G = \left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\frac{\sigma }{{{\rho _l}{R^3}}} - }\\ {\frac{3}{{4{R^2}}}{{\left( {\frac{{{\rm{d}}R}}{{{\rm{d}}t}}} \right)}^2} - \frac{{\left( {n + 0.5} \right)}}{R}\frac{{{{\rm{d}}^2}R}}{{{\rm{d}}{t^2}}}} \end{array} $ | (28) |
When the expression of R is replaced by Eq. (11), the equation above is changed into
| $ \begin{array}{l} G = \left[ { - 3\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\frac{\sigma }{{{\rho _l}R_0^3}} + } \right.\\ \;\;\;\;\;\;\left. {\left( {n + \frac{1}{2}} \right){\omega ^2}} \right] \times \frac{{{P_{\rm{A}}}}}{{{\rho _l}R_0^2\left| {\omega _0^2 - {\omega ^2}} \right|}} \cdot \cos \left( {\omega t + \phi } \right) + \\ \;\;\;\;\;\;\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\frac{\sigma }{{{\rho _l}R_0^3}} \end{array} $ | (29) |
Here, an is the nth order coefficient of the spherical harmonics; Yn is the nth order spherical harmonics; n is the mode number of spherical harmonics. With further analysis, we found that the parameter G is quite influential by the acoustic pressure amplitude (PA) for fixed equilibrium radius of the gas bubble (R0). Therefore, to satisfy G > 0, there exists a critical pressure amplitude (PA*) of acoustic pressure amplitude in Eq. (29)[16]
| $ P_{\rm{A}}^ * = \frac{{\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\sigma \left| {\omega _0^2 - {\omega ^2}} \right|}}{{{R_0}\left| {\frac{{ - 3\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\sigma }}{{{\rho _l}R_0^3}} + \left( {n + \frac{1}{2}} \right){\omega ^2}} \right|}} $ | (30) |
If ω ≫ ω0, the critical pressure amplitude of spherical stability in Eq. (30) above will reach a high-frequency limit as
| $ P_{\rm{A}}^ * = \frac{{\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\sigma }}{{{R_0}\left( {n + 0.5} \right)}} = {P_{\rm{H}}} $ | (31) |
If ω ≪ ω0, Eq. (30) can be changed into the case of low-frequency limit as
| $ P_{\rm{A}}^ * = \frac{{2\sigma }}{{3{R_0}}} = {P_{\rm{L}}} $ | (32) |
When the denominator of Eq. (30) is set as zero, an angular frequency corresponding to the singular mathematically is
| $ \omega = \sqrt {\frac{{3\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)\sigma }}{{{\rho _l}R_0^3\left( {n + \frac{1}{2}} \right)}}} = {\omega _d} $ | (33) |
where PH is the critical pressure amplitude when angular frequency is far above the natural frequency; PL is the critical pressure amplitude when angular frequency is far below the natural frequency; ωd is the angular frequency at the singular point.
2.4 Experimental Verification of the Rectified Diffusion ModelIn this section, the numerical model of rectified diffusion above is verified by the experimental data collected from the former research. Fig. 1 shows the comparison of the present numerical results of Eq. (24) (red line) and the former experimental data from Crum's work[31] during the rectified diffusion process(black points).The measurements of the bubble growth during rectified diffusion is the function of the acoustic pressure amplitude and the surface tension. The corresponding parameters of the surface tension and the acoustic frequency employed by Crum are 0.068 N/m and 22.1 kHz, respectively. The motion of the bubble was observed by the microscope and the acoustic data was collected by the hydrophone under water. From Fig. 1 we can find that the experimental data match the numerical analysis well for bubble radius from 100 μm to 70 μm. The average difference between the values of experiment and the numerical model is 8.3%. Therefore, it is feasible to employ the numerical model of rectified diffusion in the present paper when the bubble radius oscillation is smaller compared with the bubble radius.
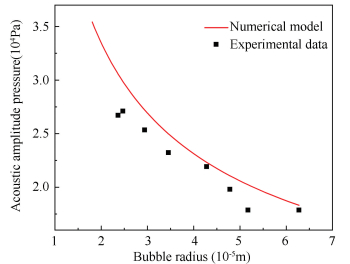
|
Fig.1 Comparison of threshold pressure during rectified diffusion changing with the bubble radius |
3 Diffusional and Spherical Stability Status
In this section, the diffusional and spherical stability status of gas bubbles are discussed by the stability maps (including the acoustic angular frequency and bubble radius) under the conditions of different acoustic amplitudes. The logarithmic coordinate was employed to express the variation of the parameters more clearly.
Fig. 2 shows stability maps divided by the four stability zones determined by spherical stability (PA* > PA) and diffusional stability (PT < PA). The four zones represent four different instability statues: spherical and diffusional stability (purple zone), spherical stability but diffusional instability (red zone), spherical instability but diffusional stability (yellow zone), and the both spherical and diffusional instability (blue zone). Ci/C0=1. PA=103, 104, 105, and 106 Pa, respectively.
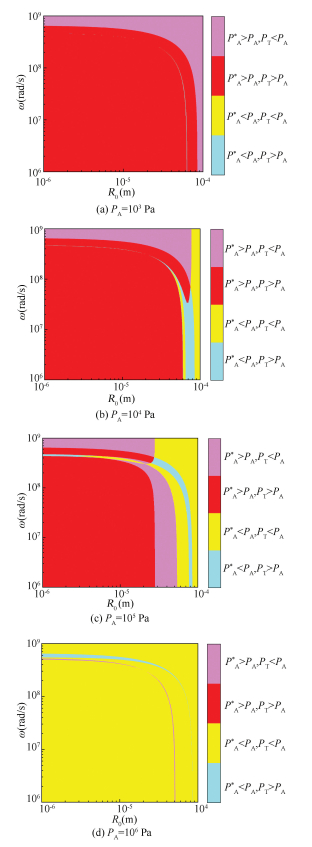
|
Fig.2 Four different kinds of stability zones determined by diffusional stability (PT < PA) and spherical stability(PA* > PA) |
From Fig. 2, it can be found that the amplitude of the acoustic field has deep impacts on the spherical and diffusional stability. With the increase of the acoustic field, the spherical stability weakens while the diffusional stability is enhanced. Furthermore, the boundaries of spherical stability (lines between purple and yellow, or red and blue areas) move toward left with the increasing acoustic pressure while the boundaries of diffusional stability do not change. The results of enhanced diffusional stability under the condition of increased acoustic pressure amplitude match the former trend of rectified diffusion [22]. We can speculate that if the acoustic pressure is high enough, the gas bubble will not be spherical but experience a shape and rectified diffusion oscillation for diffusional stability like Fig. 2(d) within a large range of bubble radius. For fixed pressure amplitude, bubbles with small radii and high frequency excited are much easier to be spherically and diffusionally stable.
4 Influential Factors of Acoustic Fields on the Gas Bubble StabilityIn this section, the influential parameters (including the concentration of gas and the angular frequency of external acoustic fields) on the stability of gas bubbles are discussed in detail.
4.1 Concentration of Gas on the Bubble StabilityFig. 3 shows the threshold pressure of diffusional stability (PT represented by the solid line) and critical pressure amplitude of spherical stability (PA* represented by the dashed line) versus bubble equilibrium radius (R0). ω=104, 105, 106 rad/s and Ci/C0=0.8, 0.9, 1.0, and 1.1, respectively.
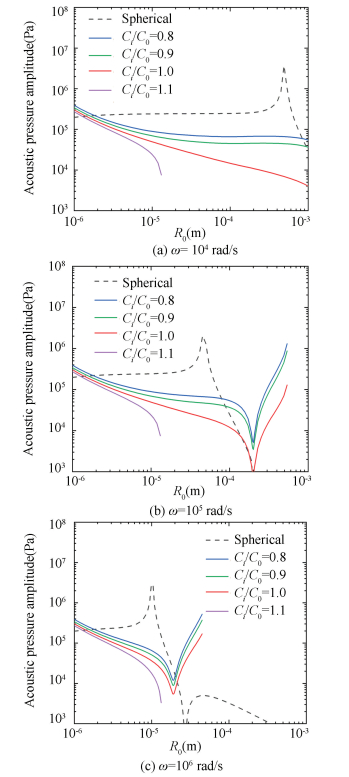
|
Fig.3 Threshold pressure of diffusional stability and critical pressure amplitude of spherical stability versus bubble equilibrium radius |
In Fig. 3, the areas surrounded by the dashed line and one solid line are both the spherical and diffusional stability areas. When the angular frequency of acoustic fields increases, the stable area moves towards left and becomes smaller. Meanwhile, the positions of singular points move towards left, too. However, the gas bubble could form diffusional nonlinearity excited by high frequency, especially for large bubbles as shown in Fig. 3(b)-(c). For increased concentrations of the gas in liquids, it can be found that the bubble achieves diffusional stability. The bubble is harder to be stable subject to the higher angular frequency, especially for larger bubbles. For fixed angular frequency cases, the higher gas concentration in liquids, the easier it is for the gas bubble to achieve diffusional stability. On the other hand, the concentration of the gas in liquids has no effects on the spherical stability. It can be found that for such a large bubble or high gas concentration, the present expressions are not enough to illustrate the stability.
4.2 Angular Frequency of Acoustic FieldsFig. 4 shows the critical pressure amplitude of spherical stability (PA* represented by the dashed line) and the threshold pressure amplitude of diffusional stability (PT represented by the solid line) with different acoustic angular frequencies.

|
Fig.4 Threshold pressure of diffusional stability and critical pressure amplitude of spherical stability versus bubble equilibrium radius |
The section between the two lines represents both the spherical and diffusional stability area. With the increase of angular frequency, the curves of spherical and diffusional stabilities move towards left. The stable area shrinks and the spherical instability has the singular point and the minimum point. The results also match the stable areas from those of Fig. 3. Specifically, the gas bubble is nonlinear to be diffusional stable if the bubble radius is too large.
Fig. 4(b)-(d) show the maximum value of PA* corresponding to singular points which are derived from Eq. (33) and the minimum value corresponding to the zero numerator of Eq. (30), which are not shown in Fig. 4(a). The expression explains that the positions of the singular points decrease with the growth of bubble radii. When the angular frequency is near the natural frequency, the gas bubble could experience the minimum values of PA*, which can be explained by the numerator of Eq. (30) (from Fig. 4(c)-(d)). Besides, the minimum values of PT could be found out in Fig. 4(c)-(d) which means the spherical stability corresponding to the zero numerator in Eq. (24).
According to the results obtained above, Table 1 concludes the relationship between the relative parameters considered above and the bubble stability. From the discussions, it can be found that for an oscillating bubble with a fixed equilibrium bubble radius, the external parameters (e.g., acoustic pressure amplitude and angular frequency) and the internal parameter as concentration of the gas in liquids codetermine its stability status.
| Table 1 Relationship between the relative parameters and the bubble stabilities |
5 High-Frequency and Low-Frequency Limits
Fig. 5 shows the threshold pressure of diffusional stability (PT represented by the solid line) and critical pressure amplitude of spherical stability (PA* represented by the dashed line) versus the angular frequency of the acoustic field (ω) bubble equilibrium radius (R0) is 10-6 m. The critical pressure amplitude of spherical stability is usually higher than the threshold pressure amplitude of diffusional stability. Spherical stability has two critical pressure amplitudes corresponding to the low and high frequency limits, PL and PH.
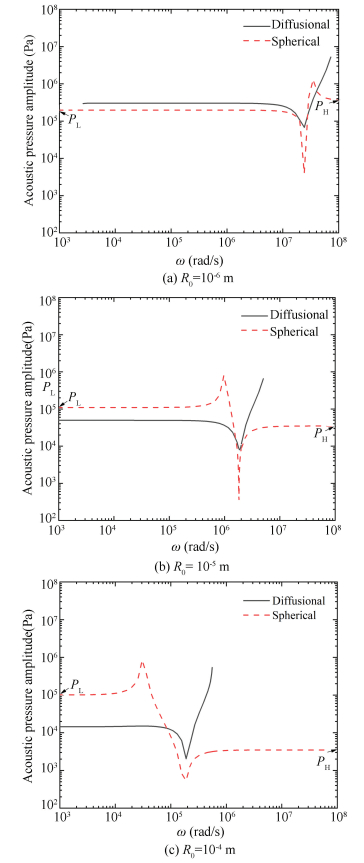
|
Fig.5 The threshold pressure of diffusional stability and critical pressure amplitude of spherical stability versus acoustic angular frequency |
The diffusional stability only has one PL under the condition of low-frequency limit, because large bubbles are easier to be nonlinear for the diffusional stability, especially under high-frequency conditions. The difference between PL of two kinds of stabilities is getting larger when angular frequency increases. In other words, the bubble stability is enhanced for the larger bubble under conditions of low acoustic angular frequency.
6 ConclusionsIt is critical to identify the stability status of oscillating gas bubbles subject to ultrasonic fields. In the present paper, we explained the spherical stability and the diffusional stability status which represent the linear and non-linear motion of gas bubble interfaces, respectively. The spherical shape of the gas bubble is affected by the internal and external factors (e.g., equilibrium bubble radius, acoustic angular frequency, and pressure amplitude). The diffusional stability is not only determined by the above parameters but also the gas concentration of the bubbles in liquids. The stable status of the gas bubble was divided into four different situations. For fixed bubble radius, the gas bubble experienced an area of spherical stability and diffusional stability when the external acoustic pressure was set between the two critical parameters, PA* and PT. The increase of gas concentration in the liquids enhanced both spherical and diffusional stabilities. The variation trend of the stable area and the limitation situation were also discussed which demonstrated that the increasing acoustic angular frequency weakens the stability of the gas bubble and alters the position of critical pressure amplitude in the limitation cases.
| [1] |
Lauterborn W, Kurz T. Physics of bubble oscillations. Reports on Progress in Physics, 2010, 73(10): 106501. DOI:10.1088/0034-4885/73/10/106501 (  0) 0) |
| [2] |
Yu T, Xiong S, Mason T J, et al. The use of a microbubble agent to enhance rabbit liver destruction using high intensity focused ultrasound. Ultrasonics Sonochemistry, 2006, 13(2): 143-149. DOI:10.1016/j.ultsonch.2005.02.001 (  0) 0) |
| [3] |
Huang B, Yin L Y, Wang G, et al. Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation. Journal of Fluids Engineering, 2013, 135(7): 071301. DOI:10.1115/1.4023650 (  0) 0) |
| [4] |
Longuet-Higgins M S. Monopole emission of sound by asymmetric bubble oscillations. Part 1. Normal modes. Journal of Fluid Mechanics, 1989, 201: 525-541. DOI:10.1017/S0022112089001035 (  0) 0) |
| [5] |
Datta S, Coussios C C, Ammi A Y, et al. Ultrasound-enhanced thrombolysis using Definity© as a cavitation nucleation agent. Ultrasound in Medicine and Biology, 2008, 34(9): 1421-1433. DOI:10.1016/j.ultrasmedbio.2008.01.016 (  0) 0) |
| [6] |
Fan C H, Liu H L, Ting C Y, et al. Submicron-bubble-enhanced focused ultrasound for blood-brain barrier disruption and improved CNS drug delivery. PloS One, 2014, 9(5): e96327. DOI:10.1371/journal.pone.0096327 (  0) 0) |
| [7] |
Yasui K, Tuziuti T, Lee J, et al. Numerical simulations of acoustic cavitation noise with the temporal fluctuation in the number of bubbles. Ultrasonics Sonochemistry, 2010, 17(2): 460-472. DOI:10.1016/j.ultsonch.2009.08.014 (  0) 0) |
| [8] |
Ashokkumar M. The characterization of acoustic cavitation bubbles - An overview. Ultrasonics Sonochemistry, 2011, 18(4): 864-872. DOI:10.1016/j.ultsonch.2010.11.016 (  0) 0) |
| [9] |
Merouani S, Hamdaoui O, Rezgui Y, et al. Theoretical procedure for the characterization of acoustic cavitation bubbles. Acta Acustica United with Acustica, 2014, 100(5): 823-833. DOI:10.3813/AAA.918762 (  0) 0) |
| [10] |
Tronson R, Muthupandian Ashokkumar M, Grieser F. Multibubble sonoluminescence from aqueous solutions containing mixtures of surface active solutes. The Journal of Physical Chemistry B, 2003, 107(30): 7307-7311. DOI:10.1021/jp034360v (  0) 0) |
| [11] |
van Wijngaarden L. Mechanics of collapsing cavitation bubbles. Ultrasonics Sonochemistry, 2016, 29: 524-527. DOI:10.1016/j.ultsonch.2015.04.006 (  0) 0) |
| [12] |
Reuter F, Mettin R. Mechanisms of single bubble cleaning. Ultrasonics Sonochemistry, 2016, 29: 550-562. DOI:10.1016/j.ultsonch.2015.06.017 (  0) 0) |
| [13] |
Mettin R, Cairós C, Troia A. Sonochemistry and bubble dynamics. Ultrasonics Sonochemistry, 2015, 25: 24-30. DOI:10.1016/j.ultsonch.2014.08.015 (  0) 0) |
| [14] |
Brennen C E. Cavitation and Bubble Dynamics. Cambridge: Cambridge University Press, 1995.
(  0) 0) |
| [15] |
Bai L, Chen X, Zhu G, et al. Surface tension and quasi-emulsion of cavitation bubble cloud. Ultrasonics Sonochemistry, 2017, 35(Part A): 405-414. DOI:10.1016/j.ultsonch.2016.10.019 (  0) 0) |
| [16] |
Zhang Y, Gao Y, Du X. Stability mechanisms of oscillating vapor bubbles in acoustic fields. Ultrasonics Sonochemistry, 2018, 40(Part A): 808-814. (  0) 0) |
| [17] |
Mei C C, Zhou X. Parametric resonance of a spherical bubble. Journal of Fluid Mechanics, 1991, 229: 29-50. DOI:10.1017/S0022112091002926 (  0) 0) |
| [18] |
Brenner M P, Lohse D, Dupont T F. Bubble shape oscillations and the onset of sonoluminescence. Physical Review Letters, 1995, 75(5): 954-957. DOI:10.1103/PhysRevLett.75.954 (  0) 0) |
| [19] |
Kang I S, Leal L G. Bubble dynamics in time-periodic straining flows. Journal of Fluid Mechanics, 1990, 218(218): 41-69. DOI:10.1017/S0022112090000921 (  0) 0) |
| [20] |
Zhang Y, Du X, Xian H, et al. Instability of interfaces of gas bubbles in liquids under acoustic excitation with dual frequency. Ultrasonics Sonochemistry, 2015, 23: 16-20. DOI:10.1016/j.ultsonch.2014.07.021 (  0) 0) |
| [21] |
Yang S M, Feng Z C, Leal L G. Nonlinear effects in the dynamics of shape and volume oscillations for a gas bubble in an external flow. Journal of Fluid Mechanics, 1993, 247(247): 417-454. DOI:10.1017/S0022112093000515 (  0) 0) |
| [22] |
Fyrillas M M, Szeri A J. Dissolution or growth of soluble spherical oscillating bubbles. Journal of Fluid Mechanics, 1994, 277: 381-407. DOI:10.1017/S0022112094002806 (  0) 0) |
| [23] |
Plesset M S, Zwick S A. A nonsteady heat diffusion problem with spherical symmetry. Journal of Applied Physics, 1952, 23(1): 95-98. DOI:10.1063/1.1701985 (  0) 0) |
| [24] |
Eller A, Flynn H G. Rectified diffusion during nonlinear pulsations of cavitation bubbles. The Journal of the Acoustical Society of America, 1965, 37(3): 493-503. DOI:10.1121/1.1909357 (  0) 0) |
| [25] |
Crum L A, Hansen G M. Generalized equations for rectified diffusion. The Journal of the Acoustical Society of America, 1982, 72(5): 1586-1592. DOI:10.1121/1.388494 (  0) 0) |
| [26] |
Zhang Y, Li S. Mass transfer during radial oscillations of gas bubbles in viscoelastic mediums under acoustic excitation. International Journal of Heat and Mass Transfer, 2014, 69(2): 106-116. DOI:10.1016/j.ijheatmasstransfer.2013.10.019 (  0) 0) |
| [27] |
Plesset M S. The dynamics of cavitation bubbles. Journal of Applied Mechanics, 1949, 16(3): 277-282. (  0) 0) |
| [28] |
Zhang Y. Analysis of Radial Oscillations of Gas Bubbles in Newtonian or Viscoelastic Mediums Under Acoustic Excitation. Coventry: The University of Warwick, 2012.
(  0) 0) |
| [29] |
Zhang Y, Li S. A general approach for rectified mass diffusion of gas bubbles in liquids under acoustic excitation. Journal of Heat Transfer, 2014, 136(4): 042001. DOI:10.1115/1.4026089 (  0) 0) |
| [30] |
Plesset M S. On the stability of fluid flows with spherical symmetry. Journal of Applied Physics, 1954, 25(1): 96-98. DOI:10.1063/1.1721529 (  0) 0) |
| [31] |
Crum L A. Measurements of the growth of air bubbles by rectified diffusion. The Journal of the Acoustical Society of America, 1980, 68(1): 203-211. DOI:10.1121/1.384624 (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


