2. Guangzhou Urban Planning & Design Survey Research Institute, Guangzhou 510060, China
Bus travel time prediction is vital component of advanced public transportation system (APTS) and advanced traveler information system (ATIS). With the rapid development of communication and network technology, an accurate and real-time travel time forecast is increasingly important. For bus operation management, it can help optimize bus route planning, stop site and distance between stations selection, and choose appropriate road section to implement bus priority tragedy, which will realize better bus priority on the premise of limited traffic supply. On the other hand, real-time and dynamic bus arrival time forecast released by mobile communication applications can help passengers make more suitable travel plans, which not only reduces the long waiting process, but also improves the service level of public transportation and attracts more passengers.
Previously, various methods have been adopted by researchers to forecast bus travel time using historical average model[1], time series model[2], statistical regression model[3] and kalman filter algorithms[4]. However, the prediction of bus travel time is very complex and highly nonlinear in nature as it depends upon many influence factors such as ridership, traffic flow, weather and traffic signals in bus system. It is difficult for those predicting methods to consider all of factors, so the prediction quality, in practice, is unsatisfactory.
In the recent decade, machine learning models have better capability to handle nonlinear mapping problems that are complex in nature, particularly in the field of travel time prediction where an artificial neutral network (ANN) has been widely applied. Park and Rilett analyzed the performance of ANN applications in bus travel time modeling[5]; Chien et al.[6] put forward two ANN models based on link and bus station respectively, which are applied to bus travel time prediction. It has been shown that ANN model has good applicability in bus travel time prediction. Further, there is a lot of research proving that ANN model outperforms historical average, statistical regression and kalman filter models in bus travel time prediction[7-8]. However, ANN model follows the principle of empirical risk minimization, which has some drawbacks, like local optimal, over-fitting or under-fitting problems and generalization ability defects[9-10], which may reduce the effect of artificial neural network application in travel time prediction to a certain degree.
Support vector machine (SVM), which is based on statistical learning theory, is a relatively new classification and regression technique from the artificial intelligence field. It is good at finding the statistical laws under the small sample and has a strong learning ability. Moreover, this technique has better generalization performance and is easy to be balanced between the level of generalization and fitness. Due to the structural risk minimization principle, SVM can effectively overcome the defects of ANN, which has gained attention in the transportation domain. Besides, urban public transport is a non-stationary, time-variant, and stochastic system, therefore using SVM in bus travel time prediction has important significance, which has been found to perform well compared to the other predictors[11-13].
Wavelet transform (WT), which can decompose the original data into various frequency components, has been successfully used in the fields like data analysis and signal processing. The application of wavelet transform provides useful information about sub-series components of original data so that forecasting capability of a model can be improved by extracting useful information at different levels. In recent years, wavelet transforms has been applied to a number of research fields such as temperature[14], water resource[15-16], wind energy[17] and share price prediction[18], which combine the wavelet transform to form a hybrid tool in their models. Research findings indicate that the hybrid model can be efficient and effective in improving the accuracy of forecasts and has been gradually adopted in transport domain. In hybrid prediction model, several techniques are combined to take advantages of their unique features in data analysis and modeling. In fact, every method has its strong points, for example wavelet transform (WT) has an advantage of frequency decomposition in time domain, while a support vector machine (SVM) is good at handling nonlinear optimization problems. So it is really meaningful to unite those methods in bus travel time prediction domain for the purpose of improving the accuracy of prediction results[19-21].
In this study, wavelet transform is used to capture the detailed information of bus travel time variation and decompose original data into several components at different frequency. The SVR models for predicting the components from high frequency to low frequency are constructed respectively. The final prediction result is derived from the summation of model outputs for each component. The main purpose of this study are to analyze the performances of applying wavelet transform-support vector regression model into bus travel time prediction and to compare the performances of the WT-SVR models with other widely used models like SVR and ANN models.
2 Theory of the ModelWavelet transform (WT) has excellent characteristics of multi-resolution analysis. On one hand, the signals can be decomposed into different levels, and the information features of different levels can be displayed, which helps to give a deep insight into the variation of signal. On the other hand, the components of transient abnormal phenomenon entrained in normal signal can be detected, and their components are displayed[22]. Compared to traditional artificial neural network, support vector machine method replaces traditional empirical risk with structure risk minimization and solves a quadratic optimization problem with the global optimal solution in theory. Therefore, the application of hybrid wavelet transform-support vector regression (WT-SVR) model in bus travel time prediction can capture the regularity of bus running behind the seemingly random and improve the prediction accuracy.
2.1 Wavelet TransformSuppose the function φ(t)∈L2(R) and its Fourier transform ψ(ω) satisfies the condition (t and ω are random variables):
| $ \int\limits_{R} \frac{|\hat{\psi}(\omega)|^{2}}{|\omega|} \mathrm{d} \omega<+\infty $ | (1) |
Then φ(t) can be called wavelet base or mother wavelet. By dilations and translations of mother wavelet, a family of wavelet functions can be obtained:
| $ \psi_{a, b}(t)=\frac{1}{\sqrt{a}} \psi\left(\frac{t-b}{a}\right)(a \neq 0, b \in R) $ | (2) |
where a represents the scale factor and b represents the translation factor. Let a=2j and b=k·2j, discrete wavelet transform (DWT) can be transformed as follow:
| $ \psi_{j, k}(t)=2^{\frac{-j}{2}} \psi\left(2^{-j} \cdot t-k\right) $ | (3) |
where k denotes the shift parameter and j denotes the resolution level. If the value of j is larger, the frequency of wavelet decomposition is lower.
An effective way to apply the wavelet transform is the multi-resolution technique based on scale function and wavelet base function, which extracts the low frequency components and the high frequency components of the series respectively. The process of multi-scales decomposition can be expressed as:
| $ \begin{array}{c}{V_{0}=V_{1} \oplus W_{1}=V_{2} \oplus W_{2} \oplus W_{1}=} \\ {V_{3} \oplus W_{3} \oplus W_{2} \oplus W_{1}=\cdots}\end{array} $ | (4) |
where, V0 is original signal; Vi is the approximate components of signal, i=1, 2, …, n; Wi is the detail components of signal, i=1, 2, …, n.
For a given section of a bus route, the bus travel time in this section at time step t can be defined as f(t), and t=1, 2, …, n, f(t)∈L2(R). Therefore, the bus travel time series f(t) can be treated as a signal input, which can be decomposed into different frequency bands through wavelet decomposition. The reconstruction expression of f(t) can be obtained by Mallat multi-scales analysis algorithm as follows:
| $ \begin{aligned} f(t)=& \sum\limits_{k} c_{j, k} \varphi_{j, k}(t)+\sum\limits_{k} \sum\limits_{j} d_{j, k} \psi_{j, k}(t)=\\ & A_{j}(t)+\sum\limits_{j} D_{j}(t) \end{aligned} $ | (5) |
where cj, k is wavelet coefficient and dj, k is scale coefficient; φj, k(t) denotes wavelet base function and ψj, k(t) denotes scale function; Aj and Dj are the approximate and detail sequences of original data after reconstruction, respectively. The flow chart of Mallat wavelet decomposition is shown in Fig. 1.

|
Fig.1 Mallat wavelet decomposition |
2.2 Support Vector Regression
For the case of regression problems, suppose that given a series of data points, namely {(x1, y1), (x2, y2), …, (xn, yn)} (xi is the input vector; yi relates to the target value; and n is the number of observation). In order to solve nonlinear regression problems, a set of non-linear transfer functions are used to map the input space into high dimension feature space, where theoretically a simple linear regression can be found to approximate a given sample. According to statistical learning theory[23], the linear estimation function of SVR can be formulated as follows:
| $ f(x)=\omega \cdot \phi(x)+b $ | (6) |
where ϕ(x) denotes a non-linear transfer function in the feature space; ω is weight vector, b is a constant. The coefficients ω and b can be calculated by minimizing the regularized risk function:
| $ R(f)=C \frac{1}{n} \sum\limits_{i=1}^{n} L_{\varepsilon}\left(y_{i}, f\left(x_{i}\right)\right)+\frac{1}{2}\|w\|^{2} $ | (7) |
| $ L_{\varepsilon}(y , f(x))=\left\{\begin{array}{l}{0, \text { if }(y-f(x)) \leqslant \varepsilon} \\ {|y-f(x)|-\varepsilon, \text { otherwise }}\end{array}\right. $ |
where Lε(y, f(x))is called ε-insensitive loss function, the constant C>0 specifies a trade-off between an approximation error and the weight vector ||w||. ε is called as the tube size that is equivalent to the approximation accuracy placed on the training data points. Both C and ε must be chosen beforehand by the user. Two non-negative slack variables ξ and ξ* can be introduced, which represent the distance from the actual values to the corresponding boundary values of ε-tube; then, Eq.(7) is transformed to the following convex quadratic programming problem:
| $ \begin{array}{*{20}{l}} {\mathop {\min }\limits_{_{w, b, \xi , \xi } \cdot } \frac{1}{2}||w|{|^2} + C\sum\limits_{i = 1}^N {\left( {{\xi _i} + \xi _i^*} \right)} }\\ {{\rm{ Subject}}\;{\rm{to }}\left\{ {\begin{array}{*{20}{l}} {{w_i} \cdot \phi \left( {{x_i}} \right) + {b_i} - {y_i} \le \varepsilon + \xi _i^*}\\ {{y_i} - {w_i} \cdot \phi \left( {{x_i}} \right) - {b_i} \le \varepsilon + {\xi _i}}\\ {{\xi _i}, \xi _i^* \ge 0, i = 1, 2, \cdots , N} \end{array}} \right.} \end{array} $ | (8) |
After optimizing above equation by Lagrange function and condition, a non-linear regression function can be given as:
| $ \begin{array}{*{20}{c}} {f(x) = \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} k\left( {{x_i}, x} \right) + b}\\ {k\left( {{x_i}, x} \right) = \sum\limits_{j = 1}^D \phi \left( {{x_i}} \right)\phi \left( {{x_j}} \right)} \end{array} $ | (9) |
where αi and αi* are two Lagrange multipliers. k(xi, xj)=ϕ(xi)ϕ(xj) is a kernel function which describes the inner products in the high dimension feature space. By using kernel functions, all calculation processes can be finished directly in the input space without mapping into the high dimension feature space. The structure of SVR is shown in Fig. 2.

|
Fig.2 The topology structure of SVR |
The performance and efficiency of SVM depends greatly on the kernel function, so choosing the kernel function and corresponding parameters properly according to different problems is very important. The common kernel functions are shown in Table 1.
| Table 1 Common kernel functions of SVR |
3 Model Development in Bus Travel Time Prediction
In this study, a hybrid WT-SVR model is used for predicting bus travel time, which is formed by combining the model of support vector machine with wavelet transform technique. The details of model input and details regarding the wavelet decomposition are discussed briefly in this section.
Considered to the variation of bus running, four input variables and an output variable are used, which are advised by Ji et al.[24]. Firstly, bus travel time is non-stationary and fluctuates during a day. Especially at morning and afternoon peak hours, the bus travel times will increase significantly; then, different road segments have different number of intersections, road segment length, traffic conditions, and traffic flow composition. All these differences can result in the changes of bus travel times. Thus, the time of day should be classified into several periods, and road segments should also be considered as input factors in this model. Moreover, bus travel time is easily influenced by many random factors such as traffic flow, ridership, weather, stops delay and traffic signals delay, but it is very difficult to estimate the traffic condition of road segments by obtaining this information in real time. Based on the research of Yu[25], this paper chooses the latest bus travel time of the predicted section and the latest bus travel time of the previous section to represent the current traffic condition of predicted section and the running status of the bus, assuming that the latest travel time can be obtained by bus information system in real time. Therefore, four input variables include time of day (x1), road segment (x2), the latest bus travel time of at predicted section (x3) and the latest bus travel time of current bus at preceding segment (x4); y denotes output vector, which represents the bus travel times from stop i to stop j. While a bus reaches the stop i, the latest travel time from stop i-1 to stop i will be updated.
For a bus route, the bus travel time series at each segment can be decomposed into sub-series component (approximation components A's and detail components D's) using wavelet multi-scales decomposition beforehand. The input data such as the latest bus travel time in current section and the latest bus travel time in preceding section can be obtained by the corresponding bus travel time sub-series. The sub-series (A's and D's) components of future travel time at predicted section are predicted by different SVR models separately. Finally, the prediction result is the aggregation of each model outputs.
With respect to the model parameters, radial basis function (RBF) is selected as the kernel function, which is able to fit high-dimension data with a few hyper parameters thus reducing the complexity of prediction model. The definition of RBF kernel function can be expressed as:
| $ k\left(x_{i}, x\right)=\exp \left(-\gamma| | x-x_{i}| |^{2}\right), \gamma>0 $ | (10) |
When RBF kernel is used, three SVR parameters including penalty parameter C and kernel function's parameter γ and tube size ε are considered. The general accuracy of prediction depends on a proper setting of these parameters, and the best combination of parameters (C, γ and ε) can be determined by the methods such as k-fold cross validation (CV), genetic algorithm (GA), and particle swarm optimization (PSO). For simplicity, five-fold cross validation is chosen to optimize the parameters of all SVR models.
The structure of prediction model is shown in Fig. 3, of which details are demonstrated as follows.
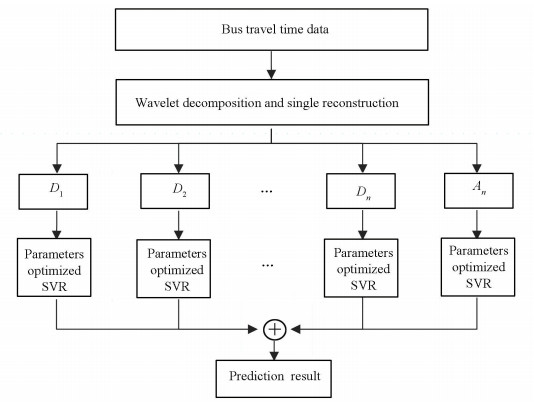
|
Fig.3 Diagram of bus travel time prediction model based on wavelet transform and SVR |
1) The bus route under study is separated into k segments according to the bus stops. For the convenience of this study, the time of day variable is classified into peak hours (7:00-9:00 a.m. and 17:00-19:00 p.m.) and off-peak hours.
2) The original bus travel time data is decomposed into a set of various subsequences using wavelet multiresolution technique and single branch reconstruction method.
3) After wavelet transform, each sub-series components are learned and trained separately by support vector regression models. The parameters including penalty parameter C, kernel function's parameter γ and tube size ε are optimized by cross-validation and grid search approach.
4) The final predicting results is obtained by the combination of prediction results from all SVR models, which can be expressed as
| $ \begin{aligned} y_{\text { predict }}=& \sum\limits_{i=1}^{n} D_{i}^{\prime}+A_{n}^{\prime}=\sum\limits_{i=1}^{n} f_{D i}\left(x_{1}, x_{2}, x_{3 D i}, x_{4 D i}\right)+\\ & f_{A}\left(x_{1}, x_{2}, x_{3 A n}, x_{4 A n}\right) \end{aligned} $ | (11) |
where f(*) denotes non-linear mapping function trained by SVR; D denotes detail components of predict value and A denotes approximation components of predict value; n is decomposition level.
5) Performance measures are conducted by comparing the final forecasting value with ANN and SVR prediction results.
4 Numerical Test 4.1 Study Area and DataTo evaluate the applicability of proposed WT-SVR model for bus travel time prediction, a south-eastbound corridor on Daqiao Rd. and a north-westbound from Jianning Rd. to Rehe Rd. of bus No.550 in Nanjing, China were selected, as experimental route sections. The route of Bus No. 550 is 10.2 km length and has 27 bus stops in the upstream direction, which starts from Taifeng Road terminus to Mochou Lake Park terminus. The bus headway varies from about 10 min in peak hours and about 15 min in off-peak hours. The study region of bus No.550 in this paper starts from Qiaobei Coach station to Agricultural Trade Center stops, which is divided into two sections as shown in Fig. 4.
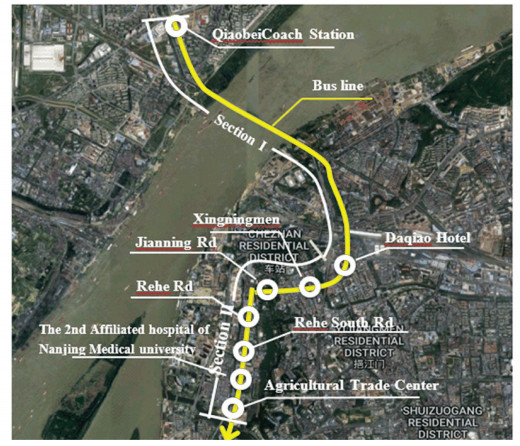
|
Fig.4 Layout of study area of bus No.550 |
a) Section Ⅰ: from Qiaobei Coach Station to Daqiao Hotel stop.
b) Section Ⅱ: from Daqiao Hotel stop to Agricultural Trade Center stop.
The buses on this route are equipped with the GPS and AVL devices that can obtain the real-time travel time information. The bus travel time data was collected from November 2, 2015 to November 10, 2015 in weekdays during the bus operation time (05:10 am -21:10 pm). After preprocessing of collected data, a total of 560 sets of data are valid, and each set of data contains the travel time of a bus through a road segment. All the bus travel time data sets are divided into two parts for training and testing. The bus travel time observations from the six weekdays from November 2, 2015 to November 9, 2015 are set as training set, and the data of November 10, 2015 is set as the testing set. To avoid numerical difficulties, normalization of the samples is conducted before modeling as follows:
| $ x_{i}^{\prime}=\frac{x_{i}-\min \left(x_{i}\right)}{\max \left(x_{i}\right)-\min \left(x_{i}\right)} $ | (12) |
where, xi denotes the ith value of the input or output data set X={x1, x2, …, xn}.
4.2 Model Identification 4.2.1 WT-SVR modelThe history and real-time bus travel time data series are decomposed into several components by wavelet transform at different levels, and each sub-series component is predicted by different SVR models. The decomposed level is the most key parameter in wavelet transform. If the decomposed level is too low, high-frequency noise remains in the low-frequency components, which will directly affect the prediction accuracy of low-frequency components; but when the level is too large, the complexity and training time of the model will be increased. Thus, in this study 'db3' function is selected as the mother wavelet and decomposed level is three, according to the requirement of multi-scale decomposition and single branch reconstruction. All levels components received by decomposition are forecasted respectively by SVR models. At last, the future bus travel time is equal to the summation of prediction results of each component. During the process, RBF is selected as kernel function of SVR models. The best combination of parameters for each SVR is shown in Table 2.
| Table 2 Parameters selection of each SVR model |
4.2.2 SVR model
For the purpose of investigating the performance of the model, the proposed WT-SVR model is compared with the normal SVR and BPANN, which are trained and tested with the same data sets. The normal support vector regression model consists of four model inputs (x1, x2, x3, x4) and one output vector (y) without wavelet decomposition. The best combination of parameters for SVR is C=1, γ=0.062 5 and ε=0.003 125.
4.2.3 ANN modelThe ANN model with the hyperbolic tangent sigmoid transfer function is used in this study, which consists of an input layer, a hidden layer, and an output layer. Different number of neurons in the hidden layer is tested in the back-propagation neural network model in order to identify the suitable well-trained one. By trial and error process the optimal number of neurons in the hidden layer is determined to be 8. The final ANN architecture consists of the same input features as the SVR and the model parameters are optimized by the back propagation algorithm.
4.3 Results and DiscussionIn order to evaluate the performance of the prediction, the performance measurement of proposed WT-SVR model is mean absolute percentage error (EMAP), mean absolute error (EMA) and the root mean square error (ERMS). The formula can be expressed as follows:
| $ E_{\mathrm{MA}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right| $ | (13) |
| $ E_{\mathrm{MAP}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|\frac{y_{i}-\hat{y}_{i}}{y_{i}}\right| $ | (14) |
| $ E_{\mathrm{RMS}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}} $ | (15) |
where, yi is the observed value in future;
The future travel time of bus can be forecasted by WT-SVR model proposed in the above section, and the prediction results of two testing sections in the bus route NO.550 are shown in Fig. 5. it can be seen that the proposed hybrid model can capture the underlying dynamics of bus travel time variations and achieve high fitness in both two sections, with the regression coefficient R square 0.754 7 and 0.630 6 respectively. Considering the different traffic conditions on the two testing sections, difference between R square can be easily understood. There are many traffic signal intersections and bus stops in section Ⅱ, which may cause the travel time of this section to be more fluctuant and non-stationary than section Ⅰ.
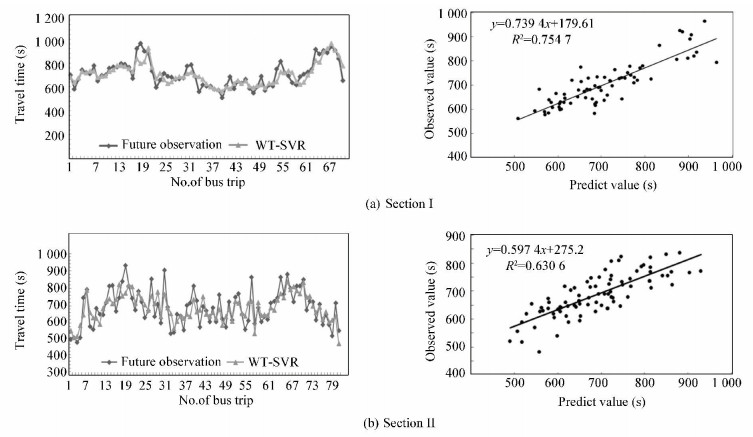
|
Fig.5 Prediction results of WT-SVR in two testing sections |
Additionally, traditional BP neural networks and support vector regression model are also experimented with in this paper as comparisons. Fig. 6 gives the absolute error of prediction for ANN, SVR and hybrid WT-SVR model in the testing links of the bus No.550. The maximum prediction error of ANN, SVR and WT-SVR are 244, 223 and 167 respectively for section Ⅰ and 331, 256 and 140 respectively for section Ⅱ. It is observed that the hybrid WT-SVR model is able to forecast accurately and gain a lower prediction error in almost all trips when compared to other models. Moreover, Table 2 gives a comparison of EMA, EMAP and ERMS obtained by the WT-SVR, SVR, and ANN models for two testing sections. In comparison with single SVR model, the proposed hybrid model gives a decrease in EMA, EMAP and ERMS values of 15 seconds, 2% and 20 seconds respectively for section Ⅰ and 18 seconds, 2.5% and 23 seconds for section Ⅱ. Similarly when compared to BPANN model, EMA, EMAP and ERMS values for WT-SVR are lowered by 26 seconds, 4% and 30 seconds respectively for section Ⅰ and 31 seconds, 4.5% and 45 seconds for section Ⅱ. According to Lewis[26], a EMAP value of less than 10% can be considered quite accurate. As shown in Table 3, the EMAP values of the two reference models constructed in this paper are close to 10% or even greater than 10% indicating that their performance is between "more accurate" and "accurately accurate". However, the EMAP values of the WT-SVR shows that its predictive performance is "pretty accurate". It shows that the prediction results of the model constructed in this paper are more accurate and reliable, which is feasible and effective in bus travel-time prediction. For the arrival time forecast of passengers issued to passengers, the value of the information depends heavily on the reliability of the forecast results, reducing the prediction error can prevent passengers from missing the bus due to wrong information and improve the availability of information.
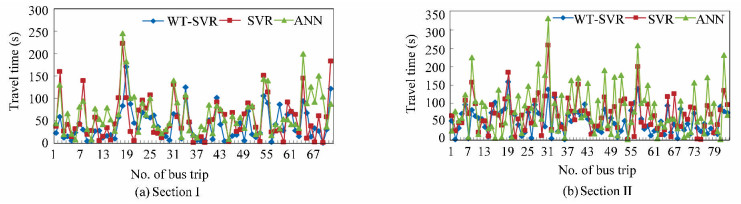
|
Fig.6 Prediction error of three models in testing sections |
| Table 3 Comparison of WT-SVR with ANN and SVR models |
5 Conclusions
In this paper, the applicability of a hybrid WT-SVR model has been investigated for predicting the bus travel time of the route No.550 in Nanjing, China. The WT-SVR model was developed by integrating wavelet transform technique with support vector regression model. In the developed model, the original travel time data were decomposed into approximate components and detail components by wavelet transform, and SVR model was constructed for each components of future travel time. The model was tested using four input variables including time of day, road segment, and the latest travel time of previous section as well as the latest travel time in predicted section, which is also compared with regular SVR and ANN model with the same dataset. From the results, it was determined that bus travel time prediction based on the wavelet SVR provided higher accuracy when compared to regular SVR and ANN models, as the wavelet transform can capture travel time variations in different scale and thus enhances the forecasting ability of SVR model. Therefore, the proposed model can greatly improve the prediction performance of bus travel times, which would contribute to the increase of the service level and predictive reliability.
| [1] |
Chen M, Chien S I, Liu X, et al. Application of APC/AVL archived data support system. 82 nd Annual Meeting of the Transportation Research Board, 2003.
(  0) 0) |
| [2] |
D'Angelo M P, Al-Deek H M, Wang M C. Travel-time prediction for freeway corridors. Transportation Research Record Journal of the Transportation Research Board, 1999, 1676: 184-191. DOI:10.3141/1676-23 (  0) 0) |
| [3] |
Patnaik J, Chien S, Bladikas A. Estimation of bus arrival times using APC data. Physical Review Letters, 2004, 7(1): 128001-128100. (  0) 0) |
| [4] |
Vanajakshi L, Subramanian S C, Sivanandan R. Travel time prediction under heterogeneous traffic conditions using global positioning system data from buses. Iet Intelligent Transport Systems, 2009, 3(1): 1-9. DOI:10.1049/iet-its:20080013 (  0) 0) |
| [5] |
Park D, Rilett L R. Forecasting freeway link travel times with a multilayer feedforward neural network. Computer-Aided Civil and Infrastructure Engineering, 1999, 14(5): 357-367. DOI:10.1111/mice.1999.14.issue-5 (  0) 0) |
| [6] |
Chien I J, Ding Y, Wei C. Dynamic bus arrival time prediction with artificial neural networks. Journal of Transportation Engineering, 2002, 128(5): 429-438. DOI:10.1061/(ASCE)0733-947X(2002)128:5(429) (  0) 0) |
| [7] |
Jeong R, Rilett L R. Bus arrival time prediction using artificial neural network model.International IEEE Conference on Intelligent Transportation Systems, 2004. Proceedings of IEEE Xplore, 2004.988-993. https://www.researchgate.net/publication/224756438_Bus_arrival_time_prediction_using_artificial_neural_network_model
(  0) 0) |
| [8] |
Gurmu Z, Wei F. Artificial neural network travel time prediction model for buses using only GPS data. Journal of Public Transportation, 2014, 17(2): 45-65. DOI:10.5038/2375-0901 (  0) 0) |
| [9] |
Yu Bin, Jiang Y L, Yu Bo, et al. Application of support vector machines in bus travel time prediction. Journal of Dalian Maritime University, 2008, 34(4): 158-160. (  0) 0) |
| [10] |
Chien I J, Ding Y, Wei C. Dynamic bus arrival time prediction with artificial neural networks. Journal of Transportation Engineering, 2002, 128(5): 429-438. DOI:10.1061/(ASCE)0733-947X(2002)128:5(429) (  0) 0) |
| [11] |
Wu C H, Ho J M, Lee D T. Travel-time prediction with support vector regression. IEEE Transactions on Intelligent Transportation Systems, 2005, 5(4): 276-281. (  0) 0) |
| [12] |
Vanajakshi L, Rilett L R. Support vector machine technique for the short term prediction of travel time. Intelligent Vehicles Symposium. IEEE Xplore, 2007.600-605. https://www.researchgate.net/publication/4268836_Support_Vector_Machine_Technique_for_the_Short_Term_Prediction_of_Travel_Time
(  0) 0) |
| [13] |
Wang J, Yu B, Yang Z Z. Bus travel-time prediction based on bus speed. Transport, 2010, 163(1): 3-7. (  0) 0) |
| [14] |
Liu X, Yuan S, Li L. Prediction of temperature time series based on wavelet transform and support vector machine. Journal of Computers, 2012, 7(8): 32-42. (  0) 0) |
| [15] |
Suryanarayana C, Sudheer C, Mahammood V, et al. An integrated wavelet-support vector machine for groundwater level prediction in Visakhapatnam, India. Neurocomputing, 2014, 145(18): 324-335. (  0) 0) |
| [16] |
Kalteh A M. Wavelet genetic algorithm-support vector regression (wavelet GA-SVR) for monthly flow forecasting. Water Resources Management, 2015, 29(4): 1283-1293. DOI:10.1007/s11269-014-0873-y (  0) 0) |
| [17] |
Liu Y, Shi J, Yang Y, et al. Short-term wind-power prediction based on wavelet transform-support vector machine and statistic-characteristics analysis. IEEE Transactions on Industry Applications, 2011, 48(4): 1136-1141. (  0) 0) |
| [18] |
Fang X, Bai T. Share price prediction using wavelet transform and ant colony algorithm for parameters optimization in SVM. Intelligent Systems, 2009. GCIS '09. WRI Global Congress on IEEE, 2009.288-292.
(  0) 0) |
| [19] |
Yu B, Yang Z Z, Chen K, et al. Hybrid model for prediction of bus arrival times at next station. Journal of Advanced Transportation, 2010, 44(3): 193-204. (  0) 0) |
| [20] |
Ge Y, Wang G. Study of traffic flow short-time prediction based on wavelet neural network. Electrical Engineering and Control, 2011, 98: 509-516. DOI:10.1007/978-3-642-21765-4 (  0) 0) |
| [21] |
Yusuf A, Madisetti V K. Configuration for predicting travel-time using wavelet packets and support vector regression. Journal of Transportation Technologies, 2013, 3(3): 220-231. DOI:10.4236/jtts.2013.33023 (  0) 0) |
| [22] |
Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory, 1990, 36(5): 961-1005. DOI:10.1109/18.57199 (  0) 0) |
| [23] |
Vapnik V N. The nature of satistical learning theory. New York: Springer-Verlag Inc, 1999.988 - 999.
(  0) 0) |
| [24] |
Ji Y J, Lu J W, Chen X S, et al. Prediction model of bus arrival time based on particle swarm optimization and wavelet neural network. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(3): 60-66. (  0) 0) |
| [25] |
Yu B, Yang Z Z, Chen K, et al. Hybrid model for prediction of bus arrival times at next station. Journal of Advanced Transportation, 2010, 44(3): 193-204. DOI:10.1002/atr.136 (  0) 0) |
| [26] |
Lewis C D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting.London: Butterworth Heinemann, 1982.
(  0) 0) |
 2019, Vol. 26
2019, Vol. 26


