Switched systems, an important class of hybrid systems, are often encountered in many practical situations. Normally, the switched system is defined as dynamical system which is comprised by series of continuous-time or discrete-time subsystems and a logical rule that decides the switching mechanism among the individual subsystems[1]. In the past two decades, more and more researchers and experts have been drawn by switched systems because of a number of applications and the theoretical importance. It is well known that the stability problem is one of key issues of studying switched systems. In order to study the stability of switched systems, some approaches have been proposed; for example, the common Lyapunov function method, dwell time or average dwell time method, multiple Lyapunov function method[2-15]. Among them, the common Lyapunov function method is a particular method which only finds a common Lyapunov function that ensures stability of the whole switched systems and switching signals is arbitrary[2-4]. This method is usually used when we cannot know the switching signal or it is too complex to apply directly in studying the stability problem.
In the real world, many control systems often company with uncertainties including parametric, structural and environmental uncertainties[9, 12]. Such uncertainties often appear in aircraft engine, mechanical systems, chemical engineering and so on. The existence of uncertainties makes the study of system stability more complicated. As is well known, adaptive control is a powerful tool to deal with uncertainties, which provides adaptive control laws to real-time adjust controllers or system parameters for obtaining desired system performance[16]. From a perspective of practicality, the adaptive control can be classified into three types: model reference adaptive control (MRAC), self-tuning control and other adaptive control[17]. Among them, MRAC is an extensively used method and has been matured theoretically[18-22]. The purpose of MRAC is to make the state (or output) of the controlled system track the state (or output) of a preset reference model by designing the controller and adaptive law. In the last decades, there are many results in this field for non-switched systems[18-22].
However, few results on MRAC for switched systems with parametric uncertainties have been reported so far.Chiang and Fu[23] studied a class of signal-input-signal-output switched systems by means of a variable structure MRAC method, while the requirement limits the design flexibility which the reference model is common for all subsystems. When the state of the system is fully measurable, Liu and Xiang[24] solved the exponential H∞ output tracking control problem for a class of uncertain switched neutral systems. They presented a concurrent learning model reference adaptive control architecture for this switched systems and the problem of closed loop parameter estimation was solved in the paper[25].Based on the minimal control synthesis algorithm, Bernardo, Montanaro and Santini[26] presented a generic MRAC scheme so that the state of a multimodal piecewise affine system can track asymptotically a given multimodal piecewise affine (or smooth) reference model. But, what needs to point out is that all the above results require the state of controlled system being measurable while it is not reasonable for many practical systems. Therefore, how to deal with the MRAC problem for switched systems which have parametric uncertainties is a practical problem when the state of the system is immeasurable, which is a motivation for this paper.
On the other hand, as we all know, what restricts the application of MRAC is the poor transient performance. So it must do something to improve MRAC. Recently, several researchers proposed a new class of closed-loop reference model in which the reference model has an observer-like feedback term containing the state error and a feedback gain[18-22]. Because of the introduction of the feedback term, the transient performance can be improved by adjusting the feedback gain. In the paper, Gibson, Annaswamy and Lavertsky[18] analyzed how the closed-loop reference model improved the transient performance of MRAC and compared the transient performance of the closed-loop reference model adaptive control system with the classical open-loop reference model control system. Lately, Zheng[22] studied the MRAC state tracking problem with the closed-loop reference model when the state is not available for measurement. However, only non-switched systems are studied. A natural problem arises: how to improve the transient performance of switched systems. Clearly, this is a challenge problem for the switched systems. This is another motivation for this paper.
This paper studies the MRAC problem for switched systems with parametric uncertainties under arbitrary switching while it is not required the state of the controlled system should be fully measurable. In this paper, the contributions are as follows: first of all, we only use the output and the state of the given closed-loop reference model to design controllers and adaptive laws because the requirement that the controlled system state is fully measurable for is hard to achieve in many practical systems. Secondly, all reference models and controllers for subsystems are not common which remarkably add the flexibility of designing. Finally, the introduction of the closed-loop reference model can improve the transient performance of the switched system.
The organization of this paper is as follows. Section 2 gives the problem statement and preliminaries.The design of controllers and adaptive laws and the stability theorem of switched error system are in Section 3.A numerical Simulink example is established to prove the correctness of this theory in Section 4. Section 5 is the conclusion.
Notation: The standard Euclidean or the induced matrix two-norm is denoted as ‖·‖. The positive-definite matrix is P >0. A-1 represents the inverse of a matrix A and AT represents the transpose of a matrix A. The smallest eigenvalue of matrix A is defined as λmin(A) and the trace of square matrix A is defined as tr(A). We use I and 0 to denote identity matrix and zero matrix in a block matrix respectively.
2 System Statement and PreliminariesThe switched system with parametric uncertainties in this paper can be described as:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{A}}_\sigma }\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_\sigma }\mathit{\boldsymbol{u}}}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{C}}_\sigma ^{\rm{T}}\mathit{\boldsymbol{x}}} \end{array}} \right. $ | (1) |
where x∈Rn is the plant vector, the control input is denoted as u∈Rm, y∈Rm denotes the plant output. σ(t):[0, +∞)→I={1, 2, …, N} denotes switching signal of this switched systems and the quantity of the subsystems is N.Bi∈Rn×m and Ci∈Rn×m are known constant matrices while Ai∈Rn×n and Λi∈Rm×m are unknown, and only y is measurable.
The closed-loop switched reference model is:
| $ \left\{\begin{array}{l}{\dot{\boldsymbol{x}}_{m}=\boldsymbol{A}_{m \sigma} \boldsymbol{x}_{m}+\boldsymbol{B}_{\sigma} \boldsymbol{r}-\boldsymbol{L}_{\sigma}\left(\boldsymbol{y}-\boldsymbol{y}_{m}\right)} \\ {\boldsymbol{y}_{m}=\boldsymbol{C}_{\sigma}^{\mathrm{T}} \boldsymbol{x}_{m}}\end{array}\right. $ | (2) |
where r∈Rm is the input signal of reference model and Li∈Rn×m are feedback gains that will be designed suitably. e=x-xm denotes the state error. There is one-to-one correspondence between the subsystems of the reference model and the controlled system. In this paper, the control objective is to design a switched controller and switched adaptive laws so that the state error converges to 0 i.e., the state of controlled system x tracks the state of given closed-loop reference model xm.
Remark 1 In the classical switched MRAC control problem[23-27], the switched reference model is open-loop switched reference model and the form is given by:
| $ \left\{\begin{array}{l}{\dot{\overline{\boldsymbol{x}}}_{m}=\boldsymbol{A}_{m \sigma} \overline{\boldsymbol{x}}_{m}+\boldsymbol{B}_{\sigma} \boldsymbol{r}} \\ {\overline{\boldsymbol{y}}_{m}=\boldsymbol{C}_{\sigma}^{\mathrm{T}} \overline{\boldsymbol{x}}_{m}}\end{array}\right. $ |
Compared with the open-loop reference model, the closed-loop reference model has an additional feedback term. When we choose Li=0, i∈M or the state error e→0, xm→xm, thus x→xm, so the closed-loop switched reference model in Eq.(2) degenerates into the open reference switched reference model. Besides, the introduction of the feedback Li can improve the transient performance due to the additional degree of freedom for each subsystem[18-22].
The following assumptions are requisite to achieve the control objective.
Assumption 1 The product CiT Bi is full rank, i∈I.
Assumption 2 The pair (Ami, CiT) is observable, i∈I.
Assumption 3 The subsystems in controlled system (1) are minimum phase.
Assumption 4 There exists Θi*∈Rn×m and Ki*∈Rm×m such that Ai+BiΛiΘi*T=Ami and ΛiKi*T=I, i∈I, respectively.
Assumption 5 Λi is diagonal with positive elements, i∈I.
Assumption 6 The unknown control input matrices Λi and the uncertain matching parameters Θi* have priori known upper bounds and the following hold:
| $ \bar \lambda = \mathop {\max }\limits_{i \in I} \left( {\sup \left\| {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}} \right\|} \right), {\bar \theta ^*} = \mathop {\max }\limits_{i \in I} \left( {\sup \left\| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}} \right\|} \right) $ | (3) |
Remark 2 Assumption 1 actually is the requirement that Mi is nonsingular. Assumption 2 is needed since the feedback gains of the reference model Li are required to use in the following result. Assumption 3 makes the condition of the KYP lemma hold. Assumption 4 is the matching conditions and is commonly used in MRAC[17]. Assumption 5 is about the uncertainties and it is routinely satisfied in the area of aerospace industry in which control directions are generally known but we do not know their magnitudes[27]. Assumption 6 is for a suitable choice of Li(i∈M).
Lemma 1[21, 28] For each subsystem of the switched system (1) satisfying Assumptions 1-3, and Mi choose as in Eq.(8). There always exists Lsi such that MiTCiT(sI-Ami-LsiCiT)-1Bi are strict positive realness (SPR).
Lemma 2[21, 29] If Li=Lsi-ρiBiMiT are chosen and ρi>0 are arbitrary, then the transfer functions MiTCiT(sI-Ami-LsCiT)-1Bi are SPR and the following hold:
| $ \left(\boldsymbol{A}_{m i}+\boldsymbol{L}_{i} \boldsymbol{C}_{i}^{\mathrm{T}}\right)^{\mathrm{T}} \boldsymbol{P}_{i}+\boldsymbol{P}_{i}\left(\boldsymbol{A}_{m i}+\boldsymbol{L}_{i} \boldsymbol{C}_{i}^{\mathrm{T}}\right)=-\boldsymbol{Q}_{i} $ | (4a) |
| $ \boldsymbol{Q}_{i} \triangleq \boldsymbol{Q}_{s i}+2 \rho_{i} \boldsymbol{C}_{i} \boldsymbol{M}_{i} \boldsymbol{M}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}^{\mathrm{T}} $ | (4b) |
| $ \boldsymbol{P}_{i} \boldsymbol{B}_{i}=\boldsymbol{C}_{i} \boldsymbol{M}_{i}, i \in \boldsymbol{I} $ | (4c) |
where Lsi are in Lemma 1, Pi=PiT>0 and Qsi=QsiT>0 are ρi and Mi.
3 Stability AnalysisFor the switched system in Eqs. (1) and (2) satisfying the all above assumptions, we design the following switched adaptive controller and adaptive laws:
| $ \boldsymbol{u}_{i}(t)=\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i}^{\mathrm{T}}(t) \boldsymbol{x}_{m}+\boldsymbol{K}_{i}^{\mathrm{T}}(t) \boldsymbol{r}, i \in \boldsymbol{I} $ | (5) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}_i}(t) = \left\{ {\begin{array}{*{20}{l}} { - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\mathit{\Theta }_i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{m}}}(\mathit{\boldsymbol{t}})\mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{M}}_i}, }&{i = \sigma }\\ {0, }&{i \ne \sigma } \end{array}} \right. $ | (6) |
| $ {\mathit{\boldsymbol{\dot K}}_i}(t) = \left\{ {\begin{array}{*{20}{l}} { - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{K_i}}}{\mathit{\boldsymbol{x}}_m}(t)\mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{M}}_i}, i}&{ = \sigma }\\ {0, }&{i \ne \sigma } \end{array}} \right. $ | (7) |
where Θi(t) and Ki(t) are the estimated values of Θi* and Ki* respectively. ΓΘi and ΓKi are both positive diagonal matrices which can be designed freely. ey=y-ym is the output tracking error and where
| $ \boldsymbol{M}_{i} \triangleq \boldsymbol{C}_{i}^{\mathrm{T}} \boldsymbol{B}_{i} $ | (8) |
Remark 3 In general, it is hard to measure all the state of the controlled systems in many practical systems. Therefore, we choose the state of the given reference model instead of the controlled system to design the control input Eq.(5).
From Eqs.(1), (2) and (5), we can easily get the following expression of the state error
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{\dot e}}=\left(\boldsymbol{A}_{m_{\sigma}}+\boldsymbol{L}_{\sigma} \boldsymbol{C}_{\sigma}^{\mathrm{T}}\right) \boldsymbol{e}+\\ \boldsymbol{B}_{\sigma} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{\sigma}\left(\tilde{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}_{\sigma}^{\mathrm{T}} \boldsymbol{x}_{m}+\tilde{\boldsymbol{K}}_{\sigma}^{\mathrm{T}} \boldsymbol{r}-\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{\sigma}^{* \mathrm{T}} \boldsymbol{e}\right) \\ \boldsymbol{e}_{y}=\boldsymbol{C}_{\sigma}^{\mathrm{T}} \boldsymbol{e} \end{array}\right. $ | (9) |
where
In the following, we give a sufficient condition under which the MRAC problem is solved.
Theorem 1 If there exist P=PT>0 and Q=QT>0, such that the following holds:
| $ \left(\boldsymbol{A}_{m i}+\boldsymbol{L}_{i} \mathrm{C}_{i}^{\mathrm{T}}\right)^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P}\left(\boldsymbol{A}_{m i}+\boldsymbol{L}_{i} \boldsymbol{C}_{i}^{\mathrm{T}}\right) \leqslant-\boldsymbol{Q} $ | (10a) |
| $ \boldsymbol{Q}_{s i}+2 \rho \boldsymbol{C}_{i} \boldsymbol{M}_{i} \boldsymbol{M}_{i}^{\mathrm{T}} \boldsymbol{C}_{i}^{\mathrm{T}} \leqslant \boldsymbol{Q} $ | (10b) |
| $ \boldsymbol{P B}_{i}=\boldsymbol{C}_{i} \boldsymbol{M}_{i} $ | (10c) |
The MRAC problem of switched adaptive system described by Eqs.(1), (2), (5), (6) satisfying Assumptions 1-6 with Li defined in Eq.(4), Mi stated in Eq. (8), ρ>ρ* is solved with
| $ \rho^{*}=\frac{\overline{\lambda}^{2} \overline{\theta}^{* 2}}{2 \min\limits_{i \in I} \lambda_{\min }\left(\boldsymbol{Q_{s i}}\right)} $ | (11) |
Proof The Lyapunov function we choose is:
| $ \begin{array}{l} \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Pe}} + \sum\limits_{i = 1}^M {{\bf{Tr}}} \left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}(t)\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}}^{ - 1}{{\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}}_i}(t)} \right) + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^M {{\bf{Tr}}} \left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}(t)\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}}^{ - 1}{{\mathit{\boldsymbol{\widetilde K}}}_i}(t)} \right) \end{array} $ | (12) |
Differentiating V along the active subsystem trajectories in Eq. (9) gives:
| $ \begin{array}{l} \mathit{\boldsymbol{\dot V}} = {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{A}}_{mi}} + {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{C}}_i^{\rm{T}} + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\left( {\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_m} + \mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}\mathit{\boldsymbol{r}} - } \right.} \right.\\ \;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}\mathit{\boldsymbol{e}}){)^{\rm{T}}}\mathit{\boldsymbol{Pe}} + {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {{\mathit{\boldsymbol{A}}_{mi}} + {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{C}}_i^{\rm{T}} + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\left( {\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_m} + } \right.} \right.\\ \;\;\;\;\;\;\;\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}\mathit{\boldsymbol{e}})) + 2{\bf{Tr}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}(t)\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}}^{ - 1}{{\mathit{\boldsymbol{\dot { \boldsymbol{\tilde \varTheta} }}}}_i}(t)} \right) + \\ \;\;\;\;\;\;\;2{\bf{Tr}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}(t)\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{K_i}}^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde K}}}}_i}(t)} \right) = {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {{{\left( {{\mathit{\boldsymbol{A}}_{mi}} + {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{C}}_i^{\rm{T}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} + } \right.\\ \;\;\;\;\;\;\;\mathit{\boldsymbol{P}}\left( {{\mathit{\boldsymbol{A}}_{mi}} + {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{C}}_i^{\rm{T}}} \right))\mathit{\boldsymbol{e}} - 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}\mathit{\boldsymbol{e}} + \\ \;\;\;\;\;\;\;2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_m} + 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}\mathit{\boldsymbol{r}} - \\ \;\;\;\;\;\;\;2{\bf{Tr}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}(t){\mathit{\boldsymbol{x}}_m}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}} \right) - \\ \;\;\;\;\;\;\;2{\bf{Tr}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}(t)\mathit{\boldsymbol{r}}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}} \right) \end{array} $ | (13) |
According to the property of the matrix trace, we have:
| $ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_m} = {\bf{Tr}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\widetilde \varTheta} }}_i^{\rm{T}}(t){\mathit{\boldsymbol{x}}_m}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}} \right) $ | (14a) |
| $ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}\mathit{\boldsymbol{r}} = {\bf{Tr}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{\widetilde K}}_i^{\rm{T}}(t)\mathit{\boldsymbol{r}}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}} \right) $ | (14b) |
By Eqs. (8), (10) and (14), Eq. (13) can be written as:
| $ \begin{array}{l} \mathit{\boldsymbol{\dot V}} = {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {{{\left( {{\mathit{\boldsymbol{A}}_{mi}} + {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{C}}_i^{\rm{T}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {{\mathit{\boldsymbol{A}}_{mi}} + {\mathit{\boldsymbol{L}}_i}\mathit{\boldsymbol{C}}_i^{\rm{T}}} \right)} \right)\mathit{\boldsymbol{e}} - \\ \;\;\;\;\;\;2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}\mathit{\boldsymbol{e}} \le \\ \;\;\;\;\;\; - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe}} - 2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}\mathit{\boldsymbol{e}} \le \\ \;\;\;\;\;\; - {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{Q}}_{si}} + 2\rho {\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{M}}_i}\mathit{\boldsymbol{M}}_i^{\rm{T}}\mathit{\boldsymbol{C}}_i^{\rm{T}}} \right) - \\ \;\;\;\;\;\;2{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{*{\rm{T}}}\mathit{\boldsymbol{e}} \end{array} $ | (15) |
By the fact that ey=CiTe, we can get
| $ \boldsymbol{Q}(\rho)=\left[\begin{array}{cc}{2 \rho \boldsymbol{M}_{i} \boldsymbol{M}_{i}^{\mathrm{T}}} & {\boldsymbol{M}_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{i} \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i}^{* \mathrm{T}}} \\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i}^{* \mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{i} \boldsymbol{M}_{i}^{\mathrm{T}}} & {\boldsymbol{Q}_{s i}}\end{array}\right]\\ ~~~~~~~~~~~\boldsymbol{\varepsilon}=\left[\begin{array}{l}{\boldsymbol{e}_{y}} \\ {\boldsymbol{e}}\end{array}\right] $ |
Due to ρ>ρ*>0 and Eq.(11), we have
| $ 2 \boldsymbol{M}_{i} \rho \boldsymbol{M}_{i}^{\mathrm{T}}-\boldsymbol{M}_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{i} \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i}^{* \mathrm{T}} \boldsymbol{Q}_{s i}^{-1} \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{i}^{*} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{i} \boldsymbol{M}_{i}^{\mathrm{T}}>0 $ |
According to the Schur complement Lemma, Q(ρ) is a positive-definite matrix. Thus
In this section, we provide a numerical example to prove the effectiveness of the theorem in this paper.
Considering the switched system (1) and the switched closed-loop reference model (2), the system matrices and parameters are given by:
| $ A_{1}=\left[\begin{array}{rr}{-2} & {0} \\ {0} & {-3}\end{array}\right], \quad \boldsymbol{B}_{1}=\left[\begin{array}{l}{4} \\ {2}\end{array}\right]\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{1}=0.5, \quad \boldsymbol{C}_{1}=\left[\begin{array}{l}{1} \\ {1}\end{array}\right]\\ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{r}} { - 1.8}&0\\ 0&{ - 3.2} \end{array}} \right], \;\;\;{\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{l}} 4\\ 2 \end{array}} \right]\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{2}=0.5, \quad \quad \boldsymbol{C}_{2}=\left[\begin{array}{l}{1} \\ {1}\end{array}\right] $ |
The plant parameters of the closed-loop reference model are:
| $ \begin{array}{c} {\mathit{\boldsymbol{A}}_{m1}} = \left[ {\begin{array}{*{20}{c}} { - 3}&{ - 2}\\ { - 0.5}&{ - 4} \end{array}} \right]\\ {\mathit{\boldsymbol{B}}_{m1}} = \left[ {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right], \;\;\;{\mathit{\boldsymbol{C}}_{m1}} = \left[ {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right]\\ {\mathit{\boldsymbol{A}}_{m2}} = \left[ {\begin{array}{*{20}{c}} { - 2.8}&{ - 2}\\ { - 0.5}&{ - 4.2} \end{array}} \right]\\ {\mathit{\boldsymbol{B}}_{m2}} = \left[ {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right], \;\;\;{\mathit{\boldsymbol{C}}_{m2}} = \left[ {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right] \end{array} $ |
The reference input is r(t)=4sin(0.2πt). From Assumption 4, we have
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^* = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2^* = {\left[ {\begin{array}{*{20}{c}} { - 0.5}\\ { - 1} \end{array}} \right]^{\rm{T}}}, K_1^{*{\rm{T}}} = K_2^{*{\rm{T}}} = 2 $ |
The parameters of the adaptive laws in Eqs.(6) and (7) are designed as
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\mathit{\Theta }_1}}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\mathit{\Theta }_2}}} = \left[ {\begin{array}{*{20}{c}} {400}&0\\ 0&{400} \end{array}} \right], {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{K_1}}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{K_2}}} = 450 $ |
A direct calculation gives
| $ \boldsymbol{L}_{s 1}=\left[\begin{array}{c}{2} \\ {1.333}\end{array}\right], \boldsymbol{L}_{s 2}=\left[\begin{array}{c}{1.4} \\ {-1.87}\end{array}\right] $ |
Then, we choose ρ=1. The feedback gains of the reference model are
| $ \boldsymbol{L}_{1}=\left[\begin{array}{c}{-22} \\ {-10.6667}\end{array}\right], \boldsymbol{L}_{2}=\left[\begin{array}{c}{-22.6} \\ {-10.13}\end{array}\right] $ |
so we have
| $ \begin{array}{c} \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{r}} {16.730}&0&{ - 24.331}&2\\ { - 24.331}&2&{51.563}&1 \end{array}} \right]\\ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} { - 350}&0\\ 0&{ - 350} \end{array}} \right] \end{array} $ |
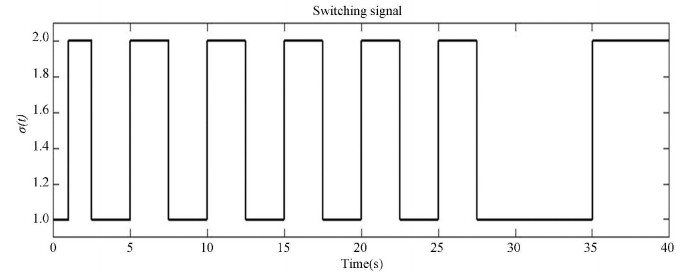
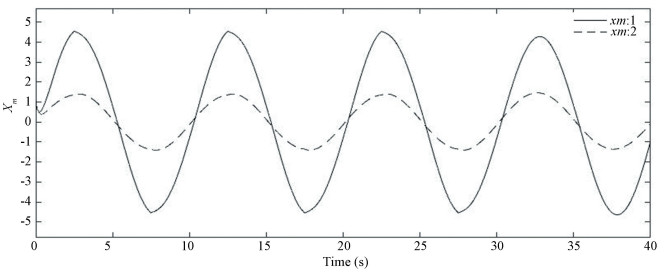
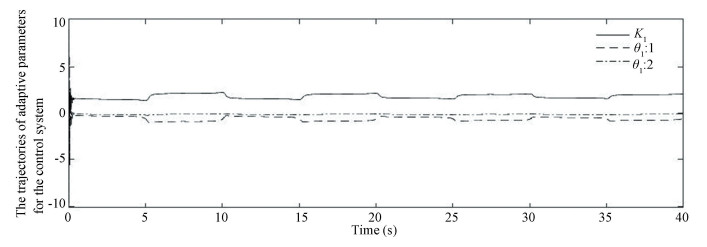
From Figs. 1-5, it can be concluded that the switched MRAC problem in Eqs.(1), (2) and (9) with the closed-loop reference model is solved under the adaptive controller (5). Fig. 1 is the switching signal. Fig. 2 shows that the trajectories of the closed-loop reference model are bounded. It shows us that the adaptive parameters of the error systems are bounded from Figs. 3-4. From Fig. 5, we can get the fact that the state error converges to 0 which implies the state of controlled system can track the state of given switched reference model.
|
Fig.1 The switching signal |
|
Fig.2 Trajectories of the reference model |
|
Fig.3 Trajectories of adaptive parameters for the control system |

|
Fig.4 Trajectories of adaptive parameters for the reference model |

|
Fig.5 The state error |
5 Conclusions
The MRAC problem for the switched systems with parametric uncertainties which has closed-loop reference model for each subsystem under arbitrary switching signals has been solved in this paper. Firstly, the reference model and the controller were not common for all subsystems. Secondly, to get a better transient performance of the whole switched system, the closed-loop reference model has been introduced. Finally, it is hard to measure all of the state of system in many piratical systems, so the design of control input is depended on the state of closed-loop reference model and the measurable output error in this paper. By appropriate design of the adaptive control laws and the gain of the closed-loop reference models for switched systems, the state tracking errors converged to 0.
| [1] |
Lierzon D. Switching in Systems and Control. Boston: Birkhäuser, 2003.
(  0) 0) |
| [2] |
Liberzon D, Morse A S. Basic problems in stability and design of switched systems. IEEE Control Systems Magazine, 1999, 19(5): 59-70. DOI:10.1109/37.793443 (  0) 0) |
| [3] |
Lin H, Antsaklis P J. Stability and stabilizability of switched linear systems: A survey of recent results. IEEE Transactions on Automatic Control, 2009, 54(2): 308-322. DOI:10.1109/TAC.2008.2012009 (  0) 0) |
| [4] |
He Xu, Dimirovski G M, Zhao Jun. Control of switched LPV systems using common Lyapunov function method and an F-16 aircraft application. 2010 IEEE International Conference on Systems Man and Cybernetics. Pisacataway: IEEE, 2010. 386-392. DOI: 10.1109/ICSMC.2010.5641742.
(  0) 0) |
| [5] |
Xie Jing, Zhao Jun. Model reference adaptive control for switched LPV systems and its application. IET Control Theory & Applications, 2016, 10(17): 2204-2212. DOI:10.1049/iet-cta.2015.1332 (  0) 0) |
| [6] |
Xie Jing, Zhao Jun. Model reference adaptive control for nonlinear switched systems under asynchronous switching. International Journal of Adaptive Control & Signal Processing, 2016, 31(1): 3117-3122. DOI:10.1002/acs.2666 (  0) 0) |
| [7] |
Long Lijun, Zhao Jun. H∞ control of Switched Nonlinear Systems in ρ-Normal form using multiple Lyapunov functions. IEEE Transactions on Automatic Control, 2012, 57(5): 1285-1291. DOI:10.1109/TAC.2012.2191835 (  0) 0) |
| [8] |
Long Lijun, Zhao Jun. Switched adaptive stabilization of switched nonlinearly parameterized cascade systems and its application to a two inverted pendulums. International Journal of Adaptive Control & Signal Processing, 2015, 29(3): 346-361. DOI:10.1002/acs.2474 (  0) 0) |
| [9] |
Long Lijun, Zhao Jun. Adaptive output-feedback neural control of switched uncertain nonlinear systems with average dwell time. IEEE Transactions on Neural Networks & Learning Systems, 2015, 26(7): 1350-1362. DOI:10.1109/TNNLS.2014.2341242 (  0) 0) |
| [10] |
Wu Caiyun, Zhao Jun. H∞ adaptive tracking control for switched systems based on an average dwell-time method. International Journal of Systems Science, 2013, 46(14): 1-13. DOI:10.1080/00207721.2013.871371 (  0) 0) |
| [11] |
Wu Caiyun, Zhao Jun, Sun Ximing. Adaptive tracking control for uncertain switched systems under asynchronous switching. International Journal of Robust & Nonlinear Control, 2015, 25(17): 3457-3477. DOI:10.1002/rnc.3275 (  0) 0) |
| [12] |
Wang Xia, Zhao Jun, Tang Yujun. State tracking model reference adaptive control for switched nonlinear systems with linear uncertain parameters. Control Theory and Technology, 2012, 10(3): 354-358. DOI:10.1007/s11768-012-1018-6 (  0) 0) |
| [13] |
Wang Yufei, Jiang Changsheng, Wu Qingxian, et al. Adaptive fuzzy tracking control for a class of switched MIMO nonlinear systems. Journal of Harbin Institute of Technology (New Series), 2012, 19(1): 44-49. (  0) 0) |
| [14] |
Li Erpeng, Long lijun, Zhao Jun. Global output-feedback stabilization for a class of switched uncertain nonlinear systems. Applied Mathematics & Computation, 2015, 256(2): 551-564. DOI:10.1016/j.amc.2015.01.039 (  0) 0) |
| [15] |
Zhao Xudong, Ling Mingxiang, Zeng Qingshuang, et al. Robust H∞ output feedback controller design for linear uncertain discrete-time switched systems via state reset. Journal of Harbin Institute of Technology (New Series), 2010, 17(3): 328-332. DOI:10.11916/j.issn.1005-9113.2010.03.007 (  0) 0) |
| [16] |
Astolfi A, Ortega R. Immersion and invariance: A new tool for stabilization and adaptive control of nonlinear systems. IEEE Transactions on Automatic Control, 2003, 48(4): 590-606. DOI:10.1109/TAC.2003.809820 (  0) 0) |
| [17] |
Tao G. Adaptive Control Design and Analysis. Hoboken: Wiley-IEEE Press, 2003.
(  0) 0) |
| [18] |
Gibson T E, Annaswamy A M, Lavretsky E. Adaptive systems with closed-loop reference-models, part Ⅰ: Transient performance. Proceedings of the American Control Conference, IEEE American Control Conference. Piscataway: IEEE, 2013. 3376-3383. DOI: 10.1109/ACC.2013.6580353.
(  0) 0) |
| [19] |
Gibson T E, Annaswamy A M, Lavretsky E. Closed-loop reference models for output-feedback adaptive systems. Proceedings of European Control Conference. Piscataway: IEEE, 2013. 365-370.
(  0) 0) |
| [20] |
Gibson T E, Annaswamy A M, Lavretsky E. Adaptive systems with closed-loop reference models: Composite control and observer feedback. IFAC Proceedings Volumes, 2013, 46(11): 440-445. DOI:10.3182/20130703-3-FR-4038.00144 (  0) 0) |
| [21] |
Gibson T E, Zheng Q, Annaswany A M, et al. Adaptive output feedback based on closed-loop reference models. IEEE Transactions on Automatic Control, 2015, 60(10): 2728-2733. DOI:10.1109/TAC.2015.2405295 (  0) 0) |
| [22] |
Zheng Q, Annaswamy A. Adaptive output-feedback control with closed-loop reference models and applications to very flexible aircraft. Journal of Guidance, Control and Dynamics, 2015. Citable URI: http://hdl.handle.net/1721.1/96428.
(  0) 0) |
| [23] |
Chiang Mingli, Fu Lichen. Variable structure model reference adaptive control of unknown switched linear systems with relative degree greater than one. Proceedings of 2009 Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference. Pisacataway: IEEE, 2009. 4240-4245. DOI: 10.1109/CDC.2009.5400303.
(  0) 0) |
| [24] |
Liu Shilong, Xiang Zhengrong. Exponential H∞ output tracking control for switched neutral system with time-varying delay and nonlinear perturbations. Circuits, Systems, and Signal Processing, 2013, 32(1): 103-121. DOI:10.1007/s00034-012-9450-x (  0) 0) |
| [25] |
Yazdani M, Nazari S, Sinafar B. Concurrent learning based finite time parameter estimation in adaptive control of uncertain switched systems. Proceedings of the 4th International Conference on Robotics and Mechatronics. Piscataway: IEEE, 2016. 1-13. DOI: 10.1109/ICRoM.2016.7886856.
(  0) 0) |
| [26] |
di Bernardo M, Montanaro U, Santini S. Hybrid model reference adaptive control of piecewise affine systems. IEEE Transactions on Automatic Control, 2013, 58(2): 304-316. DOI:10.1109/TAC.2012.2212516 (  0) 0) |
| [27] |
Lavretsky E. Adaptive output feedback design using asymptotic properties of LQG/LTR controllers. IEEE Transactions on Automatic Control, 2012, 57(6): 1587-1591. DOI:10.1109/TAC.2011.2174692 (  0) 0) |
| [28] |
Yu Jente, Chiang Mingli, Fu Lichen. Synthesis of static output feedback SPR systems via LQR weighting matrix design. 2010 19th IEEE Conference on Decision and Control. Pisacataway: IEEE, 2010, 58(8): 4990-4995. DOI: 10.1109/CDC.2010.5718006.
(  0) 0) |
| [29] |
Huang C H, Ioannou P A, Maroulas J, et al. Design of strictly positive real systems using constant output feedback. IEEE Transactions on Automatic Control, 1999, 44(3): 569-573. DOI:10.1109/9.751352 (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


