In recent years, there are a lot of researches on the target tracking, but most studies on maneuvering target tracking are based on the assumption of Gaussian white noise.While in the actual radar target tracking system, the scattering of target in different positions and random fluctuating of target with radar echo make the measuring errors, which cause the observation noise called glint noise.The long tail glint noise dissatisfy the Gaussian white noise assumption and cannot be described by Gaussian distribution, so modeling of glint noise is an essential issue in current research of maneuvering target tracking.But up to now, the results of maneuvering target tracking in glint noise environment are really rare. So, this problem has become a difficult point in nonlinear non-Gaussian system, as well as a research hotspots in the field of target tracking[1-2].
For maneuvering target tracking, IMM is a common effective algorithm, in which multiple models transformation are achieved by Markov chain[3-6]. But the standard IMM is put forward based on linear Kalman Filter (KF) or Extended Kalman Filter (EKF), which can only deal with a simple linear system with Gaussian assumption. For nonlinear systems with non-Gaussian hypothesis, the performance showed by the standard IMM is poor.
The emergence of PF gradually solves the state estimation problem of nonlinear non-Gaussian system, more and more attention has been paid to the application of PF in target tracking[7-13]. IMMPF algorithm was presented to track the maneuvering target based on some previous work[14-15]. However, the system state transition probability in these papers was selected as the importance density function of standard PF, without using the latest observation information, the resulting particle samples are often concentrated at the tail of posterior probability distribution, which leads to the blindness of selecting particle, so it can easily cause particle degradation and cannot meet the filtering performance. To solve this problem, Ref.[16] developed an Interacting Multiple Model Iterative Extended Kalman Particle Filter, in which the importance density function was generated by Iterated Extended Kalman Filter, and it improved tracking accuracy of maneuvering target to a certain extent.
In addition, due to the poor tracking performance of the standard PF in the glint noise environment[17], some improvements have been made to describe the real noise density function and obtain the more liable state estimation in the presence of glint noise[18].
It is worth emphasizing that most of researches about IMM and PF are only for maneuvering target tracking, or state estimation of nonlinear systems. And the existed research in view of glint noise are just dealing with the target state estimation in a single model without considering the maneuvering targets. Thus we aim at solving the problem of maneuvering target tracking affected by glint noise and optimizing the selection of importance density function of PF in IMMPF, the main contributions of this paper are: 1) observation noises are modeled as mixture Gaussian model for processing the glint noise; 2) the importance density function that we choose fuses the latest observations and it is easier to sample in PF; 3) the improved PF is extended into the IMM in dealing with the tracking of high maneuvering target.
The outline of the rest of this paper is as follows: Section 2 is a brief introduction of system model and observation noise model; the selection of importance density function and the updating of importance weights are given in Section 3, as well as the algorithm design in this paper; Section 4 provides the numerical simulation to prove effectiveness of the obtained algorithm; Section 5 draws the conclusions.
2 Model Building 2.1 Tracking ModelAssume that the target in the two-dimensional plane does nonlinear motion with turns, the motion equation and observation equation are respectively as follows:
| $ {X_l}\left( {k + 1} \right) = {\mathit{\boldsymbol{F}}_l}\left( k \right){X_l}\left( k \right) + {\mathit{\boldsymbol{B}}_l}\left( k \right)W\left( k \right) $ | (1) |
| $ {Z_l}\left( k \right) = \mathit{\boldsymbol{H}}\left( k \right)X\left( k \right) + V\left( k \right) $ | (2) |
The state vector of the target at time instant k in the l-th model is given as
| $ {\boldsymbol{X}_l}(k) = {\left[ {{x_l}(k),{{\dot x}_l}(k),{y_l}(k),{{\dot y}_l}(k),\varphi } \right]^{\rm{T}}} $ |
where the components xl(k) and yl(k) represent position coordinates of the moving target, whereas,
The transition probability between the system models is defined as follows:
| $ p_{l_{1} l_{2}}=P\left\{m_{k+1}=l_{1} | m_{k}=l_{2}\right\}, l_{1}, l_{2}=1,2, \cdots, N_{m} $ | (3) |
In this way, the state X(k) of the target can be estimated by initializing X(0) and model probability
Glint noise cannot be described by Gaussian distribution because of its own characteristics, so the modeling of glint noise is mainly realized by the combination of the Gaussian distribution and other noise distribution. Therefore, by establishing the relationship between observation noise and the observation likelihood function, a glint noise model based on Gaussian mixture distribution is obtained.
In general, observation likelihood function can be constituted by Eq.(4), which is a Gaussian distribution density, with the assumption that the observation noises are white noises with zero mean and covariance of R.
| $ p\left(z_{k} | x_{k}^{j}\right)=N\left(z_{k} ; H_{k} x_{k}^{j}, R\right) $ | (4) |
where j=1, 2, …, N represents the number of particles.
But for non-Gaussian non-stationary glint noise, Gaussian distribution cannot approximately describe the observation likelihood function. We endeavor to explore the central relationship between observation likelihood function and observation noise to design another approximation method. Based on the conclusion from Ref.[19], the observation likelihood of the j-th particle can be described as:
| $ p\left(z_{k} | x_{k}\right)=p\left(z_{k}-H_{k} x_{k}\right)=p\left(v_{k}\right) $ | (5) |
For each particle, noise samples are defined as:
| $ v_{k}^{j}=z_{k}-H_{k} x_{k}^{j} $ | (6) |
and for the j-th particle, its observation likelihood function is:
| $ p\left(z_{k} | x_{k}^{j}\right)=p\left(v_{k}^{j}\right) $ | (7) |
Thus the construction of the observation likelihood function can be converted to the modeling of observation noise.
Suppose that K is a non-Gaussian non-stationary glint noise having a non-zero mean. The PDF at instant k can be presented as a Gaussian mixture with K weighted Gaussian components:
| $ p\left(v_{k}\right)=\sum\limits_{i=1}^{K} \alpha_{i},_{k} p_{i}\left(v_{k}\right)=\sum\limits_{i=1}^{K} \alpha_{i, k} N\left(v_{k} ; \mu_{i, k}, \sigma_{i, k}^{2}\right) $ | (8) |
where pi(vk) is called probability density function of the i-th Gaussian components at the instant k, μi, k, σi, k2 and αi, k > 0 are mean, variance and the weight of the each component, respectively. i=1, 2, …, K,
| $ p\left\{v_{k}^{j} | p_{i}\left(v_{k}^{j}\right)\right\}=p_{i}\left\{v_{k}^{j} | \mu_{i, k}, \sigma_{i, k}^{2}\right\} $ | (9) |
As a result, the probability of the i-th component based on the j-th noise sample can be computed through the Bayes rule:
| $ P\left\{ {{p_i}\left( {v_k^j} \right)|v_k^j} \right\} = \frac{{{\alpha _{i,k}}{p_i}\left\{ {v_k^j|{\mu _{i,k}},\sigma _{i,k}^2} \right\}}}{{\sum\limits_{i = 1}^K {{\alpha _{i,k}}} {p_i}\left\{ {v_k^j|{\mu _{i,k}},\sigma _{i,k}^2} \right\}}} $ | (10) |
And all the distribution parameters of each Gaussian component are derived below.
First, the Gaussian component of the observation noise model is initialized and for k=1, 2, …, the prior distribution parameters of each component are estimated.
Initialize the prior weight as:
| $ \alpha_{i, k^{-}}=\frac{1}{K} $ | (11) |
When K is an odd number, the priori mean is set as:
| $ \mu_{i, k^{-}}=\overline{\mu}_{k-1}\left(1+\left(i-\frac{K-1}{2}\right) \frac{1}{K}\right) $ | (12) |
and when K is even, the priori mean is expressed as:
| $ \mu_{i, k^{-}}=\overline{\mu}_{k-1}\left(1+\left(i-\frac{K}{2}\right) \frac{1}{K}\right) $ | (13) |
where
| $ \overline{\mu}_{k-1}=\sum\limits_{i=1}^{K} \alpha_{i, k-1} \mu_{i, k-1} $ | (14) |
The prior variance is:
| $ \sigma_{i, k^{-}}^{2}=\sigma_{i, k-1}^{2} $ | (15) |
Secondly, calculate the j-th observation noise samples:
| $ v_{k}^{j}=z_{k}-h\left(x_{k^{-}}^{j}\right) $ | (16) |
where
| $ x_{k^{-}}^{j}=f\left(x_{k-1}^{j}\right) $ | (17) |
Then the conditional probability of each noise component are calculated by the prior parameters:
| $ P\left\{ {{p_i}\left( {v_k^j} \right)\left| {v_k^j} \right.} \right\} = \frac{{{\alpha _{i,k ^- }}{p_i}\left\{ {v_k^j\left| {{\mu _{i,k ^- }},\sigma _{i,k ^- }^2} \right.} \right\}}}{{\sum\limits_{i = 1}^K {{\alpha _{i,k ^- }}{p_i}\left\{ {v_k^j\left| {{\mu _{i,k ^- }},\sigma _{i,k ^- }^2} \right.} \right\}} }} $ | (18) |
Next, the posterior parameters of each noise component are updated. The posterior weight is expressed as:
| $ {\alpha _{i,{k^ + }}} = \frac{1}{K}\sum\limits_{j = 1}^N {P\left\{ {{p_i}\left( {v_k^j} \right)\left| {v_k^j} \right.} \right\}} $ | (19) |
The posterior mean is:
| $ {\mu _{i,{k^ + }}} = \frac{{\sum\limits_{j = 1}^N {P\left\{ {{p_i}\left( {v_k^j} \right)\left| {v_k^j} \right.} \right\}v_k^j} }}{{\sum\limits_{j = 1}^N {P\left\{ {{p_i}\left( {v_k^j} \right)\left| {v_k^j} \right.} \right\}} }} $ | (20) |
and the posterior variance is built as:
| $ \sigma _{i,k ^+ }^2 = \frac{{\sum\limits_{j = 1}^N {P\left\{ {{p_i}\left( {v_k^j} \right)\left| {v_k^j} \right.} \right\}{{\left( {v_k^j - {\mu _{i,k ^+ }}} \right)}^2}} }}{{\sum\limits_{j = 1}^N {P\left\{ {{p_i}\left( {v_k^j} \right)\left| {v_k^j} \right.} \right\}} }} $ | (21) |
After establishing the Gaussian mixture model of observation noise, a new IMMPF is developed in this paper by improving the likelihood PF in the IMM. That is to say, particles are extracted from observation likelihood function that depends on the observation noise, and the latest observation information is fused into the importance density function, so as to get a posteriori probability distribution which is more in line with the real state of the target. At the same time, interactive operation of each particle with the estimation of other models is taken to reflect the impact of each model on different particles. Not only can it solve the problem of glint noise, but also overcome the influence of the sudden maneuver of the target.
3.1 Updating Weights in the PFThe estimation performance of the PF mainly depends on the importance density function we have selected, and the minimization of the weighted variance is the central rule of selecting optimal importance density function. According to the theorem of Ref.[20]:q(xk|xk-1j, zk)=p(xk|xk-1j, zk) is an optimal importance density function based on the minimizing variance of importance weights, and the corresponding importance weight is updated as follows:
| $ \omega _k^j = \omega _{k - 1}^jp\left( {{z_k}\left| {x_{k - 1}^j} \right.} \right) $ | (22) |
However, there are two problems need to be solved in optimal importance density function. One is the difficulty to sample from the non-standard distribution, which makes it hard to get the posterior distribution of the state. Another is the difficulty of integrating, namely, when the importance weight is updated as shown in Eq.(22), the following integral are required:
| $ p\left( {{z_k}\left| {x_{k - 1}^j} \right.} \right) = \int {p\left( {{z_k}\left| {{x_k}} \right.} \right)p\left( {{z_k}\left| {x_{k - 1}^j} \right.} \right){\rm{d}}x} $ | (23) |
But the integral is always non-analytic which leads to a large amount of calculation and even the filter is difficult to achieve.
To overcome the difficulties caused by the above problems, it is necessary to improve the PF according to the selection of importance density function. So, some researchers first select
| $ q\left( {{x_k}\left| {x_{k - 1}^j,{z_k}} \right.} \right) = p\left( {x_k^j\left| {x_{k - 1}^j} \right.} \right) $ | (24) |
as another importance density function, and the corresponding important weight is updated to:
| $ \omega _k^j = \omega _{k - 1}^jp\left( {{z_k}\left| {x_k^j} \right.} \right) $ | (25) |
As a result, the sampling is prone to implement.But in the actual environment with glint noise, the latest observations cannot be fused by priori distribution, and sample particles may drift in posterior distribution, which can lead to the degradation of filtering performance.
Therefore, the importance weight of the PF is improved and the observation likelihood function is converted to the probability density of observation noise, and from which the particles are extracted. So that, the improved importance weight which is updated to:
| $ \begin{array}{l} \omega _k^j = \omega _{k - 1}^j\frac{{p\left( {{z_k}\left| {x_k^j} \right.} \right)p\left( {x_k^j\left| {x_{k - 1}^j} \right.} \right)}}{{q\left( {x_k^j\left| {x_{k - 1}^j} \right.,{z_k}} \right)}} = \\ \;\;\;\;\;\;\;\;\;\omega _{k - 1}^j\frac{{p\left( {{z_k}\left| {x_k^j} \right.} \right)p\left( {x_k^j\left| {x_{k - 1}^j} \right.} \right)}}{{p\left( {{z_k}\left| {x_k^j} \right.} \right)}} = \\ \;\;\;\;\;\;\;\;\;\omega _{k - 1}^jp\left( {x_k^j\left| {x_{k - 1}^j} \right.} \right) \end{array} $ | (26) |
With the above improvements, the PF has the following advantages: 1) the latest observation information can be fused into the importance density function and get the posteriori probability distribution which is more in line with the target's state in a glint noise environment; 2) it can avoid the drift of particles in the posterior distribution and particle impoverishment; 3) the computational complexity caused by a large number of particles is greatly reduced; 4) the tracking accuracy is improved as well as the problem caused by glint noise is solved.
Then, we integrate the modified PF which the important weight is improved into the IMM to develop a novel IMMPF algorithm. And it is used to realize the exactly real-time tracking of the high maneuvering targets in the glint noise environment as well as the accurate estimation of target states. A detailed description of the IMMPF is given below.
3.2 Implementation of the new IMMPFAiming at the problem of maneuvering target tracking under the mixture Gaussian noise model that we have discussed, the IMMPF is put forward and the main steps include: Interaction, filtering, probability updating of models and outputting. The detailed processes are as follows:
(1) Interaction: initialize the state vector
Given the transition probability pl1l2(l1=l2=1, 2, …, Nm) of the models and the probability
| $ {\hat x_{k - 1\left| {k - 1,{l_1}} \right.}} = \sum\limits_{{l_2} = 1}^{{N_m}} {{{\hat x}_{k - 1\left| {k - 1,{l_2}} \right.}}{u_{k - 1,{l_2}\left| {{l_1}} \right.}}} $ | (27) |
| $ \begin{array}{l} {P_{k - 1\left| {k - 1,{l_1}} \right.}} = \sum\limits_{{l_2} = 1}^M {{u_{k - 1,{l_2}\left| {{l_1}} \right.}}\left[ {{P_{k - 1\left| {k - 1,{l_2}} \right.}} + \left( {{x_{k - 1\left| {k - 1,{l_2}} \right.}} - } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{x_{k - 1\left| {k - 1,{l_1}} \right.}}} \right){{\left( {{x_{k - 1\left| {k - 1,{l_2}} \right.}} - {{\hat x}_{k - 1\left| {k - 1,{l_1}} \right.}}} \right)}^{\rm{T}}}} \right] \end{array} $ | (28) |
where uk-1, l2| l1=(1/ck-1, l1)pl1l2uk-1, l2 is known as mixed probability,
(2) Filtering: randomly take N samples
| $ x_{k|k - 1,{l_1}}^j = {F_{{l_1}}}\left( {x_{k - 1|k - 1,{l_1}}^j} \right) $ | (29) |
| $ P_{k1k - 1,{l_1}}^j = {Q_{{l_1}}} + {F_{{l_1}}}{P_{k - 1|k - 1,{l_1}}}{F_{{l_1}}} $ | (30) |
| $ z_{k\left| {k - 1,{l_1}} \right.}^j = h\left( {\hat x_{k\left| {k - 1,{l_1}} \right.}^j} \right) $ | (31) |
Calculating residual:
| $ \delta _{k,{l_1}}^j = {z_k} - z_{k\left| {k - 1,{l_1}} \right.}^j $ | (32) |
we can get
Then, observation likelihood functions can be constructed:
| $ \begin{array}{l} p\left( {{z_k}\left| {x_k^j} \right.} \right) = p\left( {v_k^j} \right) = \sum\limits_{i = 1}^K {\frac{{{\alpha _{i,{k^ + }}}}}{{\sqrt {2{\rm{ \mathsf{ π} }}\sigma _{i,{k^ + }}^2} }}\exp \left[ - \right.} \\ \;\;\;\left. {\frac{{{{\left( {v_k^j - {\mu _{i,{k^ + }}}} \right)}^2}}}{{2\sigma _{i,{k^ + }}^2}}} \right] \end{array} $ | (33) |
Sampling particles xk| k, l1j~p(zk|xkj) and generating the prediction samples.The importance weight of each particle can be calculated as:
| $ \omega _{k,{l_1}}^j = \omega _{k - 1,{l_1}}^jp\left( {x_{k\left| {k,{l_1}} \right.}^j\left| {x_{k\left| {k - 1,{l_1}} \right.}^j} \right.} \right) $ | (34) |
and then normalizing the importance weight:
| $ \omega _{k,{l_1}}^j = \frac{{\omega _{k,{l_1}}^j}}{{\sum\limits_{j = 1}^N {\omega _{k,{l_1}}^j} }} $ | (35) |
Another set of particles
The estimation of state and its covariance are:
| $ {\hat x_{k\left| {k,{l_1}} \right.}} = \frac{1}{{{N_s}}}\sum\limits_{n = 1}^{{N_s}} {\hat x_{k\left| {k,{l_1}} \right.}^n} $ | (36) |
| $ {P_{k\left| {k,{l_1}} \right.}} = \frac{1}{{{N_s}}}\sum\limits_{n = 1}^{{N_s}} {\left[ {{{\hat x}_{k\left| {k,{l_1}} \right.}} - \hat x_{k\left| {k,{l_1}} \right.}^n} \right]{{\left[ {{{\hat x}_{k\left| {k,{l_1}} \right.}} - \hat x_{k\left| {k,{l_1}} \right.}^n} \right]}^{\rm{T}}}} $ | (37) |
(3) The probability updating of models:
Likelihood function of the model is calculated as:
| $ {\Lambda _{k,{l_1}}} = \frac{1}{{{N_s}}}\sum\limits_{n = 1}^{{N_s}} {N\left( {\delta _{k,{l_1}}^n;0,{S_{k,{l_1}}}} \right)} $ | (38) |
where
| $ \begin{array}{*{20}{c}} {{S_{k,{l_1}}} = R + \frac{1}{{{N_s}}}\sum\limits_{n = 1}^{{N_s}} {\left[ {z_{k\left| {k - 1,{l_1}} \right.}^n - \hat z_{k\left| {k - 1,{l_1}} \right.}^n} \right]} }\\ {{{\left[ {z_{k\left| {k - 1,{l_1}} \right.}^n - \hat z_{k\left| {k - 1,{l_1}} \right.}^n} \right]}^{\rm{T}}}} \end{array} $ |
| $ \hat z_{k\left| {k - 1,{l_1}} \right.}^n = \frac{1}{{{N_s}}}\sum\limits_{n = 1}^{{N_s}} {z_{k\left| {k - 1,{l_1}} \right.}^n} $ |
Thus, the probability of each model is updated to:
| $ {u_{k,{l_1}}} = \frac{1}{{{c_k}}}{\mathit{\Lambda }_{k,{l_1}}}{c_{k - 1,{l_1}}} $ | (39) |
where
(4) Outputting:
| $ {\hat x_{k|k}} = \sum\limits_{{l_1}}^{{N_m}} {{u_{k,{l_1}}}} {\hat x_{k|k,{l_1}}} $ | (40) |
The proposed algorithm is simulated and analyzed in this section, including the presented IMMPF and conventional IMM algorithm. The simulation is completed by MATLAB 2014 to compare the performance for maneuvering target tracking in glint noise environment.The parameters and system model in the simulation are as follows:
In order to simplify the simulation implementation and make the result easy to observe, the number of particles in IMMPF and the conventional IMM algorithm are set as 200 and 100, respectively. Besides, simulations of both algorithms are executed independently for 150 Monte Carlo runs. To evaluate the performance of this algorithm intuitively, we select the root mean square error (RMSE) of the target's location estimation as the evaluation index.
The system model for moving target is:
| $ \boldsymbol{X}_{k}=\boldsymbol{F} \boldsymbol{X}_{k-1}+\boldsymbol{G} w_{k} $ | (41) |
where
| $ {\mathit{\boldsymbol{F}}_1} = \left[ {\begin{array}{*{20}{c}} 1&T&0&0\\ 0&1&0&0\\ 0&0&1&T\\ 0&0&0&1 \end{array}} \right] $ |
where T represents the observation period of the sensor.
When in anticlockwise or clockwise motion, F is defined as:
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_2} = \\ \;\;\left[ {\begin{array}{*{20}{c}} 1&{\sin \left( {\varphi T} \right)/\varphi }&0&{\left( {\cos \left( {\varphi T} \right) - 1} \right)/\varphi }\\ 0&{\cos \left( {\varphi T} \right)}&0&{ - \sin \left( {\varphi T} \right)}\\ 0&{\left( {1 - \cos \left( {\varphi T} \right)} \right)/\varphi }&1&{\sin \left( {\varphi T} \right)/\varphi }\\ 0&{\sin \left( {\varphi T} \right)}&0&{\cos \left( {\varphi T} \right)} \end{array}} \right] \end{array} $ |
where φ denotes the steering angular velocity (φ > 0 corresponds to anticlockwise motion, while φ < 0 means clockwise motion). F3 is the same as F2 except that φ < 0. The following equation
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} {T^2}/2\\ T\\ 0\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ {T^2}/2\\ 0 \end{array} \end{array}} \right] $ |
refers to the noise gain matrix. The process noise wk follows the Gaussian distribution with zero mean and covariance of Qi(i=1, 2, 3), where
| $ {\mathit{\boldsymbol{Q}}_1} = {\mathit{\boldsymbol{Q}}_2} = {\mathit{\boldsymbol{Q}}_3} = {\rm{diag}}\left( {\left[ {{Q_0},{Q_0}} \right]} \right) $ |
And
| $ {\mathit{\boldsymbol{Q}}_0} = 50\left[ {\begin{array}{*{20}{c}} \begin{array}{l} {T^3}/3\\ {T^2}/2 \end{array}&\begin{array}{l} {T^2}/2\\ T \end{array} \end{array}} \right] $ |
Sensor is be situated at (0, 0) to measure the angle between the target and x axis, the observation period T=1s, and observation model is:
| $ {Z_k} = \arctan \frac{{{y_k}}}{{{x_k}}} + {v_k} $ | (42) |
where vk denotes the glint noise existing in each viewing angle.
The trajectory of the target is set as follows: the initial state for target is (6000 m, 20 m/s, 6000 m, 20 m/s). In the first 25 sample intervals, the target is turning anticlockwise at the turn rate of 0.1 rad/s, then going to do uniform linear motion for 10 sampling intervals, and in the last 25 intervals, the target turns clockwise, and the turning rate is 0.1 rad/s.
The initial probabilities of each model are specified as: μ0, 1=0.2, μ0, 2=0.2 and μ0, 3=0.6, and the model transition probability matrix is:
| $ \mathit{\boldsymbol{p}} = \left[ {\begin{array}{*{20}{c}} {0.8}&{0.1}&{0.1}\\ {0.1}&{0.8}&{0.1}\\ {0.1}&{0.1}&{0.8} \end{array}} \right] $ |
The simulation results are shown in Figs. 1-2.
|
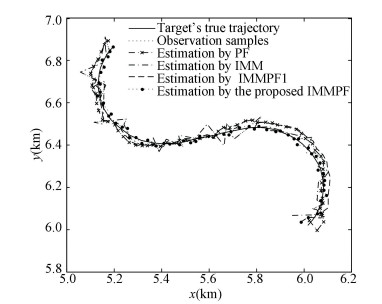
Fig.1 Target trajectory and the estimated trajectory |
|
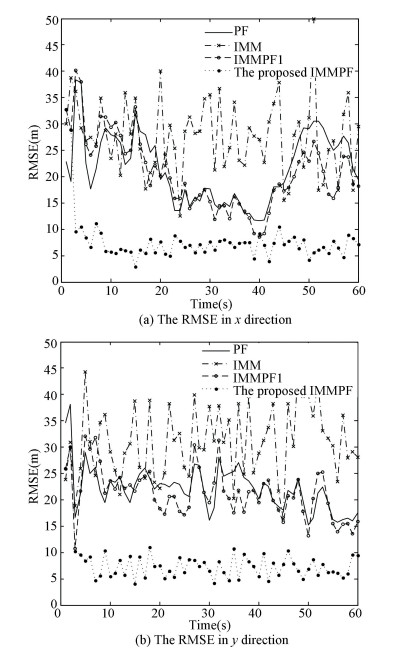
Fig.2 RMSE of target location estimation |
Curves in Fig. 1 are target's true trajectory, observation samples, the estimation by some existed filtering algorithms and the result of presented IMMPF in this paper, respectively. It can be seen that throughout the tracking process, the estimation by IMMPF we have proposed is closer to the true trajectory of the target than any other algorithm. Although target is turning, the IMMPF also estimates the target state more accurately and tracks the target better than the existed algorithms because there is no major deviation from the actual trajectory. That is to say, the improved IMMPF can flexibly deal with the maneuvering problem of target tracking and the glint noise, and the tracking result is satisfactory.
Curves in Fig. 2(a) and (b) refer to the RMSE of the conventional PF, IMM, IMMPF1 improved by the previous researchers and the IMMPF we have proposed, respectively. It's obvious that he RMSE of the presented method is much smaller during the tracking, and that the IMMPF performs still relatively stable and the superiority is more obvious even if the target suddenly maneuvers.
Furthermore, the importance density function we have selected in this paper reduces the computation load of a single PF, so the computational complexity of the whole IMMPF algorithm in which multiple PF are executed simultaneously is lower than that of the existed IMMPF1.
Overall, the introduced IMMPF has good tracking performance and feasibility as well as strong robustness. What's more, the tracking accuracy of maneuvering targets in the glint noise environment is better than that of the conventional algorithms, getting an expected tracking effect.
5 ConclusionsA novel IMMPF algorithm is improved based on the mixture Gaussian glint noise model in this paper so that the problem of maneuvering target tracking affected by glint noise is solved. The discussion and simulation indicate that it is of great significance to use the proposed scheme to track the maneuvering targets with glint noise. Furthermore, the IMMPF has the characteristics of faster convergence rate and robust adaptation, which can deal with the nonlinear non-Gaussian systems very well.
| [1] |
Wang Min, Zhang Bing, Zhu Zhiyu. Research on mobile multi-target tracking algorithm based on pf method under glint noise environment. Journal of Gun Launch & Control, 2008, 3(7): 29-32. DOI:10.19323/j.issn.1673-6524.2008.03.007 (  0) 0) |
| [2] |
Zhou Taoyun, Zhang Yi, Cai Chenglin. Research on maneuvering target tracking algorithm in glint noise environment. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(2): 149-152. DOI:10.15892/j.cnki.djzdxb.2014.02.048 (  0) 0) |
| [3] |
Gao Liang, Xing Jianping, Ma Zhenliang, et al. Improved IMM algorithm for nonlinear maneuvering target tracking. 2012 International Workshop on Information and Electronics Engineering, 2012, 29: 4117-4123. DOI:10.1016/j.proeng.2012.01.630 (  0) 0) |
| [4] |
Mazor E, Averbuch A, Bar-Shalom Y, et al. Interacting multiple model methods in target tracking: A survey. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 103-123. DOI:10.1109/7.640267 (  0) 0) |
| [5] |
Kim B D, Lee J S. IMM algorithm based on the analytic solution of steady state Kalman filter for radar target tracking. IEEE International Radar Conference. Piscataway: IEEE, 2005. 757-762. DOI: 10.1109/RADAR.2005.1435927.
(  0) 0) |
| [6] |
Li Liangqun, Ji Hongbing, Luo Junhui. Iterated extended Kalman particle filtering. Journal of Xidian University(Natural Science), 2007, 34(2): 233-238. DOI:10.3969/j.issn.1001-2400.2007.02.015 (  0) 0) |
| [7] |
Rui Ting, Zhang Qi, Zhou You, et al. Object tracking using particle filter in the wavelet subspace. Neurocomputing, 2013, 119: 125-130. DOI:10.1016/j.neucom.2012.03.036 (  0) 0) |
| [8] |
Xia Yuanqing, Deng Zhihong, Li Li, et al. A new continuous-discrete particle filter for continuous-discrete nonlinear systems. Information Sciences, 2013, 242(1): 64-75. DOI:10.1016/j.ins.2013.04.030 (  0) 0) |
| [9] |
Fu Xiaoyan, Jia Yingmin. An improvement on resampling algorithm of particle filters. IEEE Transactions on Signal Processing, 2010, 58(10): 5414-5420. DOI:10.1109/TSP.2010.2053031 (  0) 0) |
| [10] |
Li P, Goodall R, Kadirkamanathan V. Estimation of parameters in a linear state space model using a Rao-Blackwellised particle filter. IEE Proceedings Control Theory and Applications, 2004, 151(6): 727-738. DOI:10.1049/ip-cta:20041008 (  0) 0) |
| [11] |
Bolic M, Djuric P M, Hong Sangjin. Resampling algorithms and architectures for distributed particle filters. IEEE Transactions on Signal Processing, 2005, 53(7): 2442-2450. DOI:10.1109/TSP.2005.849185 (  0) 0) |
| [12] |
Gao J P, Wei Z H, Meng Y J, et al. Particle filter based on observation likelihood importance sampling. Journal of System Simulation, 2009, 21(12): 3705-3709. DOI:10.16182/j.cnki.joss.2009.12.040 (  0) 0) |
| [13] |
Mukherjee A, Sengupta A. Likelihood function modeling of particle filter in presence of non-stationary non-Gaussian measurement noise. Signal Process, 2010, 90(6): 1873-1885. DOI:10.1016/j.sigpro.2009.12.005 (  0) 0) |
| [14] |
Boers Y, Driessen J N. Interacting multiple model particle filter. IEE Proceedings Radar Sonar Navigation, 2003, 150(5): 344-349. DOI:10.1049/ip-rsn:20030741 (  0) 0) |
| [15] |
Morelande M R, Challa S. Manoeuvring target tracking in clutter using particle filters. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(1): 252-270. DOI:10.1109/TAES.2005.1413760 (  0) 0) |
| [16] |
Zhang Jungen, Ji Hongbing. IMM Iterated Extended Kalman Particle Filter Based Target Tracking. Journal of Electronics & Information Technology, 2010, 32(5): 1116-1120. (  0) 0) |
| [17] |
Li Wenling, Jia Yingmin, Du Junping, et al. PHD filter for multi-target tracking with glint noise. Signal Process, 2014, 94: 48-56. DOI:10.1016/j.sigpro.2013.06.012 (  0) 0) |
| [18] |
Hangyuan Du, Wenjian Wang, Liang Bai. Observation noise modeling based particle filter: An efficient algorithm for target tracking in glint noise environment. Neurocomputing, 2015, 158(22): 155-166. DOI:10.1016/j.neucom.2015.01.057 (  0) 0) |
| [19] |
Maybeck P S. Stochastic Models, Estimation and Control. New York: Academic Press, 1982.
(  0) 0) |
| [20] |
Doucet A, Gordon N J, Krishnamurthy V. Particle filters for state estimation of jump Markov linear systems. IEEE Transactions on Signal Processing, 2001, 49(3): 613-624. DOI:10.1109/78.905890 (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


