2. School of Logistics Engineering, Wuhan University of Technology, Wuhan 430070, China
Cloud manufacturing (CM) is a computing and service-oriented manufacturing model developed from existing advanced manufacturing models and enterprise information technologies[1]. It is supported by cloud computing, IoT (Internet of Things), virtualization and service-oriented technologies, and advanced computing technologies. CM aims to realize full sharing and circulation, and on-demand use of various manufacturing resources and capabilities.
In CM, distributed resources are packaged into cloud services and are centrally managed. Cloud users can use the cloud services according to their requirements. They can request services ranging from product designing, manufacturing, testing, managing and all other stages of a product life cycle[2]. CM provides enterprises, especially those lack of precise equipment and technologies, with high-quality cloud services.
The manufacturing resource allocation (MRA) is one of the key points of CM. Its optimal configuration model and solving mechanism directly affect the rapid and accurate sharing of cloud resources. Resource allocation (RA) problems have been paid close attention by many researchers. A hybrid fuzzy evolutionary algorithm for a multi-objective resource allocation problem, the student project allocation problem, was presented by Rachmawati and Srinivasan[3]. Lin et al.[4] proposed a multi-objective hybrid genetic algorithm approach based on the multistage decision-making model to obtain a set of Pareto solutions. Chaharsooghi et al.[5] proposed a modified version of ant colony optimization, and the updated algorithm was applied to multi-objective resource allocation problems (MORAPs). Grid systems were used by Li et al.[6] to consider the MORAP and scheduling problem in a grid computing environment. Ko & Lin[7] employed neural network to make portfolio selection as a resource allocation problem. Yin & Wang[8] employed the particle swarm optimization (PSO) paradigm and presented a hybrid execution plan that embeded a hill-climbing heuristic into the particle swarm optimization (PSO) for expediting the convergence to deal with the MORAPs. Fan et al.[9] proposed a modified binary particle swarm optimization algorithm to solve the MORAPs. Garg & Sharma[10] utilized the PSO algorithm to solve the multi-objective reliability-redundancy allocation problem. Liu et al.[11] proposed an improved NSGA-Ⅱ to solve multi-objective resource allocation and activity scheduling for fourth party logistics. Song et al.[12] presented the latest development and future directions of resource allocation in different full duplex systems by exploring the network resources in different domains. Deb and Myburgh[13] used a computationally fast heuristic algorithm handling the resource allocation problem. Zheng et al.[14] proposed a hybrid energy-aware resource allocation approach to help requestors acquire energy-efficient and satisfied manufacturing services.
Known from the above analysis, less attention has been paid to the integrated optimization of the MRA problem. The resource allocation models are incomplete open-loop model. MRA is researched based on the assumption that the preliminary selection of resources has been accomplished. Meanwhile, the cases that manufacturing resources (MRs) malfunction has not been considered. In the mode of optimization, MRA is optimized as a multi-objective optimization problem, not as a many-objective optimization problem[15-16].
In this paper, MRA considering the geographical distribution in CM environment is solved. A MRA model considering the geographical distribution is established. The model is a closed-loop cloud environment model that starts from the MRs' demand enterprise to the MRs' supply enterprise, then from one supply enterprise to another supply enterprise, at last, from the last supply enterprise return to the demand enterprise. The model is established based on the cross-geographical supply chain. The model includes two stages, preliminary selection stage and optimal selection stage. MRs are preliminarily selected by using the membership function, then MRs that have been chosen will be selected again by PSO based on the method of relative entropy of fuzzy sets (REFS_PSO). An optimal manufacturing resource supply chain (MRSC) is obtained at last. At optimal selection stage, the states whether the MRs malfunction or not are considered, the objective function is an eight-objective function. The performance of REFS_PSO is compared with NSGA-Ⅱ, PSO based on random weighting (RW_PSO).
The remainder of this paper is organized as follows. In Section 2, The MRA model considering the geographical distribution is introduced, in that two stages of the model are described. In Section 3, how things work in the optimal selection stage is elaborated. Section 4 describes the procedure of solving MRA problem considering geographical distribution in cloud manufacturing platform (CMP). In Section 5, experiments are implemented for validating the effectiveness of REFS_PSO. And finally, the conclusion is obtained in Section 6.
2 The MRA model Considering the Geographical Distribution 2.1 The DescriptionFig. 1 shows the MRA model considering the geographical distribution in CM environment. In the figure, the solid lines represent the allocation process of manufacturing resource. At this time, no malfunctioning MRs occurred. When malfunctioning MRs appeared, the dashed lines were used to show the process of removing the malfunctioning MRs and reconfiguring MRs excluding the malfunctioning MRs. The dot-and-dash lines indicate the real-time monitoring process for MRs by the cloud platform. By this model, the MR's demand enterprises would get an optimal manufacturing resource supply chain (MRSC). In this model, the suppliers' MRs are aggregated to cloud resource pool (CRP) by cloud computing, the Internet of Things (IoT), and so on. The information of MRs in CRP can be shared with CMP. The MR's demand enterprises need to log in CMP and submit tasks, then they will have a chance to rent the MRs that can complete the submitted tasks.
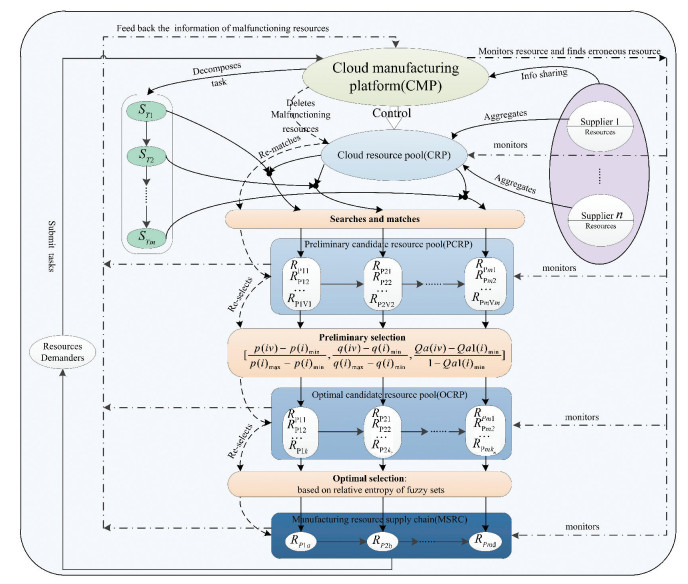
|
Fig.1 MRA model considering the geographical distribution in CM environment |
The process obtaining an optimal manufacturing resource supply chain with this model is as follows. When CMP obtains the submitted task T, the task T is immediately decomposed into m sub-tasks STi(i=1, 2, …, m) according to the production process. For each sub-task STi, the manufacturing resources RPiv are selected by searching and matching mechanism from CMP, and those manufacturing resources RPiv can complete STi, where v=1, 2, …, Vi; Vi indicates the amount of the matched resources with STi. These resources constitute the preliminary candidate resource pool (PCRP). Because the quantity of RPiv is huge, certain candidate sources RPij are selected from RPiv by using the membership function, where j=1, 2, …, Ki, Ki indicates the amount of the candidate resources. During this preliminary selection stage, the optimal candidate resources pool (OCRP) is obtained. Then, the optimal manufacturing resource RPi for each sub-task STi is selected as integrated optimization for task T. The optimization is performed with REFS_PSO. This is the optimal selection stage. All RPi of sub-task SPi constitute an optimal manufacturing resource supply chain.
During the above process, CMP keep monitoring the status of MRs in real time. If there are malfunctioning MRs, including occupied resources, the information will be returned to CMP. Meanwhile, the command is sent from CMP to the cloud resource pool to reconfigurate the resources. In the cloud resource pool, the malfunctioning MR is removed, then a new one is matched with sub-task STi, the malfunctioning MR is replaced by this new one. After the operation preliminary selection and optimal selection, a new optimal manufacturing resource supply chain would be obtained by the integrated optimization.
Three types of requirements are focused in the optimization of MRA problem considering the geographical distribution in CM environment. The first one is the production fare including the production time and the production cost. The second one is the supply chain requirements including logistics time, logistics cost, and tardiness. The supply chains refer to the resource demanders to suppliers, between the suppliers of adjacent sub-tasks, and from suppliers to demanders. The third one is quality requirements including the processing quality, reliability, and credibility. These three kinds of requirements are modeled as eight objective functions. MRA problem considering the geographical distribution is optimized by these eight objective functions, and an optimal manufacturing resource supply chain is obtained.
2.2 Preliminary Selection StageThe manufacturing resources that can meet the requirement of sub-task STi are selected on CMP according to the factors including production time, production cost, processing quality and credibility. The manufacturing resources selected on CMP are regarded as the candidate resource, and a candidate resource pool is built accordingly. The factors of time, cost and quality are the basis for the MRA, so these factors are translated into the membership function. In this paper, the membership functions including production time, production cost, processing quality are as follows:
| $ \left[ {\frac{{p\left( {iv} \right) - p{{\left( i \right)}_{\min }}}}{{p{{\left( i \right)}_{\max }} - p{{\left( i \right)}_{\min }}}},\frac{{q\left( {iv} \right) - q{{\left( i \right)}_{\min }}}}{{q{{\left( i \right)}_{\max }} - q{{\left( i \right)}_{\min }}}},\frac{{{Q_a}\left( {iv} \right) - {Q_{a1}}{{\left( i \right)}_{\min }}}}{{1 - {Q_{a1}}{{\left( i \right)}_{\min }}}}} \right] $ | (1) |
where p(iv), q(iv), Qa(iv) represent the production time, production cost, and processing quality of the vth resource of ith sub-task respectively. The lower bound, p(i)min, q(i)min, Qa1(i)min, and the upper bound p(i)max, q(i)max are set based on the requirement a sub-task STi for production time, production cost, and processing quality. Qa(iv) is a real number in range of [0, 1], that are obtained from the assessment of various users in CMP. Formula (1) is a matrix and the matrix elements of it are the membership grade. The resources can be added to the OCRP, only when its first dimension (p(iv)-p(i)min)/(p(i)max-p(i)min) is in range of (0, 0.5], second dimension (q(iv)-q(i)min)/(q(i)max-q(i)min) is in range of (0, 0.5], and third dimension (Qa(iv)-Qa1(i)min)/(1-Qa1(i)min) is in range of (0.5, 1].
2.3 The Optimal Selection StageAfter the candidate resource pool is built, an optimal manufacturing resource supply chain will be decided across three type of information. This information includes production fare information, the information of MRSC considering geographical locations, and the dynamic quality rating of the resource supplier. This information is translated to an eight-objective mathematical model. The mathematical model is as follows:
| $ F = \min \left( {{f_1},{f_2},{f_3},{f_4},{f_5},1 - {f_6},1 - {f_7},1 - {f_8}} \right) $ |
where
| $ {f_1} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{K_i}} {\left( {{x_{ij}} \times p(ij)} \right)} } $ | (2) |
| $ \begin{array}{l} {f_2} = \sum\limits_{j = 1}^{{K_1}} {\left( {{a_{0j}} \times l(0j)} \right)} + \\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = 1}^{{K_i}} {\sum\limits_{k = 1}^{{K_{i + 1}}} {\left( {{b_{ij,(i + 1)k}} \times l(ij,(i + 1)k)} \right)} } } + \\ \;\;\;\;\;\;\;\sum\limits_{j = 1}^{{K_m}} {\left( {{a_{j0}} \times l(j0)} \right)} \end{array} $ | (3) |
| $ {f_3} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{K_i}} {\left( {{x_{ij}} \times q(ij)} \right)} } $ | (4) |
| $ \begin{array}{l} {f_4} = \sum\limits_{j = 1}^{{K_1}} {\left( {{a_{0j}} \times g(0j)} \right)} + \\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = 1}^{{K_i}} {\sum\limits_{k = 1}^{{K_{i + 1}}} {\left( {{b_{ij,(i + 1)k}} \times g(ij,(i + 1)k)} \right)} } } + \\ \;\;\;\;\;\;\;\sum\limits_{j = 1}^{{K_m}} {\left( {{a_{j0}} \times g(j0)} \right)} \end{array} $ | (5) |
| $ {f_5} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{K_i}} {\left( {{x_{ij}} \times \gamma \times \max \left\{ {0,{D_i} - {C_{ij}}} \right\}} \right)} } $ | (6) |
| $ {f_6} = \left( {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{K_i}} {\left( {{x_{ij}} \times {Q_a}(ij)} \right)} } } \right)/m $ | (7) |
| $ {f_7} = \left( {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{K_i}} {\left( {{x_{ij}} \times {R_e}(ij)} \right)} } } \right)/m $ | (8) |
| $ \begin{array}{l} {f_8} = \left( {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{K_i}} {\left( {{x_{ij}} \times {R_{ep}}(ij)} \right)} } } \right)/m \end{array} $ | (9) |
s.t.
| $ \sum\limits_{j = 1}^{{K_i}} {{x_{ij}}} = 1 $ |
| $ \sum\limits_{j = 1}^{{K_i}} {{a_{0j}}} = 1 $ |
| $ \sum\limits_{j = 1}^{{K_i}} {\sum\limits_{k = 1}^{{K_{i + 1}}} {{b_{ij,(i + 1)k}}} } = 1 $ |
| $ \sum\limits_{j = 1}^{{K_m}} {{a_{j0}}} = 1 $ |
| $ {f_6} > {Q_{a\min }} $ | (10) |
| $ {f_7} > {R_{e\min }} $ | (11) |
| $ {f_8} > {R_{ep\min }} $ | (12) |
| $ {x_{ij}} = \left\{ \begin{array}{l} 1,{\rm{the}}\;j{\rm{th}}\;{\rm{candidate}}\;{\rm{is}}\;{\rm{chosen}}\;{\rm{when}}\;{\rm{processing}}\\ \;\;\;{\rm{the}}\;i{\rm{th}}\;{\rm{subtask}}\\ 0,{\rm{otherwise}} \end{array} \right. $ |
| $ {a_{0j}} = \left\{ {\begin{array}{*{20}{l}} {1,{\rm{there}}\;{\rm{is}}\;{\rm{logistics}}\;{\rm{connection}}\;{\rm{between}}\;{\rm{the}}}\\ {\;\;\;j{\rm{th}}\;{\rm{supplier}}\;{\rm{of}}\;{\rm{the}}\;{\rm{first}}\;{\rm{subtask}}\;{\rm{and}}\;{\rm{the}}}\\ {\;\;\;{\rm{resource}}\;{\rm{demander}}}\\ {0,{\rm{otherwise}}} \end{array}} \right. $ |
| $ {b_{ij,(i + 1)k}} = \left\{ \begin{array}{l} 1,{\rm{ there}}\;{\rm{is}}\;{\rm{logistic}}\;{\rm{connection}}\;{\rm{between}}\;{\rm{the}}\\ \;\;\;j{\rm{th}}\;{\rm{supplier}}\;{\rm{of}}\;{\rm{the }}i{\rm{th}}\;{\rm{subtask}}\;{\rm{and}}\;{\rm{the}}\\ \;\;\;k{\rm{th}}\;{\rm{supplier}}\;{\rm{of}}\;{\rm{the }}(i + 1){\rm{th}}\;{\rm{subtask}}\\ 0,{\rm{ otherwise}} \end{array} \right. $ |
| $ {a_{j0}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{1, there}}\;{\rm{is}}\;{\rm{logistics}}\;{\rm{connection}}\;{\rm{between}}\;{\rm{the }}}\\ {{\rm{ }}\;\;j{\rm{th}}\;{\rm{supplier}}\;{\rm{of}}\;{\rm{the}}\;{\rm{las}}\;{\rm{subtask}}\;{\rm{and}}\;{\rm{the }}}\\ {{\rm{ }}\;\;{\rm{resource}}\;{\rm{demander }}}\\ {0{\rm{, otherwise }}} \end{array}} \right. $ |
The production fare information is expressed by f1 function and f3 function. The function f1 is the production time function that indicates the whole production time of suppliers in the chain, where p(ij) presents the production time of the jth supplier in the ith sub-task. Function f3 is the production cost function that indicates the whole production cost of suppliers in the chain, where q(ij) presents the production cost of the jth supplier in the ith sub-task.
The information of MRSC considering geographical locations is expressed by f2, f4 and f5 function. Function f2 is the logistics time function. In this function,
| $ \sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = 1}^{{K_i}} {\sum\limits_{k = 1}^{{K_{i + 1}}} {\left( {{b_{ij,(i + 1)k}} \times l(ij,(i + 1)k)} \right)} } } $ |
indicates the logistics time between two candidate resource suppliers in different place in adjacent sub-tasks.
| $ \sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = 1}^{{K_i}} {\sum\limits_{k = 1}^{{K_{i + 1}}} {\left( {{b_{ij,(i + 1)k}} \times g(ij,(i + 1)k)} \right)} } } $ |
indicates the logistics cost between two candidate resource suppliers in different place in adjacent sub-tasks.
The dynamic quality rating of the resource supplier is expressed by f6, f7 and f8 functions. Function f6 is the average processing quality function. Function f7 is the average reliability function. Function f8 is the average credibility function of suppliers in the chain. The larger value of these three functions means the better quality. Qa(ij), Re(ij), Rep(ij) are real numbers in range of [0, 1] that respectively denote the minimum value of processing quality, reliability and credibility that required for the supplier. Eqs.(10)-(12) show that the candidate resource suppliers are likely to be selected when f6, f7 and f8 function values are greater then the minimum of these three indicators.
3 The Relative Entropy of Fuzzy Sets for the Optimal Selection StageThe mathematical model established in the optimal selection stage contains eight objective functions. Thus, this is a many-objective optimization problem. The relative entropy of fuzzy sets (REFS) is a significant part of the information entropy of fuzzy sets. The relative entropy coefficient of fuzzy sets (Ce) is very important in the relative entropy of fuzzy sets. This coefficient can indicate the similarity of different fuzzy sets[17]. If the Pareto solution can be transferred to the fuzzy set and a fuzzy set of the ideal solution can be obtained, the similarity between the Pareto solution and the ideal solution can be determined by this coefficient. Then multi-objective optimization problems can be optimized based on this coefficient. In this paper, the method of REFS could be used to optimize the eight-objective mathematical model in the optimal selection stage.
3.1 The Construction and Mapping of the Fuzzy Set from the Many-objective Function ValueFirstly, the eight-objective function values will be converted into fuzzy sets. In this paper, the objective function value Y =(f1, f2, …, fM) will be mapped to S=(u1, u2, …, uM), where fM is the M-th objective function value, S is the fuzzy set of membership function. uM is the M-th membership function value. The membership function is used in the mapping process. Thus, the connection between function value and fuzzy set is established.
3.1.1 The mapping from the function value to the fuzzy setFunction value of objective function M is mapped to the membership grade by the membership function. The membership function is given as follows.
| $ {u_M}(i) = \left\{ {\begin{array}{*{20}{l}} {1,}&{{f_M}(i) \le {y_{M1}}}\\ {\frac{{{f_M}(i) - {y_{M1}}}}{{{y_{M2}} - {y_{M1}}}},}&{{y_{M1}} < {f_M}(i) < {y_{M2}}}\\ {0,\quad }&{{f_M}(i) \ge {y_{M2}}} \end{array}} \right. $ | (13) |
In the formula, uM(i) is the membership grade, where i=0, 1, …, N and N is the number of the solution, yM1, yM2 are the lower and upper bound of the objective function M respectively. It can be seen from the membership function that how to decide the upper and the lower bound is important. In this paper, the objective function M as a single-objective function is optimized α times by using PSO algorithm, and then λ (λ∈(0.5, 1)) times of the average optimal result is taken as the lower bound of the objective function M, recorded as yM1. Meanwhile, the maximum function value of function M in the first generation is recorded and the greatest one in α times optimization is set as the upper bound, recorded as yM2.
3.1.2 Construct the fuzzy set of ideal solutionEach objective function is optimized as a single-objective function by PSO algorithm to obtain the optimal solution. And the function values of these optimal solutions constitute of the ideal solution set
| $ {Y_0} = \left\{ {{f_1}(0),{f_2}(0), \cdots ,{f_M}(0)} \right\} $ |
where fM(0) is the single-objective optimum function value of Mth function. Then Y0 is mapped to the fuzzy set of ideal solution by using Eq.(13).
| $ S\left( 0 \right) = \left\{ {{u_1}(0),{u_2}(0), \cdots ,{u_M}(0)} \right\} $ |
is the fuzzy set of ideal solution, where uM(0) is the membership grade of Mth function after mapping with Eq.(13).
3.1.3 Construct the fuzzy set of Pareto frontWhile solving many-objective optimization problems with PSO algorithm, the Pareto front can be obtained. The ith Pareto front
| $ {Y_i} = \left\{ {{f_1}\left( i \right),{f_2}\left( i \right), \cdots ,{f_M}\left( i \right)} \right\} $ |
is mapped to the fuzzy set of Pareto front, S(i)={u1(i), u2(i), …, uM(i)}, according to Eq.(13).
3.2 The Relative Entropy Coefficient of the Fuzzy SetsOnce these two fuzzy sets are constructed, the relative entropy coefficient of fuzzy sets is calculated and is used to evaluate the similarity between two fuzzy sets. The calculation process is as follows.
1) The relative entropy between S(i) and S(0).
The relative entropy of two fuzzy sets is labelled as E(S(i); S(0)). The formula of E(S(i); S(0)) is given as follow:
| $ \begin{array}{l} E(S(i);S(0)) = - \left( {\sum\limits_{j = 1}^M {\{ {u_j}(i)\ln {u_j}(0))} + (1} \right. - \\ \;\;\;\;\;\left. {\left. {{u_j}(i)} \right)\ln \left( {1 - {u_j}(0)} \right)} \right\} + \sum\limits_{j = 1}^n {\left\{ {{u_j}(0)} \right.} \cdot \\ \;\;\;\;\left. {\left. {\ln {u_j}(i) + \left( {1 - {u_j}(0)} \right)\ln \left( {1 - {u_j}(i)} \right)} \right\}} \right) \end{array} $ |
2) The relative entropy coefficient of fuzzy sets.
The relative entropy coefficient is labelled as Ce(S(i); S(0)) and the calculative process is given as follows.
| $ {C_e}(S(i);S(0)) = \frac{{(M\ln 2)(E(S(0)) + E(S(i)))}}{{E(S(i);S(0))}} $ | (14) |
where
| $ \begin{array}{*{20}{c}} {E(S(0)) = - \frac{1}{{M\ln 2}}\sum\limits_{j = 1}^M {\left\{ {{u_j}(0)\ln {u_j}(0) + (1 - } \right.} }\\ {\left. {\left. {{u_j}(0)} \right)\ln \left( {1 - {u_j}(0)} \right)} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {E(S(i)) = - \frac{1}{{M\ln 2}}\sum\limits_{j = 1}^M {\left\{ {{u_j}(i)\ln {u_j}(i) + (1 - } \right.} }\\ {\left. {\left. {{u_j}(i)} \right)\ln \left( {1 - {u_j}(i)} \right)} \right\}} \end{array} $ |
where E(S(0) is the entropy of fuzzy set of ideal solution, E(S(i)) is the entropy of fuzzy set of Pareto front.
3.3 The Realization of Many-Objective MRA Problem by REFS_PSOThe relative entropy coefficient can indicate the similarity of different fuzzy sets. The greater coefficient means much similar. Thus it is reasonable to adopt this coefficient as the criterion to judge the quality of Pareto solution. When optimizing many-objective problems with evolutionary algorithm combined with REFS, this coefficient is used as the fitness value to lead the individual evolution. The larger the coefficient is, the better the solution is.
The PSO algorithm, a modern evolutionary-based computation technique, was originally developed by Kennedy and Eberhart[18] to solve continuous optimization problems. Recently there are several successful studies about PSO focusing on discrete problems such as the travelling salesman problem (TSP), project selection problem and job-shop scheduling problems[19].
In this paper, PSO is combined with REFS. The PSO based on REFS (REFS_PSO) is built to optimize the eight-objective mathematical model of an optimal MRSC. The scheduling process is encoded in integer, then the real numbers are transformed to the discrete process through the LOV(Largest-Order- the Value)[20]. The solving process is as follows:
1) Get the optimal solutions of eight single-objective function with PSO algorithm, and use these solutions to form the ideal solution set Y0 for an optimal MRSC. Y0 is mapped to the fuzzy set of ideal solution S(0).
2) Initialize the population. Generate NP particles with random positions Xigen(gen =0) and velocities vigen, where gen is the current iteration of evolution, and then calculate each particle's objective function values with Eqs.(2) - (9). Obtain Pareto front Yigen, Yigen is mapped to the fuzzy set of Pareto front S(i).
3) Calculate the relative entropy coefficient of the fuzzy sets (Ce(S(i); S(0))) with Eq.(14). This coefficient is regarded as the fitness value to lead particle evolution. Let Pigen of each particle and its coefficient Ce equal to its current position and Ce(S(i); S(0)); and let Gigen and its coefficient Ce equal to the position and Ce of the best initial particle.
4) Maintain and update the external archive based on Ce.
5) Update the velocity and position of each particle according to follow formulas.
| $ \begin{array}{l} v_i^{\left( {gen + 1} \right)} = \omega v_i^{gen} + {c_1}{r_1}\left( {P_i^{gen} - X_i^{gen}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{c_2}{r_2}\left( {G_i^{gen} - X_i^{gen}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;X_i^{\left( {gen + 1} \right)} = X_i^{gen} + v_i^{\left( {gen + 1} \right)} \end{array} $ |
where, ω is the inertia weight; c1, c2 are influence factors in the range of [0, 1];
6) Calculate each particle's objective function values with Eqs. (2)- (9). Pareto front Yigen is obtained and mapped to the fuzzy set of Pareto front S(i).
7) Calculate the relative entropy coefficient (Ce(S(i); S(0))) with Eq.(14). For each particle, its current coefficient with the coefficient of its Pigen is compared. If current value is better, then update Pigen and its Ce with the current position and Ce.
8) Determine the best particle of the current swarm with the best coefficient Ce. If the Ce is better than Ce of Gigen, then Gigen and its Ce with the position and Ce of the current best particle are updated.
9) Verify the termination conditions of the algorithm. If the termination conditions are not reached, then gen = gen+1, return to Step 4), else, output the external archive.
4 Procedure of Solving MRA Considering the Geographical DistributionThe MRA considering the geographical distribution in CMP is solved from the perspective of the supply chain. In this process, the states whether the MRs malfunction or not are considered. The process is as follows.
Step 1 Task decomposition. The task is decomposed to several sub-tasks according to the process requirement. The state of manufacturing resources is monitored in real time. If the manufacturing resources malfunction, the malfunctioning resources can be found and deleted immediately.
Step 2 Match. After the task is decomposed in CMP, the MRs that satisfy the requirement of sub-task are matched from the cloud resource pool.
Step 3 Preliminary selection. Each MR that can match with sub-task is estimated by Eq. (1), the MRs that are selected by this membership function are regarded as the candidate MRs. The candidate resource pool is built.
Step 4 Optimal selection. Utilize PSO algorithm containing REFS to optimize MRA considering the geographical distribution. REFS_PSO is built, and is used to obtain the optimal manufacturing resource supply chain.
Step 5 If no MR malfunctions in Step 2, Step 3, and Step 4, then go to Step 6, otherwise, the malfunctioning MRs are removed from the cloud resource pool, return to Step 2.
Step 6 Termination. An optimal manufacturing resource supply chain is outputted.
5 Simulation ExperimentsFor validating the effectiveness of MRA model considering the geographical distribution and REFS_PSO, the simulation example is designed. The processing time, the logistic time, and the quality information are given with Refs. [21-22]. The simulation example is a task that can be decomposed to five sub-tasks. In order to embody that the model has the instantaneity, the dynamic and the fault-tolerance, the states whether the MRs malfunction or not are set. In optimal selection stage, REFS_PSO is used to get the optimal manufacturing resource supply chain, NSGA-Ⅱ and PSO based on Random Weight (RW_PSO) are adopted as comparison algorithms.
5.1 Parameters SettingsThe parameters setting of MRA is as follows, which refer to Refs. [21, 23]. In the preliminarily selecting stage, the amount (Vi) of MR that each sub-task can be matched are all set to 15, the amount (Ki) of candidate resources of each sub-task are all set to 5. p(i)min=10, q(i)min=10, Qa1(i)min=0.65, p(i)max=100, q(i)max=100. These parameters are set according to some actual tasks, and the Qa1(i)min is obtained by the evaluations of users who have utilized the related resources. This parameter setting in preliminary stage can effectively filter some resources with longer production time, higher production cost, but lower processing quality. And in the optimal selection stage, the unit delay cost γ=1.5, Qamin=0.75, Remin=0.8, Repmin=0.8. Qamin here is greater than Qa1(i)min because it is reasonable to set a higher quality threshold in optimal stage than that in preliminary stage.
For three algorithms, the population size is set to 50, the scale of individuals in the external archive Wmax is set to 30, and the maximum number of iteration genmax is 1000. In PSO, vmax=1, c1=c2=2.0, To improve the convergence performance of PSO, the adaptive adjustment strategy[24-25] is adopted to reduce ω linearly. In NSGA-Ⅱ, crossover rate Pc=0.9 and mutation rate Pm=0.1.
For calculating the membership grade, λ=0.9 and α=10.
5.2 Result Analysis 5.2.1 The state that the MRs work normallyIn Fig. 1, the solid lines represent the allocation process of MA, at this time, the malfunctioning MRs do not occur. For each sub-task, from ST1 to ST5, at most fifteen MRs that can realize the requirement of sub-task are searched from CMP. The searched MRs constitute the resource set. For example, the resource set of ST1 is (RP11, RP12, RP13, …, RP113, RP114, RP115), the resource set of ST3 is (RP31, RP32, RP33, …, RP313, RP314, RP315). Then the preliminary selection stage of the allocation process begins. Five MRs are matched for each sub-task from these fifteen MRs with the membership function. The matched MRs as the candidate resources constitute the candidate resource pool. Thus there will be 55=3125 schemes of the manufacturing resource supply chain for further selection.
Continually, the optimal selection stage of the allocation process now starts. MRA is optimized by REFS_PSO. Table 1 shows the optimal results obtained by REFS_PSO and two comparison algorithms, NSGA-Ⅱ and RW_PSO. Known from the table, REFS_PSO obtains the smallest value for the minimum optimization objective function fi(i=1, 2, 3, 4, 5), and achieves the largest value in the maximum optimization objective function f6, f7 and f8. The solutions obtained by REFS_PSO are superior to those by other two algorithms. The optimal manufacturing resource supply chain is resource demander→ RP12→RP23→RP37→RP49→RP57→ resource demander. For REFS_PSO, the fitness value (Ce) is 0.745, that if far greater than 0.5. The relative entropy coefficient is larger, so the similarity between the Pareto solution and the ideal solution is good, then function values of the Pareto solution obtained by REFS_PSO is excellent.
| Table 1 Optimal results while MRs work normally |
5.2.2 The state that the MRs malfunction
Fig. 2 shows the process of MRA when MRs malfunction. The process that MRs are allocated is described in solid line before MRs malfunction. The process after MRs malfunction is described in the dashed line.
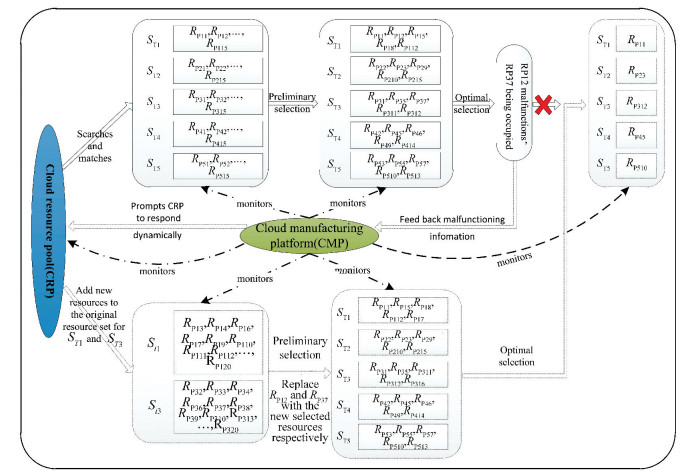
|
Fig.2 The optimal allocation process during MRs malfunction |
Before MRs malfunction, the process of match and preliminary selection is the same with the process described in Section 5.2.1. If there is certain MRs malfunction before the optimal selection stage begins. The malfunctioning messages are sent to CMP through IoT system, the malfunctioning MRs will be replaced immediately. For example, RP12 breaks down, and RP37 turns from idle state to occupied state. The procedure that the malfunctioning MRs are replaced is as follows. For the sub-task ST1 and ST3, there are malfunctioning MRs, RP12 and RP37 respectively. Then RP12 and RP37 are removed from the cloud resource pool and the resource set. Including original MRs exceptremoved MRS, at most fifteen new MRs that can realize the requirement of ST1 are searched from the cloud resource pool. The resource set of ST1 is updated. For example, the new resource set of ST1 is (RP11, RP13, RP14, RP15, … RP114, RP115, RP116). In a similar way, the new resource set of ST3 is (RP31, RP32, …, RP36, RP38, …, RP314, RP315, RP316). The new MRs for ST1 or ST3 are selected from the new resource set with the membership function, and a new candidate resource pool is built. Then through the optimal selection stage, the manufacturing resource supply chain can be obtained.
Table 2 shows the optimal results obtained by three algorithms while MRs malfunction. Known from Table 2, the performance of REFS_PSO is still as good as ever. For five minimum optimization objective function fi(i=1, 2, 3, 4, 5), the results obtained by REFS_PSO are smaller than the values of other two algorithms. For three maximum optimization objective function f6, f7 and f8, the results obtained by REFS_PSO are larger than the values of other two algorithms. The optimal manufacturing resource supply chain obtained by REFS_PSO is resource demander→RP11→RP23→RP312→RP45→RP510→ resource demander. For REFS_PSO, the fitness value (Ce) is 0.718, indicating that the similarity between the Pareto solution and the ideal solution is good, the results obtained by REFS_PSO are close to function values of ideal solution, then function values of the Pareto solution obtained by REFS_PSO is excellent.
| Table 2 Optimal results while MRs malfunction |
In the above experiment, the time that the MRs malfunction is the time that preliminary selection stage is to be finished and the optimal selection stage is about to begin. However, in practice, the time is uncertain. But the method proposed is still effective in solving the problem no matter when the MRs malfunction. The malfunctioning MRs will be removed by the proposed method, the new MRs are matched and added to the resource set. This process embodies the instantaneity, the dynamic, and the fault-tolerance of CM.
6 ConclusionsIn this paper, manufacturing resource allocation (MRA) problems are studied from the perspective of considering the geographical distribution in CM environment. Main work is as follows. First, the MRA model considering the geographical distribution is built, the model is closed-loop cloud environment model that includes two stages, preliminary selection stage and optimal selection stage. At optimal selection stage, the states whether the MRs malfunction or not are considered. Second, a many-objective optimization algorithm, REFS_PSO, is described for optimizing MRA problem considering the geographical distribution. An optimal manufacturing resource supply chain is obtained at last. The results of experiments indicate that the proposed model is effective, and REFS_PSO can obtain better manufacturing resource supply chain while compared with other two algorithms.
| [1] |
Tao F, Zhang L, Venkatesh V C, et al. Cloud manufacturing: A computing and service-oriented manufacturing model. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2011, 225(10): 1969-1976. DOI:10.1177/0954405411405575 (  0) 0) |
| [2] |
Xu X. From cloud computing to cloud manufacturing. Robotics and Computer-Integrated Manufacturing, 2012, 28(1): 75-86. DOI:10.1016/j.rcim.2011.07.002 (  0) 0) |
| [3] |
Rachmawati L, Srinivasan D. A hybrid fuzzy evolutionary algorithm for a multi-objective resource allocation problem. Fifth International Conference on Hybrid Intelligent Systems(HIS'05), 2005. Piscataway: IEEE, DOI: 10.1109/ICHIS.2005.10.
(  0) 0) |
| [4] |
Lin C-M, Gen M. Multiobjective resource allocation problem by multistage decision-based hybrid genetic algorithm. Applied Mathematics and Computation, 2007, 187(2): 574-583. DOI:10.1016/j.amc.2006.08.170 (  0) 0) |
| [5] |
Chaharsooghi S K, Meimand Kermani A H. An effective ant colony optimization algorithm (ACO) for multi-objective resource allocation problem (MORAP). Applied Mathematics and Computation, 2008, 200(1): 167-177. DOI:10.1016/j.amc.2007.09.070 (  0) 0) |
| [6] |
Li C, Li L. A new optimal approach for multiple optimisation objectives grid resource allocation and scheduling. International Journal of Systems Science, 2008, 39(12): 1127-1138. DOI:10.1080/00207720802299036 (  0) 0) |
| [7] |
Ko P-C, Lin P-C. Resource allocation neural network in portfolio selection. Expert Systems with Applications, 2008, 35(1-2): 330-337. DOI:10.1016/j.eswa.2007.07.031 (  0) 0) |
| [8] |
Yin P-Y, Yu S-S, Wang P-P, et al. A hybrid particle swarm optimization algorithm for optimal task assignment in distributed systems. Computer Standards & Interfaces, 2006, 28(4): 441-450. DOI:10.1016/j.csi.2005.03.005 (  0) 0) |
| [9] |
Fan K, You W, Li Y. An effective modified binary particle swarm optimization (mBPSO) algorithm for multi-objective resource allocation problem (MORAP). Applied Mathematics and Computation, 2013, 221: 257-267. DOI:10.1016/j.amc.2013.06.039 (  0) 0) |
| [10] |
Garg H, Sharma S P. Multi-objective reliability-redundancy allocation problem using particle swarm optimization. Computers & Industrial Engineering, 2013, 64(1): 247-255. DOI:10.1016/j.cie.2012.09.015 (  0) 0) |
| [11] |
Liu Q, Zhang C, Zhu K, et al. Novel multi-objective resource allocation and activity scheduling for fourth party logistics. Computers & Operations Research, 2014, 44: 42-51. DOI:10.1016/j.cor.2013.10.010 (  0) 0) |
| [12] |
Song L, Li Y, Han Z. Resource allocation in full-duplex communications for future wireless networks. IEEE Wireless Communications, 2015, 22(4): 88-96. DOI:10.1109/MWC.2015.7224732 (  0) 0) |
| [13] |
Deb K, Myburgh C. A population-based fast algorithm for a billion-dimensional resource allocation problem with integer variables. European Journal of Operational Research, 2017, 261(2): 460-474. DOI:10.1016/j.ejor.2017.02.015 (  0) 0) |
| [14] |
Zheng H, Feng Y, Tan J. A hybrid energy-aware resource allocation approach in cloud manufacturing environment. IEEE Access, 2017, 5: 12648-12656. DOI:10.1109/ACCESS.2017.2715829 (  0) 0) |
| [15] |
Chand S, Wagner M. Evolutionary many-objective optimization: A quick-start guide. Surveys in Operations Research and Management Science, 2015, 20(2): 35-42. DOI:10.1016/j.sorms.2015.08.001 (  0) 0) |
| [16] |
Purshouse R C, Fleming P J. On the evolutionary optimization of many conflicting objectives. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 770-784. DOI:10.1109/TEVC.2007.910138 (  0) 0) |
| [17] |
Guo X Z, Xin X L. Partial entropy and relative entropy of fuzzy sets. Fuzzy Systems and Mathematics, 2005, 19(2): 97-102. DOI:10.3969/j.issn.1001-7402.2005.02.019 (  0) 0) |
| [18] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of IEEE International Conference on Neural Networks. Piscataway: IEEE, 1995, 4: 1942-1948, DOI: 10.1109/ICNN.1995.488968.
(  0) 0) |
| [19] |
Zhang W B, Zhu G Y. Comparison and application of four versions of particle swarm optimization algorithms in the sequence optimization. Expert Systems with Applications, 2011, 38(7): 8858-8864. DOI:10.1016/j.eswa.2011.01.097 (  0) 0) |
| [20] |
Qian B, Wang L, Huang D X, et al. An effective hybrid DE-based algorithm for multi-objective flow shop scheduling with limited buffers. Computers & Operations Research, 2009, 36(1): 209-233. DOI:10.1016/j.cor.2007.08.007 (  0) 0) |
| [21] |
Song W Y. Cloud Manufacturing Resources Optimization Configuration Research. Chongqing: Chongqing University, 2013. DOI: 10.7666/d.D355131.
(  0) 0) |
| [22] |
Wang S, Guo L, Kang L, et al. Research on selection strategy of machining equipment in cloud manufacturing. International Journal of Advanced Manufacturing Technology, 2014, 71(9-12): 1549-1563. DOI:10.1007/s00170-013-5578-5 (  0) 0) |
| [23] |
He L. Workshop manufacturing resources scheduling optimization research considering the supply chain in Cloud Manufacturing environment. Fuzhou: Fuzhou University, 2016.
(  0) 0) |
| [24] |
Shi Y, Eberhart R. A modified particle swarm optimizer. The 1998 IEEE International Conference on Evolutionary Computation Proceedings, 1998. IEEE World Congress on Computational Intelligence, Piscataway: IEEE, 1998. 69-73. DOI: 10.1109/ICEC.1998.699146.
(  0) 0) |
| [25] |
Zhu G Y, Feng Z C, Yang Z F. Solving multi-objective optimization problem with particle swarm algorithm guided by grey entropy parallel analysis method. Systems Engineering and Electronics, 2014, 36(11): 2233-2238. DOI:10.3969/j.issn.1001-506X.2014.11.19 (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


