2. Shenzhen Research Institute of Northwestern Polytechnical University, Shenzhen 518057, Guangdong, China
The exceptional structural design of the tilt rotor aids in the vertical take-off and landing capacity of the helicopter, and also facilitates characteristics such high cruise speed, long operational range, and heavy load of fixed wing aircraft[1]. Quad tilt rotor (QTR) is a class of controlled unmanned aerial vehicles with complex structure, the QTR's attitude control system exhibits characteristics such as strong coupling, multi input, multi output, and nonlinearity and the system possesses modeling error and external disturbance, which causes the design of the flight control system to be exceedingly demanding[2]. To solve these problems, many scholars have carried out extensive research, for instance, designing flight control system of the tilting rotor using nonlinear control strategy[3-5], design of a tilting rotor flight control system based on full mode flight strategy[6-7], unified velocity control of unmanned tilt-wing aircraft[8], the flight control system in a large attitude change [9], the optimal control theory [10-11], tilt rotorcraft flight control method based on switch controller initialization[12], four tilt rotor unmanned aerial vehicle control system with adaptive control [13]. Especially in the stage of vertical take-off and landing, it is exceedingly important that the attitude control of the aircraft, throughout the tilting of the Rotorcraft V-22 four major accidents occurred, these were all caused by out of control attitude during the vertical take-off and landing stages, therefore, this study focuses on the QTR's attitude control during the vertical takeoff and landing modes. As a nonlinear control method, because of its characteristic of significant robustness, the sliding mode variable structure control has been given considerable attention, it has been widely used in the design of motor control and aircraft control systems[14-15]. In the general sliding mode variable structure control, usually select a linear sliding surface, the state of the system can only asymptotically converging to the equilibrium point, and the convergence rate is slow, thus when the system state error is large, the control effect of linear sliding mode is not ideal. To solve this problem, Zak et al.[16] proposed terminal sliding mode (TSM), it is a finite time convergent sliding mode control strategy. Introducing nonlinear term in the sliding mode, the convergence characteristics of the system are improved, so that the system state is exhibits finite time convergence with respect to the desired trajectory. In Ref.[17], the final attractor in the neural network is introduced so that the state error converges to zero within a limited time. However, there is a problem of singularity and slow convergence rate in the traditional terminal sliding mode control when situated far from the sliding mode surface, this is owing to the introduction of nonlinear components the convergence speed with respect to the equilibrium state is improved, and the closer it is to the equilibrium state, the faster is the convergence rate, but, when the state of the system is away from the equilibrium point, the convergence rate of the nonlinear sliding mode is slower than that of the linear. To solve the singularity problem, scholars have studied several methods, such as switching between nonlinear and linear sliding mode surfaces[18]; the trajectory is transformed to the prescribed interval and the terminal sliding mode in this interval is non-singular[19]; however, these methods are incorporated to avoid the singularity problem indirectly. In Ref.[20], the redesigned terminal sliding mode directly avoids the singularity problems. In order to solve the shortcomings of convergence rate, the characteristics of a linear sliding surface is used in Ref.[21] to improve the convergence speed of the terminal sliding mode far away from the equilibrium point. In Refs.[22-23], an exponential and logarithmic type of sliding mode surface is designed, which improves the convergence speed away from the equilibrium point. However, the previous studies only consider one of the two problems, but do not consider the singular problem and the convergence speed problem simultaneously, therefore, this study is based on the aforementioned research a logarithmic form of the global fast nonsingular terminal sliding surface is designed, which avoids the singularity directly and improves the convergence speed of the sliding surface of the terminal away from the equilibrium point.
To realize the sliding mode, Gao[24]proposed the concept of reaching law, but to reduce the chattering and convergence time, the traditional reaching law still possesses a scope for improvement. In Refs.[25-27], "double power reaching law", "variable exponent reaching law", and "an improved the power reaching law" were proposed, thereby improving the system state of convergence and suppressing the chattering of variable structure control. Based on the aforementioned research, a fast double power reaching law with variable coefficients is proposed in this study, which renders the motion quality in the process of system state approaching the sliding mode outstanding.
Because of the existence of the modeling error and external disturbance term in the QTR attitude model, it is difficult to eliminate the chattering of the controller, managing the complex disturbance becomes the problem that should be considered when designing the controller. The appearance of the extended state observer(ESO) theory[28] provides a new method to solve the complex disturbance. The ESO is the principal component of the active disturbance rejection control (ADRC) technique. It can be used to estimate the complex disturbance and compensate it in the control system. Based on the comprehensive analysis of the above, in this study, a new logarithmic fast nonsingular terminal sliding mode controller with ESO is designed and the relevant stability proof is provided. The simulation results show that the scheme has good tracking control performance.
2 Attitude Model of QTR Vertical Take-Off and Landing ModelThe attitude control of the QTR vertical take-off and landing mode is realized via differential adjustment of the lift force of the propellers or nacelle angle. The control of the pitching channel is achieved via differential adjustment of the two sets of front and rear propellers, the rolling channel is realized via differential adjustment of the rotation rate of the rotor on both sides of the fuselage, the yaw channel is achieved via the differential adjustment of the two groups of nacelle angles on both sides of the fuselage. The system structure is shown in Fig. 1.

|
Fig.1 QTR structure schematic diagram |
Neglecting the impact of the QTR's elastic vibration, a new state variable x is defined as follows:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}} = {{\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_6}} \end{array}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} \phi &{\dot \phi }&\theta &{\dot \theta }&\varphi &{\dot \varphi } \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
The attitude model of the QTR vertical take-off and landing model can be expressed as follows with respect to the nonlinear system with uncertainties:
| $ \left\{ \begin{array}{l} {{\dot x}_{\left( {2k - 1} \right)}}\left( t \right) = {x_{\left( {2k} \right)}}\left( t \right)\\ {{\dot x}_{\left( {2k} \right)}}\left( t \right) = {f_k}\left( {x,t} \right) + {g_k}{u_k} + {\sigma _{dk}} \end{array} \right. $ | (1) |
where k=1, 2, 3, fk is
| $ {\mathit{\boldsymbol{f}}_k} = \left[ {\begin{array}{*{20}{c}} {\frac{{{I_{xz}}\left( {{I_{xx}} - {I_{yy}} + {I_{zz}}} \right){x_4}{x_6} + \left[ {{I_{zz}}\left( {{I_{yy}} - {I_{xx}}} \right) - I_{xz}^2} \right]{x_2}{x_6}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}\\ {\frac{{\left( {{I_{zz}} - {I_{xx}}} \right){x_2}{x_6} + {I_{xz}}\left( {x_6^2 - x_2^2} \right)}}{{{I_{yy}}}}}\\ {\frac{{{I_{xx}}\left( {{I_{xx}} - {I_{yy}}} \right){x_4}{x_6} + {I_{xz}}\left( {{I_{xx}} - {I_{yy}} + {I_{zz}}} \right){x_2}{x_6}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}} \end{array}} \right] $ |
and gk is
| $ {\mathit{\boldsymbol{g}}_k} = \left[ {\begin{array}{*{20}{c}} {\frac{{{I_{zz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}&0&{\frac{{{I_{xz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}\\ 0&{\frac{1}{{{I_{yy}}}}}&0\\ {\frac{{{I_{xz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}&0&{\frac{{{I_{xz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{u}}_k} = {\left[ {\begin{array}{*{20}{l}} {{u_1}}&{{u_2}}&{{u_3}} \end{array}} \right]^{\rm{T}}} $ |
| $ {\sigma _{dk}} = \Delta {f_k}\left( {x,t} \right) + \Delta {g_k}{u_k} + {d_k} $ |
where, Δfk, Δgk are the modeling error terms; σdkis composite disturbance; φ, θ, ϕ are the roll angle, pitch angle, and yaw angle; Ixx, Iyy, Izz are the moment of inertia around the x, y, z axis of the fuselage; Ixz is the inertial product; dk refers to the external disturbances of each channel; u1, u2, u3 are the control input of each channel, the specific expression is
| $ {u_1} = {L_\varphi }{k_T}\left( {w_1^2 - w_2^2 + w_3^2 - w_4^2} \right) $ |
| $ {u_2} = {L_\theta }{k_T}\left( {w_1^2 + w_2^2 - w_3^2 - w_4^2} \right) $ |
| $ {u_3} = {L_\phi }mgv $ |
where kT is the propeller thrust coefficient, wi is the corresponding propeller speed, m is the aircraft mass, υ is the nacelle angle, Lφ, Lθ, Lϕ are the arms of each channel.
3 Terminal Sliding Mode ControlThe common terminal sliding mode surface (TSM) is designed as [17]
| $ {s_T} = \dot x + {\beta _T}{\rm{sig}}{(x)^{{q_T}}} $ | (2) |
where, sliding surface parameters βT>0, and 0 < pT < 1.
The state of the system based on the sliding mode surface of Eq.(2) can be stable for a limited time, however, when the state is far from the equilibrium, the convergence rate is slow, thus the design described in Ref.[18] is as follows, fast terminal sliding mode surface (FTSM):
| $ {s_F} = \dot x + {\alpha _F}x + {\beta _F}{\rm{sig}} {(x)^{{p_F}}} $ | (3) |
where, αF, βF>0;pF∈(0, 1). The convergence time of the system is Ts=max{Tsi} (i=1, 2, …, N), where:
| $ {T_{si}} = \frac{1}{{{\alpha _F}\left( {1 - {P_F}} \right)}}\ln \frac{{{\alpha _F}{{\left| {{x_{si}}} \right|}^{1 - {p_F}}} + {\beta _F}}}{{{\beta _F}}} $ | (4) |
where, xsi∈ R is the state of the system when it reaches the sliding surface.
However, the above two types of sliding surface designs will inevitably exhibit the singularity phenomenon, thus, in Ref.[18] a nonsingular terminal sliding mode surface (NTSM) is designed, in Refs. [29] and [30] a fast nonsingular terminal sliding mode surface (FNTSM) is designed; the FNTSM surface described in Ref.[30] is as follows:
| $ {s_N} = x + \frac{1}{{{\alpha _N}}}{\rm{sig}}{\left( x \right)^{{q_N}}} + \frac{1}{{{\beta _N}}}{\rm{sig}}{\left( {\dot x} \right)^{{p_N}}} $ | (5) |
where, αN, βN>0;pN∈(1, 2);qN>pN. The convergence time of the system is
| $ \begin{array}{l} {T_{si}} = \frac{{{p_N}}}{{{p_N} - 1}}\beta _N^{ - 1/{P_N}}{\left| {{x_{si}}} \right|^{1 - 1/{p_N}}} \cdot \bar F\left( {\frac{1}{{{P_N}}},} \right.\\ \;\;\;\;\left. {\frac{{{P_N} - 1}}{{{P_N}\left( {{q_N} - 1} \right)}},1 + \frac{{{P_N} - 1}}{{{P_N}\left( {{q_N} - 1} \right)}}, - \frac{1}{{{\alpha _N}}}{{\left| {{x_{si}}} \right|}^{{q_N} - 1}}} \right) \end{array} $ | (6) |
where F is Gauss hypergeometric function[31].
4 New Logarithmic Nonsingular Fast Terminal Sliding ModeBased on the aforementioned research, a new logarithmic fast nonsingular terminal sliding mode (LFNTSM) surface is designed in this study:
| $ \begin{array}{l} {s_k} = {\left( {{I_k} + \left| x \right|} \right)^p}{\rm{diag}}\left( {{{\ln }^{\left( {1 + \left| x \right|} \right)}}} \right){\rm{sgn}}(x) + \\ \;\;\;\;\;\;\frac{1}{\alpha }{\left( {{I_k} + \left| x \right|} \right)^p}{\rm{diag}}{\left( {{{\ln }^{\left( {1 + \left| x \right|} \right)}}} \right)^q}{\rm{sgn}}(x) + \\ \;\;\;\;\;\;\frac{1}{\beta }{\rm{sig}}{\left( {\dot x} \right)^p} \end{array} $ | (7) |
where |x|=diag(xk)sgn(x).
Lemma 1 For Gaussian hypergeometric functions[20]
| $ \bar F\left( {A,B,C,z} \right) = \sum\limits_{k = 0}^{ + \infty } {\frac{{{{\left( A \right)}_k}{{\left( B \right)}_k}}}{{{{\left( C \right)}_k}k!}}{z^k}} $ | (8) |
If A, B, and C are positive real numbers, and C-B-A>0, then F(A, B, C, z) is convergent on the domain z < 0.
Theorem 1 For the nonlinear system described in Eq.(1), if the sliding mode surface of Eq.(7) is used to design the controller, and the parameters satisfy the condition α, β>0, p∈(1, 2), q>p, then the state of the system will slide to x≡0 in the finite time Tsk after reaching the sliding surface, where:
| $ \begin{array}{l} {T_{sk}} = \frac{{{p_L}}}{{{p_L} - 1}}\beta _L^{ - 1/{P_L}}{\left| {{{\ln }^{\left( {1 + \left| {{x_k}} \right|} \right)}}} \right|^{1 - 1/{p_L}}} \cdot \\ \;\;\;\;\bar F\left( {\frac{1}{{{P_L}}},\frac{{{P_L} - 1}}{{{P_L}\left( {{q_L} - 1} \right)}},1 + \frac{{{P_L} - 1}}{{{P_L}\left( {{q_L} - 1} \right)}},} \right.\\ \;\;\;\;\left. { - \frac{1}{{{\alpha _L}}}{{\left| {{{\ln }^{\left( {1 + \left| {{x_k}} \right|} \right)}}} \right|}^{{q_N} - 1}}} \right) \end{array} $ | (9) |
Proof When s=0, Eq. (7) is transformed as follows:
| $ \begin{array}{l} \dot x = - {\left[ {\beta \left[ {{{\ln }^{(1 + |x|)}}} \right] + \frac{\beta }{\alpha }{{\left[ {{{\ln }^{(1 + |x|)}}} \right]}^q}} \right]^{1/p}}(1 + \\ \;\;\;|x|) {\rm{sgn}} (x) \end{array} $ |
which can be obtained using
Remark 1 Comparing the convergence time of FNTSM and LFNTSM, the term ln(1+|x|) is observed to be the only difference between Eq.(6) and Eq.(9), and when xi≠0, the term ln(1+|x|) < |x| is always tenable. Therefore, under the same parameters, the terminal sliding mode based on Theorem 1 is faster than the existing fast nonsingular terminal sliding mode technique with regard to avoiding singularity.
5 New Fast Reaching LawTo realize the system state fast reaching sliding surface, Professor Gao [24] proposed the following exponential reaching law:
| $ {{\dot s}_k} = - {\varepsilon _{k1}} sgn \left( {{s_k}} \right) - {\varepsilon _{k2}}{s_k},{\varepsilon _{k1}} > 0,{\varepsilon _{k2}} > 0 $ | (10) |
Based on the form of the exponential reaching law, it can be observed that the derivative of the sliding mode surface is not zero when the state of system converges to s=0, it slides the system state out of the sliding surface, and the reaching law does not possess the two order sliding mode characteristics, the chattering is relatively large, if the saturation function is used instead of the switching function, the robustness of the system will be eliminated. In this study, to realize the fast chattering free approach to sliding surface, a double power reaching law of variable coefficients with two order sliding mode characteristics is proposed:
| $ \begin{array}{l} {{\dot s}_k} = - \left( {{I_k} + \left| {{{\dot \lambda }_k}} \right|} \right)\left[ {{\varepsilon _{k1}}{\rm{diag}}\left\{ {\left| {{s_k}} \right|} \right\}{\rm{sgn}}\left( {{s_k}} \right) + } \right.\\ \;\;\;\left. {{\varepsilon _{k2}}{\rm{diag}}\left\{ {{{\left| {{s_k}} \right|}^{m/n}}} \right\}{\rm{sgn}}\left( {{s_k}} \right)} \right]\\ \;\;\;{\varepsilon _{k1}} > 0,{\varepsilon _{k2}} > 0,n > m > 0,k = 1,2,3\\ \;\;\;\left| {{{\dot \lambda }_k}} \right| = {\rm{diag}}\left( {\left| {{{\dot \lambda }_1}} \right|,\left| {{{\dot \lambda }_2}} \right|,\left| {{{\dot \lambda }_3}} \right|} \right) \end{array} $ | (11) |
When the state of system is far away from the sliding surface, the convergence rate of the new reaching law is primarily determined via the term
| $ {t_{rk}} < \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{1 + \left| {{{\dot \lambda }_k}} \right|}} \cdot \frac{1}{{{\varepsilon _{k2}}(1 - m/n)}},\left| {s\left( 0 \right)} \right| > 1}\\ {\frac{1}{{1 + \left| {{{\dot \lambda }_k}} \right|}} \cdot \frac{{{{\left| {s\left( 0 \right)} \right|}^{1 - m/n}}}}{{{\varepsilon _{k2}}(1 - m/n)}},0 < \left| {s\left( 0 \right)} \right| < 1} \end{array}} \right. $ | (12) |
It can be observed that the system state converges to the sliding mode surface in a finite time, and it is
Introducing the new logarithmic fast nonsingular fast terminal sliding surface:
| $ \begin{array}{l} {s_k} = {\left( {{I_k} + \left| {{\lambda _k}} \right|} \right)^p}{\rm{diag}}\left( {{{\ln }^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}} \right){\rm{sgn}}\left( {{\lambda _k}} \right) + \\ \;\;\;\;\;\;\frac{1}{\alpha }{\left( {{I_k} + \left| {{\lambda _k}} \right|} \right)^p}{\rm{diag}}{\left[ {{{\ln }^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}} \right]^q}{\rm{sgn}}\left( {{\lambda _k}} \right) + \\ \;\;\;\;\;\;\frac{1}{\beta }{\rm{sig}}{\left( {{{\dot \lambda }_k}} \right)^p} \end{array} $ | (13) |
where,
| $ \left| {{\lambda _k}} \right| = {\rm{diag}}\left( {{\lambda _k}} \right){\rm{sgn}}\left( {{\lambda _k}} \right) $ |
| $ {\lambda _k} = {x_{(2k - 1)}} - {x_{d(2k - 1)}},k = 1,2,3 $ |
The following is obtained via the derivation of Eq.(13):
| $ {{\dot s}_k} = h\left( {{\lambda _k},{{\dot \lambda }_k}} \right) + \frac{p}{\beta }{\left( {{{\dot \lambda }_k}} \right)^{p - 1}}{{\ddot \lambda }_k} $ | (14) |
where:
| $ \begin{array}{l} h\left( {{\lambda _k},} \right.\left. {{{\dot \lambda }_k}} \right) = \left[ {p{{\left( {1 + \left| {{\lambda _k}} \right|} \right)}^{p - 1}} \cdot {{\ln }^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}} \right] \cdot \\ \;\;\;\;\;\;\;{{\dot \lambda }_k} + {\left( {1 + \left| {{\lambda _k}} \right|} \right)^{p - 1}}{{\dot \lambda }_k} + \\ \;\;\;\;\;\;\frac{p}{\alpha }{\left( {1 + \left| {{\lambda _k}} \right|} \right)^{p - 1}}{\ln ^{{{\left( {1 + \left| {{\lambda _k}} \right|} \right)}^q}}}{{\dot \lambda }_k} + \\ \;\;\;\;\;\;\frac{q}{\alpha } \cdot {\left( {1 + \left| {{\lambda _k}} \right|} \right)^{p - 1}} \cdot {\ln ^{\left( {1 + {{\left| {{\lambda _k}} \right|}^{q - 1}}} \right)}}{{\dot \lambda }_k} \end{array} $ |
Combined with the new fast approaching law proposed in the previous section of this paper, the corresponding control law is designed as follows:
| $ \begin{array}{l} {u_k} = - g_k^{ - 1}\left\{ {\frac{\beta }{p}{{\left( {{{\dot \lambda }_k}} \right)}^{1 - p}}h\left( {{\lambda _k},{{\dot \lambda }_k}} \right) + {f_k} - {{\ddot x}_{d(2k - 1)}} + } \right.\\ \;\;\;\;\;\;\;{\sigma _{dk}} + \left[ {{\varepsilon _{k1}}{\rm{diag}}\left\{ {\left| {{s_k}} \right|} \right\}{\rm{sgn}}\left( {{s_k}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\left. {{\varepsilon _{k2}}{\rm{diag}}\left\{ {{{\left| {{s_k}} \right|}^{m/n}}} \right\}{\rm{sgn}}\left( {{s_k}} \right)} \right]\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)} \right\} \end{array} $ | (15) |
where, εkj∈R+(k=1, 2, 3, j=1, 2), and σdk is the compound disturbance to be estimated.
6.2 Disturbance Observer Based on ESOFor system (1), the effect of the modeling error and external disturbance is exceedingly serious. To ensure the control precision and robustness and to minimize the chattering as much as possible, this study incorporates the extended state observer (ESO) to conduct the estimation and compensation of the online real-time disturbance. In this study, a disturbance observer is designed using the ESO model proposed in Ref.[17],
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot {\hat x}}_{(2k - 1)}} = {{\hat x}_{(2k)}} + \frac{{{\rho _{k1}}}}{{{\xi _k}}}\left( {{x_{(2k - 1)}} - {{\hat x}_{(2k - 1)}}} \right)}\\ {{{\dot {\hat x}}_{(2k)}} = {{\hat f}_{(k)}} + {{\hat g}_{(k)}}{u_k} + {{\hat \sigma }_{(k)}} + \frac{{{\rho _{k2}}}}{{\xi _k^2}}\left( {{x_{(2k - 1)}} - {{\hat x}_{(2k - 1)}}} \right)}\\ {{{\dot {\hat \sigma} }_{(k)}} = \frac{{{\rho _{k3}}}}{{\xi _k^3}}\left( {{x_{(2k - 1)}} - {{\hat x}_{(2k - 1)}}} \right)} \end{array}} \right. $ | (16) |
where k=1, 2, 3.
| $ \begin{array}{l} {u_k} = - g_k^{ - 1}\left\{ {\frac{\beta }{p}{{\left( {{{\dot {\hat \lambda} }_k}} \right)}^{1 - p}}h\left( {{{\hat \lambda }_k},{{\dot {\hat \lambda} }_k}} \right) + {{\hat f}_k} - {{\ddot x}_{d(2k - 1)}} + } \right.\\ \;\;\;\;{{\hat \sigma }_{dk}} + \left[ {{\varepsilon _{k1}}{\rm{diag}}\left\{ {\left| {{s_k}} \right|} \right\}{\rm{sgn}}\left( {{s_k}} \right) + } \right.\\ \left. {\left. {\;\;\;\;{\varepsilon _{k2}}{\rm{diag}}\left\{ {{{\left| {{s_k}} \right|}^{m/n}}} \right\}{\rm{sgn}}\left( {{s_k}} \right)} \right]\left( {1 + \left| {{{\hat \lambda }_k}} \right|} \right)} \right\} \end{array} $ | (17) |
Assumption 1 Composite disturbance σdk and composite disturbance estimate
| $ \left| {{\sigma _{dk}} - {{\hat \sigma }_{dk}}} \right| \le \sigma _{dk}^* $ | (18) |
Theorem 2 For the attitude control system of QTR, if the composite disturbance σdk satisfies the condition of Assumption 1, using the new type of nonsingular terminal sliding mode controller with ESO disturbance observer as shown in Eq.(15), the system state trajectory will reach a neighborhood Ωk of the sliding surface in a finite time, and
| $ \left\{ {\begin{array}{*{20}{l}} {\left| {{\mathit{\Omega }_k}} \right| \le \Delta = \min \left( {{\Delta _1},{\Delta _2}} \right)}\\ {{\Delta _1} = \frac{{\sigma _{dk}^*}}{{{\varepsilon _{k1}}\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)}}}\\ {{\Delta _2} = {{\left( {\frac{{\sigma _{dk}^*}}{{{\varepsilon _{k2}}\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)}}} \right)}^{n/m}}} \end{array}} \right. $ | (19) |
λk and
| $ \left\{ {\begin{array}{*{20}{l}} {\left| {{\lambda _k}} \right| \le {\Delta _{{\lambda _k}}}}\\ {\left| {{{\dot \lambda }_k}} \right| \le {\Delta _{{{\dot \lambda }_k}}}} \end{array}} \right. $ | (20) |
where,
| $ {\Delta _{{\lambda _k}}} = \min \left[ {{{\left( {\frac{{a\sigma _{dk}^*}}{{{\varepsilon _{k1}}}}} \right)}^{1/q}},{{\left( {\frac{{{a^{m/n}}\sigma _{dk}^*}}{{{\varepsilon _{k2}}}}} \right)}^{n/qm}}} \right] $ |
| $ {\Delta _{{{\dot \lambda }_k}}} = \min \left[ {{{\left( {\frac{{\beta \sigma _{dk}^*}}{{{\varepsilon _{k1}}}}} \right)}^{1/p}},{{\left( {\frac{{{\beta ^{m/n}}\sigma _{dk}^*}}{{{\varepsilon _{k2}}}}} \right)}^{n/pm}}} \right] $ |
Proof The selected Lyapunov function is
| $ {\mathit{\boldsymbol{V}}_k} = \frac{1}{2}\mathit{\boldsymbol{S}}_k^{\rm{T}}{\mathit{\boldsymbol{S}}_k} $ | (21) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_k} = {\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {h + p{{(\dot \lambda )}^{p - 1}}\ddot \lambda /\beta } \right) = \\ \;\;\;\;\;{\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {h + p{{(\dot \lambda )}^{p - 1}}\left( {{f_k}(x,t) + {g_k}{u_k} + {\sigma _{dk}}} \right)/\beta } \right) \end{array} $ | (22) |
where k=1, 2, 3.
The following formula can be obtained by substituting Eq.(17) into Eq.(22):
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_k} = {\mathit{\boldsymbol{S}}^{\rm{T}}}\frac{p}{\beta }{\left( {\mathit{{\dot \lambda }}} \right)^{p - 1}}\left\{ {\left( {{\sigma _{dk}} - {{\hat \sigma }_{dk}}} \right) - } \right.\\ \;\;\;\;\left[ {{\varepsilon _{k1}}{\rm{diag}}\left\{ {\left| {{s_k}} \right|} \right\}{\rm{sgn}}\left( {{s_k}} \right) + } \right.\\ \;\;\;\;\left. {{\varepsilon _{k2}}{\rm{diag}}\left\{ {{{\left| {{s_k}} \right|}^{m/n}}} \right\}{\rm{sgn}}\left( {{s_k}} \right)\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)} \right\} = \\ \;\;\;\; - \eta \left( {{\delta _{k1}}{{\left| {{s_k}} \right|}^2} + {\varepsilon _{k2}}{{\left| {{s_k}} \right|}^{1 + \frac{m}{n}}}} \right)\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right) = \\ \;\;\;\; - 2\eta \left( {{\delta _{k1}}{V_k} + {\varepsilon _{k2}}V_k^{(n + m)/2n}} \right)\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)\\ \;\;\;\;k = 1,2,3 \end{array} $ | (23) |
where,
| $ \eta = \frac{p}{\beta }{\left( {{{\dot \lambda }_k}} \right)^{p - 1}} $ |
| $ {\delta _{k1}} = \frac{{ - {s_k}\left( {{\sigma _{dk}} - {{\hat \sigma }_{dk}}} \right)}}{{\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right){{\left| {{s_k}} \right|}^2}}} + {\varepsilon _{k1}} $ |
| $ k = 1,2,3 $ |
when, δk1>0,
| $ \left| {{s_k}} \right| \le \frac{{\sigma _{dk}^*}}{{{\varepsilon _{k1}}\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)}} $ | (24) |
| $ {{\dot V}_k} = - \eta \left( {{\varepsilon _{k1}}{V_k} + {\delta _{k2}}V_k^{(n + m)/2n}} \right)\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right) $ | (25) |
where, k=1, 2, 3
| $ {\delta _{k2}} = \frac{{ - {s_k}\left( {{\sigma _{dk}} - {{\hat \sigma }_{dk}}} \right)}}{{\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right){{\left| {{s_k}} \right|}^{1 + m/n}}}} + {\varepsilon _{k2}},{\delta _{k2}} > 0 $ |
Using the same analysis method, we can obtain another description of the convergence domain:
| $ \left| {{s_k}} \right| \le {\left( {\frac{{\sigma _k^*}}{{{\varepsilon _{k2}}\left( {1 + \left| {{{\dot \lambda }_k}} \right|} \right)}}} \right)^{n/m}} $ | (26) |
It can be derived from Eqs. (24) and (26) that the region where the system state converges within a finite time is as described in Eq. (19).
When
| $ \begin{array}{l} {{\dot x}_{(2k)}}(t) = - \left[ {{\varepsilon _{k1}}{\rm{diag}}\left\{ {\left| {{s_k}} \right|} \right\}{\rm{sgn}}\left( {{s_k}} \right) + {\varepsilon _{k2}}{\rm{diag}}\left\{ {{{\left| {{s_k}} \right|}^{m/n}}} \right\}} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;{\rm{sgn}}\left( {{s_k}} \right)} \right] - \left( {{\sigma _{dk}} - {{\hat \sigma }_{dk}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{l}} { - \left( {{\delta _{k1}}\left| {{s_k}} \right| + {\varepsilon _{k2}}{{\left| {{s_k}} \right|}^{m/n}}} \right)}\\ { - \left( {{\varepsilon _{k1}}\left| {{s_k}} \right| + {\delta _{k2}}{{\left| {{s_k}} \right|}^{m/n}}} \right)} \end{array}} \right. \end{array} $ | (27) |
for the sliding surface sk outside the region Δ1, Δ2, there exists δk1, δk2>0, sk≠0, thus we can obtain
When the state of the system enters the |sk| ≤Δ region, there is the |τ| ≤Ωk
| $ \begin{array}{l} {\left( {1 + \left| {{\lambda _k}} \right|} \right)^p}{\ln ^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}{\rm{sgn}}\left( {{\lambda _k}} \right) + \\ \;\;\;\;\;\frac{1}{\alpha }{\left( {1 + \left| {{\lambda _k}} \right|} \right)^p}{\left[ {{{\ln }^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}} \right]^q}{\rm{sgn}}\left( {{\lambda _k}} \right) + \\ \;\;\;\;\;\frac{1}{\beta } {\rm{sig}} {\left( {{{\dot \lambda }_k}} \right)^p} = \tau \end{array} $ | (28) |
Eq. (28) can be converted to
| $ \begin{array}{l} {\left( {1 + \left| {{\lambda _k}} \right|} \right)^p}{\ln ^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}{\rm{sgn}}\left( {{\lambda _k}} \right) + \\ \;\;\;\;\;\frac{1}{\alpha }{\left( {1 + \left| {{\lambda _k}} \right|} \right)^p}{\left[ {{{\ln }^{\left( {1 + \left| {{\lambda _k}} \right|} \right)}}} \right]^q}{\rm{sgn}}\left( {{\lambda _k}} \right) + \left( {\frac{1}{\beta } - } \right.\\ \;\;\;\;\;\;\left. {\frac{\tau }{{ {\rm{sig}} {{\left( {{{\dot \lambda }_k}} \right)}^p}}}} \right) {\rm{sig}} {\left( {{{\dot \lambda }_k}} \right)^p} = 0 \end{array} $ | (29) |
When β-1-τsig(
The QTR's quality is 6.65 kg, the moment of inertia are
| $ {I_{xx}} = 4.782{\rm{kg}} \cdot {{\rm{m}}^2} $ |
| $ {I_{yy}} = 3.258{\rm{kg}} \cdot {{\rm{m}}^2} $ |
| $ {I_{zz}} = 2.837{\rm{kg}} \cdot {{\rm{m}}^2} $ |
The product of inertia is Ixz=0.032 kg·m2, the initial state is ϕ0=θ0=φ0=0°, the target instructions are φd=3°, θd=5°, ϕd=2°, the moment of inertia is applied to 12% uncertainty, assumptions from the beginning of the simulation, the attitude angle measurement exhibits a Gauss white noise with a magnitude of 0.05, and filters 50/(s+50) are used, the time-varying disturbance torque applied to the system is
| $ \Delta \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{l}} {3\sin (0.9t) + 6\cos (0.2t)}\\ {2\sin (0.3t) + 7\cos (0.6t)}\\ {6\sin (0.7t) + 2\cos (0.5t)} \end{array}} \right] $ |
In order to verify the validity of the method proposed in this paper, the following two control schemes are compared.
Control scheme 1 Applying the new logarithmic fast nonsingular terminal sliding mode (LFNTSM) controller proposed in this study, the reaching law uses a new fast reaching law with two order sliding mode characteristics.
Control scheme 2 Using the traditional fast nonsingular terminal sliding mode (FNTSM) controller, the reaching law is selected based on the traditional exponential reaching law, the corresponding control law is as follows:
| $ \begin{array}{l} {u_k} = - g_k^{ - 1}\left\{ {\frac{\beta }{p}{{\left( {{{\dot {\hat \lambda} }_k}} \right)}^{2 - p}}{\rm{sgn}}\left( {{{\dot {\hat \lambda} }_k}} \right)\left( {1 + \frac{q}{\alpha }{{\left| {{{\hat \lambda }_k}} \right|}^{q - 1}}} \right) + } \right.\\ \;\;\;\;\;\;\left. {{{\hat f}_k} - {{\ddot x}_{d(2k - 1)}} + {{\hat \sigma }_{dk}} + {\varepsilon _{k1}}{\rm{sgn}}\left( {{s_k}} \right) + {\varepsilon _{k2}}{s_k}} \right\} \end{array} $ |
In control schemes 1 and 2, the extended state disturbance observer is used to estimate and compensate the complex disturbances. For the two sliding mode control schemes, the selected controller parameters are as follows:
In control scheme 1:
| $ \begin{array}{*{20}{l}} {p = {\rm{diag}}\left[ {1.7,1.7,1.7} \right],q = {\rm{diag}}\left[ {3,3,3} \right]}\\ {\alpha = {\rm{diag}}\left[ {10,10,10} \right],\beta = {\rm{diag}}\left[ {40,40,40} \right]}\\ {{\varepsilon _{k1}} = {\rm{diag}}\left[ {0.6,0.6,0.6} \right],{\varepsilon _{k2}} = {\rm{diag}}\left[ {1.8,1.8,1.8} \right]}\\ {n = 4,m = 3} \end{array} $ |
In control scheme 2:
| $ \begin{array}{*{20}{l}} {p = {\rm{diag}}\left[ {1.7,1.7,1.7} \right],q = {\rm{diag}}\left[ {3,3,3} \right]}\\ {\alpha = {\rm{diag}}\left[ {10,10,10} \right],\beta = {\rm{diag}}\left[ {40,40,40} \right]}\\ {{\varepsilon _{k1}} = {\rm{diag}}\left[ {0.8,0.8,0.8} \right],{\varepsilon _{k2}} = {\rm{diag}}\left[ {2,2,2} \right]} \end{array} $ |
In the two control schemes, the extended state disturbance observer has the same parameter setting, ρk1=ρk2=ρk3=10, ξk=3.
7.2 Simulation Result AnalysisIt can be observed from Fig. 2 that although the disturbance estimation curve with the extended disturbance observer exhibits a brief oscillation at the initial stage, the time-varying complex disturbance is tracked in a short time and it coincides with the actual time-varying perturbation curve. Thus, on-line continuous disturbance compensation can be provided in the execution of the controller, the effect of the complex disturbance on the system is effectively suppressed, and the control accuracy and robustness of the two kinds of control methods are improved.
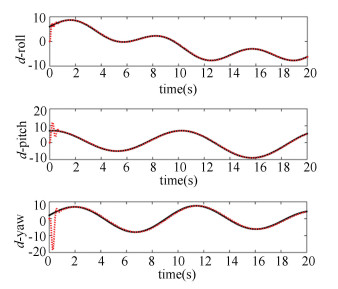
|
Fig.2 Disturbance and disturbance estimation of each channel in LFNTSM |
Fig. 3 is the attitude angle response curve of the QTR under two control schemes. It can be observed from the diagram that the control scheme 1 tracks the control instructions, and exhibits no overshoot, with steady state accuracy, and a fast convergence speed, control scheme 2 does not track the instructions satisfactorily, and the UAV attitude angle around the control command fluctuates and the steady-state performance is poor. This is because the logarithmic nonsingular terminal sliding mode presented in this study compared with the traditional fast non-singular terminal sliding surface, the convergence rate becomes faster and in the control scheme 1, a double power reaching law of variable coefficients with two order sliding mode characteristics is applied, which softens the motion trajectory of the controlled system.
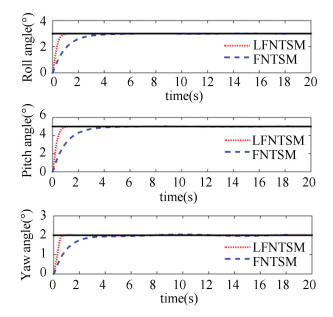
|
Fig.3 Attitude angle response curve |
As shown in Fig. 4, in the process of arrival of the system from the initial state to the sliding surface, the convergence rate of the sliding surface in control scheme 1 is higher than that in control scheme 2, reducing the movement time of the system in the approaching stage. When the state of system is far away from the sliding surface, the system state in control scheme 1 can move to the sliding surface rapidly. But, when the motion is close to the sliding surface, the approaching speed is significantly reduced and the smooth transition of sliding mode surface is realized; the chattering is also effectively reduced.
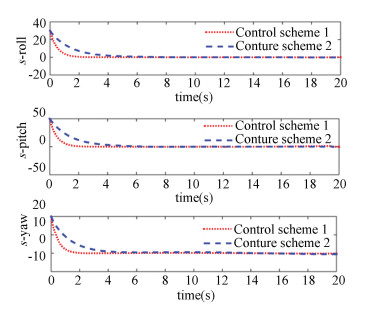
|
Fig.4 Changing curve of each channel sliding surface |
Fig. 5 shows a change in the curve of each channel control quantity using the control scheme 1, it can be observed from the graph that the curve of each channel control moment is smooth and chattering free. This is because the new fast reaching law used in the control scheme 1 possesses two order sliding mode characteristics, thus when the system enters the sliding mode, no tendency exists to leave the sliding surface, which effectively suppresses the chattering of the system. In summary, the control strategy proposed in this study exhibits satisfactory control effect, and achieves the design purpose.
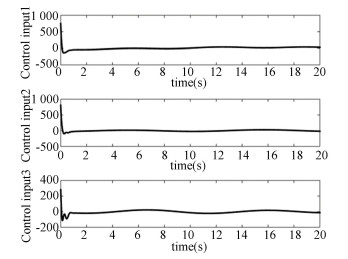
|
Fig.5 Changing curve of each channel control moment |
8 Conclusions
In this study, a new type of logarithmic fast non-singular terminal sliding mode surface is designed regarding the QTR attitude control problem, which significantly improves the convergence speed of the state of system, and a new fast reaching law with two order sliding mode characteristics is proposed, smooth and chattering free to increase the system convergence speed, the extended state observer is adopted to compensate the controller on-line, which effectively suppresses the effect of complex disturbance on the system. The simulation analysis indicates that the proposed method is effective and exhibits significant practical value.
| [1] |
Hwang S-J, Choi S-W. Ironbird ground test for tilt rotor unmanned aerial vehicle. International Journal of Aeronautical and Space Science, 2010, 11(4): 313-318. DOI:10.5139/IJASS.2010.11.4.313 (  0) 0) |
| [2] |
Barkai S M, Rand O, Peyran R J, et al. Modeling and analysis of tilt-rotor aeromechanical phenomena. Mathematical and Computer Modeling, 1998, 27(12): 17-43. DOI:10.1016/S0895-7177(98)00071-5 (  0) 0) |
| [3] |
Yoo Chang-Sun, Ryu Si-Dae, Park Bum-Jin, et al. Actuator controller based on fuzzy sliding mode control of tilt rotor unmanned aerial vehicle. International Journal of Control, Automation and Systems, 2014, 12(6): 1257-1265. DOI:10.1007/s12555-013-0009-9 (  0) 0) |
| [4] |
De Almeida M M, Raffo G V. Nonlinear control of a TiltRotor UAV for load transportation. IFAC-PapersOnLine, 2015, 48(19): 232-237. DOI:10.1016/j.ifacol.2015.12.039 (  0) 0) |
| [5] |
Liu Haibo, Wang Heping, Sheng Liding. Attitude control for vertical take off and landing mode of QTR based on fractional order sliding mode control. Systems Engineering and Electronics, 2017, 39(1): 156-161. DOI:10.3969/j.issn.1001-506X (  0) 0) |
| [6] |
Czyba R, Szafranski G, Rys A. Design and control of a single tilt tri-rotor aerial vehicle. Journal of Intelligent & Robotic Systems, 2016, 84(1-4): 53-66. DOI:10.1007/s10846-016-0353-0 (  0) 0) |
| [7] |
Chen C, Zhang J Y, Zhang D B. Control and flight test of a tilt-rotor unmanned aerial vehicle. International Journal of Advanced Robotic Systems, 2017, 14(1): 1-12. DOI:10.1177/1729881416678141 (  0) 0) |
| [8] |
Hartmann P, Meyer C, Moormann D. Unified velocity control and flight state transition of unmanned tilt-wing aircraft. Journal of Guidance, Control and Dynamics, 2017, 40(6): 1348-1360. DOI:10.2514/1.G002168 (  0) 0) |
| [9] |
Oosedo A, Abiko S, Narasaki S, et al. Large attitude change flight of a quad tilt rotor unmanned aerial vehicle. Advanced Robotics, 2016, 30(5): 326-337. DOI:10.1080/01691864.2015.1134344 (  0) 0) |
| [10] |
Yan Xufei, Chen Renliang. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 520865-1. DOI:10.7527/S1000-6893.2017.520865 (  0) 0) |
| [11] |
Panza S, Guastalla L, Roda B, et al. Tilt-rotor multivariable attitude control with rotor state feedback. IFAC-PapersOnLine, 2016, 49(17): 100-105. DOI:10.1016/j.ifacol.2016.09.018 (  0) 0) |
| [12] |
Wang Qi, Wu Wenhai. Robust controller initialization for switching flight control of tilt rotor. Transaction of Beijing Institute of Technology, 2015, 35(2): 176-179. DOI:10.15918/j.tbit1001-0645.2015.02.013 (  0) 0) |
| [13] |
Senkul A F, Altug E. System design of a novel tilt-roll rotor quadrotor UAV. Journal of Intelligent & Robotic Systems, 2016, 84(1-4): 575-599. DOI:10.1007/s10846-015-0301-4 (  0) 0) |
| [14] |
Zhang Q, Wu Q X, Jiang C S, et al. Robust reconfigurable tracking control of near space vehicle with actuator dynamic and input constraints. Control Theory & Applications, 2012, 29(10): 1263-1271. (  0) 0) |
| [15] |
Khatri A K, Singha N K, Sinha N K. Aircraft maneuver design using bifurcation analysis and sliding mode control techniques. Journal of Guidance, Control, and Dynamics, 2012, 35(5): 1435-1449. DOI:10.2514/1.56361 (  0) 0) |
| [16] |
Zak M. Terminal attractors in neural networks. Neural Networks, 1989, 2(4): 259-274. DOI:10.1016/0893-6080(89)90036-1 (  0) 0) |
| [17] |
Man Z H, Paplinski A P, Wu H R. A robust MIMO terminal sliding mode control scheme for rigid robot manipulators. Transaction on Automatic Control, 1994, 39(12): 2464-2469. DOI:10.1109/9.362847 (  0) 0) |
| [18] |
Man Z H, Yu X H. Terminal sliding mode control of MIMO linear systems. Transactions on Circuits and Systems Ⅰ: Fundamental Theory and Applications, 1997, 44(11): 1065-1070. DOI:10.1109/81.641769 (  0) 0) |
| [19] |
Wu Y, Yu H, Man Z H. Terminal sliding mode control design for uncertain dynamic systems. Systems and Control Letters, 1998, 34(5): 281-287. DOI:10.1016/S0167-6911(98)00036-X (  0) 0) |
| [20] |
Feng Yong, Yu Xinhuo, Man Zhihong. Non-singular terminal sliding mode control of rigid manipulators. Automatica, 2002, 38(12): 2159-2167. DOI:10.1016/S0005-1098(02)00147-4 (  0) 0) |
| [21] |
Park K B, Tsuiji T. Terminal sliding mode control of second-order nonlinear uncertain system. International Journal of Robust and Nonlinear Control, 1999, 9(11): 769-780. DOI:10.1002/(SICI)1099-1239(199909)9:11<769::AID-RNC435>3.0.CO;2-M (  0) 0) |
| [22] |
Lei Junwei, Wang Yue, Gu Wenjin. Synchronization control for unified chaos systems by using a kind of exponential Terminal huper-surface. Journal of Naval Aeronautical Engineering Institute, 2007, 22(3): 308-312. DOI:10.3969/j.issn.1673-1522.2007.03.003 (  0) 0) |
| [23] |
Xu Shixu, Ma Jianmin. Fast terminal sliding mode control of uncertain multivariable linear systems. Aerospace Shanghai, 2011, 28(2): 7-11. DOI:10.19328/j.cnki.1006-1630.2011.02.002 (  0) 0) |
| [24] |
Gao W B. Theory and Design Method for Variable Sliding Mode Control. Beijing: Science Press, 1996: 241-254.
(  0) 0) |
| [25] |
Zhang H X, Fan J S, Meng F, et al. A new double power reaching law for sliding mode control. Control and Decision, 2013, 28(2): 289-293. DOI:10.13195/j.cd.2013.02.132.zhanggx.028 (  0) 0) |
| [26] |
Tong K W, Zhang X, Zhang Y, et al. Sliding mode variable structure control of permanent magnet synchronous machine based on a novel reaching law. Proceedings of the CSEE, 2008, 28(21): 102-106. (  0) 0) |
| [27] |
Xi L P, Chen Z L, Zhang S H. Design of sliding mode control scheme based on improved idempotent trending law for robotic manipulators. Computer Measurement & Control, 2012, 20(2): 380-382. DOI:10.16526/j.cnki.11-4762/tp.2012.02.071 (  0) 0) |
| [28] |
Han J Q. Active Disturbance Rejection Control Technique—The Technique for Estimating and Compensating the Uncertainties. Beijing: National Defense Industry Press, 2008: 183-242.
(  0) 0) |
| [29] |
Yang L, Yang J Y. Nonsingular fast terminal sliding mode control for nonlinear dynamical systems. International Journal of Robust and Nonlinear Control, 2010, 21(16): 1865-1879. DOI:10.1002/rnc.1666 (  0) 0) |
| [30] |
Li H, Dou L H, Su Z. Adaptive nonsingular fast terminal sliding mode control for electromechanical actuator. International Journal of Systems Science, 2013, 44(3): 401-415. DOI:10.1080/00207721.2011.601348 (  0) 0) |
| [31] |
Abramowitz M, Stegun I A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. New York: Dover Publications, 1972. DOI:10.2307/1402037
(  0) 0) |
 2019, Vol. 26
2019, Vol. 26


