2. Department Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China
In recent decades, the fault estimation of sampled-data systems by the observer design method has received more and more attention[1-5]. However, for a well-known reason, if the sampling process is relatively slow, the stability and stabilization condition of the continuous-time observers may be lost which makes the fault estimation results unfeasible. In many practice, this unfeasibility cannot be solved. So, a new model by transforming the sampled-data systems into descriptor ones is proposed.
Descriptor systems, which can be also defined as the singular systems or differential-algebraic equation systems, are widely used to describe plenty of practical systems such as electrical networks[6], constrained mechanical systems[7], aircraft modeling[8] and so on. A lot of models have been established to guarantee the feasibility of the fault estimation in descriptor systems by the observer designing[9-11]. However, little existing work focuses on the fault estimation problem of sampled-data descriptor systems, and the observability of some descriptor systems in practical works may not be realized[12-14]. So there is a great incentive for us to develop a novel sampled-data descriptor observer for the estimation of system faults, and furthermore to improve the detectability of the designed system.
Recently, a novel design method of observation is proposed in Ref.[15] to investigate sensor fault reconstruction and sensor compensation for discrete-time systems. Based on the results in Ref.[15], a new approach of sensor fault estimation for sampled-data systems is considered. The sampled-data systems are firstly discretized to obtain a discrete-time model. Then a fault estimation model is established by designing a discrete-time observer of the discretized descriptor system, the necessary and sufficient condition for the existence and convergence of the proposed observer is given and proved. In the paper, many results have been proposed to design observers for discrete-time systems by using the linear matrix inequality (LMI) techniques, so the observer design is formulated as an LMI feasible problem, which can be easily solved by standard convex optimization algorithms[16].
Autonomous land vehicle control system is a class of norm bounded parameter uncertainty of generalized continuous piecewise affine systems[17].In view of the lack of an autonomous land vehicle system in previous switching control strategies and system delays, the case of unknown external interference and noise on the adverse effects of the performance of the control system, a method with a linear matrix inequality LMI algorithm in the papercan be put forward[18-20].Then discussion is needed for the detectability of descriptor system since a pair of parameters T and N are introduced[21-23].
This paper is organized as follows. In Section 2, a model of the sampled-data system is proposed to be studied, and then we discretize the system into a descriptor one by an efficient way. In Section 3, sensor fault estimation observer is presented for the evaluated discrete-time linear descriptor systems which is presented and formulated as an LMI formulation. The detectability of the designed observer is discussed. In Section 4, two simulation examples are given to demonstrate the validity of our results. Finally, several conclusions are drawn in Section 5.
2 Problem StatementConsider the following sampled-data system:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_c}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{B}}_c}\mathit{\boldsymbol{u}}\left( t \right) + {\mathit{\boldsymbol{D}}_c}\mathit{\boldsymbol{d}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( {k{T_s}} \right) = \mathit{\boldsymbol{Cx}}\left( {k{T_s}} \right) + \mathit{\boldsymbol{Ffx}}\left( {k{T_s}} \right)} \end{array}} \right. $ | (1) |
where x(t)∈
Additional remark: At first, the following system representation is considered:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_c}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{B}}_c}\mathit{\boldsymbol{u}}\left( t \right) + {\mathit{\boldsymbol{D}}_c}\mathit{\boldsymbol{d}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( {k{T_s}} \right) = \mathit{\boldsymbol{Cx}}\left( {k{T_s}} \right) + \mathit{\boldsymbol{Ffx}}\left( {k{T_s}} \right)} \end{array}} \right. $ |
In this situation, the following descriptor system will be obtained:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{E\bar x}}(k + 1) = \mathit{\boldsymbol{\bar A\bar x}}(k) + \mathit{\boldsymbol{\bar B}}{\boldsymbol{u}}(k) + \mathit{\boldsymbol{\bar Dd}}(k)}\\ {\mathit{\boldsymbol{y}}(k) = \mathit{\boldsymbol{\bar C\bar x}}(k)} \end{array}} \right. $ |
where:
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}&0\\ 0&0 \end{array}} \right],\mathit{\boldsymbol{\bar A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ 0&0 \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\bar B}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{B}}\\ 0 \end{array}} \right],\mathit{\boldsymbol{\bar D}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{D}}\\ 0 \end{array}} \right],\mathit{\boldsymbol{\bar C}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{C}}&{{\mathit{\boldsymbol{I}}_m}} \end{array}} \right] $ |
To obtain TE + NC = In+m, we must choose:
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}&0\\ { - \mathit{\boldsymbol{C}}}&{{\mathit{\boldsymbol{I}}_m}} \end{array}} \right],\mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{I}}_m}} \end{array}} \right] $ |
Unfortunately, this may lead to the loss of observability. It can be seen that
In many practical systems,
Denoting x(k) = x(kTs), u(k) = u(kTs), and y(k) = y(kTs), the discretized representation of System(1) can be derived as:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{Bu}}\left( k \right) + \mathit{\boldsymbol{Dd}}\left( k \right) + \mathit{\boldsymbol{O}}\left( {\mathit{\boldsymbol{T}}_s^2} \right)}\\ {\mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right)} \end{array}} \right. $ | (2) |
where:
| $ \mathit{\boldsymbol{A}} = {e^{{A_c}\tau }} $ |
| $ \mathit{\boldsymbol{B}} = \int_0^T {{e^{{A_c}\tau }}{\mathit{\boldsymbol{B}}_c}{\rm{d}}\tau } $ |
| $ \mathit{\boldsymbol{D}} = \int_0^T {{e^{{A_c}\tau }}{\mathit{\boldsymbol{D}}_c}{\rm{d}}\tau } $ |
In this paper, the sampling interval Ts assumed to be sufficiently small such that the term in the order of O(Ts2) can be omitted.
However, if we consider the System (2), the pair (
So, we have to combine the descriptor system approach to the dedicated observer scheme, as used in Professor Wu's paper (IEEE Transactions on Fuzzy Systems) 2015[16].
The following Lemma [17] is needed.
Lemma 1 Given a scalar γ>0, the discrete-time system described by:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{Bu}}\left( k \right)}\\ {\mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right)} \end{array}} \right. $ | (3) |
Which is stable and its transfer function Hyu(z) = C(zI-A)-1B,
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}} - \mathit{\boldsymbol{P}}}&{{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PB}}}\\ {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PA}}}&{{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} - {\gamma ^2}\mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (4) |
In this section, a descriptor system is firstly constructed for System(6). Then, an observer is designed to simultaneously estimate the state x(k) and the sensor fault f(k).
Defining:
| $ \mathit{\boldsymbol{\bar x}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( k \right)}\\ {\mathit{\boldsymbol{f}}\left( k \right)} \end{array}} \right] $ | (5) |
Then the System (2) is rewritten as the following descriptor system:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{E\bar x}}(k + 1) = \mathit{\boldsymbol{\bar A\bar x}}(k) + \mathit{\boldsymbol{\bar B}}{\boldsymbol{u}}(k) + \mathit{\boldsymbol{\bar Dd}}(k)}\\ {\mathit{\boldsymbol{y}}(k) = \mathit{\boldsymbol{\bar C\bar x}}(k)} \end{array}} \right. $ | (6) |
where:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}&0\\ 0&0 \end{array}} \right],\mathit{\boldsymbol{\bar A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ 0&0 \end{array}} \right]}\\ {\mathit{\boldsymbol{\bar B}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{B}}\\ 0 \end{array}} \right],\mathit{\boldsymbol{\bar D}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{D}}\\ 0 \end{array}} \right],\mathit{\boldsymbol{\bar C}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{C}}&\mathit{\boldsymbol{F}} \end{array}} \right]} \end{array} $ | (7) |
For the descriptor System(6), the following observer is constructed:
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\bar x}}}\left( {k + 1} \right) = \mathit{\boldsymbol{T\bar A\hat {\bar x}}}(k) + \mathit{\boldsymbol{T\bar Bu}}(k) + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{L}}(\mathit{\boldsymbol{y}}(k) - \mathit{\boldsymbol{\bar C\hat {\bar x}}}(k)) + \mathit{\boldsymbol{Ny}}(k + 1) \end{array} $ | (8) |
where
Suppose that matrices T and N are chosen such that:
| $ \mathit{\boldsymbol{TE}} + \mathit{\boldsymbol{NC}} = {\mathit{\boldsymbol{I}}_{n + m}} $ | (9) |
where the matrix
Based on Lemma 1, the following Theorem is proposed to synthesize a robust sensor fault estimation observer.
Theorem 1 Given a scalar γ>0, the dynamic System (8) is a robust sensor fault estimation observer with
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{P}} > 0\\ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{P}}}&{{{\left( {\mathit{\boldsymbol{T\bar A}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{W}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{T\bar A}}} \right) - \mathit{\boldsymbol{W\bar C}}}&{ - \mathit{\boldsymbol{P}}} \end{array}} \right] < 0 \end{array} \right. $ | (10) |
and the gain matrix L in observer (8) is determined by L = P-1W.
Proof Using Eq. (9), the descriptor System (6) is written as:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar x}}\left( {k + 1} \right) = \mathit{\boldsymbol{T\bar A\bar x}}\left( k \right) + \mathit{\boldsymbol{T\bar Bu}}\left( k \right) + }\\ {\mathit{\boldsymbol{\bar Dd}}(k) + \mathit{\boldsymbol{Ny}}(k + 1)} \end{array} $ | (11) |
The augmented state estimation error is defined as:
| $ \mathit{\boldsymbol{e}}(k) = \mathit{\boldsymbol{x}}(k) - \mathit{\boldsymbol{\hat x}}(k) $ | (12) |
Subtracting Eq. (8) from Eq.(11), the error dynamic equation is obtained as:
| $ \mathit{\boldsymbol{e}}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{T\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)\mathit{\boldsymbol{e}}\left( k \right) + \mathit{\boldsymbol{\bar Dd}}\left( k \right) $ | (13) |
Applying Lemma 1 to Eq.(13), we obtain that
| $ \left[ {\begin{array}{*{20}{c}} {\Delta + {\mathit{\boldsymbol{I}}_n} - \mathit{\boldsymbol{P}}}&{{{(\mathit{\boldsymbol{T\bar A}} - \mathit{\boldsymbol{L\bar C}})}^{\rm{T}}}\mathit{\boldsymbol{PT\bar D}}}\\ *&{{{(\mathit{\boldsymbol{T\bar D}})}^{\rm{T}}}\mathit{\boldsymbol{PT\bar D}} - {\gamma ^2}{\mathit{\boldsymbol{I}}_q}} \end{array}} \right] < 0 $ | (14) |
where
By the well-known Schur complement Lemma in Ref. [22], Inequality (14) is equivalent to:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{P}} > 0\\ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{I}}_n}}&0&{{{\left( {\mathit{\boldsymbol{T\bar A}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{P}}}\\ * &{ - {\gamma ^2}{\mathit{\boldsymbol{I}}_q}}&{{{\left( {\mathit{\boldsymbol{T\bar D}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}}\\ * & * &{ - \mathit{\boldsymbol{P}}} \end{array}} \right] < 0 \end{array} \right. $ | (15) |
Letting W=PL, Eq.(15) comes to Eq.(10). Then the gain matrix L is determined by L=P-1W.
From Eq. (13), it is known that there exists a stable sensor fault estimation observer if the pair
For the convenience of discussion, the definition of detectability for the descriptor systems is introduced in Ref.[1].
Definition 1 The descriptor System (6) is called R-detectable, if the following condition holds:
| $ {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {z\mathit{\boldsymbol{E}} - \mathit{\boldsymbol{\bar A}}} \\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = n + m,\forall z \in \mathbb{C},\left| z \right| \geqslant 1 $ | (16) |
To discuss the detectability of the (TA C), the following Theorem is presented.
Theorem 2 The pair
Proof It is obvious that:
| $ {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {z{\mathit{\boldsymbol{I}}_{n + m}} - \mathit{\boldsymbol{T\bar A}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}}{\mathit{\boldsymbol{I}}_{n + m}} - \mathit{\boldsymbol{T\bar A}}}\\ {z\mathit{\boldsymbol{\bar C}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] $ | (17) |
Using Eq. (9), we obtain:
| $ \begin{array}{l} {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}}{\mathit{\boldsymbol{I}}_{n + m}} - \mathit{\boldsymbol{T\bar A}}}\\ {\mathit{\boldsymbol{z\bar C}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = \\ \;\;\;\;\;\;\;{\rm{rank}}\left( {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{T}}&\mathit{\boldsymbol{N}}&0\\ 0&{{\mathit{\boldsymbol{I}}_m}}&0\\ 0&0&{{\mathit{\boldsymbol{I}}_m}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{zE}} - \mathit{\boldsymbol{\bar A}}}\\ {z\mathit{\boldsymbol{\bar C}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right]} \right) \end{array} $ | (18) |
Since T is of full rank, we have:
| $ {\rm{rank}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{T}}&\mathit{\boldsymbol{N}}&0\\ 0&{{\mathit{\boldsymbol{I}}_m}}&0\\ 0&0&{{\mathit{\boldsymbol{I}}_m}} \end{array}} \right] = n + 3m $ | (19) |
Applying Sylvester's equality to Eq. (18) gives:
| $ \begin{array}{l} {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}}{\mathit{\boldsymbol{I}}_{n + m}} - \mathit{\boldsymbol{T\bar A}}}\\ {\mathit{\boldsymbol{z\bar C}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = \\ \;\;{\rm{ }}\;\;\;\;\;{\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{zE}} - \mathit{\boldsymbol{\bar A}}}\\ {\mathit{\boldsymbol{z\bar C}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{zE}} - \mathit{\boldsymbol{\bar A}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] \end{array} $ | (20) |
Considering Eq. (17) and Eq.(20), it becomes:
| $ {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {z{\mathit{\boldsymbol{I}}_{n + m}} - \mathit{\boldsymbol{T\bar A}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{zE}} - \mathit{\boldsymbol{\bar A}}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] $ | (21) |
If the descriptor system (6) is R-detectable, we have:
| $ \begin{array}{*{20}{c}} {{\rm{rank}}\left[ {\begin{array}{*{20}{c}} {z{\mathit{\boldsymbol{I}}_{n + m}} - \mathit{\boldsymbol{T\bar A}}} \\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{zE}} - \mathit{\boldsymbol{\bar A}}} \\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = } \\ {n + m,\forall \mathit{\boldsymbol{z}} \in \mathbb{C},\left| \mathit{\boldsymbol{z}} \right| \geqslant 1} \end{array} $ | (22) |
which means that the pair
Since rank
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{T}}&\mathit{\boldsymbol{N}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]^{\rm{T}}} + \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{I}}_{n + m}} - \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]}^{\rm{T}}}} \right) $ | (23) |
where
In this section, a simulation example is given to show the effectiveness of the proposed method.
Firstly, a fault estimation observer for Sensor 1 is designed.
Case 1 Consider the following sampled-data system in the form of System(1) with the following parameters:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{l}} 0&1&0&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}} 1\\ 0 \end{array}} \right] $ |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {0.1}\\ 1\\ 0\\ {0.1} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 0.277}&0&{ - 32.9}&{9.81}\\ { - 0.1033}&{ - 8.525}&{3.75}&0\\ {0.3649}&0&{ - 0.639}&0\\ 0&1&0&0 \end{array}} \right] $ |
with the sampling interval Ts=0.1 s, Choosing:
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&0&0&0&{ - 1}&0\\ 1&{ - 1}&0&1&0&0&{ - 1}\\ 0&{ - 1}&0&1&0&0&{ - 1}\\ 0&0&{ - 1}&{ - 1}&{ - 1}&{ - 1}&{ - 1}\\ 0&{ - 1}&0&0&{ - 1}&{ - 1}&{ - 1} \end{array}} \right] $ |
We obtain:
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&1&0&{ - 0.5}&1\\ 0&0&1&1&0\\ 0&0&0&{0.5}&{ - 1}\\ 0&{ - 1}&0&{0.5}&{ - 1} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{r}} 0&0\\ 0&{0.5}\\ 0&{ - 1}\\ 0&{0.5}\\ 1&{ - 0.5} \end{array}} \right] $ |
It is obvious that T is of full rank. Then, by letting γ=0.4 and applying Theorem 1, it comes:
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {0.0002}&{1.2671}\\ {0.4567}&{9.2066}\\ {0.0048}&{4.3691}\\ {0.0024}&{1.2483}\\ { - 0.4567}&{ - 9.2066} \end{array}} \right] $ |
The disturbance d(t) is chosen as random noise with d(t)~N(0, 1). The following sensor fault (of Sensor 1) is considered:
| $ \mathit{\boldsymbol{f}}\left( k \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{k < 100}\\ {1\sin \left( {0.1k} \right),}&{k \ge 100} \end{array}} \right. $ |
The fault estimation result is shown in Fig. 1.
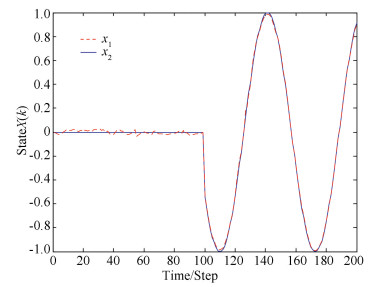
|
Fig.1 The fault estimation result in Case 1 |
Then, a fault estimation observer for Sensor 2 is designed.
Case 2 Consider the following sampled-data system in the form of System (1) with the following parameters.
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 0.277}&0&{ - 32.9}&{9.81}\\ { - 0.1033}&{ - 8.525}&{3.75}&0\\ {0.3649}&0&{ - 0.639}&0\\ 0&1&0&0 \end{array}} \right] $ |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {0.1}\\ 1\\ 0\\ {0.1} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{l}} 0&1&0&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}} 0\\ 1 \end{array}} \right] $ |
Choosing:
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{r}} { - 1}&0&0&0&0&{ - 1}&0\\ 1&{ - 1}&0&1&0&0&{ - 1}\\ 0&{ - 1}&0&1&0&0&{ - 1}\\ 0&0&{ - 1}&{ - 1}&{ - 1}&{ - 1}&{ - 1}\\ 0&{ - 1}&0&0&{ - 1}&{ - 1}&{ - 1} \end{array}} \right] $ |
We obtain:
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{r}} 1&{0.5}&0&0&0\\ 0&{0.5}&0&0&1\\ 0&{ - 0.5}&1&0&0\\ 0&{0.5}&0&1&{ - 1}\\ 0&0&0&{ - 1}&{ - 1} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{r}} { - 0.5}&0\\ {0.5}&0\\ {0.5}&0\\ { - 0.5}&0\\ 0&1 \end{array}} \right] $ |
Let γ=0.4 and apply Theorem 1, it comes:
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{r}} {1.5732}&{0.6053}\\ {0.4878}&{0.0143}\\ { - 1.1456}&{ - 0.3431}\\ {0.9857}&{0.7585}\\ { - 0.4979}&{ - 0.7441} \end{array}} \right] $ |
The disturbance d(t) is chosen as random noise with d(t)~N(0, 1). The following sensor fault (of Sensor 2) is considered.
| $ \mathit{\boldsymbol{f}}(k) = \left\{ {\begin{array}{*{20}{c}} {0,}&{k < 100}\\ {0.5,}&{k \ge 100} \end{array}} \right. $ |
The fault estimation result is shown in Fig. 2.
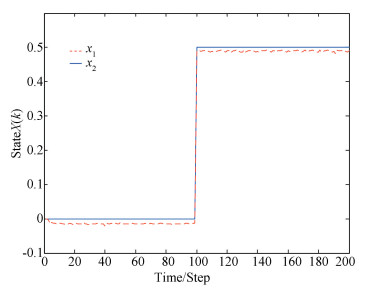
|
Fig.2 The fault estimation result in Case 2 |
Case 3 Finally, we consider a practical example of the tunnel diode circuit, in order to confirm the analysis and synthesis measures established in the priorsections[23]. In the tunnel diode circuit system, x1 (k), x2(k), x3(k) can be described by the following Table 1.
| Table 1 The significance of state variable xi(k) |
The practical example can be abstracted as a system which is given by the prior dynamics system(1). y(k)= Cix(k), i=1, 2.The data we used is given in Ref.[23]. Now, we also need some more data:
| $ {\mathit{\boldsymbol{D}}_{11}} = \left[ {\begin{array}{*{20}{l}} {0.3}\\ {0.5}\\ {0.6} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{D}}_{21}} = \left[ {\begin{array}{*{20}{c}} {1.1}\\ {2.1}\\ {1.7} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{D}}_{22}} = 1.5,{\mathit{\boldsymbol{D}}_{12}} = 0.6 $ |
The other parameters are obtained by Case 2. Let γ=0.9 and apply Theorem 1, it comes:
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{r}} {5.5342}&{0.5435}\\ {0.9878}&{0.9843}\\ { - 0.1876}&{ - 12.2151}\\ {0.3257}&{0.6544}\\ { - 5.4349}&{ - 6.7331} \end{array}} \right] $ |
The disturbance d(t) is chosen as random noise with d(t)~N(0, 1). The following sensor fault (of Sensor 2) is considered.
| $ \mathit{\boldsymbol{f}}\left( k \right) = \left\{ {\begin{array}{*{20}{l}} {0.7,}&{k < 100}\\ {1\cos (0.1k),}&{k \ge 100} \end{array}} \right. $ |
The fault estimation method for sampled-data systems with sensor faults is addressed in this paper, based on designing observers for discrete-time descriptor systems, and a novel approach of sensor fault estimation for sampled-data systems is presented. The paper has established the necessary and sufficient conditions for the convergence of the proposed observer for the discretized discrete-time descriptor systems, and expressed it in a linear matrix inequalities formulation [LMI], and the detectability of the designed system is proved as well. Then two simulation examples are used to demonstrate the effectiveness of the design procedure which can be implemented.
| [1] |
Zhang Yu, Feng Gang, Sun Jitao. Stability of impulsive piecewise linear systems. International Journal of Systems Science, 2013, 44(1): 139-150. DOI:10.1080/00207721.2011.598957 (  0) 0) |
| [2] |
Kazantzis N, Kravaris C. Nonlinear observer design using Lyapunov's auxiliary theorem.Proceedings of the 36th IEEE Conference on Decision and Control, 1997. Piscataway: IEEE, 1997.4802-4807. DOI: 10.1109/CDC.1997.649779.
(  0) 0) |
| [3] |
Bemporad A, Ferrari-Trecate G, Morari M. Observability controllability of piecewise affine hybrid systems. Proceedings of the 38th IEEE Conference onDecision and Control. Piscataway: IEEE, 1999.3966-3971. DOI: 10.1109/CDC.1999.827980.
(  0) 0) |
| [4] |
Ferrari-Trecate G, Cuzzola F A, Mignone D, et al. Analysis of discrete-time piecewise affine and hybrid systems. Automatica, 2002, 38(12): 2139-2146. DOI:10.1016/S0005-1098(02)00142-5 (  0) 0) |
| [5] |
Rajamani R. Observers for Lipschitz nonlinear systems. IEEE Transactions on Automatic Control, 1998, 43(3): 397-401. DOI:10.1109/9.661604 (  0) 0) |
| [6] |
Blondel V D, Tsitsiklis J N. Complexity of stability and controllability of elementary hybrid systems. Automatica, 1999, 35(3): 479-489. DOI:10.1016/S0005-1098(98)00175-7 (  0) 0) |
| [7] |
Dueker K J, Butler J A. A geographic information system framework for transportation data sharing. Transportation Research Part C:Emerging Technologies, 2000, 8(1-6): 13-36. DOI:10.1016/S0968-090X(00)00006-1 (  0) 0) |
| [8] |
Barbosa K A, de Souza C E, Trofino A. Robust H2 filtering for discrete-timeuncertain linear systems using parameter-dependent Lyapunov functions. Proceedings of the American Control Conference.Piscataway: IEEE, 2002, 4: 3224-3229. DOI: 10.1109/ACC.2002.1025287.
(  0) 0) |
| [9] |
Koenig D, Mammar S. Design of proportional-integral observer for unknown input descriptor systems. IEEE Transactions on Automatic Control, 2002, 47: 2057-2062. DOI:10.1109/TAC.2002.805675 (  0) 0) |
| [10] |
Koenig D. Observer design for unknown input nonlinear descriptor systems via convex optimization. IEEE Transactions on Automatic Control, 2006, 51(6): 1047-1052. DOI:10.1109/TAC.2006.876807 (  0) 0) |
| [11] |
Cao Yong-Yan, Lin Zongli. A descriptor system approach to robust stability analysis and controller synthesis. IEEE Transactions on Automatic Control, 2004, 49(11): 2081-2084. DOI:10.1109/TAC.2004.837749 (  0) 0) |
| [12] |
Geromel J C, de Oliveira M C, Bernussou J. Robust filtering of discrete-timelinear systems with parameter dependent Lyapunov functions. SIAM Journal on Control and Optimization, 2003, 41(3): 700-711. DOI:10.1137/S0363012999366308 (  0) 0) |
| [13] |
Leite V J S, Peres P L D. An improved LMI condition for robust D-stability of uncertain polytopic systems. IEEE Transactions on Automatic Control, 2003, 48(3): 500-504. DOI:10.1109/TAC.2003.809167 (  0) 0) |
| [14] |
Zemouche A, Boutayeb M. Observer design for Lipschitz nonlinear systems: The discrete-time case. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2006, 53(8): 777-781. DOI:10.1109/TCSⅡ.2006.876465 (  0) 0) |
| [15] |
Shaked U. Improved LMI representations for the analysis and the design of continuous-time systems with polytopic type uncertainty. IEEE Transaction and Automatic Control, 2001, 46(4): 652-656. DOI:10.1109/9.917671 (  0) 0) |
| [16] |
Wu Zheng-Guang, Shi Peng, Su Hongye, et al. Dissipativity-based sampled-data fuzzy control design and its application to truck-trailer system. IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1669-1679. DOI:10.1109/TFUZZ.2014.2374192 (  0) 0) |
| [17] |
Wu Zheng-Guang, Shi Peng, Su Hongye, et al. Local synchronization of chaotic neural networks with sampled-data and saturating actuators. IEEE Transactions on Cybernetics, 2014, 44(12): 2635-2645. DOI:10.1109/TCYB.2014.2312004 (  0) 0) |
| [18] |
Wu Zheng-Guang, Shi Peng, Su Hongye, et al. Exponential stabilization for sampled-data neural-network-based control systems. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(12): 2180-2190. DOI:10.1109/TNNLS.2014.2306202 (  0) 0) |
| [19] |
Wu Zheng-Guang, Shi Peng, Su Hongye, et al. Sampled-data fuzzy control of chaotic systems based on T-S fuzzy model. IEEE Transactions on Fuzzy Systems, 2014, 22(1): 153-163. DOI:10.1109/TFUZZ.2013.2249520 (  0) 0) |
| [20] |
Wu Zheng-Guang, Shi Peng, Su Hongye, et al. Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled-data. IEEE Transactions on Cybernetics, 2013, 43(6): 1796-1806. DOI:10.1109/TSMCB.2012.2230441 (  0) 0) |
| [21] |
Qiu Jianbin, Feng Gang, Gao Huijun. Approaches to robust H∞ static output feedback control of discrete-time piecewise-affine systems with norm-bounded uncertainties. International Journal of Robust and Nonlinear Control, 2011, 21(7): 790-814. DOI:10.1002/rnc.1627 (  0) 0) |
| [22] |
Boyd S, El Ghaoui L, Feron E, et al. Linear Matrix Inequality in Systems and Control Theory. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM), 1994.
(  0) 0) |
| [23] |
Wang Mao, Wei Yanling, Qiu Jianbin. Static output feedback control of discrete-time piecewise affine singular systems. Journal of Harbin Institute of Technology, 2013, 45(3): 14-21. (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


