Porous tubes have been employed in many areas, such as petrochemicals, agriculture irrigation, water supply, and drainage[1-2]. The uniformity of fluid distribution is an important indicator of engineering quality[3-4], which is used to determine the pressure head and the length in many irrigation systems, and the design requirements of uniformity should be achieved to ensure quality and efficiency. In actual engineering systems, uniformity can be affected by many factors, including working pressure changes of emitter, manufacturing deviation of emitter, congestion, water temperature changes, and micro topography changes[5-10]. To date, some results for calculating flow uniformity have been achieved by domestic scholars. Examples for the method of hydraulics design, as studied by Kang[11], is in accordance with both average flow rate and emitter uniformity[11-12]. The methods for calculating comprehensive flow and ultimate flow deviation rates were proposed based on the analysis of the existing rates of hydraulic deviation and flow deviation[3, 6-9]. Scaloppi and Allen[13] applied a differential approach to multiple outlet pipes with constant and continuously variable outflows and simulated the pressure distributions along uniform sprinkle systems, trickle irrigation laterals, manifolds, and gated pipes, considering the effect of ground slope and velocity head on the pipeline hydraulics. Hathoot et al.[14-15] investigated the problem of a lateral pipe with equally spaced emitters and a uniform slope, and estimated the head loss between emitters using the Darcy-Weisbach formula with variation in the Reynolds number, different zones on the Moody diagram, and a friction coefficient formula corresponding to each zone. Many results were achieved by predecessors scholars, but few have studied the interaction relation between flow uniformity and laying length, pressure head, laying slope, as well as perforation spacing[16-21], which has effects on practical engineering applications.
Another problem with the momentum method is that it ignores the influence of the slope on the flow in the process of establishing a variable mass momentum equation, which is only regarded as a horizontal slope. According to mechanics, the momentum method only considers the influence of hydrodynamic pressure, friction, and momentum changes on the flow, but neglects the effect of gravity. For most perforated pipes used in micro-irrigation, slope is not horizontal and gravity might have a significant influence on the flow. Therefore, gravity should be introduced into the momentum equation of the variable mass to investigate the influence of the slope.
Flow uniformity in porous tubes is significantly affected by the hole system. Gravitational pressure and forced pressure have different effects on the porous tubes distribution systems. Being the primary problem of flow uniformity, free porous flow relies on gravity and can be affected by many factors, so it is necessary to be further studied. This paper analyzes the flow uniformity in porous tubes, which is affected by laying length, pressure head, laying slope, and perforation spacing. The results of this study are helpful to improve the flow uniformity of porous tubes, reduce investment, and guide the construction and operation of porous tubes. The objectives are to develop a momentum equation of variable mass flow using the momentum conservation method under the condition of a certain slope, as well as solve the flow deviation rate and the deviation rate of working head.
2 Expression of the Flow Deviation RateWhile designing water distribution projects, engineers only consider the influence of flow uniformity affected by the manufacturing deviation of the emitter and the hydraulic friction loss. Of the two factors, manufacturing deviation is determined by the production technology level, and if it is high, flow uniformity is low, despite of hydraulic friction loss. Although manufacturers have improved the level of technology and produced emitters with smaller manufacturing deviations, the flow uniformity of the system remains poor without a reasonable hydraulic design. In the present study, manufacturing deviation was ignored and the factors of hydraulic design were considered to analyze data. The flow uniformity can be expressed in many ways, and the following computational formula[22] was adopted in this study:
1) The flow deviation rate:
| $ {q_{\rm{v}}} = \frac{{{q_{{\rm{max}}}} - {q_{{\rm{min}}}}}}{{{q_{\rm{a}}}}} \times 100\% $ | (1) |
where qv represents the flow deviation rate of emitter; qmax (L/h) represents the maximum flow of emitter; qmin (L/h) represents the minimum flow of emitter; and qa (L/h) represents the flow of design.
When the flow index is 0.5, the flow formula of the pipe hole of porous tubes[8] is
| $ {q_i} = {k_p}\sqrt h $ | (2) |
where qi (L/h) represents the flow of perforation; h (m) represents the working pressure head of perforation; and kp represents the coefficient.
If the flow of pipe hole is regarded as the design flow, the formula can be expressed as
| $ {q_{\rm{a}}} = {k_p}\sqrt {\bar h} $ | (3) |
where qa (L/h) represents the flow of design, and h (m) represents the average pressure head.
Combining with the formulas in Eqs.(1)-(3), the following formula is obtained:
| $ {q_{\rm{v}}} = \frac{{\sqrt {{h_{\max }}} - \sqrt {{h_{\min }}} }}{{\sqrt {\bar h} }}100\% $ | (4) |
where hmax (m) represents the maximum of working head, and hmin (m) represents the minimum of working head.
2) Deviation rate of the working head.
In irrigation systems, the pressure head varies according to the position of the emitter, thus causing a change in flow, which leads to flow deviation. The difference between the working pressure and the design of the pressure heads is called head deviation. The difference between the maximum and the minimum deviations in the entire system to the design pressure head is the deviation rate of the working head. Therefore, it can be written as
| $ {h_{\rm{v}}} = \frac{{\Delta {h_{\max }} - \Delta {h_{\min }}}}{{{h_{\rm{a}}}}} = \frac{{{h_{\max }} - {h_{\min }}}}{{{h_{\rm{a}}}}} $ | (5) |
where ha (m) represents the design of working head; Δhmax (m) represents the maximum of head deviation; and Δhmin (m) represents the minimum of head deviation.
In light of previous research results, the formula of the relationship between the deviation of working head and the flow deviation rate is obtained by using the binomial expansion method[23]
| $ {q_{\rm{v}}} = k{h_{\rm{v}}} $ | (6) |
where k represents the state index of emitter.
3 Analysis of the Deviation Rate in the Working HeadSince mass decreases along the flow in the porous tube flow or the embranchment flow, it is characterized as variable mass flow. Pressure distribution is affected by momentum exchange, head loss, and slope. The velocity of the flow decreases with changes in mass because of the holes in the sidewall, so the momentum changes along the flow and a certain amount of kinetic energy is converted into the pressure head, which causes the pressure to increase along the flow. Friction produces pressure losses that lead to the decrease of the pressure, and at the same time, the flow might result in rough waves at the outlet of the hole, which can increase energy losses. The head change induced by the slope of the pipe has a significant effect on the pressure distribution. Therefore, it is necessary to simultaneously take these influence factors into consideration if the pressure change is maintained in a certain range.
Fig. 1 shows the schematic of the pipeline with multiple outlets. It can be observed that the perforated tube is closed at the end of one side and the cross-sectional area is the same along the flow, which has one row of radial holes. In practical engineering, factors such as laying length, laying slope, pressure head, and perforation spacing simultaneously exert effects, which influence the deviation rate of the working head of the system concurrently. The average pressure head should be considered as the design pressure head during the design process to make the average pressure consistent with the design pressure.
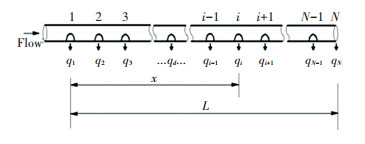
|
Fig.1 Schematic of pipeline with multiple holes |
Then, Eq.(5) can be rewritten as
| $ {h_{\rm{v}}} = \frac{{{h_{\max }} - {h_{\min }}}}{{\bar h}} $ | (7) |
The average, maximum, and minimum pressure heads with different laying lengths, pressure heads, and slopes can be computed by the calculation formula for the flow, as well as processing the head loss and the pressure head along the pipe[24-25]. In practical engineering, long porous tubes are more commonly used than other porous tubes. Therefore, the following formula investigates the influence of the deviation rate of the working head as a factor that affects flow uniformity in long porous tubes. According to the general principle, the conditions of 2 000 < Re < 105, z=1, b=4.75, and m=1.75 are mainly analyzed, among which the velocity head can be ignored. Re represents the Reynolds number, z represents the velocity distribution index, m represents the flow index, and b represents the caliber index.
The different formula for resistance coefficient along the way was adopted in the range of different Reynolds numbers. Different results of the calculating head loss were analyzed, and the formula for calculating the head loss along the pipe is as follows[24]:
| $ {H_f} = \chi f\frac{{Q_0^m}}{{{D^b}}}\frac{L}{{m \cdot z + 1}} $ | (8) |
where χ represents correction coefficient; f represents friction coefficient; D (m) represents the diameter of pipe; Q0 (m3/s) represents the flow of porous tubes inlet; and L represents the length of pipe. This formula is closer to the true head loss in the physical model than those in previous studies.
3.1 Analysis of the Deviation Rate of the Working Head on a Flat SlopeIn the case of a flat slope, the pressure curve was in decline, the pressure head of the first hole was the maximum, and that of the last hole was the minimum. Therefore,
| $ {h_{\max }} = {h_1},{h_{\min }} = {h_z} = {h_1} - {H_f} $ |
| $ \bar h = {h_1} - \frac{{m \cdot z + 1}}{{m \cdot z + 2}} = {h_1} - \frac{{2 \cdot 75}}{{3.75}}{H_f} = {h_1} - 0.733{H_f} $ |
where h1 represents the pressure head of the first hole, and hz represents the pressure head of the last hole.
Combined with Eq.(7), then
| $ {h_{\rm{v}}} = \frac{{{H_f}}}{{{h_1} - 0.733{H_f}}} $ | (9) |
It can be inferred from Eq.(9) that the deviation rate of the working head as well as the difference between the first pressure head and the frictional head loss were inversely related, provided that there was a flat slope for the long porous tubes without a velocity head. The greater the increase in the head loss was, the greater the deviation in the increase in the working head was. The deviation rate of the working head decreased with an increase in the first pressure head, which showed that the flow uniformity was high when the deviation rate of the working head was small. Thus, the first pressure head could be increased to improve the flow uniformity and reduce the deviation rate of the working head.
The frictional head loss along the pipe was related to the total flow and the laying length of the porous tubes. If the length of the pipe was longer, the head loss was greater, the deviation rate of working head was bigger, and the flow uniformity was smaller. The head loss is controlled by the first pressure head and the total flow of the pipe, so a steady flow occurred when they were balanced. When the first pressure head increased, the deviation rate of the working head also decreased. Moreover, the total flow increased with the increase in the first pressure head, while it caused a deviation in the rate of increase in the working head. Therefore, the deviation rate of the working head decreased with an increase in the first pressure head, though the influence was not obvious, which was also observed for flow uniformity.
3.2 Analysis of the Deviation Rate of the Working Head on an Adverse SlopeIn adverse slope (I < 0) conditions, the pressure curve declined. The pressure head of the first hole was the maximum, and that of the last hole was the minimum. Combining the maximum and the minimum pressure heads, as well as the average pressure head and Eq. (7), we can obtain
| $ {h_{\rm{v}}} = \frac{{{H_f} - IL}}{{{h_1} + \frac{{IL}}{2} - 0.733{H_f}}} $ | (10) |
where L represents the length of pipe, and I represents the slope of pipe.
Compared with Eqs.(9) and (10), the numerator obtained in Eq.(10) was greater than that in Eq.(9), and the denominator in Eq.(10) was smaller than that in Eq.(9). Therefore, in the same conditions, the deviation rate of the working head of the adverse slope was greater than that of the flat slope, because under the condition of an adverse slope, the first pressure head not only compensated for the head loss caused by the adverse slope but also overcame the frictional head loss. From Eq.(10), it can also be observed that the influence was similar to the laying length and the first pressure head for the deviation rate of the working head of the adverse slope. Thus, it can improve flow uniformity and decrease the deviation rate of the working head by reducing the laying length or increasing the first pressure head.
3.3 Analysis of the Deviation Rate of the Working Head on a Positive SlopeIn positive slope (I>0) conditions, the head change along the porous tubes was complicated. The maximum pressure head appeared on the first hole section or the end section, and the minimum pressure head was random. Therefore, the analysis of the deviation rate of the working head should depend on the location of the minimum pressure head. When the minimum pressure head is in the middle of the pipe, the formula for the minimum pressure head is
| $ {h_{\min }} = {h_1} + IL\left[ {1 - {{\left( {\frac{{IL}}{{2.75{H_f}}}} \right)}^{\frac{1}{{1/5}}}}} \right] - {H_f}\left[ {1 - {{\left( {\frac{{IL}}{{2.75{H_f}}}} \right)}^{1.57}}} \right] $ | (11) |
| $ {h_z} = {h_0} + IL - {H_f} $ | (12) |
| $ \bar h = {h_1} + \frac{{IL}}{2} - 0.733{H_f} $ | (13) |
The first condition is that the pressure head of the end section equals to the pressure head of the first section, and the maximum pressure head appears in the first section. IL=Hf and hmax=h1. According to Eq. (7), the deviation rate of the working head can be calculated as
| $ {h_{\rm{v}}} = \frac{{0.357{H_f}}}{{{h_1} - 0.233{H_f}}} $ | (14) |
A comparison of Eqs.(14) and (9) showed that the structures of the two formulas were similar. The deviation rate of the working head decreased as the first pressure head increased. The frictional head loss was larger, which could lead to an increase in the deviation rate of the working head. Under the same conditions, the numerator in Eq.(14) was smaller than that in Eq.(9), and the denominator in Eq.(14) was greater than that in Eq.(9). The result illustrated that the deviation rate of the working head of the positive slope was smaller than that of the flat slope in the same conditions. Thus, the flow uniformity of the flat slope was higher than that of the flat slope in the same condition. Besides, it could improve flow uniformity and decrease the deviation rate of the working head by reducing the laying length or increasing the first pressure head.
The second condition is that the pressure head of the end section is smaller than that of the first section, and the maximum pressure head appears in the first section. hmax=h1 and 0 < IL/Hf < 1. According to Eq.(7), the deviation rate of the working head is as follows:
| $ {h_{\rm{v}}} = \frac{{{H_f}\left[ {1 - {{\left( {\frac{{IL}}{{2.75{H_f}}}} \right)}^{\frac{1}{{1.73}}}}} \right] - {H_f}{{\left( {\frac{{IL}}{{2.75{H_f}}}} \right)}^{1.57}}}}{{{h_1} + \frac{{IL}}{2} - 0.733{H_f}}} $ | (15) |
In this formula, the numerator in Eq.(15) was smaller than that in Eq.(9), and the denominator in Eq.(14) was larger than that in Eq.(9). Thus, the deviation rate of the working head of the positive slope was smaller than that of the flat slope in the same conditions. The flow uniformity of the flat slope was bigger than that of the flat slope in the same condition. This is because the head loss was compensated by the head increment on the positive slope. Hence, improved flow uniformity could be improved by increasing the slope appropriately. In construction design, the slope of the terrain can be adopted to improve the flow uniformity.
The third condition is that the pressure head of the end section is bigger than that of the first section, and the maximum pressure head occurs in the end section. 0 < IL/Hf < 2.75 and hmax=h1-Hf. According to Eq.(7), the deviation rate of the working head is expressed as follows:
| $ {h_{\rm{v}}} = \frac{{IL{{\left( {\frac{{IL}}{{2.75{H_f}}}} \right)}^{0.57}} - {H_f}{{\left( {\frac{{IL}}{{2.75{H_f}}}} \right)}^{1.57}}}}{{{h_1} + \frac{{IL}}{2} - 0.733{H_f}}} $ | (16) |
For Eq.(16), under the same conditions, the slope increased, and both the denominator and the numerator increased. However, the numerator increased faster than the denominator, indicating that the deviation rate of the working head of the positive slope was bigger than that of the flat slope in this condition. Thus, increasing only the slope would decrease the flow uniformity.
According to the above analysis, when I>0, the deviation rate of the working head could be decreased by reducing the laying length and increasing the first pressure head, which could also improve the flow uniformity. When 0 < IL/Hf < 1, increasing the slope could reduce the deviation rate of the working head and improve the flow uniformity. When 0 < IL/Hf < 2.75, increasing the slope would increase the deviation rate of the working head, thus improving the flow uniformity to reduce the slope. When IL=Hf, with the other factors being definite values, the deviation rate of the working head had a minimum value, and the flow uniformity was the best. In engineering design, the terrain slope can be applied to improve the flow uniformity and reduce the investment.
The fourth condition is that the pressure head on the end section is the maximum, and the first section is the minimum.
| $ IL/{H_f} > 2.75,{h_{\min }} = {h_1},{h_{\max }} = {h_1} + IL - {H_f} $ |
According to Eq.(7), the deviation rate of the working head is as follows:
| $ {h_{\rm{v}}} = \frac{{IL - {H_f}}}{{{h_1} + \frac{{IL}}{2} - 0.733{H_f}}} $ | (17) |
For Eq.(17), the increase of the first pressure head could reduce the deviation rate of the working head. Moreover, if (IL-Hf) is increased, the deviation rate of the working head is increased. Thus, the flow uniformity can be improved by increasing the first pressure head or reducing (IL-Hf).
4 Analysis of the Laying LengthThe laying length of the porous tubes was dependent on the flow uniformity. Thus, the utilization efficiency of water was the best when the flow uniformity was higher and the flow deviation rate was lower. However, it would increase the investment and the operating cost. Therefore, flow deviation rate should be determined on the basis of the requirement with a suitable laying length. Currently, the flow deviation rate of less than 20% of the system is considered good. Although the chemical industry has a higher demand for flow deviation rates, most rates fall below 10%. Thus, the total flow computational formula, the head loss computational formula, and the pressure head computational formula can be utilized in different conditions, such as different slopes and pressure heads, to calculate the average pressure head, the maximum pressure head, and the minimum pressure head. Hence, Eq.(4) was used to calculate the flow deviation rate in this study.
4.1 Effect of the Slope on Laying LengthWhen the pressure head of inlet H=1 m, the perforation spacing S=0.2 m, the diameter of pipe D=40 mm, and the diameter of perforation d=2 mm. The porous tubes are made of steel. The calculated results are listed in Table 1.
| Table 1 Laying length L (m) under H =1 m, S =0.2 m, D =40 mm (d =2 mm) |
It can be seen from Fig. 2 that the flow deviation rates and the laying lengths of the porous pipe were different when the slope was fixed. With the decrease of the flow deviation rate, the laying length of the porous tube was gradually reduced. This is because the longer the laying length is, the greater Hf is, and the greater the flow deviation rate is, the smaller the outflow uniformity is. Under the premise of keeping the flow deviation rate unchanged, with the laying slope changed from the inverse slope (I < 0) to the positive slope (0≤I≤0.1), the laying length first increased and then decreased. Table 1 shows different flow deviation rates for the best-laid slope in different conditions. For example, when qv=15%, the longest laying length was I=0.003, and the pipe could be laid on this slope with the length of 38.2 m. With the pressure head being constant, an appropriate increase in the slope could increase the laying length. The reason is that the head loss is less than the slope head increment caused by the slope. However, when the slope increased to a certain extent and continued to increase as I>0.003, the laying length would become shorter, because the friction head loss was less than the enhanced head due to the slope. It indicated that there is an optimal slope that can ensure the pipe has the longest length. From the table, it can be inferred that when the slope was constant, the laying length was longer, the flow deviation rate was bigger, and the flow uniformity was lower. The cause is that the increase of the length of the laying pipe accelerates the head loss, leading to the porous tube hole flow unstable and the difference between the maximum flow and the minimum flow greater, thus resulting in larger flow deviation rate. In summary, the maximum laying length of the porous pipe can be obtained at the slope of 0.002-0.003.
|
Fig.2 Scatter plot of Table 1 |
4.2 Effect of the Slope on Pressure Head
To explore the relationship between the pressure head and the laying length, the laying length in a different slope condition was discussed when the perforation spacing S=0.2 m, the diameter of pipe D=40 mm, the diameter of perforation d=2 mm, and the flow deviation rate qv=15%, as shown in Table 2.
| Table 2 Laying length L (m) under S =0.2 m, qv =15%, D =40 mm (d =2 mm) |
It can be seen from Table 2 that when the slope is on the inverse slope (I < 0) and remains unchanged, the laying length of the porous tube increased with the increase of pressure head. When the slope 0 < I < 0.004 and is unchanged, the laying length of the porous pipe decreased with the increase of pressure head. At this moment, increasing the pressure head would lead to the increase of the head loss, but the pressure head increment caused by the slope could not completely offset the head loss, so it is necessary to reduce the laying length to ensure the flow deviation rate. When the slope I>0.004 and is unchanged, the laying length increased first and then decreased with the increase of pressure head. Under the premise of qv=15%, where the best laying slope was different under different pressure heads, indicating that the optimum laying length was different. It can be seen from Table 2 that the laying length increased with the increase in the pressure head when the pressure head H=0.4 m and the slope I≤0.003. If I≥0.004, for a constant slope, increasing the pressure head properly could increase the laying length under the premise of ensuring the flow deviation rate. However, if the pressure head is too large, the laying length should be reduced to ensure the flow deviation rate.
4.3 Effect of Slope on Perforation SpacingTable 3 shows the laying length of porous tubes with different perforation spacing and slopes, when the diameter of pipe D=40 mm, the diameter of perforation d=2 mm, and the flow deviation rate qv=15%.
| Table 3 Laying length L (m) under qv =15%, D =40 mm (d =2 mm) |
It can be seen in Table 3 that different perforation spacing corresponded to an optimal slope. In this slope, the porous tubes were longer than the lengths of other slopes. The optimal laying slope corresponding to different perforation spacing was varied. For example, when S=0.2 m, the optimal slope I=0.003, and the laying length was 38.2 m. When S=0.3 m, the optimal slope I=0.007, and the laying length was 53.1 m. When the slope was not changed, the laying length increased with the increase in perforation spacing. This occurred because with a larger perforation spacing, the total flow of the porous tubes was smaller, which could reduce the head loss.
In summary, when I>0 and the pressure head is not changed, there is always a best slope for laying the longest porous tubes. In this case, the head loss is exactly equal to the incremental head obtained by the slope, and the maximum length can thus be achieved. Notably, influencing factors of flow uniformity are laying length, pressure head, pipe diameter, and perforation spacing. As these factors change, the total flow, first pressure head, and total head loss along the pipe change. Therefore, the best laying length is variable. The above test was only performed in a certain pipe diameter and a certain perforation diameter to get the maximum laying length and the best slope, while the maximum laying length would be different with different pipe diameters or perforation spacing. Therefore, the best slope can only be obtained in a positive slope, because only in the positive slope will an incremental head be produced to compensate for the head loss, and the slope can reach the best only when the two are balanced. In the flat slope and the adverse slope, the weight of the component was inversely related to the flow, thus making the pressure distribution gap larger and the flow uniformity smaller, which however, did not appear to be the best slope. The above analysis was consistent with the law of the deviation rate of the working head analysis. Considering the problem of ground flatness in practical engineering, the head loss would increase slightly, and the optimum laying length would be reduced accordingly.
5 ConclusionsFor flat slope, the longer the length was, the larger the deviation rate of the working head was. The flow uniformity decreased withthe increase in laying length. The change in the first pressure head had only a slight effect on the deviation rate of the working head, and the increase in pressure head was not significant for increasing the flow uniformity. Under the same condition, for the adverse slope, the deviation rate of the working head was larger than that of the flat slope of the pipe. Thus, the flow uniformity was less than that of the flat slope. The effects of the laying length and the pressure head on the deviation rate of the working head of the adverse slope were similar to those of the flat slope porous tubes.
The positive slope based on the ratio of IL and Hf was used to analyze the effect of the slope, the pressure head, and other factors on the deviation rate of the working head and the flow uniformity of the impact. For maintaining a certain flow deviation rate, there was an optimal slope that could make the pipe obtain the longest laying length, which was greater than the laying length in the other slope. Moreover, this optimal slope must be in the positive slope. Increasing the pressure head appropriately would increase the length of the pipe. However, if the pressure head was too large to ensure the flow deviation rate, the length of the pipe would decrease. For the same slope, increasing the perforation spacing would increase the length of pipe.
| [1] |
Zhang L, Wu P T, Fan X K, et al. Experimental research on drip irrigation uniformity at low-pressure. Journal of Northwest A & F University (Natural Science Edition), 2009, 12: 207-212. (in Chinese) DOI:10.3321/j.issn:1671-9387.2009.12.035 (  0) 0) |
| [2] |
Zhang G X. Method of determining locations of branch pipe on slope with paired capillaries in micro-irrigation system. Transactions of Chinese Society of Agricultural Engineering, 2012, 28(21): 98-104. (in Chinese) DOI:10.3969/j.issn.1002-6819.2012.21.014 (  0) 0) |
| [3] |
Niu Q W, Zhang R C, Luo C Y. Drip irrigation uniformity calculation considering distribution location of clogged emitters. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 147-152, 174. (in Chinese) DOI:10.6041/j.issn.1000-1298.2015.06.021 (  0) 0) |
| [4] |
Ju X L, Wu P T, Zhu D L, et al. Estimation of micro-irrigation water application uniformity based on sample emitter flow variation. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(2): 173-178. (in Chinese) DOI:10.3969/j.issn.1674-8530.15.0174 (  0) 0) |
| [5] |
Chang H H, Li Y N. Research on pressure head distribution and allowed maximum length of orifice outlet drip irrigation laterals. China Rural Water and Hydropower, 2014(1): 41-44. (in Chinese) DOI:10.3969/j.issn.1007-2284.2014.01.010 (  0) 0) |
| [6] |
Ju X L, Wu P T, Weckler R P, et al. Simplified method for designing diameter of drip irrigation laterals based on emitter flow variation. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(5): 14-20. (in Chinese) DOI:10.11975/j.issn.1002-6819.2016.05.002 (  0) 0) |
| [7] |
Zhang G X, Wu P T. Determination of the design working head of emitter. Transactions of the Chinese Society of Agricultural Engineering, 2005, 21(9): 20-22. (in Chinese) DOI:10.3321/j.issn:1002-6819.2005.09.005 (  0) 0) |
| [8] |
Ju X L, Wu P T, Weckler R P, et al. Appropriate layouts of micro-irrigation laterals laid on uniformly sloping ground. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(5): 123-128. (in Chinese) DOI:10.6041/j.issn.1000-1298.2016.05.017 (  0) 0) |
| [9] |
Zheng C, Wu P T, Zhu D L, et al. Research on flow resistance and pressure head distribution of multiple outlets pipeline. Water Saving Irrigation, 2014, 3: 24-29. (in Chinese) (  0) 0) |
| [10] |
Zhang L, Wu P T, Zhu D L, et al. Integrated flow deviation rate of drip irrigation system based on manufacturing variation. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(12): 135-139. (in Chinese) DOI:10.6041/j.issn.1000-1298.2013.12.022 (  0) 0) |
| [11] |
Kang Y H. Hydraulic Analysis and Design of Micro-irrigation System. Xi'an: Shaanxi Science and Technology Press, 1999. (in Chinese)
(  0) 0) |
| [12] |
Chang F S, Zhang D S. Discussion on uniformity of drip irrigation. Water Resource & Hydropower of Northeast China, 2003, 12: 38-39. (in Chinese) (  0) 0) |
| [13] |
Scaloppi E J, Allen R G. Hydraulics of irrigation laterals: Comparative analysis. Journal of Irrigation and Drainage Engineering, 1993, 119(1): 91-115. DOI:10.1061/(asce)0733-9437(1993)119:1(91) (  0) 0) |
| [14] |
Hathoot H M, AI-Amoud A I, Mohammad F S. Analysis and design of trickle-irrigation laterals. Journal of Irrigation and Drainage Engineering, 1993, 119(5): 756-767. DOI:10.1061/(asce)0733-9437(1993)119:5(756) (  0) 0) |
| [15] |
Hathoot H M, Abo-Ghobar H M, AI-Amoud A I, et al. Analysis and design of sprinkler irrigation laterals. Journal of Irrigation and Drainage Engineering, 1994, 120(3): 534-549. DOI:10.1061/(asce)0733-9437(1994)120:3(534) (  0) 0) |
| [16] |
Murphy P, Kaye N B, Khan A A. Hydraulic performance of aggregate beds with perforated pipe under drains flowing full. Journal of Irrigation and Drainage Engineering, 2014, 140(8): 04014023-1-04014023-7. DOI:10.1061/(ASCE)IR.1943-4774.0000740 (  0) 0) |
| [17] |
Afrin T, Kaye N B, Khan A A, et al. Parametric study of perforated pipe under drains surrounded by loose aggregate. Journal of Hydraulic Engineering, 2016, 142(12): 04016066. DOI:10.1061/(ASCE)HY.1943-7900.0001214 (  0) 0) |
| [18] |
Zhang L, Wu P T, Niu Q W, et al. Method for calculating flow deviation in drip irrigation system under uniform slope. Transactions of the Chinese Society of Agricultural Engineering, 2007, 23(8): 40-44. (in Chinese) DOI:10.3321/j.issn:1002-6819.2007.08.007 (  0) 0) |
| [19] |
Zhu D L, Wu P T, Zhang L. Calculation method of the maximum flow variation and evaluation of factors for micro-irrigation engineering. Journal of Drainage and Irrigation Machinery Engineering, 2013(4): 340-344. (in Chinese) DOI:10.3969/j.issn.1674-8530.2013.04.013 (  0) 0) |
| [20] |
Fan Y S, Wu F, Zai S M, et al. Experimental study on hydraulic property of emitters with tiny water pressure. Journal of Irrigation and Drainage, 2006, 25(5): 39-41. (in Chinese) DOI:10.3969/j.issn.1672-3317.2006.05.011 (  0) 0) |
| [21] |
Zhang T J, Wu F, Deng Z, et al. Experimental study on effect of pressure on capillary tube uniformity in drip irrigation at different slopes. Advances in Science and Technology of Water Resources, 2007, 27(3): 24-26. (in Chinese) DOI:10.3880/j.issn.1006-7647.2007.03.007 (  0) 0) |
| [22] |
Department of Rural Water Resources in Ministry of Water. Resources Water-saving Irrigation Technology Standards. Beijing: China Water & Power Press, 1999. (in Chinese)
(  0) 0) |
| [23] |
Niu Q W, Wu P T, Fan X K. Method for calculating integrated flux deviation rate of micro-irrigation system. Transactions of the Chinese Society of Agricultural Engineering, 2004(6): 85-88. (in Chinese) DOI:10.3321/j.issn:1002-6819.2004.06.020 (  0) 0) |
| [24] |
Liu H F. Study on Hydraulic Characteristics of Micro-pressure Perforated Flexible Hose. Shaanxi: Northwest A & F University, 2008: 56-66. (in Chinese)
(  0) 0) |
| [25] |
Wang Y M, Liu H F, Du T, et al. An analysis of the influence of slopes on the pressure head distribution of porous tubes. China Rural Water and Hydropower, 2017(7): 14-17. (in Chinese) (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


