2. Changzhou Vocational Institute of Light Industry Technology, Changzhou 213000, Jiangsu, China
Fault diagnosis is significant for practical systems as the existing faults in the actuator or the sensor may lead inefficient work of the systems. The research on descriptor systems (also defined as singular system) in recent decades is more in depth as it has a better characterization than the space description method for some practice systems[1-4]. Our research is based on this background to solve the problem of fault diagnosis for descriptor systems and process in a further study.
Existing literature has provided many methods for diagnosing the faults of the descriptor system, and one of the efficient ways is the fault diagnosis observer design. In Ref.[5], a residual generator was proposed for continuous-time linear descriptor systems. In Ref.[6], a robust state space observer was designed for Lipschitz non-linear descriptor systems with bounded input disturbance to solve the actuator fault diagnosis problems. In Ref.[7], a sensor fault observer was proposed for attitude control systems model of satellite upon on fuzzy descriptor systems. In Ref.[8], a model-based fault estimation observer which meets the H-/H∞ performance index was proposed for Linear Parameter Varying (LPV) descriptor system models. In Ref.[9], an augmented proportional plus observer(PD) was proposed for fault estimation of descriptor systems with system uncertainties, where the augmented residal has a robustness against the sensor noise, disturbance as well as the uncertainties. In Ref.[10], for Takagi-Sugeno (T-S) fuzzy model upon on descriptor systems with unknown bounded, a fault detection observer was proposed and the observer design problem is formulating as the H-/H∞ filtering one.
As the state time-delay exists in most of the actual systems, the fault diagnosis problem for descriptor systems with state time-delay is significant. For time-delay descriptor models, in Ref.[11], a fault detection filer was proposed based on the admissible augmented measurement residual for Markovian jump descriptor systems. In Ref.[12], a robust fault diagnosis filter was proposed for a continuous-time linear time-delay descriptor system with uncertainties based on the observer design, its core idea is that the filter is seen as the residual generator so that the design of the filter problem is transformed into H∞ filtering, the research method in Ref.[12] was developed to realize fault diagnosis for time-vary state delay descriptor models in Ref.[13].
In the aforementioned literature, all of the observers are realized based on the singular structure, which makes the design workings more complex. For more convenient and accurate fault diagnosis, a new observer design approach is needed for descriptor systems. In Refs.[14-16], the author proposed non-singular structure observers and filters to solve the fault diagnosis problem for descriptor systems, and these working have enlightened the next study. In this paper, a new type of fault diagnosis observer is proposed for linear sampled-data descriptor systems with state time-vary delay based on the augmented state estimation error and the measurement residual. The augmented measurement residual meets the H∞ performance index at zero initial condition, which means the augmented measurement residual has a robustness against the sensor faults and the disturbance. Different from the former studies in the domain of fault diagnosis of time-delay descriptor systems, our fault diagnosis observer has a non-singular structure which is easy to implement. For detecting the faults as soon as possible, a residual evaluation function and threshold are introduced in for judging if faults occur. Additionally, for time-vary delay descriptor systems, the confining matrix of the observer parameters is not a standard LMI and is very difficult to solve directly. Thus, a CCL algorithm is introduced in to solve this problem.
This paper is organized as follows. In Section 2, by introducing a pair of parameters and using the Euler discretization method, the sampled-data descriptor model with state time-vary delay is transformed into a non-singular equivalent discrete-time one. In Section 3, a non-singular structure fault diagnosis observer is proposed, by applying the Lyapunov-Kravoskii function, the existence of the observing parameters which meet the H∞ performance index is proved. A CCL iteration algorithm is proposed for aiding the calculation of the observing parameter matrices in the forms of LMI. In Section 4, simulating example is given to show the effectiveness of our method. Finally, the conclusion is drawn.
2 Problem StatementFirstly, consider a continuous-time descriptor system with time-vary delay as follows
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{E\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}\left( {t - {d_1}\left( t \right)} \right) + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{u}}\left( t \right) + {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{w}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{Cx}}\left( t \right) + {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( t \right) + \mathit{\boldsymbol{Ff}}\left( t \right)}\\ {\mathit{\boldsymbol{x}}\left( t \right) = \phi \left( t \right)} \end{array}} \right. $ | (1) |
where t∈[-τM, 0], E represents the singular matrix and satisfies that rank(E) =r≤n, x∈Rn denotes the state vector, u∈Rl denotes the input of the system, f∈Rq is the sensor fault, y∈Rm denotes the output of the system, w∈Rd denotes the disturbance, d1(t) denotes the time-vary delay which satisfies 0≤τm'≤d1(t)≤τM', A1, A2, Bc, Dc, C, Dd, F separately represents the constant matrix, ϕ(·) denotes the initial function.
In this paper,
| $ {\rm rank}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right] = n $ | (2) |
If the measurement of the system (1) is the sampling model, then Eq.(1) is rewritten as
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{E\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}\left( {t - {d_1}\left( t \right)} \right) + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{u}}\left( t \right) + {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{w}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{Cx}}\left( {{t_k}} \right) + {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( {{t_k}} \right) + \mathit{\boldsymbol{Ff}}\left( {{t_k}} \right)}\\ {\mathit{\boldsymbol{x}}\left( t \right) = \phi \left( t \right)} \end{array}} \right. $ | (3) |
where t∈[-τM, 0], tk is the sampling time, the sampling interval is defined as τ=tk+1-tk.
For the system (3), as the singular matrix E exists in the dynamic model, it is very difficult to process in the calculation of the constraint matrix for the observer design. In this paper, parameters are introduced in to transform the descriptor model into non-singular one.
Lemma 1[15] If there exist matrix R1∈Ra1×b1, matrix R2∈Rb1×c1 and matrix R3∈Ra1×c1, where R2 satisfies that rank(R2)=c1, then
| $ {\mathit{\boldsymbol{R}}_1}{\mathit{\boldsymbol{R}}_2} = {\mathit{\boldsymbol{R}}_3} $ | (4) |
has a general solution as
| $ {\mathit{\boldsymbol{R}}_1} = {\mathit{\boldsymbol{R}}_3}\mathit{\boldsymbol{R}}_2^\dagger + \xi \left[ {{\mathit{\boldsymbol{I}}_{{b_1}}} - {\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{R}}_2^\dagger } \right] $ | (5) |
where ξ is an arbitrary matrix, R2† denotes the pseudo-inverse of R2.
According to Lemma 1, since rank
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{H}}&\mathit{\boldsymbol{G}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right] = {\mathit{\boldsymbol{I}}_n} $ | (6) |
where [H G] is calculated by the Eq. (7)
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{H}}&\mathit{\boldsymbol{G}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]^\dagger } + \Gamma \left( {{\mathit{\boldsymbol{I}}_{n + m}} - \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]}^\dagger }} \right) $ | (7) |
Γ∈Rn×(n+m) denotes the design freedom.
It is seen that the dynamic model of Eq.(3) is continuous-time one, and the measurement is the discrete-time one, the Eq. (7) can not be used directly. So we firstly discretize the system (3) to be a discrete non-singular model.
For the system (3), using the Eq. (7), the following equation is obtained as
| $ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( t \right) = \left( {\mathit{\boldsymbol{HE}} + \mathit{\boldsymbol{GC}}} \right)\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{HE\dot x}}\left( t \right) + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{GC\dot x}}\left( t \right) = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}\left( {t - {d_1}\left( t \right)} \right) + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{u}}\left( t \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{w}}\left( t \right) + \mathit{\boldsymbol{GC\dot x}}\left( t \right) \end{array} $ | (8) |
In Ref.[17], the author discretized a continuous constant time-delay system into a discrete-time one, the dynamic model of this system is represented as
| $ \mathit{\boldsymbol{\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}\left( {t - {\tau _h}} \right) $ | (9) |
where τh is a positive constant time-delay.
Using the Euler discretization method, it is obtained that
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{x}}\left( k \right) + \tau {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}\left( k \right) + \tau {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}\left( {k - h} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;O\left( {{\tau ^2}} \right) \end{array} $ | (10) |
where
| $ h = \frac{{{\tau _h}}}{\tau } $ |
| $ \begin{array}{*{20}{c}} {O\left( {{\tau ^2}} \right) = \mathit{\boldsymbol{H}}\left[ {\frac{{{\tau ^2}}}{{2!}}\mathit{\boldsymbol{A}}_1^2{\mathit{\boldsymbol{x}}^2}\left( t \right) + \frac{{{\tau ^3}}}{{3!}}\mathit{\boldsymbol{A}}_1^{\left( 3 \right)}{\mathit{\boldsymbol{x}}^3}\left( t \right) + } \right.}\\ {\left. { \cdots + \frac{{{\tau ^k}}}{{k!}}\mathit{\boldsymbol{A}}_1^{k - 1}{\mathit{\boldsymbol{x}}^{k - 1}}\left( t \right)} \right]} \end{array} $ |
Similarly with the Eq.(9) and Eq.(10), using the Euler discretization method, the Eq. (8) is rewritten as
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{H\tau }}{\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{H\tau }}{\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{H\tau }}{\mathit{\boldsymbol{B}}_c}\mathit{\boldsymbol{u}}\left( k \right) + \mathit{\boldsymbol{H\tau }}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{w}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{GCx}}\left( {k + 1} \right) + O\left( {{\tau ^2}} \right) \end{array} $ | (11) |
where
| $ d\left( k \right) = \frac{{{d_1}\left( k \right)}}{\tau } $ |
| $ \begin{array}{*{20}{c}} {O\left( {{\tau ^2}} \right) = \mathit{\boldsymbol{H}}\left[ {\frac{{{\tau ^2}}}{{2!}}\mathit{\boldsymbol{A}}_1^2{\mathit{\boldsymbol{x}}^2}(t) + \frac{{{\tau ^3}}}{{3!}}\mathit{\boldsymbol{A}}_1^{(3)}{\mathit{\boldsymbol{x}}^3}(t) + } \right.}\\ {\left. { \cdots + \frac{{{\tau ^k}}}{{k!}}\mathit{\boldsymbol{A}}_1^{k - 1}{\mathit{\boldsymbol{x}}^{k - 1}}\left( t \right)} \right]} \end{array} $ |
The measurement in Eq.(3) is rewritten as the Eq.(12)
| $ \mathit{\boldsymbol{Cx}}\left( k \right) = \mathit{\boldsymbol{y}}\left( k \right) - {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( k \right) - \mathit{\boldsymbol{Ff}}\left( k \right) $ | (12) |
The third term of Eq.(3) is rewritten as the Eq.(13)
| $ \mathit{\boldsymbol{x}}\left( k \right) = \phi \left( k \right),k \in \left[ { - {d_M},0} \right] $ | (13) |
where dM=τM/τ.
Combining Eqs.(11), (12) and (13), the system (3) is descretized as
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\mathit{\boldsymbol{HBu}}\left( k \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( k \right) + \mathit{\boldsymbol{Gy}}\left( {k + 1} \right) - \\ \;\;\;\;\;\;\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_d}\mathit{\boldsymbol{w}}\left( {k + 1} \right) - \mathit{\boldsymbol{GFf}}\left( {k + 1} \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right) + {\mathit{\boldsymbol{D}}_d}\mathit{\boldsymbol{w}}\left( k \right) + \mathit{\boldsymbol{Ff}}\left( k \right)\\ \mathit{\boldsymbol{x}}\left( k \right) = \phi \left( k \right) \end{array} \right. $ | (14) |
where k∈[-dM, 0], A=τHA1+In, Ad=τA2, B=τBc, Bd=τDc.
Define
| $ \mathit{\boldsymbol{f}}\left( {k + 1} \right) = \mathit{\boldsymbol{f}}\left( k \right) + \Delta \mathit{\boldsymbol{f}}\left( k \right) $ | (15) |
Then the system (14) is transformed into the system (16)
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\mathit{\boldsymbol{HBu}}\left( k \right) + \mathit{\boldsymbol{Gy}}\left( {k + 1} \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( k \right) - \\ \;\;\;\;\;\;\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( {k + 1} \right) - \mathit{\boldsymbol{GFf}}\left( k \right) - \mathit{\boldsymbol{GF \boldsymbol{\varDelta} f}}\left( k \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right) + {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( k \right) + \mathit{\boldsymbol{Ff}}\left( k \right)\\ \mathit{\boldsymbol{x}}\left( k \right) = \phi \left( k \right) \end{array} \right. $ | (16) |
where k∈[-dM, 0].
So the problem for designing the fault diagnosis observer for the sampled-data descriptor system (3) is transformed into one for designing the fault diagnosis observer for the system (16).
Remark 1 In this paper, the sampling interval τ is chosen to be sufficiently small so that the high order O(τ2) can be omitted. Additionally, the sampling interval and the time-delay satisfy that τ≤dm, the discretized d(k) satisfies 0≤dm≤d(k)≤dM, where dm=τm'/τ, dm and dM are assumed to be the integer.
3 Robust Sensor Fault Diagnosis Observer DesignIn this section, a robust sensor fault diagnosis observer is designed upon on the measurement residual. As the fault diagnosis includes two parts, the residual produce and the residual evaluation[12], our purpose is to find an observer as a residual generator based on the H∞ filtering as the residual producer which makes
| $ {\left\| {\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{f}}}\left( z \right)f} \right\|_2} < \gamma {\left\| {\mathit{\boldsymbol{\bar w}}} \right\|_2} $ | (17) |
where γ>0, Wf is a stable weighing function, w=[fT wT ΔfT].
Remark 2 When Wf = I, the measurement residual r is the H∞ estimation of the fault, which means the faults occur in the whole frequency. For enhancing the performance index of the fault estimation, the weighting function Wf is proposed, and the inequality (17) represents that the calculated residual is the H∞ estimation of the fault in the frequency of Wf.
Assume Wf has a minimal realization as the following equation:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_f}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_W}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{f}}}\left( k \right) + {\mathit{\boldsymbol{B}}_W}\mathit{\boldsymbol{f}}\left( k \right),{\mathit{\boldsymbol{x}}_f}\left( 0 \right) = 0\\ {\mathit{\boldsymbol{r}}_\mathit{\boldsymbol{f}}}\left( k \right) = {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{W}}}{\mathit{\boldsymbol{x}}_f}\left( k \right) \end{array} \right. $ | (18) |
where xf∈Rnf, rf∈Rq, AW, BW, CW separately represents the constant matrix.
Combining the system (16) and the system (18), the following augmented system is obtained as
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\bar x}}\left( {k + 1} \right) = \mathit{\boldsymbol{\bar A\bar x}}\left( k \right) + {{\mathit{\boldsymbol{\bar A}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\bar x}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\bar Bu}}\left( k \right) + {{\mathit{\boldsymbol{\bar B}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{w}}\left( k \right) + \mathit{\boldsymbol{\bar Gy}}\left( {k + 1} \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{\bar C\bar x}}\left( k \right) + {{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\bar w}}\left( k \right)\\ {\mathit{\boldsymbol{r}}_\mathit{\boldsymbol{f}}}\left( k \right) = {{\mathit{\boldsymbol{\bar C}}}_\mathit{\boldsymbol{w}}}\mathit{\boldsymbol{\bar x}}\left( k \right)\\ \mathit{\boldsymbol{\bar x}}\left( k \right) = \bar \phi \left( k \right) \end{array} \right. $ | (19) |
where k∈[-dM, 0],
| $ \mathit{\boldsymbol{\bar x}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( k \right)}\\ {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{f}}}\left( k \right)} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\bar x}}\left( {k - d\left( k \right)} \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right)}\\ {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{f}}}\left( k \right)} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{{0_{n \times {n_f}}}}\\ {{0_{{n_f} \times n}}}&{{\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{W}}}} \end{array}} \right],{{\mathit{\boldsymbol{\bar A}}}_\mathit{\boldsymbol{d}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{d}}}}&{{0_{n \times {n_f}}}}\\ {{0_{{n_f} \times n}}}&{{0_{{n_f} \times {n_f}}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\bar B}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{B}}\\ {{0_{{n_f} \times l}}} \end{array}} \right],\mathit{\boldsymbol{\bar G}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{G}}\\ {{0_{{n_f} \times m}}} \end{array}} \right],\mathit{\boldsymbol{\bar C}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{C}}&{{0_{m \times {n_f}}}} \end{array}} \right] $ |
| $ {{\mathit{\boldsymbol{\bar B}}}_\mathit{\boldsymbol{d}}} = \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{GF}}}&{\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{d}}}}&{ - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}}&{ - \mathit{\boldsymbol{GF}}}\\ {{\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{w}}}}&{{0_{{n_f} \times d}}}&{{0_{{n_f} \times d}}}&{{0_{{n_f} \times q}}} \end{array}} \right] $ |
| $ {{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{F}}&{{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{d}}}}&{{0_{m \times d}}}&{{0_{m \times q}}} \end{array}} \right] $ |
| $ {{\mathit{\boldsymbol{\bar C}}}_\mathit{\boldsymbol{w}}} = \left[ {\begin{array}{*{20}{l}} {{0_{q \times n}}}&{{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{w}}}} \end{array}} \right],\bar \phi \left( k \right) = \left[ {\begin{array}{*{20}{c}} {\phi \left( \mathit{\boldsymbol{k}} \right)}\\ {{0_{{n_f} \times n}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\bar w}}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( {k + 1} \right)}&{\Delta {\mathit{\boldsymbol{f}}^{\rm{T}}}\left( k \right)} \end{array}} \right]^{\rm{T}}} $ |
For the system (19), the observer has the non-singular structure as follows:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat {\bar x}}}\left( {k + 1} \right) = \mathit{\boldsymbol{\bar A\hat {\bar x}}}\left( k \right) + {{\mathit{\boldsymbol{\bar A}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\hat {\bar x}}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{\bar Bu}}\left( k \right) + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{y}}\left( k \right) - \mathit{\boldsymbol{\bar C\hat {\bar x}}}\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{\bar Gy}}\left( {k + 1} \right),\mathit{\boldsymbol{\hat {\bar x}}}\left( 0 \right) = 0\\ \mathit{\boldsymbol{r}}\left( k \right) = \mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{y}}\left( k \right) - \mathit{\boldsymbol{\bar C\hat {\bar x}}}\left( k \right)} \right) + {C_\mathit{\boldsymbol{w}}}\mathit{\boldsymbol{\hat {\bar x}}}\left( k \right)\\ \mathit{\boldsymbol{\hat y}}\left( k \right) = \mathit{\boldsymbol{\bar C\hat {\bar x}}}\left( k \right) \end{array} \right. $ | (20) |
where
Define
| $ \mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) = \mathit{\boldsymbol{\bar x}}\left( k \right) - \mathit{\boldsymbol{\hat {\bar x}}}(k) $ | (21) |
Then it is obtained that
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k + 1} \right) = \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k + 1} \right) - \mathit{\boldsymbol{\hat {\bar x}}}\left( {k + 1} \right) = \\ \;\;\;\;\;\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + {{\mathit{\boldsymbol{\bar A}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) - \\ \;\;\;\;\;\left( {{{\mathit{\boldsymbol{\bar B}}}_\mathit{\boldsymbol{d}}} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}}} \right)\mathit{\boldsymbol{\bar w}}\left( k \right) \end{array} $ | (22) |
where
| $ \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) = \mathit{\boldsymbol{\hat {\bar x}}}\left( {k - d\left( k \right)} \right) - \mathit{\boldsymbol{\bar x}}\left( {k - d\left( k \right)} \right) $ |
Define
| $ \mathit{\boldsymbol{\tilde r}}\left( k \right) = \mathit{\boldsymbol{r}}\left( k \right) - {\mathit{\boldsymbol{r}}_f}\left( k \right) $ | (23) |
Then it is obtained that
| $ \mathit{\boldsymbol{\tilde r}}\left( k \right) = \left( {\mathit{\boldsymbol{V\bar C}} - {{\mathit{\boldsymbol{\bar C}}}_\mathit{\boldsymbol{w}}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + \mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\bar w}}\left( k \right) $ | (24) |
So the following augmented system is obtained as
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + {{\mathit{\boldsymbol{\bar A}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\left( {{{\mathit{\boldsymbol{\bar B}}}_\mathit{\boldsymbol{d}}} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}}} \right)\mathit{\boldsymbol{\bar w}}\left( k \right)\\ \mathit{\boldsymbol{\tilde r}}\left( k \right) = \left( {\mathit{\boldsymbol{V\bar C}} - {{\mathit{\boldsymbol{\bar C}}}_\mathit{\boldsymbol{w}}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + \mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\bar w}}\left( k \right)\\ \mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) = \bar \phi \left( k \right) \end{array} \right. $ | (25) |
where k∈[-dM, 0].
So the inequality (17) is transformed into the following performance index:
| $ {\left\| {\mathit{\boldsymbol{\tilde r}}} \right\|_2} < \gamma {\left\| {\mathit{\boldsymbol{\bar w}}} \right\|_2} $ | (26) |
Define the augmented error in Eq.(25) as
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + {{\mathit{\boldsymbol{\bar A}}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\left( {{{\mathit{\boldsymbol{\bar B}}}_\mathit{\boldsymbol{d}}} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_\mathit{\boldsymbol{d}}}} \right)\mathit{\boldsymbol{\bar w}}\left( k \right)\\ \mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) = \bar \phi \left( k \right) \end{array} \right. $ | (27) |
where k∈[-dM, 0].
The designed observer should satisfies that
(ⅰ)When w(k)=0, Eq.(27) is asymptotically stable.
(ⅱ)At zero initial condition, ϕ(k)=0, the performance index Eq.(26) is satisfied.
Theorem 1 If there exists matrix P, Q, Z which satisfies the following inequality
| $ \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{P}}^{ - 1}}}&{\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}}&{{{\mathit{\boldsymbol{\bar A}}}_d}}&0\\ * &\mathit{\boldsymbol{\varpi}} &{\frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&{{{\mathit{\boldsymbol{\bar A}}}^{{\bf T}}} - {{\mathit{\boldsymbol{\bar C}}}^{{\bf T}}}{\mathit{\boldsymbol{L}}^{{\bf T}}} - \mathit{\boldsymbol{I}}}\\ * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}}}&{\mathit{\boldsymbol{A}}_d^{\rm{T}}}\\ * & * & * &{ - \frac{1}{{{d_M}}}{\mathit{\boldsymbol{Z}}^{ - 1}}} \end{array}} \right] < 0 $ | (28) |
where
Proof Define
| $ \mathit{\boldsymbol{\tilde e}}\left( k \right) = \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k + 1} \right) - \mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) $ | (29) |
The Lyapunov-Krasovskii function about the error is chosen as
| $ \mathit{\boldsymbol{V}}\left( k \right) = {\mathit{\boldsymbol{V}}_1}\left( k \right) + {\mathit{\boldsymbol{V}}_2}\left( k \right) + {\mathit{\boldsymbol{V}}_3}\left( k \right) + {\mathit{\boldsymbol{V}}_4}\left( k \right) $ | (30) |
where
| $ {\mathit{\boldsymbol{V}}_1}\left( k \right) = {{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{P\tilde {\bar x}}}\left( k \right) $ |
| $ {\mathit{\boldsymbol{V}}_2}\left( k \right) = \sum\limits_{i = k - \mathit{\boldsymbol{d}}\left( k \right)}^{k - 1} {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( i \right)} $ |
| $ {\mathit{\boldsymbol{V}}_3}\left( k \right) = \sum\limits_{\pi = - {d_{M + 1}}}^{ - {d_m}} {\sum\limits_{i = k + \pi }^{k - 1} {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( i \right)} } $ |
| $ {\mathit{\boldsymbol{V}}_4}\left( k \right) = \sum\limits_{\pi = - {d_M}}^{ - 1} {\sum\limits_{i = k + {\rm{ \mathsf{ π} }}}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Z\tilde e}}\left( i \right)} } $ |
If w(k) is not considered, then the following deduction are obtained as
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_1}\left( {k + 1} \right) - {\mathit{\boldsymbol{V}}_1}\left( k \right) = \left( {{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( k \right){{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}^{\rm{T}}} + } \right.\\ \;\;\;\;\left. {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( {k - d\left( k \right)} \right)\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}} \right) \cdot \mathit{\boldsymbol{P}}\left( {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right)} \right. + \\ \;\;\;\left. {{{\mathit{\boldsymbol{\bar A}}}_d}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right)} \right) - {\mathit{\boldsymbol{V}}_1}\left( k \right) = \\ \;\;\;{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right)\left( {{{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right) - \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + \\ \;\;\;2{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right){\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( {k - d\left( k \right)} \right)\mathit{\boldsymbol{\bar A}}_{\rm{d}}^{\rm{T}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) = \\ \;\;\;{\mathit{\boldsymbol{\eta }}^{\rm{T}}}{{\bf \Omega }}\mathit{\boldsymbol{\eta }} \end{array} $ | (31) |
where
| $ \mathit{\boldsymbol{\eta }} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right)}\\ {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( {k - d\left( k \right)} \right)} \end{array}} \right] $ |
| $ {{\bf \Omega }} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right) - \mathit{\boldsymbol{P}}}&{{{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}}\\ * &{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}} \end{array}} \right] $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_2}\left( {k + 1} \right) - {\mathit{\boldsymbol{V}}_2}\left( k \right) = \sum\limits_{i = k + 1 - d(k + 1)}^k {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( i \right) - } \\ \;\;\;\;\;\;\sum\limits_{i = k - d\left( k \right)}^{k - 1} {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( i \right)} \le {{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( k \right) - \\ \;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( {k - d\left( k \right)} \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) + \\ \;\;\;\;\;\;\sum\limits_{i = k + 1 - {d_M}}^{k - {d_m}} {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( i \right)} \end{array} $ | (32) |
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_3}\left( {k + 1} \right) - {\mathit{\boldsymbol{V}}_3}\left( k \right) = \left( {{d_M} - {d_m}} \right){{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( \mathit{\boldsymbol{k}} \right) - \\ \;\;\;\;\;\sum\limits_{i = k + 1 - {d_M}}^{k - {d_m}} {{{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Q\tilde {\bar x}}}\left( i \right)} \end{array} $ | (33) |
Additionally, from the Eq.(30), it is obtained that
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde e}}\left( k \right) = \mathit{\boldsymbol{\tilde {\bar x}}}\left( {k + 1} \right) - \mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) = \\ \;\;\;\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) + {{\mathit{\boldsymbol{\bar A}}}_d}\mathit{\boldsymbol{\tilde {\bar x}}}\left( {k - d\left( k \right)} \right) \end{array} $ | (34) |
So it is obtained that
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_4}\left( {k + 1} \right) - {\mathit{\boldsymbol{V}}_4}\left( k \right) = \\ \;\;\;\;\;{d_M}{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Z\tilde e}}\left( k \right) - \sum\limits_{i = k - {d_M}}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Z\tilde e}}\left( i \right)} \le \\ \;\;\;\;\;{d_M}{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Z\tilde e}}\left( k \right) - \sum\limits_{i = k - d\left( k \right)}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Z\tilde e}}\left( i \right)} \le \\ \;\;\;\;\;{d_M}{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Z\tilde e}}\left( k \right) - \\ \;\;\;\;\;\frac{1}{{{d_M}}}\left( {\sum\limits_{i = k - d\left( k \right)}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( i \right)} } \right)\mathit{\boldsymbol{Z}}\left( {\sum\limits_{i = k - d\left( k \right)}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( i \right)} } \right) = \\ \;\;\;\;\;{d_M}{\mathit{\boldsymbol{\eta }}^{\rm{T}}}{{\bf \bar \Omega }}\mathit{\boldsymbol{\eta }} - \frac{1}{{{d_M}}}{\mathit{\boldsymbol{\eta }}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{Z}}&{ - \mathit{\boldsymbol{Z}}}\\ * &\mathit{\boldsymbol{Z}} \end{array}} \right]\mathit{\boldsymbol{\eta }} \end{array} $ | (35) |
where
| $ {{\bf \bar \Omega }} = \left[ {\begin{array}{*{20}{c}} {{{{{\bf \bar \Omega }}}_{11}}}&{{{{{\bf \bar \Omega }}}_{12}}}\\ * &{{{{{\bf \bar \Omega }}}_{22}}} \end{array}} \right] $ |
| $ {{{{\bf \bar \Omega }}}_{11}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right) $ |
| $ {{{{\bf \bar \Omega }}}_{12}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}{{\mathit{\boldsymbol{\bar A}}}_d} $ |
| $ {{{{\bf \bar \Omega }}}_{22}} = \mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}{{\mathit{\boldsymbol{\bar A}}}_d} $ |
From Eq.(31) to (35), it is obtained that
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{V}}\left( k \right) = \mathit{\boldsymbol{V}}\left( {k + 1} \right) - \mathit{\boldsymbol{V}}\left( k \right) \le \\ \;\;\;\;\;\;{\mathit{\boldsymbol{\eta }}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{11}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{12}}}\\ * &{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{22}}} \end{array}} \right]\mathit{\boldsymbol{\eta }} \buildrel \Delta \over = {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} \eta }} \end{array} $ | (36) |
where
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{11}} = - \mathit{\boldsymbol{P}} + {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right) + \\ \;\;\;\;\;\left( {{d_M} - {d_m} + 1} \right)\mathit{\boldsymbol{Q}} - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} + \\ \;\;\;\;\;{d_M}{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right) \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{12}} = \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} + {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d} + \\ \;\;\;\;\;\;\;{d_M}{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}{{\mathit{\boldsymbol{\bar A}}}_d} \end{array} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{22}} = - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d} + {d_M}\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}{{\mathit{\boldsymbol{\bar A}}}_d} $ |
Using the Schur complement, Θ < 0 is equivalent to the inequality (37).
| $ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{P}}}&{\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}&{\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}}&0\\ * & \mathit{\boldsymbol{\varpi}} &{\frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}& \mathit{\boldsymbol{\bar \varpi}} \\ * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}}}&{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}}\\ * & * & * &{ - \frac{1}{{{d_M}}}Z} \end{array}} \right] < 0 $ | (37) |
where
Pre- and post-multiply the Eq.(37) by diag (P-1, In+nf, In+nf, Z-1) and its transpose, the inequality (28) is obtained.
As Θ < 0, there exists a sufficiently small positive scalar δ which satisfies
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} + {\rm{diag}}\left( {\delta \mathit{\boldsymbol{I}},0} \right) < 0 $ | (38) |
From Eq.(36) and Eq.(38), it is obtained that
| $ \Delta \mathit{\boldsymbol{V}}\left( k \right) < - \delta {{\mathit{\boldsymbol{\tilde {\bar x}}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\tilde {\bar x}}}\left( k \right) $ | (39) |
So when w(k)=0, the augmented estimation error Eq.(27) is asymptotically stable, Theorem 1 is proved.
Remark 3 As P-1, Z-1 exist in the inequality (28), inequality (28) is not a standard LMI. Nevertheless, the CCL algorithm can solve the non-convex problem effectively, and its process is seen in Algorithm 1.
Theorem 2 For given scalars dm and dM, if there exists matrix P, Q, Z and γ>0, which satisfy the inequality (40)
| $ \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{P}}^{ - 1}}}&{\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}}&{{{\mathit{\boldsymbol{\bar A}}}_d}}&{{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}}&0&0\\ * &\mathit{\boldsymbol{\varpi}} &{\frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&0&{{{\mathit{\boldsymbol{\bar A}}}^{\rm{T}}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}} - \mathit{\boldsymbol{I}}}&{{{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{V}}^{\rm{T}}} - \mathit{\boldsymbol{\bar C}}_w^{\rm{T}}}\\ * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}}}&0&{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}}&0\\ * & * & * &{ - {\gamma ^2}{\mathit{\boldsymbol{I}}_{2d + 2q}}}&{\mathit{\boldsymbol{\bar B}}_d^{\rm{T}} - \mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{L}}^{\rm{T}}}}&{\mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{V}}^{\rm{T}}}}\\ * & * & * & * &{ - \frac{1}{{{d_M}}}{\mathit{\boldsymbol{Z}}^{ - 1}}}&0\\ * & * & * & * & * &{ - {\mathit{\boldsymbol{I}}_q}} \end{array}} \right] < 0 $ | (40) |
Then at zero initial condition, ϕ(k)=0, the performance index Eq.(26) is satisfied.
Proof Define
| $ \mathit{\boldsymbol{J}} = \Delta \mathit{\boldsymbol{V}}\left( k \right) + {{\mathit{\boldsymbol{\tilde r}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\tilde r}}\left( k \right) - {\gamma ^2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{\bar w}}\left( k \right) $ | (41) |
Choosing the Lyapunov-Krasovskii function as Eq.(30), then the following inequalities are obtained as
| $ {\mathit{\boldsymbol{V}}_1}\left( {k + 1} \right) - {\mathit{\boldsymbol{V}}_1}\left( k \right) = {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{\varUpsilon}} \mathit{\boldsymbol{\zeta }} $ | (42) |
where
| $ \mathit{\boldsymbol{\zeta }} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde x}}\left( k \right)}\\ {\mathit{\boldsymbol{\tilde x}}(k - d(k))}\\ {\mathit{\boldsymbol{\bar w}}(k)} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\varUpsilon}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varUpsilon}} _{11}}}&{{{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}}&{{\mathit{\boldsymbol{\varUpsilon}} _{13}}}\\ * &{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}}&{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right)}\\ * & * &{{\mathit{\boldsymbol{\varUpsilon}} _{33}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{\varUpsilon}} _{11}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right) - \mathit{\boldsymbol{P}} $ |
| $ {\mathit{\boldsymbol{\varUpsilon}} _{13}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) $ |
| $ {\mathit{\boldsymbol{\varUpsilon}} _{33}} = {\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_4}\left( {k + 1} \right) - {\mathit{\boldsymbol{V}}_4}\left( k \right) \le {d_M}{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Z\tilde e}}\left( k \right) - \\ \;\;\;\;\;\frac{1}{{{d_M}}}\left( {\sum\limits_{i = k - d(k)}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}} (i)} \right)\mathit{\boldsymbol{Z}}\left( {\sum\limits_{i = k - d(k)}^{k - 1} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}} (i)} \right) = \\ \;\;\;\;\;{d_M}{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{\varUpsilon}} \mathit{\boldsymbol{\zeta }} - \frac{1}{{{d_M}}}{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\left[ {\begin{array}{*{20}{r}} \mathit{\boldsymbol{Z}}&{ - \mathit{\boldsymbol{Z}}}&0\\ *&\mathit{\boldsymbol{Z}}&0\\ *&*&0 \end{array}} \right]\mathit{\boldsymbol{\zeta }} \end{array} $ | (43) |
where
| $ \mathit{\boldsymbol{\bar \varUpsilon}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{11}}}&{{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{12}}}&{{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{13}}}\\ * &{{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{22}}}&{{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{23}}}\\ * & * &{{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{33}}} \end{array}} \right] $ |
| $ {{\mathit{\boldsymbol{\bar \varUpsilon}} }_{11}} = {{{{\bf \bar \Omega }}}_{11}},{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{12}} = {{{{\bf \bar \Omega }}}_{12}} $ |
| $ {{\mathit{\boldsymbol{\bar \varUpsilon}} }_{13}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) $ |
| $ {{\mathit{\boldsymbol{\bar \varUpsilon}} }_{22}} = {{{{\bf \bar \Omega }}}_{22}},{{\mathit{\boldsymbol{\bar \varUpsilon}} }_{23}} = \mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) $ |
| $ {{\mathit{\boldsymbol{\bar \varUpsilon}} }_{33}} = {\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) $ |
From Eqs.(41), (32), (33) and (43) it is obtained that
| $ \begin{array}{*{20}{c}} {{{\bf \Delta }}\mathit{\boldsymbol{V}}\left( k \right) + {{\mathit{\boldsymbol{\tilde r}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\tilde r}}(k) - {\gamma ^2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\bar w}}(k) \le }\\ {{\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{11}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{12}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{13}}}\\ {\; * }&{{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{22}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{23}}}\\ {\; * }&{\; * }&{{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{33}}} \end{array}} \right]\mathit{\boldsymbol{\zeta }} \buildrel \Delta \over = {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varXi} \zeta }}} \end{array} $ | (44) |
where
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{11}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right) - \mathit{\boldsymbol{P}} + \\ \;\;\;\;\;\;\;\left( {{d_M} - {d_m} + 1} \right)\mathit{\boldsymbol{Q}} - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} + \\ \;\;\;\;\;\;\;{d_M}{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right) + \\ \;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{V\bar C}} - {{\mathit{\boldsymbol{\bar C}}}_\mathit{\boldsymbol{w}}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{V\bar C}} - {{\mathit{\boldsymbol{\bar C}}}_w}} \right) \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{12}} = \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} + {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d} + \\ \;\;\;\;{d_M}{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}{{\mathit{\boldsymbol{\bar A}}}_d} \end{array} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{22}} = - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d} + {d_M}\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}{{\mathit{\boldsymbol{\bar A}}}_d} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{13}} = {\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) + \\ \;\;\;\;\;\;\;\;{d_M}{\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) + \\ \;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{V\bar C}} - {{\mathit{\boldsymbol{\bar C}}}_w}} \right)^{\rm{T}}}\mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{\bar D}}}_d} \end{array} $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{23}} = \mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) + {d_M}\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_{33}} = {\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) + \\ \;\;\;\;\;{d_M}{\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right)^{\rm{T}}}\mathit{\boldsymbol{Z}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right) + \\ \;\;\;\;\;\mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{\bar D}}}_d} - {\gamma ^2}{\mathit{\boldsymbol{I}}_{2d + 2q}} \end{array} $ |
Using the Shcur complement for Ξ, Ξ < 0 is equivalent to the inequality (45)
| $ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{P}}}&{\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}&{\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}}&{\mathit{\boldsymbol{P}}\left( {{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}} \right)}&0&0\\ * &\mathit{\boldsymbol{\varpi}} &{\frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&0&{\left( {{{\mathit{\boldsymbol{\bar A}}}^{\rm{T}}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}} - \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{Z}}}&{{{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{V}}^{\rm{T}}} - \mathit{\boldsymbol{\tilde C}}_w^{\rm{T}}}\\ * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}}}&0&{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}}&0\\ * & * & * &{ - {\gamma ^2}{\mathit{\boldsymbol{I}}_{2d + 2q}}}&{\left( {\mathit{\boldsymbol{\bar B}}_d^{\rm{T}} - \mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{L}}^{\rm{T}}}} \right)\mathit{\boldsymbol{Z}}}&{\mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{V}}^{\rm{T}}}}\\ * & * & * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&0\\ * & * & * & * & * &{ - {\mathit{\boldsymbol{I}}_q}} \end{array}} \right] < 0 $ | (45) |
Pre- and post-multiply the Eq. (45) by diag (P-1, In+nf, In+nf, I2d+2q, Z-1, Iq) and its transpose, the inequality (40) is obtained, i.e., J < 0.
From Eq.(41), it is obtained that
| $ \Delta \mathit{\boldsymbol{V}}(k) + {{\mathit{\boldsymbol{\tilde r}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\tilde r}}(\mathit{\boldsymbol{k}}) - {\gamma ^2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\bar w}}(k) < 0 $ | (46) |
Adding the both sides of Eq.(46) from k=0 to ∞, it is obtained that
| $ \begin{array}{l} \mathit{\boldsymbol{V}}\left( \infty \right) - \mathit{\boldsymbol{V}}\left( 0 \right) + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{k = 0}^\infty {\left( {{{\mathit{\boldsymbol{\tilde r}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\tilde r}}(\mathit{\boldsymbol{k}}) - {\gamma ^2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\bar w}}(k)} \right)} < 0 \end{array} $ | (47) |
Notice that, at zero initial condition, ϕ(k)= 0, ϕ(k)=0, so V(0) =0, V(∞) ≥0, from Eq.(47), the following inequality is obtained as
| $ \begin{array}{l} \sum\limits_{k = 0}^\infty {\left( {{{\mathit{\boldsymbol{\tilde r}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\tilde r}}(k) - {\gamma ^2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}(k)\mathit{\boldsymbol{\bar w}}(k)} \right)} < \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{V}}\left( 0 \right) - \mathit{\boldsymbol{V}}\left( \infty \right) < 0 \end{array} $ | (48) |
i.e., for w(k)≠0, w(k)∈L2[0, +∞), performance index Eq.(26) is satisfied.
So the Theorem 2 is proved.
Remark 4 In Theorem 2, when w(k)=0, Eq.(45) is represented as
| $ \mathit{\boldsymbol{ \boldsymbol{\varXi} '}} < 0 $ | (49) |
where
| $ \mathit{\boldsymbol{ \boldsymbol{\varXi} '}} = \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{P}}}&{\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar C}}} \right)}&{\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_d}}&0&0\\ * &\mathit{\boldsymbol{\varpi}} &{\frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&{\left( {{{\mathit{\boldsymbol{\bar A}}}^{\rm{T}}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}} - \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{Z}}}&{{{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{V}}^{\rm{T}}} - \mathit{\boldsymbol{\tilde C}}_w^{\rm{T}}}\\ * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}}}&{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}\mathit{\boldsymbol{Z}}}&0\\ * & * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&0\\ * & * & * & * &{ - {\mathit{\boldsymbol{I}}_q}} \end{array}} \right] $ |
By calculating, Eq. (49) is equivalent to the following inequality
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} + \mathit{\boldsymbol{ \boldsymbol{\varPi} }} < 0 $ | (50) |
where
| $ \mathit{\boldsymbol{ \boldsymbol{\varPi} }} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{\bar CV}} - {{\mathit{\boldsymbol{\bar C}}}_w}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{\bar CV}} - {{\mathit{\boldsymbol{\bar C}}}_w}} \right)}&0&0\\ * &0&0\\ * &0&0 \end{array}} \right] $ |
Notice that Π ≥0, so Θ < 0. From the deduction of Theorem 1, when Θ < 0, Eq.(27) is asymptotically stable, so if the Theorem 2 is satisfied, performance (ⅰ) and (ⅱ) are met, then our designed fault diagnosis observer is a robust H∞ one for sampled-data descriptor system.
The CCL algorithm is used to solve the non-convex problem caused by P-1 and Z-1 in the inequality (40).
Define the maximum iteration as Kmax, the minimum iteration which satisfies the performance index 2 as βmin, for the given time-vary delay parameters dm and dM, the process of CCL algorithm for Theorem 2 is as follows.
Algorithm 1
Step 1. For given dm>0, dM>0 and Kmax >0, give a initial value of γ which is sufficiently large and satisfies the inequality(51) and (52), let βmin=γ.
Step 2. Find a group of feasible solution L0, V0, P0, Q0, Z0 which satisfy the inequality (51) and (52), if there is none, exist. Otherwise, set k=0 and jump to Step 3.
Step 3. Solving the LMI problems as Eq.(51) and Eq. (52)
| $ {\mathop{\rm minTr}\nolimits} \left( {\mathit{\boldsymbol{PW}}_1^k + {\mathit{\boldsymbol{P}}^k}{\mathit{\boldsymbol{W}}_1} + \mathit{\boldsymbol{ZW}}_2^k + {\mathit{\boldsymbol{Z}}^k}{\mathit{\boldsymbol{W}}_2}} \right) $ | (51a) |
| $ \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{W}}_1}}&{\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{L\bar Cq}}}&{{{\mathit{\boldsymbol{\bar A}}}_d}}&{{{\mathit{\boldsymbol{\bar B}}}_d} - \mathit{\boldsymbol{L}}{{\mathit{\boldsymbol{\bar D}}}_d}}&0&0\\ * &\mathit{\boldsymbol{\varpi}} &{\frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}}}&0&{{{\mathit{\boldsymbol{\bar A}}}^{\rm{T}}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}} - \mathit{\boldsymbol{I}}}&{{{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{V}}^{\rm{T}}} - \mathit{\boldsymbol{\bar C}}_w^{\rm{T}}}\\ * & * &{ - \frac{1}{{{d_M}}}\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Q}}}&0&{\mathit{\boldsymbol{\bar A}}_d^{\rm{T}}}&0\\ * & * & * &{ - {\gamma ^2}{\mathit{\boldsymbol{I}}_{2d + 2q}}}&{\mathit{\boldsymbol{\bar B}}_d^{\rm{T}} - \mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{L}}^{\rm{T}}}}&{\mathit{\boldsymbol{\bar D}}_d^{\rm{T}}{\mathit{\boldsymbol{V}}^{\rm{T}}}}\\ * & * & * & * &{ - \frac{1}{{{d_M}}}{\mathit{\boldsymbol{W}}_2}}&0\\ * & * & * & * & * &{ - {\mathit{\boldsymbol{I}}_q}} \end{array}} \right] < 0 $ | (51b) |
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{P}}&\mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{I}}&{{\mathit{\boldsymbol{W}}_1}} \end{array}} \right] \ge 0,\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{Z}}&\mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{I}}&{{\mathit{\boldsymbol{W}}_2}} \end{array}} \right] \ge 0 $ | (52) |
Find the feasible solution L, V, P, Q, Z, W1, W2, define Pk+1=P, Zk+1=Z, W1k+1=W1, W2k+1=W2.
Step 4. Verify the inequality (40), if it is satisfied, set γmin=γ, reduce the value of γ, and return to the the Step 2. If the Eq.(40) is not satisfied and k=Kmax, exist. otherwise, set k=k+1, and then jump to the Step 3.
It is easy to know Theorem 1 is also adopted by Algorithm 1, and its process is omitted here.
The final step of a successful fault diagnosis is the residual evaluate, which includes the design of the residual evaluate function and the threshold[13]. In this paper, the residual evaluate function Jr and the threshold Jth are choosing as
| $ {\mathit{\boldsymbol{J}}_r} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left\| {\mathit{\boldsymbol{\tilde r}}\left( {k + n} \right)} \right\|}^2}} } $ | (53) |
| $ {\mathit{\boldsymbol{J}}_{{\rm{th}}}} = \mathop {\sup }\limits_{\mathit{\boldsymbol{w}}\left( k \right),\mathit{\boldsymbol{f}}\left( k \right) = 0} {\left\| {\mathit{\boldsymbol{\tilde r}}\left( k \right)} \right\|_2} $ | (54) |
where N denotes the time window of the residual evaluate. Notice that the width of N is finite, i.e. ∞ is replaced by N, as the fault should be diagnosed as soon as possible, and evaluating the residual in the whole time domain is meaningless.
Based on Eqs.(53) and (54), the decision logic of residual can be formulated as
| $ {\mathit{\boldsymbol{J}}_r} > {\mathit{\boldsymbol{J}}_{{\rm{th}}}} \Rightarrow {\rm{fault - alarm}} $ |
| $ {\mathit{\boldsymbol{J}}_r} \le {\mathit{\boldsymbol{J}}_{{\rm{th}}}} \Rightarrow {\rm{fault - free}} $ |
In this section, a sampled-data descriptor system is given, and the proposed fault diagnosis method is verified. At the zero initial condition, the parameters of the proposed system are given as follows:
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{l}} 1&0\\ 0&0 \end{array}} \right],{\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} { - 1}&0\\ 1&{ - 2} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} { - 0.1}&0\\ 1&{ - 0.1} \end{array}} \right]\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{l}} 1&0\\ 1&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{C}}} = \left[ {\begin{array}{*{20}{c}} {0.2}\\ {0.1} \end{array}} \right],\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {0.7}\\ {0.5} \end{array}} \right],{\mathit{\boldsymbol{D}}_d} = \left[ {\begin{array}{*{20}{c}} {0.1}\\ {0.1} \end{array}} \right] $ |
| $ {d_1}\left( t \right) = 0.6 + 0.2\sin t,{\tau _m} = 0.4,{\tau _M} = 0.8 $ |
w(t) is the white noise which satisfies E(w(t)wT(t)) =2.5×10-4I2.
Using the Eq.(7), choosing
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left[ {\begin{array}{*{20}{c}} 1&0&1&0\\ 0&1&0&{ - 1} \end{array}} \right] $ |
Then H and G are obtained as
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{r}} {0.5}&0\\ { - 0.5}&1 \end{array}} \right],\mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{r}} {0.5}&0\\ { - 0.5}&1 \end{array}} \right] $ |
It is easy to verify that H is non-singular, and H, G satisfy the Eq.(6).
Choosing Aw=-1, Bw=1, Cw=1, γ=1.26. Using the CCL algorithm, the observer parameters are obtained as
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {2.151\;2}&{ - 0.412\;3}\\ { - 0.435\;2}&{0.262\;0}\\ {0.134\;6}&{ - 0.459\;8} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} {1.382\;6}&{ - 0.459\;8} \end{array}} \right] $ |
As the fault includes the gradual and abrupt one, in this paper, the descretized faults in the sensor are choosing as
| $ {\mathit{\boldsymbol{f}}_1}\left( k \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{0 \le k < 130}\\ {\sin \left( {\frac{{{\rm{ \mathsf{ π} }}(k - 130)}}{{32}}} \right),}&{130 \le k < 770}\\ {0,}&{k \ge 770} \end{array}} \right. $ |
| $ {\mathit{\boldsymbol{f}}_2}\left( k \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{0 \le k < 200}\\ {1,}&{200 \le k < 400}\\ { - 0.5,}&{,400 \le k < 600}\\ { - 1,}&{600 \le k < 800}\\ {0,}&{k \ge 800} \end{array}} \right. $ |
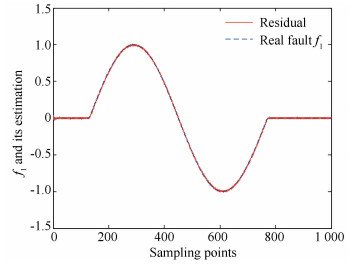
where f1 is the gradual fault, and f2 is the abrupt one. Fig. 1 and Fig. 2 show the fault diagnosis results of f1 and f2.
|
Fig.1 f1 and its estimation (gradual scenario) |

|
Fig.2 f2 and its estimation (abrupt scenario) |
Table 1 shows the Root Mean Square Error (RMSE) of f1 and f2.
| Table 1 RMSE of f1 and f2 |
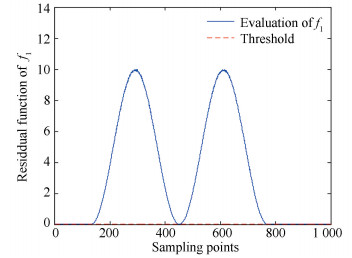
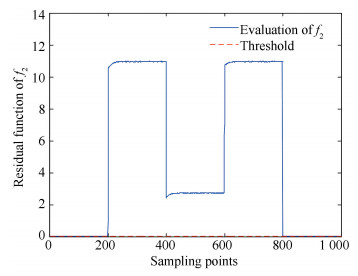
The threshold Jth is set as Jth=0.04, and Fig. 3, Fig. 4 show the residual evaluation function of f1 and f2.
|
Fig.3 Residual evaluation function of f1 |
|
Fig.4 Residual evaluation function of f2 |
From Fig. 1 and Fig. 2, it can be seen that, for both gradual and abrupt faults, accurate fault diagnosis results are obtained by our designed observer, and Table 1 further verifies this accuracy. From Table 1, for both gradual fault and abrupt fault, the estimation error is about 0.05, which means our designed fault diagnosis observer implements an accurate fault diagnosis. When the evaluation functions in Fig. 3 and Fig. 4 beyond the threshold, the faults are detected.
Now we analyze the robust H∞ performance index of our designed fault diagnosis observer. In Ref.[13], the author has argued that, for the augmented system (25), the designed observer is a robust H∞ one if the residual and the augmented disturbance (which includes the faults and the disturbance) satisfy that
| $ {\left\| {{\mathit{\boldsymbol{T}}_{\mathit{\boldsymbol{\tilde r\bar w}}}}\left( \mathit{\boldsymbol{Z}} \right)} \right\|_\infty } = \mathop {\sup }\limits_{\bar w \in {L_2},\bar w \ne 0} \frac{{{{\left\| {\mathit{\boldsymbol{\tilde r}}} \right\|}_2}}}{{{{\left\| {\mathit{\boldsymbol{\bar w}}} \right\|}_2}}} < \gamma $ |
By calculation, for fault f1, the maximum value of
In this paper, a robust sensor fault diagnosis observer with a new type of non-singular structure is proposed for linear sampled-data descriptor systems with time-vary delay. The sampled-data descriptor model is transformed into a non-singular discrete-time one for an easy processing by the introducing parameters and the Euler discretization method. The designed observer is proposed based on the augmented estimation error and the measurement residual of this transformed model. A CCL algorithm is introduced in for aiding the calculation of the observer parameters in the form of LMI. The robust H∞ performance index is satisfied at zero initial condition, residual evaluation function is introduced in for judging if the faults occur. Simulating results show that, for both the abrupt fault and the gradual sensor fault, the designed observer implements an accurate fault diagnosis for linear sampled-data descriptor systems with time-vary delay.
| [1] |
Zhou Z H. Robust Control and Filtering for Singular Piecewise-Affine Systems with Norm-bounded Uncertainties. Harbin: Harbin Institute of Technology, 2016.
(  0) 0) |
| [2] |
Duan G R. Analysis and Design of Descriptor Linear Systems. New York: Springer, 2010.
(  0) 0) |
| [3] |
Liu P Y, Zhang Q L, Yang X G, et al. Passivity and optimal control of descriptor biological complex systems. IEEE Transactions on Automatic Control, 2008, 53(Special Issue): 122-125. DOI:10.1109/TAC.2007.911341 (  0) 0) |
| [4] |
Stevens B L, Lewis F L. Aircraft Modeling, Dynamics and Control. New York: Wiley, 1991.
(  0) 0) |
| [5] |
Nyberg M, Frisk E. Residual generation for fault diagnosis of systems described by linear differential-algebraic equations. IEEE Transactions on Automatic Control, 2006, 51(12): 1995-2000. DOI:10.1109/TAC.2006.884960 (  0) 0) |
| [6] |
Gao Z W, Ding S X. Actuator fault robust estimation and fault-tolerant control for a class of nonlinear descriptor systems. Automatica, 2007, 43(5): 912-920. DOI:10.1016/j.automatica.2006.11.018 (  0) 0) |
| [7] |
Cheng Y H, Jiang B, Fu Y P, et al. Robust sensor fault diagnosis for satellite attitude control system based on fuzzy descriptor system approach. Proceedings of 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA). Piscataway: IEEE, 2010.1431-1436. DOI: 10.1109/ISSCAA.2010.5632718.
(  0) 0) |
| [8] |
Astorga-Zaragoza C M, Theilliol D, Ponsart J C, et al. Fault diagnosis for a class of descriptor linear parameter-varying systems. International Journal of Adaptive Control & Signal Processing, 2012, 26(3): 208-223. DOI:10.1002/acs.1259 (  0) 0) |
| [9] |
Shi F M, Patton R J. Simultaneous state and fault estimation for descriptor systems using an augmented PD observer. IFAC Proceedings Volumes, 2014, 47(3): 8006-8011. DOI:10.3182/20140824-6-ZA-1003.01383 (  0) 0) |
| [10] |
Chadli M, Abdo A, Ding S X. H-/H∞ fault detection filter design for discrete-time Takagi-Sugeno fuzzy system. Automatica, 2013, 49(7): 1996-2005. DOI:10.1016/j.automatica.2013.03.014 (  0) 0) |
| [11] |
Yao X M, Wu L G, Zheng W X. Fault detection filter design for Markovian jump singular systems with intermittent measurements. IEEE Transactions on Signal Processing, 2011, 59(7): 3099-3109. DOI:10.1109/TSP.2011.2141666 (  0) 0) |
| [12] |
Chen L, Zhong M Y. Designing robust H∞ fault detection filter for singular time-delay systems with uncertainty. Acta Automatica Sinica, 2008, 34(8): 943-949. (  0) 0) |
| [13] |
Chen L, Zhong M Y, Zhang M Y. H∞ fault detection for linear singular systems with time-varying delay. International Journal of Control, Automation and Systems, 2011, 9(1): 9-14. (  0) 0) |
| [14] |
Wang Z H, Shen Y, Zhang X L, et al. Observer design for discrete-time descriptor systems: an LMI approach. Systems & Control Letters, 2012, 61(6): 683-687. DOI:10.1016/j.sysconle.2012.03.006 (  0) 0) |
| [15] |
Wang Z H, Rodrigues M, Theilliol D, et al. Fault estimation filter design for discrete-time descriptor systems. IET Control Theory & Applications, 2015, 9(10): 1587-1594. DOI:10.1049/iet-cta.2014.0641 (  0) 0) |
| [16] |
Wang Z, Shen Y, Zhang X L. Actuator fault estimation for a class of nonlinear descriptor systems. International Journal of Systems Science, 2014, 45(3): 487-496. DOI:10.1080/00207721.2012.724100 (  0) 0) |
| [17] |
Xu Y X. Some Bifurcation Problems and Their Numerical Analysis in Delay Differential Systems. Changchun: Jilin University, 2005.
(  0) 0) |
 2019, Vol. 26
2019, Vol. 26


