Forecasting volatility of financial assets is a crucial research direction in the field of financial measurement that the accurate measurement of volatility is vital in options pricing and risk management. The autoregressive conditional heteroscedasticity (ARCH) model is one of the most important volatility models for financial time series proposed by Engle [1]and extended by Bollerslev [2] to the generalized ARCH (GARCH) model.
Although the univariate GARCH models can well characterize the volatility of financial time series, it is difficult to study multivariate time series. Bollerslev et al.[3] proposed an extension model of the univariate GARCH, the VEC model, while it is difficult to estimate multiple parameters of high dimensional matrix or guarantee the constraint conditions of positive definite of conditional covariance matrix. Baillie [4]developed conditional correlation coefficient GARCH (CCC-GARCH) models, in which the conditional correlations are constant. This restriction greatly simplifies the estimation but it is not applicable to real financial data. The BEKK model of Caporin and Mcaleer[5] can well describe the volatility of multivariable and guarantee the positive qualitative of covariance matrix, while it has a limitation on model recognition. Considering the interaction between conditional variances, Tsukuda[6]applied the DCC-GARCH model and the dynamic conditional variance decomposition method to analyze the degree of integration of East Asian and global bond markets. Chen[7] proposed the orthogonal GARCH (O-GARCH) models by using principal component analysis (PCA) technology to extract the principal component. Wu and Yu[8] formed the ICA-GARCH models that decompose multivariate time series using independent component analysis (ICA), whose results show that the ICA-GARCH models are more effective to estimate volatilities than the PCA-GARCH methods. Broda[9] used the ICA method to extract the independent components from the multidimensional financial asset returns. García-Ferrer et al.[10] proposed the GICA-GARCH model which combines the ICA and multivariate GARCH (MGARCH) models. Jin[11] imulated the dynamic heterogeneity covariance breakdown in the MGARCH model by a random component. Francq[12] proposed the multivariate log-GARCH-X model. Karanasos[13] applied the vector AR-DCC-FIAPAPARCH model to estimate the long-term volatility correlation and asymmetric volatility response of stock market daily returns. Almeida[14] analyzed the trade-off between the feasibility and flexibility of the MGARCH model. Dua[15] used the vector autoregressive-multivariate GARCH-BEKK model to study the correlation between Indian and American stock markets. Hyvarinen et al.[16] proposed a linear non-Gaussian acyclic model (LiNGAM) based on the structural equation model, which used the ICA method to obtain the cause effects and applied the ICA-LiNGAM algorithm as the estimation method. Tashiro et al.[17] utilized a direct method to estimate the cause effects based on the non-Gaussianity and proposed a new direct estimation algorithm named DirectLiNGAM.
Based on the combination of structural autoregressive moving-average (ARMA) model and the GARCH model, we present the ARMA-GARCH model in this paper. The relationship between conditional heteroscedasticity of the independent component of error term vector and that of residual vector was constructed. The estimation of the impulse response of conditional volatility of MGARCH models was translated to the estimation of the impulse response of the independent component of error term vector, and the causal structure was maintained.
The rest of this paper is organized as follows. In Section 2, we present the ARMA-GARCH model and demonstrate the procedure of applying impulse response of conditional volatility in multivariate volatilities modeling. In Section 3, we introduce the ICA-LiNGAM and the Direct-LiNGAM algorithms with the mean squared error (MSE) as the evaluation method of the algorithm performance. In Section 4, the specific steps of the ARMA-GARCH model parameter estimation are described. An empirical application of the model in finance is given in Section 5 and the conclusions are drawn in Section 6.
2 The ARMA-GARCH Model 2.1 Model DefinitionBased on the combination of instantaneous model and the ARMA model with the external influence of non-Gaussian, Kawahara [18]proposed an ARMA-LiNGAM model and presented an estimation method. The error term vector e(t) of ARMA-LiNGAM can describe the volatility of financial data well, so taking the e(t) as GARCH process, the ARMA-GARCH model is proposed in this paper. Let y(t)=[y1(t), y2(t), .…, yn(t)]T, (t=1, 2, …, T) represents the observed variable over a period of time. Without loss of generality, assuming that each y(t) has zero mean vectors, the ARMA-GARCH model is defined as
| $ \mathit{\boldsymbol{y}}(t) = \sum\limits_{j = 0}^p {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_j}} \mathit{\boldsymbol{y}}(t - j) + \mathit{\boldsymbol{e}}(t) - \sum\limits_{j = 1}^q {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_j}} \mathit{\boldsymbol{e}}(t - j) $ | (1) |
where Ψj(j=0, 1, …, p) are n×n matrices, which represent the causal effects between the variables y(t) and y(t-j)(j=0, 1, …, p). For τ>0, the effects are general autoregressive effects from the past to the present, while for τ=0, the effects are contemporaneous. In addition, Ωj(j=1, 2, …, q) are the n×n moving average coefficient matrices and the error term vector e(t) is the vector of external influences ei(t)(i=1, 2, …, n). Hence, the following assumptions on the ei(t) are made.
1) The ei(t) are GARCH process, i.e., each ei(t) is treated as a univariate GARCH (k, l) model
| $ {e_i}(t) = \sqrt {{h_i}(t)} {\eta _i}(t) $ | (2) |
where ηi(t) is a sequence of independent and identically distributed random variables, Eηt=0 and Eηt2=1;hi(t) are conditional variance of series ei(t):hi(t)=V(ei(t)|It-1), It-1 is the past information up to time t-1, and
| $ {h_i}(t) = {\omega _i} + \sum\limits_{j = 1}^l {{\alpha _{ij}}} {e_i}{(t - j)^2} + \sum\limits_{j = 1}^k {{\beta _{ij}}} {h_i}(t - j) $ |
To ensure a positive hi(t)>0, we assume that ωi>0, αij≥0(j=1, 2, …, l), βij≥0(j=1, 2, …, k), and
2) The instantaneous effects matrix Ψ0 in the model corresponds to a directed acyclic graph. The acyclicity is equivalent to the existence of a permutation matrix P which makes P Ψ0 PT a lower triangular. The acyclicity also ensures that I-Ψ0 is invertible.
From Eq. (1), we have
| $ \begin{array}{l} \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right)\mathit{\boldsymbol{y}}(t) = \sum\limits_{j = 1}^p {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\tau }} \mathit{\boldsymbol{y}}(t - j) + \mathit{\boldsymbol{e}}(t) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^q {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_j}} \mathit{\boldsymbol{e}}(t - j) \end{array} $ | (3) |
By multiplying A = (I -Ψ0)-1 from the left on the both sides, we can obtain
| $ \mathit{\boldsymbol{y}}(t) = \sum\limits_{j = 1}^p {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_j}} \mathit{\boldsymbol{y}}(t - j) + \mathit{\boldsymbol{n}}(t) - \sum\limits_{j = 1}^q {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_j}} \mathit{\boldsymbol{n}}(t - j) $ | (4) |
where Φτ= A Ψτ, n(t)= Ae(t), and Θj = AΩjA-1. Eq. (4) is a standard ARMA model, which can be estimated by conditional maximum likelihood[19] of Φj(j=1, 2, …, p) and Θj(j=1, 2, …, q).
We calculate the residual vector n(t) in Eq. (4) and separate the instantaneous effects matrix Ψ0 and the error term vector e(t) from the n (t). According to the conclusion of Hyvarinen et al.[16], the non-Gaussian of e(t) in the GARCH model and the acyclic of instantaneous effects matrix Ψ0 ensure that e(t) and Ψ0 can be uniquely identified. Therefore, the volatility structure of n(t) can be estimated by Ψ0 and the volatility structure of e(t). Eq. (4) shows that the conditional covariance matrix of n(t) is
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_t} = cov\left( {\mathit{\boldsymbol{n}}(t)|{\mathit{\boldsymbol{I}}_{t - 1}}} \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{H}}_t}{\mathit{\boldsymbol{A}}^{\rm{T}}} = \sum\limits_{i = 1}^n {{a_i}} a_i^\prime {h_{it}} $ | (5) |
where Ht=diag(h1t, h2t, …, hnt), hit is the conditional variance of the ith component of e(t) given by Eq. (2), A =(a1, a2, …, an), and ai is the ith column vector of A.
2.2 Impulse Response of Conditional VolatilityEq. (5) indicates the relationship between conditional heteroscedasticity of the independent component of error term vector e(t) and that of residual vector n(t). The estimation of the impulse response of conditional volatility of MGARCH models is translated to the estimation of the impulse response of the independent component of error term vector. The volatility of Γt can be inferred by analyzing the response of one unit shock to the system in e(t). The impulse response of conditional volatility can well describe the volatile effects of one unit shock on the system.According to Eq. (5), the impulse response of the conditional volatility of the residual vector n(t) can be expressed as
| $ {\mathit{\boldsymbol{R}}_{s,i}} = \frac{{\partial {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{t + s/t}}}}{{\partial {e_i}{{(t)}^2}}} = \sum\limits_{i = 1}^n {{a_i}} a_i^\prime \frac{{\partial {h_{i,t + s/t}}}}{{\partial {e_i}{{(t)}^2}}} $ | (6) |
where Rs, i is the s order lag impulse response of the ith element in e(t) after one unit shock, and Γt+s/t is the conditional covariance information set of Γt+s at time t. According to Hafner [20], the impulse response function of the univariate GARCH (k, l) model can be obtained as follows:
| $ {\rm{For}}\;s \le q,{r_{s,i}} = \sum\limits_{j = 1}^{s - 1} {\left( {{\alpha _j} + {\beta _j}} \right){r_{s - j,i}}} + {\alpha _s} $ | (7.1) |
| $ {\rm{For}}\;q < s \le m,{r_{s,i}} = \sum\limits_{j = 1}^{s - 1} {\left( {{\alpha _j} + {\beta _j}} \right){r_{s - j,i}}} $ | (7.2) |
| $ {\rm{For}}\;s > m,{r_{s,i}} = \sum\limits_{j = 1}^m {\left( {{\alpha _j} + {\beta _j}} \right){r_{s - j,i}}} $ | (7.3) |
where
In this section, we briefly introduce the ICA-LiNGAM and Direct-LiNGAM algorithms. Then we use MSE as the evaluation method of algorithm performance.
LiNGAM, the linear non-Gaussian acyclic model proposed by Hyvarinen et al. [16], is a variant of structural equation model and Bayesian network, which satisfies the following two conditions: 1) the adjacency matrix B corresponds to a directed acyclic graph; 2) the components of e are independent and non-Gaussian. Under the above non-Gaussian acyclic conditions, LiNGAM can be formally expressed as
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{Bx}} + \mathit{\boldsymbol{e}} $ | (8) |
where x is a p dimensional random vector, B is an adjacency matrix of p×p, and e is a p dimensional non-Gaussian random noise vector.
The original solution to the LiNGAM model was proposed by Hyvarinen et al.[16]based on the ICA method, i.e., the ICA-LiNGAM algorithm, which separates the adjacency matrix B and the non-Gaussian e vector from the observed data x[21]. Because of the directed acyclic graph hypothesis, the existence of a permutation matrix P∈Rp×p makes B′=PBPT as close as possible to strictly lower triangular. Then, the causal order is obtained by combining B′ with strictly triangular characteristics. Finally, a certain pruning algorithm is used to get the final causal network. The ICA-LiNGAM algorithm relies on the selection of initial values, which may not converge to a correct solution. Shimizu et al. [22]proposed the DirectLiNGAM algorithm using the principle of residual independence, in which exogenous variables were selected on the basis of the Darmois-Skitovitch theorem[23], i.e., the judgment variable is a regression residual independent of all other variables.
Assuming x is a set of variables, the exogenous variable xe can be calculated from Eqs. (9)-(11)
| $ r_i^{(j)} = {x_i} - \frac{{cov\left( {{x_i},{x_j}} \right)}}{{var\left( {{x_j}} \right)}}{x_j} $ | (9) |
| $ {T_k}\left( {{x_j};x} \right) = \sum\limits_{i \in x,i \ne j} {{\rm{M}}{{\rm{I}}_k}} \left( {{x_j},r_i^{(j)}} \right) $ | (10) |
| $ {x_e} = \arg \mathop {\min }\limits_{j \in x} {T_k}\left( {{x_j};x} \right) $ | (11) |
where Tk is the degree of independence of the two variables, and MIk is the kernel-based measure of mutual information based on the Gaussian kernel. Assuming xj is the first selected exogenous variable, the following only needs to update the current variable xi with the current residual ri(j) to make it satisfies the acyclic and non-Gaussian assumptions of the basic LiNGAM model. The process of updating the exogenous variable and eliminating the effect of exogenous variables is completed recursively, and the whole cause and effect order is then obtained. Finally, the pruning is completed by using the least square regression method.
In this paper, the performance of the above algorithm is tested by simulation data and we use MSE as the evaluation indicator of causal structure model algorithm. The MSE of B is defined as follows:
| $ {\rm{MSE}} = \sqrt {\frac{1}{{{n^2}}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{\left( {{b_{ij}} - {{\hat b}_{ij}}} \right)}^2}} } } $ | (12) |
where n is the number of all variables in the dataset, bij is the true value of the adjacency matrix corresponding to the causality network, and
We randomly generated artificial data sets with each combination of number of variables p and sample size N(p=15, 30, 60; N=500, 1000, 2000, 3000) by following steps.
1) We constructed an adjacency matrix with all elements equal to zero and used the Bernoulli random variable to replace each element of the lower triangle.
2) We replaced the non-zero elements in adjacency matrix by the randomly generated numbers from the interval [-1.5, -0.5]∪[0.5, 1.5] and used the generated matrix as the adjacency matrix B. We also randomly selected the noise ei from the interval [1, 3].
3) The values of the observed variables xi were generated according to Eq. (8). Finally, we randomly permuted the order of xi to make the order of observation inconsistent with the causal order. Then the DirectLiNGAM algorithm and ICA-LiNGAM algorithm were tested on the generated data sets.
Table 1 and Table 2 show the MSE between the true value B and the estimated value
|
Table 1 MSE between true B and estimated |
|
Table 2 MSE between true B and estimated |
4 Estimation of the ARMA-GARCH Model
The estimation procedure and the specific steps of the ARMA-GARCH model parameter estimation are described as follows:
1) Use the conditional maximum likelihood to estimate the autoregressive matrix Φj and the moving average matrix Θj of Eq. (4), and calculate the residual vector n(t).
2) Use the DirectLiNGAM algorithm to estimate the causal order and calculate the instantaneous effects matrix Ψ0 and the error term vector e(t) :
| $ \mathit{\boldsymbol{n}}\left( t \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}\mathit{\boldsymbol{n}}\left( t \right) + \mathit{\boldsymbol{e}}\left( t \right) $ |
3) Use the estimation matrix Ψ0 to calculate the parameters in Eq. (1) as in
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_j} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_j},{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_j} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_j}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right)^{ - 1}} $ |
4) Use the maximum likelihood function to estimate the univariate GARCH parameters from the error term vector e(t).
5) Use Eq. (7) to estimate the univariate impulse response function for each element in e(t).
6) Use the univariate impulse response function, the matrix Ψ0, and Eq. (6) to estimate the impulse response of the conditional volatility.
5 Applications in FinanceWe applied the ARMA-GARCH model to estimate the volatility of stock market. The chosen indices are A share index of Shanghai stock Exchange (000002.ss), B share index of Shanghai stock Exchange (000003.ss), A share index of Shenzhen stock Exchange (399107.sz), and B share index of Shenzhen stock Exchange (399108.sz). The dataset was from September 2, 2014 to December 30, 2017, representing 1150 daily observations. The daily return ri(t) were calculated by ri(t)=log(pi(t))-log(pi(t-1)), where the closing price of index i on the trading day is t by pi(t). We fitted the ARMA-GARCH to the dataset, where the order (p, q) = (1, 2) was selected based on Bayesian information criteria (BIC). The ARMA (1, 2)-GARCH (1, 1) model is
| $ \begin{array}{l} \mathit{\boldsymbol{y}}\left( t \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}\mathit{\boldsymbol{y}}(t) + {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_1}\mathit{\boldsymbol{y}}(t - 1) + \mathit{\boldsymbol{e}}(t) - \\ \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1}\mathit{\boldsymbol{e}}(t - 1) - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}\mathit{\boldsymbol{e}}(t - 2) = \\ \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}\mathit{\boldsymbol{y}}(t - 1) + \mathit{\boldsymbol{n}}(t) - {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}\mathit{\boldsymbol{n}}(t) - {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\mathit{\boldsymbol{n}}(t) \end{array} $ | (13) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1} = {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right)^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_1},\mathit{\boldsymbol{n}}(t) = {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right)^{ - 1}}\mathit{\boldsymbol{e}}(t) $ | (14.1) |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1} = {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right)^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0}} \right),{\mathit{\boldsymbol{e}}_i}(t) = \\ \;\;\;\;\;\;\sqrt {{h_i}(t)} {\eta _i}(t) \end{array} $ | (14.2) |
| $ {h_i}(t) = {\omega _i} + {\alpha _{i1}}{e_i}{(t - 1)^2} + {\beta _{i1}}{h_i}(t - 1) $ | (14.3) |
The estimated parameters in ARMA (1, 2) are as follows:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0\\ { - 0.0081}&0&0&0\\ { - 0.0054}&{ - 0.0132}&0&0\\ {0.0023}&{2.0307}&{0.1207}&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_1} = \left[ {\begin{array}{*{20}{c}} {0.021\;900\;0}&{ - 0.334\;800\;00}&{ - 0.038\;800\;0}&{0.531\;000\;0}\\ {0.171\;977\;4}&{0.046\;388\;12}&{ - 0.415\;914\;3}&{0.882\;301\;1}\\ { - 0.626\;414\;0}&{ - 0.187\;959\;80}&{ - 0.838\;795\;4}&{0.978\;457\;0}\\ { - 0.732\;828\;5}&{ - 0.197\;190\;57}&{0.909\;103\;3}&{ - 1.231\;530\;7} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} = \left[ {\begin{array}{*{20}{r}} { - 0.0313253}&{0.7118711}&{0.0670461}&{0.5230000}\\ {0.1717016}&{1.5644540}&{ - 0.4118527}&{0.8102363}\\ { - 0.5186029}&{1.2924046}&{ - 0.7380915}&{0.7564634}\\ { - 0.6773514}&{ - 2.6223737}&{1.0576904}&{ - 1.3016272} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2} = \left[ {\begin{array}{*{20}{r}} {0.02865116}&{0.10285811}&{ - 0.0063182}&{0.0653000}\\ {0.03911375}&{0.22505402}&{ - 0.1020263}&{0.0645289}\\ { - 0.02903928}&{0.10795147}&{ - 0.0920588}&{0.0659974}\\ { - 0.17477920}&{ - 0.08299763}&{0.1904511}&{0.0485636} \end{array}} \right] $ |
Fig. 1 shows the direction of the estimated instantaneous causal structure obtained by the DirectLiNGAM algorithm. 000002.ss had strong negative impacts on 000003.ss and 399108.sz, while it had a weaker positive impact on 399107.sz. 399108.sz had a strong positive impact on 399107.sz and a strong negative impact on 000003.ss, whereas 000003.ss only had a strong positive impact on 399107.sz and 399107.sz did not affect other variables.These results were justified in the Chinese stock market.
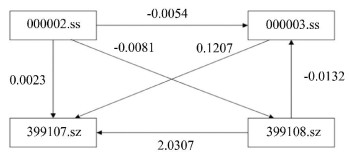
|
Fig.1 Direction of the estimated instantaneous causal structure direction by DirectLiNGAM |
The DirectLiNGAM algorithm was used to separate n(t), obtain the estimation matrix A, and extract e(t), as shown in Fig. 2. The estimated parameters in univariate GARCH (1, 1) model to each ei(t) are shown in Table 3. It can be seen from the estimated GARCH that 000002.ss, 000003.ss, 399107.sz, and 399108.sz had a characteristic of volatility clustering.
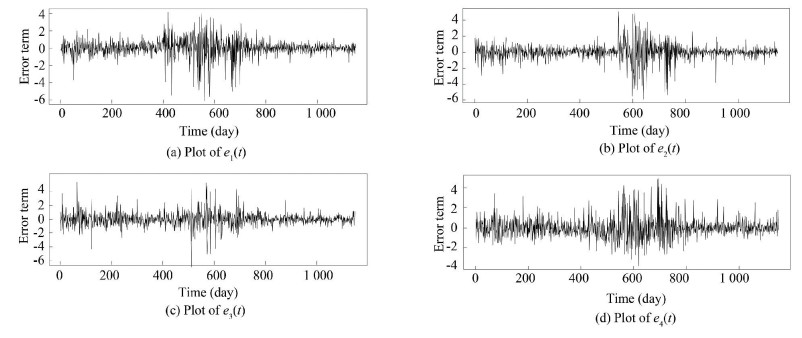
|
Fig.2 Residual series |
| Table 3 Estimation of parameters in GARCH (1, 1) |
Fig. 3 shows the impulse response functions of 000002.ss, 000003.ss, 399107.sz, and 399108.sz to one unit shock, where the dashed lines are 95% confidence interval and the solid line indicates the impulse response. The volatility of 000002.ss had the greatest impact on other variables, and the unit shock of 000002.ss had a longer lasting effect on other variables. The unit shock of 000003.ss had little effect on other variables. The unit shock of 399107.sz only had a positive influence on 399108.sz and the duration was relatively short. The impact amplitude of unit shock on 399107.sz was not very large, but it had a positive impact on 000003.ss with a short duration, which had a negative impact on 399107.sz with a longer duration. As discussed, these results proved that volatility does shift in the impulse response of conditional volatility. The unit shock of 000002.ss had the greatest impact on other variables, and the unit shock of 000003.ss had little effect on other variables, which is consistent with the stock market in China.
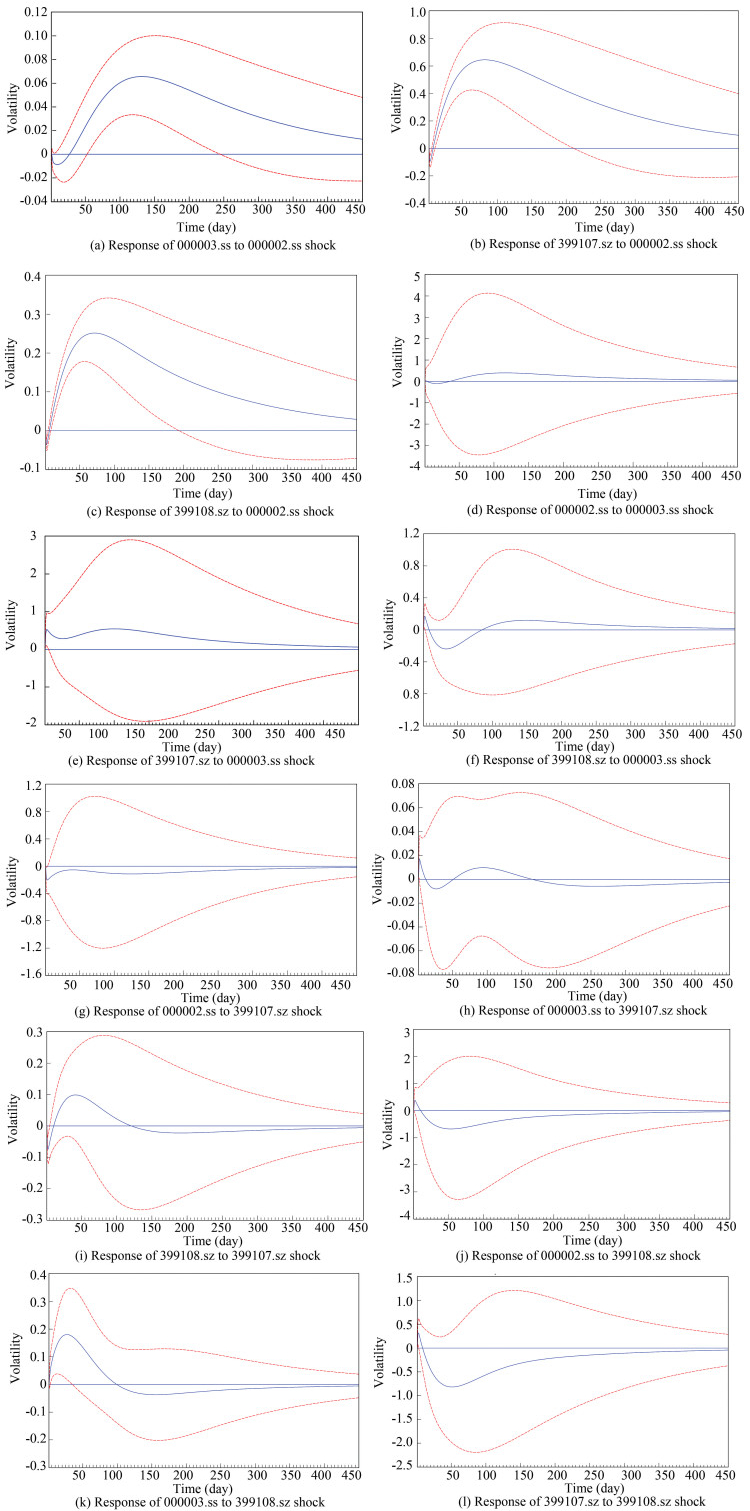
|
Fig.3 Impulse response of conditional volatility |
6 Conclusions
In this paper, we propose an ARMA-GARCH model to estimate the multivariate volatility. The model provides an effective estimation method for the traceability of the dynamic volatility. We can identify the causal structure of the ARMA-GARCH model under data driven. The univariate GARCH model was used to estimate the impulse response of conditional volatility of the MGARCH models with the causal structure maintained at the same time. In practical application, we analyzed the causal structure and volatility structure of 000002.ss, 000003.ss, 399107.sz, and 399108.sz. The results show that 000002.ss had a significant impact on other variables. The volatility shifted in the impulse response of conditional volatility. The impact of 000002.ss largely affected other variables, whereas that of 000003.ss had little effect. The result is in accordance with the stock market in China. The experimental results also show that the ARMA-GARCH model is effective for estimating multivariate volatility.
| [1] |
Engle R F. Autogressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica, 1982, 50(4): 987-1007. DOI:10.2307/1912773 (  0) 0) |
| [2] |
Bollerslev T. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 1986, 31(3): 307-327. DOI:10.1016/0304-4076(86)90063-1 (  0) 0) |
| [3] |
Bollerslev T, Engle R F, Wooldridge J M. A capital asset pricing model with time-varying covariances. Journal of Political Economy, 1988, 96(1): 116-31. DOI:10.1086/261527 (  0) 0) |
| [4] |
Baillie R T, Bollerslev T. The message in daily exchange rates. Journal of Business & Economic Statistics, 2002, 20(1): 60-8. DOI:10.1198/073500102753410390 (  0) 0) |
| [5] |
Caporin M, Mcaleer M. Scalar BEKK and indirect DCC. Journal of Forecasting, 2010, 27(6): 537-49. DOI:10.1002/for.1074 (  0) 0) |
| [6] |
Tsukuda Y, Shimada J, Miyakoshi T. Bond market integration in East Asia: Multivariate GARCH with dynamic conditional correlations approach. International Review of Economics & Finance, 2017, 51: 193-213. DOI:10.1016/j.iref.2017.05.013 (  0) 0) |
| [7] |
Chen R, Yi L, Liu J. Portfolio VaR computation based on O-GARCH. 2008 International Workshop on Modelling, Simulation and Optimization. Piscataway: IEEE, 2008.133-138. DOI: 10.1109/WMSO.2008.32. http://www.onacademic.com/detail/journal_1000037051382010_bc97.html
(  0) 0) |
| [8] |
Wu Edmond H C, Yu Philip L, Li W K. Value at risk estimation using independent component analysis-generalized autoregressive conditional heteroscedasticity (ICA-GARCH) models. International Journal of Neural Systems, 2008, 16(5): 371-382. DOI:10.1142/S0129065706000779 (  0) 0) |
| [9] |
Broda S A, Haas M, Krause J, et al. Stable mixture GARCH models. Journal of Econometrics, 2013, 172(2): 292-306. DOI:10.1016/j.jeconom.2012.08.012 (  0) 0) |
| [10] |
García-Ferrer A, Gomzález-Prieto E, Peña D. A conditionally heteroskedastic independent factor model with an application to financial stock returns. International Journal of Forecasting, 2012, 28(1): 70-93. DOI:10.1016/j.ijforecast.2011.02.010 (  0) 0) |
| [11] |
Jin X, Maheu J M. Modeling covariance breakdowns in multivariate GARCH. Journal of Econometrics, 2016, 194(1): 1-23. DOI:10.1016/j.jeconom.2016.03.003 (  0) 0) |
| [12] |
Francq C, Sucarrat G. An equation-by-equation estimator of a multivariate log-GARCH-X model of financial returns. Journal of Multivariate Analysis, 2017, 153: 16-32. DOI:10.1016/j.jmva.2016.09.010 (  0) 0) |
| [13] |
Karanasos M, Yfanti S, Karoglou M. Multivariate FIAPARCH modelling of financial markets with dynamic correlations in times of crisis. International Review of Financial Analysis, 2016, 45(4): 332-349. DOI:10.1016/j.irfa.2014.09.002 (  0) 0) |
| [14] |
de Almeida D, Hotta L K, Ruiz E. MGARCH models: Trade-off between feasibility and flexibility. International Journal of Forecasting, 2018, 34(1): 45-63. DOI:10.1016/j.ijforecast.2017.08.003 (  0) 0) |
| [15] |
Dua P, Tuteja D. Linkages between Indian and US financial markets: Impact of global financial crisis and Eurozone debt crisis. Macroeconomics & Finance in Emerging Market Economies, 2018, 9(3): 217-240. DOI:10.1080/17520843.2016.1166144 (  0) 0) |
| [16] |
Hyvarinen A, Zhang K, Shimizu S, et al. Estimation of a structural vector autoregression model using non-Gaussianity. Journal of Machine Learning Research, 2010, 11: 1709-1731. (  0) 0) |
| [17] |
Tashiro T, Shimizu S, Hyvärinen A, et al. ParceLiNGAM: A causal ordering method robust against latent confounders. Neural Computation, 2014, 26(1): 57-83. DOI:10.1162/NECO_a_00533 (  0) 0) |
| [18] |
Kawahara Y, Shimizu S, Washio T. Analyzing relationships among ARMA processes based on non-Gaussianity of external influences. Neurocomputing, 2011, 74(12-13): 2212-2221. DOI:10.1016/j.neucom.2011.02.008 (  0) 0) |
| [19] |
Tsay R S. Multivariate time series analysis: With R and financial applications. Wiley, 2013, 3(4): 1-40. (  0) 0) |
| [20] |
Hafner C M, Herwartz H. Volatility impulse responses for multivariate GARCH models: An exchange rate illustration. Journal of International Money & Finance, 2006, 25(5): 719-740. DOI:10.1016/j.jimonfin.2006.04.006 (  0) 0) |
| [21] |
Tashiro T, Shimizu S, Washio T. Estimation of causal orders in a linear non-Gaussian acyclic model: A method robust against latent confounders. Proceedings of the International Conference on Artificial Neural Networks and Machine Learning, ICANN 2012., 2012, 491-198. DOI:10.1007/978-3-642-33269-2_62 (  0) 0) |
| [22] |
Shimizu S, Inazumi T, Sogawa Y, et al. DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model. Journal of Machine Learning Research, 2011, 12(2): 1225-1248. (  0) 0) |
| [23] |
Kagan A, Wesolowski J. An extension of the Darmois-Skitovitch theorem to a class of dependent random variables. Statistics & Probability Letters, 2000, 47(1): 69-73. DOI:10.1016/S0167-7152(99)00139-X (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


