2. Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Anhui University, Hefei 230601, China
Memristor, a type of two-terminal nonlinear circuital element, was put forward by Professor Chua in 1971[1]. As a contemporary hot topic, the study of the nature of memristor has drawn wide attention from researchers. Compared with general differential systems, memristive differential systems with properties of memory, non-volatility, and nonlinearity may exhibit more complicated chaotic behaviors, which has potential application prospects. The current methods of building memristive circuit systems are no more than introducing the memristor in the existing circuit or replacing the nonlinear resistance element in the original circuit with memristor[2-5].For instance, Ruan et al.[2] introduced the simplified Lorenz system that uses memristor as a positive feedback and studied its dynamics. In Ref. [3] and Ref. [4], memristor was substituted for the resistor in the existing circuitry system to construct a new hyperchaotic memristive system with multi-winged attractors. On the contrary, many other scholars focused on the applications of memristor such as secure communications[6], artificial neural networks[7], and non-volatile random access memory[8].
Fractional calculus has been highly favored in the study of chaos theory[9-10] because it makes dynamic systems show more complex chaotic phenomena. As an exceptional case of system that is not linear, fractional-order chaotic systems have more complex dynamics than general nonlinear systems. It was a big hit when Hartley et al.[11] first raised the Chua's system with fractional order in 1995. Then, in Ref. [12] a simple memristive chaos system with fractional order was studied, which is the extension of the integer order chaotic system. To sum up, the current research on fractional order is mostly based on the expansion of the corresponding system into its fractional order form[13-15].
Time-delay (time interval) refers to the period from the initiation of a certain behavior to the results, which is frequently cited in the differential equations. Such delay differential dynamical systems are commonly used and studied in the fields of biological systems[16], economy[17], neural networks[18], chaos[19], physics[20], etc. Delay seems to be very small, but sometimes it has a certain potential impact on the system's oscillation and may affect the dynamics of the entire system. Therefore, it is necessary to investigate time-delay in complex dynamic systems theoretically and practically.
Chaotic synchronization has always been a significant contemporary topic in the study of non-linear science. At present, there are various methods to realize synchronization of chaotic system schemes, such as Laplace transform theory[21], adaptive feedback control method[22], a sinusoidal state coupling control method[23], active control method[24], and sliding model control method[25-27]. Some other methods were reported in Refs. [28-30]. In this paper, we derive sufficient criteria and design a linear feedback controller for system synchronization.
Motivated by what has been discussed, our research object is a fractional-order delayed memristive system without equilibrium. The main contributions are summarized as follows:
1) Taking the parameter a as bifurcation parameter, the evolution law of the proposed system with the change of parameter a was observed. It was found that this system exhibited more complicated chaotic behaviors than the integer order counterpart[31];
2) A simple active control method was designed to cope with chaos synchronization. Then the stability of the error system was discussed to obtain the conditions for system synchronization;
3) The effects of three factors (i.e., parameter a, fractional order q, and time delay τ) on synchronization were discussed by providing examples and the results were analyzed.
The rest of this paper is arranged as follows. Section 2 gives the related definitions regarding to fractional calculus and proposes a delayed memristive chaotic differential system. Section 3 presents the evolution process with the variation of the coefficient parameter a. Section 4 introduces the process of chaos synchronization of the system and provides the stability conditions for the error system. The effects of these factors on the system synchronization are discussed in Section 5 and Section 6 summarizes the obtained findings.
2 Preliminaries 2.1 DefinitionsDefinition 1: Given that f(t) is a continuous function, the Caputo derivative adopting fractional order q is defined as
| $ _0^CD_t^qf(t) = \frac{1}{{\Gamma (m - q)}}\int_0^t {\frac{{{f^{(q)}}(\tau )}}{{{{(t - \tau )}^{q - m + 1}}}}{\rm{d}}\tau } $ | (1) |
| $ \Gamma (x) = \int_0^\infty {{t^{x - 1}}} {e^{ - t}}{\rm{d}}t $ | (2) |
where Γ is the Gamma function, 0≤m-1 < q≤m.
Definition 2: Laplace function defined by the Caputo definition is written as
| $ L\left\{ {_0^CD_t^qf(t)} \right\} = {s^q}F(s) - \sum\limits_{k = 0}^{n - 1} {{s^{q - k - 1}}} {f^k}(0) $ | (3) |
where m-1 < q≤m.F(s) is obtained by the Laplace transform of f(t).
2.2 Fractional-Order Delayed Memristive System without Equilibrium PointTo introduce memristive systems, we generalize the original concept of the memristor and describe it as
| $ \left\{ {\begin{array}{*{20}{l}} {n = W(m,u,t)u}\\ {\dot m = F(m,u,t)} \end{array}} \right. $ | (4) |
in which u, m, and n represent the internal state, input, and output of the memristive model.
The memristive model discussed in this paper is written as
| $ \left\{ {\begin{array}{*{20}{l}} {h\left( {{x_1},{x_2}} \right) = \left( {0.1{x_2} - 1} \right){x_1}}\\ {{x_2} = c{x_1}} \end{array}} \right. $ | (5) |
Fig. 1 shows the circuit principle diagram of the discussed system[31]. The delayed chaotic system consists of four resistors R1, R2, R3, R4, two integrators U1, U2, a delay unit, a capacitor C1, a voltage follower U3, DC voltage (Vc=1VDC), and a generalized memory element.

|
Fig.1 Circuital schematic diagram of a time-delay memristive chaotic system |
By using the Kirchhoff's circuit laws, the characteristic equations of this system can be deduced as
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{x_1}}}{{{\rm{d}}t}} = - \frac{1}{{{R_1}{C_1}}}{x_1}(t - \tau ) + \frac{{{V_{{\rm{sat}}}}}}{{{R_2}{C_1}}}\text{sgn}\left( {{x_1}(t - \tau )} \right) - }\\ {\quad \frac{1}{{{R_3}{C_1}}}h\left( {{x_1},{x_2}} \right) - \frac{{{V_{\rm{C}}}}}{{{R_4}{C_1}}}}\\ {\frac{{{\rm{d}}{x_2}}}{{{\rm{d}}t}} = c{x_1}} \end{array}} \right. $ | (6) |
in which τ is the time delay, Vsat represents the saturation voltage of the operational amplifier U2, and VC=1VDC.
Assume that
| $ a = \frac{1}{{{R_1}{C_1}}},b = \frac{1}{{{R_3}{C_1}}} $ |
| $ d = \frac{{{V_{\rm{C}}}}}{{{R_4}{C_1}}},\frac{{{V_{{\rm{sat}}}}}}{{{R_2}{C_1}}} = 1 $ |
| $ h\left( {{x_1},{x_2}} \right) = \left( {0.1{x_2} - 1} \right){x_1} $ |
then the dimensionless form of Eq. (6) is written as
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - a{x_1}(t - \tau ) + sgn \left( {{x_1}(t - \tau )} \right) - }\\ {\quad bh\left( {{x_1},{x_2}} \right) - d}\\ {{{\dot x}_2} = c{x_1}} \end{array}} \right. $ | (7) |
Eq. (7) is generalized to fractional-order form and expressed as
| $ \left\{ \begin{array}{l} {D^q}{x_1} = - a{x_1}(t - \tau ) + sgn \left( {{x_1}(t - \tau )} \right) - \\ \;\;\;\;\;\;\;bh\left( {{x_1},{x_2}} \right) - d\\ {D^q}{x_2} = c{x_1} \end{array} \right. $ | (8) |
in which 0 < q < 1, τ > 0, and a, b, c, d are positive constants.
| $ \begin{array}{l} {\rm{Let}}\;{D^q}{x_1} = {D^q}{x_2} = 0,\text{then}\\ \left\{ {\begin{array}{*{20}{l}} { - a{x_1} + \text{sgn}\left( {{x_1}} \right) - b\left( {0.1{x_2} - 1} \right){x_1} - d = 0}\\ {c{x_1} = 0} \end{array}} \right. \end{array} $ | (9) |
Clearly, Eq. (9) has no real solution if d≠0, which means system (8) has no equilibrium point when d≠0. We also found that system (8) can exhibit chaotic attractors by numerical simulations although it has no equilibrium point. Therefore, the next step is to study the chaotic property of system (8) when there is no equilibrium.
3 Occurrence of Multiple Hidden Attractors in System (8)At present, there are mainly three methods to solve the problem of chaotic systems with fractional order, namely, frequency domain method (FDM)[32-33], Adams bashforth-moulton algorithm (ABM)[34-35], and Adomian decomposition (ADM)[36-37]. When detecting and analyzing chaotic behaviors in non-linear systems, it is relatively more precise and convenient for ABM and ADM, while FDM is not always useful and trustworthy. Thus we adopted the modified ABM in numerical simulations.
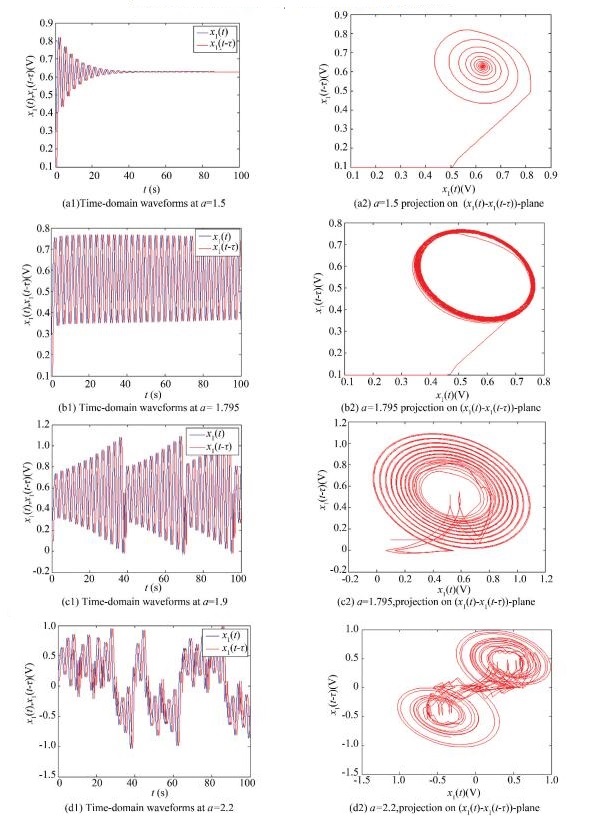
The simulation results of bifurcation diagram can be used to effectively determine the important dynamical properties of chaotic systems with fractional order. When fixing q=0.84, the parameters were set as b=0.02, c=0.1, d=0.001, τ=0.9. The initial conditions (0.1, 0.1) and the parameter a were adjusted. Then system (8) produced abundant phenomena with the variation of the parameter a (Fig. 2(a)). The asymptotically stable state of system (8) was observed in the interval a < 1.58. The stable state at a=1.5 is depicted in Fig. 3(a1)-(a2). Then Hopf bifurcation occurred and system (8) generated the limit cycle. Further, the increase of the parameter a led to the chaotic state of the system. The specific situation at a=1.795 is shown in Fig. 3(b1)-(b2). When a=1.9, the single scroll attractor appeared in system (8) as illustrated in Fig. 3(c1)-(c2). System (8) entered the hyperchaotic regime at a≥1.929 and the two-scroll hyperchaotic attractor of system (8) was generated at a≥1.969. The situation of the double hyperchaotic attractor for a=2.2 is depicted in Fig. 3(d1)-(d2).

|
Fig.2 Numerical bifurcation diagram with parameter a |
|
Fig.3 Chaotic attractors of delayed system (8) with the parameter a change |
When fixing q=0.9, system (8) exhibited a dynamic evolution law similar to q=0.84, from the asymptotically stable state to the appearance of the Hopf bifurcation to enter the chaotic area. Comparing Fig. 2(a) with Fig. 2(b), it was found that the larger the value of the order q was, the faster the evolution law accompanying the coefficient parameter a changed.
4 Synchronization of System (8)System (8) is the drive system. By adding the controller to Eq. (8), the response system is rewritten as
| $ \left\{ \begin{array}{l} {D^q}{y_1} = - a{y_1}\left( {t - \tau } \right) + \text{sgn}\left( {{y_1}\left( {t - \tau } \right)} \right) - \\ \;\;\;\;\;\;\;\;\;\;b\left( {0.1{y_2} - 1} \right){y_1} + {u_1}\left( t \right)\\ {D^q}{y_{\rm{2}}} = c{y_1} + {u_2}\left( t \right) \end{array} \right. $ | (10) |
in which u1(t), u2(t) are the appropriate control terms. The error of drive-response system can be set as
| $ \begin{array}{*{20}{c}} {{e_1} = {y_1} - {x_1},{e_2} = {y_2} - {x_2}}\\ {{e_1}\left( {t - \tau } \right) = {y_1}\left( {t - \tau } \right) - {x_1}\left( {t - \tau } \right)} \end{array} $ | (11) |
For Eqs. (8)-(10), the following error system can be written as
| $ \left\{ \begin{array}{l} {D^q}{e_1} = - a{e_1}(t - \tau ) + \text{sgn} \left( {{y_1}(t - \tau ) - } \right.\\ \;\;\;\;\;\;\;\text{sgn}\left( {{x_1}(t - \tau )} \right) + b{e_1} - 0.1b\left( {{x_1}{x_2} - {y_1}{y_2}} \right) + \\ \;\;\;\;\;\;\;{u_1}(t)\\ {D^q}{e_2} = c{e_1} + {u_2}(t) \end{array} \right. $ | (12) |
The nonlinear control input is defined as
| $ \left\{ {\begin{array}{*{20}{l}} {{u_1} = \text{sgn} \left( {{x_1}(t - \tau )} \right) - \text{sgn} \left( {{y_1}(t - \tau )} \right) + }\\ {\;\;\;0.1b\left( {{x_1}{x_2} - {y_1}{y_2}} \right) - {K_1}{e_1}}\\ {{u_2} = - {K_2}{e_2}} \end{array}} \right. $ | (13) |
where K1, K2 are control parameters.
Substituting Eq. (13) into Eq.(12), then we obtain
| $ \left\{ {\begin{array}{*{20}{l}} {{D^q}{e_1} = - a{e_1}(t - \tau ) + \left( {b - {K_1}} \right){e_1}}\\ {{D^q}{e_2} = c{e_1} - {K_2}{e_2}} \end{array}} \right. $ | (14) |
By discussing and analyzing the stability of error system (14) with zero solution, it is possible to reach synchronization between the drive system (8) and the response system (10). Then we studied the state of the positive and negative real parts of all the roots of the characteristic equation det(Δ(s)). If all of them possess negative real parts, the error system (14) with equilibrium point can be asymptotically stable[38], and the antisense is not.
The characteristic equation is
| $ \begin{array}{l} \text{det} (\mathit{\Delta} (s)) = \left| {\begin{array}{*{20}{l}} {{s^q} - \left( {b - {K_1}} \right) + a{{\rm{e}}^{ - s\tau }}}&0\\ { - c}&{{s^q} + {K_2}} \end{array}} \right| = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{s^{2q}} + \left( {{K_1} + {K_2} - b} \right){s^q} + a{s^q}{{\rm{e}}^{ - s\tau }} + \\ \;\;\;\;\;\;\;\;\;a{K_2}{{\rm{e}}^{ - s\tau }} - {K_2}\left( {b - {K_1}} \right) = 0 \end{array} $ | (15) |
Let
| $ \left\{ {\begin{array}{*{20}{l}} {{\psi _1} = {K_1} + {K_2} - b}\\ {{\psi _2} = a}\\ {{\psi _3} = a{K_2}}\\ {{\psi _4} = - {K_2}\left( {b - {K_1}} \right)} \end{array}} \right. $ |
Simplify Eq. (15), then we can obtain
| $ {s^{2q}} + {\psi _1}{s^q} + {\psi _2}{s^q}{{\rm{e}}^{ - s\tau }} + {\psi _3}{{\rm{e}}^{ - s\tau }} + {\psi _4} = 0 $ | (16) |
| $ \left\{ \begin{array}{l} |w{|^{2q}}\cos q\mathtt{π} + {\psi _1}|w{|^q}\cos \frac{{q\mathtt{π} }}{2} + \left( {{\psi _2}|w{|^q}\cos \frac{{q\mathtt{π} }}{2} + } \right.\\ \;\;\;\;\left. {{\psi _3}} \right)\cos \tau w + {\psi _2}|w{|^q}\sin \left( { \pm \frac{{q\mathtt{π} }}{2}} \right)\sin \tau w + {\psi _4} = 0\\ |w{|^{2q}}\sin ( \pm q\mathtt{π} ) + {\psi _1}|w{|^q}\sin \left( { \pm \frac{{q\mathtt{π} }}{2}} \right) - \\ \;\;\;\;\left( {{\psi _2}|w{|^q}\cos \frac{{q\mathtt{π} }}{2} + {\psi _3}} \right)\sin \tau w + \\ \;\;\;\;{\psi _2}|w{|^q}\sin \left( { \pm \frac{{q\mathtt{π} }}{2}} \right)\cos \tau w = 0 \end{array} \right. $ | (17) |
Simplify Eq. (17), then
| $ \left\{ {\begin{array}{*{20}{l}} {{A_1} + B\cos \tau w + C\sin \tau w = 0}\\ {{A_2} - B\sin \tau w + C\cos \tau w = 0} \end{array}} \right. $ | (18) |
where
| $ \left\{ {\begin{array}{*{20}{l}} {{A_1} = |w{|^{2q}}\cos q\mathtt{π} + {\psi _1}|w{|^q}\cos \frac{{q\mathtt{π} }}{2} + {\psi _4}}\\ {{A_2} = |w{|^{2q}}\sin ( \pm q\mathtt{π} ) + {\psi _1}|w{|^q}\sin \left( { \pm \frac{{q\mathtt{π} }}{2}} \right)}\\ {B = {\psi _2}|w{|^q}\cos \frac{{q\mathtt{π} }}{2} + {\psi _3}}\\ {C = {\psi _2}|w{|^q}\sin \left( { \pm \frac{{q\mathtt{π} }}{2}} \right)} \end{array}} \right. $ | (19) |
From Eq. (18), we can get
| $ {B^2} + {C^2} = A_1^2 + A_2^2 $ | (20) |
Then
| $ \begin{array}{l} |w{|^{4q}} + {F_1}|w{|^{3q}} + {F_2}|w{|^{2q}} + {F_3}|w{|^q} + \\ \;\;\;\;\;{F_4} = 0 \end{array} $ | (21) |
where
| $ \left\{ {\begin{array}{*{20}{l}} {{F_1} = 2{\psi _1}\left( {\cos q\mathtt{π} \cos \frac{{q\mathtt{π} }}{2} + \sin ( \pm q\mathtt{π} )\sin \left( { \pm \frac{{q\mathtt{π} }}{2}} \right)} \right)}\\ {{F_2} = 2{\psi _4}\cos q\mathtt{π} + \psi _1^2 - \psi _2^2}\\ {{F_3} = 2\cos \frac{{q\mathtt{π} }}{2}\left( {{\psi _1}{\psi _4} - {\psi _2}{\psi _3}} \right)}\\ {{F_4} = \psi _4^2 - \psi _3^2} \end{array}} \right. $ | (22) |
Apparently, for 0 < q < 1, Eq. (21) has no real solution if and only if Fi>0(i=1, 2, 3, 4) and ψ3+ψ4≠0, meaning that Eq. (15) has no purely imaginary root for all τ≥0. Thus we need to satisfy the following condition
| $ {K_1} \ge b,{K_2} \ge 0 $ | (23) |
Suppose that Eq. (15) has two negative eigenvalues, which means if all the roots have negative parts for Eq. (15) with τ=0, all the principal minors Δi(i=1, 2) must be non-negative.
| $ {\mathit{\Delta} _1} = {\psi _1} + {\psi _2} > 0,{\mathit{\Delta} _2} = \left| {\begin{array}{*{20}{l}} {{\psi _1} + {\psi _2}}&0\\ 1&{{\psi _3} + {\psi _4}} \end{array}} \right| > 0 $ |
Thus we can obtain the following condition holds
| $ {K_1} > b - a,{K_2} > 0 $ | (24) |
On the basis of Corollary 3[39], we drew the following conclusions:
Stability criterion of Eq.(15): System (15) with zero solution is Lyapunov globally asymptotically stable if and only if K1 and K2 meet both conditions (23) and (24), which means that system (8) is synchronized with system (10).
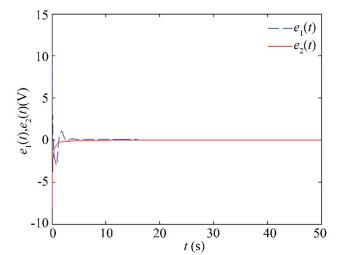
5 Simulations ResearchThe parameters b, c, and d in system (8) are the same as those in Section 3. The suitable control parameters satisfying conditions (23) and (24) were selected as K1=K2=5. The initial values of system (8) and (10) were set as (x1(0), x2(0))=(-4, 5) and (y1(0), y2(0))=(8, -4), so the initial condition of the error Eq. (14) was (e1(0), e2(0))=(12, -9). Let a= 1.795, q=0.84, τ=0.9, as shown in Fig. 4, then system (8) synchronized with system (10). Meanwhile, the error synchronization was zero in Fig. 5.

|
Fig.4 Evolutions of drive-response system |
|
Fig.5 Synchronization errors e1, e2 |
5.1 Effect of Parameter a
In order to stabilize the chaotic state of the system (8) as the parameter a varies, the effects of the parameter a on synchronization were discussed when setting q=0.84, τ=0.9, a=1.795, 1.9, 2.2, as shown in Fig. 6. It is clear that the synchronization state of e1 was slower as the parameter a increased in Fig. 6(a). Since the error e2 of system (14) was independent of the parameter a, the synchronization state of e2 remained unchanged with the increase of a, as shown in Fig. 6(b).

|
Fig.6 Synchronization errors at a=1.795, 1.9, 2.2 |
5.2 Effect of Fractional Order q
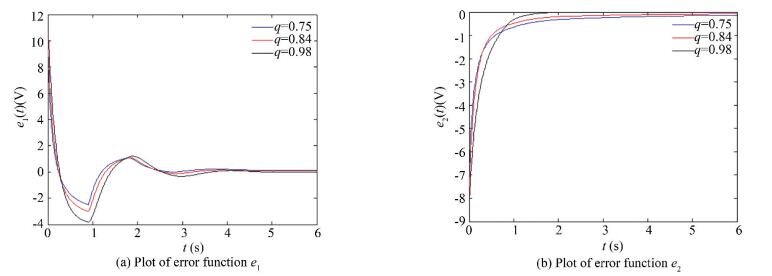
When fixing a=1.795, τ=0.9, simulations about the effects of the order q on synchronization are shown in Figs. 7 by giving three cases of the order q, namely, 0.75, 0.84, and 0.98. It can be found that the faster the order increased, the slower the error e1 trended to synchronize, and the faster the error e2 tended to synchronize.
|
Fig.7 Synchronization errors at q=0.75, 0.84, 0.98 |
5.3 The effect of time delay τ
In this part, we discuss the impact of time delay τ on the synchronization. For a=1.795, q=0.84, three cases of the time delay τ, i.e., 0.7, 0.8, and 0.9 were analyzed and the simulation outcomes of the effects of the time delay τ on synchronization are depicted in Figs. 8. As shown in Fig. 8(a), the synchronization error e1 went faster with the decrease of time delay τ. The e2 of the error system (14) was unrelated to the time delay τ, and thus the synchronization of the e2 remained unchanged with the increase of τ in Fig. 8(b).

|
Fig.8 Synchronization errors at τ=0.7, 0.8, 0.9 |
6 Conclusions
This paper mainly introduces a fractional-order time-delayed memristive differential system without equilibrium point. As the parameter a changed, complex and rich chaotic attractors emerged in the system. Sufficient stability criteria of the factional-order delayed system were derived to deal with chaos synchronization of the proposed systems. Besides, the parameter a, fractional order q, and time delay τ were used as bifurcation parameters to study the impact of the system on synchronization. Results showed that as the parameter a increased, the synchronization state of e1 went slower and the synchronization of e2 remained unchanged. With the growth of the order q, the slower the error e1 trended to synchronize, and the faster the error e2 tended to synchronize. The synchronization of the error e1 was faster with the decrease of the time delay τ, while the e2 of the error system (14) was independent of the time delay τ, and thus the synchronization of the e2 remained unchanged with the increase of τ. The simulation results proved that the parameter a, order q, and delay τ have certain impacts on chaos synchronization, which verified the effectiveness and feasibility of the proposed method.
| [1] |
Chua L O. Memristor - The missing circuit element. IEEE Transactions on Circuit Theory, 1971, 18(5): 507-519. DOI:10.1109/TCT.1971.1083337 (  0) 0) |
| [2] |
Ruan J, Sun K, Mou J. Memristor-based Lorenz hyper-chaotic system and its circuit implementation. Acta Physica Sinica, 2016, 65(19): 190502. (in Chinese) DOI:10.7498/aps.65.190502 (  0) 0) |
| [3] |
Zhou L, Wang C, Zhou L. Generating hyperchaotic multi-wing attractor in a 4D memristive circuit. Nonlinear Dynamics, 2016, 85(4): 2653-2663. DOI:10.1007/s11071-016-2852-8 (  0) 0) |
| [4] |
Zhou L, Wang C, Zhou L. A novel no-equilibrium hyperchaotic multi-wing system via introducing memristor. International Journal of Circuit Theory and Applications, 2017, 46(1): 84-98. DOI:10.1002/cta.2339 (  0) 0) |
| [5] |
Wang C, Liu X, Xia H. Multi-piecewise quadratic nonlinearity memristor and its 2N-scroll and 2N+1-scroll chaotic attractors system. Chaos, 2017, 27(3): 033114. DOI:10.1063/1.4979039 (  0) 0) |
| [6] |
Abunahla H, Shehada D, Yeun C Y, et al. Novel microscale memristor with uniqueness property for securing communications. Proceedings of 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS). Piscataway: IEEE, 2017, 6(2): 1-4. DOI:10.1109/MWSCAS.2016.7870134 (  0) 0) |
| [7] |
Hu M, Graves C E, Li C, et al. Memristor-based analog computation and neural network classification with a dot product engine. Advanced Materials, 2018, 30(9): 1705914. DOI:10.1002/adma.201705914 (  0) 0) |
| [8] |
Vijay H M, Ramakrishnan V N. Radiation effects on memristor-based non-volatile SRAM cells. Journal of Computational Electronics, 2018, 17(1): 279-287. DOI:10.1007/s10825-017-1080-x (  0) 0) |
| [9] |
Oldham K B, Spanier J. The Fractional Calculus. New York: Academic Press, 1974.
(  0) 0) |
| [10] |
Tavazoei M S, Haeri M, Jafari S, et al. Some applications of fractional calculus in suppression of chaotic oscillations. IEEE Transactions on Industrial Electronics, 2008, 55(11): 4094-4101. DOI:10.1109/TIE.2008.925774 (  0) 0) |
| [11] |
Hartley T T, Lorenzo C F, Qammer H K. Chaos in a fractional order Chua's system. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1995, 42(8): 485-490. DOI:10.1109/81.404062 (  0) 0) |
| [12] |
Cafagna D, Grassi G. On the simplest fractional-order memristor-based chaotic system. Nonlinear Dynamics, 2012, 70(2): 1185-1197. DOI:10.1007/s11071-012-0522-z (  0) 0) |
| [13] |
Atangana A, Koca I. Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos, Solitons & Fractals, 2016, 89: 447-454. DOI:10.1016/j.chaos.2016.02.012 (  0) 0) |
| [14] |
Yang N, Xu C, Wu C, et al. Modeling and analysis of a fractional-order generalized memristor-based chaotic system and circuit implementation. International Journal of Bifurcation and Chaos, 2017, 27(13): 1750199. DOI:10.1142/S0218127417501991 (  0) 0) |
| [15] |
Ding D, Li S, Wang N. Dynamic analysis of fractional-order memristive chaotic system. Journal of Harbin Institute of Technology(New series), 2018, 25(2): 50-58. DOI:10.11916/j.issn.1005-9113.16136 (  0) 0) |
| [16] |
Feng J, Sevier S A, Huang B, et al. Modeling delayed processes in biological systems. Physical Review E, 2016, 94(3): 032408. DOI:10.1103/PhysRevE.94.032408 (  0) 0) |
| [17] |
Lain S J, Roberts C L, Bond D M, et al. An economic evaluation of planned immediate versus delayed birth for preterm prelabour rupture of membranes: Findings from the PPROMT randomised controlled trial. BJOG, 2017, 124(4): 623-630. DOI:10.1111/1471-0528.14302 (  0) 0) |
| [18] |
Huang C, Meng Y, Cao J, et al. New bifurcation results for fractional BAM neural network with leakage delay. Chaos, Solitons & Fractals, 2017, 100: 31-44. DOI:10.1016/j.chaos.2017.04.037 (  0) 0) |
| [19] |
Biswas D, Banerjee T. A simple chaotic and hyperchaotic time-delay system: Design and electronic circuit implementation. Nonlinear Dynamics, 2016, 83(4): 2331-2347. DOI:10.1007/s11071-015-2484-4 (  0) 0) |
| [20] |
Braun J, Mian W A, Rechenberger S. Delayed magnetic catalysis. Physics Letters B, 2016, 755: 265-269. DOI:10.1016/j.physletb.2016.02.017 (  0) 0) |
| [21] |
Li C, Deng W. Chaos synchronization of fractional-order differential systems. International Journal of Modern Physics B, 2006, 20(7): 791-803. DOI:10.1142/S0217979206033620 (  0) 0) |
| [22] |
Odibat Z M. Adaptive feedback control and synchronization of non-identical chaotic fractional order systems. Nonlinear Dynamics, 2010, 60(4): 479-487. DOI:10.1007/s11071-009-9609-6 (  0) 0) |
| [23] |
Li C, Zhang M, Zhou F, et al. Projective synchronization for a fractional-order chaotic system via single sinusoidal coupling. Optik, 2016, 127(5): 2830-2836. DOI:10.1016/j.ijleo.2015.11.197 (  0) 0) |
| [24] |
Ding D, Qian X, Wang N, et al. Synchronization and anti-synchronization of a fractional order delayed memristor-based chaotic system using active control. Modern Physics Letters B, 2018, 32(14): 1850142. DOI:10.1142/S0217984918501427 (  0) 0) |
| [25] |
Bigdeli N, Ziazi H A. Finite-time fractional-order adaptive intelligent backstepping sliding mode control of uncertain fractional-order chaotic systems. Journal of the Franklin Institute, 2017, 354(1): 160-183. DOI:10.1016/j.jfranklin.2016.10.004 (  0) 0) |
| [26] |
Wen S, Huang T, Yu X, et al. Sliding-mode control of memristive Chua's systems via the event-based method. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2017, 64(1): 81-85. DOI:10.1109/TCSⅡ.2016.2538727 (  0) 0) |
| [27] |
Ding D, Li S, Wang N. Sliding mode control of fractional-order memristive system. Journal of Beijing Institute of Technology, 2017, 26(3): 418-426. DOI:10.15918/j.jbit1004-0579.201726.0319 (  0) 0) |
| [28] |
Luo R, Su H, Zeng Y. Synchronization of uncertain fractional-order chaotic systems via a novel adaptive controller. Chinese Journal of Physics, 2017, 55(2): 342-349. DOI:10.1016/j.cjph.2016.10.024 (  0) 0) |
| [29] |
Bouzeriba A, Boulkroune A, Bouden T. Projective synchronization of two different fractional-order chaotic systems via adaptive fuzzy control. Neural Computing and Applications, 2016, 27(5): 1349-1360. DOI:10.1007/s00521-015-1938-4 (  0) 0) |
| [30] |
Singh P P, Singh J P, Roy B K. Tracking control and synchronization of Bhalekar-Gejji chaotic systems using active backstepping control. Proceedings of 2018 IEEE International Conference on Industrial Technology (ICIT). Piscataway: IEEE, 2018, 322-326. DOI:10.1109/ICIT.2018.8352197 (  0) 0) |
| [31] |
Pham V T, Vaidyanathan S, Volos C K, et al. A novel memristive time-delay chaotic system without equilibrium points. The European Physical Journal Special Topics, 2016, 225(1): 127-136. DOI:10.1140/epjst/e2016-02625-8 (  0) 0) |
| [32] |
Sun H, Abdelwahab A, Onaral B. Linear approximation of transfer function with a pole of fractional power. IEEE Transactions on Automatic Control, 1984, 29(5): 441-444. DOI:10.1109/TAC.1984.1103551 (  0) 0) |
| [33] |
Tavazoei M S, Haeri M. Limitations of frequency domain approximation for detecting chaos in fractional order systems. Nonlinear Analysis: Theory, Methods & Applications, 2008, 69(4): 1299-1320. DOI:10.1016/j.na.2007.06.030 (  0) 0) |
| [34] |
Diethelm K, Ford N J, Freed A D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dynamics, 2002, 29(1-4): 3-22. DOI:10.1023/A:1016592219341 (  0) 0) |
| [35] |
Danca M F. Numerical approximation of a class of discontinuous systems of fractional order. Nonlinear Dynamics, 2011, 66(1-2): 133-139. DOI:10.1007/s11071-010-9915-z (  0) 0) |
| [36] |
Ibijola E A, Adegboyegun B J, Halid O Y. On Adomian Decomposition Method (ADM) for numerical solution of ordinary differential equations. Advances in Natural & Applied Sciences, 2008, 2(3): 165-169. (  0) 0) |
| [37] |
Zhang L, Sun K, He S, et al. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. The European Physical Journal Plus, 2017, 132: 31. DOI:10.1140/epjp/i2017-11310-7 (  0) 0) |
| [38] |
Bhalekar S. A necessary condition for the existence of chaos in fractional order delay differential equations. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineer, 2013, 7(3): 28-32. (  0) 0) |
| [39] |
Deng W, Li C, Lü J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dynamics, 2007, 48(4): 409-416. DOI:10.1007/s11071-006-9094-0 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


