2. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China
Three-level (3L) converters have several advantages over conventional two-level six-switch converters, such as reduction of harmonic component in the line current, suppression of voltage stress on switching devices, and increase of efficiency[1-2]. The typical topology of 3L converters can be classified into three types: flying-capacitor (FC)[3], cascade H-bridge (CHB)[4], and neutral-point-clamped (NPC)[5]. As the most prevailing 3L converter, the three-level neutral-point-clamped (3L-NPC) converter is applied in the field of railway traction, ship propulsion, mine lifting, wind power generation, and other medium-voltage high-power motor drive applications[6-8].
When applied in the above mentioned fields, the output performance of 3L converter is significantly reduced during the process of pulse width modulation (PWM) on account of the switching frequency of switching devices. The harmonic distortion of the converter and the torque ripple of the motor are both increased[9]. Thus, how to evaluate and improve the output waveform quality of 3L converter has been studied by researchers worldwide.
Several evaluation indexes, such as weighted total harmonic distortion (VWTHD)[10-11], RMS value of stator flux ripple[12-13], and the amplitude of mean error current vector[14-15], have been adopted to represent the output waveform quality of converters in recent years.
For VWTHD, double Fourier series (DFS) method should be adopted to calculate the individual harmonic of the output waveform. The calculation is highly complicated[10]. For RMS value of stator flux ripple, the d and q axis components of the stator flux ripple are calculated to synthesize RMS value of stator flux ripple[12]. The computational burden is greatly reduced compared with that of VWTHD. For the amplitude of mean error current vector, the distance between the centroid of the error current vector trajectory and the coordinate origin point is calculated on the basis of space vector modulation (SVM). Then the amplitude of mean error current vector can be obtained[15]. The computational burden is further reduced compared with the above mentioned two methods.
All the above evaluation methods are based on the premise that DC-link voltage is constant. Only the high frequency error caused by the space vector synthesis is considered. However, for 3L-NPC converter, the neutral point is directly connected to the load by the clamping diode. The load current will charge and discharge upper and lower capacitors of the DC-link. If the charge is not equal to the discharge, there will be low-frequency oscillation in the neutral-point (NP), which leads to the ripple in the output of the 3L-NPC converter[16]. At this time, if the traditional evaluation method is still used, the quantitative evaluation results of the output waveform will be inaccurate.
In order to solve the above issue, the NP voltage is regarded as a variable in this paper. The mathematical model of the NP voltage offset affected by the switching sequence was derived. On this basis, the amplitude and phase angle of basic voltage vectors were modified. Then an accurate evaluation method of the output waveform quality for 3L-NPC converter was established. The proposed method will be helpful in the design of switching sequence and the selection of modulation strategy.
2 SVM of 3L-NPCFig. 1 illustrates the topology of 3L-NPC converter. Each leg has 3 switching states (defined as S, S∈{0, 1, 2}, 2 represents Sx1 and Sx2 switch on, Sx3 and Sx4 switch off; 1 represents Sx2 and Sx3 switch on, Sx1 and Sx4 switch off; 0 represents Sx3 and Sx4 switch on, Sx1 and Sx2 switch off; x=A, B and C). So there are 33 = 27 switching states for three phases. According to Eq. (1), the output voltage for each switch state can be transformed into the space vector in the space vector diagram.
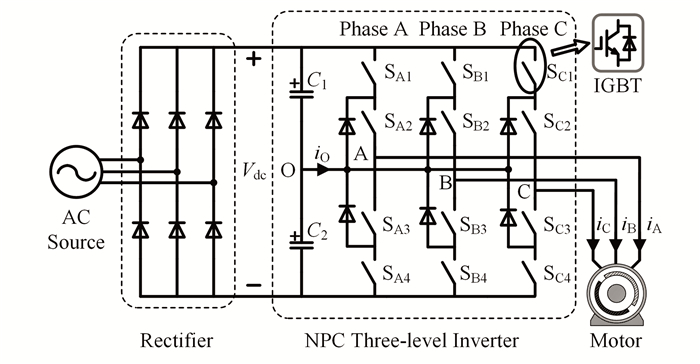
|
Fig.1 Topology of 3L-NPC converter fed motor system |
| $ {\mathit{\boldsymbol{V}}_j} = ({v_{{\rm{AO}}}} \cdot {{\rm{e}}^{j0}} + {v_{{\rm{BO}}}} \cdot {{\rm{e}}^{j\frac{{2\pi }}{3}}} + {v_{{\rm{CO}}}} \cdot {{\rm{e}}^{j\frac{{4\pi }}{3}}}) $ | (1) |
whereVj, j=0, 1, 2, …, 18is the basic vector, as can be seen in Fig. 2. According to the amplitude, basic vectors can be classified into large vectorV1 ~ V6, medium vectorV13 ~ V18, small vectorV7~V12, and zero vectorV0. Zero vector has three switching states, and each small vector has two switching states. If medium vector is taken as the center, Fig. 2 can be divided into sectors Ⅰ~Ⅵ, and each sector can be further partitioned into triangle 1~6.

|
Fig.2 Space vector diagram of 3L-NPC converter |
For SVM of 3L converter, the nearest three voltage vectors are commonly applied to compose the reference vector Vref. The duty cycle of Vj is determined by the theory of volt-second balance. Take Vref lying in triangle 1 of sector I as an example:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_{{\rm{ ref }}}}{T_{\rm{s}}} = {\mathit{\boldsymbol{V}}_7}{T_1} + {\mathit{\boldsymbol{V}}_{13}}{T_2} + {\mathit{\boldsymbol{V}}_1}{T_0}}\\ {{T_{\rm{s}}} = {T_1} + {T_2} + {T_0}} \end{array}} \right. $ | (2) |
In each sample period Ts, the sequence of space voltage vectors used to compose Vref could be arranged arbitrarily. More than one switching state corresponds to basic vector V0 and V7~V12. Therefore, there are several switching sequences that can be applied to synthesize Vref in each sample period. The continuous PWM (CPWM) and four kinds of discontinuous PWM (DPWM0~ DPWM3) strategies are presented in Refs. [16] and [17], respectively. Switching sequences of CPWM and DPWM0~DPWM3 are shown in Table 1. The output performance of the converter will be different for different strategies. It is necessary to establish the output current ripple model. Then the output performance can be analyzed quantitatively and accurately.
| Table 1 Switching sequences of different modulation strategies in sector Ⅰ |
3 Error Model of Space Vector Synthesis
According to the theory of SVM, difference still exists between the actual output voltage vector and the reference vector at any arbitrary instant of the sample period. In order to analyze the influence of space vector synthesis process on the output performance of the converter, the above errors need to be analyzed and modeled.
3.1 Trajectory of Error Current VectorThe error voltage vector Δ Vj is considered as the difference between Vj and Vref. As shown in Fig. 3, when Vref lies in triangle 1 of sector Ⅰ, error voltage vectors generated by basic voltage vectors V7, V1, and V13 are Δ V7, Δ V1, and Δ V13, respectively.

|
Fig.3 Error voltage vector and trajectory of error current vector |
The stator resistance can be neglected when 3L converter feeds the motor. The error current vector Δij will be generated by Δ Vj. The relationship between the error voltage vector and the error current vector can be derived as
| $ \Delta {\mathit{\boldsymbol{V}}_j} = {L_\sigma }\frac{{{\rm{d}}\Delta {\mathit{\boldsymbol{i}}_j}}}{{{\rm{d}}t}} $ | (3) |
where Lσ is the inductance of the motor. According to Eq. (3), the error current vector Δij changes linearly with the error voltage vector. Take switching sequence 211↔210↔200 as an example. When t is between 0 and T1/2, the switching state 211 corresponding to V7 is applied to the converter. The error current vector Δi7 starts from point O, and the terminal travels from point O to point A. When t=T1/2, error current vector Δi7=ΔV7 ·T1/2Lσ. Similarly, when switch states 210 and 200 apply for T2/2 and T0/2, respectively, the corresponding error current vectors are Δi13=ΔV13 ·T2/Lσ and Δi1=ΔV1·T0/Lσ, respectively. The trajectory of the terminal of error current vector Δij during [0, Ts/2] is triangle OAB, and the trajectory during (Ts/2, Ts] is triangle OCD.
The modulation index can be defined as
| $ m = \sqrt 3 {V_{{\rm{ref}}}}/{V_{{\rm{dc}}}} $ | (4) |
From Fig. 3, the amplitudes of error voltage vectors ΔV7, ΔV1, and ΔV13 are
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta {V_7} = \sqrt {(1 + 3{m^2})V_{{\rm{dc}}}^2 - 2\sqrt 3 m{V_{{\rm{dc}}}}{\rm{cos}}\theta } /3}\\ {\Delta {V_1} = \sqrt {(4 + 3{m^2})V_{{\rm{dc}}}^2 - 4\sqrt 3 m{V_{{\rm{dc}}}}{\rm{cos}}\theta } /3}\\ {\Delta {V_{13}} = \sqrt {(1 + 3{m^2})V_{{\rm{dc}}}^2 - 6m{V_{{\rm{dc}}}}{\rm{cos}}(\pi /6 - \theta )} /3} \end{array}} \right. $ | (5) |
According to Eq. (2), the duty cycle of voltage vectors V1, V7, and V13 in Ts are
| $ \left\{ {\begin{array}{*{20}{l}} {{T_0} = {T_{\rm{s}}}[2m{\rm{sin}}(\pi /3 - \theta ) - 1]}\\ {{T_1} = 2{T_{\rm{s}}}[1 - m{\rm{sin}}(\pi /3 + \theta )]}\\ {{T_2} = 2m{T_{\rm{s}}}{\rm{sin}}\theta } \end{array}} \right. $ | (6) |
As can be deduced from Fig. 4(a), angles δ1, δ2, and δ3 between Δi7, Δi1, Δi13, and d-axis are:

|
Fig.4 d-q axis decoupling of error current vector |
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _1} = \frac{\pi }{2} - {\rm{arccos}}\frac{{V_{{\rm{ref}}}^2 + \Delta V_7^2 - V_{{\rm{dc}}}^2/9}}{{2{V_{{\rm{ref}}}} \cdot \Delta {V_7}}}}\\ {{\delta _2} = {\rm{arccos}}\frac{{V_{{\rm{ref}}}^2 + \Delta V_{13}^2 - V_{{\rm{dc}}}^2/3}}{{2{V_{{\rm{ref}}}} \cdot \Delta {V_{13}}}} - \frac{\pi }{2}}\\ {{\delta _3} = {\rm{arccos}}\frac{{V_{{\rm{ref}}}^2 + \Delta V_1^2 - 4V_{{\rm{dc}}}^2/9}}{{2{V_{{\rm{ref}}}} \cdot \Delta {V_1}}} - \frac{\pi }{2}} \end{array}} \right. $ | (7) |
Error current vectors Δ i7, Δi1, and Δi13 are then decoupled into d-axis and q-axis components, as illustrated in Fig. 4(a).
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta {i_{7d}} = - \frac{{\Delta {V_7}{T_1}}}{{2{L_\sigma }}}{\rm{cos}}{\delta _1},\Delta {i_{7q}} = \frac{{\Delta {V_7}{T_1}}}{{2{L_\sigma }}}{\rm{sin}}{\delta _1}}\\ {\Delta {i_{13d}} = \frac{{\Delta {V_{13}}{T_2}}}{{2{L_\sigma }}}{\rm{cos}}{\delta _2},\Delta {i_{13q}} = - \frac{{\Delta {V_{13}}{T_2}}}{{2{L_\sigma }}}{\rm{sin}}{\delta _2}}\\ {\Delta {i_{1d}} = - \frac{{\Delta {V_1}{T_0}}}{{2{L_\sigma }}}{\rm{cos}}{\delta _3},\Delta {i_{1q}} = - \frac{{\Delta {V_1}{T_0}}}{{2{L_\sigma }}}{\rm{sin}}{\delta _3}} \end{array}} \right. $ | (8) |
By substituting Eqs. (5)-(7) into Eq. (8), it can be deduced that the expressions of d-axis and q-axis components of error current vector are both functions of m and θ.
3.2 Expression of RMS Value of Output Current RippleRMS value of output current ripple in one sample period is usually considered as the index to evaluate the quality of output current waveform.
| $ {I_{{\rm{ ripple }}}} = \sqrt {\frac{1}{{{T_{\rm{s}}}}}\int_0^{{T_{\rm{s}}}} | \varDelta \mathit{\boldsymbol{i}}{|^2}{\rm{d}}t} $ | (9) |
As can be seen from Fig. 3, trajectories of error current vector during the first and the second half of each sample period are symmetrical with respect to the origin O. Therefore, only the RMS value of the output current ripple during (0, Ts/2] needs to be calculated. Thus, Eq. (9) can be transformed into
| $ {I_{{\rm{ ripple }}}} = \sqrt {\frac{2}{{{T_{\rm{s}}}}}\int_0^{{T_{\rm{s}}}/2} {(\Delta {i_d}^2 + \Delta {i_{dq}}^2)} {\rm{d}}t} $ | (10) |
From Figs. 4(b) and 4(c), Δid and Δiq can be derived as
| $ \Delta {i_d} = \left\{ \begin{array}{l} \Delta {i_{{\rm{7d}}}}\frac{t}{{{T_1}}},0 \le t < {T_1}/2\\ \Delta {i_{{\rm{7d}}}} + \Delta {i_{13d}}\frac{t}{{{T_2}}},{T_1}/2 \le t < ({T_1} + {T_2})/2\\ \Delta {i_{{\rm{7d}}}} + \Delta {i_{13d}} + \Delta {i_{1d}}\frac{t}{{{T_0}}},({T_1} + {T_2})/2 \le t \le {T_{\rm{s}}}/2 \end{array} \right. $ | (11) |
| $ \Delta {i_q} = \left\{ \begin{array}{l} \Delta {i_{{\rm{7}}q}}\frac{t}{{{T_1}}},0 \le t < {T_1}/2\\ \Delta {i_{{\rm{7}}q}} + \Delta {i_{13q}}\frac{t}{{{T_2}}},{T_1}/2 \le t < ({T_1} + {T_2})/2\\ \Delta {i_{{\rm{7}}q}} + \Delta {i_{13q}} + \Delta {i_{1q}}\frac{t}{{{T_0}}},({T_1} + {T_2})/2 \le t \le {T_{\rm{s}}}/2 \end{array} \right. $ | (12) |
By substituting Eq. (8) into Eqs. (11) and (12), and then substituting Eqs. (11) and (12) into Eq. (10), the RMS value of output current ripple can be obtained. It is also the function of modulation index and phase angle of reference vector. According to Eq. (10), the output waveform quality under different switching sequence can be calculated. Moreover, the arithmetic mean value of RMS value of output current ripple in one fundamental period can be easily calculated to compare the output performance of various modulation methods.
4 Error Model of NP Voltage RippleFrom Fig. 1, the neutral-point O is directly connected to the load through the clamping diode. When CPWM or DPWM0-DPWM3 is adopted, the unbalanced charge and discharge of upper and lower capacitor caused by the NP current iO will lead to low-frequency oscillation in the NP voltage[16]. However, the error model established in Section 3 is based on the premise that basic vectors are not changed. Only the high-frequency error caused by space vector synthesis is taken into account, which is not suitable for 3L-NPC converter. It is necessary to analyze the low-frequency error caused by the NP voltage ripple so as to evaluate the output waveform quality of 3L-NPC converter accurately. Then a unified error model considering both high-frequency error and low-frequency error needs to be established.
4.1 Calculation of NP Voltage OffsetThe three-phase load current can be defined as
| $ \left\{ {\begin{array}{*{20}{l}} {{i_{\rm{A}}} = \sqrt 2 I{\rm{cos}} (\theta - \varphi )}\\ {{i_{\rm{B}}} = \sqrt 2 I{\rm{cos}} (\theta - \varphi - 2\pi /3)}\\ {{i_{\rm{C}}} = \sqrt 2 I{\rm{cos}} (\theta - \varphi + 2\pi /3)} \end{array}} \right. $ | (13) |
where I is the RMS value of load current, φ is the power factor angle. With the change of modulation index, the reference vector rotates through different triangles in each fundamental period. The space vector diagram can be divided into three regions with regard to the modulation index. Take sector I as an example (as shown in Fig. 5), when 0≤m < 0.5 (region ①), the reference vector Vref passes through triangle 3 and 4; when 0.5≤m < 0.577 (region ②), the reference vector Vref passes through triangle 3, 2, 5, and 4; when 0.577≤m < 1 (region ③), the reference vector Vref passes through triangle 1, 2, 5, and 6.

|
Fig.5 Regions of modulation index segmentation |
By taking triangle 1 of region ③ as an example, switching states 211, 210, and 200 will be applied to the converter one by one if DPWM1 is adopted. The phase angle θ of reference vector can be considered as a constant in each sample period. The offset of the NP voltage Δv can be obtained according to Eq. (14).
| $ \begin{array}{l} \Delta v\left( t \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} { - \frac{{\sqrt 2 I{\rm{cos}} (\theta - \varphi )}}{{2C}}t,0 \le t < {T_1}/2}\\ { - \frac{{\sqrt 2 I}}{{2C}}[{\rm{cos}}(\theta - \varphi ){T_1}/2 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}(\theta - \varphi - 2\pi /3)t],\quad {T_1}/2 \le t < {T_1} + {T_2}/2}\\ { - \frac{{\sqrt 2 I}}{{2C}}[{\rm{cos}}(\theta - \varphi ){T_1}/2 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}(\theta - \varphi - 2\pi /3){T_2}/2],{T_1} + {T_2}/2 \le t < {T_s}/2} \end{array}} \right. \end{array} $ | (14) |
When capacitance C, sample period Ts, load current I, and load power factor φ are not changed, Δv can be regarded as a linear function of t, where C is capacitance of C1 and C2. Fig. 6 shows the trend of the offset Δv against the phase angle θ.

|
Fig.6 Neutral point voltage offset during reference vector synthesis |
Take the reference vector Vref located at θ=0 as an example. In the first half of sample period, when t=0 (k-th instant), vC1 is equal to vC2, where vC1 and vC2 are voltages of C1 and C2, respectively, and NP voltage offset Δv=0; when t is between 0 and T1/2, the switching state 211 is adopted, C1 is discharged and C2 is charged by the NP current io, and NP voltage offset Δv is increased; when t=T1/2 ((k+1)-th instant), Δv=-
When NP voltage ripple occurs, the output phase voltage is also shifted. The output voltage of each phase at (k+1)-th instant can be determined by the output voltage at k-th instant, the switching state, and the offset of the NP voltage, which yields
| $ \left\{ {\begin{array}{*{20}{l}} {v_{{\rm{AO}}}^{k + 1} = v_{{\rm{AO}}}^k + (S - 1)\Delta v}\\ {v_{{\rm{BO}}}^{k + 1} = v_{{\rm{BO}}}^k + (S - 1)\Delta v}\\ {v_{{\rm{CO}}}^{k + 1} = v_{{\rm{CO}}}^k + (S - 1)\Delta v} \end{array}} \right. $ | (15) |
By substituting Eq.(15) into Eq.(1), the amplitude and phase of Vj can be determined. Define NP voltage ripple coefficient λ as
| $ \lambda = \frac{{\varDelta v}}{{{V_{{\rm{dc}}}}/2}} $ | (16) |
From Fig. 7, when NP voltage is shifted (assuming λ= 0.25), the phase angle of V7 is unchanged, while the amplitude is changed, and V7 is changed to V′7. The amplitude and phase angle of V13 are both changed, and V13 is changed to V′13. Consequently, during the reference vector synthesis, error voltage vector Δ V7 and Δ V13 are changed into Δ V′7 and Δ V′13, respectively. The trajectory of error current vector is also changed, and the calculation results of the error model are inaccurate.

|
Fig.7 The change of current ripple trajectory caused by neutral point voltage ripple |
Therefore, the amplitude and phase angle modification model, i.e., the error model of NP voltage ripple, needs to be added to the error model of space vector synthesis. The high-frequency error caused by space vector synthesis and the low-frequency error caused by NP voltage ripple are both considered. Then the unified model can be established. The output waveform quality of 3L-NPC converter can be evaluated accurately. Fig. 8 shows the algorithm flow of the unified error model.
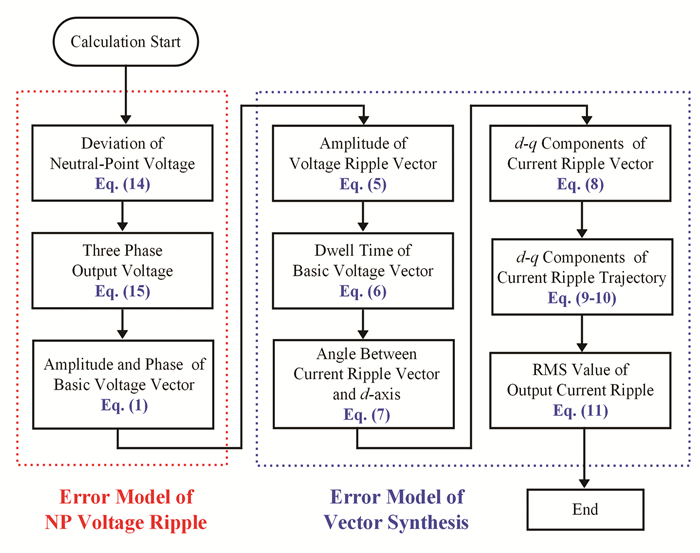
|
Fig.8 Flow diagram of the unified error model |
5 Experimental Analysis and Verification
As shown in Fig. 9, a rapid control prototype dSPACE DS1007 was adopted as the control circuit, and IGBT module Infineon F3L75R07W2E3_B11 was used as the power circuit to compose 3L-NPC converter. Parameters of the experimental prototype are listed in Table 2.

|
Fig.9 The prototype of dSPACEⒸDS1007 driven 3L-NPC converter |
| Table 2 Parameters of the experimental platform |
Based on the above experimental prototype, the experimental results of the output current are sampled. Instead of total harmonic distortion (ITHD), total demand distortion of output current (ITDD) is introduced to describe the output performance of 3L-NPC. ITDD varies slightly throughout the modulation range compared with ITHD, which is beneficial for the comparison of the performance of different modulation strategies. Define ITDD as[18]
| $ {I_{{\rm{TDD}}}} = \frac{{\sqrt {0.5\sum\limits_{h = 2}^\infty {I_h^2} } }}{{{I_{{\rm{nom}}}}}} $ | (17) |
where Ih represents the h-th harmonic of load current and Inom represents normal load current. Then the curve of ITDD versus the modulation index can be obtained by the Fourier analysis. On this basis, the RMS value of the output current ripple calculated by the traditional error model and the unified error model are compared and analyzed.
Fig. 10 shows the experimental results of output line voltage vAB, output current iA, and neutral-point voltage vC1-vC2 for DPWM3 when m=0.8, DC-link capacitance C=1 000 μF, and C=180 μF, respectively.

|
Fig.10 Experimental results of DPWM3 when m=0.8 |
As can be seen, the neutral-point voltage ripple increases with the reduction of DC-link capacitor, and ITDD increases consequently.
Fig. 11 shows the variation of ITDD under CPWM and DPWM0~DPWM3 when the DC-link capacitance C=1 000 μF and C=180 μF, respectively. From Fig. 11, the decrease of the DC-link capacitance will lead to the increase of ITDD. From Eq. (14), the smaller the C is, the larger the NP voltage offset Δv is. Thus, the output waveform quality of the converter decreases visibly.

|
Fig.11 Variation of the total demand distortion ITDD versus the modulation index m |
Fig. 12 shows the calculation results Iripple of the traditional error model. It can be deduced from Section 3 that the NP voltage offset Δv is not introduced into the traditional error model. The influence of NP voltage ripple on the output performance cannot be measured. Comparison of Fig. 11 and Fig. 12 shows that the calculation results of the traditional error model coincide with the curve of ITDD when the DC-link capacitance is relatively high. When the DC-link capacitance is low, NP voltage offset Δv increases. There is a large deviation between the calculation results of Iripple and ITDD, which indicates that they are inaccurate.

|
Fig.12 Curve of Iripple versus the modulation index m(traditional error model) |
Fig. 13 illustrates the calculation results Iripple of the unified error model presented in this paper.

|
Fig.13 Curves of Iripple versus the modulation index m(unified error model) |
When the modulation index m=0.3, the RMS value of output current ripple Iripple of DPWM3 (C=180 μF) is 0.1 A and the amplitude of output current is 1.2 A. Thus, according to the unified error model, the ripple component accounts for 8.3% of the output current, while for the experimental results shown in Fig. 10, the value of ITDD is 9.05%. The output current is obviously affected by the error during reference vector synthesis and the neutral-point voltage ripple. So the calculation results are in accordance with the experimental results.
Comparison of Fig. 11 and Fig. 13 shows that the calculation results of the unified error model are consistent with the curve of ITDD under different DC-link capacitance conditions. It shows that the influence of NP voltage ripple on the output waveform quality can be represented by the error model of NP voltage ripple. The disadvantage of the traditional error model, which only evaluates the high-frequency error caused by space vector synthesis and does not consider the low-frequency error introduced by NP voltage ripple, can thus be modified.
It is worth noting that the value of L is only a proportional coefficient in Eq. (3). The comparison of RMS value of output current ripple for different modulation strategies is not affected by the variation of L. Even if L is changed to L′, the results in Fig. 12 only need to be multiplied by L/L′, and the comparative relationship between Iripples remains the same.
6 ConclusionsAn accurate evaluation method of the output waveform quality for 3L-NPC converter is presented in this paper. RMS value of output current ripple was used as the index. The influence of the NP voltage ripple on the output waveform quality was fully considered. The mathematical model of NP voltage offset was established and used to modify the amplitude and phase angle of the basic vector. The unified error model considering both the high frequency error caused by space vector synthesis and the low frequency error introduced by NP voltage ripple simultaneously was established. The accurate evaluation of the output waveform quality of 3L-NPC converter was realized.
| [1] |
Rodriguez J, Bernet S, Steimer P K, et al. A survey on neutral-point-clamped inverters. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2219-2230. DOI:10.1109/TIE.2009.2032430 (  0) 0) |
| [2] |
Abu-Rub H, Holtz J, Rodriguez J, et al. Medium-voltage multilevel converters-state of the art, challenges, and requirements in industrial applications. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2581-2596. DOI:10.1109/TIE.2010.2043039 (  0) 0) |
| [3] |
Stillwell A, Candan E, Pilawa-Podgurski R C N. Active voltage balancing in flying capacitor multi-level converters with valley current detection and constant effective duty cycle control. IEEE Transactions on Power Electronics, 2019, 34(11): 11429-11441. DOI:10.1109/TPEL.2019.2899899 (  0) 0) |
| [4] |
Rahman S, Iman-Eini H, Bakhshizadeh M K, et al. Selective harmonic elimination technique with control of capacitive DC-link voltages in an asymmetric cascaded H-bridge inverter for STATCOM application. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8788-8796. DOI:10.1109/TIE.2018.2811365 (  0) 0) |
| [5] |
Zhang G Z, Wei B X, Gu X, et al. Sector subdivision based SVPWM strategy of neutral-point-clamped three-level inverter for current ripple reduction. Energies, 2019, 12(14): 2734. DOI:10.3390/en12142734 (  0) 0) |
| [6] |
Kouro S, Malinowski M, Gopakumar K, et al. Recent advances and industrial applications of multilevel converters. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2553-2580. DOI:10.1109/TIE.2010.2049719 (  0) 0) |
| [7] |
Zhang Z B, Li Z, Kazmierkowski M P, et al. Robust predictive control of three-level NPC back-to-back power converter PMSG wind turbine systems with revised predictions. IEEE Transactions on Power Electronics, 2018, 33(11): 9588-9598. DOI:10.1109/TPEL.2018.2796093 (  0) 0) |
| [8] |
Mukherjee S, Giri S K, Kundu S, et al. A generalized discontinuous PWM scheme for three-level NPC traction inverter with minimum switching loss for electric vehicles. IEEE Transactions on Industry Applications, 2019, 55(1): 516-528. DOI:10.1109/TIA.2018.2866565 (  0) 0) |
| [9] |
Gu X, Wei B X, Zhang G Z, et al. Improved synchronized space vector PWM strategy for three-level inverter at low modulation index. Electronics, 2019, 8(12): 1400. DOI:10.3390/electronics8121400 (  0) 0) |
| [10] |
Chen W, Sun H W, Gu X, et al. Synchronized space vector PWM for three level VSI with lower harmonic distortion and switching frequency. IEEE Transactions on Power Electronics, 2016, 31(9): 6428-6441. DOI:10.1109/TPEL.2015.2499774 (  0) 0) |
| [11] |
Beig A R, Kanukollu S, Hosani K A, et al. Space-vector-based synchronized three-level discontinuous PWM for medium-voltage high-power VSI. IEEE Transactions on Industrial Electronics, 2014, 61(8): 3891-3901. DOI:10.1109/TIE.2013.2288194 (  0) 0) |
| [12] |
Das S, Narayanan G, Pandey M. Space-vector-based hybrid pulsewidth modulation techniques for a three-level inverter. IEEE Transactions on Power Electronics, 2014, 29(9): 4580-4591. DOI:10.1109/TPEL.2013.2287095 (  0) 0) |
| [13] |
Das S, Narayanan G. Analytical closed-form expressions for harmonic distortion corresponding to novel switching sequences for neutral-point-clamped inverters. IEEE Transactions on Industrial Electronics, 2014, 61(9): 4485-4497. DOI:10.1109/TIE.2013.2293708 (  0) 0) |
| [14] |
Casadei D, Serra G, Tani A, et al. Theoretical and experimental analysis for the rms current ripple minimization in induction motor drives controlled by SVM technique. IEEE Transactions on Industrial Electronics, 2004, 51(5): 1056-1065. DOI:10.1109/TIE.2004.834967 (  0) 0) |
| [15] |
Xia C L, Zhang G Z, Yan Y, et al. Discontinuous space vector PWM strategy of neutral-point-clamped three-level inverters for output current ripple reduction. IEEE Transactions on Power Electronics, 2017, 32(7): 5109-5121. DOI:10.1109/TPEL.2016.2611687 (  0) 0) |
| [16] |
Xia C L, Shao H J, Zhang Y, et al. Adjustable proportional hybrid SVPWM strategy for neutral-point-clamped three-level inverters. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4234-4242. DOI:10.1109/TIE.2012.2213558 (  0) 0) |
| [17] |
McGrath B P, Holmes D G, Lipo T. Optimized space vector switching sequences for multilevel inverters. IEEE Transactions on Power Electronics, 2003, 18(6): 1293-1301. DOI:10.1109/TPEL.2003.818827 (  0) 0) |
| [18] |
Geyer T. A comparison of control and modulation schemes for medium-voltage drives: emerging predictive control concepts versus PWM-based scheme. IEEE Transactions on Industry Applications, 2011, 47(3): 1380-1389. DOI:10.1109/TIA.2011.2127433 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


