In recent years, much research attention has been devoted to wave-structure interactions in open seas and nonlinear waves. The numerical research on wave-structure interaction take interest in large-scale model and real-sea state simulations. This gives a big challenge on modeling the nonlinear wave propagation in large domain and the application of computational fluid dynamics (CFD). With the development of computer science, the CFD method becomes a popular approach due to its ability to resolve the complicated wave-structure interaction problems such as impact pressure on structures and wave patterns around high-speed ship. The ability of the CFD method to deal with large-scale model and refinement fluid simulations makes it become the main method in the future. However, the cost of propagating open-state waves or freak waves in the CFD method cannot be ignored. As is known, the viscous effect in incident wave is small, therefore employing the potential theory to do the fast wave generation is a good choice in numerical simulations. The traditional potential theories are mature in generating nonlinear waves, but a spectral method called high-order-spectral (HOS) method has salient ability on dealing with long-time wave evolution and large domain propagation in an efficient way. Yet its shortcomings are obvious: it has difficulties in simulating large amplitude motion of structures and complicated wave phenomena such as wave breaking. Therefore, combining the HOS method with the CFD method seems to be the best way to solve complex wave-structure interactions efficiently and accurately. This paper reviews the development of the HOS method and includes the coupling method in recent years. Besides, based on the strength as well as shortcomings of the combined method, this paper discusses the future research work of this combined method.
2 HOS MethodThe HOS method is a robust numerical method for solving nonlinear wave equations. With the application of pseudo-spectral method and Fast Fourier Transform, the HOS method embodies the feature of efficiency and fast convergence. This method has another name called Dirichlet-Neumann Operator[1]. Its accelerated version[2] is equivalent to the HOS method[3]. Ducrozet et al.[4] gave a comparison and conclusion that HOS models are more efficient than advanced models with finite-difference discretization. Dommermuth and Yue[5] compared spectral method with fully nonlinear mixed-Eulerian-Lagrangian (MEL)[6], and this spectral method accomplishes a more rapid convergence in calculation as well as total energy conservation. With the computational effort increasing only linearly with modes and orders, the spectral method costs less computational time.
2.1 Theory of the HOS MethodDommermuth and Yue[5] gave the numerical description of the HOS method. They extended Zakharov equation[7-8]/model coupling idea[9-11] to steeper waves, and modified this equation and the approach to a higher order for gravity waves. It can simulate the wave nonlinearity into a specified order and use a large number of free Fourier modes in nonlinear simulations. The computational effort increases only proportional to the order and modes. The fluid is considered to be irrotational, homogeneous, incompressible, and inviscid. They considered a velocity potential which satisfies Laplace's equation. With the pseudo-spectral method, the equation only accounts for the free surface, thus they defined the surface potential as ϕs(x, t) = ϕ(x, η (x, t), t). The kinematic and dynamic boundary conditions on the free surface of ϕs are[5]
| $ {{\eta _t} + {\nabla _x}{\phi ^s} \cdot {\nabla _x}\eta - (1 + {\nabla _x}\eta \cdot {\nabla _x}\eta ){\phi _z}(\mathit{\boldsymbol{x}},\eta ,t) = 0} $ | (1) |
| $ \begin{array}{l} \phi _t^s + \eta + \frac{1}{2}{\nabla _x}{\phi ^s} \cdot {\nabla _x}{\phi ^s} - \frac{1}{2}(1 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\nabla _x}\eta \cdot {\nabla _x}\eta )\phi _z^2(\mathit{\boldsymbol{x}},\eta ,t) = - {P_a} \end{array} $ | (2) |
They assumed a measure of the wave steepness ε as a small parameter. ϕ and η are O(ε) quantities. For a given order M in ε, ϕ can be written in a perturbation series based on ε[5]. Thus ϕ(m) is the same quantity with O(εm). They expanded each ϕ(m) on z = η in a Taylor series, then[5]
| $ \begin{array}{*{20}{l}} {{\phi ^s}(x,t) = \phi (\mathit{\boldsymbol{x}},\eta ,t) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{m - 1}^M {\sum\limits_{k = 0}^{M - m} {\frac{{{\eta ^k}}}{{k!}}} } \frac{{{\partial ^k}}}{{\partial {z^k}}}{\phi ^{(m)}}(\mathit{\boldsymbol{x}},0,t)} \end{array} $ | (3) |
When expanding Eq. (3)[12-13], they got a sequence of equations of ϕ(m):
| $ \begin{array}{l} {\phi ^s}(\mathit{\boldsymbol{x}},t) = {\phi ^{(1)}}(\mathit{\boldsymbol{x}},0,t) + \eta \frac{{\partial {\phi ^{(1)}}}}{{\partial z}}(\mathit{\boldsymbol{x}},0,t) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{\phi ^{(1)}}}}{{\partial {z^2}}}(\mathit{\boldsymbol{x}},0,t) + \ldots + {\phi ^{(2)}}(\mathit{\boldsymbol{x}},0,t) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta \frac{{\partial {\phi ^{(2)}}}}{{\partial z}}(\mathit{\boldsymbol{x}},0,t) + \frac{{{\eta ^2}}}{2}\frac{{{\partial ^2}{\phi ^{(2)}}}}{{\partial {z^2}}}(\mathit{\boldsymbol{x}},0,t) + \ldots + \ldots \end{array} $ |
Collecting η in the same order, Eq. (3) is a Dirichlet boundary condition. The surface potential ϕs(x, 0) and η(x, 0) are known in
| $ \begin{array}{l} {\phi ^{(m)}}(\mathit{\boldsymbol{x}},0,t) = - {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^{m - 1} {{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\eta ^k}}}{{k!}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^k}}}{{\partial {z^k}}}{\phi ^{(m - k)}}(\mathit{\boldsymbol{x}},0,t),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m = 2,3, \ldots ,M \end{array} $ | (4) |
where m = 1, ϕs = ϕ(m)(x, 0, t). Eq. (4) is the final formulation of the HOS method. While in a mode-coupling approach, except Dirichlet free-surface condition (4), Eq. (3) can be solved by using eigenfunction[5].
The eigenfunction φn has analytical solutions for simple geometries. For example, the 2π-periodic boundary conditions can be represented as[5]
| $ \begin{array}{*{20}{l}} {{\phi ^{(m)}}(\mathit{\boldsymbol{x}},z,t) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n = 0}^\infty {\phi _n^{(m)}} (t){\rm{exp}}[|{\mathit{\boldsymbol{k}}_\mathit{\boldsymbol{n}}}|z + {\rm{i}}{\kern 1pt} {\mathit{\boldsymbol{k}}_\mathit{\boldsymbol{n}}} \cdot \mathit{\boldsymbol{x}}]} \end{array} $ |
For constant finite deep water, with depth h[5],
| $ \begin{array}{*{20}{l}} {{\phi ^{(m)}}(\mathit{\boldsymbol{x}},z,t) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n = 0}^\infty {\phi _n^{(m)}} (t)\frac{{{\rm{cosh}}[|{\mathit{\boldsymbol{k}}_\mathit{\boldsymbol{n}}}|(z + h)]}}{{{\rm{cosh}}(|{\mathit{\boldsymbol{k}}_\mathit{\boldsymbol{n}}}|h)}}{\rm{exp}}({\rm{i}}{\kern 1pt} {\mathit{\boldsymbol{k}}_\mathit{\boldsymbol{n}}} \cdot \mathit{\boldsymbol{x}})} \end{array} $ |
The study of Dommermuth and Yue[5] is essential for developing the the HOS method. With its high efficiency and accuracy, it opens up a path in simulating nonlinear gravity waves for succeeding researchers. With the existence of the exponential profile, the HOS method can provide rapid convergence and consume less time. The boundary-value problems are solved rapidly through Fast Fourier Transform, which connects spatial derivatives in spectral representation and nonlinear products in physical space.
West et al.[14] presented using the HOS method to study the free and bound waves on nonlinear ocean surface. The descriptions of the HOS method is similar to Dommermuth and Yue[5]. However, there is a little difference in dealing with the vertical velocity in West[14].They first assumed a power series in ε:
| $ {{\phi _z}(\mathit{\boldsymbol{x}},\eta ,t) = \sum\limits_{m = 1}^M {\varphi _z^{(m)}} (\mathit{\boldsymbol{x}},0,t)} $ | (5) |
| $ {\phi _z^{(m)}(\mathit{\boldsymbol{x}},\eta ,t) = \sum\limits_{k = 0}^{m - 1} {\frac{{{\eta ^k}}}{{k!}}} \frac{{{\partial ^{k + 1}}}}{{\partial {z^{k + 1}}}}{\varphi ^{m - k}}(\mathit{\boldsymbol{x}},0,t)} $ | (6) |
In this way, all the terms under boundary condition which contain the vertical velocity are consistent with the ordering ε, making the comparison with analytical data easier.
Although the advantages of the HOS method are obvious, some errors exist due to its features. Because the velocity potential is single value in the HOS method, it cannot simulate overturn phenomenon in waves. Besides, the HOS method has a limit in wave steepness, and it will fail when wave steepness is very large.
The first error is the truncation in the number of modes N and order M. For the singularity in the analytic continuation of velocity potential in the HOS method, the convergence breaks when the wave steepness is large. The second is amplification of round-off errors. The error at any order in high wavenumber modes will be amplified. The unstable growth of this error in many nonlinear free-surface simulations will occur when high wave number is used[15-16]. Dommermuth and Yue[5] used Longuet-Higgins and Cokelet's methods to make a low-pass filter to eliminate such high-wavenumber instabilities.
The aliasing errors[17-18] happen because the nonlinear products in free-surface boundary conditions are performed in physical space instead of in spectral space. West et al.[14] removed this error by changing the numbers of mesh points Nx, Ny in the physical plane to satisfy the condition
| $ {N_x} > (M + 1){k_{{\rm{max}}}},{N_y} > (M + 1){l_{{\rm{max}}}} $ |
De-aliased computation can be performed by extending spectra in zero padding[19-20]. The zero-padding applies half-rule and are defined on a number of points:
| $ {N_d} = \frac{{p + 1}}{2}M $ |
Liu et al.[21] extended the HOS method to study nonlinear wave-body interactions. They considered the submerged body as a dipole distributed on the free surface and a source affected on the body surface. They showed the ability and accuracy of the spectral method in simulating submerged body. However, they also pointed out the method is not available when the body submergence is small and in wave breaking case.
Unlike many numerical models[8,10,22] which have difficulties in simulating deep-water dispersive waves due to the complexity of the nonlinear terms, the HOS method is more suitable for strong nonlinearity terms. However, it has difficulty in simulating the progress of nonlinear wave which may give spurious high-frequency waves. It can be eliminated by either giving sufficient time when initialized with linear wave or changing initialization procedures. Dommermuth[23] developed an adjustment for simulating the turbulent free-surface flows. In case of turbulent free surface flows, Dommermuth[24] also developed an adjustment that allows nonlinear free-surface simulations to be initialized with linear solutions. By introducing the vertical component velocity ϕz|z = η = Ws(x, t), and letting the first order vertical velocity denote the leading-order, the free-surface Eqs. (1)-(2) can be expressed as[24]
| $ \begin{array}{*{20}{c}} {{\eta _t} - {W^{(1)}} = - {W^{(1)}} - {\nabla _x}{\phi ^s} \cdot {\nabla _x}\eta + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 + {\nabla _x}\eta \cdot {\nabla _x}\eta ){W^s}}\\ {\phi _t^s + \eta = - \frac{1}{2}{\nabla _x}{\phi ^s} \cdot {\nabla _x}{\phi ^s} + \frac{1}{2}(1 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\nabla _x}\eta \cdot {\nabla _x}\eta ){{({W^s})}^2}} \end{array} $ |
Then the nonlinear terms were all collected on the right-hand side. They applied a term Ta which is the duration of the transition period. They replaced right-hand terms into terms with Ta(named F and G), which smoothed the linear initial conditions to nonlinear computations. As the partial derivatives of the nonlinear terms F and G are equal to zero at any order, the procedure reduces the imbalance under the initial conditions. Dommermuth[23,25] also used atmosphere pressure terms to balance the dynamic free-surface boundary conditions. It needs to be mentioned that the work of Refs. [23] and [25] requires the adjustment of dynamic boundary condition, while that of Ref. [24] requires adjustment of both dynamic and kinematic boundary condition.
The solution of the initial condition and less computational time of the HOS method make extreme waves with long time generation in open seas more available. Brandini and Grilli[26] used the HOS method to do the first stage of growth of wave modulations and then applied the results as the initial conditions for extreme waves generation. It is worth noting that Brandini and Grilli presented the 2D HOS method as initial condition in transversal and longitudinal direction and it showed typical 3D wave modulations. Tanaka[27] employed the HOS method as the basis numerical scheme, and in order to study the energy spectrum or time evolution of skewness and kurtosis of wave elevation, they introduced a complex amplitude function[8]. The complex amplitude function b(k, t) is defined as[8]
| $ \begin{array}{*{20}{c}} {b(\mathit{\boldsymbol{k}},t) = \sqrt {\frac{{\omega (\mathit{\boldsymbol{k}})}}{{2\mathit{\boldsymbol{k}}}}} \hat \eta (\mathit{\boldsymbol{k}},t) + {\rm{i}}\sqrt {\frac{\mathit{\boldsymbol{k}}}{{2\omega (\mathit{\boldsymbol{k}})}}} \hat \phi (\mathit{\boldsymbol{k}},t)}\\ {\omega (\mathit{\boldsymbol{k}}) = \sqrt {gk} ,k = |\mathit{\boldsymbol{k}}|} \end{array} $ |
where
| $ f(\mathit{\boldsymbol{x}}) = \frac{1}{{2\pi }}\int {\hat f} (\mathit{\boldsymbol{k}}){{\rm{e}}^{{\rm{i}}kx}}{\rm{d}}\mathit{\boldsymbol{k}} $ |
ϕs and η are described with b(k, t) :
| $ \begin{array}{*{20}{l}} {\eta (\mathit{\boldsymbol{x}}) = \frac{1}{{2\pi }}\int {\sqrt {\frac{k}{{2\omega }}} } \{ b(\mathit{\boldsymbol{k}}) + {b^*}( - \mathit{\boldsymbol{k}})\} {{\rm{e}}^{{\rm{i}}kx}}{\rm{d}}\mathit{\boldsymbol{k}}}\\ {\phi (\mathit{\boldsymbol{x}}) = \frac{{ - {\rm{i}}}}{{2\pi }}\int {\sqrt {\frac{\omega }{{2k}}} } \{ b(\mathit{\boldsymbol{k}}) - {b^*}( - \mathit{\boldsymbol{k}})\} {{\rm{e}}^{{\rm{i}}kx}}{\rm{d}}\mathit{\boldsymbol{k}}} \end{array} $ |
The complex amplitude b (k) is given by the value of k in discretized space, and for each k,
| $ {b_k} = \sqrt {\frac{{{\omega _k}}}{{2k}}} {\hat \eta _k} + i\sqrt {\frac{k}{{2{\omega _k}}}} {\hat \phi _k},\quad {\omega _k} = \omega (\mathit{\boldsymbol{k}}) $ |
The energy density E can be given according to bk on the wave field:
| $ E \approx \sum\limits_k {{\omega _k}} |{b_k}{|^2} $ |
where E can also be given in terms of directional spectrum Φ(ω, θ) as
| $ \begin{array}{l} E = \int\limits_0^{2\pi } {\int\limits_0^\infty \varPhi } (\omega ,\theta ){\rm{d}}\omega {\rm{d}}\theta = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int {\frac{{{g^2}}}{{2{\omega ^3}}}} \varPhi (\omega ,\theta ){\rm{d}}k \approx \sum\limits_k {\frac{{{g^2}}}{{2\omega _k^3}}} \varPhi (\omega ,\theta )\varDelta {S_k} \end{array} $ | (7) |
| $ \varDelta {S_k} = \varDelta {k_x} \times \varDelta {k_y} $ | (8) |
Eqs. (7)-(8) gives the relation between |bk| and Φ(ω, θ):
| $ |{b_k}{|^2} \approx \sum\limits_k {\frac{{{g^2}}}{{2\omega _k^4}}} \varPhi (\omega ,\theta )\varDelta {S_k} $ | (9) |
Through Eq. (9), the directional spectrum Φ(ω, θ) can be determined by calculating the norm |bk(t = 0)|, and the phase of bk(t = 0) is determined by a random number in [0, 2π]. Φ(ω, θ) can be expressed with JONSWAP spectrum.
Ducrozet et al.[28] followed the initializing condition of Dommermuth[23] and simulated a forced focusing event wave based on the method of Tanaka[27], and then a natural freak waves during a long time simulation were considered as well, as shown in Fig. 1. Their study gives a definite description on generating freak wave in an open-sea state, discusses the selection of parameters in directional spreading, and gives a proper solution to it. This encourages the exploration on the freak wave mechanics and the developments of the HOS method. Li et al.[29] computed the sloshing wave in 3D tank which shows the efficiency of the HOS method in simulating focusing wave.

|
Fig.1 3-D surface elevation at t = 20.3Tp[28](Reprinted with the permission from Ref.[28] copyright © Author(s) 2007. This work is Licensed under a Great Commons License) |
Zhao et al.[30-32] applied an improved Adams-Bashforth-Moulton (ABM) numerical integration instead of Runge-Kutta forth (RK4) scheme to reduce simulation time and studied focusing wave simulation in experimental scale and real scale. The improved ABM scheme can reach a truncation error of O(Δt6), while RK4 scheme can only reach O(Δt5). However, as mentioned in Dommermuth and Yue's work[5], they employed RK4 instead of ABM because RK4 can provide a lower global truncation error and a larger stability region. The improved ABM only increases the precise order, and they did not mention the global truncation error and numerical stability in their work. Therefore, it needs to be discussed in the future which numerical integration method has wider application scope.
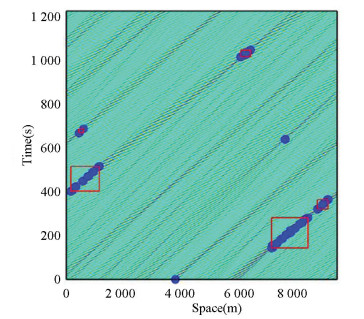
Sergeeva and Slunyaev[33] studied the characteristics of rogue waves by the HOS method. They produced space-time wave data sheets using the HOS method, and observed the detailed picture of individual rogue waves. They simulated 10 km field with 20 min sheets of data with surface elevation, fluid velocity, and so on. Fig. 2 illustrates rogue waves and rogue events, where markers indicate rogue waves and rectangles assemble them into rogue events. Rogue waves are difficult to observe for its long-time duration, short time appearance, and high crests with shallow troughs. Their study applies the HOS method to give the probability of appearance and lifetime of rogue waves, showing the possibility to study the rogue waves and wave-structure interactions in rogue waves. The application of the HOS method makes the study of rogue waves possible.
|
Fig.2 Spatio-temporal sheet of the surface elevation[33](Reprinted with the permission from Ref.[33] © Author(s) 2013.CC Attribution 3.0 License) |
Xiao et al.[34] studied the occurrence and dynamics of rogue waves employing the HOS method in three dimensions. They compared the HOS results to nonlinear Schrodinger equations, giving a quasi-stationary evolution in long-time prediction, which cannot be predicted by the nonlinear Schrodinger equations. They also introduced the definition of rogue wave occurrence which related to the occurrence probability, and discussed different situations of narrow spread seas. Along with the study mentioned above, the research on probability of rogue wave occurrence provides valuable reference for studying the structures which were emerged and changed in the rogue waves.
Those studies focused on unbounded domains of open-sea states, with periodic boundary conditions applied. However, unbounded domain means that the wave propagates without wave generation, absorption, and beach reflections, which makes experimental validations more difficult. Bonnefoy et al.[35] developed a non-periodic HOS technique and presented a linear wave maker motion in the numerical wave tank. They considered an additional potential[36] added on the original potential to make sure the potential satisfied the wave maker condition. By numerically solving the additional potential also in time domain, they extended the idea of Agnon and Bingham[36], and adjusted a linear piston wavemaker to a generic wavemaker, as shown in Fig. 3. They presented 2D cases of focusing wave packet with extending second order initial decomposition and target phase signal iterative corrections.
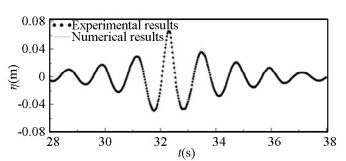
Li[37] employed the high-order-spectral tank (HOST) derived from Bonnefoy et al.[35] to simulate 2-D focusing wave and made comparison with the experimental results. Li and Liu[38] also applied the HOST method to generate directional focusing waves. Fig. 4 shows the comparison between experimental results and 2-D focusing wave generated by HOST. The surface elevation of 3-D focusing wave generation is displayed in Fig. 5. They studied the properties of the focusing wave and gave conclusions that shift of focusing point and maximum crest decreases when spreading parameter decreases in 3-D case. In addition, Li et al.[39] used the HOST method to study the influence of current on the focusing wave. The potential velocity are expressed as the uniform current velocity added with wave potential velocity in their study. The numerical model revealed strong nonlinear interaction in the wave-current interaction.
|
Fig.4 Comparison between experimental data and numerical results[38](Reprinted with the permission from Ref.[38] © 2015 Chinese Ocean Engineering Society and Springer-Verlag Berlin Heidelberg) |
|
Fig.5 Surface elevation of 3-D focusing waves at selected time[38](Reprinted with the permission from Ref.[38] © 2015 Chinese Ocean Engineering Society and Springer-Verlag Berlin Heidelberg) |
Based on the previous works on HOST[35] and its successful results compared with experiments, Ducrozet et al.[40] developed this method into second-order wave maker motion. They combined the model developed by Bonnefoy et al.[13,15] with the HOS method wave tank, and then extended HOST to second order. Fig. 6 shows the calculation process of this new HOST. A 2D focusing wave packet embedded in irregular wave fields was considered and showed apparent improvement in results compared with those in linear HOST.
|
Fig.6 The 2nd HOST calculation setup (in Runge Kutta)[40](Reprinted with the permission from Ref.[40] Copyright © by the International Society of offshore and Polar Engineers) |
Bonnefoy et al.[41] applied both second-order wave maker motion and fully nonlinear numerical wave tanks and gave the validation results to experimental complex sea-states in 3-D.
Those improvements and developments of the HOS method lays the foundation for more application of the HOS method. In order to make the method more conveniently applied in many fields, Ecole Centrale Nantes, LHEEA Lab developed an open-source HOS model[42] named HOS-Ocean. The software is available on the Github (https://github.com/LHEEA/HOS-ocean/wiki). The HOS method is realized in a numerical simulation way, and provides possibility to couple the CFD software.
Assuming the simulation based on a rectangular fluid domain with periodic boundary condition, the velocity potential of surface boundary condition can be written as Eqs. (5)-(6), where kn = n(2π)/Lx is the wave numbers. Fig. 7 presents the brief description of code working in HOS-Ocean according to Ref.[42]. For the wave spectra used in HOS-Ocean is only JONSWAP spectrum, Song et al.[43] made an attempt to add two new wave spectrum P-M spectrum and ITTC 2-parameter spectrum in it.
|
Fig.7 Procedure of time-stepping in HOS-Ocean according to Ref.[42] |
Meanwhile, Ducrozet et al.[44] developed the open-source numerical wave tank based on HOS (HOS-NWT). The HOS-NWT is also available on Github (https://github.com/LHEEA/HOS-NWT/wiki). They extended wave maker modeling into three-order generation.
Seiffert and Ducrozet[45] included the wave breaking mechanism into HOS-NWT. As the HOS method assumes free-surface as single-valued, they approximated the broken surface as a single value. They suggested a threshold of water particle velocity to crest velocity between a broken and an unbroken wave in HOS solvers. Seiffert et al.[46] implemented a wave breaking onset criteria in HOS-NWT, which predicts good wave-breaking onset time and location compared with the experiments. Seiffert and Ducrozet[47] validated this wave-breaking mechanism through energy dissipation by adding an eddy viscosity parameter under boundary conditions. This kind of wave breaking onset can be incorporated with other nonlinear potential solver to reduce the risk of numerical instabilities, thus increasing the scope of application.
The development of the HOS method shows a perspective in ocean and ship engineering. The ability of generating large-domain wave field with fast convergence and accuracy gives researchers the chance to study rogue waves. The difficulties in studying rogue waves are due to its transient time appearance and long-time with large space simulation, which requires huge investment in resources. With the help of the HOS method, the parameters of rogue waves and the position of its occurrence can be found out. This lays the foundation for simulating severe conditions in ocean and sail engineering.
The applications and extensions of the HOS method are not limited to wave simulations. Many physical mechanisms are included by employing and validating the the HOS method, which include nonlinear energy transfers[48], bi-modal seas[49], modulation instabilities[50-51], and so on (cf.[42]). There are also some developments based on the HOS method, including wind forcing effects[52], jet current effects[53], variable bathymetry[54-58], and so on.
3 Combined Method of the HOS and CFD MethodIn order to simulate the wave-structure interaction in a more realistic and flexible way, the CFD method is carried out. This approach functions extremely well in resolving complex surface problem, large amplitude motion of structures, and so on. However, even though the development of computational science is rapid, the time duration and cost of the CFD method is still nonnegligible. In fact, when wave-structure interaction is considered, wave loads extending on the structures can be focused even more. Besides, the viscous effects are not obvious in wave simulation, and long-time wave simulation in the CFD method may cost a long time and cause numerical dissipation. Therefore, combining the potential and viscous flow together can improve the simulation in an efficient and realistic way.
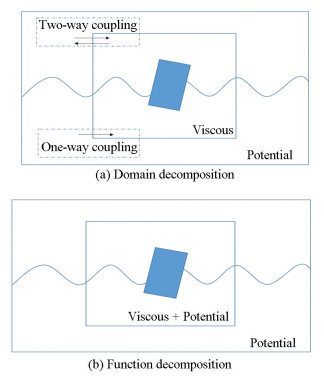
Li[59] gave a view of two groups which divides the combined potential and viscous flow: Domain Decomposition and Function Decomposition, the schematic diagram is shown in Fig. 8. He mentioned Domain Decomposition sets viscous domain and potential domain apart, while Function Decomposition sets viscous part and potential part in viscous domain.
|
Fig.8 View of two groups of combined potential and viscous flow according to Ref.[59] |
3.1 Function Decomposition
Many studies have been conducted[60-64] to solve a wave-structure interaction employing function decomposition approaches. These studies applied BEM as potential solver and RANS or Lattice Boltzmann Method (LBM) as viscous solver. Later on, a new approach was carried out focused on solving diffracted flow only, which is named Spectral Wave Explicit Navier-Stokes Equations (SWENSE). It is derived from a frame of potential theory[65-66] and splits all unknown variables into incident terms and diffracted terms[67]. SWENSE modifies the variables in RANS equations as follows[68]:
| $ \left\{ {\begin{array}{*{20}{l}} {{u^\alpha } = u_{\rm{I}}^\alpha + u_{\rm{D}}^\alpha }\\ {p = {p_{\rm{I}}} + {p_{\rm{D}}}}\\ {h = {h_{\rm{I}}} + {h_{\rm{D}}}} \end{array}} \right. $ |
where α∈{1, 2}, the unknown variables u, p, and h stands for Cartesian components of velocity, pressure, and free-surface elevation, respectively. The subscripts I and D represent incident and diffracted variables, respectively.
According to Navier-Stokes equations[59],
| $ \begin{array}{*{20}{c}} {\nabla {u^\alpha } = 0}\\ {\frac{{\partial {u^\alpha }}}{{\partial t}} + {u^\alpha }\nabla {u^\alpha } = - \frac{{\nabla p}}{\rho } + \mathit{\boldsymbol{g}} + \mathit{\boldsymbol{v}}{\kern 1pt} {\kern 1pt} {\nabla ^2}{u^\alpha }} \end{array} $ |
and Euler equations[59],
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla u_{\rm{I}}^\alpha = 0}\\ {\frac{{\partial u_{\rm{I}}^\alpha }}{{\partial t}} + u_{\rm{I}}^\alpha \nabla u_{\rm{I}}^\alpha = - \frac{{\nabla p}}{\rho } + \mathit{\boldsymbol{g}}} \end{array} $ |
The transport equations are obtained by substituting the Euler equations from the NS equations[59],
| $ \begin{array}{l} \frac{{\partial u_{\rm{D}}^\alpha }}{{\partial t}} + (u_{\rm{I}}^j + u_{\rm{D}}^j)\frac{{\partial u_{\rm{D}}^\alpha }}{{\partial {x^j}}} - v\frac{{{\partial ^2}u_{\rm{D}}^\alpha }}{{\partial {x^{{j^2}}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{1}{\rho }\frac{{\partial {p_{\rm{D}}}}}{{\partial {x^\alpha }}} = u_{\rm{D}}^j\frac{{\partial u_{\rm{I}}^\alpha }}{{\partial {x^j}}} + \mathit{\boldsymbol{v}}\frac{{{\partial ^2}u_{\rm{I}}^\alpha }}{{\partial {x^{{j^2}}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial u_{\rm{D}}^j}}{{\partial {x^j}}} = 0} \end{array} \end{array} $ |
With those equations, the incident variables were explicitly computed, thus named the solver SWENSE Equations. The incident nonlinear regular wave was obtained by a stream function model[69] while the nonlinear wave trains were derived from a spectral formulation combined with BEM[70] first, and then from the HOS method. The SWENSE method using the spectral formulation combined with BEM was validated both in 2D cases[71-72] and 3D cases[73].
Luquet et al.[74] employed the HOS method to play the role as incident wave model. Compared with the previous potential theories, the HOS method makes the simulation of arbitrary complex sea-state or freak waves more convenient and efficient. They used this method to simulate a Tension Leg Platform (TLP) in regular and irregular waves.
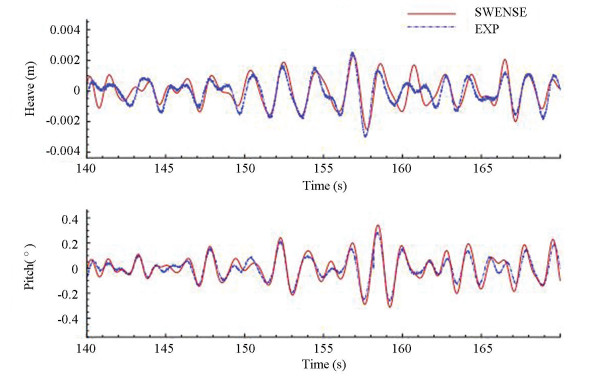
Other studies such as ship maneuvering with 6DOF, CALM buoy, and ship motion in 2DOF have been done in SWENSE model[75-78]. A validation of ship motion in SWENSE in irregular head wave was carried out (Fig. 9).
|
Fig.9 Comparison of ship motion with experimental results[77](Reprinted with the permission from Ref.[77] Copyright © 2009 ISOPE) |
However, those original SWENSE methods are based on one-phase CFD solver, which solve the free surface through the boundary condition. Li et al.[79-80] extended the SWENSE model into two-phase SWENSE model. They modified Euler momentum equation by introducing an incident pressure to balance the governing equations both in water and air phases.
The SWENSE model divides the total field into two parts: incident field and diffraction field. In this way, the incident field was solved by potential theory, thus the computational grids can be a coarse mesh while only the grids near diffraction field need to be refined. It not only improves efficiency when using the HOS method as incident model, but also decreases the cost when simulating wave structure interactions due to less grids in far field.
Gatin et al.[81-82] combined HOS with CFD RANS equation to solve 6DOF ships in extreme waves, as shown in Fig. 10 and Fig. 11. The combination was performed based on open source CFD software OpenFOAM[83]. They obtained free surface elevation and velocity from the HOS method, thus the velocity field is presented as[81-82]
| $ \begin{array}{l} {v_x}(x,y,z,t) = \sum\limits_k {\sum\limits_l {{c_{k.l}}} } (t){\rm{i}}{K_k}\frac{{{\rm{cosh}}({K_{k.l}}({z^\prime } + d))}}{{{\rm{cosh}}({K_{k.l}}d)}}{{\rm{e}}^{{\rm{i}}{K_k}x}}{{\rm{e}}^{{\rm{i}}{K_l}y}}\\ {v_y}(x,y,z,t) = \sum\limits_k {\sum\limits_l {{c_{k.l}}} } (t){\rm{i}}{K_l}\frac{{{\rm{cosh}}({K_{k.l}}({z^\prime } + d))}}{{{\rm{cosh}}({K_{k.l}}d)}}{{\rm{e}}^{{\rm{i}}{K_k}x}}{{\rm{e}}^{{\rm{i}}{K_l}y}}\\ {v_z}(x,y,z,t) = \sum\limits_k {\sum\limits_l {{c_{k.l}}} } (t){\rm{i}}{K_{k.l}}\frac{{{\rm{cosh}}({K_{k.l}}({z^\prime } + d))}}{{{\rm{cosh}}({K_{k.l}}d)}}{{\rm{e}}^{{\rm{i}}{K_k}x}}{{\rm{e}}^{{\rm{i}}{K_l}y}}\\ {\rm{where}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {z^\prime } = zd/\left( {d + \eta } \right) + d\left( {d/\left( {d + \eta } \right) - 1} \right). \end{array} $ |
where z' = zd/(d+η)+d(d/(d+η)-1).
They coupled the HOS method with the the CFD method using a two-phase SWENSE method[84-86] in level set method[87]. This two-phase SWENSE method is different from that in Li[79-80]. It deals with incident wave as a source term in CFD meshes. Therefore, the incident domain in CFD mesh still needs to be refined to keep accurate.
3.2 Domain DecompositionThe domain decomposition sets computational domains apart into viscous flow sub-domain and potential flow sub-domain. In general, with advantages of solving complex free surface and viscous effect around structure, the CFD method takes the inner domain and potential flow method takes the outer domain. The two methods solve separately in each sub-domain and communicate through the common boundary. Therefore, the domain decomposition method can be two-way coupling or one-way coupling.
Before the emergence of the HOS method, either two-way coupling[88-91] or one-way coupling[92-94] employed BEM method in potential flow sub-domain. Kim et al.[95] applied an overlay zone to do the communication between CFD and Euler wave, which is named Euler-Overlay Method (EOM). They combined EOM with mooring and riser model to do the simulation of Vortex-Induced Motion (VIM). Paulsen et al.[96] combined Oceanwave3D[97] with the CFD method and gave validations under different sea bed conditions.
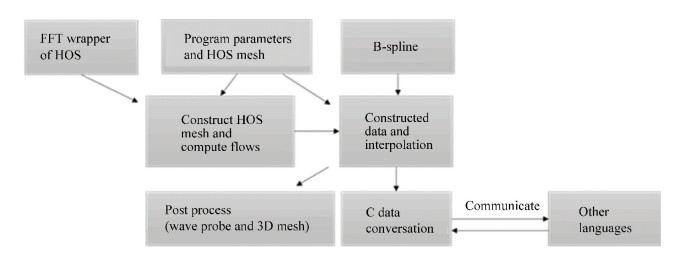
Choi et al.[98] combined the HOS method with OpenFOAM (foamStar) through a HOS wrapper program named Grid2Grid[99] which can be obtained from GitHub (https://github.com/LHEEA/Grid2Grid). Grid2Grid reconstructs HOS wave results and interpolates at demanded time and position in viscous flow field. The frame of program of Grid2Grid is shown in Fig. 12. Choi et al.[98] tested the new solver in empty wave tank and validated the stable and accuracy of this solver.
|
Fig.12 Frame of program in Grid2Grid according to Ref.[99] |
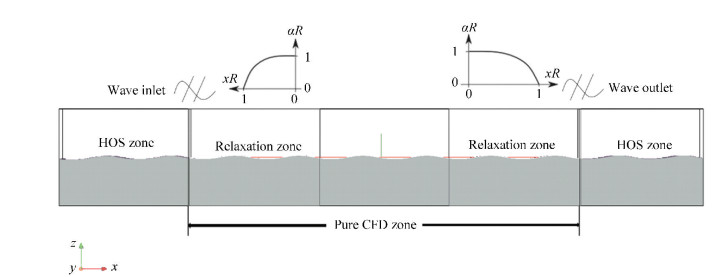
Zhuang et al.[100] developed the HOS method into an in-house CFD solver naoe-FOAM-SJTU[101-108]. They applied relaxation zone[109] as the common boundary to communicate information, as shown in Fig. 13. They tested the ability and accuracy of the new combined solver in empty wave tank, and gave good results. Song et al.[110] also applied this new solver to simulate freak waves in the empty tank. The CFD zone can obtain wave elevation and velocity from the HOS method in arbitrary time spot and positions, thus the new combined solver reduces the simulation cost in the CFD method.
|
Fig.13 Sketch of the HOS method combined with naoe-Foam-SJTU[100](Reprinted with permission from Ref.[100]) |
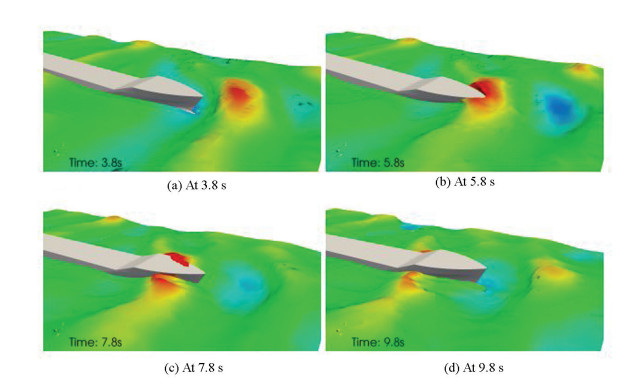
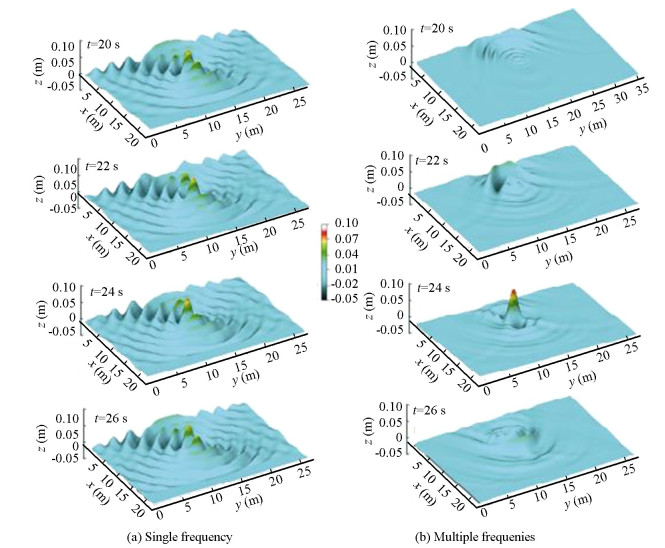
The CFD solver naoe-FOAM-SJTU is based on OpenFOAM and develops many modules and functions in recent years, such as 6DOF module[111], overset grids[112-114], internal flow coupled with external flow[115-117], and so on. Combined with the HOS method, the new solver has advantages on solving structures in open-sea states in an efficient way. A number of simulations have been carried out[118] by the new combined solver, presenting the ability to simulate the cylindrical structure in multi-directional sea-state (Fig. 14) as well as focusing wave (Fig. 15).
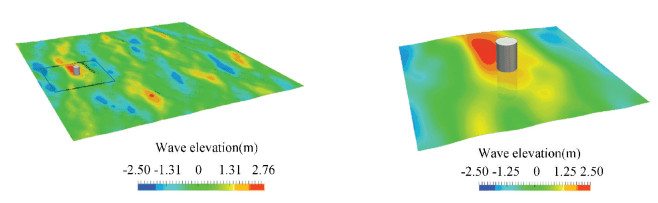
|
Fig.14 Wave pattern of a cylinder in directional wave in HOS-CFD domain (left) and in CFD domain (right)[118](Reprinted with permission from Ref.[118]) |

|
Fig.15 Focusing wave passing through a cylinder in CFD domain |
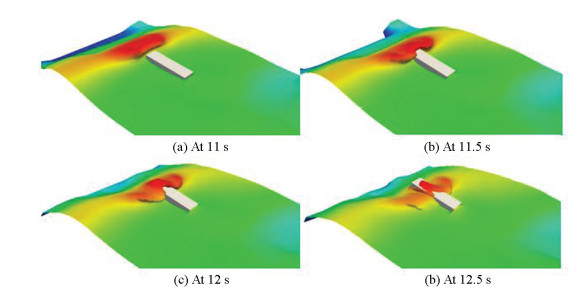
In general, a ship sailing in the seas is assumed to be sailing in the encountered added current. But a ship sailing in a large domain constitutes realistic ship maneuvering. With the help of overset grids and the HOS method, ship can sail in open seas without large computational domain requirement, as shown in Fig. 16. KCS ship model in model scale is chosen as the ship model and the Lpp of the ship is 6.070 2 m. The ship speed is 2.017 m/s, and the wave is first order Stokes wave in λ/L = 1.15. Through the results of heave motion and pitch motion as shown in Ref. [118], the coupled method is closer to experimental results than pure CFD method.

|
Fig.16 A ship maneuvering in the regular wave ((a) and (b) show the ship sailing in HOS domain; (c)-(f) show the details of the ship in a period in CFD domain)[118](Reprinted with permission from Ref.[118]) |
Quinn[119] combined HOS-NWT with OpenFOAM to study the breaking waves. The HOS-NWT replicates a 2D waves conducted in experiments with a 3D long-crest irregular wave and the results were analyzed with different breaking onset criteria. However, the breaking process was not visible in the coupled method. Quinn pointed out that this may due to the diminishing of crest value in HOS-NWT, which provided flows in OpenFOAM. Meanwhile, Quinn also simulated freak and rouge waves in HOS-NWT, and gave a conclusion that with the increase of the wave steepness, the discrepancy between HOS results and experimental results becomes large.
The review of application with the coupled method gives a huge possibility in wave-structure interactions. Nowadays, with the help of overset grids, the large amplitude of structures is achieved in the CFD method. The coupled method solved a big problem which the CFD method cannot solve at this moment. The HOS method gives the input information of large-scale or large domain of wave or sea states, the CFD method can simulate any situations in ocean and naval engineering. The given results of the coupled method are not enough though. Many research such as large-scale simulations, fine wave fields, and ship sailing in freak waves need to be done.
4 ConclusionsThe HOS method has been developed in the 1980s. With the feature of efficient wave generation and fast numerical convergence, an increasing number of applications using the HOS method have been carried out. The HOS method is popular in recent years for its ability in simulating large-domain wave generation and long-time evolution. From the very beginning, the HOS method was applied for studying nonlinear gravity wave and wave-wave interaction. After that, the attempt in studying wave-body interaction in the HOS method was carried out. The extreme wave and long-time simulation was completed from 2D to 3D, along with the observation of occurrence of freak wave in open-sea state. Then the application of the HOS method extended to bounded boundary condition which is wave tank simulation. With the development of computer science, the open source software of using the HOS method is well developed. Although many studies have been conducted to eliminate numerical error or employed assumptions to solve the shortfalls, development of the HOS method should not be stopped.
The combined method of the HOS and CFD method is a new theory in numerical simulations. The idea of combining the HOS with CFD method was put forward in recent decades. The development and application of the integrated method is all about fixed structure to test the accuracy of the combination. Some studies have been done to simulate ships in freak waves, showing the ability of the combined method in dealing with large motion of structure in freak waves.
Although the combined method of the HOS and CFD method only rises in recent years, its achievement is a progress in numerical simulation. The ability and advantages of the combined method are listed as follows:
1) Because the HOS method can give incident wave information in arbitrary space and time spot, the CFD method can choose required position and time spot in wave propagation. For example, the HOS method can be employed to do a real-sea state generation. After observing the appearance of freak wave, the CFD method can be used to receive the freak wave signal to simulate the freak wave-structure interactions. It is well known that the capture of freak wave needs thousands of seconds of simulation, which is impossible for the CFD method, while the combined method provides the possibility to do the freak wave structure interactions.
2) The large-scale model simulation in the HOS method coupled with the CFD method can also be achieved. The HOS method has the advantage in generating wave in large field efficiently, thus it can be an economic way to simulate large-scale model, especially in two-way coupling. The domain of the CFD method can be minimized around the large-scale model, and the wave field outside can be solved by the HOS method. Therefore, it will save lots of time and resources compared with pure CFD method.
3) The combined method has the ability and advantages in simulating fine wave field. When the simulations are based on focusing wave or fully developed nonlinear wave, the CFD method needs to spend lots of time to make sure the nonlinear wave or focusing wave are fully developed. The viscous effects in the CFD method may diminish the wave amplitude during the wave propagation. In this way, it costs splendid time and resources when the fine wave field is considered. With the help of HOS wave field which is a fully developed wave field, the time during wave propagation can be ignored in the CFD method. Therefore, the meshes in CFD can be as fine as possible to achieve the accuracy as required.
As stated above, the combined method has great ability in simulating some kinds of wave-structure interactions, which include ships or platforms in freak waves that may encounter impact pressure, breaking wave, and air gap phenomenon; large-scale model simulations; realistic wave-structure interactions such as real-sea state simulation, and so on.
5 Future WorksSome research perspectives and corresponding solutions are given below.
1) There are two kinds of coupled method of the HOS and CFD method: one is function decomposition of two-phase SWENSE[59,79-80], the other is SWENSE in Naval hydropack[81-82,84-86] and domain decomposition[98,100]. The first two-phase SWENSE model is limited to fixed structure up till now, therefore a 6DOF module and dynamic mesh needs to be applied. These modules can be implemented through OpenFOAM. The second SWENSE and the domain decomposition have the 6DOF module and dynamic/overset grids, but they have to refine the mesh in incident wave domain.
2) For coupled method of the HOS and CFD method in domain decomposition, it is one-way coupling at present. It does not need extra iterations between potential and viscous flow. However, it requires larger domain to realize complete radiation flow of wave-interaction influence than that in two-way coupling. Considering the ship maneuvering in the coupled method, the one-way coupling will end with misplaced wave patterns in the view of whole domain. Nevertheless, the two-way coupling of the HOS and CFD method needs to change the formulation of the HOS method and improvement of the common boundary condition, thus it is still under consideration.
3) The simulations based on the HOS method[28,42,44] are conducted on single-processor, while simulations in the CFD method often need multiple processors. This leads to separate calculation in the HOS method and the CFD method. In domain decomposition, the CFD calculation in multiple processors will duplicate the results of the HOS method. When the internal memory of HOS results is large, the duplication in parallel running may cause a huge work in CFD simulation. The HOS method has no apparent solutions on parallel running at present, therefore the CFD method can solve this problem by sparing an extra processor for the HOS method. This will prevent the duplication of HOS results files.
4) The studies of breaking waves are often included in wave-structure interactions. With the assumption of single value of breaking waves[45-47], the HOS method has the ability to predict breaking wave onset criteria. However, the assumption is not realistic and cannot be obviously visible in CFD domain. Therefore, the study of breaking phenomena needs to be done in viscous flow in the future. The CFD method can capture arbitrary time spot of HOS results, thus the thought is to map the breaking time spot of HOS to CFD domain, thus the breaking in waves happens under viscous flow solution. It requires further tests, because the incident information of the HOS method is absent, and the breaking wave in CFD domain may collapse or propagate in a wrong way.
5) There are some numerical instabilities with the combined HOS and CFD method. As all the variables are solved on free surface in the HOS method, the interaction with the CFD method will cause instability in sharp free surface. For function decomposition of two-phase SWENSE[59,79-80], it applies Ghost Flow Method (GFM)[120-122]to keep discontinuity in the CFD method. For domain decomposition of the combined method, the accumulated velocity on sharp free surface can be solved by an adding inversed velocity.
| [1] |
Craig W, Sulem C. Numerical simulation of gravity waves. Journal of Computational Physics, 1993, 108(1): 73-79, 82-83. DOI:10.1006/jcph.1993.1164 (  0) 0) |
| [2] |
Vijfvinkel E. Focused Wave Groups on Deep and Shallow Water. Groningen: University of Groningen, 1996.
(  0) 0) |
| [3] |
Schäffer H A. On the Dirichlet-Neumann Operator for nonlinear water waves. Proceedings of the 20th Intertional Workshop on Water Waves and Floating Bodies. 2005. 41-60.
(  0) 0) |
| [4] |
Ducrozet G, Bingham H B, Engsig-Karup A P, et al. A comparative study of two fast nonlinear free-surface water wave models. International Journal for Numerical Methods in Fluids, 2012, 69(11): 1818-1834. DOI:10.1002/fld.2672 (  0) 0) |
| [5] |
Dommermuth D G, Yue D K P. A high-order spectral method for the study of nonlinear gravity waves. Journal of Fluid Mechanics, 1987, 184: 267-288. DOI:10.1017/S002211208700288X (  0) 0) |
| [6] |
Longuet-Higgins M S, Cokelet E D. The deformation of steep surface waves on water-I. A numerical method of computation. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1976,350(1660): 1-26. DOI: 10.1098/rspa.1976.0092.
(  0) 0) |
| [7] |
Huang Y, Sclavounos P D. Nonlinear ship motions. Journal of Ship Research, 1998, 42(2): 120-130. (  0) 0) |
| [8] |
Zakharov V E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. Journal of Applied Mechanics and Technical Physics, 1968, 9(2): 190-194. (  0) 0) |
| [9] |
Crawford D R, Lake B M, Saffman P G, et al. Stability of weakly nonlinear deep-water waves in two and three dimensions. Journal of Fluid Mechanics, 1981, 105: 177-191. DOI:10.1017/S0022112081003169 (  0) 0) |
| [10] |
Phillips O M. On the dynamics of unsteady gravity waves of finite amplitude Part 1. The elementary interactions.. Journal of Fluid Mechanics, 1960, 9(2): 193-217. DOI:10.1017/S0022112060001043 (  0) 0) |
| [11] |
West B J, Watson K M, Thomson J A. Mode coupling description of ocean wave dynamics. The Physics of Fluids, 1974, 17(6): 1059-1067. DOI:10.1063/1.1694844 (  0) 0) |
| [12] |
Cohen B I, Watson K M, West B J. Some properties of deep water solitons. The Physics of Fluids, 1976, 19(3): 345-354. DOI:10.1063/1.861481 (  0) 0) |
| [13] |
Bonnefoy F, Le Touzé D, Ferrant P. A fully-spectral 3D time-domain model for second-order simulation of wavetank experiments. Part A: Formulation, implementation and numerical properties. Applied Ocean Research, 2006, 28(1): 33-43. DOI:10.1016/j.apor.2006.05.004 (  0) 0) |
| [14] |
West B J, Brueckner K A, Janda R S, et al. A new numerical method for surface hydrodynamics. Journal of Geophysical Research: Oceans, 1987, 92(C11): 11803-11824. DOI:10.1029/JC092iC11p11803 (  0) 0) |
| [15] |
Bonnefoy F, Le Touzé D, Ferrant P. A fully-spectral 3D time-domain model for second-order simulation of wavetank experiments. Part B: Validation, calibration versus experiments and sample applications. Applied Ocean Research,, 2006, 28(2): 121-132. DOI:10.1016/j.apor.2006.05.004 (  0) 0) |
| [16] |
Vinje T, Brevig P. Nonlinear ship motions. Proceedings of the 3rd International Symposium of Num. Ship Hydro., 1981.257.
(  0) 0) |
| [17] |
Dold J W, Peregrine D H. An Efficient Boundary-Integral Method for Steep Unsteady Water Waves. Morton K W, Baines M J. Numerical Methods for Fluid Dynamics Ⅱ. London: Oxford University Press, 1986. 671-679.
(  0) 0) |
| [18] |
Boyd J P. Chebyshev and Fourier Spectral Methods. New York: DOVER Publications, Inc., 2000.
(  0) 0) |
| [19] |
Hussaini M Y, Zang T A. Spectral methods in fluid dynamics. Annual Review of Fluid Mechanics, 1987, 19(1): 339-367. DOI:10.1146/annurev.fl.19.010187.002011 (  0) 0) |
| [20] |
Fructus D, Clamond D, Grue J, et al. An efficient model for three-dimensional surface wave simulations: Part Ⅰ: Free space problems. Journal of Computational Physics, 2005, 205(2): 665-685. DOI:10.1016/j.jcp.2004.11.027 (  0) 0) |
| [21] |
Liu Y M, Dommermuth D G, Yue D K P. A high-order spectral method for nonlinear wave-body interactions. Journal of Fluid Mechanics, 1992, 245: 115-136. DOI:10.1017/S0022112092000375 (  0) 0) |
| [22] |
Zakharov V E. The instability of waves in nonlinear dispersive media. Soviet Physics JETP, 1967, 24(4): 740-744. (  0) 0) |
| [23] |
Dommermuth D G. The initialization of vortical free-surface flows. Journal of Fluids Engineering, 1994, 116(1): 95-102. DOI:10.1115/1.2910249 (  0) 0) |
| [24] |
Dommermuth D. The initialization of nonlinear waves using an adjustment scheme. Wave Motion, 2000, 32(4): 307-317. DOI:10.1016/S0165-2125(00)00047-0 (  0) 0) |
| [25] |
Dommermuth D G. Efficient simulation of short and long-wave interactions with applications to capillary waves. Journal of Fluids Engineering, 1994, 116(1): 77-82. DOI:10.1115/1.2910246 (  0) 0) |
| [26] |
Brandini C, Grilli S. Modeling of freak wave generation in a 3D-NWT. The Eleventh International Offshore and Polar Engineering Conference. Los Angeles: International Society of Offshore and Polar Engineers, 2001.124-131.
(  0) 0) |
| [27] |
Tanaka M. A method of studying nonlinear random field of surface gravity waves by direct numerical simulation. Fluid Dynamics Research, 2001, 28(1): 41-60. DOI:10.1016/S0169-5983(00)00011-3 (  0) 0) |
| [28] |
Ducrozet G, Bonnefoy F, Le Touzé D, et al. 3-D HOS simulations of extreme waves in open seas. Natural Hazards and Earth System Science, 2007, 7(1): 109-122. DOI:10.5194/nhess-7-109-2007 (  0) 0) |
| [29] |
Li J X, Liu S X, Hong K Y. Numerical simulation of nonlinear waves. Journal of Dalian University of Technology, 2008, 48(3): 430-435. (in Chinese) (  0) 0) |
| [30] |
Zhao X Z, Sun Z C, Liang S X. A high order spectral method and its application to nonlinear water waves. Journal of Ship Mechanics, 2008, 12(5): 685-691. (in Chinese) (  0) 0) |
| [31] |
Zhao X P, Sun Z C, Liang S X. Focusing models for generating freak waves. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(4): 447-454. (in Chinese) (  0) 0) |
| [32] |
Zhao X P, Sun Z C, Liang S X. Focusing model for generating 3-D freak waves based on HOS method. The Ocean Engineering, 2009, 27(1): 33-39. (in Chinese) DOI:10.16483/j.issn.1005-9865.2009.01.011 (  0) 0) |
| [33] |
Sergeeva A, Slunyaev A. Rogue waves, rogue events and extreme wave kinematics in spatio-temporal fields of simulated sea states. Natural Hazards and Earth System Sciences, 2013, 13(7): 1759-1771. DOI:10.5194/nhessd-1-39-2013 (  0) 0) |
| [34] |
Xiao W T, Liu Y M, Wu G Y, et al. Rogue wave occurrence and dynamics by direct simulations of nonlinear wave-field evolution. Journal of Fluid Mechanics, 2013, 720: 357-392. DOI:10.1017/jfm.2013.37 (  0) 0) |
| [35] |
Bonnefoy F, Touz L, Ferrant P. Generation of fully-nonlinear prescribed wave fields using a high-order spectral model. The Fourteenth International Offshore and Polar Engineering Conference. Los Angeles: International Society of Offshore and Polar Engineers, 2004. 257-263.
(  0) 0) |
| [36] |
Agnon Y, Bingham H B. A non-periodic spectral method with application to nonlinear water waves. European Journal of Mechanics-B/Fluids, 1999, 18(3): 527-534. DOI:10.1016/S0997-7546(99)80047-8 (  0) 0) |
| [37] |
Li J X. The Numerical and Experimental Studying on the Multi-directional Focusing and Extreme Waves. Dalian: Dalian University of Technology, 2007. (in Chinese)
(  0) 0) |
| [38] |
Li J X, Liu S X. Focused wave properties based on a high order spectral method with a non-periodic boundary. China Ocean Engineering, 2015, 29(1): 1-16. DOI:10.1007/s13344-015-0001-7 (  0) 0) |
| [39] |
Li J X, Liu D Y, Liu S X. Numerical investigation of the effect of current on wave focusing. China Ocean Engineering, 2012, 26(1): 37-48. DOI:10.1007/s13344-012-0003-7 (  0) 0) |
| [40] |
Ducrozet G, Bonnefoy F, Le Touzé D, et al. Implementation and validation of nonlinear wavemaker models in a HOS numerical wave tank. International Journal of Offshore and Polar Engineering, 2006, 16(3): 161-167. (  0) 0) |
| [41] |
Bonnefoy F, Ducrozet G, Le Touzé D, et al. Time Domain Simulation of Nonlinear Water Waves Using Spectral Methods. Ma Q W. Advances in Numerical Simulation of Nonlinear Water Waves. London: World Scientific, 2010. 129-164. DOI: 10.1142/7087.
(  0) 0) |
| [42] |
Ducrozet G, Bonnefoy F, Le Touzé D, et al. HOS-ocean: open-source solver for nonlinear waves in open ocean based on High-Order Spectral method. Computer Physics Communications, 2016, 203: 245-254. DOI:10.1016/j.cpc.2016.02.017 (  0) 0) |
| [43] |
Song J Q, Zhuang Y, Wan D C. New wave spectrums models developed based on HOS method. The Twenty-Eighth International Ocean and Polar Engineering Conference Sapporo. Los Angeles: 2018. The International Society of Offshore and Polar Engineers, 2018. 524-531.
(  0) 0) |
| [44] |
Ducrozet G, Bonnefoy F, Le Touzé D, et al. A modified high-order spectral method for wavemaker modeling in a numerical wave tan. European Journal of Mechanics-B/Fluids, 2012, 34: 19-34. DOI:10.1016/j.euromechflu.2012.01.017 (  0) 0) |
| [45] |
Seiffert B, Ducrozet G. Deep water wave-breaking in a High-Order Spectral Model. Proceedings of the 31th International Workshop on Water Waves and Floating Bodie. Plymouth, 2016.
(  0) 0) |
| [46] |
Seiffert B R, Ducrozet G, Bonnefoy F. Simulation of breaking waves using the high-order spectral method with laboratory experiments: wave-breaking onset. Ocean Modelling, 2017, 119: 94-104. DOI:10.1016/j.ocemod.2017.09.006 (  0) 0) |
| [47] |
Seiffert B R, Ducrozet G. Simulation of breaking waves using the high-order spectral method with laboratory experiments: wave-breaking energy dissipation. Ocean Dynamics, 2018, 68: 65-89. DOI:10.1007/s10236-017-1119-3 (  0) 0) |
| [48] |
Tanaka M. Verification of Hasselmann's energy transfer among surface gravity waves by direct numerical simulations of primitive equations. Journal of Fluid Mechanics, 2001, 444: 199-221. DOI:10.1017/S0022112001005389 (  0) 0) |
| [49] |
Toffoli A, Onorato M, Bitner-Gregersen E M, et al. Development of a bimodal structure in ocean wave spectra. Journal of Geophysical Research: Oceans, 2010, 115(C3): C03006. DOI:10.1029/2009JC005495 (  0) 0) |
| [50] |
Fernández L, Onorato M, Monbaliu J, et al. Modulational instability and wave amplification in finite water depth. Natural Hazards and Earth System Sciences, 2014, 14(3): 705-711. DOI:10.5194/nhess-14-705-2014 (  0) 0) |
| [51] |
Toffoli A, Gramstad O, Trulsen K, et al. Evolution of weakly nonlinear random directional waves: laboratory experiments and numerical simulations. Journal of Fluid Mechanics, 2010, 664: 313-336. DOI:10.1017/S002211201000385X (  0) 0) |
| [52] |
Kharif C, Giovanangeli J P, Touboul J, et al. Influence of wind on extreme wave events: experimental and numerical approaches. Journal of Fluid Mechanics, 2008, 594: 209-247. DOI:10.1017/S0022112007009019 (  0) 0) |
| [53] |
Shrira V I, Slunyaev A V. Nonlinear dynamics of trapped waves on jet currents and rogue waves. Physical Review E, 2014, 89(4): 041002. DOI:10.1103/physreve.89.041002 (  0) 0) |
| [54] |
Guyenne P, Nicholls D P. A high-order spectral method for nonlinear water waves over moving bottom topography. SIAM Journal on Scientific Computing, 2007, 30(1): 81-101. DOI:10.1137/060666214 (  0) 0) |
| [55] |
Gouin M, Ducrozet G, Ferrant P. Development and validation of a non-linear spectral model for water waves over variable depth. European Journal of Mechanics-B/Fluids, 2016, 57: 115-128. DOI:10.1016/j.euromechflu.2015.12.004 (  0) 0) |
| [56] |
Gouin M, Ducrozet G, Ferrant P. Propagation of 3D nonlinear waves over an elliptical mound with a High-Order Spectral method. European Journal of Mechanics-B/Fluids, 2017, 63: 9-24. DOI:10.1016/j.euromechflu.2017.01.002 (  0) 0) |
| [57] |
Li J X, Hao J, Wang L, et al. A fully nonlinear numerical model for wave propagation over variable bathymetry based on High Order Spectral method. Chinese Journal of Hydrodynamics, 2017, 32(3): 293-300. (in Chinese) DOI:10.16076/j.cnki.cjhd.2017.03.004 (  0) 0) |
| [58] |
Hao J. Numerical Investigations on the Influences of Two-dimensional Bathymetry on the Occurrence Probability of Freak Waves. Dalian: Dalian University of Technology, 2017. (in Chinese)
(  0) 0) |
| [59] |
Li Z B. Two-phase Spectral Wave Explicit Navier-Stokes Equations Method for Wave-structure Interactions. Nantes: Ecole Centrale de Nantes, 2018.
(  0) 0) |
| [60] |
Kim K, Sirviente A I, Beck R F. The complementary RANS equations for the simulation of viscous flows. International Journal for Numerical Methods in Fluids, 2005, 48(2): 199-229. DOI:10.1002/fld.892 (  0) 0) |
| [61] |
Janssen C F, Krafczyk M, Grilli S. Modeling of wave breaking and wave-structure interactions by coupling of fully nonlinear potential flow and Lattice-Boltzmann models. Proceedings of the Twentieth International Offshore and Polar Engineering Conference. Los Angeles: International Society of Offshore and Polar Engineers, 2010. 686-693.
(  0) 0) |
| [62] |
Edmund D O, Maki K J, Beck R F. A velocity-decomposition formulation for the incompressible Navier-Stokes equations. Computational Mechanics, 2013, 52: 669-680. DOI:10.1007/s00466-013-0839-6 (  0) 0) |
| [63] |
Rosemurgy W J, Beck R F, Maki K J. A velocity decomposition formulation for 2D steady incompressible lifting problems. European Journal of Mechanics-B/Fluids, 2016, 58: 70-84. DOI:10.1016/j.euromechflu.2016.03.007 (  0) 0) |
| [64] |
Chen Y, Maki K J. A velocity decomposition approach for three-dimensional unsteady flow. European Journal of Mechanics-B/Fluids, 2017, 62: 94-108. DOI:10.1016/j.euromechflu.2016.11.011 (  0) 0) |
| [65] |
Schønberg T, Chaplin J R. Computation of nonlinear wave reflections and transmissions from submerged horizontal cylinder. International Journal of Offshore and Polar Engineering, 2003, 13(1): 29-37. (  0) 0) |
| [66] |
Ferrant P. Simulation of strongly nonlinear wave generation and wave-body interactions using a 3-D MEL model. Proceedings of the 21st ONR Symposium on Naval Hydrodynamics. Washington, D.C.: The National Academy of Sciences Engineering Machine, 1997. 93-109.
(  0) 0) |
| [67] |
Ferrant P, Gentaz L, Le Touzé D. A new RANSE/Potential approach for water wave diffraction. Proceedings of Numerical Towing Tank Symposium. 2002.
(  0) 0) |
| [68] |
Luquet R, Alessandrini B, Ferrant P, et al. RANSE analysis of 2D flow about a submerged body using explicit incident wave models. Proceedings of the Numerical Towing Tank Symposium.Rome, 2003. (  0) 0) |
| [69] |
Rienecker M M, Fenton J D. A Fourier approximation method for steady water waves. Journal of Fluid Mechanics, 1981, 104: 119-137. DOI:10.1017/S0022112081002851 (  0) 0) |
| [70] |
Ferrant P, Touze L. Fully-nonlinear spectral/BEM solution for irregular wave interactions with a 3D body. ASME 2002 21st International Conference on Offshore Mechanics and Arctic Engineering. New York: ASME, 2002. 747-754. DOI: 10.1115/OMAE2002-28521.
(  0) 0) |
| [71] |
Ferrant P, Gentaz L, Alessandrini B, et al. A potential/RANSE approach for regular water wave diffraction about 2-D structures. Ship Technology Research, 2003, 50(4): 165-171. DOI:10.1179/str.2003.50.4.004 (  0) 0) |
| [72] |
Luquet R, Alessandrini B, Ferrant P, et al. RANSE analysis of 2D flow about a submerged body using explicit incident wave models. Proceedings of the Numerical Towing Tank Symposium. Rome, 2003.1-6.
(  0) 0) |
| [73] |
Gentaz L, Luquet R, Alessandrini B, et al. Numerical simulation of the 3D viscous flow around a vertical cylinder in non-linear waves using an explicit incident wave model. Proceedings of the ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering. New York: ASME, 2004. 157-163. DOI: 10.1115/OMAE2004-51098.
(  0) 0) |
| [74] |
Luquet R, Ferrant P, Alessandrini B, et al. Simulation of a TLP in waves using the SWENSE scheme. Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. Los Angeles: Proceedings of the International Society of Offshore and Polar Engineers, 2007. 1916-1992.
(  0) 0) |
| [75] |
Ferrant P, Gentaz L, Alessandrini B, et al. Fully nonlinear potential/RANSE simulation of wave interaction with ships and marine structures. Proceedings of the ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering. New York: ASME, 2008. 379-387. DOI: 10.1115/OMAE2008-57952.
(  0) 0) |
| [76] |
Luquet R, Ducrozet G, Gentaz L, et al. Applications of the SWENSE Method to seakeeping simulations in irregular waves. Proceedings of the 9th International Conference on Numerical Ship Hydrodynmics, 2007, 1-20. (  0) 0) |
| [77] |
Monroy C, and Ducrozet G, Roux de Reilhac, et al. RANS simulations of ship motions in regular and irregular head seas using the SWENSE method. Proceedings of the 19th International Conference on Offshore and Polar Engineering. Los Angeles: International Society of Offshore and Polar Engineers, 2009. 6-13.
(  0) 0) |
| [78] |
Monroy C, Ducrozet G, Bonnefoy F, et al. RANS simulations of a CALM buoy in regular and irregular seas using the SWENSE method. International Journal of Offshore and Polar Engineering, 2011, 21(4): 264-271. (  0) 0) |
| [79] |
Li Z, Bouscasse B, Gentaz L, et al. Progress in coupling potential wave models and two-phase solvers with the SWENSE methodology. Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering. New York: ASME, 2018. OMAE2018-77466-V009T13A027. DOI: 10.1115/OMAE2018-77466.
(  0) 0) |
| [80] |
Li Z B, Bouscasse B, Ducrozet G, et al Challenges in developing a SWENSE two-phase CFD solver for complex wave conditions. Proceedings of the 33rd International Workshop on Water Waves and Floating Bodies (IWWWFB), 2018, 1-4.
(  0) 0) |
| [81] |
Gatin I, Vukčević V, Jasak H. CFD validation of a container ship in calm water and head seas. Proceedings of the 18th Numerical Towing Tank Symposium. TuTech, 2015: 53-58.
(  0) 0) |
| [82] |
Gatin I, Vukčević V, Jasak H. Coupling of higher order spectral method and computational fluid dynamics. Proceedings of the 22th Symposium Sorta/ Degiuli, Nastia; Žiha, Kalman; Flesch, Nenad; Šoda-Cotić, Stipan, Kokeza, Vesna. 2016. 127-133.
(  0) 0) |
| [83] |
CFD Direct Ltd. OpenFOAM User Guide. https://www.openfoam.com, 2018-08-15.
(  0) 0) |
| [84] |
Vukčević V. Numerical Modelling of Coupled Potential and Viscous Flow for Marine Applications. Zagreb: University of Zagreb, 2016.
(  0) 0) |
| [85] |
Vukčević V, Jasak H, Malenica Š. Decomposition model for naval hydrodynamic applications, Part Ⅰ: Computational method. Ocean Engineering, 2016, 121: 37-46. DOI:10.1016/j.oceaneng.2016.05.022 (  0) 0) |
| [86] |
Vukčević V, Jasak H, Malenica Š. Decomposition model for naval hydrodynamic applications, Part Ⅱ: Verification and validation. Ocean Engineering, 2016, 121: 76-88. DOI:10.1016/j.oceaneng.2016.05.021 (  0) 0) |
| [87] |
Sussman M, Smereka P, Osher S. A level set approach for computing solutions to incompressible two-phase flow. Journal of Computational physics, 1994, 114(1): 146-159. DOI:10.1006/jcph.1994.1155 (  0) 0) |
| [88] |
Campana E, di Mascio A, Esposito P G, et al. Viscous-inviscid coupling in free surface ship flows. International Journal for Numerical Methods in Fluids, 1995, 21(9): 699-722. DOI:10.1002/fld.1650210902 (  0) 0) |
| [89] |
Chen H C, Lee S K. RANS/Laplace calculations of nonlinear waves induced by surface-piercing bodies. Journal of Engineering Mechanics, 1999, 125(11): 1231-1242. DOI:10.1061/(ASCE)0733-9399(1999)125:11(1231) (  0) 0) |
| [90] |
Colicchio G, Greco M, Faltinsen O M. A BEM-level set domain-decomposition strategy for non-linear and fragmented interfacial flows. International Journal for Numerical Methods in Engineering, 2006, 67(10): 1385-1419. DOI:10.1002/nme.1680 (  0) 0) |
| [91] |
Zhang Y, Peszynska M, Yim S C. Coupling of viscous and potential flow models with free surface for near and far field wave propagation. International Journal of Numerical Analysis and Modeling, Series B, 2013, 4(3): 256-282. (  0) 0) |
| [92] |
Guignard S, Grilli S T, Marcer R, et al. Computation of shoaling and breaking waves in nearshore areas by the coupling of BEM and VOF methods. Proceedings of the Ninth International Offshore and Polar Engineering Conference. Los Angeles: International Society of Offshore and Polar Engineers, 1999.
(  0) 0) |
| [93] |
Lachaume C, Biausser B, Fraunié P, et al. Modeling of breaking and post-breakingwaves on slopes by coupling of BEM and VOF methods. Proceedings of the Thirteenth International Offshore and Polar Engineering Conference. Los Angeles: International Society of Offshore and Polar Engineers, 2003.
(  0) 0) |
| [94] |
Biausser B, Grilli S T, Fraunié P, et al. Numerical analysis of the internal kinematics and dynamics of 3-D breaking waves on slopes. International Journal of Offshore and Polar Engineering, 2004, 14(4): 247-256. (  0) 0) |
| [95] |
Kim J W, Jang H, Baquet A, et al. Technical and economic readiness review of CFD-Based numerical wave basin for offshore floater design. Proceedings of the Offshore Technology Conference. Houston: Offshore Technology Conference, 2016.1-16.
(  0) 0) |
| [96] |
Paulsen B T, Bredmose H, Bingham H B. An efficient domain decomposition strategy for wave loads on surface piercing circular cylinders. Coastal Engineering, 2014, 86: 57-76. DOI:10.1016/j.coastaleng.2014.01.006 (  0) 0) |
| [97] |
Engsig-Karup A P, Bingham H B, Lindberg O. An efficient flexible-order model for 3D nonlinear water waves. Journal of Computational Physics, 2009, 228(6): 2100-2118. DOI:10.1016/j.jcp.2008.11.028 (  0) 0) |
| [98] |
Choi Y, Benjamin B, Seng S, et al. Generation of regular and irregular waves in Navier-Stokes CFD solvers by matching with the nonlinear potential wave solution at the boundaries. Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering. New York: ASME, 2018. V002T08A020. DOI: 10.1115/OMAE2018-78077.
(  0) 0) |
| [99] |
Choi Y M, Gouin M, Ducrozet G, et al. Grid2Grid: HOS Wrapper Program for CFD Solvers. https://arXiv.xilesou.top/pdf/1801.00026.pdf, 2020-02-29.
(  0) 0) |
| [100] |
Zhuang Y, Wan D C, Bouscasse B, et al. Regular and Irregular Wave Generation in OpenFOAM Using High Order Spectral Method. https://dcwan.sjtu.edu.cn/userfiles/OFW13-8-102.pdf, 2020-02-29.
(  0) 0) |
| [101] |
Zha R S, Ye H X, Shen Z R, et al. Numerical computations of resistance of high speed catamaran in calm water. Journal of Hydrodynamics, Series B, 2014, 26(6): 930-938. DOI:10.1016/S1001-6058(14)60102-5 (  0) 0) |
| [102] |
Shen Z R, Wan D C. An irregular wave generating approach based on naoe-FOAM-SJTU solver. China Ocean Engineering, 2016, 30(2): 177-192. DOI:10.1007/s13344-016-0010-1 (  0) 0) |
| [103] |
Wang J H, Zhao W W, Wan D C. Free Maneuvering Simulation of ONR Tumblehome Using Overset Grid Method in Naoe-FOAM-SJTU Solver. https://dcwan.sjtu.edu.cn/userfiles/No_16-WangJH-WanDC-31st-SNH-full-paper.pdf, 2020-02-29.
(  0) 0) |
| [104] |
Wang J H, Wan D C. Investigations of self-propulsion in waves of fully appended ONR Tumblehome model. Applied Mathematics and Mechanics, 2016, 37(12): 1345-1358. (  0) 0) |
| [105] |
Wang J H, Wan D C. CFD investigations of ship maneuvering in waves using naoe-FOAM-SJTU Solver. Journal of Marine Science and Application, 2018, 17(3): 443-458. DOI:10.1007/s11804-018-0042-4 (  0) 0) |
| [106] |
Liu C, Wang J H, Wan D C. CFD computation of wave forces and motions of DTC ship in oblique waves. International Journal of Offshore and Polar Engineering, 2018, 28(2): 154-163. DOI:10.17736/ijope.2018.sh21 (  0) 0) |
| [107] |
Wang J H, Zhao W W, Wan D C. Development of naoe-FOAM-SJTU solver based on OpenFOAM for marine hydrodynamics. Journal of Hydrodynamics, 2019, 31(1): 1-20. DOI:10.1007/s42241-019-0020-6 (  0) 0) |
| [108] |
Wang J H, Wan D C. CFD Study of Ship Stopping Maneuver by Overset Grid Technique. Ocean Engineering, 2020, 197: 106895. DOI:10.1016/j.oceaneng.2019.106895 (  0) 0) |
| [109] |
Jacobsen N G, Fuhrman D R, Fredsøe J. A wave generation toolbox for the open-source CFD library: OpenFoam ©. International Journal for numerical methods in fluids, 2012, 70(9): 1073-1088. DOI:10.1002/fld.2726 (  0) 0) |
| [110] |
Song J Q, Wan D C. Application of coupling model based on High-Order Spectral method and CFD calculation in simulating irregular waves. Chinese Journal of Hydrodynamics (A), 2019, 34(1): 1-12. (in Chinese) DOI:10.16076/j.cnki.cjhd.2019.01.001 (  0) 0) |
| [111] |
Shen Z R V, Wan D C. RANS Computations of added resistance and motions of ship in head waves. Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference. Los Angeles: International Journal of Offshore and Polar Engineering, 2013. 263-271.
(  0) 0) |
| [112] |
Wan D C, Shen Z. Overset-RANS Computations of Two Surface Ships Moving in Viscous Fluids. International Journal of Computational Methods, 2012, 9(1): 1240013. DOI:10.1142/S0219876212400130 (  0) 0) |
| [113] |
Shen Z R, Wan D C, Pablo P M. Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering. Ocean Engineering, 2015, 108: 287-306. DOI:10.1016/j.oceaneng.2015.07.035 (  0) 0) |
| [114] |
Wang J, Zou L, Wan D C. CFD simulations of free running ship under course keeping control. Ocean Engineering, 2017, 141: 450-464. DOI:10.1016/j.oceaneng.2017.06.052 (  0) 0) |
| [115] |
Zhuang Y, Wan D C. Numerical study on coupling effects of FPSO ship motion and LNG tank sloshing in low-filling condition. Applied Mathematics and Mechanics, 2016, 37(12): 1378-1393. DOI:10.21656/1000-0887.370516 (  0) 0) |
| [116] |
Zhuang Y, Wan D C. Numerical study on ship motion fully coupled with LNG tank sloshing in CFD method. International Journal of Computational Methods, 2019, 16(6): 1840022. DOI:10.1142/S0219876218400224 (  0) 0) |
| [117] |
Zhuang Y, Wan D C. Numerical simulation of ship motion fully coupled with sloshing tanks by naoe-FOAM-SJTU solver. Engineering Computations, 2019, 36(8): 2787-2810. DOI:10.1108/EC-10-2018-0482 (  0) 0) |
| [118] |
Zhuang Y, Wan D C. Numerical simulation based on a coupled method with High-Order Spectral method and CFD method. Proceedings of the 30th National Symposium on hydrodynamics and the 15th National Symposium on hydrodynamics. 2019. 37-49. (in Chinese)
(  0) 0) |
| [119] |
Quinn B. Validation of the High Order Spectral (HOS) Method for Extreme and Breaking Waves and Coupling of the HOS-Numerical Wave Tank Model with OpenFOAM. Stavanger, Norway: University of Stavanger, 2019.
(  0) 0) |
| [120] |
Fedkiw R P, Aslam T, Merriman B, et al. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). Journal of Computational Physics, 1999, 152(2): 457-492. DOI:10.1006/jcph.1999.6236 (  0) 0) |
| [121] |
Huang J T, Carrica P M, Stern F. Coupled ghost fluid/ two-phase level set method for curvilinear body-fitted grids. International Journal for Numerical Methods in Fluids, 2007, 55(9): 867-897. DOI:10.1002/fld.1499 (  0) 0) |
| [122] |
Osher S, Fedkiw R P. Level set methods: an overview and some recent results. Journal of Computational Physics, 2001, 169(2): 463-502. DOI:10.1006/jcph.2000.6636 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27