As a new class of potential structural and functional materials, metallic glasses (MGs) present a number of superior physical and chemical properties[1], which have stimulated widespread research enthusiasm. Nevertheless, under the quasistatic loading, these amorphous materials always break in an apparently brittle manner at ambient temperature, severely compromising their engineering applications[2]. To overcome this shortcoming, lots of efforts have been made to improve their plasticity[3-5].
Based on the experimental and computational results, the mechanical behavior of MGs should be dependent on their chemical composition. Park et al.[6] surveyed the mechanical properties of CuxZr100-x binary MGs; with the increment of Cu contents, the yield strength continuously increases, while the plastic strain decreases rapidly. In addition, Kumar et al.[7] reported a few percent of Al innovated into Cu50Zr50 amorphous alloys leads to the same mechanical behavior change as the increase of Cu contents. Since many Zr-Cu-based systems manifest excellent performance, Cheng et al.[8-9]established the correlation between their internal structure and mechanical behavior employing molecular dynamics (MD) simulations. Following these results, one can penetrate how and why the alloying elements influence the mechanical properties of MGs.
Nowadays, MGs employed as hydrogen-separable membranes have received a great attention due to their comparable H permeability, lower cost, and higher durability in hydrogen atmosphere than Pd and Pd-based crystalline membranes[10-12]. Meanwhile, during the H charging, it was found that H additions can induce the emergence and propagation of shear bands from the tip of notch in MGs under the continuous load[13]. Subsequently, Zhao et al.[14-15] studied the impact of charging H atoms on the yield shear stress and the volume of shear transformation zones (STZs) of Zr-bearing amorphous alloys based on the first pop-in load from the tests of nanoindentation. The mechanical response of hydrogenated alloys is significantly dependent on Zr contents, i.e., the addition of hydrogen can induce softening in low-Zr samples by increasing the volume of STZs while reversing in high-Zr alloys.
In our recent work, hydrogen was doped into Zr-Cu-based MGs by alloying with a gaseous mixture of hydrogen/argon, i.e., the so-called melt hydrogenation, which is also a hydrogen microalloying technology[16]. Amazingly, minor addition of H atoms could notably optimize the deformability of MGs at ambient temperature[17]. However, the internal mechanism of this H-dependent mechanical behavior remain unclear. Therefore, in this context, we employed molecular dynamics (MD) simulations to elucidate the evolution of structure and mechanical behavior of MGs after hydrogen microalloying, with the purpose of accounting for the structural origin of H-induced plasticity enhancement.
2 MethodsMD simulations were performed to investigate the characteristic of atomic arrangement and its evolution during the deformation of MGs employing the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) codes[18]. All the atomistic simulations employed the recently developed 2NN MEAM (second nearest-neighbor modified embedded atom method) potential as the interatomic interaction of Cu-Zr-H system, which could reproduce certain fundamental physical properties (the lattice parameter and bulk modulus of intermetallic compounds) of alloys in consistence with the results from experimental measurements or first-principle calculations[19-20]. It can also generate a relatively reliable amorphous structure for the amorphous system.
The original Cu50Zr50 sample with 10 000 atoms was firstly melt and equilibrated at 2 000 K for 2 ns (time step 1 fs), and then quenched into glassy states (300 K) at a cooling rate of 1 K/ps. The external pressure of each three-dimensional (3D) direction was held at zero by using an isothermal-isobaric ensemble (NPT) during the whole process. The cooled sample was sufficiently relaxed at 300 K for 1 ns. Periodic boundary conditions (PBCs) were applied for all directions in order to eliminate the surface effect. A typical amorphous configuration is shown in Fig. 1(a).
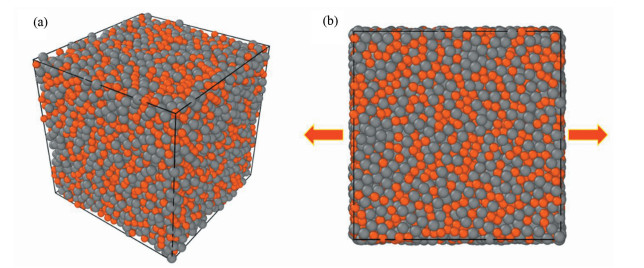
|
Fig.1 (a) 3D-configuration for Cu50Zr50 amorphous sample with 10 000 atoms achieved by MD simulation; (b) Schematic for the uniaxial tensile loading. The Cu and Zr atoms are respectively colored by orange and grey |
During the experimental process of melt hydrogenation, master alloys are melt under the gaseous mixture of H2/Ar to make the H atoms diffuse into the liquid alloy, i.e., hydrogen atoms are introduced into matrix (Cu50Zr50) during the melt stage. Thus, in our simulations, hydrogen atoms were randomly doped into the systems with molten state (2 000 K) before quenching. The amount of inserted hydrogen atoms defined as the ratio of the number of inserted H atoms (H) to that of the Cu and Zr atoms (M) was respectively 0%, 5%, and 10%, since only a small quantity of hydrogen atoms could be absorbed by matrix.
Fig. 1(b) gives the loading schemes adopted for deformation. Uniaxial tensile loading with a strain rate of 108 s-1 was imposed on each final sample (300 K). To ensure the stress-free state, the direction perpendicular to the loading direction should undergo a Parrinello-Rahman barostat. PBCs were applied for all directions.
3 Results and Discussion 3.1 Atomic Structure from SimulationsFig. 2 presents the distribution for the coordination numbers (CNs) of MGs with different H contents. In Fig. 2(a), the distribution about the CN of total atoms indicates that the fractions of small-sized clusters (CN = 11-12) and medium-sized clusters (CN = 15) decrease while those of medium-sized clusters (CN = 13) and large-sized (CN = 17-18) ones increase after the addition of H atoms. As only the Cu-centered clusters given in Fig. 2(b) are considered, the CN distribution presents a similar H-induced trend, i.e., the proportions of small-sized clusters (CN = 10-12) decline, in turn the large-sized clusters (CN = 13-16) increase. Considering the relationship of atomic radii r among the three elements (rH < rCu < rZr), the dominant polyhedra become 12, 13-coordination for Cu-centered one (Fig. 2(b)), 15, 16-coordination for Zr-centered one (Fig. 2(c)), and 11, 12-coordination for H-centered one (Fig. 2(d)).
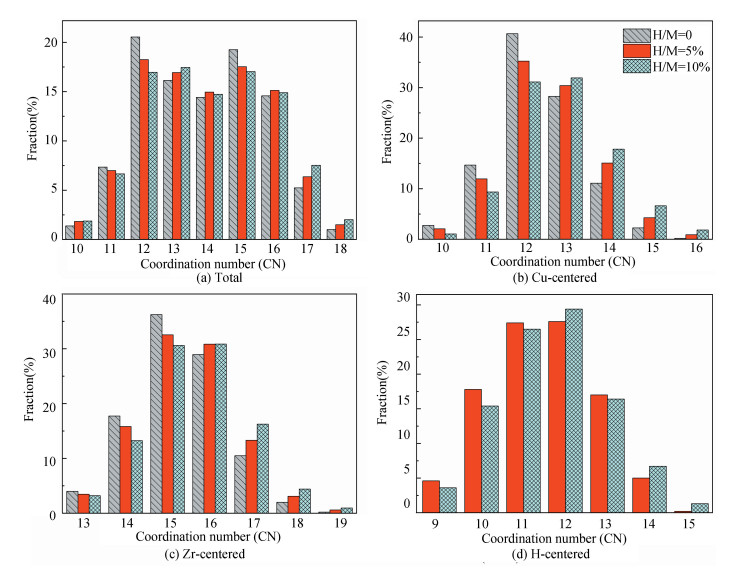
|
Fig.2 Distributions of major CNs for (a) total, (b) Cu, (c) Zr, and (d) H atoms in samples with different H contents. Only the fraction over 1.0% is listed |
The fraction of major Voronoi polyhedra in each sample can be seen in Fig. 3(a); it gradually reduces with the addition of H atoms. In addition, some polyhedra centered by Cu, Zr, or H atoms are individually depicted in Figs. 3(b)-(d). Ma et al.[21] found that there is the highest possible packing efficiency for the atomic arrangement around Cu atoms with a given partial CNs, whereas a less efficient packing can be found around Zr atoms through using XRD and neutron diffraction. These findings are also consistent with the results from MD simulations[22]. It can be deduced that the structure of ZrCu-based MGs can be better analyzed from the perspective of Cu-centered coordination polyhedra. In Fig. 3(b), three characteristic clusters are respectively indexed as < 0, 0, 12, 0>, < 0, 2, 8, 2>, and < 0, 2, 8, 1>, in line with the previous results[8-9]. Their variation after hydrogen microalloying presents a decreased behavior. In contrast, some high-coordinated clusters are found to increase, such as < 0, 1, 10, 2> polyhedra. As displayed in Fig. 3(d), the dominant polyhedra centered by H atoms are respectively indexed as < 0, 4, 4, 2>, < 1, 2, 5, 2>, and < 0, 4, 4, 3>, which can be regarded as the trigonal prisms attributed to a type of distorted bi-capped square Archimedean antiprism (BASP) with two half octahedral (AA) and defect-AA. In addition, the < 0, 3, 6, 0> polyhedra, corresponding to the tricapped trigonal prism (TTP) consisting of three half octahedral, is also noteworthy. Hence, the local atomic packing environment around most of H atoms should be featured by the trigonal prisms.
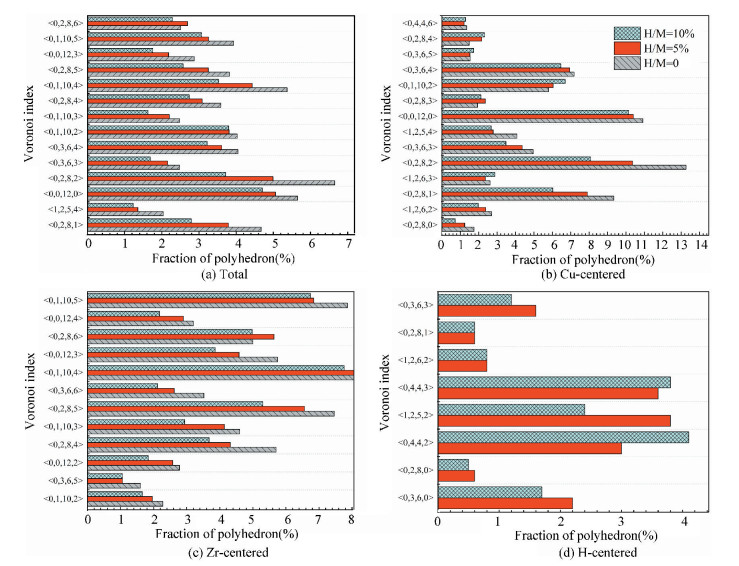
|
Fig.3 Histogram displaying the fraction of major Voronoi polyhedra in samples with different H contents (a) Total atoms; (b) Cu atoms; (c) Zr atoms; (d) H atoms. Only the fraction over 1.0% is plotted |
3.2 Stress-Strain Curves and Local Atomic Strain
As is known, the deformability of MGs must be correlated with the initiation and proliferation of shear bands[2]. Therefore, the various deformabilities owned by the amorphous samples can be properly accounted by probing the flow characteristics inside a shear band and its corresponding structural evolution. Fig. 4 illustrates the simulated stress-strain curves of the deformed MGs with different H contents. Considering the typical thickness of shear band is 10-20 nm that is much larger than the size of each specimen, its mechanical response can be treated as the characteristics inside the shear band. For each specimen, stress increases step by step as deformation progresses in the elastic stage. As it exceeds the critical yield strength τy, a precipitous drop can be seen; finally, beyond ~2% loading strain, the stress tends to be saturated.
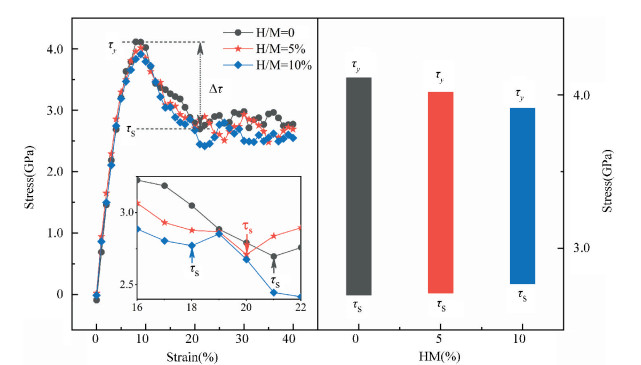
|
Fig.4 Simulated stress-strain curves (left panel) and variation in the values of stress drop Δτ (right panel) under uniaxial tensile loading imposed on the amorphous samples with different H contents. The steady-state stress τs for each sample is highlighted in the inset |
Meanwhile, it can be perceived from Fig. 4 that τy decreases with the addition of H atoms. However, the steady-state stress τs, corresponding to the first minimum of stress after global yielding[23], presents a slight increase in the H-alloyed samples. Correspondingly, the value of stress drop (Δτ = τy-τs) declines after hydrogen microalloying, as shown in the right panel of Fig. 4. Following the recent simulated studies, the softening degree of deformed MGs can be evaluated by Δτ, which corresponds to an indicator for plastic response stemming from the structural change of MGs; this may be concomitant by strain localization in shear bands[24-25]. Thus, the magnitude of Δτ maps the extent of strain localization in flow region[9], and a lower Δτ of the H-alloyed samples means weaker degree of localization than in the H-free one. Therefore, minor additions of hydrogen can improve the plasticity of MGs through inducing local softening behavior, which is consistent with the previous results from nanoindentation test demonstrating that a decreased elastic modulus and hardness can be found in the nano-scale regions of MGs with the similar H contents[26].
As reflected in the central materials science paradigm that "structure determines properties", the different degrees of softening (Δτ) for MGs in Fig. 4 must relate to their various atomic structures. The local irreversible rearrangement in each simulated configuration was assessed by the nonaffine displacement of the central atom i relative to its neighbor atoms j, which can be defined as[27]
| $ \begin{array}{l} {D_{i, {\rm{min}}}}^2 = \frac{1}{{{N_i}}}\sum\limits_{{\rm{ }}j} {} {\rm{ }}\{ {\overrightarrow r _j}\left( t \right) - {\overrightarrow r _i}\left( t \right) - {J_i}[{\overrightarrow r _j}\left( {t - \Delta t} \right) - \\ {\rm{ }}\;\;\;\;\;\;\;\;\;\;{\overrightarrow r _i}\left( {t - \Delta t} \right)]{\} ^2} \end{array} $ | (1) |
where Ni is the total nearest neighbors of the ith atoms within the reference configuration,
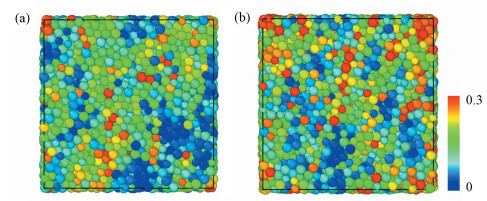
|
Fig.5 Projected views of atomic arrangement in response to tensile loading captured from (a) H/M = 0 and (b) H/M = 10% samples at the strain of 8% (before global yielding).Each atom is colored by its own value of nonaffine displacement |
3.3 Structural Evolution during Deformation
Peng et al.[28] have demonstrated that a structural indicator correlated with the degree of local fivefold symmetry (LEFS) can be correlated with the deformation of MGs. The degree of LEFS d5 is defined as the ration of the number of pentagons n5 to that of the nearest-neighbor atoms ni in Voronoi polyhedra:
| $ {d_5} = {n_5}/\sum\limits_i {{n_i}} $ | (2) |
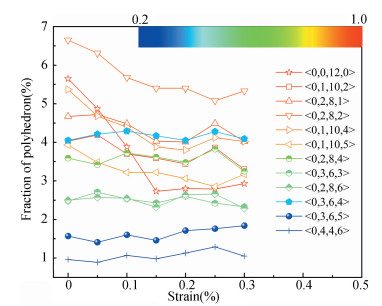
In order to examine the role of the polyhedra with different degrees of LEFS during deformation, the evolution for the fraction of dominant polyhedra associated with deformation in H-free Cu50Zr50 is firstly monitored, as shown in Fig. 6. The color bar maps the various levels of LEFS.
|
Fig.6 Variations of the fraction of dominant polyhedra during tensile deformation of Cu50Zr50 (H/M = 0). Note that the color bar maps the various levels of LEFS |
As the stress ascends and reaches the yielding point, the polyhedra with higher degree of LEFS, especially < 0, 0, 12, 0> (d5 = 1.0), begins to breakdown; conversely, the clusters with lower degree of LEFS increase, such as < 0, 3, 6, 4>. Accordingly, the polyhedra with medium degree of LEFS keeps almost constant. This process seems to saturate when the stress approaches τs. Therefore, it can be suggested that τy is the stress required to break the dense polyhedra with higher degree of LEFS, converting to the loose one with lower degree, such that flow can be initiated. That is, the polyhedra with a higher degree of LEFS is "harder", while the polyhedra with lower degree of LEFS is "softer" in the initial amorphous system. Following the results from Fig. 3, the fraction of dominant polyhedra with higher degree of LEFS significantly decreases with the addition of H atoms; it should be noted that diverse low fractions of polyhedra with lower degree of LEFS cannot be seen in Fig. 3. In a word, hydrogen microalloying can develop more "soft spots" with distorted atomic packing in MGs; these fertile sites afford the nucleation of shear bands, which could mitigate the degree of strain localization and finally promotes their deformability.
4 ConclusionsDoping hydrogen into Cu50Zr50 amorphous matrix can induce structural change by increasing the average CN, i.e., the hydrogenated sample is more compact. Moreover, the fraction of dominant polyhedra with higher degree of LEFS significantly decreases with the addition of H atoms, while diverse low fraction of polyhedra with lower degree of LEFS appears in hydrogenated alloys. This structural evolution can induce local softening, weaken the degree of strain localization, and further improve the plasticity of MGs.
| [1] |
Inoue A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Acta Materialia, 2000, 48(1): 279-306. DOI:10.1016/S1359-6454(99)00300-6 (  0) 0) |
| [2] |
Schuh C A, Hufnagel T C, Ramamurty U. Mechanical behavior of amorphous alloys. Acta Materialia, 2007, 55(12): 4067-4109. DOI:10.1016/j.actamat.2007.01.052 (  0) 0) |
| [3] |
Hays C C, Kim C P, Johnson W L. Microstructure controlled shear band pattern formation and enhanced plasticity of bulk metallic glasses containing in situ formed ductile phase dendrite dispersions. Physical Review Letters, 2000, 84(13): 2901-2904. DOI:10.1103/PhysRevLett.84.2901 (  0) 0) |
| [4] |
Fan C, Ott R T, Hufnagel T C. Metallic glass matrix composite with precipitated ductile reinforcement. Applied Physics Letters, 2002, 81(6): 1020-1022. DOI:10.1063/1.1498864 (  0) 0) |
| [5] |
Hofmann D C, Suh J Y, Wiest A, et al. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature, 2008, 451: 1085-1089. DOI:10.1038/nature06598 (  0) 0) |
| [6] |
Park K-W, Jang J, Wakeda M, et al. Atomic packing density and its influence on the properties of Cu-Zr amorphous alloys. Scripta Materialia, 2007, 57(9): 805-808. DOI:10.1016/j.scriptamat.2007.07.019 (  0) 0) |
| [7] |
Kumar G, Ohkubo T, Mukai T, et al. Plasticity and microstructure of Zr-Cu-Al bulk metallic glasses. Scripta Materialia, 2007, 57(2): 173-176. DOI:10.1016/j.scriptamat.2007.02.013 (  0) 0) |
| [8] |
Cheng Y Q, Cao A J, Ma E. Correlation between the elastic modulus and the intrinsic plastic behavior of metallic glasses: the roles of atomic configuration and alloy composition. Acta Materialia, 2009, 57(11): 3253-3267. DOI:10.1016/j.actamat.2009.03.027 (  0) 0) |
| [9] |
Cheng Y Q, Cao A J, Sheng H W, et al. Local order influences initiation of plastic flow in metallic glass: effects of alloy composition and sample cooling history. Acta Materialia, 2008, 56(18): 5263-5275. DOI:10.1016/j.actamat.2008.07.011 (  0) 0) |
| [10] |
Lai T M, Yin H D, Lind M L. The hydrogen permeability of Cu-Zr binary amorphous metallic membranes and the importance of thermal stability. Journal of Membrane Science, 2015, 489: 264-269. DOI:10.1016/j.memsci.2015.03.098 (  0) 0) |
| [11] |
Paglieri S N, Pal N K, Dolan M D, et al. Hydrogen permeability, thermal stability and hydrogen embrittlement of Ni-Nb-Zr and Ni-Nb-Ta-Zr amorphous alloy membranes. Journal of Membrane Science, 2011, 378(1-2): 42-50. DOI:10.1016/j.memsci.2011.04.049 (  0) 0) |
| [12] |
Yamaura S I, Sakurai M, Hasegawa M, et al. Hydrogen permeation and structural features of melt-spun Ni-Nb-Zr amorphous alloys. Acta Materialia, 2005, 53(13): 3703-3711. DOI:10.1016/j.actamat.2005.04.023 (  0) 0) |
| [13] |
Shan G B, Li J X, Yang Y Z, et al. Hydrogen-enhanced plastic deformation during indentation for bulk metallic glass of Zr65Al7.5Ni10Cu17.5.. Materials Letters, 2007, 61(8-9): 1625-1628. DOI:10.1016/j.matlet.2006.07.181 (  0) 0) |
| [14] |
Zhao Y K, Choi I C, Seok M Y, et al. Effect of hydrogen on the yielding behavior and shear transformation zone volume in metallic glass ribbons. Acta Materialia, 2014, 78: 213-221. DOI:10.1016/j.actamat.2014.06.046 (  0) 0) |
| [15] |
Zhao Y K, Choi I C, Seok M Y, et al. Hydrogen-induced hardening and softening of Ni-Nb-Zr amorphous alloys: dependence on the Zr content. Scripta Materialia, 2014, 93: 56-59. DOI:10.1016/j.scriptamat.2014.08.029 (  0) 0) |
| [16] |
Dong F Y, Su Y Q, Luo L S, et al. Deoxidation of bulk metallic glasses by hydrogen arc melting. Materials Letters, 2012, 83: 1-3. DOI:10.1016/j.matlet.2012.05.101 (  0) 0) |
| [17] |
Dong F Y, Su Y Q, Luo L S, et al. Enhanced plasticity in Zr-based bulk metallic glasses by hydrogen. International Journal of Hydrogen Energy, 2012, 37(19): 14697-14701. DOI:10.1016/j.ijhydene.2012.07.034 (  0) 0) |
| [18] |
Plimpton S. Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics, 1995, 117(1): 1-19. DOI:10.1006/jcph.1995.1039 (  0) 0) |
| [19] |
Lee B-J, Ko W-S, Kim H-K, et al. The modified embedded-atom method interatomic potentials and recent progress in atomistic simulations. Calphad, 2010, 34(4): 510-522. DOI:10.1016/j.calphad.2010.10.007 (  0) 0) |
| [20] |
Lee B-M, Lee B-J. A comparative study on hydrogen diffusion in amorphous and crystalline metals using a molecular dynamics simulation. Metallurgical and Materials Transactions A, 2014, 45: 2906-2915. DOI:10.1007/s11661-014-2230-4 (  0) 0) |
| [21] |
Ma D, Stoica A D, Wang X L, et al. Efficient local atomic packing in metallic glasses and its correlation with glass-forming ability. Physical Review B, 2009, 80(1): 014202. DOI:10.1103/PhysRevB.80.014202 (  0) 0) |
| [22] |
Cheng Y Q, Sheng H W, Ma E. Relationship between structure, dynamics, and mechanical properties in metallic glass-forming alloys. Physical Review B, 2008, 78(1): 014207. DOI:10.1103/PhysRevB.78.014207 (  0) 0) |
| [23] |
Park K-W, Shibutani Y, Falk M L, et al. Shear localization and the plasticity of bulk amorphous alloys. Scripta Materialia, 2010, 63(2): 231-234. DOI:10.1016/j.scriptamat.2010.03.063 (  0) 0) |
| [24] |
Manning M L, Daub E G, Langer J S, et al. Rate-dependent shear bands in a shear-transformation-zone model of amorphous solids. Physical Review E, 2009, 79(1): 016110. DOI:10.1103/PhysRevE.79.016110 (  0) 0) |
| [25] |
Shi Y F, Katz M B, Li H, et al. Evaluation of the disorder temperature and free-volume formalisms via simulations of shear banding in amorphous solids. Physical Review Letters, 2007, 98(18): 185505. DOI:10.1103/PhysRevLett.98.185505 (  0) 0) |
| [26] |
Dong F Y, He M Y, Zhang Y, et al. Effects of hydrogen on the nanomechanical properties of a bulk metallic glass during nanoindentation. International Journal of Hydrogen Energy, 2017, 42: 25436-25445. DOI:10.1016/j.ijhydene.2017.08.141 (  0) 0) |
| [27] |
Falk M L, Langer J S. Dynamics of viscoplastic deformation in amorphous solids. Physical Review E, 1998, 57(6): 7192-7205. DOI:10.1103/PhysRevE.57.7192 (  0) 0) |
| [28] |
Peng H L, Li M Z, Wang W H. Structural signature of plastic deformation in metallic glasses. Physical Review Letters, 2011, 106(13): 135503. DOI:10.1103/PhysRevLett.106.135503 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


