With the rapid development of resource-intensive mobile services (e.g., AI, AR/VR, high-resolution video streaming, and mobile gaming), mobile devices are facing great challenges of providing high-quality services due to the limited computation resource on single device. Mobile Edge Computing (MEC) is emerging as one of the promising solutions to tackle the upcoming computing tsunami in 5G/6G era[1]. The basic idea of MEC is to utilize the idle computing resources at the network edge (e.g., base stations, mobile devices, and routers) through the appropriate task division and offloading strategy[2], instead of sending tasks to remote cloud servers. Compared with the traditional centralized cloud computing paradig m, MEC tends to execute the task as close as to where it is generated, which thus can reduce the backhaul data traffic and improve the user experience and quality-of-service (QoS).
In the area of MEC, one of the important problems is whether and how to offload tasks to the appropriate positions at the mobile edge to reduce the operational cost and/or improve the QoS. Some researchers proposed to deploy edge cloud on the edge network facilities (e.g., base stations and routers) and offload tasks to the edge cloud on the edge network facilities[3-6]. Kwak et al.[3] studied the dynamic resource allocation and task offloading problem and proposed a Lyapunov optimization framework to optimize energy consumption given the delay constraints. You et al.[4] investigated the multi-user task offloading problem and formulated the problem into a convex optimization problem under TDMA and a mixed-integer programming problem under OFDMA, respectively. Liu et al.[5] discussed the joint optimization of energy consumption and delay and proposed an energy-constrained delay-optimal task offloading strategy based on the Markov decision process. Jiang et al.[6] analyzed the tradeoff between delay and energy consumption and further proposed an online algorithm based on the Lyapunov optimization framework to optimize the delay and energy consumption jointly. In practice, however, it is often costly to deploy and maintain an MEC server due to both technical and economic reasons. To overcome the shortcomings of edge cloud, some researchers proposed a complementary approach which offloads tasks to nearby mobile devices with idle resources[7-9]. To achieve this, the nearby mobile devices need to cooperate and share resources with each other through D2D communications. However, previous research did not consider the heterogeneous resource demands of tasks, whereas in practice, tasks often have heterogeneous and multi-dimensional demands for resource. For example, an AR task needs the communication resource to upload the real-time video data and the computing resource to process the video data. Due to the limit of single device capability, a single mobile device may not be able to satisfy the multi-dimensional demand of a task.
For this purpose, researchers further proposed to divide a task into multiple micro-tasks according to their resource demands and offload different micro-tasks to different mobile devices appropriately[10-12]. Specifically, Chen et al.[10] constructed an incentive-aware resource sharing framework via D2D collaboration, in which each task can employ multiple mobile devices to accomplish different jobs. Tang et al.[11] proposed a general framework for multi-dimensional resource sharing among mobile devices, in which each task is divided into three micro-tasks (i.e., data downloading, data processing, and data uploading) and different micro-tasks can be offloaded to different devices. Pan et al.[12] established a more general task model, where each task is divided into five micro-tasks (i.e., data downloading, data processing, data uploading, and two D2D micro-tasks for data transmission between mobile devices). Clearly, with such a task division, the tasks can be offloaded in a more flexible and efficient manner.
However, the above work only considered one-hop D2D communication, where the downloaded data can only be transmitted to a one-hop neighboring mobile device via D2D for processing, and the generated data can only be transmitted to a one-hop neighboring mobile device via D2D for uploading. It restricts the collaboration of mobile devices in a very small range where one-hop D2D can reach, which hence greatly limits the potential of mobile edge collaboration. This motivates us to study a more flexible D2D-enabled MEC system, where data can be transmitted via multi-hop D2D communications, thus enlarging the collaboration range of mobile devices.
1.2 Solution and ContributionsIn this work, a multi-hop D2D-enabled MEC scenario was proposed, where mobile devices at network edge connect and share resources with each other via multi-hop D2D communications. Inspired by Ref. [12], each task is divided into five sequential micro-tasks: (i) a data downloading micro-task for downloading the necessary input data (to be processed) from the Internet, (ii) a multi-hop D2D micro-task for transmitting the input data from the data downloader to the data processer, (iii) a computing micro-task for processing the input data and generating the output data, (iv) a multi-hop D2D micro-task for transmitting the output data from the data processer to the data uploader, and (v) a data uploading micro-task for uploading the output data to the Internet. The downloading, computing, and uploading micro-tasks are necessary (called basic micro-tasks), while the D2D micro-tasks are conditionally needed. For example, if the downloading and computing micro-tasks are scheduled to the same mobile device, the first D2D micro-task is no longer needed.
Fig. 1 illustrates an example of such a D2D-enabled MEC model with eight mobile devices (MDs), where MD 8 has a resource-intensive task but does not have enough resource, and hence offloads the downloading subtask (d), computing subtask (c), and uploading subtask (u) to MDs 1, 2, and 3, respectively. Besides, MD 4 helps to form a two-hop D2D link to forward the downloaded input data from MD 1 to MD 2, and MD 5 helps to form a two-hop D2D link to forward the generated output data from MD 2 to MD 3.
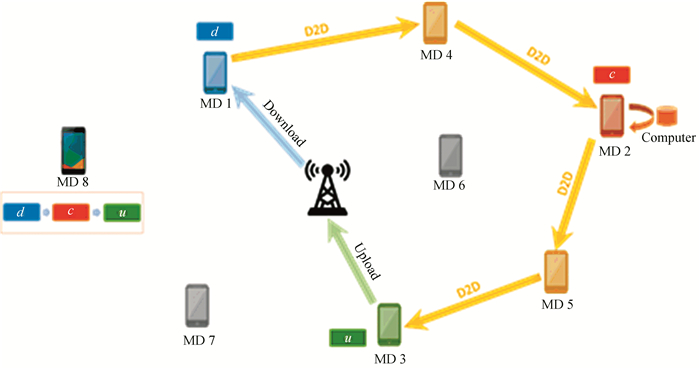
|
Fig.1 Example of D2D-enabled mobile edge computing system: MD 8 offloads the downloading subtask (d), computing subtask (c), and uploading subtask (u) to MDs 1, 2, and 3, respectively; MDs 4 and 5 help to form multi-hop D2D links to forward the downloaded data and uploaded data, respectively |
In such a model, our research interest lies in the micro-task scheduling problem of how to optimally offload micro-tasks to mobile devices with the aim of minimizing the total energy cost and maximizing the overall task completion. The problem is crucial for the practical implementation of MEC due to the following reasons. First, different from fixed data-centers which are often stable and robust, mobile devices are highly unstable and heterogeneous. For example, different devices may have very different resources at the same time and the resource of a single device may also change fast across time. Hence, tasks may not be successfully completed in an MEC system, and the overall task completion becomes an important problem in MEC. Second, mobile devices are often equipped with a limited battery, and hence is energy constraint. Therefore, minimizing the energy consumption is also critical for MEC.
To solve the above problems, a joint Task Failure Probability and Energy Consumption Minimization problem called TFP-ECM was formulated, which aims to minimize the task failure probability and the energy consumption jointly. Several linearization methods were proposed to relax the constraints and convert the original problem into an integer linear programming (ILP), which can be solved by many classic methods effectively. Simulations were conducted to evaluate the performance of the proposed solution, which was then compared with the existing solutions with indivisible tasks or without resource sharing.
In summary, the key contributions of this work are as follows. First, a multi-hop D2D-enabled MEC model was proposed, which allows mobile devices to exchange data via multi-hop D2D links and hence greatly enlarges the collaboration range of the D2D-enabled MEC system. Meanwhile, this model generalizes and extends the existing models in the literature. Second, a joint energy consumption and task failure probability optimization problem was proposed, which aims to minimize the total energy cost and maximize the overall task completion jointly. Third, simulation results show that the proposed solution outperformed the existing solutions in terms of both total cost and task failure probability. Specifically, the proposed solution reduced the total cost by 25%-85% and the task failure probability by 10%-35%.
The rest of the paper is organized as follows. In Section 2, the system model is introduced. In Section 3, the optimization problem is formulated and the original problem is transformed into an ILP problem. Simulation results are presented in Section 4, and conclusions are drawn in Section 5.
2 System ModelAs shown in Fig. 1, a set of mobile devices
Mobile devices have heterogeneous resource types. In this paper, we mainly consider the computing resources and communication resources (including download link resources and upload link resources) of mobile devices, which are used for task computing and data transmission, respectively. Since different mobile devices have different amounts of resources, the different types of resources of mobile device n are marked as:
| $ {Q_n} \buildrel \Delta \over = \{ Q_n^d,Q_n^c,Q_n^u\} $ |
where Qnd and Qnu are the download link capacity and upload link capacity of mobile device n, which can be modeled as Shannon capacity. Qnc denotes the computing capacity of mobile device n, which mainly depends on the physical properties of the mobile device itself and the percentage of CPU usage. The total CPU capacity of mobile device n is denoted as Fn. The amount of CPU used by non-shiftable applications on mobile device n is denoted by σn. Thus, Qnc is given by
| $ Q_n^c = {F_n} - {\sigma _n} $ | (1) |
When the download part and the computation part of the task are respectively scheduled to the mobile devices n and m, a D2D link will be established between mobile devices n and m for data exchange. For example, the data downloaded from the mobile device n is transmitted to the mobile device m through the D2D link for computing. Qn→mw is used to denote the D2D link capacity from mobile device n to m, which, similar as the download and upload link capacities, can be modeled as Shannon capacity.
2.2 Task ModelFor a general task, the main process from task generation to task completion can be abstracted as follows: (i) downloading the input data (to be processed) from the Internet, (ii) computing the input data, and (iii) uploading the output data to the Internet. Based on the above, each task in the system can be divided into three micro-tasks, namely, the downloading micro-task (denoted by d, ) the computing micro-task (denoted by c, ) and the uploading micro-task (denoted by u). Therefore, the task s in the system can be expressed as follows:
| $ {R_s} \buildrel \Delta \over = \{ R_s^d,R_s^c,R_s^u\} $ |
where Rds, Rcs, and Rus represent the size of input data, the number of CPU cycles needed for computing data, and the size of output data, respectively.
Since three micro-tasks of a task can be scheduled to different mobile devices, D2D transmission links are needed for transmitting the input and output data between different devices. For clarity, the D2D links used for transmitting input and output data are denoted as wi and wo, respectively. When the downloading micro-task and computing micro-task of a task are respectively scheduled to different mobile devices n and m, the system will schedule a D2D link wi for transmitting the input data from mobile device n to m. When the computing micro-task and the uploading micro-task of the task are respectively scheduled to different mobile devices k and j, the system will schedule a D2D link wo to transmit the output data from mobile device k to j.
Based on the above discussion, each task can be modeled into five micro-tasks, i.e., three basic micro-tasks {d, c, u} and two possible D2D micro-tasks {wi, wo}. Fig. 2 illustrates such a five-part task model. In the model, it was assumed that each basic micro-task is indivisible and can only be scheduled to one mobile device, while the D2D micro-task can be assisted by multiple mobile devices, hence forming a multi-hop D2D transmission network.

|
Fig.2 General task model with five micro-tasks |
2.3 Problem Statement
The research interest lies in designing a micro-task scheduling mechanism to determine which micro-task should be performed on which mobile device, aiming for jointly optimizing the energy consumption and task failure probability in the system. In this work, the task failure probability is defined as the ratio of the number of unscheduled tasks to the total number of tasks.
In the next section, an optimization problem is formulated to minimize energy consumption and task failure probability jointly, which is an NP-hard problem. Then, several linearization methods are proposed to transform the original optimization problem into a linear programming proble m, which can be solved by existing classical algorithms.
3 Problem Formulation and SolutionIn this section, the decision variables are introduced and the corresponding constraints are defined. Then, the optimization problem that jointly optimizes the energy consumption and the probability of task failure is formulated. Finally, the non-convex optimization problem is transformed into a linear programming problem through linearization method.
3.1 Decision VariablesFor task s∈
∙ xs, n→mwi≥0:indicating the amount of input data of task s transmitted over the D2D link from mobile device n to m.
∙ xs, n→mwo≥0:indicating the amount of output data of task s transmitted over the D2D link from mobile device n to m.
3.2 ConstraintsThe constraints of task scheduling are described based on the above decision variables. The first constraint is the scheduling constraints of each basic micro-task of a task. Specifically, for each task s, its downloading, computing, and uploading micro-tasks cannot be further divided into multiple parts; that is, each basic micro-task can only be scheduled to one mobile device. Therefore, the following scheduling constraints can be obtained:
| $ \sum\nolimits_{n \in \mathbb{N}} {x_{s,n}^\alpha } \le 1,\forall s \in \mathbb{S} $ | (2) |
for each basic micro-task α∈{d, c, u}.
Then, the D2D micro-tasks are divisible and can be scheduled to multiple mobile devices (to form multi-hop D2D networks). This implies that the input data and output data of a task s can flow through multiple multi-hop paths until it reaches the target mobile device. Therefore, the amount of data of task s flowing in each mobile device needs to meet the network flow balance condition; that is, the total amount of data of task s flowing into mobile device n must be the same as the total amount of data of task s flowing out of mobile device n. Formally, such network flow balance constraints can be expressed as follows:
| $ \begin{array}{*{20}{l}} {\sum\nolimits_{m \in \mathbb{N}} {x_{s,m \to n}^{{\rm{wi}}}} + x_{s,n}^d \cdot R_s^d = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\nolimits_{m \in \mathbb{N}} {x_{s,n \to m}^{{\rm{wi}}}} + x_{s,n}^c \cdot R_s^d,\forall n \in \mathbb{N},s \in \mathbb{S}} \end{array} $ | (3) |
| $ \begin{array}{*{20}{l}} {\sum\nolimits_{m \in \mathbb{N}} {x_{s,m \to n}^{{\rm{wo}}}} + x_{s,n}^c \cdot R_s^u = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\nolimits_{m \in \mathbb{N}} {x_{s,n \to m}^{{\rm{wo}}}} + x_{s,n}^u \cdot R_s^u,\forall n \in \mathbb{N},s \in \mathbb{S}} \end{array} $ | (4) |
The above restrictions indicate that for each D2D link connected to each mobile device n∈
Next, the scheduling of basic micro-tasks is also limited by the amount of available resources on each mobile device. Mobile devices cannot handle tasks that exceed their resource capacities. Therefore, the amount of task processed on mobile device n needs to satisfy the following resource constraint:
| $ \sum\nolimits_{s \in \mathbb{S}} {x_{s,n}^\alpha } \cdot R_s^\alpha \le Q_n^\alpha ,\forall n \in \mathbb{N} $ | (5) |
for each basic micro-task α∈{d, c, u}.
Similarly, each D2D link also has a capacity limit. The nearby D2D links interfere with each other and hence cannot transmit data simultaneously. For example, the D2D links connecting to the same mobile device cannot be initiated at the same time. Hence, it is further assumed that D2D works in half-duplex mode; that is, the D2D link between two mobile devices n and m can transmit data from n to m or from m to n, but not simultaneously. Therefore, the amount of data transmitted on the D2D link needs to meet the following interference restrictions:
| $ \begin{array}{l} \sum\nolimits_{m \in \mathbb{N}} ( \frac{{\sum\nolimits_{s \in \mathbb{S}} {(x_{s,n \to m}^{{\rm{wi}}} \cdot R_s^d + x_{s,n \to m}^{{\rm{wo}}} \cdot R_s^u)} }}{{Q_{n \to m}^w}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\nolimits_{s \in \mathbb{S}} {(x_{s,m \to n}^{{\rm{wi}}} \cdot R_s^d + x_{s,m \to n}^{{\rm{wo}}} \cdot R_s^u)} }}{{Q_{m \to n}^w}}) \le 1,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall n \in \mathbb{N} \end{array} $ | (6) |
where the first part and the second part in the summation denote the total time consumed by mobile device n for sending and receiving (input and output) data to mobile device m.
3.3 ObjectiveGiven the definition of decision variables and constraints, the system energy consumption and the number of task failures can be calculated. Define Es as the energy consumption for task s, which is composed of the energy consumption of each micro-task of task s, then
| $ {E_s} = E_s^d + E_s^c + E_s^u + E_s^{{\rm{wi}}} + E_s^{{\rm{wo}}} $ | (7) |
where
| $ {E_s^\alpha = \sum\nolimits_{n \in \mathbb{N}} {P_n^\alpha } \frac{{x_{s,n}^\alpha \cdot R_s^\alpha }}{{Q_n^\alpha }},\forall \alpha \in \{ d,c,u\} } $ |
| $ {E_s^{{\rm{wi}}} = \sum\nolimits_{n \in \mathbb{N}} {\sum\nolimits_{m \in \mathbb{N}} {P_n^w} } \frac{{x_{s,n \to m}^{{\rm{wi}}} \cdot R_s^d}}{{Q_{n \to m}^w}}} $ |
| $ {E_s^{{\rm{wo}}} = \sum\nolimits_{n \in \mathbb{N}} {\sum\nolimits_{m \in \mathbb{N}} {P_n^w} } \frac{{x_{s,n \to m}^{{\rm{wo}}} \cdot R_s^u}}{{Q_{n \to m}^w}}} $ |
where Pnd, Pnu, and Pnc represent the unit energy consumption of mobile device n for downloading, uploading, and computing data, respectively, and Pnw represents the energy consumption for transmitting unit data through the D2D link.
Next, the binary variable ϕs∈{0, 1} is introduced to describe whether the task s is completed. Task s is completed (i.e., ϕs=1), if and only if all the basic micro-tasks of task s are scheduled successfully, i.e., downloading, computing, and uploading successfully; otherwise, task s fails, i.e., ϕs=0. Note that when a task s is downloaded and computed (or computed and uploaded) in the same mobile device n, it can also be regarded as scheduling a virtual D2D link from mobile device n to itself. ϕsα∈{0, 1} is defined to indicate whether a basic micro-task α∈{d, c, u} of task s is completed. Therefore, the completion status of task s can be formulated as follows:
| $ {\phi _s} = \phi _s^d \cdot \phi _s^c \cdot \phi _s^u,\forall s \in \mathbb{S} $ | (8) |
where
Aiming at jointly optimizing the energy consumption and the number of tasks failure in the system, a set of parameters called penalty weights denoted by
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{min}}}\limits_x \sum\nolimits_{s \in \mathbb{S}} {({E_s} + {V_s}(1 - {\phi _s}))} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }},(1) - (8)} \end{array} $ | (9) |
where
Based on the above analysis, it can be seen that the formulation of (9) requires the complete information of the whole network, including the capabilities of all mobile devices and the capacities of all wireless links. To obtain such information, the classic route protocols such as Ad hoc On demand Distance Vector (AODV) and Dynamic Source Routing (DSR) were introduced. Nevertheless, such an information collection process will consume some energy, which depends on how fast the network is changed and how often the information is updated. As mentioned above, a quasi-static network scenario was proposed, where the network state changes very slowly or remains unchanged in the scheduling period, and hence such energy consumption is neglectable.
In the optimization problem (9), the definition of ϕs involves the multiplication of decision variables, which makes the optimization problem non-convex and difficult to solve. Then, a linearization method was introduced to transform the optimization problem into a linear programming problem.
3.5 Linearization and SolutionAccording to the definition of ϕs, when one micro-task α∈{d, c, u} of task s is not scheduled successfully, then the task fails, i.e., ϕs=0. That is, only if all basic micro-tasks of task s are scheduled successfully, we have ϕsα=1. To linearize ϕs, a set of new variables are introduced as follows:
| $ {\varphi _s} \buildrel \Delta \over = \frac{{(\phi _s^d + \phi _s^c + \phi _s^u)}}{3},\forall s \in \mathbb{S} $ | (10) |
By analyzing the value of φs, it can be found that when ϕsα=1 (α∈{d, c, u}), then φs=1; otherwise, φs < 1. Therefore, linear constraint can be built on ϕs through φs. Formally,
Lemma: Binary decision variable ϕs can be fully characterized by the following linear constraints:
| $ {\varphi _s} - \varepsilon \le {\phi _s} \le {\varphi _s},\forall s \in \mathbb{S} $ | (11) |
where 0 < ε < 1 is a constant and φs is defined in Eq. (10).
Proof: Based on the above linear constraints and the definition of φs in Eq.(10), we have:
i) When all basic micro-tasks α∈{d, c, u} of task s are completed, we have: φs=1 according to Eq.(10). Then, the above constraints become:0 < 1-ε≤ϕs≤1. Since ϕs is binary variable, we must have: ϕs=1.
ii) When one or multiple basic micro-tasks α∈{d, c, u} of task s are not completed, we have: φs < 1 according to Eq.(10). Then, the above constraints become: φs-ε≤ϕs≤φs < 1. Since ϕs is binary variable, we must have: ϕs=0.
The above linearization method converts the original non-convex constraint into a linear constraint, hence transforming the non-convex optimization problem (9) into a linear programming problem:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_{x,\varPhi } \sum\nolimits_{s \in \mathbb{S}} {({E_s} + {V_s}(1 - {\phi _s}))} }\\ {{\rm{s}}{\rm{.t}}{\rm{. }},(1) - (7),(10) - (11)} \end{array} $ | (12) |
where Φ={ϕs, s=1, 2, …, S}. The key difference between (9) and (12) is that the variables ϕs are relaxed into a set of free decision variables with linear constraints (11). Hence, the optimization problem (12) is a linear programming, which can be solved by many classic methods. Due to space limit, we skip the detailed solutions in this work.
4 SimulationsIn this section, a simulation scenario is proposed, where mobile devices are uniformly distributed in a square of 1 km× 1 km and a base station is located at the center of the square to serve mobile devices. The downlink, uplink, and D2D links follow the free space path loss equation in Ref. [13], and the instantaneous channel gains were modeled as Gaussian random variables with corresponding path loss as mean values. Other wireless link-related parameters such as the bandwidth and transmitting power of base station and mobile devices were normalized to one. The instantaneous CPU capacity was modeled as a Gaussian variable with 10 G (in CPU cycles per time slot) as the mean value.
To better understand the performance difference, the following three schemes were compared: (i) the proposed D2D-enabled resource sharing scheme with divisible tasks (named as RS-divisible); (ii) the D2D-disabled resource sharing scheme with indivisible tasks (named as RS-indivisible), where tasks cannot be divided into subtasks; that is, all micro-tasks of a task can only be scheduled to the same mobile device; and (iii) no resource sharing scheme (named as No-RS), where tasks have to be processed on their own devices. For fair comparison, each simulation was run for 1 000 times under randomly generated parameters and the average value of 1 000 outputs was adopted for comparison.
Fig. 3 illustrates the total cost under different penalty weights, including both energy cost and task failure cost. Fig. 4 shows the task failure probability under different penalty weights. It can be seen that the proposed RS-divisible outperformed RS-indivisible and No-RS in the aspects of total cost and task failure probability. More specifically, compared with RS-indivisible, the proposed RS-divisible reduced the total cost by up to 25% and the task failure probability by up to 10%. In comparison with No-RS, the proposed RS-divisible reduced the total cost by up to 85% and the task failure probability by up to 35%. Moreover, under all the three schemes, the total cost increased with the penalty weight while the task failure probability decreased with the penalty weight, both at a decreasing rate. The results coincided with our previous analysis that with a larger penalty weight, it tends to optimize the number of completed tasks preferentially.
Based on the above simulation results, it can be summarized that for the applications (e.g., distributed learning and federated learning) that require a low task failure probability (e.g., 10%), the penalty weight can be set a large value, e.g., between 6 and 20. For the applications (e.g., mobile crowdsensing and crowdsourcing) that rely on a large amount of participants but not on the failure probability of each single task, the penalty weight can be set a small value, e.g., between 1 and 5.

|
Fig.3 Relation between total cost and penalty weight Vs |

|
Fig.4 Relation between task failure probability and penalty weight Vs |
5 Conclusions
In this work, a micro-task scheduling problem was studied in the multi-hop D2D-enabled MEC system, where each task was divided into five sequential micro-tasks. A joint TFP-ECM problem was proposed, aiming at minimizing the task failure probability and the energy consumption jointly. Several linearization methods were developed to relax the constraints and convert the original problem into an ILP. Simulations were performed and results show that the proposed solution outperformed the existing solutions in terms of both total cost and task failure probability. Specifically, the solution reduced the total cost by 25%-85% and the task failure probability by 10%-35%. In terms of the future research, there are several interesting directions to be investigated. First, mobile devices are often self-motivated, and hence a well-designed incentive mechanism is necessary to motivate these devices to collaborate with each other. Second, in practice, a micro-task can be further divided into multiple mini-tasks. For example, the downloading micro-task can be divided into multiple mini-tasks, and each can be scheduled to a different mobile device. Thus, it is intriguing and critical to investigate a more complicated task model with more micro-tasks.
| [1] |
Zhou Z, Chen X, Li E, et al. Edge intelligence: Paving the last mile of artificial intelligence with edge computing. Proceedings of the IEEE, 2019, 107(8): 1738-1762. DOI:10.1109/JPROC.2019.2918951 (  0) 0) |
| [2] |
Mao Y, You C, Zhang J, et al. A survey on mobile edge computing: The communication perspective. IEEE Communications Surveys & Tutorials, 2017, 19(4): 2322-2358. DOI:10.1109/COMST.2017.2745201 (  0) 0) |
| [3] |
Kwak J, Kim Y, Lee J, et al. DREAM: Dynamic resource and task allocation for energy minimization in mobile cloud systems. IEEE Journal on Selected Areas in Communications, 2015, 33(12): 2510-2523. DOI:10.1109/JSAC.2015.2478718 (  0) 0) |
| [4] |
You C, Huang K, Chae H, et al. Energy-efficient resource allocation for mobile-edge computation offloading. IEEE Transactions on Wireless Communications, 2017, 16(3): 1397-1411. DOI:10.1109/TWC.2016.2633522 (  0) 0) |
| [5] |
Liu J, Mao Y, Zhang J, et al. Delay-optimal computation task scheduling for mobile-edge computing systems. Proceedings of 2016 IEEE International Symposium on Information Theory (ISIT). Piscataway: IEEE, 2016, 1451-1455. DOI:10.1109/ISIT.2016.7541539 (  0) 0) |
| [6] |
Jiang Z, Mao S. Energy delay trade-off in cloud offloading for multi-core mobile devices. IEEE Access, 2015, 1-6. DOI:10.1109/ACCESS.2015.2499300 (  0) 0) |
| [7] |
Xing H, Liu L, Xu J, et al. Joint task assignment and resource allocation for D2D-enabled mobile-edge computing. IEEE Transactions on Communications, 2019, 67(6): 4193-4207. DOI:10.1109/TCOMM.2019.2903088 (  0) 0) |
| [8] |
Jiang C, Gao L, Duan L, et al. Scalable mobile crowdsensing via peer-to-peer data sharing. IEEE Transactions on Mobile Computing, 2017, 17(4): 898-912. DOI:10.1109/TCOMM.2019.2903088 (  0) 0) |
| [9] |
Iosifidis G, Gao L, Huang J, et al. Efficient and fair collaborative mobile Internet access. IEEE/ACM Transactions on Networking, 2017, 25(3): 1386-1400. DOI:10.1109/TNET.2016.2638939 (  0) 0) |
| [10] |
Chen X, Pu L, Gao L, et al. Exploiting massive D2D collaboration for energy-efficient mobile edge computing. IEEE Wireless Communications, 2017, 24(4): 64-71. DOI:10.1109/MWC.2017.1600321 (  0) 0) |
| [11] |
Tang M, Gao L, Huang J. Enabling edge cooperation in tactile Internet via 3C resource sharing. IEEE Journal on Selected Areas in Communications, 2018, 36(11): 2444-2454. DOI:10.1109/JSAC.2018.2874123 (  0) 0) |
| [12] |
Pan Y, Gao L, Luo J, et al. A Multi-Dimensional Resource Crowdsourcing Framework for Mobile Edge Computing. IEEE ICC, 2020, 1-6. (  0) 0) |
| [13] |
Foerster J. Channel Modeling Sub-Committee Report Final. IEEE P802.15-02/368r5-SG3a, 2002.
(  0) 0) |
 2020, Vol. 27
2020, Vol. 27


