Interpolation of missing traces is a critical stage in seismic data processing workflow. It is not only used to remove sampling artifacts but also to improve amplitude analysis. Many methods have been proposed for the seismic data interpolation. Wave-equation based methods need the wave propagation simulation to reconstruct seismic data, so a precise subsurface velocity model is required. Signal-processing based methods use sparse transforms to construct the data such as the Radon transform[1], Fourier transform[2-8], curvelet transform[9-12], seislet transform[13], and data-driven tight frame[14-15]. Another popular technique in the signal-processing based method is to use prediction filters[10, 16-20]. The low-frequency non-aliased components of the observed data are applied to design anti-aliasing prediction-error filters, and then the filters are used to reconstruct high-frequency aliased components. This strategy makes the prediction filters suitable for interpolating linear events with regularly missing traces.
In the past few years, rank-reduced methods have been applied to seismic data reconstruction. These methods mainly fall into two categories: the Cadzow method and nuclear-norm minimization (NNM). The motivation of the Cadzow method is that a Hankel matrix constructed using a frequency slice of the data in f-x(frequency-spatial) domain, should be low rank. Trickett et al.[21] presented a truncated singular value decomposition (SVD) based matrix-rank reduction of constant-frequency slices. Oropeza and Sacchi[22] presented a multichannel singular spectrum analysis (MSSA) for simultaneous seismic reconstruction and random noise attenuation. The MSSA rebuilds seismic data at a given temporal frequency into a block Hankel matrix, and then introduces the projection onto convex sets (POCS) algorithm with a randomized SVD to reduce the matrix rank. Gao et al.[23] proposed a fast pre-stack seismic volume reconstruction method by applying Lanczos bidiagonalization. Naghizadeh and Sacchi[24] proposed multidimensional de-alised Cadzow reconstruction of seismic records by combining Cadzow reconstruction with Spitz's prediction filtering. More recently, Cheng et al.[25] proposed a computational efficient MSSA for pre-stack seismic data reconstruction.
On the other hand, seismic data interpolation can be formulated as an NNM problem[26-27]. This is based on the sparsity regularization of matrix singular values. Yang et al.[26] first designed a pre-transformation, the so-called texture-patch mapping[28], to reorganize the data into a texture-patch matrix of low rank, then applied a fast NNM algorithm to recover the low-rank matrix. Ma[29] extended the NNM matrix completion (MC) for three-dimensional (3D) irregular seismic data reconstruction. Recently, Yao et al.[30] applied the texture-patch based method in the f-x domain. Kumar et al.[31] applied a coordinate transformation from source-receiver domain to midpoint-offset domain, and then used the NNM MC algorithm for the m-h data frequency by frequency in the f-k (frequency-wave number) domain, Aravkin et al.[32] presented a robust SVD-free approach to MC. In comparison with the f-x domain Hankel matrix based Cadzow methods, the NNM MC algorithm is faster and can deal with larger-scale data[26]. Applications of rank-reduced methods (specially named tensor completion) for 4D and 5D seismic data interpolation have also been implemented[23, 33-36].
Generally speaking, sparse-transform based methods mainly capture large magnitude components and ignore small magnitude components for high-frequency band. Most of them are local methods. However, the NNM methods mainly capture the patterned components (because of the relatively large singular values), and ignore the small singular values described by non-pattern components. The Hankel matrix based rank-reduced methods assume a superposition of linear events for seismic data. In this case, multidimensional data embedded in a Hankel matrix form a low rank matrix with a rank that is equal to the number of dips in the data[37]. Our patch low-rank method has less stringent constraints on curvature and linear events[26, 29]. It is assumed that seismic data consist of repeated texture patterns. In this case, the data after the patch mapping lead to a low rank matrix. Thus, the patch low-rank methods can cope with the problem that waveform dips vary in space.
According to MC theory, any columns (and any rows) of the observed matrix must be required to have at least one non-zero entry, to achieve successful reconstruction. However, the interpolation of missing traces will lead to a higher matrix rank rather than a lower matrix rank, which is opposite to the basic requirement of low-rank MC. Thus, the seismic data cannot be directly interpolated successfully because "zero" columns are resulted from the missed traces. A pre-transform or mapping needs to be designed. To make the MC theory work, the new matrix in the transform domain should have lower rank, and more importantly, the missing traces should increase the rank of the new matrix.
The texture-patch mapping suggested in Ref.[26] avoids such zero columns in the new matrix. After the texture-patch transform, the missing traces in observed data are shifted with zero pixels in the new matrix. The missed pixels increase the rank of matrix. Generally, for seismic data consisting of texture components (events), the texture-patch mapping leads to lower rank[28]. In fact, for the Cadzow method, the Hankel matrix in the f-x domain can be also seen as a pre-transformation, which makes the rank-reduced method suitable for seismic data interpolation.
However, the previous method presented in Refs.[26, 29] does not work for interpolation of regularly missing traces. Because the regularly missing traces in seismic data often lead to aliasing the in f-k domain, these data are referred to as aliasing data. Using the suggested patch mapping method in Refs.[26, 29], the new matrix after the texture-patch mapping is applied to aliasing data that still include "zero" rows. That is to say, the mapping transforms the "zero" columns to "zero" rows instead of expected distributed "zero" pixels.
The challenge motivating this paper is how to make the low-rank methods work for aliased data without additional prediction techniques. To solve this key problem, a 3D random overlapped texture-patch transform was designed, which maps the 3D sub-blocks into column vectors that compose a new low-rank matrix. Then a low-rank factorization matrix fitting method (so-called LMaFit) and an orthogonal rank-one matrix pursuit (OR1OMP) method[38] were applied to efficiently solving the presented patch low-rank MC. The method presented in the paper may not replace current state-of-the-art methods for interpolation of seismic data, but can offer a new perspective on the problem.
Recently, machine learning methods have also been applied for seismic data interpolation[39-42]. Discussion of the learning based methods is beyond the scope of this paper.
2 Theory 2.1 Random-Overlapped Texture-Patch MappingA seismic data interpolation problem can be considered as
| $ \mathit{\boldsymbol{Y}} = {P_\Omega }(\mathit{\boldsymbol{X}}) $ | (1) |
where X denotes original data that is to reconstruct, Y means the observed or corrupted data, and PΩ stands for trace sampling.
| $ {[{P_\Omega }(\mathit{\boldsymbol{X}})]_{i,j}} = \left\{ {\begin{array}{*{20}{c}} {{X_{i,j}},}&{(i,j) \in \Omega }\\ {0,}&{{\rm{ otherwise }}} \end{array}} \right. $ | (2) |
where PΩ(X) is zeros at the locations of missing traces, and Ω is index subsets for sampling traces. The missing traces in X decrease the rank of matrix X, i.e., the rank of Y is lower than the rank of X. Thus, X cannot be reconstructed via the classic low-rank method. In Refs.[26, 29], the non-overlapped texture-patch mapping was considered for the randomly missing traces. In this paper, for the regularly missing traces, a random overlapped texture-patch mapping was designed.
The 3D random-overlapped texture-patch mapping, T:Mn, m, q→Mnmqα/r3, is defined as follows: for a v∈Mn, m, q, partition up v into r×r×r subblocks, labeled as {Bi}i=1, …, nmqα/r3. α indicates an overlapping factor. Each subblock is randomly shifted to the original of coordinates δ:=(δx, δy, δt), where the δx, δy, δt denote shift step numbers in X, y and t directions, respectively. In this paper, δx, δy∈(0, 1, 2, 3, 4, 5) and δt=0 are taken. That is to say, for the neighbor subblocks, they may have overlapping no more than 5 columns/rows in two spatial directions. Each Bi is rearranged into a column vector wi of length r3 following the same ordering. Thus the new matrix is formatted as
| $ T\mathit{\boldsymbol{v}}: = \left[ {{w_1},{w_2}, \cdots ,w\frac{{nmq\alpha }}{{{r^3}}}} \right] $ | (3) |
As mentioned in Ref. [28], the texture-patch mapping reduces the nuclear norm of 2D matrices for texture images, ‖TX‖* ≪ ‖X‖*.For the 3D case, ‖Tv‖* ≪ ‖v‖*, in which ‖v‖* is defined by the trace norm of the tensor[43].
Fig. 1 is an illustration of the random-overlapped texture-patch mapping.

|
Fig.1 Illustration of random-overlapped texture-patch mapping from 3D volume to 2D matrix |
The new matrix is noted by X=TX. Eqs. (4)-(5) illustrate details for the mapping. Here it is assumed that data X of size 4×4×2 are mapped into a new matrix by a 2×2×2 patch.
| $ \mathit{\boldsymbol{X}}(:,:,1) = \left( {\begin{array}{*{20}{c}} {{x_{111}}}&{{x_{121}}}&{{x_{131}}}&{{x_{141}}}\\ {{x_{211}}}&{{x_{221}}}&{{x_{231}}}&{{x_{241}}}\\ {{x_{311}}}&{{x_{321}}}&{{x_{331}}}&{{x_{341}}}\\ {{x_{411}}}&{{x_{421}}}&{{x_{431}}}&{{x_{441}}} \end{array}} \right) $ | (4a) |
| $ \mathit{\boldsymbol{X}}(:,:,2) = \left( {\begin{array}{*{20}{l}} {{x_{112}}}&{{x_{122}}}&{{x_{132}}}&{{x_{142}}}\\ {{x_{212}}}&{{x_{222}}}&{{x_{232}}}&{{x_{242}}}\\ {{x_{312}}}&{{x_{322}}}&{{x_{332}}}&{{x_{342}}}\\ {{x_{412}}}&{{x_{422}}}&{{x_{432}}}&{{x_{442}}} \end{array}} \right) $ | (4b) |
| $ \mathit{\boldsymbol{\bar X}} = T\mathit{\boldsymbol{X}} = \left( {\begin{array}{*{20}{l}} {{x_{111}}}&{{x_{121}}}&{{x_{131}}}&{{x_{311}}}&{{x_{331}}}\\ {{x_{211}}}&{{x_{221}}}&{{x_{231}}}&{{x_{411}}}&{{x_{431}}}\\ {{x_{121}}}&{{x_{131}}}&{{x_{141}}}&{{x_{321}}}&{{x_{341}}}\\ {{x_{221}}}&{{x_{231}}}&{{x_{241}}}&{{x_{421}}}&{{x_{441}}}\\ {{x_{112}}}&{{x_{122}}}&{{x_{132}}}&{{x_{312}}}&{{x_{332}}}\\ {{x_{212}}}&{{x_{222}}}&{{x_{232}}}&{{x_{412}}}&{{x_{432}}}\\ {{x_{122}}}&{{x_{132}}}&{{x_{142}}}&{{x_{322}}}&{{x_{342}}}\\ {{x_{222}}}&{{x_{232}}}&{{x_{242}}}&{{x_{422}}}&{{x_{442}}} \end{array}} \right) $ | (5) |
One column overlap is used between the first and second block (i.e., δx=1, δy=0, δt=0), and another column overlap between the second and third block. Due to the overlapping, data X are partitioned into 5 subblocks, and after the mapping a new matrix of size 8×5 is obtained. In the illustration, how the elements move can be easily seen. The repeated elements resulted from overlapping will be averaged in the reconstruction. It should be noted that the method guarantees that the rank is decreased only for texture-pattern data after the texture-patch mapping. It models texture-like seismic components as an alignment of patches, which are almost linearly dependent. Thus low-rank promoting NNM can be used to reconstruct the texture-like events.
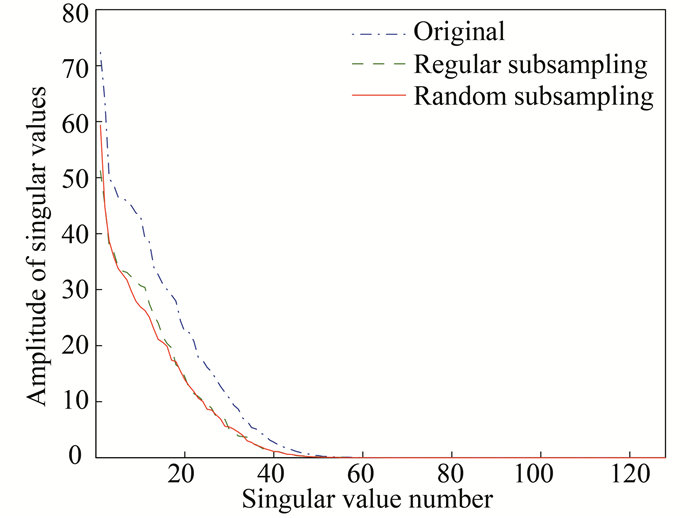
A synthetic 3D data with dimensions 128×128×128 that will be used in example section is taken as an example here. Fig. 2 shows the singular value plot for original data X (dot-dashed line), X with regular subsampling (dashed line), and X with random subsampling (solid line). Both subsampling patterns decrease the rank of matrix, thus the classic low-rank method cannot be used to directly reconstruct X from its subsampling data.
|
Fig.2 Singular values plot with decreasing amplitude for one section of a synthetic seismic data(The dot-dashed line corresponds to original data X as shown in Eq. (1); the dashed and solid lines correspond to X with regularly missing traces and randomly missing traces, respectively; both subsampling patterns decrease the rank of matrix) |
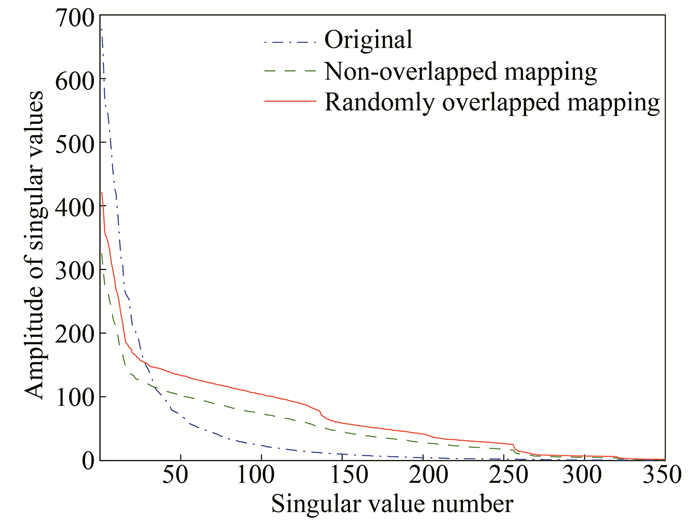
Fig. 3 shows the singular value plot for X via non-overlapped mapping and random-overlapped mapping for a random subsampling pattern. Both mappings make the random subsampling increase the rank of matrix. But the random-overlapped texture-patch mapping increases the rank more.
|
Fig.3 Singular value plot for X with 50% randomly missing traces (The dot-dashed line corresponds to original data after non-overlapped mapping; the dashed and solid lines correspond to the subsampling data after non-overlapped mapping and random-overlapped mapping, respectively.) |
Fig. 4 shows the singular value plot for X via non-overlapped mapping and random-overlapped texture-patch mapping for regularly subsampling pattern. It is obvious to see that only the random-overlapped texture-patch mapping increases the rank of the matrix. This is why the random-overlapped texture-patch mapping works for our low-rank reconstruction, while previous non-overlapped texture-patch mapping fails.

|
Fig.4 Singular value plot for X with 50% regular missing/subsamping traces (The dot-dashed line corresponds to original data after Non-overlapped mapping; the dashed and solid lines correspond to the subsampling data after Non-overlapped mapping and random-overlapped mapping, respectively.) |
It is also worth noting that the amplitude of singular value of randomly overlapped mapping is smaller than the original when the amplitude is large. In experiments, it does not affect the final results. The main concern of this paper is the decay of curves, i.e., how many non-zero significant singular values does it have after a thresholding. But that will be addressed in the next work.
2.2 Low Patch-Rank Model and AlgorithmX is reconstructed by a rank minimizing model[44-45]:
| $ \mathop {{\rm{ min }}}\limits_{\bar X} {\kern 1pt} {\kern 1pt} {\rm{rank }}(\mathit{\boldsymbol{\bar X}}),{\rm{ s}}{\rm{.t}}{\rm{. }}{\bar X_{i,j}} = {\bar Y_{i,j}}{\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} (i,j) \in \Omega $ | (6) |
Here rank (X) is the number of singular values of X·Y=TY, meaning the observed data Y should also be reshaped into corresponding patch-mapping domain. After finding X, X can be easily obtained by inverse patch mapping.
For efficient computation, its relaxation version is often considered:
| $ \mathop {{\rm{ min }}}\limits_{\bar X} {\left\| {{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\bar X}}{\kern 1pt} {\kern 1pt} } \right\|_ * },{\rm{ s}}{\rm{.t}}{\rm{. }}{\bar X_{i,j}} = {\bar Y_{i,j}}{\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} (i,j) \in \Omega $ | (7) |
The nuclear norm ‖X‖* stands for the L1 norm of the singular values of X. The model can be rewritten as
| $ \mathop {{\rm{ min }}}\limits_X {\left\| {{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{X}}{\kern 1pt} {\kern 1pt} } \right\|_R},{\rm{ s}}{\rm{.t}}{\rm{. }}{X_{i,j}} = {Y_{i,j}}{\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} (i,j) \in \Omega $ | (8) |
where the R-norm ‖X‖R=‖TRX‖*, and TR denotes the random-overlapped texture-patch mapping. As put forward by the theory of MC, suppose one observes m entries selected uniformly and randomly from a matrix of size n×n, then most low-rank matrices can be completed by solving a simple convex optimization problem, if the number m of sampled entries obeys m≥Cn1.2rlogn. Here C denotes a positive numerical constant, and r denotes the rank of the matrix.
Most rank-reduction algorithms require SVD in each iteration, which is the main computational cost for large-scale problems. In order to avoid the SVD computation in solving the NNM model, the low-rank factorization model[46] is applied.
| $ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{A}},\mathit{\boldsymbol{B}},\mathit{\boldsymbol{Z}}} \left\| {\mathit{\boldsymbol{AB}} - \mathit{\boldsymbol{Z}}} \right\|{\kern 1pt} _F^2,{Z_{i,j}} = {\bar Y_{i,j}}{\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} (i,j) \in \Omega $ | (9) |
The motivation is that any matrix X∈Rm×n of a rank up to κ has matrix factorization X=AB, where A∈Rm×κ and B∈Rκ×n. Here variable Z∈Rm×n is introduced for a computational purpose, and κ is a predicted rank bound that will be dynamically adjusted. With an appropriate κ, this low-rank factorization model provides results very close to the NNM model[46].
In this paper, an orthogonal rank-one matrix pursuit (OR1MP) algorithm[38] is applied to solve the seismic interpolation model. The OR1MP only computes the largest singular value in each iteration, thus it is competitive to LMaFit. The motivation of OR1MP is that any matrix X can be written as a linear combination of rank-one matrices:
| $ \mathit{\boldsymbol{\bar X}} = \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{\theta }}) = \sum\limits_{i \in I} {{\theta _i}} {\kern 1pt} {M_i} $ | (10) |
where Mi:i∈I is the set of rank-one matrices with unit Frobenius norm. M can be taken as a basis and θ the weight/coefficient of the basis. The original low-rank MC problem can be written to minimize the zero-norm of θ.
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{\theta }} \left\| {{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\theta }}{\kern 1pt} {\kern 1pt} } \right\|{{\kern 1pt} _0},{\rm{ s}}{\rm{.t}}{\rm{. }}{P_\Omega }(\mathit{\boldsymbol{M}}(\mathit{\boldsymbol{\theta }})) = \mathit{\boldsymbol{\bar Y}} $ | (11) |
The above equation can be reformulated as
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{\theta }} \left\| {{\kern 1pt} {P_\Omega }(\mathit{\boldsymbol{M}}(\mathit{\boldsymbol{\theta }})) - \mathit{\boldsymbol{\bar Y}}{\kern 1pt} } \right\|{\kern 1pt} _F^2,{\rm{ s}}{\rm{.t}}{\rm{. }}{\left\| {{\kern 1pt} \mathit{\boldsymbol{\theta }}{\kern 1pt} } \right\|_0} \le r $ | (12) |
The model shown in Eq. (12) can be solved by an orthogonal-matching-pursuit (OMP) type greedy algorithm using rank-one matrices as the basis. It is a natural extension of OMP from previous vector case to the matrix case. The detailed algorithm is provided in the appendix.
3 ExamplesIn our experiments, the maximum overlap is taken as 5 (i.e., the overlap will be a number randomly chosen from {0, 1, 2, 3, 4, 5}) in the spatial directions. The proposed algorithm was first tested on synthetic 3D data with dimensions 256×32×32 and four linear events.
Fig. 5(a) shows the original data, and Fig. 5(b) shows the corrupted data with approximately 50% regularly missing traces (section subsampling in x direction). Fig. 5(c) is the reconstruction and Fig. 5(d) is the difference between the reconstruction and original data. In order to demonstrate how the amplitude is reconstructed, the center t-x section by waveform display is shown in Fig. 5(e). The left part is the original data and the right part is corrupted data. Fig. 5(f) shows the reconstruction and its reconstruction errors (difference between the reconstruction and original data).

|
Fig.5 (a) Original data; (b) Corrupted data with 50% regularly missing trace; (c) Reconstructed data, signal-to-noise ratio(SNR)=16.32;(d) Difference between the reconstruction and original data; (e-f) Waveform display of a center section for original data, corruption, reconstruction, and difference, respectively |
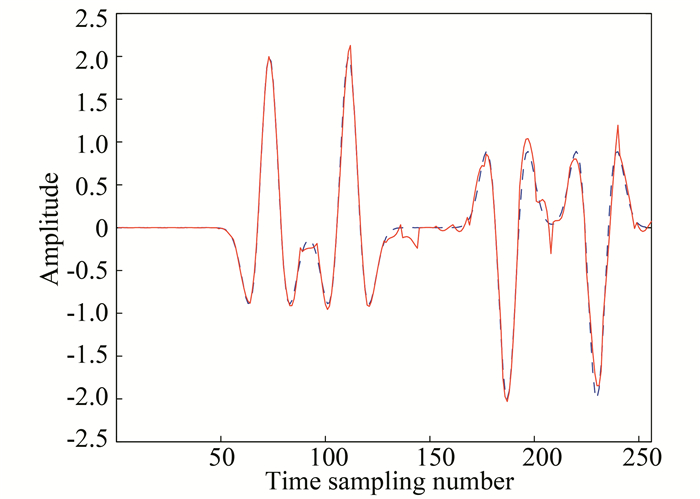
Fig. 6 displays the trace comparison. The dashed line is the original trace that was missed, and the solid line is the reconstructed trace. The amplitude of the trace is kept well except for some slight artifacts.
|
Fig.6 A central trace comparison (The dashed line denotes the original trace that was missed; the solid line denotes the reconstructed trace.) |
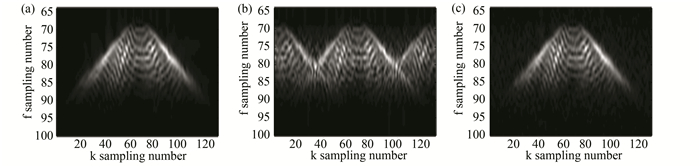
In Fig. 7, a simulated 3D data with dimensions 128×128×128 was tested. The center slices in three directions of the 3D volume are displayed. From the top row to the bottom row, the original data, corruption, reconstruction, and the error are shown. The reconstruction performance is satisfied in this case.The result presented in Fig. 7(g) may not look so good. This is because the profile/section in Fig. 7(g) is totally missed as shown in Fig. 7(d). It should be interpolated from other sections. Fig. 8 displays the f-k spectra of the original data, corruption, and the reconstruction. Most f-k aliasing resulted from regularly missing traces are suppressed by the proposed method.

|
Fig.7 Test on a synthetic 3D data. The center slices in three direction (t-x, t-y, x-y sections) of the 3D volume are displayed; (a-c) Original data; (d-f) Corrupted data with regularly missing traces; (g-i) Reconstructed data by the proposed method; (j-l) Difference between the reconstruction and original data |
|
Fig.8 (a)-(c) The f-k spectra of original data, corrupted data, and reconstruction as shown in Fig. 7(b), (e), and (h) |
In this method, the random shift is an important parameter. How to design the random shift of each overlapped texture-patch and how to control the random overlapped texture-patch without zero rows are two common questions. In fact, it is not necessary to design the random shift of each overlapping patch. Instead solely randomly choosing a number will do, e.g., 1-5 columns for the shift. It does not need adaptive design. The method itself is a breakthrough that makes the low-rank patch methods work for regular downsampling. Previous low-rank patch methods only work for irregular downsampling.
The sensitivity of random overlapping to reconstruction SNR values and sensitivity of random overlapping to computational time were tested for the simulated 3D data, as shown in Fig. 9. Six random low patch-rank cases for each overlapping from 1 to 5 were tested, and then the six SNR values and computational time were averaged to obtain the final value for each overlapping. It seems the overlapping size can be taken as 3 to balance reconstruction SNR value and computational time.

|
Fig.9 (a) SNR of reconstructed data v.s. overlapping; (b) Computational time v.s. overlapping |
The shifts of overlap are random, so the size of matrix is different in each compute time. The random shift parameters need to be recorded and kept the same size when the matrix was transformed to the original domain. It is an easy operation, but a little bit additional memory is needed. It is also fine to use 0 to shift some patches. It is acceptable if it causes the matrix with zero row, because it is almost impossible to use 0 in all patches along the row direction. Randomness plays an important role here.
The performance of the proposed method on a real seismic data with a size of 256×256×16 is presented. A central t-x section is displayed in Fig. 10 as an example. For the real data, the OR1MP shows competitive performance in terms of SNR value and computational time.

|
Fig.10 Test on real seismic data; (a) Original data; (b) Corrupted data with 50% missing traces; (c) Reconstruction by LMaFit (SNR=6.15, time=73.97 s); (d) Difference between the LMaFit reconstruction and the original data; (e) Reconstruction by R1OMP (SNR=6.99, time=46.96 s); (f) Difference between the OR1MP reconstruction and the original data |
Fig. 11 shows the close-up for a patch of the data. Fig. 11(a) is the original data (left part) and the corrupted data (right part). Fig. 11(b) and (c) are the LMaFit and OR1MP reconstruction (left part) and their error (right part). Because random-overlapped texture-patch mapping was used, the reconstruction results show a slight difference compared with the original data. To average them can further improve the result. For instance, the code was run four times for the real data while keeping the parameters unchanged. Averaging the four results, SNR=9.98 (a 62.89% improvement) and SNR=9.02 (a 29.04% improvement) can be obtained for LMaFit and OR1MP, respectively.

|
Fig.11 The close-up of data; (a) Original data (left part) and corrupted data with missing traces (right part); (b) LMaFit reconstruction (left part) and its error (right part); (c) OR1MP reconstruction and its error |
4 Conclusions and Future Work
A new low patch-rank method is proposed for the reconstruction of regularly missing traces in seismic data. Opposite to previous work where a regular texture-patch mapping based low-rank method was applied for randomly missing traces, random-overlapped mapping for regularly missing trace is considered in this paper. The basic assumption is that missing traces should increase the rank of the mapped matrix, or at least mapping should avoid zero or blank columns in the new mapped matrix, where the classic low-rank MC theory can be applied for reconstruction. The singular value plots show the performance of random-overlapped texture-patch mapping. Experiments show that the fast rank reduction algorithms, LMaFit and OR1MP, are efficient to solve the interpolation problem.
The low patch-rank method aligns all patches into a new matrix (mapping one patch from original matrix into one column in the new matrix), and then employs the NNM to reduce the rank. It works well for seismic data that have a globally similar texture pattern, but is not suitable for data that contain various different patterns. If the data does not have a globally similar texture pattern, one can add locally adaptive information into the model. A block method is the simplest model that enjoys globally dissimilar but locally similar seismic features. Other computationally expensive strategies such as shearing the patch data and defining a so-called block nuclear norm[47], and finding nonlocal similar cubes, can also be used to build a lower-rank matrix.
Frankly speaking, it is difficult for the current method to handle high missing-rate traces, especially for complex field data. One can incorporate it into other techniques to further improve the method. Application of the low patch-rank methods to 5D seismic data interpolation is straightforward. But the question of how to make use of the structures of high-dimensional data remains a problem for future research.
5 AcknowledgementsThe author would like to thank Dr. Xinxin Li, Dr. Wenyi Tian, and Dr. Zheng Wang for their help and discussion in programming the code.
6 Appendix: OR1MPThe OR1MP algorithm to solve Eq. (12) includes two stages: pursuing the basis and then weighting the basis[38].
In the k-th iteration, one can pursue Mk that is mostly correlated with the residual Rk=Y - PΩ(Xk-1), where
| $ \mathop {{\rm{max}}}\limits_\mathit{\boldsymbol{M}} \{ < \mathit{\boldsymbol{M}},{\mathit{\boldsymbol{R}}_k} > : {\rm{rank}} (\mathit{\boldsymbol{M}}) = 1,\left\| {{\kern 1pt} \mathit{\boldsymbol{M}}{\kern 1pt} } \right\|{{\kern 1pt} _F} = 1\} $ | (13) |
Furthermore, M can be written as the product of two unit vectors: M=uvT. Thus the above problem can be reformulated as
| $ \mathop {{\rm{max}}}\limits_{u,v} \{ {\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{v}}:\left\| {{\kern 1pt} \mathit{\boldsymbol{u}}{\kern 1pt} } \right\| = \left\| {{\kern 1pt} \mathit{\boldsymbol{v}}{\kern 1pt} } \right\| = 1\} $ | (14) |
Actually, the optimal solution (u*, v*) is a pair of top left and right singular vector of Rk, which can be efficiently computed by some fast algorithms. After obtaining the Mk=u*v*T, one can look for the weights θk by the least squares regression model:
| $ \mathop {{\rm{min}}}\limits_\theta \left\| {{\kern 1pt} \sum\limits_{i = 1}^k {{\mathit{\boldsymbol{P}}_\Omega }} ({\theta _i}{M_i}) - \mathit{\boldsymbol{\bar Y}}{\kern 1pt} } \right\|_F^2 $ | (15) |
In order to reduce the memory storage, one can simplify the orthogonal projection step by only tracking the estimated Xk-1 and the rank-one updated matrix Mk, i.e.,
| $ {\rm{argmi}}{{\rm{n}}_{{\alpha _1},{\alpha _2}}}\left\| {{\kern 1pt} {\mathit{\boldsymbol{P}}_\Omega }({\alpha _1}{{\mathit{\boldsymbol{\bar X}}}_{k - 1}} + {\alpha _2}{\mathit{\boldsymbol{M}}_k}) - \mathit{\boldsymbol{\bar Y}}{\kern 1pt} } \right\|{\kern 1pt} _F^2 $ | (16) |
Then one has Xk=α1kXk-1+α2k(Mk), θkk=α2k and θik=θik-1α1k. Repeat the above two-stage iteration until a stopping criterion is satisfied.
| [1] |
Kabir M M N, Verschuur D J. Restoration of missing offsets by parabolic Radon transform. Geophysical Prospecting, 1995, 43(3): 347-368. DOI:10.1111/j.1365-2478.1995.tb00257.x (  0) 0) |
| [2] |
Liu B, Sacchi M D. Minimum weighted norm interpolation of seismic records. Geophysics, 2004, 69(6): 1560-1568. DOI:10.1190/1.1836829 (  0) 0) |
| [3] |
Xu S, Zhang Y, Pham D, et al. Antileakage Fourier transform for seismic data regularization. Geophysics, 2005, 70(4): V87-V95. DOI:10.1190/1.1993713 (  0) 0) |
| [4] |
Sacchi M D, Ulrych T J, Walker C J, et al. Interpolation and extrapolation using a high-resolution discrete Fourier transform. IEEE Transactions on Signal Processing, 1998, 46(1): 31-38. DOI:10.1109/78.651165 (  0) 0) |
| [5] |
Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm. Geophysics, 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 (  0) 0) |
| [6] |
Zwartjes P M, Sacchi M D. Fourier reconstruction of nonuniformly sampled, aliased seismic data. Geophysics, 2007, 72(1): V21-V32. DOI:10.1190/1.2399442 (  0) 0) |
| [7] |
Trad D. Five-dimensional interpolation: recovering from acquisition constraints. Geophysics, 2009, 74(6): V123-V132. DOI:10.1190/1.3245216 (  0) 0) |
| [8] |
Naghizadeh M, Innanen K A. Seismic data interpolation using a fast generalized Fourier transform. Geophysics, 2011, 76(1): V1-V10. DOI:10.1190/1.3511525 (  0) 0) |
| [9] |
Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x (  0) 0) |
| [10] |
Naghizadeh M, Sacchi M D. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data. Geophysics, 2010, 75(6): WB189-WB202. DOI:10.1190/1.3509468 (  0) 0) |
| [11] |
Shahidi R, Tang G, Ma J W, et al. Application of randomized sampling schemes to curvelet-based sparsity-promoting seismic data recovery. Geophysical Prospecting, 2013, 61(5): 973-997. DOI:10.1111/1365-2478.12050 (  0) 0) |
| [12] |
Yu S W, Ma J W, Zhao B L. Off-the-grid vertical seismic profile data regularization by a compressive sensing method. Geophysics, 2020, 85(2): V157-V168. DOI:10.1190/geo2019-0357.1 (  0) 0) |
| [13] |
Fomel S, Liu Y. Seislet transform and seislet frame. Geophysics, 2010, 75(3): V25-V38. DOI:10.1190/1.3380591 (  0) 0) |
| [14] |
Liang J W, Ma J W, Zhang X Q. Seismic data restoration via data-driven tight frame. Geophysics, 2014, 79(3): V65-V74. DOI:10.1190/geo2013-0252.1 (  0) 0) |
| [15] |
Liu L N, Plonka G, Ma J W, et al. Seismic data interpolation and denoising by learning a tensor tight frame. Inverse Problems, 2017, 33: 105011. DOI:10.1088/1361-6420/aa7773 (  0) 0) |
| [16] |
Spitz S. Seismic trace interpolation in f-x domain. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 (  0) 0) |
| [17] |
Porsani M J. Seismic trace interpolation using half-step prediction filters. Geophysics, 1999, 64(5): 1461-1467. DOI:10.1190/1.1444650 (  0) 0) |
| [18] |
Naghizadeh M, Sacchi M D. f-x adaptive seismic-trace interpolation. Geophysics, 2009, 74(1): V9-V16. DOI:10.1190/1.3008547 (  0) 0) |
| [19] |
Crawley S, Clapp R, Claerbout J. Interpolation with smoothly non-stationary prediction-error filters. Proceedings of the 69th Annual International Meeting, SEG Technical Program Expanded Abstracts, 1999, 100: 1154-1157. DOI:10.1190/1.1820707 (  0) 0) |
| [20] |
Gulunay N. Seismic trace interpolation in the Fourier transform domain. Geophysics, 2003, 68(1): 355-369. DOI:10.1190/1.1543221 (  0) 0) |
| [21] |
Trickett S, Burroughs L, Milton A, et al. Rank-reduction-based trace interpolation. SEG Technical Program Expanded Abstracts, 2010, 3829-3833. DOI:10.1190/1.3513645 (  0) 0) |
| [22] |
Oropeza V, Sacchi M D. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics, 2011, 76(3): V25-V32. DOI:10.1190/1.3552706 (  0) 0) |
| [23] |
Gao J J, Sacchi M D, Chen X. A fast reduced-rank interpolation method for pre-stack seismic volumes that depend on four spatial dimensions. Geophysics, 2013, 78(1): V21-V30. DOI:10.1190/geo2012-0038.1 (  0) 0) |
| [24] |
Naghizadeh M, Sacchi M D. Multidimensional de-aliased Cadzow reconstruction of seismic records. Geophysics, 2013, 78(1): A1-A5. DOI:10.1190/geo2012-0200.1 (  0) 0) |
| [25] |
Cheng J K, Sacchi M D, Gao J J, et al. Computational efficient multidimensional singular spectrum analysis for prestack seismic data reconstruction. Geophysics, 2019, 84(2): V111-V119. DOI:10.1190/geo2018-0343.1 (  0) 0) |
| [26] |
Yang Y, Ma J W, Osher S, et al. Seismic data reconstruction via matrix completion. Inverse Problem and Imaging, 2013, 7(4): 1379-1392. DOI:10.3934/ipi.2013.7.1379 (  0) 0) |
| [27] |
Kreimer N, Sacchi M D. Nuclear norm minimization and tensor completion in exploration seismology.Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal. Processing. Piscataway: IEEE, 2013, 4275-4279. DOI:10.1109/ICASSP.2013.6638466 (  0) 0) |
| [28] |
Schaeffer H, Osher S. A low patch-rank interpretation of texture. SIAM Journal on Imaging Sciences, 2013, 6(1): 226-262. DOI:10.1137/110854989 (  0) 0) |
| [29] |
Ma J W. Three-dimensional irregular seismic data reconstruction via low-rank matrix completion. Geophysics, 2013, 78(5): V181-V192. DOI:10.1190/geo2012-0465.1 (  0) 0) |
| [30] |
Yao Z S, Galbraith M, Kolesar R. A low rank based seismic data interpolation via frequency-patches transform and low rank space projection. GeoConvention 2014: FOCUS, 2014, 1-7. (  0) 0) |
| [31] |
Kumar R, Aravkin A Y, Mansour H, et al. Seismic data interpolation and denoising using SVD-free low-rank matrix factorization. Proceedings of the 75th EAGE conference and Exhibition. Houton, The Netherlands: European Association of Geoscientists & Engineers, 2013. DOI:10.3997/2214-4609.20130388 (  0) 0) |
| [32] |
Aravkin A Y, Kumar R, Mansour H, et al. Fast methods for denoising matrix completion formulations, with applications to robust seismic data interpolation. SIAM Journal on Scientific Computing, 2014, 36(5): S237-S266. DOI:10.1137/130919210 (  0) 0) |
| [33] |
Kreimer N, Sacchi M D. A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation. Geophysics, 2012, 77(3): V113-V122. DOI:10.1190/geo2011-0399.1 (  0) 0) |
| [34] |
Kreimer N, Stanton A, Sacchi M D, et al. Tensor completion based on nuclear norm minimization for 5D seismic data reconstruction. Geophysics, 2013, 78(6): V273-V284. DOI:10.1190/geo2013-0022.1 (  0) 0) |
| [35] |
da Silva C, Herrmann F J. Hierarchical tucker tensor optimization-application to 4D seismic data interpolation.Proceedings of the 75th European Association of Geoscientists and Engineers Conference and Exhibition 2013 Incorporating SPE EUROPEC 2013: Changing Frontiers. Houten, The Netherlands: European Association of Geoscientists & Engineers, 2013, 1775-1779. DOI:10.3997/2214-4609.20130390 (  0) 0) |
| [36] |
Ely G, Aeron S, Hao N, et al. 5D and 4D pre-stack seismic data completion using tensor nuclear norm. SEG Technical Program Expanded Abstracts, 2013, 3639-3644. DOI:10.1190/segam2013-1143.1 (  0) 0) |
| [37] |
Stanton A, Sacchi M D. All roads lead to Rome: predictability, sparsity, rank and pre-stack seismic data reconstruction. CSEG Recorder, 2013, 38(10): 32-37. (  0) 0) |
| [38] |
Wang Z, Lai M J, Lu Z S, et al. Orthogonal rank-one matrix pursuit for matrix completion. SIAM Journal on Scientific Computing, 2015, 37(1): A488-A514. DOI:10.1137/130934271 (  0) 0) |
| [39] |
Jia Y N, Ma J W. What can machine learning do for seismic data processing? An interpolation application. Geophysics, 2017, 82(3): V163-V177. DOI:10.1190/geo2016-0300.1 (  0) 0) |
| [40] |
Jia Y N, Yu S W, Ma J W. Intelligent interpolation by Monte Carlo machine learning. Geophysics, 2018, 83(2): V83-V97. DOI:10.1190/geo2017-0294.1 (  0) 0) |
| [41] |
Wang B, Zhang N, Lu W, et al. Deep-learning-based seismic data interpolation: a preliminary result. Geophysics, 2019, 84(1): V11-V20. DOI:10.1190/geo2017-0495.1 (  0) 0) |
| [42] |
Zhang H, Yang X Y, Ma J W. Can learning from natural image denoising be used for seismic data interpolation. Geophysics, 2020, 85(4): WA115-WA136. DOI:10.1190/geo2019-0243.1 (  0) 0) |
| [43] |
Liu J, Musialski P, Wonka P, et al. Tensor completion for estimating missing values in visual data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 208-220. DOI:10.1109/TPAMI.2012.39 (  0) 0) |
| [44] |
Candes E J, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathematics, 2009, 9: 717-772. DOI:10.1007/s10208-009-9045-5 (  0) 0) |
| [45] |
Recht B, Fazel M, Parrilo P A. Guaranteed minimum rank solutions to linear matrix equations via nuclear norm minimization. SIAM Review, 2010, 52(3): 471-501. DOI:10.1137/070697835 (  0) 0) |
| [46] |
Wen Z W, Yin W T, Zhang Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Mathematical Programming Computation, 2012, 4: 333-361. DOI:10.1007/s12532-012-0044-1 (  0) 0) |
| [47] |
Ono S, Miyata T, Yamada I. Cartoon-texture image decomposition using blockwise low-rank texture characterization. IEEE Transactions on Image Processing, 2014, 23(3): 1128-1142. DOI:10.1109/TIP.2014.2299067 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


