Atomic force microscopy (AFM) has been widely used in imaging micro-surface and investigating mechanical properties of soft materials due to its high resolution in both space (nm) and force (pN)[1-4]. AFM can be operated in various environments including liquid, atmosphere, and vacuum[5-7]. To date, AFM-based single-molecule force spectroscopy (SMFS) has been developed into a powerful technique to study individual bond strength[8], polymer elasticity[9-12], and mechanical properties of biomacromolecules. When immersed in liquids, the dynamic behavior of the cantilever will be significantly altered due to the strong effects of fluid mass and damping[13-14]. In particular, immersion in a liquid will result in marked increase of the effective mass of the cantilevers. Then, the thermally driven frequency will be reduced to about 10 kHz or even lower. Meanwhile, the broadened resonance peaks make it difficult to eliminate the low frequency noise by low frequency filter[15-16]. When the cantilever is close to the surface, the liquid is squeezed out. The hydrodynamic interactions between the cantilever and the surface will then become more complicated[17].
In an AFM system, the Brownian motion of the cantilever is not negligible. One of the main noise sources is the thermal vibration of cantilever, which can be mainly attributed to the first vibration mode of the cantilever. In many researches, the higher modes of the cantilever were ignored and a simple harmonic oscillator model was used[18]. By the equipartition theorem, the potential energy of a harmonic oscillator in equilibrium with surroundings is given by[19-20]
| $ 1/2{\omega ^2} = m{q^2} = 1/2{k_{\rm{B}}}T $ | (1) |
where m is the oscillator effective mass, ω is the resonance angular frequency, kB is Boltzmann constant, T is the temperature, q2 is the mean square deflection. If the higher modes of oscillator and the situation of the optical lever measurement system are considered, a correction factor χ (about 0.8 for V-shaped cantilever) should be introduced[14, 21]. Note that ω2=k/m (k is the spring constant)[19]. As a consequence, the q2 can be expressed by the following equation:
| $ {q^2} = \chi {k_{\rm{B}}}T/k $ | (2) |
It is clear that the cantilever with smaller spring constant has good force resolution in AFM-SMFS experiments. However, Eq. (2) shows that the smaller the spring constant, the higher the thermal vibration[22]. Compared with the cantilever, the molecular size of the liquid molecules is negligibly small. However, thermal vibration of the cantilever is also affected by liquid due to the collisions between the liquid molecules and the cantilever[23]. In addition, force resolution is also related to the damping coefficient of the cantilever, which is dependent on several factors, such as liquid properties, shape and dimensions of the cantilever, distance between cantilever and surface. If there is no instrumental noise and only the noise from the cantilever is considered, according to fluctuation-dissipation theorem, the force precision (ΔF) can be expressed as[24-26]
| $ \Delta F = \sqrt {4{k_{\rm{B}}}\Delta f\beta } $ | (3) |
where Δf is the bandwidth of the measurement, β is drag coefficient. A direct consequence of Eq. (3) is that the cantilever with a smaller drag coefficient has higher resolution. Furthermore, some experimental factors will result in a poor AFM stability, including evaporation and temperature gradients in liquid, mechanical and acoustic noise[25]. For different rectangular cantilevers with similar spring constant (k=60 pN/nm), the large cantilever (200-μm-long) has the noise of 7.4 pN and the small cantilever (10-μm-long) has the noise of 1.3 pN. In other words, the smaller cantilever exhibits higher force resolution due to the lower viscous damping coefficient[27]. When the cantilever (k=27 pN/nm) is immersed in DI water, the measured noise is 4.6 pN at 100 nm from the surface, whereas a lower noise of 2.4 pN can be obtained at a larger distance of 22 μm[16]. Compared with rectangular cantilever, V-shaped cantilevers themselves and surrounding liquid-flow are more complicated, which makes the vibration more elusive[28-29]. It is known that the force resolution also strongly depends on the laser spot size[30].
Herein, the AFM-SMFS experimental process was simulated and the systematic noise and the noise of cantilevers moving at a constant velocity in various environments were measured. The results show that the V-shaped cantilever exhibited very low noise in high vacuum. The noise in atmospheric environment was also satisfactory. In liquid environments, a much larger noise was observed. The noise of rectangular cantilever was lower than that of V-shaped cantilever in the same environment. As the velocity increased, the noise increased in a similar trend. It is also found that the variation trend was more pronounced as the liquid viscosity increased.
2 Materials and Methods 2.1 MaterialsA V-shaped and rectangular silicon nitride AFM cantilever with gold-coating (MLCT type, Bruker) was employed in this study (Fig. 1). The nominal spring constant is 0.03 N/m for D cantilever and 0.02 N/m for B cantilever, respectively. The nominal resonance frequency is 15 kHz for both cantilevers. The nominal length is 225 μm for D cantilever and 210 μm for B cantilever, respectively. Both of the two types of cantilevers are frequently used in AFM-SMFS experiments due to the high force resolution and good stability. Deionized (DI) water (>15 MΩ·cm) is used when water is involved. All chemicals are analytically pure and used without further treatment.

|
Fig.1 Photo of AFM cantilevers. The B and D cantilevers are used in this study |
2.2 AFM Noise Measurements
All noise measurements in air and liquid environments were carried out on the JPK AFM (NanoWizard Ⅱ, JPK Instruments, Germany) with a signal sampling rate of 10 kHz. The cantilever velocity was 2 μm/s, if not mentioned otherwise. The noise measurements in high vacuum were carried out on the Hitachi AFM (5300E, Hitachi, Japan), with a signal sampling rate of 1 kHz. Prior to the measurements, the AFM chamber was pumped down to ~1×10-4 Pa. The cantilever velocity was 2.5 μm/s. According to literature, the resonance frequency of the cantilever in air is close to that in vacuum (with an error of 2% or less)[31]. Therefore, the spring constant measured in air by JPK AFM was used in high vacuum.
During the noise measurements, the systematic noise of AFM in air and DI water were measured firstly when the cantilever velocity was zero (i.e., the cantilever position was unchanged). Then, the noise of AFM cantilevers was measured at a constant velocity. Before the measurements of the noise of the AFM cantilevers, the cantilever was firstly manipulated far from the surface (1000 nm, the distance between the tip of cantilevers and the substrate, which is controlled by the AFM software). The force signal was recorded when the cantilever was approaching the surface. Each of the pure solvent was used as the liquid environment in the following order: DI water, butanol, pentanol, and octane. In the experimental process, several measures were taken to reduce random error[32]. Firstly, for each type of cantilever, the identical one was used in the experiments. Secondly, for the same AFM and cantilever, laser spot position was not moved during the experiments. In each experiment, efforts were made to achieve the maximum laser sum value by regulating the laser spot position. Thus, the spot positions on the cantilever for different experiments should be very similar. The intensity and spot size of two AFM lasers are different. However, because the noise in high vacuum is very low in general, the slight error caused by the small difference in the position of the laser spot can be ignored. The noise level was defined as the standard deviation (SD) of the force signals. When the cantilever is close to the substrate, the interactions between them will induce a small deflection of the cantilever, which will result in a tilted force-distance curve. This phenomenon will be more pronounced in high vacuum and air. Therefore, the force signals obtained when the cantilever is more than 200 nm away from the surface were selected for further analysis. The sample size is 220 points in high vacuum. The sample size is more than 2000 points in air and liquids. It is reported that the thermal drift of the optical lever arm system will increase with time[26]. Each measurement operation was completed in short time to minimize the thermal drift. All experiments were performed at room temperature (~24℃).
3 Results and DiscussionIn air, the resonance frequency is about 14.5 kHz, which is close to the nominal value. When the cantilever is immersed in liquids, the resonance frequency is reduced to about 3 kHz, which is about one fifth of that in air. The systematic noise of AFM in air and DI water at different distances from the substrate is shown in Fig. 2.
|
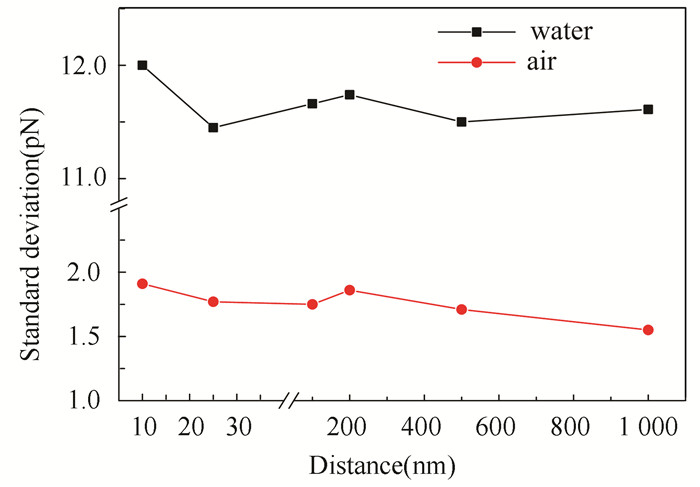
Fig.2 The magnitude of systematic noise obtained in air and DI water at different distances between the tip and substrate |
One can see that the systematic noise in DI water is much larger than that in air, which can be attributed to both the resonance effect of low frequency environmental noise and the liquid property. Besides, the systematic noise in air will gradually decrease with the increasing of distance. When the cantilever is close to the substrate (10 nm) in DI water, a slight increase of the systematic noise can be observed, which may be attributed to the squeezing effect. No significant change in the systematic noise is observed at a distance larger than 25 nm in DI water.
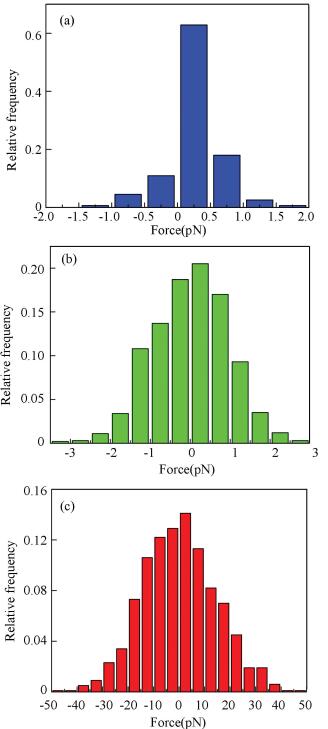
Then, the noise of V-shaped cantilever was measured at a constant velocity in air, DI water, and high vacuum. The force signals obtained in these environments are shown in Fig. 3. In high vacuum and atmospheric environments, the cantilever exhibits lower noise. The SD is 0.63 pN in high vacuum and 1.98 pN in air, respectively. By contrast, the noise drastically increases to 13.40 pN in DI water. The statistical distribution histograms of the noise in each environment are shown in Fig. 4. Meanwhile, it can be found that the noise of cantilever in air at 2 μm/s is comparable or larger than the systematic noise, which is dependent on the distance. In DI water, the noise of cantilever at 2 μm/s is markedly larger than the systematic noise.

|
Fig.3 Comparison of force noise obtained in different environments |
|
Fig.4 Statistical histograms of force noise obtained in (a) high vacuum, (b) air, and (c) DI water |
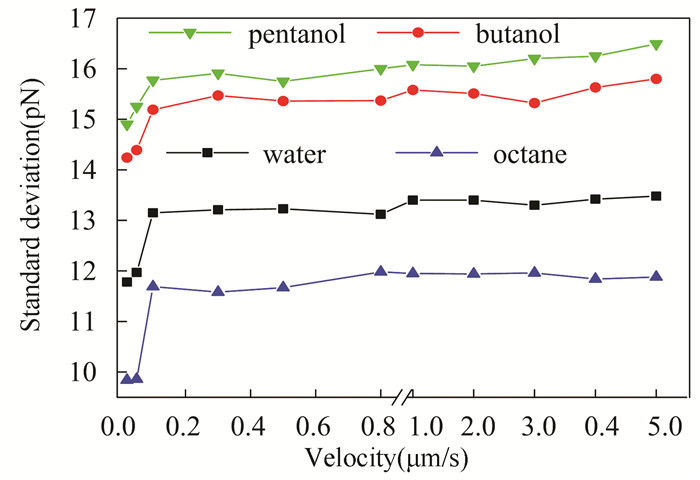
There are strong coupling effects between liquid and the cantilever (i.e., the vibration of the cantilever will act on the surrounding liquid, and the liquid also influences the cantilever). The viscous drag between the liquid and the cantilever is proportional to the velocity of the cantilever[33-34]. Various velocities have been applied in the noise measurements in DI water (Fig. 5). When the cantilever velocity is no larger than 0.05 μm/s, a lower noise is obtained with an SD of 11.78 pN at 0.02 μm/s and 11.97 pN at 0.05 μm/s, respectively. A sudden increase of the noise is obtained with an SD of 13.15 pN when the velocity increases to 0.1 μm/s. Then, the noise will be increased slowly to 13.48 pN when the velocity is increased to 5 μm/s. The noise of cantilever at 0.02 μm/s is also larger than the systematic noise obtained at a distance larger than 25 nm (the systematic noise is 12.0 pN at 10 nm). Thus, it can be concluded that when SMFS experiments with a stretching velocity between 50 and 5000 nm/s are performed in this AFM system, the minimum noise is ~12 pN in DI water. This noise is comparable to the weak intermolecular forces and unfolding force of biomacromolecules[35-37], which reduces the signal-to-noise ratio and restricts its application in the micro-force detection.
|
Fig.5 The magnitude of force noise obtained in different liquids and at various cantilever velocities |
It is well known that viscosity has significant effects on the dynamic behavior of the cantilever in liquid[31, 33]. More liquids (with various viscosity, see Table 1) are used as the environment in the noise measurements, and similar results can be observed (Fig. 5).
| Table 1 Viscosity and force noise obtained in these environments at the cantilever velocity of 2 μm/s |
In all liquid environments, the V-shaped cantilever exhibits lower noise with velocity at 0.02-0.05 μm/s. A sudden increase is observed when the velocity is increased to 0.1 μm/s. Then, the noise will increase slowly when the velocity is increased to 5 μm/s. It can be inferred that environmental noise and thermodynamic property have remarkable effects on the cantilever noise at lower velocity.
However, the hydrodynamic property of the cantilever is nonnegligible at higher velocity in liquids. Most AFM-SMFS experiments are carried out at a relatively high velocity (50- 5000 nm/s) to minimize the effects of positional and mechanical drift[26]. According to the above results, cantilever velocity has minor effects on the noise level when velocity >0.1 μm/s. At the same velocity, the maximum noise is obtained in pentanol and the minimum noise is obtained in octane. In other words, there is a positive correlation between the noise and the viscosity of the liquid environments. This correlation is different from the negative correlation between the cantilever resonance frequency and liquid viscosity[15, 33]. To further investigate the viscosity effects on the noise, the slope of linear fit of noise versus velocity in the range of 0.1-5 μm/s is calculated. The slopes are 0.038, 0.0578, 0.0751, and 0.1282 pN/(μm/s) in octane, water, butanol, and pentanol, respectively. These results indicate that both the magnitude of noise and the variation trend (slope) are dependent on liquid viscosity. The main reason is that the vibration of cantilever is closely related to the damping coefficient, which will be increased with the increasing of liquid viscosity.
According to the above results, both the cantilever velocity and liquid viscosity will affect the noise. For a better signal-to-noise ratio, both the cantilever velocity and liquid viscosity should be as low as possible. The viscosity of biological buffers (usually with low salt concentration) is very close to that of DI water[40]. The difference of noise in these two solutions should be very small. Because of the limitation of instrument, the cantilever velocity is set as 2.5 μm/s instead of 2 μm/s in high vacuum. Even at a very high velocity, the noise obtained in high vacuum is still lower than that in air since the interference from the environment is minimized. Therefore, the small difference in velocity will not affect the reliability of research results (i.e., the noise of cantilever in high vacuum is lower than that in other environments).
Besides V-shaped cantilever, the rectangular cantilever is also frequently used. Some research has shown that the dynamic behaviors of these two types of cantilevers are different. The noise data of the rectangular cantilever are shown in Table 1. It can be found that in the same environment, the noise of rectangular cantilever is slightly lower than that of V-shaped cantilever. The difference may due to the higher damping coefficient and more complicated surrounding liquid-flow for V-shaped cantilever in contrast to rectangular cantilever.
4 ConclusionsIn summary, the systematic noise and the noise of cantilevers moving at a constant velocity are measured in various environments. The experimental results show that the V-shaped cantilever exhibited very low noise in high vacuum. The noise in atmospheric environment was also satisfactory. In liquids (i.e., octane, DI water, butanol, and pentanol), the noise dramatically increased. The systematic noise (velocity is zero) was low and dependent on the distance between the tip and substrate. As the velocity increased, similar variation trend of the noise could be observed in these liquids. The V-shaped cantilever exhibited lower noise when the velocity was lower than 0.05 μm/s. A sudden increase was observed when the velocity increased to 0.1 μm/s. Then, the noise increased slowly when the velocity increased to 5 μm/s. Particularly, the variation trend was more pronounced as the liquid viscosity increased. The noise of rectangular cantilever was slightly lower than that of V-shaped cantilever in the same environment. The present study indicates that the liquid viscosity exhibits dual impacts on the noise of the AFM cantilever. High vacuum is an ideal environment for SMFS due to the lower noise and higher resolution. For a better signal-to-noise ratio, both the cantilever velocity and liquid viscosity should be as low as possible. These results will be helpful when a lower noise is desired in weak force detection.
| [1] |
Butt H J, Cappella B, Kappl M. Force measurements with the atomic force microscope: technique, interpretation and applications. Surface Science Reports, 2005, 59(1-6): 1-152. DOI:10.1016/j.surfrep.2005.08.003 (  0) 0) |
| [2] |
Cai W H, Xiao C, Qian L M, et al. Detecting van der Waals forces between a single polymer repeating unit and a solid surface in high vacuum. Nano Research, 2019, 12: 57-61. DOI:10.1007/s12274-018-2176-8 (  0) 0) |
| [3] |
Sandoval F A, Sepulveda M, Bellon L, et al. High resolution viscosity measurement by thermal noise detection. Sensors (Basel), 2015, 15(11): 27905-27916. DOI:10.3390/s151127905 (  0) 0) |
| [4] |
Cheng B, Cui S X. Supramolecular chemistry and mechanochemistry of macromolecules: recent advances by single-molecule force spectroscopy. Boulatov R. Polymer Mechanochemistry. Topics in Current Chemistry. Cham, Switzerland: Springer, 2015, 369: 97-134. DOI:10.1007/128_2015_628 (  0) 0) |
| [5] |
Cui S X, Yu J, Kuhner F, et al. Double-stranded DNA dissociates into single strands when dragged into a poor solvent. Journal of the American Chemical Society, 2007, 129(47): 14710-14716. DOI:10.1021/ja074776c (  0) 0) |
| [6] |
Pill M F, East A L L, Marx D, et al. Mechanical activation drastically accelerates amide bond hydrolysis, matching enzyme activity. Angewandte Chemie International Edition, 2019, 58(29): 9787-9790. DOI:10.1002/anie.201902752 (  0) 0) |
| [7] |
Qian L, Bao Y, Duan W L, et al. Effects of water content of the mixed solvent on the single-molecule mechanics of amylose. ACS Macro Letters, 2018, 7(6): 672-676. DOI:10.1021/acsmacrolett.8b00375 (  0) 0) |
| [8] |
Huang W M, Wu X, Gao X, et al. Maleimide-thiol adducts stabilized through stretching. Nature Chemistry, 2019, 11: 310-319. DOI:10.1038/s41557-018-0209-2 (  0) 0) |
| [9] |
Zhang S, Qian H J, Liu Z H, et al. Towards unveiling the exact molecular structure of amorphous red phosphorus by single-molecule studies. Angewandte Chemie International Edition, 2019, 58(6): 1659-1663. DOI:10.1002/anie.201811152 (  0) 0) |
| [10] |
Wang K F, Pang X C, Cui S X. Inherent stretching elasticity of a single polymer chain with a carbon-carbon backbone. Langmuir, 2013, 29: 4315-4319. DOI:10.1021/la400626x (  0) 0) |
| [11] |
Ma Z W, Yang P, Zhang X Y, et al. Quantifying the chain folding in polymer single crystals by single-molecule force spectroscopy. ACS Macro Letters, 2019, 8(9): 1194-1199. DOI:10.1021/acsmacrolett.9b00607 (  0) 0) |
| [12] |
Liu C J, Jiang Z H, Zhang Y H, et al. Intercalation interactions between dsDNA and acridine studied by single molecule force spectroscopy. Langmuir, 2007, 23(18): 9140-9142. DOI:10.1021/la7013804 (  0) 0) |
| [13] |
Basak S, Raman A, Garimella S V. Hydrodynamic loading of microcantilevers vibrating in viscous fluids. Journal of Applied Physics, 2006, 99(11): 114906. DOI:10.1063/1.2202232 (  0) 0) |
| [14] |
Pirzer T, Hugel T. Atomic force microscopy spring constant determination in viscous liquids. Review of Scientific Instruments, 2009, 80: 035110. DOI:10.1063/1.3100258 (  0) 0) |
| [15] |
Chon J W M, Mulvaney P, Sader J E. Experimental validation of theoretical models for the frequency response of atomic force microscope cantilever beams immersed in fluids. Journal of Applied Physics, 2000, 87(8): 3978-3988. DOI:10.1063/1.372455 (  0) 0) |
| [16] |
Kawakami M, Taniguchi Y, Hiratsuka Y, et al. Reduction of the damping on an AFM cantilever in fluid by the use of micropillars. Langmuir, 2010, 26(2): 1002-1007. DOI:10.1021/la902472h (  0) 0) |
| [17] |
Maali A, Cohen-Bouhacina T, Jai C, et al. Reduction of the cantilever hydrodynamic damping near a surface by ion-beam milling. Journal of Applied Physics, 2006, 99(2): 024908. DOI:10.1063/1.2163996 (  0) 0) |
| [18] |
Melcher J, Hu S Q, Raman A. Equivalent point-mass models of continuous atomic force microscope probes. Applied Physics Letters, 2007, 91(5): 053101. DOI:10.1063/1.2767173 (  0) 0) |
| [19] |
Hutter J L, Bechhoefer J. Calibration of atomic-force microscope tips. Review of Scientific Instruments, 1993, 64(7): 1868-1873. DOI:10.1063/1.1143970 (  0) 0) |
| [20] |
Butt H J, Jaschke M. Calculation of thermal noise in atomic-force microscopy. Nanotechnology, 1995, 6(1): 1-7. DOI:10.1088/0957-4484/6/1/001 (  0) 0) |
| [21] |
Levy R, Maaloum M. Measuring the spring constant of atomic force microscope cantilevers: thermal fluctuations and other methods. Nanotechnology, 2002, 13(1): 33-37. DOI:10.1088/0957-4484/13/1/307 (  0) 0) |
| [22] |
Gittes F, Schmidt C F. Thermal noise limitations on micromechanical experiments. European Biophysics Journal with Biophysics Letters, 1998, 27: 75-81. DOI:10.1007/s002490050113 (  0) 0) |
| [23] |
Pierro E, Bottiglione F, Carbone G. Thermal fluctuations and dynamic modeling of a dAFM cantilever. Advanced Theory and Simulations, 2019, 2(5): 1900004. DOI:10.1002/adts.201900004 (  0) 0) |
| [24] |
Edwards D T, Faulk J K, Sanders A W, et al. Optimizing 1-mu s-resolution single-molecule force spectroscopy on a commercial atomic force microscope. Nano Letters, 2015, 15(10): 7091-7098. DOI:10.1021/acs.nanolett.5b03166 (  0) 0) |
| [25] |
Churnside A B, Perkins T T. Ultrastable atomic force microscopy: improved force and positional stability. FEBS Letters, 2014, 588(19): 3621-3630. DOI:10.1016/j.febslet.2014.04.033 (  0) 0) |
| [26] |
Sullan R M A, Churnside A B, Nguyen D M, et al. Atomic force microscopy with sub-picoNewton force stability for biological applications. Methods, 2013, 60(2): 131-141. DOI:10.1016/j.ymeth.2013.03.029 (  0) 0) |
| [27] |
Viani M B, Schäffer T E, Chand A, et al. Small cantilevers for force spectroscopy of single molecules. Journal of Applied Physics, 1999, 86(4): 2258-2262. DOI:10.1063/1.371039 (  0) 0) |
| [28] |
Clark M T, Paul M R. The stochastic dynamics of rectangular and V-shaped atomic force microscope cantilevers in a viscous fluid and near a solid boundary. Journal of Applied Physics, 2008, 103(9): 094910. DOI:10.1063/1.2912989 (  0) 0) |
| [29] |
Stark R W, Drobek T, Heckl W M. Thermomechanical noise of a free v-shaped cantilever for atomic-force microscopy. Ultramicroscopy, 2001, 86(1-2): 207-215. DOI:10.1016/S0304-3991(00)00077-2 (  0) 0) |
| [30] |
Schäffer T E. Calculation of thermal noise in an atomic force microscope with a finite optical spot size. Nanotechnology, 2005, 16(6): 664-670. DOI:10.1088/0957-4484/16/6/007 (  0) 0) |
| [31] |
Bergaud C, Nicu L. Viscosity measurements based on experimental investigations of composite cantilever beam eigenfrequencies in viscous media. Review of Scientific Instruments, 2000, 71(6): 2487-2491. DOI:10.1063/1.1150640 (  0) 0) |
| [32] |
Proksch R, Schäffer T E, Cleveland J P, et al. Finite optical spot size and position corrections in thermal spring constant calibration. Nanotechnology, 2004, 15(9): 1344-1350. DOI:10.1088/0957-4484/15/9/039 (  0) 0) |
| [33] |
Ahmed N, Nino D F, Moy V T. Measurement of solution viscosity by atomic force microscopy. Review of Scientific Instruments, 2001, 72(6): 2731-2734. DOI:10.1063/1.1368856 (  0) 0) |
| [34] |
Cranch G A, Lane J E, Miller G A, et al. Low frequency driven oscillations of cantilevers in viscous fluids at very low Reynolds number. Journal of Applied Physics, 2013, 113(19): 194904. DOI:10.1063/1.4805072 (  0) 0) |
| [35] |
Rief M, Clausen-Schaumann H, Gaub H E. Sequence-dependent mechanics of single DNA molecules. Nature Structural Biology, 1999, 6(4): 346-349. DOI:10.1038/7582 (  0) 0) |
| [36] |
Junker J P, Ziegler F, Rief M. Ligand-dependent equilibrium fluctuations of single calmodulin molecules. Science, 2009, 323(5914): 633-637. DOI:10.1126/science.1166191 (  0) 0) |
| [37] |
Li H B, Zheng P. Single molecule force spectroscopy: a new tool for bioinorganic chemistry. Current Opinion in Chemical Biology, 2018, 43: 58-67. DOI:10.1016/j.cbpa.2017.11.014 (  0) 0) |
| [38] |
Tracy Richard, Welch William R, Pinshow Berry, et al. Properties of Air. Madison : University of Wisconsin-Madison. 2010.
(  0) 0) |
| [39] |
El-Banna M M. Densities and viscosities for mixtures of pentyl acetate and hexyl acetate with normal alkanols at 298.15 K. Journal of Chemical and Engineering Data, 1997, 42(1): 31-34. DOI:10.1021/je960193z (  0) 0) |
| [40] |
Figueira V B C, Jones J P. Viscoelastic study of the adsorption of bovine serum albumin on gold and its dependence on pH. Journal of Colloid and Interface Science, 2008, 325(1): 107-113. DOI:10.1016/j.jcis.2008.05.056 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


