Minimally invasive surgical robot (MISR) is a revolution in surgical field. Compared with traditional minimally invasive surgery, MISR performs better in surgery because it has many advantages such as accurate positioning, 3D surgical vision, action dexterity, motion scaling, master-slave control, hand-eye coordination, and fine operation[1]. Benefiting from these advantages, MISR can effectively improve the quality of surgery, reduce the dependence on the experience of surgeons, and reduce the intensity of surgeons' labor. Therefore, the research on minimally invasive surgical robot system has been on the rise, and it is also a hot spot in the robot research field in the next few years. At present, there are a number of minimally invasive surgical robots in clinical use in the world, such as Da Vinci Surgical Robot System. It can be applied to heart, digestive system, urology, gynecology, and other surgical operations [2].
There are still some deficiencies to be improved in the research and application of minimally invasive surgical robots. One of the important problems is vibration caused by physiological hand tremor. When a surgeon operates with the assistance of a robot, his physiological hand tremor causes the master manipulator to vibrate in the Master-Slave control robot system, which will cause vibration at the surgical instruments installed on the slave manipulator. Especially after the motion scaling of the Master-Slave control system, such a vibration will seriously affect surgeon's operation. It can increase the difficulty of operation, reduce the accuracy of operation, and even threaten operation safety in serious cases. So tremor suppression is highly necessary in robotically assisted minimally invasive surgery.
Physiological tremor is a tremor inherent in the human hands. Even experienced surgeons are no exception. Physiological hand tremor is a complex, high frequency signal without obvious regularity, as shown in Fig. 1. Studies have shown that the frequency of tremor signals in the hands of surgeons is between 8-12 Hz, and its amplitude is under 50 μm [3-4].
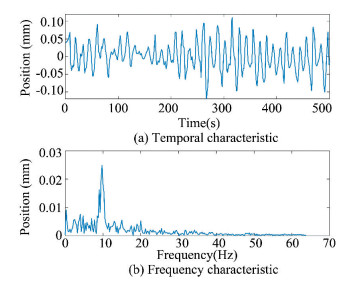
|
Fig.1 Tremor signal characteristics |
Besides the physiological hand tremor, the dynamic characteristics of the master manipulator are also related to its vibration. Nonlinear friction in the master manipulator and other dynamic terms of dimensional modeling will cause vibration at the end of the manipulator when it moves. Vibration suppression caused by these dynamic terms has been extensively studied in the field of industrial robots. Compared with the high-speed and heavy-load working conditions of industrial robots, the operating environment of medical robots is different, mostly low-speed and light-load. Therefore, the current international research on the master manipulator tremor removal of medical robots is mainly focused on the removal of physiological tremor. In this paper, physiological hand tremor and its filtering algorithm are also focuses of investigation.
Usually, the frequency of the control signal of the surgical robot is lower than that of the tremor signal. So in principle, the tremor signal can be filtered in the control signal by low pass filtering. Researchers at MIT used low pass filters to remove tremors. The results show that the filters can effectively remove tremors with low accuracy requirements [5]. Yet the biggest problem of low pass filter is time delay. For surgical robots, real-time requirements are very high, and time delay will affect the operation and safety. Some researchers have considered the tremor filtering method based on signal compensation [6]. Veluvolu and Tatinati [7] proposed a system using adaptive neural fuzzy control for multi-step estimation of hand pathological tremor. Liu et al.[8] proposed a nonlinear adaptive neural fuzzy network to filter physiological tremor. Liu and Mao[9] proposed a three-dimensional wavelet fuzzy neural network to filter tremor. Liu and Luo [10] proposed an adaptive fuzzy filter based on time-varying sequence. As a feedforward method, Kalman filter can solve the time-delay problem. But the traditional Kalman filter also has some limitations. Zhou et al. [11] proposed an improved Kalman filtering algorithm, which estimates and corrects the error of dynamic model by LS-LVM, and improves the accuracy of Kalman filtering.
In this paper, a Least Squares Support Vector Machine Kalman Filter (LSSVMKF) is proposed based on signal compensation. First, the signal was preprocessed to get the accurate physiological tremor signal by an improved Kalman filter, and then a compensation signal with the same phase and the opposite amplitude was generated, which was superimposed into the control signal in real time.
2 Filter DesignA Master-Slave control system for minimally invasive surgery consists of three subsystems: a master manipulator control system, a slave manipulator execution system, and an imaging system. This paper deals with the problem of tremor filtering in the master manipulator control system. Fig. 2 shows the control principle of the master manipulator control system. The LSSVMKF module in Fig. 2 is the focus of this paper. The design process of LSSVMKF will be described in detail below.

|
Fig.2 Control principle of the master manipulator control system |
2.1 Kalman Filtering
The key of filtering based on signal compensation is accurate prediction of tremor signal. Kalman filtering algorithm can estimate the optimal state of a system, which uses state equation and the input-output observed data of the system [12]. In our master manipulator control system, Kalman filtering algorithm can be employed to estimate the tremor signal.
The Kalman filtering model includes a process state and a measurement state. They can be expressed as:
Process state:
| $ \mathit{\boldsymbol{X}}(k) = \mathit{\boldsymbol{AX}}(k - 1) + \mathit{\boldsymbol{w}}(k) $ | (1) |
Measurement state:
| $ \mathit{\boldsymbol{Z}}(k) = \mathit{\boldsymbol{HX}}(k) + \mathit{\boldsymbol{v}}(k) $ | (2) |
where X (k) is a state vector of the tremor signal in the master manipulator control system. It contains position information of tremor signals. Matrix A denotes the state transition and matrix H denotes the measurement transition. When this time does not increase the tremor control at the last time, A is a unit matrix. Z (k) is a measured vector which contains position information of tremor signals by measurement. Vector w (k) denotes the process noise and vector v (k) denotes the measurement noise. In general Kalman filtering algorithm, it is assumed that w (k) and v (k) are linearly independent Gaussian white noises with mean 0 and satisfy the following conditions:
| $ \left\{ \begin{array}{l} E\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{w}}_k}}&{\mathit{\boldsymbol{w}}_i^{\rm{T}}} \end{array}} \right] = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{Q}},i = k}\\ {0,i \ne k} \end{array}} \right.\\ E\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_k}}&{\mathit{\boldsymbol{v}}_i^{\rm{T}}} \end{array}} \right] = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{R}},i = k}\\ {0,i \ne k} \end{array}} \right.\\ E\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{w}}_k}}&{\mathit{\boldsymbol{w}}_i^{\rm{T}}} \end{array}} \right] = 0,\forall i,k \end{array} \right. $ | (3) |
where Q is the covariance of w (k)and R is the covariance of v (k).
The Kalman filtering process is divided into two processes: transcendental prediction and measurement updating:
Transcendental prediction:
| $ {\mathit{\boldsymbol{\hat X}}(k|k - 1) = \mathit{\boldsymbol{A\hat X}}(k - 1|k - 1)} $ | (4) |
| $ {\mathit{\boldsymbol{P}}(k|k - 1) = \mathit{\boldsymbol{AP}}(k - 1|k - 1){\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{Q}}} $ | (5) |
Measurement updating:
| $ \mathit{\boldsymbol{K}}(k) = \mathit{\boldsymbol{P}}(k|k - 1){\mathit{\boldsymbol{H}}^{\rm{T}}}{[\mathit{\boldsymbol{HP}}(k|k - 1){\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}}]^{ - 1}} $ | (6) |
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat X}}(k|k) = \mathit{\boldsymbol{A\hat X}}(k|k - 1) + \mathit{\boldsymbol{K}}(k)(\mathit{\boldsymbol{Z}}(k) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{H\hat X}}(k|k - 1))} \end{array} $ | (7) |
| $ \mathit{\boldsymbol{P}}(k|k) = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}(k)\mathit{\boldsymbol{H}})\mathit{\boldsymbol{P}}(k|k - 1) $ | (8) |
where vector
Eqs.(4)-(8) are the basic formula for Kalman filtering. Kalman filtering algorithm can estimate the optimal state of a system, which uses state equation and the input-output observed data of the system. In the prediction and estimation of tremor signal, Kalman filtering makes use of the state vector and measurement vector of tremor signal at this time to recursively calculate. In each recursion, the tremor state vector at the last moment is predicted according to the tremor state vector, and the covariance is calculated (Eqs.(4)-(5)). Then the state prediction is updated by the measurement vector, and the covariance and Kalman gain are updated for the next iteration (Eqs.(6)-(8)).
The Kalman filtering algorithm can be used to predict and model the tremor signal without time delay, but the filtering effect is not very satisfactory. The Kalman filtering algorithm will be improved accordingly.
2.2 LS-SVM Kalman FilteringIn the above Kalman filtering algorithm, the covariance of the process noise and the measurement noise are regarded as a constant. The values of these two parameters need to be set before filtering. Among them, the value of process noise covariance is affected by the vibration control process, and the measurement noise covariance is affected by the sensor characteristics and working environment. Their determination can only be estimated by prior knowledge. If the two parameters are not set properly, the final filtering effect will be affected. In addition, process noise and measurement noise are not invariable, and it is unreasonable to set their covariance as a constant. The Kalman filtering algorithm designed in this paper regards the covariance of the process noise and the measurement noise as variables, and adjusts their values in real time in order to improve the accuracy of filtering.
In this paper, the regression model of the process noise covariance and the measurement noise in Kalman filtering algorithm was established using Least Squares Support Vector Machine (LS-SVM) [14]. The input of the model was the surgeon's hand control signal, and the output was the covariance of the process noise and the measurement noise. Regression model of covariance was obtained by training a set of control signal data, of which the tremor signal and covariance are known as training samples.
The following is the establishment of a regression model to measure noise covariance R.
The training set adopted by the LS-SVM regression model was
First, a nonlinear function Φ (·) was used to map the input vector into the high dimensional space F. In the feature space, the following expressions were used to estimate unknown nonlinear functions:
| $ \mathit{\boldsymbol{R}}(k) = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(\mathit{\boldsymbol{S}}) + b,\mathit{\boldsymbol{\omega }} \in \mathit{\boldsymbol{F}},b \in \mathbb{R} $ | (9) |
where ω and b are undetermined parameters.
Then, the optimization problem of LS-SVM was defined as
| $ \mathop {{\rm{min}}}\limits_{\omega ,e} \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{e}}) = \frac{1}{2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} + C\sum\limits_{i = 1}^N {e_i^2} ,C > 0 $ | (10) |
which satisfies the following equality constraints:
| $ {R_i} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{S}}_i}) + b + {e_i},i = 1,2, \ldots ,N $ | (11) |
The Lagrange functions that define the above optimization problems are as follows:
| $ \begin{array}{*{20}{l}} {L(\mathit{\boldsymbol{\omega }},b,e;\alpha ) = J(\mathit{\boldsymbol{\omega }},e) - \sum\limits_{i = 1}^N {{\alpha _i}} [{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{S}}_i}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b + {e_i} - {R_i}]} \end{array} $ | (12) |
where
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial L}}{{\partial \omega }} = 0 \Rightarrow \omega = \sum\limits_{i = 1}^N {{\alpha _i}} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{S}}_i})}\\ {\frac{{\partial L}}{{\partial b}} = 0 \Rightarrow b = \sum\limits_{i = 1}^N {{\alpha _i}} = 0}\\ {\frac{{\partial L}}{{\partial {e_i}}} = 0 \Rightarrow {\alpha _i} = C{e_i}}\\ {\frac{{\partial L}}{{\partial {\alpha _i}}} = 0 \Rightarrow {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{S}}_i}) + b + {e_i} - {R_i} = 0} \end{array}} \right. $ | (13) |
where i=1, 2, …, N.
The linear equations can be obtained from the above four conditions:
| $ \left[ {\begin{array}{*{20}{c}} 0&{{{\vec 1}^{\rm{T}}}}\\ {\vec 1}&{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + {\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{b}}\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ \mathit{\boldsymbol{R}} \end{array}} \right] $ | (14) |
where
| $ {\vec 1 = {{[1, \cdots ,1]}^{\rm{T}}},\mathit{\boldsymbol{R}} = {{[{R_1}, \cdots ,{R_N}]}^{\rm{T}}}} $ |
| $ {\alpha = {{[{\alpha _1}, \cdots ,{\alpha _N}]}^{\rm{T}}}} $ |
Ω is the kernel matrix:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{ij}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{({\mathit{\boldsymbol{S}}_i})^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{S}}_i}) = k({\mathit{\boldsymbol{S}}_i},{\mathit{\boldsymbol{S}}_j}),i,j = 1,2, \ldots ,N $ | (15) |
where k( S i, S j)is the kernel function and the Radial Basis Function(RBF) was chosen here [15]. Finally, the model expression of LSSVM was obtained as follows:
| $ R(\mathit{\boldsymbol{S}}) = \sum\limits_{i = 1}^N {{\alpha _i}} k({\mathit{\boldsymbol{S}}_i},\mathit{\boldsymbol{S}}) + b $ | (16) |
Replacing the constant R in the Kalman filtering algorithm with R(S), the Least Squares Support Vector Machine Kalman filter (LSSVMKF) can be obtained. Using the LSSVMKF, the prediction model of tremor signal can be built, and then it can be inversely superimposed into the control signal to achieve tremor filtering.
3 Simulation ResultsTo verify the filtering effect of the LSSVMKF on hand tremor signal in robotically assisted minimally invasive surgery, a simulation experiment was carried out by MATLAB.
In simulation experiments, the following signal was used to simulate the ideal control signal:
| $ y(t) = {\rm{cos}}(\pi t) + {\rm{sin}}(2\pi t) $ | (17) |
The physiological hand tremor signal was simulated by the following signal:
| $ n(t) = 0.1{\rm{cos}}(22\pi t) + 0.1{\rm{sin}}(18\pi t) $ | (18) |
where n(t) is a simplified analog tremor signal, which consists of two frequency components of 11 Hz and 9 Hz, respectively. Its signal characteristic was similar to that of human physiological tremor. Using this signal, the real human physiological tremor can be simulated approximately.
Then, the complete hand control signal was the superposition of the above signal:
| $ s(t) = y(t) + n(t) $ | (19) |
The waveform of the above signal is shown in Fig. 3.
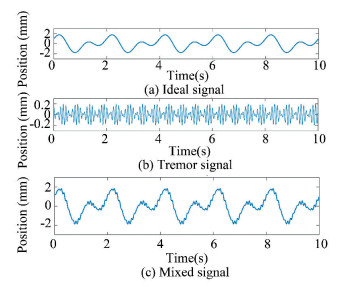
|
Fig.3 Signal for simulation |
3.1 Result of Traditional Low Pass Filtering
First, the traditional Butterworth low pass filter was used to filter out the tremor signal. Butterworth filter is a common digital filter. Here, the Butterworth filter toolbox of MATLAB was used to conduct filter. When using this toolbox to simulate low-pass filtering, only two parameters need to be determined: Filter order (N) and cut-off frequency(ωc). First, the 6th order Butterworth low pass filter was chosen, i.e., N = 6. Then, the Butterworth cut-off frequency ωc was related to cut-off frequency of low-pass filter, Fc. According to the frequency bandwidth range of the tremor signal and the control signal, Fc was set as 5 Hz. Then, ωc=0.1 was obtained according to ωc= Fc/(Fs/2), where, Fs=100, was the sampling frequency.
The original control signal was compared with the filtered signal as shown in Fig. 4.

|
Fig.4 Butterworth low pass filtering |
From Fig. 4, the tremor signal in the control signal was basically filtered out after the Butterworth low pass filtering. However, the phase of the filtered signal was shifted, i.e., the time delay was generated. The phase diagram of this filter function is shown in Fig. 5.
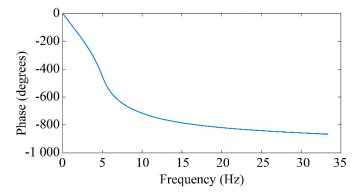
|
Fig.5 Phase diagram of Butterworth function |
In such a traditional low pass filter, the cut off frequency was designed according to the required frequency components. It was expected that all frequency components above the cut off frequency would be filtered and all frequency components below the cut off frequency would be retained without time delay. But in fact, the Butterworth function itself had phase delay (Fig. 5), so the filtering inevitably led to time delay. Other convolutional low-pass filters also have phase delay problems.
This is the shortcoming of traditional low pass filtering. Such time delay is acceptable when the phase requirement is not strict. But in surgical robots, there is strict requirement for the real-time control signal and no time delay is desired. So the low pass filter cannot be used directly in the surgical robot system.
3.2 Result of LSSVMKFThe key of LSSVMKF is to accurately model tremor signals. In order to illustrate the effect of LSSVMKF, the traditional Kalman filter was first used to model the tremor signal, and then a signal with the opposite amplitude and the same phase was generated, which was superimposed into the control signal.
Fig. 6 shows the filtering effect of the traditional Kalman filter for the modeling of tremor. There was no time delay in signal filtering based on signal compensation, for it was a feedforward compensation method. The estimated real-time tremor signal was reversely compensated to the control signal. This method eliminated tremor without phase lag, so it did not cause time delay.

|
Fig.6 Traditional Kalman filtering |
Comparison of the ideal control signal and the filtered signal is shown in Fig. 7. Although there was almost no time delay in filtering results, filtering accuracy was also a concern of the study. The Root Mean Square Error (RMSE) between the ideal control signal and filtered signal can reflect the filtering accuracy. The RMSE between those two signal after the traditional Kalman filter was 0.0201 (Fig. 7), and the measurement noise covariance R of this Kalman filter was set to 0.1.
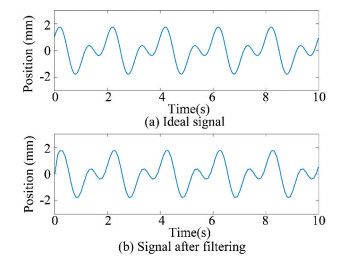
|
Fig.7 Ideal signal and filtered signal by Kalman |
As is known, R is an empirical constant in Kalman filtering, and its change affects filtering results. The value of R was changed and the filter was conducted again, the result was still basically filter out tremor and there was no time delay. But the RMSE between filtered signal and ideal signal changed as well. The result is shown in Table 1.
| Table 1 Change of RMSE with R |
Table 1 shows that the accuracy of filtering is related to the estimated value of R. If the estimation value is unreasonable, the filtering effect is poor. But it is difficult to set optimal or even reasonable R value before filtering according to the existing experience, because the current empirical research on R is not yet mature.
Then, LSSVMKF was used to model the tremor signal and it was added back to the control signal to filter out the tremor. The filtering effect is shown in Fig. 8. The comparison between the filtered signal and the ideal signal is shown in Fig. 9.

|
Fig.8 Filtering by LSSVMKF |
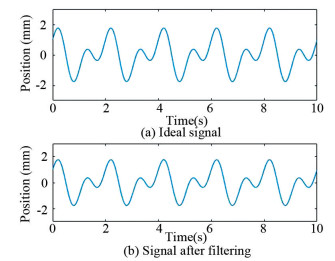
|
Fig.9 Ideal signal and filtered signal by LSSVMKF |
This time the RMSE was only 0.0020, which is significantly lower than that listed in Table 1.
Next, the simulated physiological tremor signal was changed to do the simulation again. The 6 new groups of mixed signals were composed of the following 6 groups of physiological tremor signals and Eq.(18), respectively. LSSVMKF designed in this paper was used to filter the new mixed signal.
| $ \left\{ {\begin{array}{*{20}{l}} {{n_1}(t) = 0.09{\rm{cos}}(21\pi t) + 0.1{\rm{sin}}(18\pi t)}\\ {{n_2}(t) = 0.09{\rm{cos}}(20\pi t) + 0.09{\rm{sin}}(18\pi t)}\\ {{n_3}(t) = 0.08{\rm{cos}}(19\pi t) + 0.08{\rm{sin}}(18\pi t)}\\ {{n_4}(t) = 0.09{\rm{cos}}(22\pi t) + 0.09{\rm{sin}}(19\pi t)}\\ {{n_5}(t) = 0.09{\rm{cos}}(22\pi t) + 0.09{\rm{sin}}(20\pi t)}\\ {{n_6}(t) = 0.08{\rm{cos}}(22\pi t) + 0.08{\rm{sin}}(21\pi t)} \end{array}} \right. $ | (20) |
In order to compare and verify the difference between LSSVMKF algorithm and other algorithms, the traditional Kalman filter was also used to filter the 6 groups of mixed signals. The comparison of RMSE in filtering results of these 6 groups of mixed signals are shown in Table 2.
| Table 2 RMSE of different tremor signals and different filters |
From Table 2, the filtering errors of LSSVMKF were slightly different for different tremor signals. However, for each tremor signal, the filtering error was much smaller than that of the traditional Kalman filter, which meets the requirements of robotically assisted minimally invasive surgery.
The above simulation experiments show that LSSVMKF can achieve hand tremor signal filtering effectually. It not only avoided the shortcoming of introducing time delay in low pass filter, but also improved the shortcoming that Kalman filter can only rely on empirical estimation to define the measurement noise covariance.
4 ConclusionsIn this paper, a Least Squares Support Vector Machine Kalman filter was proposed to filter the physiological tremor in minimally invasive surgical robot. LSSVMKF can estimate and model the physiological tremor signal mixed in the surgical control signal using Kalman filtering algorithm. Then a compensation signal with the same phase and opposite amplitude was generated. The physiological tremor can be removed by adding the compensation signal to the control signal. In order to overcome the dependence of parameter setting on experience in traditional Kalman filtering algorithm, the constants "measurement noise covariance" (R) was changed into a variable. Then, the LSSVM regression algorithm was employed to reconstruct the measurement noise covariance. Embedding this regression model into Kalman filtering algorithm, the LSSVMKF was obtained. In the simulation, LSSVMKF filter was first compared with traditional low-pass filter, which showed that LSSVMKF filter could effectively avoid time delay. Subsequently, the errors between LSSVMKF filter and traditional Kalman filter were compared, which showed that LSSVMKF filter could improve Kalman filter accuracy by comparing the RMSE results of LSSVMKF filter and traditional Kalman filter. In conclusion, LSSVMKF algorithm can overcome the shortcomings of traditional low pass filter and Kalman filter in minimally invasive surgical robot.
| [1] |
Sang H, Wang S, Li J, et a1. Control design and implementation of a novel master slave surgery robot system, Micro Hand A. International Journal of Medical Robotics and Computer Assisted Surgery, 2011, 7(3): 334-347. DOI:10.1002/rcs.403 (  0) 0) |
| [2] |
Carignan B, Daneault J F, Duval C. The effect of changes in joint angle on the characteristics of physiological tremor. Journal of Electromyography and Kinesiology, 2012, 22(6): 954-960. DOI:10.1016/j.jelekin.2012.04.012 (  0) 0) |
| [3] |
Morrison S, Mills P, Barrett R. Differences in multiple segment tremor dynamics between young and elderly persons. Journals of Gerontology: Medical Sciences, 2006, 61A(9): 982-990. DOI:10.1093/gerona/61.9.982 (  0) 0) |
| [4] |
Defazio G, Gigante A F, Abbruzzese G, et a1. Tremor in primary adult-onset dystonia: Prevalence and associated clinical features. Journal of Neurology Neurosurgery and Psychiatry, 2013, 84(4): 404-408. DOI:10.1136/jnnp-2012-303782 (  0) 0) |
| [5] |
Veluvolu K C, Ang W T. Estimation of physiological tremor from accelerometers for real-time applications. Sensors, 2011, 11: 3020-3036. DOI:10.3390/s110303020 (  0) 0) |
| [6] |
Veluvolu K C, Tan U X, Latt W T, et al. Bandlimited multiple Fourier linear combiner for real time tremor compensation. IEEE International Conference on Engineering in Medicine and Biology Society. Piscataway: IEEE, 2007. 2847-2850. DOI: 10.1109/IEMBS.2007.4352922.
(  0) 0) |
| [7] |
Veluvolu K C, Tatinati S, Hong S M, et al. Multistep prediction of physiological tremor for surgical robotics applications. IEEE Transactions on Biomedical Engineering, 2013, 60(11): 3074-3082. DOI:10.1109/tbme.2013.2264546 (  0) 0) |
| [8] |
Liu Z, Wu Q, Zhang Y, et al. Adaptive fuzzy wavelet neural network filter for hand tremor canceling in microsurgery. Applied Soft Computing, 2011, 11(8): 5315-5329. DOI:10.1016/j.asoc.2011.05.027 (  0) 0) |
| [9] |
Liu Z, Mao C Y, Luo J, et a1. A three domain fuzzy wavelet network filter using fuzzy PSO for robotic assisted minimally invasive surgery. Knowledge-Based Systems, 2014, 66: 13-27. DOI:10.1016/j.knosys.2014.03.025 (  0) 0) |
| [10] |
Liu Z, Luo J, Wang L Y, et a1. A time sequence-based fuzzy support vector machine adaptive filter for tremor cancelling for microsurgery. International Journal of Systems Science, 2015, 46(6): 1131-1146. DOI:10.1080/00207721.2013.821718 (  0) 0) |
| [11] |
Zhou Z, Li Y, Fu C, et al. Least-squares support vector machine-based Kalman filtering for GNSS navigation with dynamic model real-time correction. IET Radar, Sonar & Navigation, 2017, 11(3): 528-538. DOI:10.1049/iet-rsn.2016.0422 (  0) 0) |
| [12] |
Kalman R E. A new approach to linear filtering and prediction problems. Transactions of the ASME-Journal of Basic Engineering, 1960, 82: 35-45. DOI:10.1115/1.3662552 (  0) 0) |
| [13] |
Sang H, Yang C, Liu F, et al. A zero phase adaptive fuzzy Kalman filter for physiological tremor suppression in robotically assisted minimally invasive surgery. The International Journal of Medical Robotics and Computer Assisted Surgery, 2016, 12(4): 658-669. DOI:10.1002/rcs.1741 (  0) 0) |
| [14] |
Smola A J, Schölkopf B. A tutorial on support vector regression. Statistics and Computing, 2004, 14(3): 199-222. DOI:10.1023/B:STCO.0000035301.49549.88 (  0) 0) |
| [15] |
Wu Chih-Hung, Tzeng Gwo-Hshiung, Lin Rong-Ho. A novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Systems with Applications, 2009, 36(3): 4725-4735. DOI:10.1016/j.eswa.2008.06.046 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


