2. People's Liberation Army Air Force 93756, Tianjin 300000, China;
3. Department of Film and Television Technology, Tianjin Broadcasting TV and Film Institute, Tianjin 300112, China
With the rapid development of global communications, more and more wireless communications are needed. However, the conflict between heavy communication demand and limited spectrum resources has become increasingly prominent. How to increase the system capacity on a large scale on the basis of guarantee communication quality has become an important issue for the telecommunication community. The smart antenna can effectively improve the spectrum utilization rate and alleviate the problems faced by mankind, which has thus drawn more and more attention. The array antenna pattern is one of the core technologies of smart antenna. In recent years, researchers have conducted extensive and in-depth studies on it and achieved a lot of constructive results[1].
The problem of antenna array pattern synthesis is to design arrays based on the radiation characteristics of antenna patterns. In order to achieve the design goal, it is necessary to adjust some parameters of the array antenna, including element number, element spacing, array excitation amplitude, and phase coefficient. The problem is a complex nonlinear optimization problem. The more the number of the antenna elements is, the more parameters are needed to be adjusted in the optimization process, and the more complicated the computation process is. Traditional analytical methods have been utilized by the researchers of this paper to synthesize pattern. By using the classical Woodward-Lawson sampling to calculate the problem, the precision requirement in the form section can be basically achieved, but the side-lobe level is usually high and the gain is low. If the fine-tuning method is used to optimize, a lot of debugging experience and theoretical analysis are needed[2]. In order to improve efficiency, many experts and scholars have applied a variety of intelligent optimization algorithms to the optimization of antenna pattern, such as genetic algorithm (GA)[3-4], particle swarm optimization (PSO)[5], immune clone selection algorithm (ICSA)[6], and quantum particle swarm optimization (QPSO)[7]. The pattern synthesis based on these algorithms can basically meet the requirements of the antenna design, but there are still some problems. The main problem is that when the design index is relatively high, the accuracy of some algorithms is not high and the convergence speed is slow.
Wolf pack algorithm (WPA) is a new group intelligent optimization algorithm proposed by Yang et al.[8] in 2007, which imitates the predation behavior of wolves and the distribution of prey. This algorithm has good processing capability for complex nonlinear optimization problems, and has achieved good results in the optimization of sensors and the optimal scheduling of hydropower stations[9]. The researcher in Ref. [10] proposed a new cultural wolf pack algorithm (CWPA) by combining WPA with the cultural algorithm. Compared with WPA, the new algorithm has significantly improved the optimization accuracy in multidimensional optimization problems, but the convergence speed is general. In this paper, with the analysis of the shortcomings of CWPA, the Levy flight strategy in population evolution[11] is introduced to improve the performance of CWPA. A more efficient optimization algorithm was obtained, which was applied to the antenna pattern synthesis and the effect was verified by experiments.
2 Problem FormulationThe pattern of antenna array can be decided by five parameters including the number of array elements, the form of distribution, the distance between array elements, and amplitude and phase[12]. The pattern can be obtained by changing the five parameters, and the required pattern is obtained by optimizing the five parameters. According to the arrangement of the array elements, the antenna array can be divided into a linear array, a planar array, a conformal array, and so on. This paper considers a one-dimensional uniform linear array, as shown in Fig. 1.
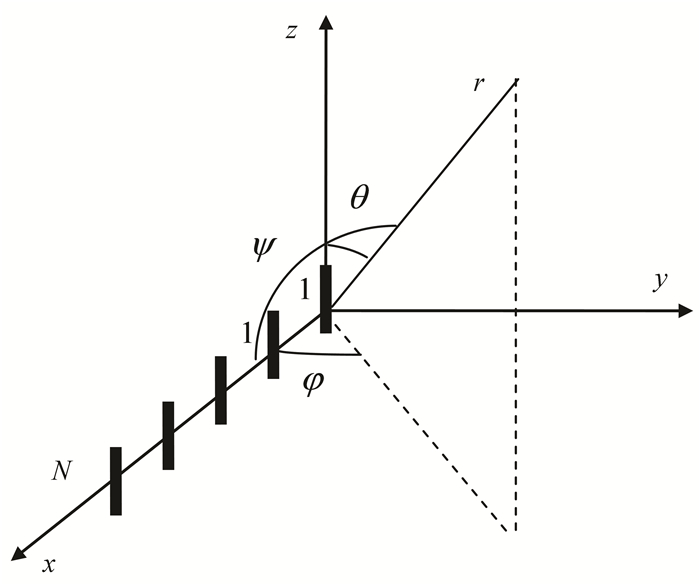
|
Fig.1 One-dimensional uniform linear array |
The problem of pattern synthesis for the uniform linear array can be described as follows. Consider the homogeneous linear array with 2N elements. Set the current phase difference as 0 and the current amplitude as center symmetric. Therefore, the pattern synthesis function is
| $ F(\theta ) = 20 \cdot {\rm{lg}}\left| {\frac{{\sum\limits_{n = 1}^N {{I_n}} {{\rm{e}}^{{\rm{j}}(kd(n - 1){\rm{cos}}\theta + {\delta _n})}}}}{{\sum\limits_{n = 1}^N {{I_n}} {{\rm{e}}^{{\rm{j}}{\delta _n}}}}}} \right| $ | (1) |
where In is the current amplitude of antenna elements, d is the space between elements, k is the wave number (k=2π/λ), λ is the wavelength, and θ is the included angle of normal and incident ray. Current amplitude is symmetric.
When the number of the elements is even, the above formula can be simplified as follows:
| $ F(\theta ) = 20 \cdot {\rm{lg}}\left| {\frac{{\sum\limits_{n = 1}^N {{I_n}} {\rm{cos}}\left[ {\left( {\frac{{2(N - n) + 1}}{2}} \right)kd \cdot {\rm{cos}}\theta } \right]}}{{\sum\limits_{n = 1}^N {{I_n}} }}} \right| $ | (2) |
When we only set request on the side-lobe level, the fitness function is described as
| $ {\rm{fitness}} = |{\rm{MSLL}} - {\rm{SLVL}}| $ | (3) |
where MSLL is the abbreviation of mean side-obe level, MSLL=max(F(θ)), θ∈S, SLVL (side-lobe valid level) is the expected level, 2θ0 is the main-lobe width, and S={0≤θ≤90°-θ0 or 90°+θ0≤θ≤180°}, which is the side-lobe region of antenna pattern[13-14].
F(θ) represents distributing power into several elements in antenna array. The fields created by the elements have mutual interference. The radiation in some directions was enhanced, while that in other directions was reduced and the value could be 0, which achieved the redistribution of the radiation power in space. The main-lobe and side-lobe were then created. Fitness function represents the absolute value of difference for MSLL and SLVL. The smaller value of the fitness function means that the real value of the side-lobe level is closer to the expected value of the side-lobe level.
Sometimes, it is also necessary to obtain the deep nulling in several specific directions with the value of NLVL(nulling lobe valid level). In the antenna array, there can be noise interference in some directions. To reduce such interface, it is suggested to minimize the radiation values in those directions, which is called deep nulling. NLVL represents the side-lobe level that is expected in the direction of deep nulling. Then the fitness function is
| $ \begin{array}{*{20}{l}} {{\rm{fitness}} = \alpha |{\rm{MSLL}} - {\rm{SLVL}}| + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta |\mathop {{\rm{max}}}\limits_{i = 1 \cdots {N_0}} \{ F({\theta _i}) - {\rm{NLVL}}\} |} \end{array} $ | (4) |
where, α=1.25, β=0.2 are set based on the simulation study in Ref. [15].
3 Proposed Method 3.1 Levy FlightLevy distribution is a probability distribution proposed by the French mathematician Levy in the 1930s. Levy flight is a random search path that obeys Levy distribution, which is a random walk mode between short distance search and occasional long distance search. With plenty of studies, it has been found that Levy flight conforms to the behavior of a variety of natural creatures such as bees and albatross, and it can explain many random phenomena in the nature such as the Brown movement[16].
In recent years, Levy flight has been widely introduced into the field of optimization. Deng et al.[17] applied it as an evolutionary strategy to improve cuckoo algorithm. Yan et al.[18] used it as an evolutionary strategy to improve particle swarm algorithm. The introduction of Levy flight enhances the diversity of the population, enlarges the scope of the search, and makes it easier to jump out of the local most advantages and effectively enhance the optimization ability of the algorithm.
The essence of Levy flight is a random step, and its location update formula is as follows[17]:
| $ x_i^{t + 1} = x_i^t + \alpha \oplus {\rm{Levy}} (\lambda ) $ | (5) |
where i∈[1, 2, …, N] stands for step size control, Levy(λ) is a random search path, and ⊕ represents point to point multiplication. The Levy distribution in the form is expressed as[17]
| $ {\rm{Levy}}\backsim \mu = {t^{ - \lambda }}, 1 < \lambda \le 3 $ | (6) |
Since Levy flight is complicated, the Mantegna algorithm is mainly used to simulate it, and the mathematical expressions are as follows[18].
The formula for calculating the step size s[18] is
| $ s = \frac{\mu }{{|v{|^{\frac{1}{\beta }}}}} $ | (7) |
where the probability distribution of μ and v satisfies the following normal distribution[18]
| $ {\mu \backsim N(0, \sigma _\mu ^2), v\backsim N(0, \sigma _v^2)} $ |
| $ {{\sigma _\mu } = {{\left( {\frac{{\Gamma (1 + \beta ) \times {\rm{sin}}\frac{{\beta \pi }}{2}}}{{\Gamma \left( {\frac{{1 + \beta }}{2}} \right) \times \beta \times {2^{\frac{{\beta - 1}}{2}}}}}} \right)}^{\frac{1}{\beta }}}} $ |
The β in various types usually takes 1.5 of the constant[18].
To prove the superiority of population updating by Levy flight, the flight trajectory of Levy was simulated in Matlab software. The step length was 1000 steps, and the result is shown in Fig. 2.

|
Fig.2 Levy flight path |

|
Fig.3 CWPA frame structure |
It can be seen that Levy flight trajectory had both short-range exploratory jumps and occasional longer walks[19]. If Levy flight is introduced into the variation rule of the CWPA, the new wolves generated by the mutation will not only be able to search carefully in their own small area, but also occasionally walk a long distance into another area and search for a wider range. It can significantly improve the ability of the algorithm to jump out of the local optimal solution and effectively develop the global optimization ability of the algorithm.
3.2 Improvement of CWPACWPA is mainly composed of two parts including main group space and belief space constrained by knowledge sources. The CWPA model framework is shown in Fig. 3.
The two spaces of the algorithm both have the ability of parallel evolution of their respective groups. The lower-level main group space contributes elite individuals to the upper-level belief space, and the upper-level belief space contributes elite individuals to the lower-level main group space after knowledge evolution. Such "double evolutionary and dual promotion" can increase the diversity of the wolves, avoid "premature", and improve the accuracy and efficiency of the algorithm.
Measures of CWPA to increase population diversity only act on the macroscopic area. Through analysis, it was found that each time the algorithm randomly selects a certain number (Gnum) of poorly performing wolves to eliminate them, and then generates the same number of new wolves as normal distribution to keep the population number P constant. This scheme prevents the convergence stagnation near the local optimal solution to some extent, but increases the computational complexity. Since the wolves are randomly initialized, the phenomenon of convergence and stagnation in wolves search is not certain, and whether the algorithm is in a convergence stagnation by certain means can be detected. When the test results are positive, as clarified in Ref. [8], it is a good solution to increase population diversity by mutation. Through variation, the wolves can jump out of the local best and try to move closer to the overall best (food). When the test result is negative, the information of the original wolves is maintained and the next search process is continued without mutation. In this way, the global search ability of the algorithm can be guaranteed and the search speed of the algorithm can be improved. Furthermore, according to Ref. [18], Levy mutation operator belongs to the thick-tailed distribution and has good disturbance ability. It can better maintain the diversity of the population and help the wolf jump out of the local optimal solution.
In response to the above issues, this paper proposes two improvements as follows:
1) In the iterative process of the algorithm, the convergence stagnation detection mechanism is introduced. In this paper, it is determined whether the algorithm is in a stagnant state by detecting changes in the fitness value of the leader wolf.
By recording the fitness value f of the leader wolf in each iteration, the vector F is obtained. When the number of the iteration steps exceeds N, the average fitness value Favg of the preceding N leader wolves is calculated, which is then compared with the tested fitness value Fi of the leader wolf as
| $ {F_{{\rm{ avg }}}} = \frac{{\sum\limits_{j = i - N}^{i - 1} {{F_j}} }}{N} $ | (8) |
where i is the serial number of the leader wolf detected in vector F. If the value of Fi/Favg still tends to 1 and the algorithm is not terminated, the algorithm is considered to be stagnant. According to Ref. [7], set N=20.
2) When the algorithm is stagnating, the wolves are selectively mutated. Based on the previous analysis, the probability of variation in the wolves should be proportional to the distance between wolves and the leader. The distance corresponds exactly to the fitness of the wolves. In the minima optimization, the smaller the adaptation value is, the smaller the distance is. Therefore, it is necessary to mutate wolves according to their fitness. The greater the fitness value of the wolf is, the higher the probability of its mutation is. This will not only maintain the diversity of the population, but also increase the iterative efficiency.
First, find out the different mutation probability ρL of the wolf that needs to be mutated. Then, assume that the size of the total wolf population is P, and the variation probability of the L-th wolf is calculated as
| $ {\rho _L} = \frac{{{f_L}}}{{\sum\limits_{k = 1}^p {{f_k}} }} $ | (9) |
Each wolf is assigned a random number between (0, 1). If the random number is less than the calculated variability probability of a wolf, then the wolf is mutated in accordance with the Levy flight mode. In contrast, the wolf population continues to remain in the original state.
The mutated wolves position update formula is changed to the following form
| $ q_{P - {G_{{\rm{num}}}} + {r_4} \cdot j}^{d + 1} = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} q_{{r_4}, j}^d + |(u_j^d - l_j^d) \oplus {\rm{ Levy }}(\lambda )|, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} q_{{r_4}, j}^d < e_j^d\\ q_{{r_4}, j}^d - |(u_j^d - l_j^d) \oplus {\rm{ Levy }}(\lambda )|, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} q_{{r_4}, j}^d > e_j^d\\ q_{{r_4}, j}^d + \eta (u_j^d - l_j^d) \oplus {\rm{Levy}} (\lambda ), {\rm{ else }} \end{array} \end{array}} \right. $ | (10) |
where r4=1, 2, …, Gnum, Gnum is a random integer in P/(2×ε), P/ε; ε is the updated scale factor; ejd is the j-th dimension of the formal knowledge E in the d-th iteration; and η is the update coefficient. Levy(λ) is calculated by Eq. (6). In order to improve the speed of the algorithm, the value of λ was set to 1.5 according to Ref. [18], and then the σμ operation result was 0.6966. Thus, Eq. (10) can be simplified as
| $ q_{P - {G_{{\rm{num}}}} + {r_4} \cdot j}^{d + 1} = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} \begin{array}{l} q_{{r_4}, j}^d + |(u_j^d - l_j^d) \times s(\mu , v)|, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} q_{{r_4}, j}^d < e_j^d\\ q_{{r_4}, j}^d - |(u_j^d - l_j^d) \times s(\mu , v)|, \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} q_{{r_4}, j}^d > e_j^d\\ q_{{r_4}, j}^d + \eta (u_j^d - l_j^d) \times s(\mu , v), {\rm{ else }} \end{array} \end{array}} \end{array}} \right. $ | (11) |
s(μ, v) can be calculated according to Eq.(7), where μ~N(0, 0.69662), v~N(0, 1).
The improved algorithm can be abbreviated as LCWPA, whose implementation steps are summarized as follows:
Step 1 Generate initial wolves in the population space;
Step 2 Calculate the fitness of each wolf and select the leader wolf;
Step 3 Establish and initialize belief space;
Step 4 Conduct wolves smart search, including three smart behaviors of scouting, summoning, and beleaguering;
Step 5 Update wolves: update the head wolves position by following the "winner is king" rule, and then selectively update the under-performing wolves according to the Levy flight strategy based on the stagnation test results;
Step 6 Update belief space;
Step 7 Determine whether the algorithm achieves the required optimization accuracy or the maximum number of iterations. If it is, the position of the leader wolf is output, otherwise the algorithm proceeds to Step 2.
The flow chart for LCWPA is shown in Fig. 4.

|
Fig.4 LCWPA flow chart |
3.3 LCWPA Performance Test
A variety of typical test functions with different characteristics were utilized to verify the effectiveness of the improved algorithm. Eight typical functions were selected according to Ref. [8], as shown in Table 1.
| Table 1 Test functions |
The characteristic "U" in Table 1 indicates that this function is a unimodal function, "M" is a multi-peak function, "S" is a separable function, and "N" is an inseparable function. The unimodal function (Easom, Matyas, and Sphere) means that the function has only global optimal values in the domain and there is no local extremum, whereas the multimodal functions (Booth, Eggcrate, Schaffer, Rastrigin, and Ackley) have many local minimum points. When the global optimization ability of the algorithm is insufficient, it is easy to converge on the local minimum point, so the accuracy of the search for this function should be carefully considered. In addition, if a function with N variables can be represented by the sum of N univariate functions, then the function is separable (Sphere, Booth, and Rastrigin), otherwise it is inseparable (Easom, Matyas, Eggcrate, Schaffer, and Ackley). Due to the complex relationship between inseparable function variables, it is relatively more difficult to optimize these functions.
The eight functions in Table 1 range from unimodal separable functions to multimodal inseparable functions, and the dimensions are from 2 D to 200 D. They all have typical representations and can fully reflect the performance of the algorithm.
The performance comparisons of LCWPA, CWPA, WPA, PSO, and GA were performed using the abovementioned eight typical functions. The PSO algorithm used the toolbox developed by Prof. Brian from the University of North Carolina, USA[10]. The GA used the algorithm toolkit developed by the University of Sheffield, UK[10]. The CWPA was programmed according to Ref. [10].
The microcomputer type Lenovo G460, Intel (R) Core (TM) i3-380-m 2.53 GHz CPU, 2.00 GB memory, 500 GB hard drive was used for the simulation environment. Windows 7 (32 bit operating system) and the simulation software Matlab 7.0 were utilized as the software platform.
In order to thoroughly compare the performance of each algorithm, LCWPA, CWPA, WPA, PSO, and GA were used to perform 100 optimization calculations on the eight complex functions. The algorithm was evaluated from different aspects such as the optimal value, the worst value, the average value, the calculation success rate, and the average time-consuming. Here, F* is the optimal function value obtained by each optimization calculation and F is the ideal optimal value of the function. When they both satisfy formula (12), the optimization calculation was considered as successful. The number of the successful calculations was divided by the total number of calculations to calculate the success rate, which can effectively reflect the stability of the algorithm and the ability to resist local extremum.
| $ \left\{ {\begin{array}{*{20}{c}} {\frac{{|F - {F^*}|}}{F} < {\rm{1e}} - 3, F \ne 0}\\ {|F - {F^*}| < {\rm{1e}} - 3, F = 0} \end{array}} \right. $ | (12) |
The maximum number of iterations for the experiment setup was set to 2000. The initial wolves, particle swarms, and chromosomes all had a scale of 50. Other parameters involved in the five algorithms were set according to Ref. [20], and the specific settings are shown in Table 2.
| Table 2 Parameter list of algorithms |
Table 3 shows the statistical results of the five algorithm optimization calculations. If the calculation result is less than 1e-16, it is regarded as 0.
| Table 3 Comparison of function optimization results |
The best values and average values in Table 3 can reflect the convergence accuracy of the algorithm. The worst value, standard deviation, and success rate reflect the robustness of the algorithm and the ability to jump out of the local optimal solution. The average time-consuming reflects the search speed of the algorithm. For simple low-dimensional functions such as Matyas and Booth, the convergence accuracy of the five algorithms was high, reaching more than 1e-7. For single-peak inseparable low-dimensional complex functions such as Easom and Matyas, PSO algorithm performed better, suggesting higher search accuracy and better algorithm execution capability. The optimization performance of WPA for these functions was slightly inferior to the PSO method. CWPA greatly improved the search ability compared with WPA because it added the overall management ability of the cultural algorithm. However, due to the increased complexity of the algorithm, the speed became slower. LCWPA performed the best among the five algorithms that it not only had the highest search accuracy, but also consumed significantly less time than WPA and CWPA.
However, as the dimension of the variable increased, the search space complexity of the algorithm increased exponentially, which is a great test for algorithm optimization. When the search space dimension increased to 30 D like Sphere function, only LCWPA, CWPA, and WPA could find the optimal solution stably. When the dimensions increased to 60 D (Rastrigin) and 200 D, PSO algorithm and GA could not find the optimal solution successfully, and the WPA search success rate was 56% and 30% respectively. The LCWPA and CWPA with cultural attributes could all be 100% successful, and the LCWPA was less time-consuming and accurate. From the above comparison, it can be concluded that the improved LCWPA greatly improved its ability to jump out of local optimum due to Levy flight variation. Moreover, the mutation was selective, which reduced the computational complexity of the algorithm and accelerated the search speed. Especially, when dealing with high-dimensional multi-peak complex function optimization problems, the advantage was more obvious.
4 LCWPA for Antenna Pattern Synthesis ExperimentThe problem of synthesizing antenna array directional diagram is to design the array according to the radiation characteristic of antenna directional diagram. In order to achieve the design goal, it is necessary to adjust some parameters of the array antenna, such as matrix number, matrix spacing, and matrix excitation amplitude phase coefficient. This problem is a complex nonlinear optimization problem[21]. Through the LCWPA for various test functions extremum optimization analysis, it can be concluded that the LCWPA proposed in this paper is suitable for solving complex nonlinear optimization problems, and therefore applicable to the pattern synthesis problem.
In order to analyze the performance of the antenna pattern synthesis of LCWPA under different conditions, simulation was first conducted under low side-lobe technical requirements, followed by the simulation under deep zero technical requirements[22]. Three intelligent optimization algorithms (i.e., QPSO[7], PSO[1], and GA[12]) were used for pattern synthesis, and they all performed well. The maximum number of iterations for the experiment set was 500, and the initial wolves and chromosomes were all 50. The remaining parameters of the three algorithms were set according to Table 2.
4.1 Simulation Example 1To compare the effectiveness of the improved algorithm, a classic example of low side-lobe pattern optimization was given in this study. A 20-element edge-fired array with a half-wavelength spacing was selected and the array element current amplitude was optimized. The main-lobe of the final pattern was required to satisfy 2θ0=20°, and the side-lobe level was lower than -40 dB.
According to Eq. (4), the fitness function was obtained and the four algorithms were used to optimize the solution. Fifty Monte Carlo experiments were performed for each algorithm and the best results were used for comparison. The simulation patterns and iterative curves are shown in Fig. 5 and Fig. 6. The optimized current source amplitudes are presented in Table 4. The best side-lobe levels optimized by the four algorithms were -40.0011, -39.9164, -37.4937, and -32.6330 dB, respectively, and the adaptive function values were 0.3246, 1.0825, 1.3234, and 2.500, respectively. It can be found that only the LCWPA basically met the design requirements. Since the design index was relatively high, all the algorithms in Fig. 6 could not be fully converged.

|
Fig.5 Synthesized array patterns for Example 1 (SLVL=-40 dB) |
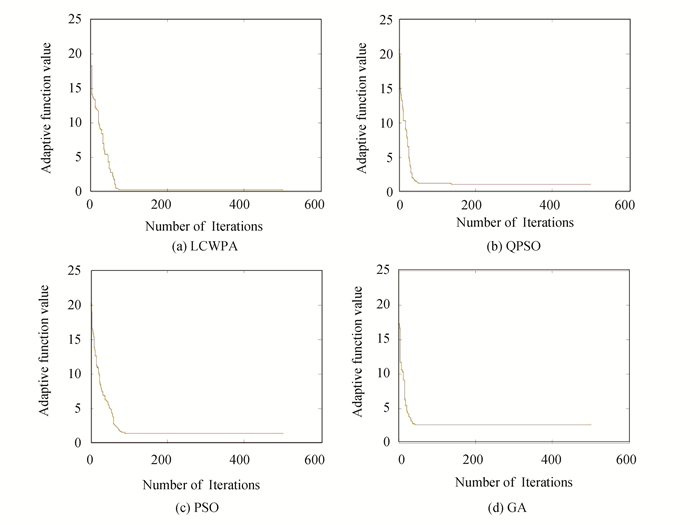
|
Fig.6 Convergence curves for Example 1 |
| Table 4 Computed element current for Example 1 |
GA had the worst global convergence, falling into early maturity in about 50 generations. PSO and QPSO were slightly better, but neither was better than LCWPA. It can be seen that LCWPA had both good optimization accuracy and good convergence speed when synthesizing low side-lobe directional diagram.
4.2 Simulation Example 2For a 20-element antenna array, the array element spacing is half-wavelength and the phase of its excitation current is 0 (edge-fired array). The pattern of the array was synthesized, which requires the width of the main-lobe to satisfy 2θ0=20° and the side-lobe level below-25 dB. It formed six nulls lower than -90 dB at the angles of 30, 40, 50, 60, 70, and 80.
According to Eq. (4), the fitness function was obtained and four algorithms were applied to optimize the solution. The simulation patterns and iterative curves are shown in Fig. 7 and Fig. 8. The optimum current source amplitudes are presented in Table 5. The minimum side-lobe levels optimized by the four algorithms were -25.3807, -25.1002, -25.0012, and -24.9981, respectively, which all met the design requirements. The LCWPA optimized pattern had the lowest side-lobe, being -25.3807, and all six nulls were lower than -90 dB. In Fig. 8, the fitness function values obtained by the four algorithms were finally optimized to be 0.0001, 0.0342, 0.0350, and 0.2136. It can be seen that the global convergence ability of the LCWPA was still the best.

|
Fig.7 Synthesized array patterns for Example 2 |
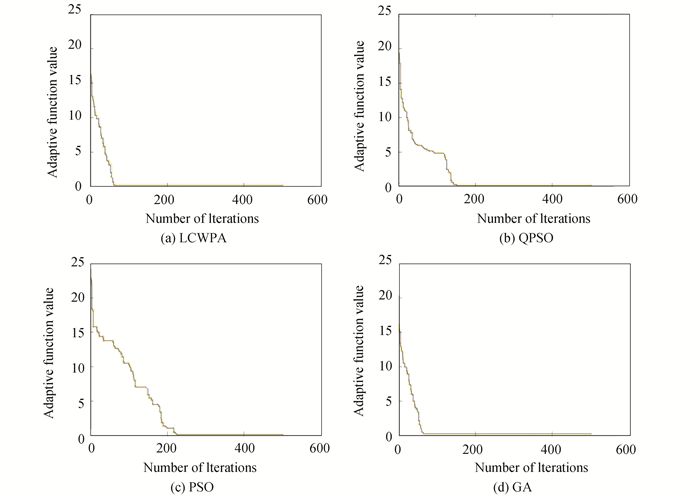
|
Fig.8 Convergence curves for Example 2 |
| Table 5 Computed element current for Example 2 |
It can be concluded that the LCWPA not only had good global convergence capability, but also had a fast speed when synthesizing the deep zero dip directional graph.
5 ConclusionsThis paper improves the CWPA proposed in Ref. [10], where a converged stagnation detection and selective Levy flight mutation mechanism is introduced and the LCWPA is proposed. The proposed algorithm selectively mutated the wolves according to the Levy flight strategy. Through the verification of the typical test function, it was found that the new algorithm not only improved the global optimization ability, but also accelerated the search speed. By applying the algorithm to array antenna pattern synthesis, the simulation results showed that the new algorithm achieved good results in the case of multi-zero and low side-lobe constraints. This paper provides a novel and efficient method for antenna pattern synthesis.
There are two aspects for the direction of future work. One is to continue to improve the LCWPA and tap its potential, and the other is to apply the algorithm to more kinds of antenna designs, such as ring arrays and plane arrays. In short, the proposed algorithm has a good ability to continue to be improved, and has a wide range of applications, suggesting a very good promotion value.
| [1] |
Jin Ronghong, Yuan Zhihao, Geng Junping, et al. The pattern synthesis of antennas based on a modified PSO algorithm. Chinese Journal of Radio Science, 2006, 21(6): 873-878. (in Chinese) (  2) 2) |
| [2] |
Elliott S R. Antenna Theory and Design. Piscataway: IEEE Press, 1981.
(  1) 1) |
| [3] |
Calvete H I, Galé C, Mateo P M. A new approach for solving linear bilevel problems using genetic algorithms. European Journal of Operational Research, 2008, 188(1): 14-28. DOI:10.1016/j.ejor.2007.03.034 (  1) 1) |
| [4] |
Holland J H. Adaption in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. Ann Arbor MI: The University of Michigan Press, 1975.
(  1) 1) |
| [5] |
Khodier M M, Christodoulou C G. Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization. IEEE Transactions on Antennas and Propagation, 2005, 53(8): 2674-2679. DOI:10.1109/TAP.2005.851762 (  1) 1) |
| [6] |
Chi Yue, Zhang Penglei, Chen Guoying, et al. Pattern synthesis based on immune clone selection algorithm. Communication Technology, 2009, 42(5): 71-74. (in Chinese) DOI:10.3969/j.issn.1002-0802.2009.05.025 (  1) 1) |
| [7] |
Wang Ting, Xia Kewen, Zhang Wenmei, et al. Pattern synthesis of array antenna with modified quantum particle swarm optimization algorithm. Acta Electronica Sinica, 2013, 41(6): 1177-1182. (in Chinese) DOI:10.3969/j.issn.0372-2112.2013.06.020 (  3) 3) |
| [8] |
Yang Chenguang, Tu Xuyan, Chen Jie. Algorithm of Marriage in Honey Bees Optimization based on the wolf pack search. Proceedings of The 2007 International Conference on Intelligent Pervasive Computing. Piscataway: IEEE, 2007. 462-467. DOI: 10.1109/IPC.2007.104.
(  3) 3) |
| [9] |
Wang Jianqun, Jia Yangyang, Xiao Qingyuan. Application of wolf pack search algorithm to optimal operation of hydropower station. Advances in Science and Technology of Water Resources, 2015, 35(3): 1-4. (in Chinese) (  1) 1) |
| [10] |
Qian Rongxin. A wolf pack algorithm based on cultural mechanism. Information Technology, 2015(12): 98-102. (in Chinese) DOI:10.13274/j.cnki.hdzj.2015.12.024 (  5) 5) |
| [11] |
Fu Qiang, Ge Hongwei, Su Shuzhi. Particle swarm optimization algorithm with firefly behavior and Levy flight. Journal of Computer Applications, 2016, 36(12): 3298-3302. (in Chinese) DOI:10.11772/j.issn.1001-9081.2016.12.3298 (  1) 1) |
| [12] |
Li S, Deng Y K, Sun H F, et al. An improved real-coded genetic algorithm for the beam forming of spaceborne SAR. IEEE Transactions on Antennas and Propagation, 2012, 60(6): 3034-3040. DOI:10.1109/TAP.2012.2194642 (  2) 2) |
| [13] |
Wang Ting, Xia Kewen, Lu Ning. Pattern synthesis for sparse arrays by compressed sensing and low-rank matrix recovery methods. International Journal of Antennas and Propagation, 2018. DOI:10.1155/2018/6403269 (  1) 1) |
| [14] |
Recioui A. Sidelobe level reduction in linear array pattern synthesis using particle swarm optimization. Journal of Optimization Theory and Applications, 2012, 153(2): 497-512. DOI:10.1007/s10957-011-9953-9 (  1) 1) |
| [15] |
Li Lei, Wang Jianming, Wu Guangxin, et al. Sparse array antenna optimization based on adaptive genetic algorithm. Modern Radar, 2017(3): 63-65, 69. (in Chinese) (  1) 1) |
| [16] |
Lee C Y, Yao Xin. Evolutionary programming using mutations based on the Levy probability distribution. IEEE Transactions on Evolutionary Computation, 2004, 8(1): 1-13. DOI:10.1109/TEVC.2003.816583 (  1) 1) |
| [17] |
Deng Kaiying, Deng Jingwei, Sun Tieli. Cuckoo search algorithm based on Tempered Lévy Flight random walk model. Application Research of Computers, 2016, 33(10): 2992-2996. DOI:10.3969/j.issn.1001-3695.2016.10.028 (  3) 3) |
| [18] |
Yan Bailu, Zhao Zheng, Zhou Yingcheng, et al. A particle swarm optimization algorithm with random learning mechanism and Levy flight for optimization of atomic clusters. Computer Physics Communications, 2017, 219: 79-86. DOI:10.1016/j.cpc.2017.05.009 (  7) 7) |
| [19] |
Mantegna R N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes. Physical Review E, 1994, 49(5): 4677-4683. DOI:10.1103/PhysRevE.49.4677 (  1) 1) |
| [20] |
Wu Husheng, Zhang Fengming, Wu Lushan. New swarm intelligence algorithm - wolf pack algorithm. Systems Engineering and Electronics, 2013, 35(11): 2430-2438. (in Chinese) (  1) 1) |
| [21] |
Khodier M M, Al-Aqeel M. Linear and circular array optimization: A study using particle swarm intelligence. Progress in Electromagnetics Research B, 2009, 15: 347-373. DOI:10.2528/PIERB09033101 (  1) 1) |
| [22] |
Mandal D, Ghoshal S P, Bhattacharjee A K. Wide null control of symmetric linear antenna array using novel particle swarm optimization. International Journal of RF and Microwave Computer-Aided Engineering, 2011, 21(4): 376-382. DOI:10.1002/mmce.20526 (  1) 1) |
 2020, Vol. 27
2020, Vol. 27



