1 Introduction

The magnetic disk consist of multi-layer structures, generally including the disk substrate, the soft magnetic layer, the intermediate layer, the magnetic medium layer, and the lubricants layer^[1]. The magnetic medium layer is used to store data, often coated with a very thin carbon layer called the Diamond-like Carbon (DLC) film. Although the DLC film is only a few nanometers thick, it is effective in reducing scatches. The DLC film, similar to the diamond film, is an amorphous carbon film, which can be prepared by multi-physical vapor deposition, chemical vapor deposition, and liquid phase method. The DLC layer is often covered with lubricant materials whose thickness is about 1 nm. Perfluoro-polyether (PFPE) is commonly used now, which can restore the original state in time when deformation occurs and repair the local loss in time to prevent local scratches caused by intermittent contact between magnetic head and disk^[2]. Tani et al.^[3] proposed a new method of depositing PFPE lubricants on DLC coating by photoelectron assisted chemical vapor deposition. Verified by experiments, the composite coating made in this way can greatly improve the storage density of the disk.

Some scholars have studied the transfer of lubricants from a macro perspective. It is found that when the flying height of the magnetic head is lower than the critical flying height, molecular transfer rate can be reduced by increasing the binding ratio of lubricant materials on the disk or increasing the lubricants film thickness^[4-5]. The head slider's specific morphology may lead to the accumulation of lubricant materials on the slider, which will affect the stability of the magnetic head flight^[6].The transfer of lubricant materials has also been researched from the perspective of molecular dynamics (MD), which is used to simulate the structure and motion characteristics of molecular systems at the atomic level, which is famous for the fast response time and high precision^[7-9]. Guo et al.^[10] simulated molecular dynamics by establishing two different molecular models of PFPE and studied the changes of lubricants transfer under different roughness of disk.Referring to secondary ion mass spectrometry, Tani et al.^[11] studied the changes of lubricants' structure and molecular weight after laser heating in the thermal assisted magnetic recording (HAMR) driver. It was found that lubricants with low molecular weight are easy to evaporate and decompose. According to the first principle, Zhang et al.^[12] calculated the molecular system's geometry, energy, and charge parameters by Materials Studio software. The diffusion coefficient of lubricant materials reflects the diffusion ability. A new model of ion self diffusion coefficient was proposed, which broadens the scope of application of ab initio approach^[13]. The basic concept of the new model is the diffusion network based on the predicted barrier energy from ab initio calculation. The related experiments showed that the new model is suitable for wider temperature range and more oxides. Based on system energetics, Bamdad et al.^[14] established a statistical mechanical model, which combines gas molecules with adsorption material molecules and simulation results were in good agreement with the experiments. The environment temperature and the molecular structure of lubricant materials both have influence on materials transfer.Wu and Bogy^[15] used near-field transducers to focus light energy on the nanopoles of the disk so that the magnetic medium reached Curie temperature instantaneously. It is proved experimentally that the heat transfer between the head and disk is strongly correlated with the distance between the head and disk.Considering hydrodynamic lubrication and temperature effect, Ghaffariet al.^[16] used various potential functions such as embedded atom method and multi-force field to simulate the molecular dynamics of lubricants. The results showed that temperature and molecular chain length both have influence on the interaction between lubricant molecules.Tani et al.^[17] studied the adsorption properties of PFPE lubricants with ionic end groups in HAMR driver.They found that PFPE lubricants with ionic end groups have strong chemical bond with DLC surface. Up to now, there is no study on different kinds of lubricant molecules' absorption on DLC layer with different carbon content and diffusion in air.In this paper, the transfer ability of different lubricant materials are studied based on molecular dynamics theory.

2 Materials and Methods

Research on the transfer of lubricant materials from molecular point of view is in accordance with the molecular dynamics theory, which is based on Newton's second law. If containing N atoms, the molecule system's total potential energy U_potential is the sum of all potential energy between all molecules U_vdw and all potential energy between N atoms U_int. The van der Waals interaction energy U_vdw is a function of the atomic position, which is equal to the local van der Waals energy sum between the atoms in the system.Eqs.(1)-(8) are all from Ref. [18]. The expression is

$ \begin{array}{l} {U_{{\rm{vdw}}}} = {u_{12}} + {u_{13}} + \cdot\cdot\cdot{u_{1N}} + {u_{23}} + {u_{24}} + \cdot\cdot\cdot = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {{\rm{ }}{u_{ij}}\left( {{r_{ij}}} \right)} } {\rm{ }} \end{array} $

(1)

The expression of the internal potential energy of a molecule U_int is

$ {U_{{\rm{int}}}} = {U_{{\rm{bond}}}} + {U_{{\rm{angle}}}} + {U_{{\rm{torsion}}}} + {U_{{\rm{elec}}}} $

(2)

where U_bond is the bond stretching energy (J); U_angle is the bond angle bending potential energy(J); U_torsion is the double-sided angular twist potential energy (J); and U_elec is the long-range electrostatic interaction energy (J).

U_bond represents the bond energy stored by molecules during the axial stretching of chemical bonds. It is expressed as follows:

$ {U_{{\rm{bond}}}} = {\rm{ }}\frac{1}{2}{\rm{ }}\sum {k_b}{\left( {{r_i} - r_i^0} \right)^2} $

(3)

where k_b is the bond length coefficient; r_i is the bond length of a molecule at any position($\mathop {\rm{A}}\limits^ \circ $); and r_i⁰ is the key length of equilibrium position($ \mathop {\rm{A}}\limits^ \circ $).

U_angle describes the potential energy stored when the bond angle between two kinds of chemical bonds bends in the process of molecular motion.Its expression is as follows:

$ {U_{{\rm{angle}}}} = {\rm{ }}\frac{1}{2}{\rm{ }}\sum {k_\theta }{\left( {{\theta _i} - \theta _i^0} \right)^2} $

(4)

where k_θ is the bond angle bending coefficient; θ_i is the molecular bond angle at any position(°); θ_i⁰ is the bond angle of the equilibrium position (°).

U_torsion represents the potential energy, which is related to the change of molecular structure caused by the rotation of molecular single chemical bond. The expression is

$ \begin{array}{l} {U_{{\rm{torsion}}}} = {\rm{ }}\frac{{1{\rm{ }}}}{2}{\rm{ }}\sum\limits_i {[{U_1}\left( {1 + {\rm{cos}}\varphi } \right) + {U_2}\left( {1 - {\rm{cos}}2\varphi } \right) + } \\ \;\;\;\;\;\;\;\;\;\;\;{U_3}\left( {1 + {\rm{cos}}3\varphi } \right){\rm{ ]}} \end{array} $

(5)

where U₁, U₂ and U₃ represent several twist coefficients of two-sided angles, respectively; φ is the bond angle of the equilibrium position (°).

U_elec is related to the amount of charge carried by the molecule and decreases with the increase of distance. The expression is

$ {U_{{\rm{elec}}}} = \sum\limits_{i, j{\rm{ }}} {\frac{{{q_i}{q_j}}}{{D{r_{ij}}}}} $

(6)

where D is a dielectric constant; q_i and q_j represent charge quantities of the i and j particles, respectively.

According to the classical mechanics formula, the force $\overrightarrow {{F_i}} $ acting on any atom i in a molecular system is the negative derivative of potential energy U_potential with the following expression:

$ \overrightarrow{F_{i}}=-\nabla_{i} U_{\text {potential }}=-\left(\vec{i} \frac{\partial}{\partial x_{i}}+\vec{j} \frac{\partial}{\partial y_{i}}+\vec{k} \frac{\partial}{\partial z_{i}}\right) U_{\text {potential }} $

(7)

According to Newton's second law, ${\overrightarrow {{a_i}}}$, the acceleration of the atom i, is generated by the following expression:

$ {\overrightarrow a _i} = {\rm{ }}\frac{{{{\overrightarrow F }_i}}}{{{m_i}}} $

(8)

where m_i is the weight of atom i.

Different algorithms have been developed for calculating the motion states and forces of atoms in the system: Verlet algorithm, leaping frog method, velocity Verlet algorithm, and Beeman numerical algorithm^[19-22]. The widely used algorithm is velocity Verlet algorithm, which can simultaneously solve the position, velocity, and acceleration of any atom in a certain time system. The calculation results generated from velocity Verlet algorithm are accurate and the calculation time is short with a few computer memories occupied. However, Beeman numerical algorithm is more common with higher accuracy. At the same time, it can increase the calculation time interval of δt so as to maintain energy conservation better. In this paper, Verlet algorithm is used and its expression is as follows:

$ \left\{\begin{array}{l} \overrightarrow{r_{i}}(t+\delta t)=\overrightarrow{r_{i}}(t)+\overrightarrow{v_{i}}(t) \delta t+\frac{1}{2} \overrightarrow{a_{i}}(t) \delta t^{2} \\ \overrightarrow{v_{i}}(t+\delta t)=\overrightarrow{v_{i}}(t)+\frac{1}{2}\left[\overrightarrow{a_{i}}(t)+\overrightarrow{a_{i}}(t+\delta t)\right] \delta t \end{array}\right. $

(9)

where $ {\overrightarrow {{v_i}}}$ is the velocity of the i atom; ${\overrightarrow {{a_i}}} $ is the acceleration of the i atom; and $ {\overrightarrow {{r_i}}}$ is the displacement of the i atom. The physical quantity labeled "0" indicates the initial values of the i atom's motion parameters. The calculation of molecular dynamics is iterative. Firstly, calculate the molecular system's total potential energy according to the position of atoms in the system at the time of t.Then, the force of each atom is able to be calculated according to Eq.(8).Next, calculate each atom's motion parameters according to Eq.(9).Based on the previous step, the new position of each atom after a very short time interval of δt can be predicted and the molecular system's total potential energy at the new position will be obtained. Finally, the predictive force is able to be calculated according to Eq.(8)and the motion parameters of each atom at the new position are calculated according to Eq.(9). The process is repeated until each atom's trajectory is obtained in the simulation time. The selection of integral step size is related to the computer memory and calculation accuracy. The small integral step size leads to many calculation steps in the same simulation time so that large computer memories are needed and the calculation accuracy will be very high.

3 Results and Discussion 3.1 Simulation Calculation and Result Analysis of Adsorption Energy 3.3.1 Establishment of adsorption model

Table 1 lists the chemical molecular formulas of four PFPE lubricants, Z-15, Z-Dol, D-SA, ZTMD, which m=5, n=6, $ \left[ Z \right] = {\rm{OC}}{{\rm{H}}_2} - {({\rm{C}}{{\rm{F}}_{\rm{2}}}{\rm{O}})_m} - {\rm{ }}{({\rm{C}}{{\rm{F}}_{\rm{2}}}{\rm{C}}{{\rm{F}}_{\rm{2}}}{\rm{O}})_n} - {\rm{C}}{{\rm{F}}_{\rm{2}}}{\rm{C}}{{\rm{H}}_{\rm{2}}}{\rm{O}}$.

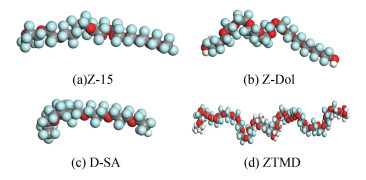
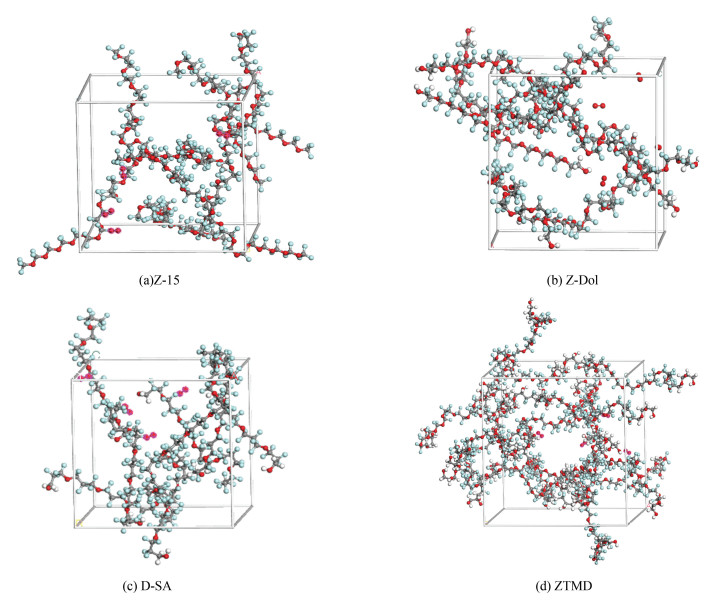
Fig. 1(a), Fig. 1(b), Fig. 1(c), and Fig. 1(d) represent three-dimensional molecular models of Z-15, Z-Dol, D-SA, and ZTMD, respectively. Green balls represent fluorine atoms; gray balls represent carbon atoms; red balls represent oxygen atoms; and white balls represent hydrogen atoms. Fig. 2 establishes the adsorption model of DLC and lubricant molecules, ZTMD represented.

3.1.2 Adsorption energy simulation of four lubricant molecules

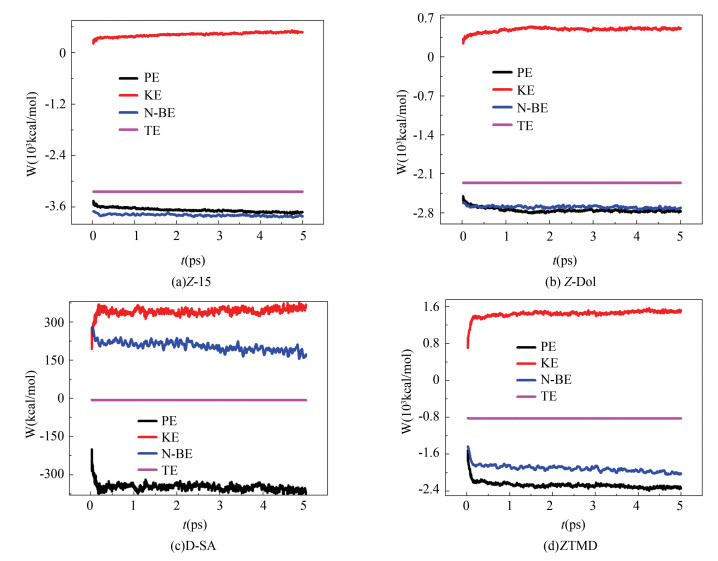
In this paper, four kinds of lubricant molecules' dynamic adsorption energy with DLC layers of different carbon content are simulated. The simulation time is 0.5 ps, simulation steps are 5000, and the initial temperature is 300 K. The volume and molecular number of the absorption system are kept unchanged. The DLC has similar structure to the diamond whose crystal cell consists of 18 carbon atoms so that an independent DLC crystal cell is constructed with a similar number of carbon atoms. DLC crystal cell models with 17 carbon atoms, 18 carbon atoms, and 20 carbon atoms are constructed, respectively. Fig. 3 is a dynamic energy adsorption diagram of the interaction between four lubricant molecules and the DLC crystal cell with 17 carbon atoms, where PE, KE, N-BE, and TE represent system's potential energy, kinetic energy, non-bonded energy, and total energy, respectively.

Comparing Fig. 3(a), Fig. 3(b), Fig. 3(c), and Fig. 3(d), it is found that the system composed of ZTMD molecules and DLC takes the longest time to reach equilibrium, almost 5 ps, while the other three systems reach dynamic equilibrium at about 0.26 ps. From Fig. 3(a) and Fig. 3(b), it is found that the energy curves of Z-15 and Z-Dol are similar. The results may be related to the molecular weight, which prolongs the dynamic equilibrium time. The energy of ZTMD molecule system changes the least, from 90.37 kcal/mol to 85.67 kcal/mol, which is a 5.201% reduction while the total energy of Z-15 subsystem changes the most, increasing 52.54 times from 8.02 kcal/mol to 429.40 kcal/mol, which results from the poorest symmetry of Z-15 molecule. With good symmetry, the molecular energy is in the lowest state so that the change of energy is little and it is easy for the system to achieve dynamic equilibrium. D-SA's dynamic energy curves have local peaks, as shown in Fig. 3(c). It may be due to its special end functional group -F.

Fig. 4 is a dynamic energy adsorption diagram of the interaction between four lubricants molecules and the DLC crystal cell with 18 carbon atoms, which is similar to Fig. 3. The total energy shown in Fig. 4 is higher than that in Fig. 3, to which the number of DLC carbon atoms may be attributed. When there are more carbon atoms, the intermolecular force will increase and it will take more energy to break internal force work. Compared with DLC crystal cell consisting of 18 carbon atoms, the energy changes of Z-15 and Z-Dol molecular systems are less while D-SA and ZTMD have opposite changes. When the carbon content increases, the structure of DLC layer is more harmonious and the DLC molecules are more nonpolar. ZTMD molecules, with many -OH end groups, have the strongest polarity. D-SA molecules are poorly symmetrical. Both of them are more different from the DLC molecules with more carbon atoms so that it takes longer for them to achieve dynamic equilibrium and their energy changes are greater.

From Fig. 5, it can be seen that the dynamic energy curve changes more greatly compared with Fig. 3 and Fig. 4. The overall dynamic energy is the minimum and has the minimum curve variation. When the DLC has more carbon atoms, its structure tends to be more stable. The system can be balanced with less structural change, resulting in the tiny energy change. Specifically, in the dynamic process, the energy of Z-15 has almost no change, so does Z-Dol. Both D-SA and ZTMD total energy curves are more smooth compared to previous figures.

After reaching dynamic equilibrium, the total energy E_total of the whole system can be calculated directly. Then calculate the DLC surface energy E_surface by deleting the lubricants molecules. Next, delete the DLC molecules and recover the lubricant molecules to calculate the molecular polymer energy E_polymer. Finally, calculate the interaction energy between the lubricants and the DLC E_Interaction using the formula ${E_{{\rm{Interaction}}}} = {E_{{\rm{total}}}} - ({E_{{\rm{surface}}}} + {E_{{\rm{polymer}}}})$. Table 2 shows that the interaction energy between lubricants and DLC with different carbon content. The negative value means that the interaction energy is adsorption energy.

3.2 Simulation Calculation and Result Analysis of Diffusion Energy 3.2.1 Establishment of diffusion model

Model the complex molecular distribution crystal cell by Materials Studio software. A disribution cystal cell is composed of lubricant molecules and air molecules, which is built as a cube with length of 50 $ \mathop {\rm{A}}\limits^ \circ $ and its density is set to 0.96 g/cm³. The initial model is uneven and there is a vacuum zone in it, so it is necessary to optimize the cell. Optimize the model to minimize the system's energy by Minimizer function in Materials Studio. Fig. 6(a), Fig. 6(b), Fig. 6(c), and Fig. 6(d) are the optimized molecular distribution crystal cell models of Z-15, Z-Dol, D-SA, and ZTMD, respectively.

3.2.2 Diffusion energy simulation of four lubricant molecules

The dynamic diffusion energy is produced in the process of lubricant molecules diffusing in the air. Compute diffusion energy by the Discover module of Materials Studio. The initial temperature is set to 300 K and the simulation time is set to 5 ps. The dynamic diffusion energy curves of four kinds of lubricant crystal cells are drawn as follows: Fig. 7(a), Fig. 7(b), Fig. 7(c), and Fig. 7(d) are the dynamic energy distribution profiles of Z-15, Z-Dol, D-SA, and ZTMD, respectively.

Both Z-15 and Z-Dol dynamic energy has insignificant changes while D-SA and ZTMD's energy changes are relatively obvious. As for the total molecular diffusion energy, the Z-15 cell's is the largest, 3239.89 kcal/mol, while the D-SA cell's is the smallest, 6.58 kcal/mol. It may be attributed to lubricant molecular structure, such as molecular structure symmetry and end functional groups.

When the system reaches dynamic equilibrium, define lubricant molecules as a group to analyze their motions so that the molecules' variation curves of the mean square displacement (D) with time (t) are obtained. Fig. 8(a), Fig. 8(b), Fig. 8(c), and Fig. 8(d) are mean shift graphs of Z-15, Z-Dol, D-SA, and ZTMD in logarithmic coordinates, respectively.

According to Fig. 8, the diffusion coefficients of Z-15, Z-Dol, D-SA, and ZTMD in air are 0.2287 cm²/s, 0.2395 cm²/s, 0.232 cm²/s, and 0.242 cm²/s, respectively. The ranking is DZTMD>D_Z-Dol>D_D-SA>D_Z-15. Although ZTMD has the largest molecular weight and the most complex structure, its diffusion coefficient is the largest, indicating that it is the easiest to diffuse. The -OH functional groups and the molecular structure symmetry may attribute to diffusion coefficient. Z-15 molecule's diffusion coefficient is the minimum due to its poor structural symmetry and the minimum -OH end functional groups.

4 Conclusions

The transfer ability of lubricant materials is assessed based on two criteria: the adsorption energy and the diffusion coefficient. Materials with large adsorption energy and low diffusion coefficient in air are uneasy to transfer. The molecular weight and structural characteristics of lubricant materials may have a direct impact on transfer ability. The molecular weight is closely related to the inter-molecular force, which means it takes much energy for molecules with large weight to break the chemical bonds. Besides, molecules with large weight often have numerous atoms, which increases the possibility of forming covalent bonds and is beneficial to the storage of chemical bond energy. In this paper, ZTMD with the largest weight, has the maximum adsorption energy. D-SA, opposite to ZTMD, has the minimum adsorption energy and its poor molecular symmetry may contribute to unsmooth dynamic adsorption curve. Z-15 and Z-Dol have similar molecular weight and molecular structure so that their adsorption energy and dynamic adsorption energy curves are similar. The DLC coating with low carbon content may be better for lubricant materials with weak adsorption capacity because the DLC coating with low carbon content is often active to form covalent bonds with foreign molecules, which attributes to enhance adsorption capacity. Besides, it can be found that the -OH functional group will reduce the interaction energy when compared with Z-15 and Z-Dol.Carbon atoms constituting DLC coatings are nonpolar while -OH functional groups are polar, which results in the structural difference among lubricant materials, DLC coatings, and the weak interaction energy. On the other hand, the -OH functional group increases the molecular diffusion activity in air, which means for lubricant materials with many -OH functional groups, such as ZTMD, it is better to fill the interface between the magnetic head and disk with the inert gas.