2. State Key Laboratory of Subtropical Building Science, School of Architecture, South China University of Technology, Guangzhou 510640, China
In the last century, experimental studies indicated that melatonin suppression of human is controlled by light and intensity dependent[1-3]. Melatonin is a hormone that is majorly secreted by pineal gland[2]. The abnormal variation of light-induced melatonin might accompany with adverse effects of human from physiology to psychology, including loss of core body temperature[3], circadian disorder, insomnia[4], and emotional negativity[5]. However, light additionally has positive effects on clinical therapy for specific diseases, such as sleep problems, circadian disruptions, and seasonal affective disorder (SAD)[4].
The discovery of intrinsically photosensitive retinal ganglion cell (ipRGCs) makes it possible to establish a distinct pathway to investigate how light impacts melatonin secretion[6]. This pathway consists of ipRGCs and a distinct intracerebral neural pathway[7]. Light stimulus signal is transmitted along this pathway to pineal gland. Then, the pineal gland designated as a major melatonin producer starts to mediate the melatonin secretion[4, 7]. The effects of light on human via this access are called circadian effects, which is also known as non-visual effects[4]. Subsequently, a study reported that Californian teachers who live in areas with high levels of ambient light at night may be at an increasing risk of getting breast cancer[8]. Another research had a similar conclusion for female nurses[9]. It is suggested that high levels of outdoor light at night may result in invasive breast cancer risk. Thus, outdoor lighting might have great potential for human health, and the mesopic evaluation model of circadian effects is worth studying.
In the past two decades, pioneers have turned to explore the evaluation, quantification, and implementation of circadian effects in lighting design[10-15]. After Brainard et al.[16] and Thapan et al.[17] had independently measured the circadian spectral sensitivity based on melatonin suppression, Gall et al.[10] and Rea et al.[12] respectively proposed a circadian sensitivity function C(λ), as is shown in Fig. 1, in which V(λ), V′(λ), and C(λ) represent photopic, scotopic, and non-visual spectral sensitivity curves, respectively. Then, Gall and Bieske[10] put forward circadian action factor (acv)model to evaluate circadian effects of light source without considering the non-linear influence of light intensity on melatonin suppression[16-18]. The acv model is analogous to scotopic/photopic ratio (RSP) which is a key parameter of mesopic lighting[19]. This model has been suitably utilized to optimize the spectral power distribution (SPD) of photobio-friendly light source[14-15]. Similarly, mesopic circadian action factor ac, mes model was used to photobiologically rationalize the SPD of outdoor light source[11]. Rea et al.[12] came up with the circadian light (CLA) model, which is usually used with a prediction model of melatonin suppression, i.e., circadian stimulus (CS) model[20]. To enhance the practicality, a simplified CLA model incorporating acv model and corneal illuminance was raised by Bellia and Seraceni[13]. Recently, many efforts have been made in the comprehensive review of light sources by analyzing non-visual, photopic, scotopic, and mesopic evaluation parameters[21-23]. The constraints between the above models and the visual parameters are ambiguous, which may be considered an obstacle to lighting design.

|
Fig.1 Spectral sensitivity curves |
This paper shows that the relationships among evaluation parameters of non-visual, photopic, scotopic, and mesopic efficacy are numerically constrained by SPD, and those constraint relationships were explored by the method of synthesizing spectral sensitivity curve. First, International Commission on Illumination (CIE) 1931 XYZ 2 deg color matching functions[24] and standard scotopic sensitivity function[24] were employed to obtain new circadian sensitivity function C′(λ) by fitting Brainard's and Thapan's spectral sensitivity data[12] with maximum coefficient of determination (R2). Note that the synthesis method is based on mathematics and independent of physiological basis. Then, C′(λ) was applied to transform the original acv model to a new one. Finally, an integrated model was obtained by revising the Bellia CLA model with the new acv model. This integrated model, which can be used to evaluate the circadian effects of mesopic light sources, showed the constraint relationships among 1931 xy chromaticity coordinate, scotopic/photopic ratio, and illuminance. To investigate the universal characteristics of the model, four-component color-mixing method[15, 25] will be wielded to optimize SPD.
2 Circadian Sensitivity FunctionA reasonable lighting can bring efficient work and health benefit[4, 26]. Traditional lighting design generally concerns photopic and mesopic efficacy, since scotopic efficacy may not be necessary and non-visual efficacy is previously unknown. With the discovery of circadian effects, a comprehensive evaluation of conventional vision efficacy and non-visual efficacy for light sources has become a consensus. Fig. 1 presents two visual spectral sensitivity curves and two non-visual spectral sensitivity curves. The mesopic sensitivity function Vmes(λ)(not given) is determined by V(λ) and V ′(λ) with various adaptation coefficients[11, 19]. Because of the difference of spectral sensitivity, various evaluation models have been adopted to estimate visual and non-visual efficacy, which troubles the practitioners. For example, RSP factor defined in Eq.(1)[19] is applicable in mesopic lighting for its indicational function on the brightness performance of light source, and the acv factor defined in Eq.(2)[13] signifies the circadian effects of light source. They are defined with different spectral sensitivity curves and individually describe the efficacy of two vision systems[22], which might increase the complexity of spectral optimization. Therefore, the distinct relationship between them is worth studying. To find out this relationship, the method of synthesizing spectral sensitivity curves rather than traditional ratio methods was adopted.
| $ {R_{{\rm{SP}}}} = \frac{{1700\smallint E\left( \lambda \right)V{'}\left( \lambda \right){\rm{d}}\lambda }}{{683\smallint E\left( \lambda \right)V\left( \lambda \right){\rm{d}}\lambda }} $ | (1) |
| $ {a_{{\rm{cv}}}} = \frac{{\smallint E\left( \lambda \right)C\left( \lambda \right){\rm{d}}\lambda }}{{\smallint E\left( \lambda \right)V\left( \lambda \right){\rm{d}}\lambda }} $ | (2) |
where E(λ) is spectral irradiance distribution, V(λ) and V′(λ) represent photopic and scotopic sensitivity functions respectively, and C(λ)is a circadian sensitivity function proposed by Gall et al.[10]
Photopic, scotopic, and mesopic evaluation models are inseparable with V(λ) and V′(λ). It was speculated that C(λ) might have a mathematical relationship with them. According to Fig. 1, the deficiency of short-wavelength makes it impossible for any effort to synthesize C(λ) by only using these two spectral sensitivity curves. In 2002, Rea et al.[27] employed S(λ), spectral sensitivity of S-cone cells, and V′(λ) to obtain a composite action spectrum, and results implied that S(λ) can play a role in compensating the deficiency of short-wavelength. However, S(λ) is incompatible with traditional lighting technology. It is known that CIE 1931 XYZ color matching functions, including x(λ), y(λ), and z(λ)[24] are widely used in lighting application, such as measuring color and calculating correlated color temperature (CCT)[28]. According to Fig. 2, the two curves are similar, which implies that they have mutual substitutability within a certain margin of error. The discrepancies between normalized S(λ) and normalized z(λ) are negligible, so S(λ) was replaced with z(λ). To improve the goodness of fit, x(λ) and y(λ) were used. Then, C'(λ) can be defined as a vector format as follows:
| $ M \cdot C{'} \left( \lambda \right) = \mathit{\boldsymbol{A}} \cdot {\mathit{\boldsymbol{S}}^{\rm{T}}} $ | (3) |

|
Fig.2 Normalized spectral sensitivity of S(λ) and z(λ) |
where M is a coefficient that normalizes the peak of C'(λ) to one. A is coefficient vector and S represents spectral sensitivity curves vector.
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\mathit{\boldsymbol{A}} = \left[ {{a_z}{a_y}{a_x}{a_s}} \right]\\ \mathit{\boldsymbol{S}} = \left[ {\bar z\left( \lambda \right)\bar y\left( \lambda \right)\bar x\left( \lambda \right)V{'} \left( \lambda \right)} \right] \end{array} $ |
Values of az, ay, ax, and as represent the proportion of z(λ), y(λ), x(λ), and V′(λ), respectively. Besides, y(λ) is equal to V(λ) and Y stimulus values are proportional to illuminance[24, 28].
Exhaustive method was employed to list possible cases of A with an accuracy of 0.01. The optimal C'(λ) was obtained with the maximum coefficient of determination that is calculated by approved data[12] and corresponding values of C′(λ). When A = [1.48 -0.45 0.29 1.92] and M=3.6377, the best fit was obtained when R2=0.86. Then, C'(λ) can be rewritten as
| $ \begin{array}{l} C{'} \left( \lambda \right) = 0.4069\bar z\left( \lambda \right) - 0.1237\bar y\left( \lambda \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;0.0797\bar x\left( \lambda \right) + 0.5278V{'} \left( \lambda \right) \end{array} $ | (4) |
Four optional circadian sensitivity functions and the data of previous studies are compared in Fig. 3(a), which shows that C'(λ) was well matched with the data of previous studies. The C'(λ) peaked at 457 nm and remedied the insufficient of z(λ) over 460 nm. The discontinuities in the Rea model seemed to be averaged in this work. More details can be observed from the perspective of residual error (Fig. 3(b)) that all four circadian sensitivity functions showed negligible difference of residual error below 460 nm. The residual errors are equal to absolute values that are gained by data of previous studies minus circadian sensitivity function values of corresponding wavelength. The main distinction of residual error for the four curves concentrated on the value above 460 nm. As can be seen, the residual error of z(λ) function, which was used to simplify acv model[10], was bigger than the other three. Gall model had larger deviation than Rea model which possessed the lowest undulation of residual error. The main residual error of synthesized model above 460 nm are mainly concentrated at about 505 nm. It can thus be prudently summarized that the performance of C'(λ) might fall between Rea and Gall models.

|
Fig.3 Circadian sensitivity functions and its residual error |
3 Integrated Model
Existing experiments have proved that SPD as well as intensity and exposure duration of light can affect circadian rhythm[2, 4, 18, 29]. In this paper, exposure duration is out of consideration and the remaining two factors will be considered. Gall acv model provides a criterion for project spectrum of light source. Rea CLA model can work as a guideline of the usage of light intensity[20]. Bellia CLA model combines the advantages of the other two models[13]. Considering the conciseness and practicability of evaluation model, the Bellia CLA model was adopted, which is defined as[13]
| $ C{L_{\rm{A}}} = (2.3748{a_{{\rm{cv}}}} - 0.67){E_{v\;{\rm{cor}}}}, \rm{if} \mathit{\Delta } \ge 0 $ | (5) |
| $ C{L_{\rm{A}}} = (2.3748{a_{{\rm{cv}}}} + 0.11){E_{v\;{\rm{cor}}}}, \rm{if} \mathit{\Delta } < 0 $ | (6) |
where
CLA:Circadian light, which was stipulated that 2856 K blackbody radiation at 1000 lux has a CLA value of 1000;
Ev cor: Corneal illuminance, and
| $ {E_{v\;{\rm{cor}}}} = 683\smallint E\left( \lambda \right)S\left( \lambda \right){\rm{d}}\lambda \left( {{\rm{lux}}} \right) $ |
E(λ) : Spectral irradiance distribution;
acv: Circadian action factor;
Δ: Discriminant factor, which was defined as
| $ \mathit{\Delta } = \smallint E\left( \lambda \right)S\left( \lambda \right){\rm{d}}\lambda - 0.33\smallint E\left( \lambda \right)V\left( \lambda \right){\rm{d}}\lambda $ |
Based on Eqs.(1), (2), and (4), the new acv model can be obtained as follows:
| $ {a_{{\rm{cv}}}} = \frac{{0.4096Z - 0.1237Y + 0.0797X + 0.2121{R_{{\rm{SP}}}}Y}}{Y} $ | (7) |
where X, Y, and Z are CIE 1931 tristimulus values, and the relationship between them is[24]
| $ X = \left( {x/y} \right)Y;Y = Y;Z = \left[ {\left( {1 - x - y} \right)/y} \right]Y $ | (8) |
Then, the new acv model is rewritten as
| $ \begin{array}{l} {a_{{\rm{cv}}}} = \left( {0.4096 - 0.5306y - 0.3272x} \right)/y + \\ \;\;\;\;\;\;\;\;0.2121{R_{{\rm{SP}}}} = {a_{{\rm{CAF}}}} + {a_{{\rm{SP}}}} \end{array} $ | (9) |
where x and y respectively represent the x-coordinate and y-coordinate values of the CIE 1931 chromaticity coordinate. Left part including x-coordinate and y-coordinate is rewritten as aCAF, and the other part is rewritten as aSP. Obviously, the new acv model is demonstrably expressed by x-coordinate, y-coordinate, and RSP values, which will be discussed later.
Rea CLA model proposed in 2012 gives a constant, 1622, to set the normalization of CLA so that 2856 K blackbody radiation at 1000 lux has a CLA value of 1000[12]. It must be noted that if the new acv model is directly combined with Bellia CLA model, then the scale condition cannot be satisfied. Therefore, the constants of Bellia CLA model should be slightly modified. Advance explanation is that 2856 K blackbody radiation at 1000 lux has acv = 0.4080 and Δ < 0. Referring to the format of Bellia CLA model, an equation can be obtained as
| $ 0.4080\alpha + {\beta _1} = 1 $ | (10) |
where α and β1 are optimization coefficients when Δ < 0.
Since one equation cannot solve two unknowns, optimization method was adopted to solve this equation. α has a value of 2.4510 when ignoring β1. Then, α around 2.4510 and β1 around zero were sought by minimizing the mean square errors that were obtained with the data of Rea CLA model and the integrated model from 1000 K to 3400 K CCT. The optimal values of α and β1 were 2.5456 and -0.0386, respectively. After acquiring the α value, CLA equation with Δ≥0 condition can be written as
| $ C{L_{\rm{A}}} = \left( {2.5456{a_{{\rm{cv}}}} + {\beta _2}} \right){E_{v\;{\rm{cor}}}} $ | (11) |
where β2 is optimization coefficient when Δ≥0.
The same optimization way was employed to hunt β2, and the optimal β2 value was -0.7224.
Furthermore, by replacing S(λ) with (λ), discriminant factor is rewritten as
| $ {\mathit{\Delta }_z} = 0.5596Z - 0.2916Y $ | (12) |
Based on Eqs. (8) and (12), the equation of discriminant factor can be further simplified. Obviously, the values of y and Y must be greater than zero. The discriminant factor is finally defined as
| $ {\mathit{\Delta }_z} = 1 - x - 1.5211y $ | (13) |
Then, the integrated model can be written as
| $ \begin{array}{l} C{L_{\rm{A}}} = \left[ {2.5456\left( {{a_{{\rm{CAF}}}} + {a_{{\rm{SP}}}}} \right) - 0.7224} \right]{E_{v\;{\rm{cor}}}}, \\ \;\;\;\;\;\;\;\;\;{\rm{if}}\;{\mathit{\Delta }_z} \ge 0 \end{array} $ | (14) |
| $ \begin{array}{l} C{L_{\rm{A}}} = \left[ {2.5456\left( {{a_{{\rm{CAF}}}} + {a_{{\rm{SP}}}}} \right) - 0.0386} \right]{E_{v\;{\rm{cor}}}}, \\ \;\;\;\;\;\;\;\;\;{\rm{if}}\;{\mathit{\Delta }_z} < 0 \end{array} $ | (15) |
The comparison between Rea CLA model and the integrated model for a blackbody radiator at different CCTs are shown in Fig. 4. Supplemental instruction is that all corneal illuminances were scaled to 300 lux. The two curves almost coincided, which implied the effectiveness of the integrated model.

|
Fig.4 Rea CLA model[12] and integrated CLA model for a blackbody radiator at different CCTs |
Once CLA is gained, circadian stimulus (melatonin suppression expressed in percentage terms) can be predicted by the following equation[13]:
| $ CS = 0.75 - \frac{{0.75}}{{1 + {{(C{L_{\rm{A}}}/215.75)}^{0.864}}}} $ | (16) |
The function of illuminance of the integrated model on circadian effects showed no special difference from Bellia CLA model[13]. Thus, this section focuses on the new acv model and the new discriminant factor Δz, which primarily reveals the nature of the integrated model. Before formal discussion, a four-component color-mixing method was established. There are many ways of dimming. Lee et al.[28] implemented a precise dimming and color control light-emitting diodes (LED) system based on bicolor LEDs, which consists of warm-white and cool-white LED. Unfortunately, bicolor LEDs are not competent for wide tuning range of chromaticity coordinate. RGB-tricolor LEDs make up for this shortcoming with possibly unsatisfactory color rendering index (CRI)[15], which can be improved by tuning full-width at half maximum (FWHM) of RGB-spectra[14]. However, it might be hard to practice. To a certain extent, red-green-blue-white (RGBW) LEDs can solve these problems[15]. Thus, the SPD (Fig. 5) of RGBW LEDs was employed. By mixing them with different proportions, a new SPD can be obtained. All optimization process was simulated in computer to ensure accuracy.

|
Fig.5 SPDs of RGBW LEDs |
According to Eq.(13), discriminant factor relies on chromaticity coordinate. The short dot line in Fig. 6(a) represents the condition of Δz =0, which separates the chromaticity diagram into two parts. All Δz above this line is smaller than zero and Eq.(15) is enabled in those areas. Otherwise, Δz is greater than or equal to zero and Eq.(14) is enabled. New discriminant factor can be obtained by XYZ sensor or RGB sensor[28] without measuring SPD. Moreover, according to the chromaticity coordinates, lighting engineers already know which CLA formula to use before they design the illumination spectrum.

|
Fig.6 Exploration of aCAF factor |
The new acv model can be divided into two factors. The aCAF factor is construed as color action factor, which is only dependent on chromaticity coordinates. The contour lines of aCAF factor are plotted in Fig. 6(a). It can be found that different combinations of x-coordinate and y-coordinate might contribute to a same aCAF value. A novel comprehension is that different colors of light might have same contribution to aCAF factor. The aCAF values around blue light were higher than those around red light, which is consistent with the traditional cognition that blue light causes serious circadian effects[30]. The short dash line, representing isothermal line of CCT = 5000 K, intersected with the contour lines of aCAF factor. Thus, identical CCT has multiple aCAF values, which is a reason why CCT is not suitable to evaluate circadian effects. The aSP factor accounts for RSP action factor. According to Eq.(9), acv factor is linear with RSP factor while fixing aCAF to a constant. Similarly, the linear nature between acv factor and aCAF factor can be obtained with a fixed RSP. However, the possible relationship between RSP and aCAF is still ambiguous.
Further exploration was carried out to understand the new acv model. Based on the theory of control variate method, let aCAF be a constant. There are two conditions: the first is to restrict aCAF at the contour line, and the second is to fix aCAF at a point. The first case is discussed primarily. Spectral optimization condition is aCAF = 0.3000±0.0001. All eligible SPDs were obtained by four-component color-mixing method and exhaustive method that list entire combinations of spectrum. Fig. 6(b) shows five selected SPDs, whose CCTs gradually decreased from upper left to bottom right along the contour line of aCAF= 0.3000 (Fig. 6(a)). A clear graphic explanation is displayed in Fig. 7. It is concluded that CCT exactly declined with the increase of x-coordinate. The RSP values also had a general downward trend, which signifies the decline of acv.According to Eqs. (14)-(16), a reasonable speculation is that circadian effects also have a weakening trend.
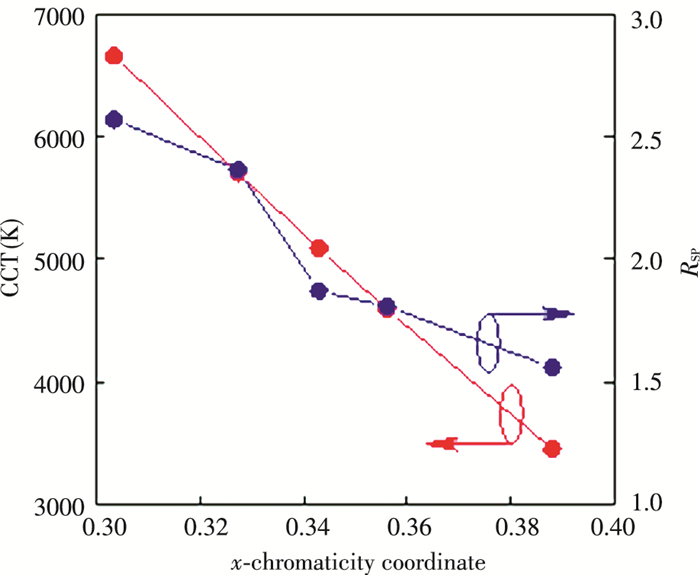
|
Fig.7 Relationship between CCT and RSP as a function of x-coordinate |
In Fig. 6(a), the solid straight lines represent the contour lines of aCAF factor, which increase from top to bottom. The short dot line represents the condition of Δz= 0. The short dash line is the isothermal line of CCT=5000 K. SPDs were obtained by four-component color-mixing method when aCAF= 0.3000±0.0001. The five diamond points in Fig. 6(a) from upper left to bottom right respectively indicate the chromaticity coordinates of the spectra from bottom to top in Fig. 6(b).
The second case was conducted by controlling (x, y) coordinate point in (0.3500±0.000 1, 0.3520 ±0.0001). In this simulation, the offset of aCAF (0.3000±0.0002) was too small to significantly impose on acv, which illuminates from an aspect that RSP is a major factor on evaluating circadian effects. Six optimal spectra with different RSP are given in Fig. 8(a), in which RSP was visibly different, despite (x, y) coordinate was almost unchanged. By comparing the tuning range of RSP with the first condition, the second condition had a fine-tuning range. The luminous efficacy of radiation (LER) and CRI are key parameters of a light source[30]. In Fig. 8(b), LER and CRI are described as a function of RSP. CRI and RSP were positively correlated within a certain range, while LER and RSP had an opposite relationship. According to Eq.(9), RSP factor plays a decisive role on acv value with a fixed aCAF value. Thus, if LER loses a bit, mesopic luminance, circadian effects, and CRI can be improved simultaneously by enlarging RSP factor.

|
Fig.8 Exploration of RSP factor at the same (x, y) |
The second condition can be verified by the experiment of Souman et al.[29] In their research, two independent light sources were developed with different melanopic efficacy factors (MEFs). The spectral properties of these two light sources are presented in Table 1. The light sources of low MEF and high MEF had almost the same values of illuminance, x-coordinate, y-coordinate, and aCAF. The main differences are the values of RSP factor. According to Eqs.(9), (15), and (16), large value of RSPleads to large values of acv and CLA, which implies higher level of melatonin suppression. Results of the experiment showed that the melatonin suppression of high MEF is higher than low MEF, which is a supporting evidence for our prediction.
| Table 1 Spectral properties for the conditions in Ref. [29] |
5 Discussion
According to Fig. 6(a) and Fig. 8(a), CCT can roughly describe the circadian effects, because same CCT maps multiple values of aCAF and RSP. When human is exposed to light environment with different absolute SPDs, melatonin suppression can be distinctly different without changing illuminance level or CCT[29]. This evidence manifests that absolute SPD of light source is the most effective tool to precisely evaluate circadian effects. Hence, an evaluation model of circadian effects that reflects the characteristic of absolute SPD is required. The integrated model proposed in this paper is a suitable model. The absolute SPD is the product of relative SPD and amplitude. To a certain extent, the corneal illuminance can be regarded as the effect of amplitude. The bracket parts in Eqs.(14)-(15) can be regarded as the effect of relative SPD.
Original intention of acv is to synthetically evaluate visual and non-visual effects by ratio. More parameters, however, are used in lighting design, whose essential relationships are worth investigating. Spectral sensitivity curves in Fig. 1 illustrate that visual and non-visual systems responded differently to spectral peaks. According to Eq.(2), it can be concluded that visual efficacy and non-visual efficacy have spectral dependence, which means that their evaluation models inevitably depend on spectrum. This objective reality induces us to find out the relationship of evaluation models through spectral sensitivity curves, and the new acv model proved its effectiveness.
Compared with Bellia CLA model[13], the integrated model showed an unequivocal link with CIE 1931 XYZ chromaticity coordinate, RSP factor, and illuminance, which suggests the compatibility between the integrated model and traditional lighting evaluation methods. It has been known that orthodox illuminance based upon V(λ) has been implemented for a long time, and conventional parameter RSP is employed in the estimation of mesopic lighting. The CIE 1931 XYZ chromaticity diagram is still useful for colorimetry. Thus, the integrated model has a practical significance in photobio-friendly mesopic lighting design, and the second condition in Section 4 is a good example.
6 ConclusionsIn this work, a well-founded theory was proposed to express circadian sensitivity function by other spectral sensitivity curves, which is practical in light engineering. The synthesis method is based on mathematics, rather than on physiological basis.
According to C′(λ), a new acv model was derived from the original model. The new acv model, consisting of CIE 1931 xy coordinates and scotopic/photopic ratio, clearly showed the intrinsic link among evaluation parameters of the light source from a novel perspective. It is helpful to analyze and design lighting spectrum, especially mesopic vision spectrum.
The integrated model was revised from Bellia CLA model with the new acv model. Then, a bridge among non-visual, photopic, scotopic, and mesopic evaluation parameters was established. The simplified discriminant factor Δz that only depends on CIE 1931 xy coordinates enhanced the flexibility of the integrated model.
Spectra analysis implied that the integrated model is not only a practical method of evaluating mesopic circadian effects, but also a helpful method to design spectrum considering non-visual, photopic, and mesopic efficacy.
Although more experimental research is needed to examine the accuracy of the integrated model in predicting melatonin suppression, it is believed that the integrated model will play a significant role in future healthy mesopic lighting design.
| [1] |
Lewy A J, Wehr T A, Goodwin F K, et al. Light suppresses melatonin secretion in humans. Science, 1980, 210(4475): 1267-1269. DOI:10.1126/science.7434030 (  0) 0) |
| [2] |
Mclntyre I M, Norman T R, Burrows G D, et al. Human melatonin suppression by light is intensity dependent. Journal of Pineal Research, 1989, 6(2): 149-156. DOI:10.1111/j.1600-079X.1989.tb00412.x (  0) 0) |
| [3] |
Shanahan T L, Czeisler C A. Light exposure induces equivalent phase shifts of the endogenous circadian rhythms of circulating plasma melatonin and core body temperature in men. The Journal of Clinical Endocrinology and Metabolism, 1991, 73(2): 227-235. DOI:10.1210/jcem-73-2-227 (  0) 0) |
| [4] |
van Bommel W J M. Non-visual biological effect of lighting and the practical meaning for lighting for work. Applied Ergonomics, 2006, 37(4): 461-466. DOI:10.1016/j.apergo.2006.04.009 (  0) 0) |
| [5] |
Ikeno T, Yan L. Chronic light exposure in the middle of the night disturbs the circadian system and emotional regulation. Journal of Biological Rhythms, 2016, 31(4): 352-364. DOI:10.1177/0748730416642065 (  0) 0) |
| [6] |
Berson D M, Dunn F A, Takao M. Phototransduction by retinal ganglion cells that set the circadian clock. Science, 2002, 295(5557): 1070-1073. DOI:10.1126/science.1067262 (  0) 0) |
| [7] |
Ostrin L A. Ocular and systemic melatonin and the influence of light exposure. Clinical and Experimental Optometry, 2019, 102(2): 99-108. DOI:10.1111/cxo.12824 (  0) 0) |
| [8] |
Hurley S, Goldberg D, Nelson D, et al. Light at night and breast cancer risk among California teachers. Epidemiology, 2014, 25(5): 697-706. DOI:10.1097/EDE.0000000000000137 (  0) 0) |
| [9] |
James P, Bertrand K A, Hart J E, et al. Outdoor light at night and breast cancer incidence in the Nurses' Health Study Ⅱ. Environmental Health Perspectives, 2017, 125(8): 087010. DOI:10.1289/EHP935 (  0) 0) |
| [10] |
Gall D, Bieske K. Definition and measurement of circadian radiometric quantities. Proceedings of 2004 CIE Symposium on Light and Health: Non-visual Effects. Vienna: Commission Internationale de L'éclairage, 2004, 129-132. (  0) 0) |
| [11] |
Žukauskas A, Vaicekauskas R, Vitta P. Optimization of solid-state lamps for photobiologically friendly mesopic lighting. Applied Optics, 2012, 51(35): 8423-8432. DOI:10.1364/AO.51.008423 (  0) 0) |
| [12] |
Rea M S, Figueiro M G, Bierman A, et al. Modeling the spectral sensitivity of the human circadian system. Lighting Research and Technology, 2012, 44(4): 386-396. DOI:10.1177/1477153511430474 (  0) 0) |
| [13] |
Bellia L, Seraceni M. A proposal for a simplified model to evaluate the circadian effects of light sources. Lighting Research and Technology, 2014, 46(5): 493-505. DOI:10.1177/1477153513490715 (  0) 0) |
| [14] |
Dai Q, Shan Q, Lam H, et al. Circadian-effect engineering of solid-state lighting spectra for beneficial and tunable lighting. Optics Express, 2016, 24(18): 20049-20059. DOI:10.1364/OE.24.020049 (  0) 0) |
| [15] |
Wu T, Lin Y, Zhu H, et al. Multi-function indoor light sources based on light-emitting diodes-A solution for healthy lighting. Optics Express, 2016, 24(21): 24401-24412. DOI:10.1364/OE.24.024401 (  0) 0) |
| [16] |
Brainard G C, Hanifin J P, Greeson J M, et al. Action spectrum for melatonin regulation in humans: evidence for a novel circadian photoreceptor. Journal of Neuroscience, 2001, 21(16): 6405-6412. DOI:10.1523/JNEUROSCI.21-16-06405.2001 (  0) 0) |
| [17] |
Thapan K, Arendt J, Skene D J. An action spectrum for melatonin suppression: evidence for a novel non-rod, non-cone photoreceptor system in humans. Journal of Physiology, 2001, 535(1): 261-267. DOI:10.1111/j.1469-7793.2001.t01-1-00261.x (  0) 0) |
| [18] |
Zeitzer J M, Dijk D J, Kronauer R E, et al. Sensitivity of the human circadian pacemaker to nocturnal light: melatonin phase resetting and suppression. Journal of Physiology, 2000, 526(3): 695-702. DOI:10.1111/j.1469-7793.2000.00695.x (  0) 0) |
| [19] |
Wu T, Lu Y, Guo Z, et al. Improvements of mesopic luminance for light-emitting-diode-based outdoor light sources via tuning scotopic/photopic ratios. Optics Express, 2017, 25(5): 4887-4897. DOI:10.1364/OE.25.004887 (  0) 0) |
| [20] |
Rea M S, Figueiro M G. Light as a circadian stimulus for architectural lighting. Lighting Research and Technology, 2018, 50(4): 497-510. DOI:10.1177/1477153516682368 (  0) 0) |
| [21] |
Yao Q. Application-dependent spectrum optimization of four-package LEDs. Lighting Researchand Technology, 2016, 48(7): 844-856. DOI:10.1177/1477153515588939 (  0) 0) |
| [22] |
Qi Y, Lei Y, Yu B. Establishment of vision effect diagram for optimization of smart LED lighting. IEEE Photonics Journal, 2017, 8(4): 1-8. DOI:10.1109/JPHOT.2016.2593262 (  0) 0) |
| [23] |
Yao Q, Zhang W, Zhang L, et al. Establishing functional model of photometric performance of trichromatic light sources in chromaticity diagrams. IEEE Photonics Journal, 2018, 10(4): 1-12. DOI:10.1109/JPHOT.2018.2842151 (  0) 0) |
| [24] |
Hunt R G W, Pointer M R. Measuring Color (4th Edition). London: Wiley, 2011.
(  0) 0) |
| [25] |
Dai Q, Cai W, Hao L, et al. Spectral optimisation and a novel lighting-design space based on circadian stimulus. Lighting Research and Technology, 2018, 50(8): 1198-1211. DOI:10.1177/1477153517733504 (  0) 0) |
| [26] |
Kraneburg A, Franke S, Methling R, et al. Effect of color temperature on melatonin production for illumination of working environments. Applied Ergonomics, 2017, 58: 446-453. DOI:10.1016/j.apergo.2016.08.006 (  0) 0) |
| [27] |
Rea M S, Bullough J D, Figueiro M G. Phototransduction for human melatonin suppression. Journal of Pineal Research, 2002, 32(4): 209-213. DOI:10.1034/j.1600-079X.2002.01881.x (  0) 0) |
| [28] |
Lee A T L, Chen H, Tan S C, et al. Precise dimming and color control of LED systems based on color mixing. IEEE Transactions on Power Electronics, 2016, 31(1): 65-80. DOI:10.1109/TPEL.2015.2448641 (  0) 0) |
| [29] |
Souman J L, Borra T, de Goijer I, et al. Spectral tuning of white light allows for strong reduction in melatonin suppression without changing illumination level or color temperature. Journal of Biological Rhythms, 2018, 33(4): 420-431. DOI:10.1177/0748730418784041 (  0) 0) |
| [30] |
Brainard G C, Hanifin J P, Warfield B, et al. Short-wavelength enrichment of polychromatic light enhances human melatonin suppression potency. Journal of Pineal Research, 2015, 58(3): 352-361. DOI:10.1111/jpi.12221 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


