Wind power is one of the most important renewable energy resources, especially when the depleting fossil fuel has raised environmental concerns. Classification of wind turbine is determined by whether the flow of air is perpendicular or parallel to rotor shaft axis Horizontal Axis wind turbine and Vertical Axis wind turbine, respectively[1]. However, this conversion of energy is dependent on the aerodynamic shape of wind turbine blade. More energy can be extracted if the design of blade is optimized with more efficiency. Many studies have dedicated to the subject of wind energy and wind turbine designs. A detailed review of aerodynamic theories related to this field was given by Eggleston and Stoddard[2]. Airfoil has a significant effect on the power and load characteristics of wind turbine. The theoretical design and optimization of airfoil have always been the research focus of experts and scholars. Different characteristics for designing airfoil have been adopted, where some are based on high lift and high drag ratio, some consider the surface roughness influence, and some focus on the characteristics of stall and thickness of airfoils. Generally, the optimization process of the airfoil can be divided into generation of geometry, simulation of numerical methods, optimization algorithm application, and surrogate model[3]. The design and optimization process of airfoils for wind turbine blade are different. Many dedicated airfoils were designed for wind turbines, for example, some airfoils for use on wind turbine adopts the most important parameter of lift-to-drag ratio using higher angle of attack even achieving stall[4]. However, these specific purpose airfoils for wind turbine blade are mainly based on theoretical studies, which lack of detailed understanding of the law of interaction between flowing air and wind turbine blades. Petrucci[5] utilized inverse design method to obtain the target optimization of pressure distribution, which has become a widely used method that most of the NACA6 series successful laminar airfoils were designed based on this method. A new direct method was proposed by Wang Quan for moderate thickness airfoil using integral expression and B-spline curve[6]. Wang[7] based on the conformal transformation and series theory, an integration equation was developed for the airfoil profile expression. Several agencies including National Aeronautics and Space Administration (NASA) (formally the originator of NACA airfoil series by USA), National Renewable Energy Laboratory (NREL) (formally Solar Energy Research Institute by USA), FOI (Sweden), Ris (Denmark), and DU (Delft University of Technology of Netherland) are developing different airfoils specifically for wind turbines. Different optimization techniques including modern computational algorithms are also employed by many researchers[8-11]. A blade is formed by configuration and connection of different airfoils, so characteristics of airfoils are crucial. Basic operation of airfoil is to create pressure difference of air between upper and lower regions, thus increasing the lift[12-13]. Aerodynamic optimization plays an important role in the performance of wind turbine[14-15]. Generally, numerical simulation method and experimental study (wind tunnel testing) are used to verify the aerodynamics of airfoil or wind turbine blade. Numerical study can be further categorized as the Computational Fluid Dynamics (CFD) method which analyzes the flow around blade surface and the Blade Element Momentum (BEM) method which analyzes the lift and drag coefficient of each airfoil element[16-22]. A cyclic design procedure was adopted to optimize, verify, and modify the performance of wind turbine blade, which can be studied by calculation and experiments[23]. A number of geometrical parameters like chord, twist angle, and airfoils of a blade were investigated by Tahani et al.[24], and the study achieved the improvement of 13.7% by delaying the separation via geometry optimization. To enhance the power output, Sayed et al.[25] numerically studied different blade profiles. The numerical study conducted by Ashrafi et al.[26] provided a significant result, which proved that different pitch angles are required at different wind velocities for optimal output of wind turbine. Similarly, the research of Sharifi and Nobari[27] showed significant improvement in the power output by using a complex pitch angle distribution at each section of blade. Shimizu et al.[28-29] studied the effect of Mei tip vane to obtain 17.5% increase in power coefficient and experimental measurement of parameters such as aspect ratio, blade number, and Reynold number. Another way to improve the performance of blade span-wise flow is to add a plate at the tip which can also reduce the vortices. The study of tip vane was first conducted by Holten[30], while van Bussel et al.[31] introduced the addition of plate at the tip vane. In summary, this paper proposed a theory of air weight analogies to pressure difference. Assuming that the entire system is in a vacuum, there is a curve in the vertical plane that the air mass slides along the curve from one point to another under the effect of gravity in a shortest time interval, and the curve was used as the profile of the airfoil. An airfoil theory was proposed on the basis of the interaction of possible number of air masses with airfoil surface in the shortest possible time under specified boundary conditions. After obtaining the nodes, airfoil was developed using CAD, and compared with three existing airfoils NACA2409-34, NACA2410, and RK40 for different characteristics.
2 Establishment of Pressure Difference Analogy TheoryA comparatively similar method named lifting line theory was utilized by Dumitrescu and Cardos[32], and the performance was measured using Biot-Savart Law along with Kutta-Joukowski theorem.
The following assumptions are adopted for the establishment of airfoil:
1) The flow of air is caused due to the pressure difference under gravity;
2) The flow is parallel to the airfoil profile with stationary state fluid motion;
3) The difference is expressed as the analogy of air weight;
4) 2D coordinate system is used, and all the viscous effects are considered under the 2D system.
2.1 Mathematical ModelAir molecules are fluid substance with no definite shape and very small density. Therefore, it suffers severe randomness or wake (turbulence) after passing through wind turbine blade, making it complicated to study its effects. It is intricate to manage the direction of the flowing air acting on blade, since air flow is caused due to the pressure difference in the air. Under the influence of gravity, the pressure difference is expressed with the analogy of air weight. In order to derive the equation of airfoil, a 2D coordinate system was established, suppose the chord length of the airfoil with a distance of r from the rotation axis of the rotor OB was assumed to be l and the torsional angle was defined as θ, as shown in Fig. 1.
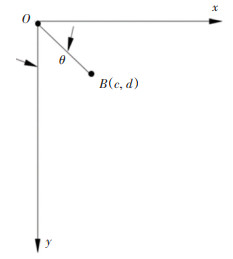
|
Fig.1 Derivation figure for the equations of blade airfoil profile |
Under the action of gravity, the mass will slide from point O to point B. If there is a curve Γ between point O and point B, which can make the air mass slide from point O to point B in a shortest time, so it shows that there is a large number of air masses that slide over the curve Γ in a certain period of time. During this time, more air masses interact with the curve Γ so that the curve acquires as much energy as possible from as many air masses as possible. Therefore, if the curve Γ is used as the airfoil profile, then the blade will be able to convert kinetic energy of more air masses into mechanical energy of the wind turbine blade. Thus, it was supposed that the curve Γ is y = f(x), the mass of air mass is m, and the air mass is stationary at point O and slides from point O to point B(c, d) under the gravity (ignore the friction) where its speed is v. Hence, kinetic energy theorem can be represented by
| $ mgy = \frac{1}{2}m{\kern 1pt} {\kern 1pt} {v^2} $ | (1) |
Then it can be obtained that
| $ v=\sqrt{2 g y} $ | (2) |
Besides, the air mass velocity v can be expressed as
| $ v = \frac{{{\rm{d}}s}}{{{\rm{d}}t}} $ | (3) |
where dt represents the time of the air mass slides over the arc length ds; ds represents the arc length of the neighborhood domain of point C (x, y), given by
| $ {\rm{d}}s = \sqrt {{{({\rm{d}}x)}^2} + {{({\rm{d}}y)}^2}} $ |
So
| $ v = \frac{{{\rm{d}}s}}{{{\rm{d}}t}} = \frac{{\sqrt {{{({\rm{d}}x)}^2} + {{({\rm{d}}y)}^2}} }}{{{\rm{d}}t}} = \sqrt {1 + \frac{{{{({\rm{d}}y)}^2}}}{{{{({\rm{d}}x)}^2}}}} \frac{{{\rm{d}}x}}{{{\rm{d}}t}} $ | (4) |
Substitute Eq.(2) into Eq.(4) and let
| $ {\rm{d}}t = \frac{{\sqrt {1 + {y^{\prime 2}}} }}{{\sqrt {2gy} }}{\rm{d}}x $ | (5) |
Supposing that the shortest time of the air mass sliding from point O to point B is T, then
| $ T = \int_a^c {\frac{{\sqrt {1 + {y^{\prime 2}}} }}{{\sqrt {2gy} }}} {\rm{d}}x $ | (6) |
Suppose that
| $ F = \frac{{\sqrt {1 + {y^{\prime 2}}} }}{{\sqrt {2gy} }} $ | (7) |
Therefore,
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial F}}{{\partial y}} = - \frac{1}{{\sqrt {2g} }}\frac{{\sqrt {1 + {y^{\prime 2}}} }}{{2{y^{\frac{3}{2}}}}}}\\ {\frac{{\partial F}}{{\partial {y^\prime }}} = \frac{1}{{\sqrt {2gy} }}\frac{{{y^\prime }}}{{\sqrt {1 + {y^{\prime 2}}} }}} \end{array}} \right. $ | (8) |
According to the Euler-Lagrange Equation[33], the necessary condition for the minimum value of Eq.(6) is
| $ \frac{{\partial F}}{{\partial y}} - \frac{{\rm{d}}}{{{\rm{d}}x}}\left( {\frac{{\partial F}}{{\partial {y^\prime }}}} \right) = 0 $ | (9) |
Substitute Eq.(8) into Eq.(9) and sort out, then
| $ \frac{{\sqrt {1 + {y^{\prime 2}}} }}{{2{y^{\frac{3}{2}}}}} + \frac{{\rm{d}}}{{{\rm{d}}x}}\left( {\frac{1}{{\sqrt y }}\frac{{{y^\prime }}}{{\sqrt {1 + {y^{\prime 2}}} }}} \right) = 0 $ | (10) |
where
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}x}}\left( {\frac{1}{{\sqrt y }}\frac{{{y^\prime }}}{{\sqrt {1 + {y^{\prime 2}}} }}} \right) = \frac{{\rm{d}}}{{{\rm{d}}y}}\left( {\frac{1}{{\sqrt y }}\frac{{{y^\prime }}}{{\sqrt {1 + {y^{\prime 2}}} }}} \right)\frac{{{\rm{d}}y}}{{{\rm{d}}x}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{{2{y^{\frac{3}{2}}}}}\frac{{{y^{\prime 2}}}}{{\sqrt {1 + {y^{\prime 2}}} }} + \frac{{{y^\prime }}}{{\sqrt y }}\frac{{\frac{{{\rm{d}}y}}{{{\rm{d}}y}}\sqrt {1 + {y^{\prime 2}}} - {y^\prime }\frac{{{y^\prime }}}{{\sqrt {1 + {y^{\prime 2}}} }}\frac{{{\rm{d}}y}}{{{\rm{d}}y}}}}{{1 + {y^{\prime 2}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{{2{y^{\frac{3}{2}}}}}\frac{{{y^{\prime 2}}}}{{\sqrt {1 + {y^{\prime 2}}} }} + \frac{{{y^\prime }}}{{\sqrt y }}\frac{{\frac{{{\rm{d}}{y^\prime }}}{{{\rm{d}}y}}\left( {1 + {y^{\prime 2}}} \right) - {y^{\prime 2}}\frac{{{\rm{d}}y}}{{{\rm{d}}y}}}}{{\left( {1 + {y^{\prime 2}}} \right)\sqrt {1 + {y^{\prime 2}}} }} \end{array} $ | (11) |
Substitute Eq.(11) into Eq.(10), and then convert it into the differential equation of y' which is about y. It can be obtained that
| $ 1 + \frac{{2yy'}}{{1 + {{y'}^2}}}\frac{{{\rm{d}}y'}}{{{\rm{d}}y}} = 0 $ | (12) |
Eq.(12) can be further converted as
| $ \frac{1}{y}{\rm{d}}y + \frac{{2y'}}{{1 + {{y'}^2}}}{\rm{d}}y' = 0 $ | (13) |
Integrate Eq.(13) to get
| $ \ln y + \ln (1 + {y'^2}) = \ln (2C) $ |
or
| $ y(1 + {y'^2}) = 2C $ | (14) |
where C represents the integral constant.
It can be obtained from Eq.(14) that
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}x}} = \sqrt {\frac{{2C - y}}{y}} $ | (15) |
Integration of Eq.(15) gives
| $ \begin{array}{l} x = \int {\sqrt {\frac{y}{{2C - y}}} } {\rm{d}}y = \int {\frac{y}{{\sqrt {2Cy - {y^2}} }}} {\rm{d}}y = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sqrt {2Cy - {y^2}} + C{\rm{arccos}}\frac{{C - y}}{C} + D \end{array} $ | (16) |
where D represents the integral constant.
Substitute the coordinate of point O (origin of coordinate), x = 0, y = 0, into Eq.(16), and obtain D = 0, then Eq.(16) is simplified as
| $ x = - \sqrt {2Cy - {y^2}} + C{\rm{arccos}} \frac{{C - y}}{C} $ | (17) |
To reveal the meaning of Eq.(17), let arccos((C-y)/C)=θ, so Eq.(17) can be expressed as
| $ \left\{ {\begin{array}{*{20}{l}} {x = C(\theta - \sin \theta )}\\ {y = C(1 - \cos \theta )} \end{array}} \right. $ | (18) |
Obviously, Eq.(18) expresses a set of cycloid families, where C is the radius of the roller which can be regarded as an air mass sliding over the cycloid curve. The smaller the air mass radius is, the more number of air masses slide over the curve, and the better the interaction effect on the curve is, which means that the wind turbine blades designed with this airfoil have better output.
It can be obtained from Eq.(17) that
| $ 2Cy - {y^2} \ge 0\quad {\rm{or}}\quad C \ge \frac{y}{2} $ | (19) |
Above is the establishment process of wind turbine blade airfoil theory and the corresponding wind turbine blade airfoil theory (Eqs.(16)-(19)).
3 Applied ResearchThree airfoils NACA2409-34, NACA2410, and RK40 were selected and compared with the SJX airfoil for aerodynamic performance. For all the four airfoils of equal chord length, similar thickness and geometric shape, traditional design method was used by considering the blade airfoil chord l = 1 m and twist angle θ =5° at a certain radius of the wind wheel. The aerodynamic characteristics of the angle of attack α from -4° to 8° were observed in the Fluent software, and the aerodynamic performances of the four airfoils were compared.
3.1 Acquisition of AirfoilWhen OB = l = 1 and torsion angle θ = 5°, then the coordinate of point B is
| $ \left\{ {\begin{array}{*{20}{l}} {c = l \cdot \sin \theta = 1 \cdot \sin {5^\circ } = 0.0870}\\ {d = l \cdot \cos \theta = 1 \cdot \cos {5^\circ } = 0.9962} \end{array}} \right. $ |
According to Eq.(19),
| $ C \ge \frac{y}{2} = \frac{d}{2} = \frac{{0.9962}}{2} = 0.4981 $ |
Set C=0.4981 and substitute it into Eq.(17) to get the airfoil profile equation as follows:
| $ x = - \sqrt {0.9962y - {y^2}} + 0.4981\arccos \frac{{0.4981 - y}}{{0.4981}} $ |
Generally, greater radius of curvature of the airfoil leading edge upper chord line helps to obtain greater lift by the airfoil. The greater the relative camber of the airfoil mid-arc is, the larger the airfoil lift coefficient is. With higher upper camber, the airflow will result in greater value of pressure coefficient. Lift coefficient is the area surrounded by the upper and lower airfoil pressure coefficient curves in the pressure distribution map. Therefore, the lift coefficient is greater[34]. Since the plane-convex type airfoil has a larger lift coefficient than a double-convex type airfoil at the same angle of attack, in order to comply with the basic characteristics of the airfoil, when the chord length l = 1 m and torsion angle θ = 5°, then the airfoil profile of coordinate (x, y) was selected with the C value of 0.52 as the upper chord of the airfoil (the curve is steeper), and the airfoil profile of coordinate (y, x) with the C value of 5 as the lower chord of the airfoil (the curve is gentler). The obtained SJX airfoil is shown in Fig. 2. To get the geometric shapes of NACA2409-34, NACA2410, and RK40 types of airfoils, the original coordinates of the NACA2409-34, NACA2410, and RK40 airfoils were acquired from the Profili software[35], which were then slightly modified by adding z = 0 at spanwise direction, and finally imported into the ANSYS ICEM software to achieve the airfoils, as shown in Figs. 3-5.

|
Fig.2 Airfoil of SJX |

|
Fig.3 Airfoil of NACA2409-34 |

|
Fig.4 Airfoil of NACA2410 |

|
Fig.5 Airfoil of RK40 |
3.2 Airfoil Grid Division
The meshing of the airfoil in this study was performed in ANSYS ICEM CFD software. As professional pre-processing software, ICEM CFD has powerful CAD model repair capabilities, automatic middle-face extraction, unique grid "sculpture" technology, grid editing technology, and extensive solver support capabilities[36]. For two-dimensional simulation of airfoil, O or C type mesh is mainly used. The C-type computational domain is used around airfoil to minimize the adverse impact on the flow field around the airfoil[37]. The four airfoil grids are shown in Figs. 6-9.

|
Fig.6 Airfoil grid of SJX |

|
Fig.7 Airfoil grid of NACA2409-34 |

|
Fig.8 Airfoil grid of NACA2410 |

|
Fig.9 Airfoil grid of RK40 |
3.3 Simulation Parameter Setting
The airfoil of wind turbine blade was simulated based on Fluent in this study. The software has advanced numerical analysis methods and powerful fore-and-aft processing functions[38], as well as significant advantages for the two-dimensional flow simulation of wind turbine blade airfoils. After importing the airfoil mesh file into Fluent, the grid quality needs to be checked to ensure that the grid file does not have a negative volume mesh. After inspection, the minimum volume of meshes for the four airfoil mesh files were 2.869×10-7 m3, 3.485×10-7 m3, 4.246×10-7 m3, and 4.312×10-7 m3, and there was no negative volume grid; the mesh qualities were 5.108×10-1, 6.160×10-1, 7.589×10-1, and 6.639×10-1, and the grid quality was good. The parameter settings are presented in Table 1[39].
| Table 1 Simulation parameter settings |
3.4 Analysis of Airfoil Aerodynamic Characteristics 3.4.1 Lift coefficient and drag coefficient
In simulation, parameters such as lift, drag, lift to drag ratio, and moment were analyzed at fixed wind velocity of 12 m/s and angle of attack from -4° to 8°. The simulation results of the lift coefficient and drag coefficient of the four airfoils are shown in Fig. 10 and Fig. 11 respectively.
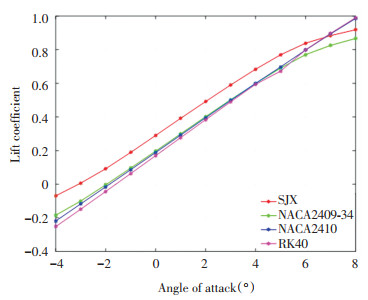
|
Fig.10 Lift coefficient curve |
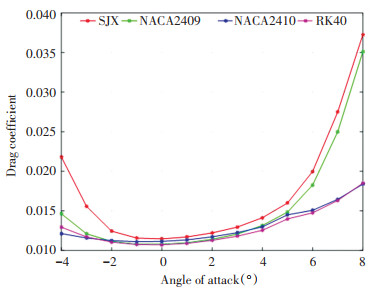
|
Fig.11 Drag coefficient curve |
It was found that the lift ratio of the SJX airfoil was 5% greater than other airfoils in the angle range of -4°-6°. The SJX airfoil had almost positive lift right from the beginning with the maximum lift rate of 49.35%, whereas the lift of other airfoils remained negative until the angle of attack reached -2°. The lift characteristics of the SJX and NACA2409-34 airfoils were similar with the difference of 5%, which were better than other two airfoils between the angles -4° to 6°; however those of the NACA2410 and RK40 airfoils were slightly better after 6°. According to Fig. 11, the drag coefficients of the four airfoil types first decreased and then increased. There was a negligible difference drag ratio value between the angles -4° to 4°. The drag coefficient curves of the SJX airfoil and the NACA2409-34 airfoil were similar in characteristics. Due to the better fit of the curve, the growth rate of drag was basically negligible, which showed that the SJX airfoil maximized the lift of the airfoil and increased the drag. Based on the lift coefficient and drag coefficient with the angle of attack curve, it can be found that the airfoil designed by weight analogies pressure difference had a better improvement in the lift coefficient. In addition, according to the mathematical formula of the lift coefficient, when the wind speed and airfoil chord length were fixed, the lift coefficient was directly proportional to the airfoil lift, which means that SJX airfoil can provide more lift than the other three airfoil types when the angle of attack changes. Although the drag coefficient was larger in value, the maximum difference rate of the drag coefficient compared with the NACA2409-34 airfoil was only 11.624%, indicating that the SJX airfoil will produce relatively large drag under simulated conditions, but it will perfectly improve the lift of the airfoil, as well the aerodynamic force increases.
3.4.2 Characteristics of lift to drag ratioLift to drag ratio of airfoil, also known as aerodynamic efficiency, is the ratio of lift coefficient and drag coefficient of the airfoil at the same angle of attack[40], or the ratio of lift and drag, which reflects the operating state of the wind turbine blade. The larger the lift to drag ratio is, the better the aerodynamic performance of the wind turbine blade is. In order to intuitively understand this characteristic of airfoil, the trend chart of the lift to drag ratios of the airfoils change with the angle of attack is plotted in Fig. 12.
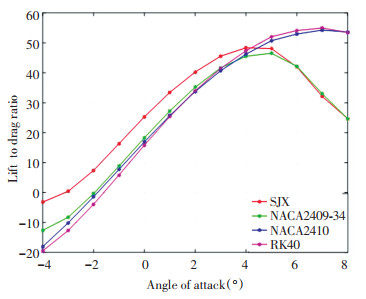
|
Fig.12 Lift to drag ratio curve |
The lift to drag ratio results show that the SJX airfoil was better than those of the other three airfoils between the angles -4°-4° with the minimum lift ratio of 2.13% and maximum lift ratio of 84.36%. The lift to drag ratio of the SJX airfoil remained positive, whereas other airfoils had negative lift to drag ratio up to angle of -2°. From the lift coefficient and drag coefficient with the angle of attack curve, it can be found that the airfoil designed by weight analogies pressure difference had a better improvement in lift coefficient. The SJX airfoil was compared with the other three types of airfoils, where the minimum increase rate of the lift to drag ratio was 2.09% and the maximum increase rate was 64.21% when the negative lift to drag ratio was removed in this range of angle of attack. It indicates that the superiority of the aerodynamic performance of the SJX airfoil is obvious in this range. In addition, as shown in Fig. 12, the SJX airfoil had the best lift to drag ratio of 48.36 at the angle of attack of 4°; the NACA2409-34 had the best lift to drag ratio of 46.51 at the angle of attack of 5°; the NACA2410 had the best lift to drag ratio of 54.25 at the angle of attack of 7°; and the RK40 had the best lift to drag ratio of 54.95 at the angle of attack of 7°. Therefore, when a certain amount of flowing air flows through the wind turbine blade and the range of angle of attack is set at -4°-4°, and if the blade is designed with the above four types of airfoils at the same radius airfoil section, then the SJX airfoil output effect is the best. The best lift to drag ratio was at the angle of attack of 4°, which means that the SJX airfoil can achieve the best output power within a small range of angle of attack, while the other three types of airfoils need a larger angle of attack to gradually reach the best output power. As for the output time, the SJX airfoil can effectively save time and output a considerable amount of power.
3.4.3 Trque analysis of airfoilAfter the Fluent flow field simulation of the above four airfoils, it was found that the lift generated by the SJX airfoil was greater than those of the other three airfoils under the same conditions, and the aerodynamic force synthesized by lift and drag was large. In addition, the synthetic aerodynamic force was decomposed, and the tangential force parallel to the plane of rotation generated a certain Moment. The magnitude of this Moment can get the output situation of a small section airfoil of blade. Fluent can monitor the change curves of airfoil moment with the changes of angle of attack, as shown in Fig. 13.

|
Fig.13 Torque curve |
According to Fig. 13, the momentum curve of the four airfoils decreased with the increase of the angle of attack. The torque of the SJX airfoil at any angle of attack was greater than those of the other three types of airfoils. The curve trends of the SJX airfoil and the NACA2409-34 airfoil were basically the same. The torque curves of the NACA2410 airfoil and the RK40 airfoil tended to be slower and basically all showed a linear decrease. The maximum torque of the SJX airfoil was generated at the angle of attack of -4°, being 7.196 N/m, and the torque of the other three types of airfoils was less than 5 N/m. The aerodynamic center of the airfoil was set (0.25c, 0), and the pressure of the flowing air acting on the airfoil surface could be simplified as an aerodynamic force and moment acting on the aerodynamic center. Moreover, the total aerodynamic force acting on the SJX airfoil produced a much higher torque than those of the other three airfoils in the aerodynamic center with the angle of attack gradually increased. It suggests that the SJX airfoil has the best output effect at a specific wind speed and range of angle of attack, and the validity and reliability of the airfoil profile theory are well verified.
3.4.4 Pressure distribution on airfoil surfaceThe airfoil surface pressure distribution reflects the pressure generated during the interaction between airfoil and the passing air, while the pressure difference between the upper and lower surfaces of the blade provides the driving force for the blade rotation, which decomposed into each airfoil section, that is, the upper and lower airfoil pressure difference. For the sake of comparison, this paper selects the NACA2409-34 airfoil with the highest similarity to the SJX airfoil to compare the simulation results when the angle of attack changes from -4°, -2°, 0°, 2°, 4°, 6°, to 8°, as shown in Fig. 14, which presents the surface pressure coefficient distribution of the SJX airfoil and the NACA2409-34 airfoil.

|
Fig.14 Pressure coefficient distribution on airfoil surface |
Pressure coefficient is represented as a ratio between chord length and selected angles of attack ranging from -4° to 8° in Figs. 14(a)-(g). The value of the ordinate above zero indicates the pressure on the pressure or lower surface and that below zero is the pressure on the suction or upper surface of the airfoil, whereas the ordinate line exactly at zero indicates the chord line of the airfoil. When the angle of attack was less than or equal to 0°, as shown in Figs. 14(a)-(c), the surface pressure of the airfoil was mainly concentrated on the leading edge, and the airfoil surface pressure and suction were staggered at certain position of the chord, resulting in low or negative lift. Lift coefficient is the area enclosed by pressure coefficient curves of the upper and lower surfaces of the airfoil. According to Figs. 14(a)-(c), the gradually increasing area indicated that the lift coefficient was increasing, which was consistent with the simulation results in Table 2. When the angle of attack was equal to or greater than 2°, the pressure near the airfoil generally increased with the increase of the angle of attack, and the pressure on the suction surface was always greater than the pressure on the pressure surface, so that the airfoil could achieve a stable lift. When the angle of attack was equal to 0°, the upper and lower surface pressure coefficient curves of the airfoils were normal. The area enclosed by the pressure coefficient curves of the upper and lower surfaces of the airfoil was basically the same when the angle of attack was between 4° and 8°. For the SJX airfoil, the pressure coefficient curves of the upper and lower surfaces were 0.4916, 0.6817, 0.8340, and 0.9127 at the angle of attack of 2°, 4°, 6°, and 8°, respectively. While the pressure coefficient curves of the upper and lower surfaces of the NACA2409-34 airfoil were 0.401, 0.597, 0.765, and 0.824, respectively. Fig. 15 presents the variation curve of the area enclosed by the upper and lower surface pressure coefficients of the two airfoils with the angle of attack changing from 2°, 4°, 6°, to 8°, which makes the difference more intuitively. It can be seen that between the angle of attack of 2°-8°, the lift coefficients of the SJX airfoil and the NACA2409-34 airfoil were gradually increasing, and the lift coefficient of the SJX airfoil was better than that of the NACA2409-34 airfoil. When the angle of attack of the airfoil ranged from 2° to 8°, the area enclosed by pressure coefficient curves of the upper and lower surfaces of the SJX airfoil increased by a minimum of 5.64%, a maximum of 18.35% and compared with the NACA2409-34 airfoil, which were consistent with the increase rate of the lift coefficients of SJX airfoil and NACA2409-34 airfoil, as presented in Table 2.
| Table 2 Simulation results of four airfoils |

|
Fig.15 Variation diagram of the area enclosed by the pressure coefficient curves of the upper and lower surfaces of the airfoil with angle of attack |
Especially, when the angles of attack were 2° and 4°, as shown in Figs. 14(d)-(e), the aerodynamic performance of the SJX airfoil was more obvious. Under this condition, the most obvious pressure difference between the upper and lower surfaces of the two kinds of airfoils appeared in the range of 0.2-0.8, which is the middle and rear part of the airfoil. When the angle of attack was 2°, the surface pressure coefficient curve of the SJX airfoil basically enveloped that of the NACA2409-34 airfoil, enabling it to obtain greater lift.
4 ConclusionsThe basic purpose of wind turbine is to extract maximum power from flowing air, which can only be achieved by optimizing its efficiency. In this study, the efficiency of Horizontal Axis Wind Turbine with air weight analogy to pressure difference was attempted to be increased. A mathematical modal based on maximum masses of air flow through the curve of airfoil in the least time was established. By comparing the SJX airfoil with NACA2409-34 airfoil, NACA2410 airfoil, and RK40 airfoil under the same conditions of the Fluent flow Field Simulation, it was found that:
1) Different airfoil profiles can be obtained by changing the C value according to the chord length and twist angle of the blade at a certain section;
2) Compared with NACA2409-34, NACA2410, and RK40, the SJX airfoil had an obvious advantage in the lift to drag ratio at the angle of attack of -4°-4°.
The inadequacies of the study are as follows:
1) It is lack of wind tunnel test data;
2) Due to the limitations of the airfoil profile, the airfoil cannot be combined according to the widely used airfoils, andthus lacks of credibility.
Subsequently, we will optimize the airfoil profile and compare the SJX airfoil with commonly usedairfoils such as NRELS series, RIS series, and FFA-W series. In addition, the model will be built for wind tunnel test, and compared with the simulation data to verify the feasibility and correctness of the theory in this paper.
| [1] |
Hau E. Wind Turbines: Fundamentals, Technologies, Application, Economics. Berlin: Springer, 2006. DOI:10.1007/3-540-29284-5 (  0) 0) |
| [2] |
Eggleston D M, Stoddard F S. Wind Turbine Engineering Design. USA, New York: Van Nostrand Reinhoid, 1987. (  0) 0) |
| [3] |
Yuan X, Xu L J, Ye Z Q, et al. Numerical simulation of an airfoil for stall regulated HAWT rotors at large angles of attack. Acta Energiae Solaris Sinica, 1997, 18(1): 36-40. (in Chinese) (  0) 0) |
| [4] |
Bao F. Geometric Design and Aerodynamic Simulation for the Wind Turbine. Dalian: Dalian University of Technology, 2008, 55-56. (in Chinese) DOI:10.7666/d.y1418730(inChinese) (  0) 0) |
| [5] |
Petrucci D R, Filho N M. A fast algorithm for inverse airfoil design using a transpiration model and an improved vortex panel method. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2007, XXIX(4): 354-365. DOI:10.1590/S1678-58782007000400003 (  0) 0) |
| [6] |
Wang Q, Chen J, Pang X P, et al. A new direct design method for the medium thickness wind turbine airfoil. Journal of Fluids and Structures, 2013, 43: 287-301. DOI:10.1016/j.jfluidstructs.2013.08.003 (  0) 0) |
| [7] |
Wang X D, Chen J, Shen W Z, et al. Integration study on airfoil profile for wind turbines. China Mechanical Engineering, 2009, 20(2): 211-213. (  0) 0) |
| [8] |
Tangler J L, Somers D M. Status of the special-purpose airfoil families. Proceedings of Windpower '87. San Francisco, 1987. (  0) 0) |
| [9] |
Veers P S, Ashwill T D, Sutherland H J, et al. Trends in the design, manufacture and evaluation of wind turbine blades. Wind Energy, 2003, 6(3): 245-259. DOI:10.1002/we.90 (  0) 0) |
| [10] |
Fuglsang P, Dahl K S. Design of the new Risϕ- A1 airfoil family for wind turbines. Proc. Ewec, 1999, 85(4): 215-219. (  0) 0) |
| [11] |
Fuglsang P, Bak C. Development of the Risø wind turbine airfoils. Wind Energy, 2004, 7(2): 145-162. DOI:10.1002/we.117 (  0) 0) |
| [12] |
Jha A R. Wind Turbine Technology. Boca Raton: CRC Press, 2010.
(  0) 0) |
| [13] |
Ye K, Ye Z Y, Qu Z. A new design concept for wind turbine airfoil. Applied Mechanics and Materials, 2015, 798: 8-14. DOI:10.4028/www.scientific.net/AMM.798.8 (  0) 0) |
| [14] |
He Y L, Agarwal R K. Shape optimization of NREL S809 airfoil for wind turbine blades using a multi-objective genetic algorithm. International Journal of Aerospace Engineering, 2014, 864210. DOI:10.1155/2014/864210 (  0) 0) |
| [15] |
Grasso F, Coiro D P, Bizzarrini N, et al. Design of advanced airfoil for stall-regulated wind turbines. Journal of Physics: Conference Series, 2016, 753(2). DOI:10.1088/1742-6596/753/2/022008 (  0) 0) |
| [16] |
Chamorro L P, Arndt R E A, Sotiropoulos F. Reynolds number dependence of turbulence statistics in the wake of wind turbines. Wind Energy, 2012, 15(5): 733-742. DOI:10.1002/we.501 (  0) 0) |
| [17] |
Yu G H, Shen X, Zhu X C, et al. An insight into the separate flow and stall delay for HAWT. Renewable Energy, 2011, 36(1): 69-76. DOI:10.1016/j.renene.2010.05.021 (  0) 0) |
| [18] |
Gharali K, Johnson D A. Numerical modeling of an S809 airfoil under dynamic stall, erosion and high reduced frequencies. Applied Energy, 2012, 93: 45-52. DOI:10.1016/j.apenergy.2011.04.037 (  0) 0) |
| [19] |
Wekesa D W, Wang C, Wei Y J, et al. Influence of operating conditions on unsteady wind performance of vertical axis wind turbines operating within a fluctuating free-stream: a numerical study. Journal of Wind Engineering and Aerodynamics, 2014, 135: 76-89. DOI:10.1016/j.jweia.2014.10.016 (  0) 0) |
| [20] |
Li Y W, Paik K J, Xing T, et al. Dynamic overset CFD simulations of wind turbine aerodynamics. Renewable Energy, 2012, 37(1): 285-298. DOI:10.1016/j.renene.2011.06.029 (  0) 0) |
| [21] |
Sicot C, Devinant P, Loyer S, et al. Rotational and turbulence effects on a wind turbine blade. Investigation of the stall mechanisms. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(8-9): 1320-1331. DOI:10.1016/j.jweia.2008.01.013 (  0) 0) |
| [22] |
Belkheir N, Dizene R, Khelladi S. A numerical simulation of turbulence flow around a blade profile of HAWT rotor in moving pulse. Journal of Applied Fluid Mechanics, 2012, 5(1): 1-9. (  0) 0) |
| [23] |
Wood D H. Dual purpose design of small wind turbine blades. Wind Energy, 2004, 28: 511-528. DOI:10.1260/0309524043028037 (  0) 0) |
| [24] |
Tahani M, Maeda T, Babayan N, et al. Investigating the effect of geometrical parameters of an optimized wind turbine blade in turbulent flow. Energy Conversion and Management, 2017, 153: 71-82. DOI:10.1016/j.enconman.2017.09.073 (  0) 0) |
| [25] |
Sayed M A, Kandil H A, Shaltot A. Aerodynamic analysis of different wind-turbine-blade profiles using finite-volume method. Energy Conversion and Management, 2012, 64: 541-550. DOI:10.1016/j.enconman.2012.05.030 (  0) 0) |
| [26] |
Ashrafi Z N, Ghaderi M, Sedaghat A. Parametric study on off-design aerodynamic performance of a horizontal axis wind turbine blade and proposed pitch control. Energy Conversion and Management, 2015, 93: 349-356. DOI:10.1016/j.enconman.2015.01.048 (  0) 0) |
| [27] |
Sharifi A, Nobari M R H. Prediction of optimum section pitch angle distribution along wind turbine blades. Energy Conversion and Management, 2013, 67: 342-350. DOI:10.1016/j.enconman.2012.12.010 (  0) 0) |
| [28] |
Shimizu Y, Imamura H, Matsumura S T, et al. Power augmentation of a horizontal axis wind turbine using a Mie type tip vane: velocity distribution around the tip of a HAWT blade with and without a Mie type tip vane. Journal of Solar Energy Engineering, 1995, 117(4): 297-303. DOI:10.1115/1.2847850 (  0) 0) |
| [29] |
Shimizu Y, Ismaili E, Kamada Y, et al. Rotor configuration effects on the performance of a HAWT with tip-mounted Mie-type vanes. Journal of Solar Energy Engineering, 2003, 125(4): 441-447. DOI:10.1115/1.1621671 (  0) 0) |
| [30] |
van Holten T. Windmills with diffuser effect induced by small tip vanes. Proceedings of International Symposium on Wind Energy Systems. Cambridge, UK, 1976.
(  0) 0) |
| [31] |
van Bussel G J W, Hensing P C, van Kuik G A M. Aerodynamic and aeroelastic research on tipvane turbines. Delft: Delft University of Technology, 1980. (  0) 0) |
| [32] |
Dumitrescu H, Cardos V. Wind turbine aerodynamic performance by lifting line method. International Journal of Rotating Machinery, 1998, 4(3): 141-149. DOI:10.1155/s1023621x98000128 (  0) 0) |
| [33] |
Khan T A, Li W, Zhang J Z, et al. Local vibrations and lift performance of low Reynolds number airfoil. Propulsion and Power Research, 2017, 6(2): 79-90. DOI:10.1016/j.jppr.2017.05.001 (  0) 0) |
| [34] |
Chen J, Wang Q, Pang X P, et al. Improvement of airfoil design using smooth curvature technique. Renewable Energy, 2013, 51: 426-435. DOI:10.1016/j.renene.2012.10.006 (  0) 0) |
| [35] |
Cong W, Song S P. 3D modeling of wind turbine blade based on SolidWorks. Applied Mechanics and Materials, 2014, 595: 123-127. DOI:10.4028/www.scientific.net/AMM.595.123 (  0) 0) |
| [36] |
Cong W, Peng C Z, Song S P, et al. Comparative study about two mesh types of NACA 0018. Mechanical Engineer, 2015, 9: 35-37. (in Chinese) (  0) 0) |
| [37] |
Esfahani J A, Barati E, Karbasian H R. Fluid structures of flapping airfoil with elliptical motion trajectory. Computers & Fluids, 2015, 108: 142-155. DOI:10.1016/j.compfluid.2014.12.002 (  0) 0) |
| [38] |
Somashekar V. A computational investigation of unsteady aerodynamics of insect-inspired fixed wing micro aerial vehicle's 2D airfoil. Advances in Aerospace Engineering, 2014, 504049. DOI:10.1155/2014/504049 (  0) 0) |
| [39] |
Seo S H, Hong C H. Performance improvement of airfoils for wind blade with the groove. International Journal of Green Energy, 2016, 13(1): 34-39. DOI:10.1080/15435075.2014.910777 (  0) 0) |
| [40] |
Rao T S, Mahapatra T, Mangavelli S C. Enhancement of lift-drag characteristics of NACA 0012. Materials Today: Proceedings, 2018, 5(2): 5328-5337. DOI:10.1016/j.matpr.2017.12.117 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


