2. College of Electrical and Control Engineering, Heilongjiang University of Science and Technology, Harbin 150022, China;
3. Handan Power Supply Company, Handan 056002, Hebei, China
Nowadays, the demand for electric power is gradually rising, which makes the voltage and capacity of the power system increased. The normal operation of a transformer can effectively ensure the safe, reliable, and stable operation of the whole power system. There are many types of fault diagnosis methods for oil immersed transformer, among which dissolved gas analysis method is more accurate and reliable for early latent faults and can effectively prevent major accidents caused by transformer faults.
Sixteen kinds of conditional attributes are commonly used in the dissolved gas method in oil. However, not all of them are meaningful, and unnecessary attributes will bring inconvenience to fault diagnosis. Therefore, in order to improve fault diagnosis performance, redundant attributes should be reduced. Since the traditional methods such as expert experience method and mathematical analysis method are subjective and require high experience, they are not suitable for transformer fault diagnosis.
Rough set theory[1-4] is a new data mining technology, which can explore the implicit relationship between data on the basis of guaranteeing the invariable classification effect. By extracting features, eliminating redundant information, and replacing original attributes with more concise attributes, it can effectively improve the data analysis ability and simplify the processing process. At present, the theory has been applied to fault diagnosis[5-7], data mining[8-10], and so on. Attribute reduction is the key content of rough set. The reduced data is a subset of the original data, whose classification ability is the same as that before reduction. Attribute reduction includes compound system reduction, mutual information reduction, Johnson algorithm, and heuristic algorithm, while they have high complexity and cannot be optimized globally. Therefore, the trend of current development is to use artificial intelligence algorithm to solve attribute reduction problems. In Ref. [11], genetic algorithm was used to reduce attributes. According to the data collection extraction criterion of genetic algorithm, the high-importance attributes set is regarded as the optimal reduction result. However, the genetic algorithm itself has the disadvantages of large amounts of computation, low efficiency, and susceptibility to local optimum, so the final effect is not satisfactory. Ant colony algorithm[12] was used to reduce attributes, but it also has shortcomings such as slow convergence speed, susceptibility to local optimum, large amounts of computation, and long solving time.
In information systems, the fewer the attributes need to be considered, the simpler the processing of information is. Hence, an improved imperialist competitive algorithm (IICA)[13-15] was used to solve the fault attribute reduction problem of oil immersed transformer, and was compared with genetic algorithm attribute reduction (GAAR), simulated annealing attribute reduction (SAAR), and particle swarm optimization attribute reduction (PSOAR).
2 Dissolved Gas AnalysisWhile using oil immersed transformer, many kinds of gases are produced, which are generally divided into normal gases and abnormal gases. Only the gas generated by the aging of the transformer is classified as normal gas. When the transformer fails and abnormal conditions occur, the gas generated by the internal material of the transformer under the combined action of electricity and heat is called fault gas[16].
The main sources of dissolved gases in transformer oil can be divided into three categories: decomposition of solid insulating materials, decomposition of insulating oil, and other sources. In addition, some operations can lead to the occurrence of some gases in the oil. For example, in the use of on-load tap-changer transformer, switching switches may cause oil leakage into the main tank of the transformer. When there is oil in the tank during welding, excessive local temperature and pollutants will also result in the production of other gases in the oil. Sometimes the original injected insulating oil contains certain gases.
For dissolved gases in transformer oil, the analyses of types, contents, and compositions, as well as the processing of related data usually conform to the thermodynamic law that the energy of fault is closely related to the chemical unsaturation of gases. Generally, the dissolved gases in oil are mainly N2 and O2, and the combustible gases only account for about one thousandth of the total dissolved gases. The aging of the transformer insulation materials will cause the generation of CO2 and CO, so if the transformer runs for a long time, the gas contents CO2 and CO will be very high. When transformer internal faults occur, gases such as CH4 and C2H6 are usually generated[17]. Different relative proportions of these gases will reflect different types of faults. Therefore, through the laboratory simulation test and the field observation experience of transformer faults, combined with the measured dissolved gas content, a certain amount of data processing and analysis can be carried out to distinguish different types of faults. However, the initial fault data are often large and complex, so the dimensionality reduction of the original data is the first step.
3 Rough Set 3.1 Discretization TheoryAttribute discretization is an important step in data preprocessing. A large number of rules need to be discretized to improve the performance of the algorithm. Therefore, before attribute reduction, it is necessary to discretize the fault data. Rough set discretization is to divide attributes into regions according to breakpoints in the data, and then classify the regions into more intervals, under the condition that the correlation between decision attributes and conditional attributes does not change before and after reduction[18].
The main methods of discretization include equal frequency discretization method, equal distance discretization method, and discretization method according to attribute importance[19].
3.2 Attribute ReductionAttribute reduction is another crucial aspect of rough set theory[20-21]. For a given system, let P(P≠ϕ) be a reduction of C, then P should satisfy two conditions: ① The discriminant relation before and after reduction remains unchanged; ② The redundant information is not included in P as far as possible, and the reduction set obtained by C is defined as RED(C).
| $ \begin{array}{l} {\mathop{\rm RED}\nolimits} (C) = \left\{ {P \subseteq C\mid {\gamma _P}(D) = {\gamma _C}(D),\forall B \subset P} \right.,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\gamma _B}(D) \ne {\gamma _C}(D)} \right\} \end{array} $ | (1) |
If any subset C′ of C is regarded as an approximate reduction of C, then the approximate accuracy of the reduction is defined as
| $ \omega = \frac{{{\gamma _{C'}}(D)}}{{{\gamma _C}(D)}} $ | (2) |
Construct reduction model of attribute dependence degree into
| $ \max F = \alpha \frac{{ {\rm Card} (C) - {\rm Card} (C')}}{{ {\rm Card}(C)}} + \beta \frac{{{\gamma _{C'}}(D)}}{{{\gamma _C}(D)}} $ | (3) |
where Card(C) is the number of conditional attributes, Card(C′) is the number of conditional attributes in reduction, γC′(D) is the degree of dependence of attributes, and α and β are the weight factors.
When γC′(D)=1, the decision attribute is completely determined by the conditional attribute. Therefore, this function guarantees that minimal reduction can be achieved without changing the dependency of the attributes.
After this step, the data will reduce some conditional attributes. At this time, the neural network needs to be used in the next step to verify whether the reduced data set has better effects.
3.3 BP Neural NetworkBP neural network is a multi-layer feedforward neural network, which consists of input layer, hidden layer, and output layer[22-23], as shown in Fig. 1.

|
Fig.1 Structural chart of BP neural network |
When the input layer signal is given, the output value can be obtained by combining the weights and thresholds of the neural network, and then compared with the actual value to calculate the error. Next, the neural network will reduce the error by adjusting the weights and thresholds in the process of reverse propagation. By repeating the forward and backward propagation processes continuously, the error will be smaller and smaller until the required range is reached. With the advantages of simple structure and strong learning ability, the BP neural network has been widely used in the field of fault diagnosis recently.
Combining data with neural network, the effect of the attribute reduction can be verified by comparing the results.
4 Improved Imperialist Competitive Algorithm (IICA) 4.1 Imperialist Competitive Algorithm (ICA)ICA is an optimization algorithm inspired by imperialist competition, whose initial population is divided into two types: imperialists and colonies, which together shape several empires. ICA mainly consists of the competition between empires, i.e., the disintegration of small and weak empires, and the occupation of colonies by powerful empires. In this algorithm, fitness value is called cost, and the state power is judged by calculating the cost. The smaller the cost is, the greater the power is. When there is only one empire at last, the colonies will have the same status and the same cost as the imperialists.
After the imperialists have allocated all the colonies and established the initial empire, the colonies begin to move towards their countries. The movement is called assimilation policy. If the cost of a colony is found to be lower than that of an imperialist in the course of its movement, the colony will become an imperialist, and the former position of the imperialist will become a new colony. Fig. 2 shows the movement of the colonies towards the imperialists, in which α and x are evenly distributed random numbers, and d is the distance between colonies and imperialists.
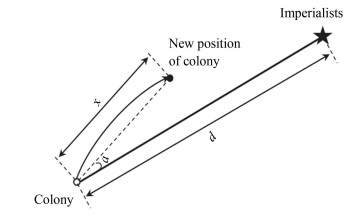
|
Fig.2 Movement process of the colony |
The power of the empire is consisted of two parts, i.e., imperialists and colonies. In ICA, the total power of the empire is defined by the power of the imperialist state plus the average power of the colonies. When an empire is unable to compete among the empires or increase its power, it will be destroyed. The imperialist competition will lead to the strengthening of the powerful empire and the weakening of the weak empire until the weak empire collapses. These movements will bring all countries together. Then there will be only one empire in the world, and all the other countries will be its colonies. The position of the empire is the best solution[24].
4.2 Improved Imperialist Competitive Algorithm (IICA)1) In the initial stage of the empire, the following forms were proposed to avoid the weakest imperial power being 0, which could lead to the number of colonies become 0.
| $ {p_i} = \left\{ \begin{array}{l} 1.3\left( {{{\max }_{1 \le j \le {N_{{\rm{imp }}}}}}\left\{ {{c_j}} \right\}} \right) - {c_i},\\ {\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if }}\left. {{{\max }_{1 \le j \le {N_{{\rm{imp }}}}}}\left\{ {{c_j}} \right\}} \right) - \left\{ {{c_i}} \right\} > 0\\ 0.7\left( {{{\max }_{1 \le j \le {N_{{\rm{imp }}}}}}\left\{ {{c_j}} \right\}} \right) - {c_i}\\ {\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if }}\left. {{{\max }_{1 \le j \le {N_{{\rm{imp }}}}}}\left\{ {{c_j}} \right\}} \right) - \left\{ {{c_i}} \right\} \le 0 \end{array} \right. $ | (4) |
| $ {\rm{N}}{{\rm{C}}_i} = {\rm{round }}(\left| {\frac{{{P_i}}}{{\sum\limits_{j = 1}^{{N_{{\rm{imp}}}}} {{p_j}} }}} \right| \times {N_{{\rm{col}}}}) $ | (5) |
where ci, pi, and NCi represent the cost, power, and number of colonies of the ith empire, respectively.
2) In the basic ICA assimilation mechanism, the movement of colonies needs to determine the direction and distance of the movement. IICA adopts Eq. (6) to realize the assimilation process.
| $ {\mathit{\boldsymbol{p}}^c} = {\mathit{\boldsymbol{p}}^c} + \beta \times \mathit{\boldsymbol{\delta }}{.^*}({\mathit{\boldsymbol{p}}^i} - {\mathit{\boldsymbol{p}}^c}) $ | (6) |
where pc and pi denote the position of colonies and imperialists, respectively.δ is an N-dimensional vector, whose elements are random numbers between[0, 1]..* denotes the multiplication of two N-dimensional vectors with the elements of the same location. Once the cost of the colony is lower than that of an imperialist in the course of its movement, the colony will become an imperialist country, and the old imperialist country will become a colony.
3) Colonial reform operations were added to IICA. For each iteration, a certain number of colonies were selected. According to the probability of reform, the same number of colonies was randomly generated to replace the original colonies, and the cost of new colonies was calculated.
| $ T.C{._n} = f({\rm{im}}{{\rm{p}}_n}) + \zeta \times \frac{{\sum\limits_{i = 1}^{N.C{._n}} f ({\rm{co}}{{\rm{l}}_i})}}{{N.C{._n}}} $ | (7) |
where impn and T.C.n are the imperialist countries and the total cost of the nth empire, respectively. ζ is the influence factor, 0 < ζ < 1. The operation increased the diversity of the samples.
4) When the distance between the two empires was less than the set search range, merging the two empires could improve the convergence speed of the algorithm to a certain extent.
5) In the original ICA algorithm, imperial competition is performed in each iteration, while IICA determines whether imperial competition is conducted by setting a probability parameter, ρ(0 < ρ < 1).
The weakest colony in the weakest empire will be chosen as the object of the competition among the empires. The stronger the empire is, the more likely it is to occupy the colony. The probability of each empire occupying the colony is expressed as follows:
| $ N.T.C{._n} = T.C{._n} - \mathop {\max }\limits_i \left\{ {T.C{._n}} \right\} $ | (8) |
| $ {p_n} = \left| {\frac{{N.T.C{._n}}}{{\sum\limits_{i = 1}^{{N_{{\rm{imp }}}}} N .T.C{._i}}}} \right| $ | (9) |
where N.T.C.n is the total cost of standardization for the n-th empire, and pn indicates the probability that the n-th empire will occupy the colony.
6) When an empire has only imperialist countries but no colonies, it means that the empire is overthrown and can be deleted. With the competition between empires, the gap between the empires will become wider and wider. When there is only one empire left, stop iterating. The position of the empire is the best solution.
Through the competition between empires and the movement of colonies, the algorithm avoids the problem of easily falling into local optimum. Meanwhile, the excellent optimization efficiency makes the algorithm receive rational results in fewer iterations, which is feasible and effective to solve the problem of transformer fault attribute reduction.
Fig. 3 shows the whole verification process of the effectiveness of the algorithm.
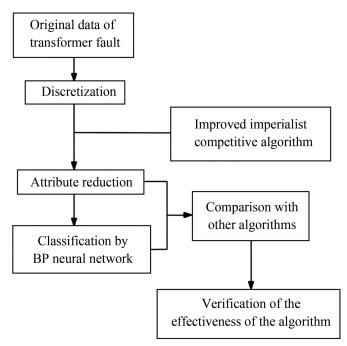
|
Fig.3 Verification process of the effectiveness of the algorithm |
5 Fault Attribute Reduction of Oil Immersed Transformer
The contents and important ratios of the dissolved gases produced by oil immersed transformer operation were taken as the original data. There are 16 conditional attributes in the data set, including C3H6, CO2, H2, C2H2, CH4, C3H8, C3H4, C2H4, CO, C2H6, C2H4/C2H6, C2H2/C2H4, C2H6/C2H2, C2H6/CH4, C2H2/CH4, and CH4/H2[25]. Some of the data are listed in Table 1. After discretization, the set of breakpoints is shown in Table 2.
| Table 1 Partial fault attribute data set of oil immersed transformer |
| Table 2 Set of breakpoints |
The improved imperialist competitive algorithm attribute reduction (IICAAR) model was used to reduce the discretized transformer fault data. The parameters were set as follows: Initial number of countries M=200, number of imperialist countries MI=8, cost coefficient ω=0.02, weight factors α=0.5, β=2, influence factor ζ=0.3, and imperial merger search space σ=0.02.
Figs. 4-7 demonstrate the operation diagrams of GAAR, SAAR, PSOAR, and IICAAR, respectively. It can be seen that when IICAAR iterated to nine times, the power of the optimal imperialist state was stabilized, and the position of the imperialist state was the optimal solution. The iteration stabilization speed of IICAAR was better than those of the other three algorithms. The fitness value was lower, and the results were stable after many tests.

|
Fig.4 Operation diagram of GAAR |
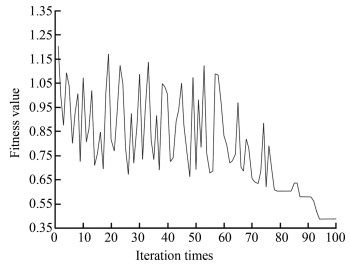
|
Fig.5 Operation diagram of SAAR |

|
Fig.6 Operation diagram of PSOAR |
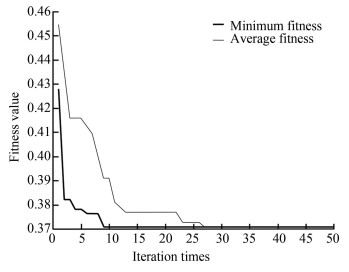
|
Fig.7 Operation diagram of IICAAR |
Tables 3-5 show the data set after reduction, including the comparison table of reduction effect and the comparison of classification results under BP neural network. The four algorithms made a lot of reduction on conditional attributes. IICAAR reduced the original data to seven conditional attributes, and the reduction rate was as high as 56.25%. In addition, its reduction accuracy and minimum fitness value were better than those of the other three algorithms. In terms of classification accuracy, IICAAR and PSOAR had the same accuracy, and the overall effect was better than other algorithms. However, since PSOAR had more conditional attributes than IICAAR, the performance of its reduction was worse than that of IICAAR.
| Table 3 Reduction attribute sets of different algorithms |
| Table 4 Performance comparison of different intelligent algorithms |
| Table 5 Comparison of classification accuracy under BP neural network |
From the above analysis and discussion, it can be found that IICA had good feasibility and adaptability in the attribute reduction of rough set. Compared with other intelligent algorithms, IICAAR had the advantages of fast convergence speed, high reduction rate, low fitness value, and high classification accuracy.
6 Conclusions1) In this paper, IICA is applied to the attribute reduction of oil immersed transformer fault. Through introducing, modeling, simulating, and comparing, it was concluded that IICA had excellent feasibility and applicability.
2) IICAAR achieved the optimal reduction of transformer fault attributes. In comparison with GAAR, SAAR, and PSOAR, IICAAR had lower iteration times, higher reduction rate, and better precision, which could reduce the requirement of data storage and improve classification accuracy.
3) On the premise of keeping the discrimination relation unchanged, removing some meaningless attributes could greatly reduce the difficulty of subsequent operations. When the data of the sample set is large, IICA should be adopted.
| [1] |
Sang Y L, Liang J Y, Qian Y H. Decision-theoretic rough sets under dynamic granulation. Knowledge-Based Systems, 2016, 91: 84-92. DOI:10.1016/j.knosys.2015.08.001 (  0) 0) |
| [2] |
Liu G J, Li L, Wang J Y. Evaluation model for capability of enterprise agent coalition based on information fusion and attribute reduction. Journal of Harbin Institute of Technology (New Series), 2016, 23(2): 23-30. DOI:10.11916/j.issn.1005-9113.2016.02.004 (  0) 0) |
| [3] |
Yu H, Wang G Y, Yao Y Y. Current research and future perspectives on decision-theoretic rough sets. Chinese Journal of Computers, 2015, 38(8): 1628-1639. DOI:10.11897/SP.J.1016.2015.01628 (  0) 0) |
| [4] |
He Y H, Wang L B, He Z Z, et al. A fuzzy TOPSIS and rough set based approach for mechanism analysis of product infant failure. Engineering Applications of Artificial Intelligence, 2016, 47: 25-37. DOI:10.1016/j.engappai.2015.06.002 (  0) 0) |
| [5] |
de Mello Oliveira A B, Moreno R L, Ribeiro E R. Short-circuit fault diagnosis based on rough sets theory for a single-phase inverter. IEEE Transactions on Power Electronics, 2019, 34(5): 4747-4764. DOI:10.1109/TPEL.2018.2861564 (  0) 0) |
| [6] |
Ghimire R, Zhang C, Pattipati K R. A rough set-theory-based fault-diagnosis method for an electric power-steering system. IEEE/ASME Transactions on Mechatronics, 2018, 23(5): 2042-2053. DOI:10.1109/TMECH.2018.2863119 (  0) 0) |
| [7] |
Chen J J. Fault diagnosis of diesel rotor vibration based on rough set and neural network. Internal Combustion Engines, 2018(3): 46-48, 53. (in Chinese) DOI:10.3969/j.issn.1000-6494.2018.03.011.(inChinese) (  0) 0) |
| [8] |
Zheng X F, Wang S. Data mining method of road transportation management information based on rough set and association rule. Journal of South China University of Technology (Natural Science Edition), 2014, 42(2): 132-138. (in Chinese) DOI:10.3969/j.issn.1000-565X.2014.02.020.(inChinese) (  0) 0) |
| [9] |
Zhang G H, Li Z H. Research on massive data mining algorithm based on rough set. Modern Electronics Technique, 2016, 39(17): 116-119, 123. (in Chinese) DOI:10.16652/j.issn.1004-373x.2016.17.029.(inChinese) (  0) 0) |
| [10] |
Maji P, Garai P. IT2 fuzzy-rough sets and max relevance-max significance criterion for attribute selection. IEEE Transactions on Cybernetics, 2015, 45(8): 1657-1668. DOI:10.1109/TCYB.2014.2357892 (  0) 0) |
| [11] |
Zhou T, Lu H L, Zhang Y N, et al. A new hybrid genetic algorithm for high dimension feature selection based on rough set. Journal of Nanjing University (Natural Sciences), 2015, 51(4): 880-893. (in Chinese) DOI:10.13232/j.cnki.jnju.2015.04.026.(inChinese) (  0) 0) |
| [12] |
Zhu H P, Li X H. Research on a new method based on improved ACO algorithm and SVM model for data classification. International Journal of Database Theory and Application, 2016, 9(1): 217-226. DOI:10.14257/ijdta.2016.9.1.19 (  0) 0) |
| [13] |
Abd-Elazim S M, Ali E S. Imperialist competitive algorithm for optimal STATCOM design in a multimachine power system. International Journal of Electrical Power & Energy Systems, 2016, 76: 136-146. DOI:10.1016/j.ijepes.2015.09.004 (  0) 0) |
| [14] |
Ali E S. Speed control of induction motor supplied by wind turbine via imperialist competitive algorithm. Energy, 2015, 89: 593-600. DOI:10.1016/j.energy.2015.06.011 (  0) 0) |
| [15] |
Khosravi M, Banejad M, Shandiz H T. Robust dynamic state estimation of power system using imperialist competitive algorithm. Canadian Journal of Electrical and Computer Engineering, 2018, 41(2): 64-76. DOI:10.1109/CJECE.2016.2629981 (  0) 0) |
| [16] |
Ayalew Z, Kobayashi K, Matsumoto S, et al. Dissolved gas analysis (DGA) of arc discharge fault in transformer insulation oils (Ester and Mineral Oils). Proceedings of 2018 IEEE Electrical Insulation Conference (EIC). Piscataway: IEEE, 2018, 150-153. DOI:10.1109/EIC.2018.8481123 (  0) 0) |
| [17] |
Islam M M, Lee G, Hettiwatte S N. Application of Parzen window estimation for incipient fault diagnosis in power transformers. High Voltage, 2018, 3(4): 303-309. DOI:10.1049/hve.2018.5061 (  0) 0) |
| [18] |
Bilski P, Wojciechowski J M. Rough-sets-based reduction for analog systems diagnostics. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 880-890. DOI:10.1109/TIM.2010.2060225 (  0) 0) |
| [19] |
Zhang H G, Xu Y, Sun Q Y. On the discretization algorithm based on fuzzy rough set for continuous system variables. Journal of Northeastern University (Natural Science), 2008, 29(1): 1-4. (in Chinese) DOI:10.3321/j.issn:1005-3026.2008.01.001.(inChinese) (  0) 0) |
| [20] |
Jing S H, Qin K Y. Relationships between several reductions in decision system. Computer Science, 2018, 45(11A): 110-112, 142. (in Chinese) (  0) 0) |
| [21] |
Huang G Q, Xiao S. Application of partheno-genetic algorithm in attributes reduction. Information Technology, 2018(5): 111-114. (in Chinese) DOI:10.13274/j.cnki.hdzj.2018.05.025.(inChinese) (  0) 0) |
| [22] |
Ahuna M N, Afullo T J, Alonge A A. Rain attenuation prediction using artificial neural network for dynamic rain fade mitigation. SAIEE Africa Research Journal, 2019, 110(1): 11-18. DOI:10.23919/SAIEE.2019.8643146 (  0) 0) |
| [23] |
de Bruin T, Verbert K, Babuška R. Railway track circuit fault diagnosis using recurrent neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(3): 523-533. DOI:10.1109/TNNLS.2016.2551940 (  0) 0) |
| [24] |
Coelho L D S, Afonso L D, Alotto P. A modified imperialist competitive algorithm for optimization in electromagnetics. IEEE Transactions on Magnetics, 2012, 48(2): 578-582. DOI:10.1109/TMAG.2011.2172400 (  0) 0) |
| [25] |
Huang J F, Luo S J, Feng J. Case study on fault diagnosis with multi-parameter for power transformers. High Voltage Apparatus, 2013, 49(3): 110-114. (in Chinese) DOI:10.13296/j.1001-1609.hva.2013.03.019.(inChinese) (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


