The surface morphology of the magnetic head slider has a great influence on the dynamic pressure of air bearing. Based on Thornton and Bogy's[1] numerical study on the performance of the air bearing slider, it was found that the shape factor of the slider can affect the film's stiffness and dampness, thus affecting the bearing capacity of air bearing. Wahl et al.[2] established the Tri-pad positive pressure head and studied the force acting on the head at stable flight altitude. He found that the influence of disk surface topography on the dynamic pressure of air bearing cannot be ignored. Zhao et al.[3] established the dynamic model of the slider-disk interface to simulate the flight characteristics. Based on this model, the air bearing pressure was calculated under loading and unloading conditions and the validity of the dynamic model has been verified by experiments. At very low flight altitude, the bulge of disk surface (micro-particles produced by manufacturing or caused by evaporation and condensation of lubricants materials or wear of hard disk) will affect the aerodynamic pressure between magnetic head and disk, and then affect the stability of magnetic head flight[4-8]. When the flight altitude is at the nanometer level, the gas between the magnetic head and disk is no longer continuous, showing a rarefied state[9]. The macroscopic properties of the gas may need to be modified. The parameters describing the physical properties of the gas, such as thermal conductivity, the molecular free path and so on, can no longer be regarded as constants and are related to pressure and temperature. These changes will affect the gas heat transfer between the magnetic head and disk. Therefore, it is necessary to further study the heat transfer of rarefied gases based on the study of the influence of disk bulge on the gas dynamic pressure. The heat conduction model has developed rapidly in recent years. Chen et al.[10] established a new three-dimensional heat transfer model, which describes the magnetic head flight altitude affecting the heat transfer of air bearing. When the flight altitude is low, the influence of aerodynamic pressure on heat transfer of air bearing could not be ignored. Zhou et al.[11] established a generalized heat transfer model of molecular dynamics, considering the impact of the collision between film molecules and solid molecules. Zhou pointed out that not only does the molecular free path contribute to heat transfer, but also air temperature and gas viscosity both have influences on heat transfer. Xiong et al.[12] studied the hard disk's thermal response time, which is mainly determined by the dominant layer. It was found that the optimization of the heat sink is the key to reduce the transient thermal process caused by the change of the linear velocity. A calculation approach based on Eulerian-description is developed, which simultaneously solves the problems of air bearing dynamics, slider thermodynamics, and disk heat dissipation. It is also suitable for transient thermal calculation of disks with different sizes and operating conditions[13]. Duan et al.[14] studied the effect of non isothermal wall temperature on heat transfer and gave a new solution to the weak boundary value according to the Boltzmann equation. Considering the different heat transfer models of the head disk interface, Poon et al.[15] studied thermal performance of the disk system numerically when the head contacts the disk and he has found that the coupling efficiency of the near-field transducer depends on the head plate gap. The air conduction model used to study the flight of the head on the disk shows that when the head disk interface is filled with the solid material formed by laser-induced accumulation, the heat transfer coefficient will become unexpectedly large and the temperature of the head will rise above the ideal level[16]. With the increase of laser input power, the thermal deformation of the magnetic head increases, and the temperature gap between the magnetic head and disk decreases, resulting in the decrease of the temperature rise of the laser. Juang and Bogy[17] studied the influence of slider morphology on thermal actuation performance and carried out numerical simulation. The thermal-structural coupling field was analyzed under the velocity slip and temperature jump boundary conditions and an iteration program was developed to find the equilibrium solution. Wang and Komvopoulos[18] have studied the influence of near-field heat transfer on the disk surface bulge and the surface temperature distribution of disk when coupling electromagnetic-thermomechanical. Li et al.[19] proposed that the laser heated head would induce a more severe curvature ratio, which would lead to an increase in bit error rate and a decrease in storage density. The curvature ratio could be reduced by altering the profile of the heat source spot, which may also affect the temperature distribution.
2 Materials and Methods 2.1 Modified Reynolds EquationThe Reynolds equation of air bearings between magnetic heads and disks is derived based on the following assumptions: gas is ideal gas; gas flow keeps laminar flow; gas is Newtonian fluid; gas viscosity is proportional to the deformation of shear stress; gas volume is negligible; molecular spacing is much smaller than that between magnetic heads and disks. Underthese assumptions, considering the rarefaction effect of ultrathin gas films, the modified Reynolds equation can be derived. The expression is that[20-22]
| $ \begin{array}{l} \frac{\partial}{\partial x}\left(Q p_{R} h_{R}^{3} \frac{\partial p_{R}}{\partial x}\right)+\frac{\partial}{\partial y}\left(Q p_{R} h_{R}^{3} \frac{\partial p_{R}}{\partial y}\right)= \\ 6 U \frac{\partial\left(\mu_{R} p_{R} h_{R}\right)}{\partial x}+6 V \frac{\partial\left(\mu_{R} p_{R} h_{R}\right)}{\partial y}+12 \frac{\partial\left(\mu_{R} p_{R} h_{R}\right)}{\partial t} \end{array} $ | (1) |
where U is x-direction of speed disk (m/s); V is y-direction of speed disk (m/s); Q is correction factor; PR is gas pressure (Pa); μR is gas viscosity (Pa·s); ρR is gas density (kg/m3); hR is the spacing between head and disk (nm); t is the time of gas flow.
2.2 Gas Heat Transfer EquationThis paper mainly considers the heat flux distribution on the central symmetrical plane of air bearing.Chen[22] developed the heat transfer model of the magnetic head/disk interface by setting the conditions of velocity slip and temperature jump. The heat flux of air bearing consists of two ways. One is heat conduction: when the temperature of air bearing is lower than that of the disk surface, the heat is transferred from the magnetic head to the gas film surface; another is viscous dissipation caused by gas flow in air bearing. Referring to Ref. [22], Eqs.(2)-(6) can be derived. The heat conduction equation is as follows:
| $ q=q_{\text {conduction }}+q_{\text {viscous }} $ | (2) |
where qviscousis viscous diffusion component of heat flux (W/m2); qconduction is heat conduction component of heat flux density (W/m2). The heat conduction equation is
| $ q_{\text {conduction }}=-k \frac{T_{s}-T_{d}}{h_{R}+2 b \lambda} $ | (3) |
where k is thermal conductivity of air; Ts, Td are the temperature of the disk and the temperature of the head, respectively; λ is average free path of the molecule.
The viscous dissipation component of heat flux density consists of two parts: one is caused by Poiseuille flow and the other is from Coriolis flow of gas. Its expression is Eq.(4):
| $ q_{\text {viscous }}=q_{\text {Couette }}+q_{\text {Poisecuille }} $ | (4) |
where qCouette is Coriolis component of heat flux density (W/m2); qPoisecuille is Poiseuille flow component of heat flux density (W/m2). The equation of qPoisecuille is
| $ \begin{aligned} q_{\text {Poiseuille }} &=-\frac{U h_{R}\left(a h_{R} \lambda+b h_{R} \lambda+2 a b \lambda^{2}\right)}{6\left(h_{R}+2 b \lambda\right)\left(h_{R}+2 a \lambda\right)} \cdot \frac{\partial p_{R}}{\partial x}+\\ & \frac{a h_{R}^{2} \lambda}{4 \mu_{R}}\left[\left(\frac{\partial p_{R}}{\partial x}\right)^{2}+\left(\frac{\partial p_{R}}{\partial y}\right)^{2}\right] \end{aligned} $ | (5) |
where a is the length of the slider of magnetic head. The equation of qCouette is
| $ q_{\text {Couette }}=\frac{\mu_{R} U^{2} h_{R}}{2\left(h_{R}+2 b \lambda\right)^{2}} $ | (6) |
The expression of heat flux for viscous dissipation of gases is obtained by substituting Eqs.(5)and (6) into Eq.(4). It is
| $ \begin{array}{l} {q_{{\rm{viscous }}}} = - \frac{{U{h_R}\left( {a{h_R}\lambda + b{h_R}\lambda + 2ab{\lambda ^2}} \right)}}{{6\left( {{h_R} + 2b\lambda } \right)\left( {{h_R} + 2a\lambda } \right)}} \cdot \frac{{\partial {p_R}}}{{\partial x}} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{ah_R^2\lambda }}{{4{\mu _R}}}\left[ {{{\left( {\frac{{\partial {p_R}}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial {p_R}}}{{\partial y}}} \right)}^2}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\mu _R}{U^2}{h_R}}}{{2{{\left( {{h_R} + 2b\lambda } \right)}^2}}} \end{array} $ | (7) |
By substituting Eqs.(3)and (7)into Eq.(2), the final expression of heat flux density of air bearing is obtained. It is shown in Eq.(8):
| $ \begin{aligned} q &=-k \frac{T_{s}-T_{d}}{h_{R}+2 b \lambda}-\frac{U h_{R}\left(a h_{R} \lambda+b h_{R} \lambda+2 a b \lambda^{2}\right)}{6\left(h_{R}+2 b \lambda\right)\left(h_{R}+2 a \lambda\right)} \cdot \\ & \frac{\partial p_{R}}{\partial x}+\frac{a h_{R}^{2} \lambda}{4 \mu_{R}}\left[\left(\frac{\partial p_{R}}{\partial x}\right)^{2}+\left(\frac{\partial p_{R}}{\partial y}\right)^{2}\right]+\frac{\mu_{R} U^{2} h_{R}}{2\left(h_{R}+2 b \lambda\right)^{2}} \end{aligned} $ | (8) |
In this paper, a complex Tri-pad barotropic head slider was used, along with a flathead slider selected as reference.
Fig. 1 shows the morphology of the two heads. The size of the flathead slider is 2 mm×1.6 mm×0.3 mm. The shape of the Tri-pad positive pressure head slider is the same as the flat plate. Besides, the height of the double rail and the tail pad are both 0.1 mm.

|
Fig.1 Structural models of the magnetic head slider |
Head slider's initial flight altitude is set as 2 nm; the rotating speed of magnetic disk is 10 m/s; the roll angle is 100 μrad; the pitch angle is 150 μrad. In this paper, the disk surface bulge is hemispherical. Its position center is set as (0.6 mm, 0), and the radius of the bulge is 0.2 mm. Considering the influence of the magnetic head's shape and the disk's bulge on the dynamic pressure of slider surface, the air bearing pressure distribution of the two kinds of magnetic head sliders were calculated. Other parameters used in calculating pressure are shown in Table 1.
| Table 1 Working parameters for calculating pressure distribution |
3.2 Air Bearing Pressure Simulation and Result of Flat Plate and Tri-Pad Barotropic Head Sliders
Fig. 2 presents two sliders' pressure distribution. From Fig. 2(a) and Fig. 2(b), it can be seen that the pressure distribution of the flathead slider is concentrated and a single peak occurs. The peak pressure without disk bulge is 4.99 ×106 Pa, which is larger than that with the disk bulge (about 4.62 ×106 Pa). The disk bulge weakens the convergence of the wedge gap between the head and disk so that the maximum pressure decreases. On the other hand, the bulge results in the decrease of the local head/disk spacing and the increase of the gas dynamic pressure, and a second peak pressure of about 1.28×106 Pa occurs near the bulge position. The range of the peak pressure is related to the bulge radius. Larger bulge radius will lead to the wider distribution of the second peak pressure. By the same method, the pressure distribution nephogram on slider surface of Tri-pad barotropic head is obtained, as shown in Fig. 2(c) and Fig. 2(d). The profile of Tri-pad barotropic head slider is bimodal. Specially, the tail pad at the end produces a peak pressure smaller than that caused by the double rail. The maximum pressure is lower than that of the flathead slider. When the disk has a bulge, the peak pressure formed by the bulge is about 0.461×106 Pa, which is smaller than that formed by the bulge of the flathead slider. This means that the Tri-pad barotropic head slider can bear more pressure.

|
Fig.2 Pressure distribution |
3.3 Heat Flux Density Simulation Result of Flathead and Tri-Pad Barotropic Head Sliders
Pressure affects the heat flux of air bearing by affecting gas heat transfer parameters whose equations are all related to pressure[11, 22]. Heat flux reflects the rate of heat exchange. In this paper, All coupling (AC) means all heat transfer parameters are coupled with pressure. Constant of thermal conductivity (CTC) means that only thermal conductivity is constant and the other parameters are influenced by pressure. Constant of dynamics viscosity (CDV) means only dynamic viscosity is constant and the other parameters are influenced by pressure. Constant of gas density (CGD) means only gas density is constant and the other parameters are influenced by pressure. Constant of molecular free path (CMFP) means only the molecular free path is constant and the other parameters are influenced by pressure. peak value of the heat flux density. Fig. 3(b) shows that when the thermal conductivity is constant, the heat flux density of air bearing changes with the different radius of the bulge, where r represents the radius of the bulge. With the increase of r, the first peak value of the heat flux curve decreases gradually and the second peak value increases gradually. Finally, it is larger than the first one. Fig. 3(c) and Fig. 3(d) show the effect of thermal conductivity on the heat flux of air bearing of Tri-pad barotropic head slider. It can be seen that thermal conductivity has a greater effect on heat flux and the heat flux curve has a single peak, which is attributed to the special structure of Tri-pad barotropic head slider.

|
Fig.3 Effect of thermal conductivity on heat flux density |
Fig. 4 shows the effect of dynamic viscosity on the heat flux density of flathead slider.
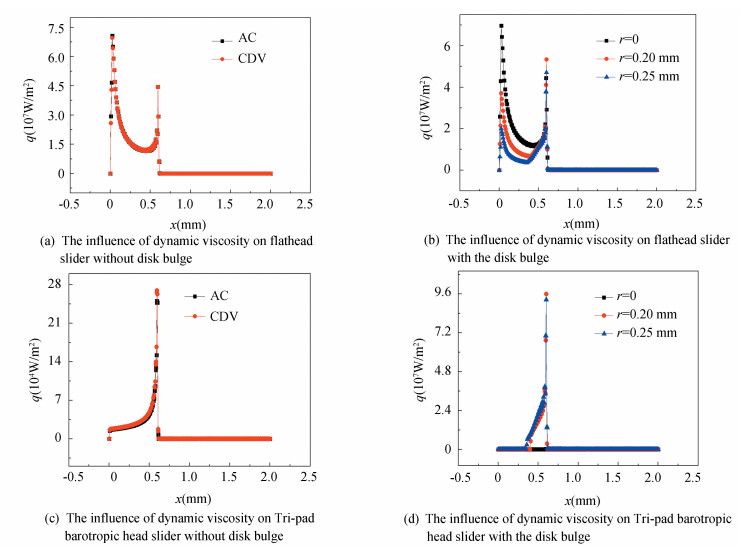
|
Fig.4 Effect of dynamic viscosity on heat flux density |
From Fig. 4(a), it can be seen that two curves nearly coincide, which means that the dynamic viscosity has little effect on the heat flux. According to Fig. 4(b), when the dynamic viscosity is constant, the heat flux decreases with the increase of the convex radius. Fig. 4(c) and Fig. 4(d) show the influence of dynamic viscosity on the heat flux density of Tri-pad barotropic head slider. From Fig. 4(c), it can be seen that the coincidence of two curves is greater than that in Fig. 4(a), indicating that dynamic viscosity has less influence on Tri-pad barotropic head slider, which may result from the special structure of Tri-pad barotropic head slider. Fig. 4(d) shows that when the dynamic viscosity is constant, the convex radius has a great influence on heat flux density of the Tri-pad barotropic head slider, and the heat flux density of the disk without convex radius is obviously smaller than that with the convex radius.
Fig. 5(a) and Fig. 5(b) reflect the influence of gas density on the heat flux density of flathead slider. From Fig. 5(a), it is known that the heat flux density with constant gas density is obviously larger than that under actual working conditions as well as the changed amplitude, which means that the pressure that influences the gas density reduces the rate of heat transfer. From Fig. 5(b), it can be seen that when the gas density is constant, the change trend curve of heat flux density under different convex radius is similar. However, with the increase of radius, the value of heat flux density changes significantly near the second peak value, and the larger the radius is, the larger the peak value will be.
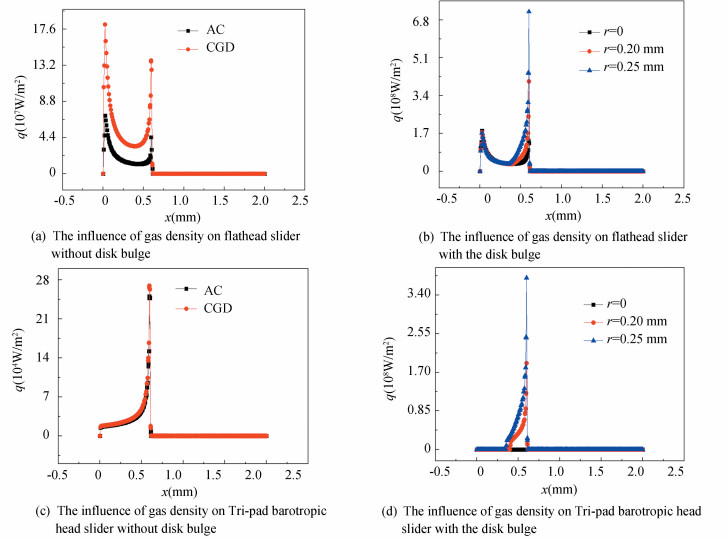
|
Fig.5 Effect of gas density on heat flux density |
Fig. 5(c) and Fig. 5(d) reflect the influence of gas density on the heat flux density of Tri-pad barotropic head slider. From Fig. 5(c), it can be seen that the heat flux curve of Tri-pad barotropic head slider has only one peak. The effect of gas density on the heat flux density is reflected in the peak value. From Fig. 5(d), it can be seen that the heat flux density increases with the increase of the bulge radius, and the ascending part of a curve varies from concave function to convex function.
Fig. 6(a) and Fig. 6(b) show the effect of the the molecular free path on the heat flux density of flathead slider. Fig. 6(a) reflects that the influence of the molecular free path on heat flux density is obvious. When the the molecular free path is constant, the heat flux density is less than the actual heat flux density and the change is more gentle, which means that when the flight altitude is very low, the influence of the molecular free path on the temperature of air bearing must be considered. The the molecular free path makes the temperature change more intense. Fig. 6(b) shows that the heat flux density of flathead slider increases with the disk bulge radius. As the radius increases, the black and red curves almost coincide as shown in Fig. 6(c), indicating that the molecular free path has little effect on Tri-pad barotropic head slider. It can be seen from Fig. 6(d) that the heat flux density of air bearing is smaller for Tri-pad barotropic head slider when the molecular free path of gas is constant but larger when the disk is no bulge. The heat flux density decreases when the radius of the bulge increases, which is different from that of flathead slider.
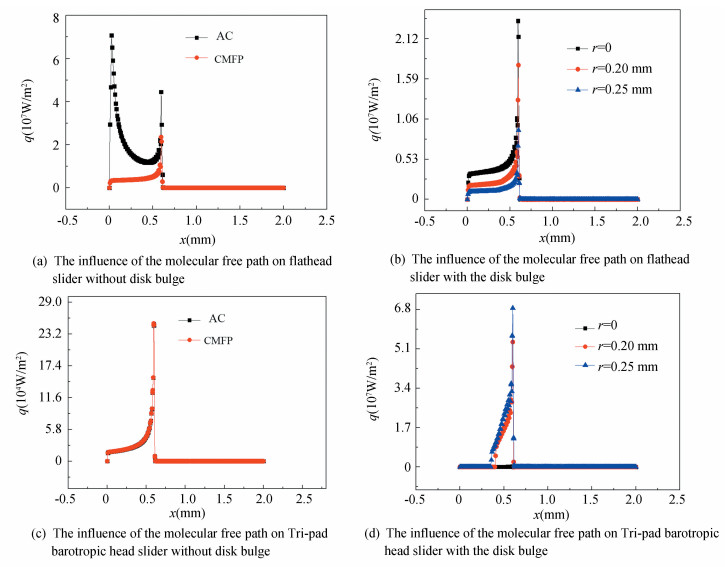
|
Fig.6 Effect of the molecular free path on heat flux density |
3.4 Simulation and Analysis of the Average Temperature on Air Bearing
Considering the influence of four gas heat transfer parameters on the temperature of air bearing, the average temperature of air bearing with two kinds of magnetic head sliders was simulated under different working conditions and different bulge sizes on disk surface. Fig. 7 shows the variation of the average temperature of air bearings with the roll angles of two magnetic head sliders, where the Ave-tem represents average temperature of air bearing.
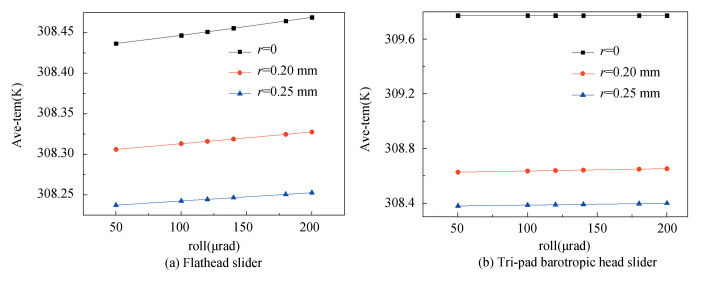
|
Fig.7 Air bearing's average temperature with the roll angle |
From Fig. 7(a) and Fig. 7(b), it can be seen that the average temperature of air bearing increases with the increase of roll angle. Large roll angle will lead to little energy dissipation of wedge clearance and high temperature of air bearing. In general, the change of rotation angle has little effect on temperature, especially on Tri-pad barotropic head slider. The convective heat transfer between the magnetic head and disk is accelerated by the disk bulge so that the temperature of air bearing decreases. The air bearing's temperature of Tri-pad barotropic magnetic head slider is higher than that of flathead slider under the same working condition, which is related to its special structure.
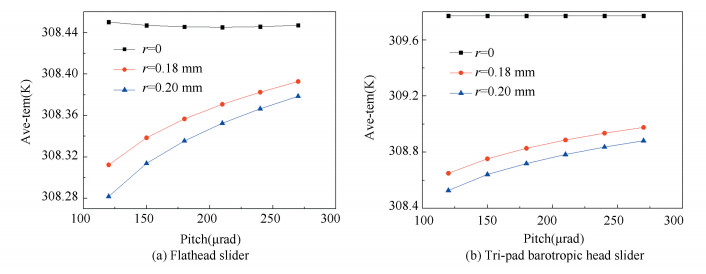
Fig. 8 illustrates that air bearing's average temperature of two magnetic head sliders changes with pitch angle. When there is no bulge on disk surface, the average temperature of air bearing surface is not affected by pitch angle. The disk bulge enlarges the effect of pitch angle on temperature, which increases with pitch angle. The convergence of the wedge space is better when the pitch angle is larger. In that case, although the gas flow is accelerated and the dynamic pressure of the gas becomes stronger, the outlet of the wedge space becomes smaller, which is equivalent to a more closed space, decreasing the heat loss. Therefore, the temperature will increase with the pitch angle.
|
Fig.8 Air bearing's average temperature with the pitch angle |
Compared with Fig. 8(a) and Fig. 8(b), the temperature change of the Tri-pad barotropic head slider is more sensitive to the pitch angle. When the pitch angle increases, it increases sharply. Therefore, it is necessary to keep flight altitude of the head as stable as possible to avoid excessive change of the pitch angle. In addition, the temperature change of Tri-pad is more sensitive to the disk bulge's radius. When the disk bulge's radius increases, the temperature will decrease faster. Therefore, it can be considered to add a bulge structure on the disk surface to reduce its average temperature.
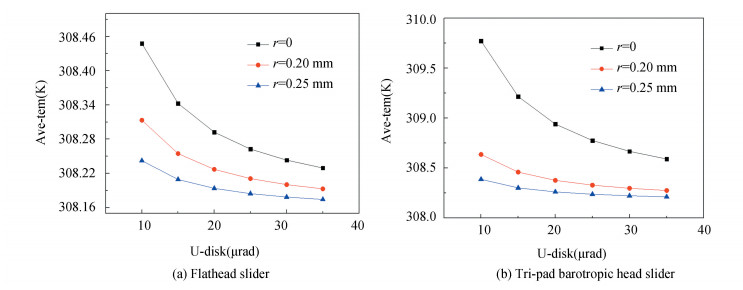
Fig. 9 shows the effect of disk speed on the average temperature of air bearings. The average temperature of air bearing decreases with the increase of disk speed and bulge radius. Gas always flows quite fast at a high disk speed, which leads to strong convective heat transfer and massive energy loss. Compared with Fig. 9(a) and Fig. 9(b), the average temperature of Tri-pad air bearing changes faster with the rotational speed under the same radius of bulge, which means the average temperature of Tri-pad is more sensitive to the rotational speed of disk and more attention should be paid to increase the stability of speed when working.
|
Fig.9 Air bearing's average temperature with disk speed |
4 Conclusions
The pressure distribution of air bearings between magnetic heads and disks will be affected by different shapes of sliders and sizes of the disk bulge. The peak pressure of Tri-pad barotropic head slider is less than that of the flathead slider and distributes more evenly, which denotes that Tri-pad barotropic head slider has a better load-carrying capacity. The bulge on disk surface weakens the convergence of the wedge gap between magnetic heads and disks, resulting in the weak peak pressure of air bearings. Pressure distribution of air bearing will affect four heat transfer parameters of gas: thermal conductivity, dynamic viscosity, gas density, and the molecular free path. Thermal conductivity, gas density, and the molecular free path all have great influences on heat flux, which cannot be simplified to a constant when the head flight altitude is very low.
The average temperature of air bearings is affected by the head shape and the disk bulge's size. The average temperature of Tri-pad barotropic head slider is lower than that of the flathead slider under the same working conditions, which results from its special head morphology characteristics. However, Tri-pad barotropic head slider is more sensitive to the change of bulge radius and working conditions, which means it requires more rigorous working conditions. The bulge on disk surface will reduce the average temperature of air bearing. Bulge reduces local space so that the probability of molecular collision increases and the temperature becomes lower. The increase of the disk roll angle reduces the heat loss in the wedge space, leading to an increase of temperature in the air bearing. With the increase of pitch angle, the space between the magnetic head and disk is closer and heat is uneasy to dissipate so that the temperature increases. The increase of disk speed enhances the convective heat transfer between the magnetic head and disk, which leads to the decrease of air bearing temperature.
| [1] |
Thornton B H, Bogy D B. A numerical study of air-bearing slider form-factors. Journal of Tribology, 2004, 126: 553-558. DOI:10.1115/1.1691435 (  0) 0) |
| [2] |
Wahl M H, Kwon H, Talke F E. Simulation of asperity contacts at the head/disk interface of tri-pad sliders during steady-state Flying©. A S L E Transactions, 1997, 40(1): 75-80. DOI:10.1080/10402009708983631 (  0) 0) |
| [3] |
Zhao D P, Li Y H, Li Q X. Modeling, design and analysis of a micro flying slider in near-field optical storage system. Microsystem Technologies, 2017, 23(10): 4753-4774. DOI:10.1007/s00542-016-3260-1 (  0) 0) |
| [4] |
Liu N, Bogy D B. Boundary effect on particle motion in the head disk interface. Tribology Letters, 2009, 33(1): 21-27. DOI:10.1007/s11249-008-9387-1 (  0) 0) |
| [5] |
Gupta V, Bogy D B. Optimal slider-disk surface topography for head-disk interface stability in hard disk drives. IEEE Transactions on Magnetics, 2007, 44(1): 138-144. DOI:10.1109/TMAG.2007.911035 (  0) 0) |
| [6] |
Song W P, Ovcharenko A, Yang M, et al. Contact between a thermal flight altitude control slider and a disk asperity. Microsystem Technologies, 2012, 18(9-10): 1549-1557. DOI:10.1007/s00542-012-1591-0 (  0) 0) |
| [7] |
Song W P, Matthes L, Ovcharenko A, et al. Experimental study of slider dynamics induced by contacts with disk asperities. Microsystem Technologies, 2013, 19(9-10): 1369-1375. DOI:10.1007/s00542-013-1822-z (  0) 0) |
| [8] |
Campbell P M, Snow E S, Mcmarr P J. Fabrication of nanometer-scale side-gated silicon field effect transistors with an atomic force microscope. Applied Physics Letters, 1995, 66(11): 1388-1390. DOI:10.1063/1.113210 (  0) 0) |
| [9] |
Ma Y, Ghafari A, Budaev B V, et al. Measurement and simulation of nanoscale gap heat transfer using a read/write head with a contact sensor. IEEE Transactions on Magnetics, 2017, 53(2): 3300105. DOI:10.1109/TMAG.2016.2604209 (  0) 0) |
| [10] |
Chen L, Bogy D B, Strom B. Thermal dependence of MR signal on slider flying state. IEEE Transactions on Magnetics, 2000, 36(5): 2486-2489. DOI:10.1109/20.908482 (  0) 0) |
| [11] |
Zhou W D, Liu B, Yu S K, et al. A generalized heat transfer model for thin film bearings at head-disk interface. Applied Physics Letters, 2008, 92(4): 339. DOI:10.1063/1.2838454 (  0) 0) |
| [12] |
Xiong S M, Smith R, Wang N, et al. Thermal response time of media in heat-assisted magnetic recording. IEEE Transactions on Magnetics, 2017, 53(10): 331906. DOI:10.1109/TMAG.2017.2721901 (  0) 0) |
| [13] |
Hu Y Q, Wu H Y, Meng Y G, et al. Head flying characteristics in heat assisted magnetic recording considering various nanoscale heat transfer models. Journal of Applied Physics, 2018, 123(3): 034303. DOI:10.1063/1.5016873 (  0) 0) |
| [14] |
Duan R J, Huang F M, Wang Y, et al. Effects of soft interaction and non-isothermal boundary upon long-time dynamics of rarefied gas. Archive for Rational Mechanics and Analysis, 2019, 234: 925-1006. DOI:10.1007/s00205-019-01405-5 (  0) 0) |
| [15] |
Poon S W, Spiece J, Robson A J, et al. Probing thermal transport and layering in disk media using scanning thermal microscopy. Proceedings of the 2017 IEEE International Magnetics Conference (INTERMAG). Piscataway: IEEE, 2017. DOI: 10.1109/INTMAG.2017.8007793.
(  0) 0) |
| [16] |
Zheng J L, Chen Y K, Zhou Q. Heat transfer across a nanoscale pressurized air gap and its application in magnetic recording. Scientific Reports, 2018, 8: 3343. DOI:10.1038/s41598-018-21673-7 (  0) 0) |
| [17] |
Juang J Y, Bogy D B. Air-bearing effects on actuated thermal pole-tip protrusion for hard disk drives. Journal of Tribology, 2007, 129(3): 570-578. DOI:10.1115/1.2736456 (  0) 0) |
| [18] |
Wang S, Komvopoulos K. Electromagnetic and Thermomechanical analysis of near-field heat transfer in heat-assisted magnetic recording heads. IEEE Transactions on Magnetics, 2018, 54(8): 1-6. DOI:10.1109/TMAG.2018.2840482 (  0) 0) |
| [19] |
Li Z Y, Chen W B, Rea C, et al. Head and media design for curvature reduction in heat-assisted magnetic recording. IEEE Transactions on Magnetics, 2017, 53(10): 9300104. DOI:10.1109/TMAG.2017.2732940 (  0) 0) |
| [20] |
Mitsuya Y. Modified reynolds equation for ultra-thin film gas lubrication using 1.5-order slip-flow model and considering surface accommodation coefficient. Journal of Tribology, 1993, 115(2): 289-294. DOI:10.1115/1.2921004 (  0) 0) |
| [21] |
Chen L, Bogy D B, Strom B. Thermal dependence of MR signal on slider flying state. IEEE Transactions on Magnetics, 2000, 36(5): 2486-2489. DOI:10.1109/20.908482 (  0) 0) |
| [22] |
Chen D, Bogy D B. Simulation of static flying attitudes with different heat transfer models for a flying-height control slider with thermal protrusion. Tribology Letters, 2010, 40(1): 31-39. (  0) 0) |
 2021, Vol. 28
2021, Vol. 28


