The beam whose bending stiffness varies along the space position is usually called variable stiffness beam. Factors that cause the change of stiffness of the beam mainly include two aspects: the change of geometric parameters (i.e., variable cross-section beams), and the change of material parameters (i.e., beams made of non-homogeneous materials such as functionally graded materials and fiber reinforced composites). Among them, variable cross-section beams have been widely used in aviation, aerospace, civil, mechanical, and other engineering fields. The spatial variation of material parameters caused by the application of composite materials provides another possibility for the change of the structural stiffness. This variable stiffness structure has good designability and has attracted the attention of scholars both at home and abroad.
At present, there have been a lot of studies on the elastic analysis of variable cross-section beams. For example, Hu et al.[1] investigated the deformations of variable cross-section beams, and provided the solution of the deformation of the cantilever beam when the width and height of the cross-section are changed linearly with the axial coordinates. Wang et al. [2] simplified the arbitrary variation of the bending stiffness along the axis of the beam to the stepped stiffness by using Heaviside function, and derived a general equation for the deformation of the beam with arbitrary variable stiffness. Li et al.[3] established a general mechanical model for the elastic analysis of statically indeterminate beams with variable axial stiffness. In the elastic analysis of functionally graded beams, researchers[4-5] assumed that the elastic modulus of functionally graded materials varies along the height of the beam section, and proposed an analytical solution for the elastic analysis of beams with uniform cross section. Yang and Lü et al.[6-7] gave a semi-analytical solution to the elastic problem of functionally graded beams of equal-section with bi-directional gradient of elastic modulus along the axis and the section height direction of the beam. Benatta et al.[8] studied the plane-bending problem of composite short beams with variable fiber spacing along the height of beams. Zhang Jinghua et al.[9] used the Differential Quadrature Method (DQM) to analyze the elastic bending of functionally graded beams with variable cross-section considering the variation of cross-section size and material parameters along the length gradient of the beam. In terms of elastic-plastic analysis of variable stiffness beams, Fertis and Taneja[10] studied the elastoplastic behavior of axially variable stiffness beams using trial method. In Refs. [11-12], scholars assumed that the elastic modulus and the yield strength vary according to the exponential function along the height of the beam, and derived the analytical solution to the elastic-plastic problem of pure bending beams with functionally graded material.
Compared with elastic analysis, little research has been performed on the elastic-plastic analysis of variable stiffness beams, and the exact solutions are particularly difficult to be obtained. However, elastic-plastic analysis is necessary for reducing the weight of structures and making full use of the post-yield strength of materials. Therefore, this paper studies the elastic and elastic-plastic bending problems of axially variable stiffness beams based on the premise of small deformation.
2 Description of the Problem 2.1 Basic AssumptionsA variable stiffness beam with rectangular cross-section is discussed in this paper, as shown in Fig. 1.

|
Fig.1 Variable stiffness beam with rectangular section and the distribution of elastic-plastic stress |
The width of the cross-section of the beam is b, and the height h(x) varies in the form of an arbitrary function along the axis of the beam. The material of the beam is a non-uniform, isotropic, ideal elastoplastic material, and the tensile and compressive properties of the beam are the same. Influences of shear on deformation and yield are not considered in this paper. During the deformation process, the beam conforms to the assumption of flat section and small deflection. The cross-section height and bending stiffness of the beam can be expressed as
| $ {h(x) = {h_0}g(x)} $ | (1a) |
| $ {E(x)I(x) = {E_0}{I_0}f(x){g^3}(x)} $ | (1b) |
where h0 and E0 are constants, representing the reference values of the section height and the elastic modulus of the materials respectively. I0=bh03/12 is the reference value of moment of inertia of the beam section. f(x) and g(x) represent the variation of elastic modulus and the cross-section height along the length of the beam respectively, and can take arbitrary function. It was further assumed that the yield strength of the material varies arbitrarily along the length of the beam, as follows:
| $ {\sigma _s}(x) = {\sigma _{s0}}s(x) $ | (2) |
When the variable stiffness beam is in the state of elastic deformation, the deflection w of any point on the beam can be expressed by we. Then the approximate differential equation of the deflection curve can be expressed as
| $ \frac{{{{\rm{d}}^2}{w_e}}}{{{\rm{d}}{x^2}}} = - \frac{{M(x)}}{{E(x)I(x)}} $ | (3) |
where M(x) is the cross-section moment. Integrate the above equation twice to get
| $ {w_e} = \frac{1}{{{E_0}{I_0}}}\int {\left[ { - \int {\frac{{M(x){\rm{d}}x}}{{f(x){g^3}(x)}}} } \right]} {\rm{d}}x + {C_1}\int {\rm{d}} x + {C_2} $ | (4) |
where C1 and C2 are the integral constants determined by the boundary conditions at both ends of the beam. When f(x), g(x), and the section moment equation M(x) are some special functions, the analytical solution of the elastic deformation of the beam can be obtained by solving the above equation. For other complex cases, numerical methods can be used.
The shear deflection of the cantilever beam was analyzed, in which the case of a plane elastic cantilever beam with shorter length and narrow rectangular cross-section was considered. For the analysis of shear deflection of slender beams, the value of shear deflection is small compared with the bending deflection, which is thus ignored. For beams with shorter length and narrow rectangular cross-section, the shear deflection in the elastic region is considered in this paper, and the shear deflection of the plastic region will be studied in another research in the future. A beam with shorter length and narrow rectangular cross-section was considered, which was subjected to a tangential load P (concentrated force) at the free end, and P can be expressed as the integral of the shear stress to the cross-section as below:
| $ P = \int_{ - h/2}^{h/2} {\int_{ - b/2}^{b/2} {{\tau _{yz}}} } {\rm{d}}y{\rm{d}}z $ | (5) |
The distribution of tangential force (shear force) at the cantilever end (free end) is defined as obeying a parabolic distribution in this paper.
Then, the Timoshenko theory in material mechanics was adopted to derive the additional shear deflection formula of the beam. According to Ref. [13], it was assumed that the direction of shear stress at each point on the cross-section is parallel to that of the shear force P, and the shear stress is distributed uniformly along the width direction of the cross-section. The shear stress in a beam section can be expressed as
| $ {\tau _{yz}} = - \frac{P}{{2I(x)}}(\frac{{{h^2}(x)}}{4} - {y^2}) $ | (6) |
Here, it can be found that the shear stress varies parabolically with the z-axis, and there is
| $ {\tau _{{\rm{max}}}} = - \frac{{P{h^2}(x)}}{{8I(x)}} = - \frac{{3P}}{{2bh(x)}} $ |
at the neutral axis (y=0).
It was assumed that the lines that parallel to the neutral axis of the beam section before the deformation of the beam are still parallel to each other after the deformation. Then we can obtain the following differential equation of the shear deflection of the beam with variable cross-section[13-14] as
| $ \frac{{{\rm{d}}{w_{sh}}}}{{{\rm{d}}x}} = - \frac{{{a_s}P}}{{GA(x)}} = - \frac{{{a_s}P}}{{Gbh(x)}} $ | (7) |
Eq.(8) can be obtained by integrating the two sides of Eq.(7), as follows:
| $ \begin{array}{l} {w_{{\rm{sh}}}} = \int_0^l {( - \frac{{{a_s}P}}{{Gbh(x)}})} {\rm{d}}x + {C_{{\rm{sh}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^l {( - \frac{{{a_s}P}}{{Gb{h_0}g(x)}})} {\rm{d}}x + {C_{{\rm{sh}}}} \end{array} $ | (8) |
Eq.(8) is the basic integral formula for solving shear deflection of the beam with variable rectangular cross-section. Here, Csh is the integral constant and can be obtained by the boundary condition of the fixed end in which the shear deflection is zero. αs is the Cowper's shear inhomogeneity coefficient, which can be obtained by the following equation:
| $ {\alpha _s} = \frac{{12 + 11\nu }}{{10(1 + \nu )}} $ | (9) |
With the increase of the external load on the beam, the bending moment of the beam section will be gradually increased. When the bending moment of a section equals to its limit of elastic bending moment, the beam enters the state of elastic limit. For variable stiffness beams with rectangular cross-section, the elastic limit moment Me is a function about the axial coordinates of the beam, as follows:
| $ {M_e}(x) = \frac{1}{{12}}bh_0^2{\sigma _{s0}}{g^2}(x)s(x) $ | (10) |
With the further increase of the external load, the beam will be changed from the elastic limit state to the elastic-plastic deformation state. For the elastic region of an elastic-plastic deformed beam, the deflection still satisfies the basic equation as shown in Eq.(4). For any section x in the plastic zone along the direction of the beam's length, in general, there are both elastic and plastic zones in this cross section. In the elastic region of the beam section, the bending normal stress is linearly distributed. In the plastic region of the beam section, the bending normal stress is equal to the yield stress (Fig. 1). The boundary line of elastic region and plastic region at beam section x was set as ys(x). According to the stress on the boundary line that has reached the yield strength, the differential equation of deflection curve in the plastic region of the beam can be obtained as follows:
| $ \frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}} = - \frac{{{\sigma _s}(x)}}{{E(x){y_s}(x)}} $ | (11) |
where wp represents the deflection of the plastic region of the beam, and ys(x) can be obtained according to the equilibrium conditions between the internal and external bending moments on the cross-section, as follows:
| $ \left( {\frac{{{I_1}(x)}}{{{y_s}(x)}} + {s_1}(x)} \right){\sigma _s}(x) = M(x) $ | (12) |
where I1(x) denotes the moment of inertia of the elastic region on the cross-section about the z-axis, and s1(x) denotes the sum of the absolute values of the static moment of the plastic region about the z-axis. ys(x) can be obtained by solving Eq.(12) as follows:
| $ {y_s}(x) = \frac{{\sqrt 3 }}{2}h(x)\sqrt {1 - \frac{{M(x)}}{{{M_p}(x)}}} $ | (13) |
where Mp(x)=(1/4)bh02σs0g2(x)s(x) is the limit value of the plastic moment of a beam with rectangular cross-section. By substituting Eq.(13) into Eq.(11), the basic equation for the deformation of the plastic region of the beam can be expressed as
| $ \frac{{{{\rm{d}}^2}{w_p}}}{{{\rm{d}}{x^2}}} = - \frac{{2\sqrt 3 {\sigma _s}(x)}}{{3E(x)h(x)}}{\left( {1 - \frac{{M(x)}}{{{M_P}(x)}}} \right)^{ - \frac{1}{2}}} $ | (14) |
Integrating the above equations twice, we can get
| $ \begin{array}{l} {w_p} = \frac{{{\sigma _{s0}}}}{{{E_0}{h_0}}}\int {\left\{ { - \int {\left[ {\frac{{2\sqrt 3 s(x)}}{{3f(x)g(x)}}{{\left( {1 - \frac{{M(x)}}{{{M_P}(x)}}} \right)}^{ - \frac{1}{2}}}} \right]} {\rm{d}}x} \right\}} {\rm{d}}x + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {D_1}\int {\rm{d}} x + {D_2} \end{array} $ | (15) |
where D1 and D2 are the integral constants. For elastoplastic deformed beams, the deflection curve needs to be solved by combining Eqs.(4), (8), and (15). Therefore, the integral constants C1 and C2 in Eq.(4), Csh in Eq.(8), and D1 and D2 in Eq.(15) were determined by the boundary conditions at both ends of the beam and the continuity conditions at the junction between the elastic and plastic zones along the length of the beam. In Eq.(15), when f(x), g(x), s(x), and M(x) are some special functions, the analytical solution of the plastic deformation of the variable stiffness beam can be obtained by integration. For other cases, Eq.(15) can be solved by numerical methods. Since the basic equations for the deformations of the elastic zone and the plastic zone along the length of the beam are different, when solving elastic-plastic deformation of the beam with variable stiffness, the coordinates xep of the boundary points between the elastic and plastic zone along the axis of the beam must be determined first.
| $ M({x_{{\rm{ep}}}}) - {M_e}({x_{{\rm{ep}}}}) = 0 $ | (16) |
where xep can be obtained by solving Eq.(16), and then the distribution of elastic and plastic zones along the axis of the beam can be determined easily. Given the cross-section moment M(x) of a variable stiffness beam, the extension depth of plasticity along the length of the beam and the height of the beam section, namely xep and ys(x), can be determined by Eqs.(13) and (16).
The analytical solutions of elastic and elastic-plastic deformations of the variable stiffness beam were proposed, whose cross-section height, elastic modulus, and yield strength varied according to some special functions. For the cases where the bending stiffness is arbitrarily changed along the axis of the beam, the numerical method DQM was used to solve the problem.
3 Solution of the Problem 3.1 Elastic Analysis 3.1.1 Uniform material beam with linear variation of the section heightIt was assumed that the section height of the variable stiffness beam varies linearly along the length of the beam, while the elastic modulus of the material was kept constant, as follows:
| $ {g(x) = 1 - {\lambda _1}\frac{x}{l}} $ | (17a) |
| $ {f(x) = {\rm{const}} } $ | (17b) |
where 0≤λ1 < 1 is a constant. Eq.(17) was substituted into Eq.(4), and then the exact expression of the deflection of the variable cross-section beam can be obtained by the direct integration of Eqs.(4) and (8). The deflection for a cantilever beam fixed at the left end and subjected to a concentrated load P at the right end is expressed as follows:
| $ \begin{array}{l} {w_e}(x) = \frac{{6p{l^2}}}{{{t_1}}}[{\lambda _1}({\lambda _1} + 1)x + 2l {\rm{In}} (l - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _1}x) + {t_2}] + \frac{{6p{l^4}({\lambda _1} - 1)}}{{{t_1}(l - {\lambda _1}x)}} \end{array} $ | (18a) |
| $ {w_{{\rm{sh}}}}(x) = \frac{{(12 + 11\nu ){\alpha _s}p{l^2}}}{{10Gb{\lambda _1}(1 + \nu )}}[{\rm{In}}|1 - \frac{{{\lambda _1}x}}{l}|] $ | (18b) |
| $ w(x) = {w_e}(x) + {w_{{\rm{sh}}}}(x) $ | (18c) |
where t1=12E0I0λ13, t2=(λ1-1)l-2lInl, and G=E/(2+2ν). G denotes the shear modulus of the beam, and v denotes the Poisson's ratio of the beam. It can be seen from Eq.(18c) that the deflection of the beam is a function of parameter λ1, representing the section height. By reasonably choosing the value of λ1, the stiffness of the beam can be effectively improved.
In Eq.(18c), when λ1→0, the limit of the deflection is
| $ \begin{array}{l} {w_0}(x) = \mathop {\lim }\limits_{{\lambda _1} \to 0} w(x) = \frac{{p{x^2}(3l - x)}}{{6{E_0}{I_0}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{p(12 + 11\nu )}}{{10Gb{h_0}(1 + \nu )}}x \end{array} $ | (19) |
The above equation is the deflection expression of a beam with uniform isotropic material, which is consistent with the solution given in the book of material mechanics [15].
3.1.2 Uniform material beam with exponential change of the section heightIt was assumed that the section height of the variable stiffness beam varies exponentially along the length of the beam, and the elastic modulus of the material was kept constant.
| $ {g(x) = {\rm{exp}}\left( {{a_1}\frac{x}{l}} \right)} $ | (20a) |
| $ {f(x) = {\rm{const}} } $ | (20b) |
where a1 is a constant. Eq.(20) was substituted into Eq.(4). To simplify the analysis, the shear deflection is not considered for the slender beam in this section. The exact solution of the deflection of a cantilever beam of variable stiffness subjected to a concentrated load P at the right end can be obtained by the direct integration of Eq.(4), as follows:
| $ \begin{array}{l} {w_e}(x) = \frac{{4p{l^2}}}{{{t_3}}}[3(3{a_1} - 1){a_1}x + (2 - 3{a_1})l] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{4{p^2}}}{{{t_3}}}[3{a_1}(l - x) - 2l]{\rm{exp}}\left( { - \frac{{3{a_1}}}{l}x} \right) \end{array} $ | (21) |
where t3=108E0I0a13. In Eq.(21), when a1→0, the limit of the deflection is consistent with the solution given in the book of material mechanics[15].
3.1.3 Uniform material beam with parabolic variation of the section heightIt was assumed that the section height of the variable stiffness beam varies in parabolic form, and the elastic modulus of the material was kept unchanged, as shown below:
| $ {g(x) = 1 - {\beta _1}{{\left( {\frac{x}{l} - \frac{1}{2}} \right)}^2}} $ | (22a) |
| $ {f(x) = {\rm{const}} } $ | (22b) |
where β1≥0 is a constant. The shear deflection will not be considered for the slender beam to simplify the analysis. Similarly, Eq.(22) was substituted into Eq.(4), and the expression of the deflection of the simply supported beam subjected to the uniform load q can be obtained by the direct integration of Eq.(4). The deflection of a simply supported beam with β1=1 is expressed as
| $ \begin{array}{l} {w_e}(x) = \frac{{9q{l^6}}}{{4{t_4}(3{l^2} + 4lx - 4{x^2})}} + \frac{{21q{l^3}}}{{32{t_4}}}(2x - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} l ) {\rm{arctan}} \left( {\frac{1}{2} - \frac{x}{l}} \right) - \frac{{12.4646q{l^4}}}{{32{t_4}}} \end{array} $ | (23) |
where t4=12E0I0. When β1 is an arbitrary value, the expression of deflection is complex, which is omitted here. When β1→0, the deflection expression of the uniformly isotropic simply supported beams with equal section can also be obtained by the limit of the deflection.
3.1.4 Equal-Section Beam with Linear Variation of Elastic ModulusIt was assumed that the elastic modulus of the material of the variable stiffness beam varies linearly along the length of the beam, while the height of the beam section remains unchanged, as shown below:
| $ {f(x) = 1 - {\lambda _2}\frac{x}{l}} $ | (24a) |
| $ {g(x) = {\rm{const}} } $ | (24b) |
where 0≤λ2 < 1 is a constant. Again, the shear deflection is considered for the slender beam for simplicity. Eq.(24) was substituted into Eq.(4), and then the deflection of a cantilever beam which is fixed at the left end and subjected to a concentrated load P at the right end can be obtained by the direct integration of Eq.(4) as
| $ \begin{array}{l} {w_c}(x) = \frac{{6pl}}{{{t_5}}}\{ 2l({\lambda _2} - 1)({\lambda _2}x - l)[{\rm{In}}l - {\rm{In}} l - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _2}x)] + 2l({\lambda _2} - 1){\lambda _2}x + \lambda _2^2x\} \end{array} $ | (25) |
where t5=12E0I0λ23. It can be seen from Eq.(25) that the deflection of the beam is a function of parameter λ2, representing the elastic modulus of the material of the beam. The deformation of the beam can be effectively controlled by reasonably choosing the value of λ2. Similarly, for Eq.(25), when λ2→0, the limit of deflection is the deflection expression of the uniform material beam with equal cross-section.
3.1.5 Equal-section beam with exponential change in elastic modulusIt was assumed that the elastic modulus of the material varies exponentially along the length of the beam, while the height of the section remains unchanged, as shown below:
| $ {f(x) = {\rm{exp}} \left( {{a_2}\frac{x}{l}} \right)} $ | (26a) |
| $ {g(x) = {\rm{const}} } $ | (26b) |
where a2 is a constant. The shear deflection will not be considered for the slender beam for the simplicity of the problem analysis. Eq.(26) was substituted into Eq.(4), and then the deflection of the variable stiffness cantilever beam subjected to a concentrated load P at the right end can be obtained by the direct integration of Eq.(4), as shown below:
| $ \begin{array}{l} {w_e}(x) = \frac{{12p{l^2}}}{{{t_6}}}\{ ({a_2} - 1){a_2}x + [({a_2} - 2)l - {a_2}x] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \exp \left( { - \frac{{{a_2}}}{l}x} \right) + (2 - {a_2})l\} \end{array} $ | (27) |
where t6=12E0I0a23. For Eq.(27), when a2→0, the limit of the deflection is the same as the case with equal cross-section described in Section 3.1.1.
3.1.6 Beam with exponential change of elastic modulus and linear change of section heightIt was assumed that the elastic modulus of the material varies exponentially along the axis of the beam, and the cross-section height of the variable stiffness beam varies linearly, as follows:
| $ {f(x) = {\rm{exp}}\left( {{a_2}\frac{x}{l}} \right)} $ | (28a) |
| $ {g(x) = 1 - {\lambda _1}\frac{x}{l}} $ | (28b) |
In this section, the shear deflectionis not considered for the slender beam (for the simplicity of the problem analysis). By substituting Eq.(28) for Eq.(4), the expression of deflection can be obtained by direct integration of Eq.(4).
The deflection of the cantilever beam fixed at the left end and acted by a concentrated load P at the right end is expressed as follows:
| $ {w_e}(x) = \frac{{p{l^2}}}{{{E_0}{l_0}\lambda _1^3a_2^2}}[{w_1}(x) - {w_2}(x) + {w_3}] $ | (29) |
where,
| $ \begin{array}{l} {w_1}(x) = {a_2}\lambda _1^2x + a_2^2{\lambda _1}({\lambda _1} - 1){\rm{exp}}\left( { - \frac{{{a_2}}}{{{\lambda _1}}}} \right){E_i}\left( {\frac{{{a_2}}}{{{\lambda _1}}}} \right)x\\ {w_2}(x) = [{a_2}({\lambda _1} - 1) - {\lambda _1}]{\lambda _1}l{\rm{exp}}\left( { - \frac{{{a_2}x}}{l}} \right) + a_2^2({\lambda _1} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 ) {\rm{exp}} \left( { - \frac{{{a_2}}}{{{\lambda _1}}}} \right) \cdot {E_i}\left( {\frac{{{a_2}}}{{{\lambda _1}}} - \frac{{{a_2}x}}{l}} \right)({\lambda _1}x - l)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_3}(x) = {\lambda _1}[{a_2}({\lambda _1} - 1) - {\lambda _1}]l - a_2^2({\lambda _1} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1)l {\rm{exp}} \left( { - \frac{{{a_2}}}{{{\lambda _1}}}} \right)Ei\left( {\frac{{{a_2}}}{{{\lambda _1}}}} \right) \end{array} $ |
where Ei(z) represents the exponential integral function. In Eq.(29), the deflection of the beam can still be the same as the case with equal cross section, when a2→0 and λ1→0. For other types of beams, such as simply supported beams and statically determinate beams with multiple spans, the analytical solution of the deflection of the variable stiffness beam can also be obtained by integration or piecewise integration, if the moment equation of the beam is relatively simple.
3.2 Elastoplastic AnalysisWhen the variable stiffness beam enters the state of elastic-plastic deformation, the extension depth of plasticity along the beam length and the section height can be determined according to Eqs.(13) and (16). The deflections of the elastic and plastic region of the beam were obtained based on Eqs.(4) and (15).
Then, the analytical solution to the plastic deformation of the variable stiffness beam with linear variation of elastic modulus was provided. For other variation forms of the beam section height and the elastic modulus, DQM was used to realize the elastic and plastic analysis of the beam.
3.2.1 Plastic deformation of equal-section beams with linear variation of the elastic modulusThe elastic modulus and section height of the variable stiffness beam conformed to the variation in Eq.(24). When the yield strength of the material of the beam is kept constant, the deformation of the plastic zone of the cantilever beam subjected to a concentrated load P at the end can be obtained from Eq.(15), as follows:
| $ {w_p}(x) = {D_1} + {D_2}x - \frac{{{T_1}(x)}}{{{T_2}(x)}} $ | (30) |
where D1 and D2 are integral constants, which can be determined according to the boundary conditions and the continuity conditions at the junction between the elastic and plastic zone.
| $ \begin{array}{l} {T_1}(x) = 4{\sigma _{s0}}l\{ - {z_1}z_2^2(x) + p({\lambda _2}x - l){z_2}(x) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arctan}}[{\lambda _2}{z_2}(x)/{z_1}]\} \end{array} $ | (31a) |
| $ {z_1} = \sqrt {({1_2} - 1){\lambda _2}pl - \lambda _2^2{M_p}} $ | (31b) |
| $ {T_2}(x) = \sqrt {3/{M_p}} {E_0}{h_0}p{\lambda _2}{z_1}{z_2}(x) $ | (31c) |
| $ {z_2}(x) = \sqrt {(x - l)p + {M_p}} $ | (31d) |
If the bending stiffness of a variable stiffness beam varies according to an arbitrary function along the length of the beam, the basic Eqs.(4) and (15) of the elastic and plastic deformation for the beam can not be solved by direct integration. Thus, the numerical solution was obtained by using the DQM, which is an effective numerical method for solving differential equations. The outstanding advantages of DQM are simple mathematical principle, strong operability, fast convergence, and high accuracy of the solution. In particular, DQM starts directly from the governing differential equation of the problem, and does not depend on the Functional Analysis or the variational principle in calculation. The boundary conditions need not be dealt with separately, whose basic principle is to approximate the partial derivative or integral of a function at a discrete point by using the weighted sum of the function values of all discrete points in the physical domain. Considering that the one-dimensional function φ(ξ) is continuously differentiable in the interval [0, 1], the approximation equation of the r-order partial derivative of the function φ(ξ) at the i-th discrete point using DQM[16-19] can be written as
| $ {\left. {\frac{{{\partial ^r}\varphi (\xi )}}{{\partial {\xi ^r}}}} \right|_{{\xi _i}}} = \sum\limits_{j = 1}^N {A_{ij}^{(r)}} \varphi ({\xi _j}),i = 1,2, \cdots ,N $ |
where N is the total number of grid dots, ξi is the coordinate value of grid dot, and φ(ξj) is the function value at the discrete point ξj. Aij(r) is the weight coefficient matrix of the r-th derivative and is expressed as follows:
| $ \begin{array}{l} A_{ij}^{(r)} = - \sum\limits_{v = 1,v \ne i}^N {A_{iv}^{(r)}} ,i = 1,2, \cdots ,N,1 \le r \le N - 1\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} A_{ij}^N = \frac{{\prod\limits_{v = 1,v \ne i}^N {({\xi _i} - {\xi _v})} }}{{({\xi _i} - {\xi _j})\prod\limits_{v = 1,v \ne j}^N {({\xi _j} - {\xi _v})} }}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} A_{ij}^{(r)} = r\left[ {A_{ii}^{(r - 1)}A_{ij}^{(1)} - \frac{{A_{ij}^{(r - 1)}}}{{{\xi _i} - {\xi _j}}}} \right] \end{array} $ |
where i, j=1, 2, ..., N, j≠i; 2≤r≤N-1.
The commonly used integration points including equidistant points and unequal spacing points are as follows:
| $ \begin{array}{*{20}{l}} {\quad \quad \quad \quad \quad {\xi _i} = \frac{{i - 1}}{{N - 1}}}\\ {{\xi _i} = \frac{1}{2}\left[ {1 - \cos \frac{{{\rm{ \mathsf{ π} }}(i - 1)}}{{N - 1}}} \right],i = 1,2, \cdots ,N} \end{array} $ |
When using DQM to realize elastic-plastic analysis of variable stiffness beams, it is necessary to first implement dimensionless for each physical quantity.
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi = \frac{x}{l},{W_e} = \frac{{{W_e}}}{l},{W_p} = \frac{{{W_p}}}{l}\\ H = \frac{h}{l},B = \frac{b}{l},\bar E = \frac{E}{{{E_0}}},{{\bar \sigma }_s} = \frac{{{\sigma _s}}}{{{E_0}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \bar M = \frac{M}{{{E_0}{l^3}}},{{\bar M}_p} = \frac{{{M_p}}}{{{E_0}{l^3}}} \end{array} $ |
The differential quadrature discretization was performed on Eqs.(3) and (14), and the following results were obtained.
Elastic zone:
| $ \sum\limits_{j = 1}^{{N_1}} {A_{ij}^{(2)}} {W_{ej}} = - \frac{{12\bar M({\xi _i})}}{{\bar E({\xi _i})B{H^3}({\xi _i})}} $ |
Plastic zone:
| $ \sum\limits_{j = 1}^{{N_2}} {A_{ij}^{(2)}} {W_{pj}} = - \frac{{2\sqrt 3 {{\bar \sigma }_s}({\xi _i})}}{{3\bar E({\xi _i})H({\xi _i})}}{\left[ {1 - \frac{{\bar M({\xi _i})}}{{{{\bar M}_p}({\xi _i})}}} \right]^{ - \frac{1}{2}}} $ |
where Aij(2) represents the weight coefficient of the second derivative, and N1 and N2 represent the total number of dots in the elastic and plastic regions respectively. After the boundary conditions and the continuity conditions between the elastic and plastic zone are discretized using DQM, the displacement of each discrete points on the variable stiffness beam can be obtained by simultaneous solution.
4 Numerical SimulationsExample 1: A cantilever beam with a fixed left end and a free right end was considered, whose section height varies linearly along the length of the beam, and the elastic modulus of the material varies according to an exponential function, as presented in Eq.(28). The geometrical parameters of the beam and the load acting on the beam are l=1000 mm, b=100 mm, and P=100 kN, respectively. The section height, elastic modulus, and yield strength of the cantilever end are h=200 mm, E=2.06×105 MPa, and σs0=235 MPa, respectively. λ1 represents the variation parameter related to the section height of the beam, and a2 represents the variation parameter related to the elastic modulus of the material. When λ1 and a2 take different values, the elastic deformation of the beam is shown in Fig. 2.
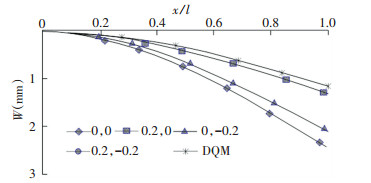
|
Fig.2 Elastic curves of the variable stiffness cantilever beam |
In Fig. 2, "0, 0" and "0.2, -0.2" represent the accuracy solutions when λ1 and a2 are taken with these values. "DQM" represents the calculated result using DQM with λ1=0.2 and a2=-0.2, where the eleven equidistant grid points were used. It can be seen from Fig. 2 that the maximum deflection of the beam would be gradually decreased with the increase of the section height and the elastic modulus of the material from the cantilever end to the fixed end. The influence of the change of the section height on the deflection of the beam was greater than that of the change of the elastic modulus of the material.
By reasonably adjusting the variation of the bending stiffness along the axis of the beam, the deformation of the beam can be effectively controlled. The calculated result using DQM was close to the exact solution, which verifies the correctness of this method in the elastic analysis of variable stiffness beams.
Example 2: Considering a variable stiffness cantilever beam, its elastic modulus varies linearly along the axis of the beam, and its section height and the yield strength were kept constant, namely, f(x)=1-λ2(x/l), g(x)=1, and s(x)=1. Other geometric and material parameters are the same as those in Example 1, and the elastoplastic analysis was carried out.
First, the elastic limit moment of the variable stiffness cantilever beam is expressed as Me=156.67 kN·m. When the maximum bending moment acting on the beam is different multiple of the elastic limit bending moment of the beam, the distribution of elastic and plastic zones along the section height and axis direction of the beam can be obtained according to Eqs.(13) and (16), as shown in Fig. 3.

|
Fig.3 Distribution of the elastic and plastic zones of the variable stiffness cantilever beam |
It can be seen from Fig. 3 that the plasticity would be expanded along the section height and axis of the beam with the increase of the load. However, the distribution of elastic and plastic zones of the variable stiffness beam was only related to the external loads, yield strength, and section height, but not the variation parameter λ2 of the elastic modulus of materials.
The deflection of the cantilever beam into the elastic-plastic deformation stage can be calculated by Eqs.(25) and (30). When λ2=0.2 and 0.5, the relationship between the displacement and the load at the right end is shown in Fig. 4.
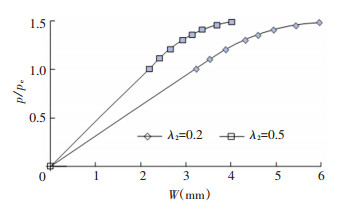
|
Fig.4 Load-displacement curves of cantilever end of the variable stiffness cantilever beam |
pe represents the elastic limit load. It can be seen from Fig. 4 that the deflection of the cantilever end acted in the same load was greatly different when λ2 takes different values. Therefore, the non-uniformity of the material can be used to improve the stiffness of the beams by reasonably choosing the parameters of elastic modulus changing along the length of the beam. When the variable parameter λ2 of the elastic modulus is 0.2 and the load acting on the cantilever end is 1.4pe, the elastic-plastic deformation of the cantilever beam with variable stiffness was calculated by DQM and analytical method, as shown in Fig. 5.
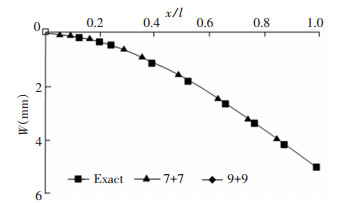
|
Fig.5 Elastic-plastic deformation of the cantilever beam with variable stiffness when the exerted load P is 1.4pe |
In Fig. 5, "7+7" and "9+9" represent the size of the grid of the differential quadrature in elastic and plastic regions respectively, namely N1 and N2. "Exact" denotes the exact solution obtained by Eqs.(25) and (30). It can be found that the calculated results using DQM were in good agreement with the exact solutions, which fully demonstrates the correctness of DQM. Meanwhile, the results obtained by using 14 nodes and 18 nodes were consistent, reflecting the convergence of DQM. Therefore, DQM can be used for the cases where the bending stiffness and yield strength of the material have special changes, as well as for elastic and plastic analysis of beams with arbitrary variable stiffness.
If yield strength varies along the axis of the beam, such as s(x)=1-0.2(x/l), the elastic limit moment of the beam is a function of the axial coordinates of the beam according to Eq.(10). The maximum value occurred at the fixed end of the beam, namely, Memax=195.83 kN·m. Further, the extension depth of plasticity along the length of the beam and the section height can be determined according to Eqs.(13) and (16), and the results are shown in Fig. 6.
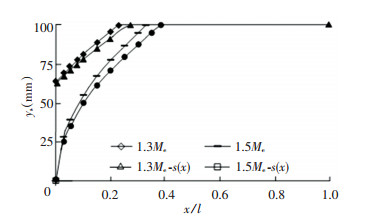
|
Fig.6 Plastic expansion of variable stiffness cantilever beam with yield strength varied by different function forms |
In Fig. 6, ″1.3Me(or 1.5Me)″ and ″1.3Me-s(x)(or 1.5Me-s(x))″ represent the distribution of elastic and plastic zones of the beam acted under different elastic limit moments when the yield strength of the beam is constant and linear. It can be seen from Fig. 6 that the change of the yield strength along the axial direction of the beam had a great influence on the plastic expansion of the beam. Under the same multiple elastic limit moment, the extension length of plasticity along the axis of the beam when the yield strength of the beam changed linearly was larger than that of the yield strength which was kept constant.
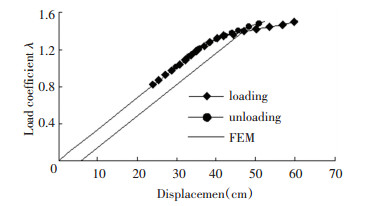
Example 3: To further verify the computational efficiency and the accuracy of DQM in analyzing the elastoplastic problem of a beam, DQM and finite element method (FEM) were used to analyze the elastic-plastic behavior of the cantilever beam subjected to a concentrated load at the free end. It was assumed that the section height of the variable stiffness beam varied in parabolic form, and the elastic modulus of the material was kept unchanged, i.e., f(x)=1 and g(x)=1-β1 (x/l)-0.52. The geometrical parameters of the beam and the load acting on the beam are l=8900 mm, b=100 mm, and P=18 kN, respectively. The section height, elastic modulus, and yield strength of the cantilever beam are h=200 mm, E=2.06×105 MPa, and σs0=235 MPa, respectively. For analysis using DQM, 11 differential quadrature grid points were selected along the length of the beam to implement calculation. For analysis using FEM, 10 Gaussian points were selected along the length of the beam to implement simulation. The calculation results of the two methods were compared, as shown in Fig. 7, where the loading and unloading curves represent the results obtained by DQM, and FEM represents the result obtained by using FEM. λ=Preal/P denotes the load coefficient.
|
Fig.7 Load-displacement curve of the cantilever beam |
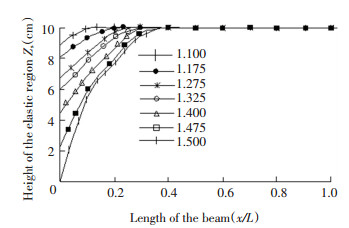
It can be seen from Fig. 7 that the load-displacement curves of the beam obtained by the two methods were very close, indicating the correctness of the analysis for the elastoplastic bending problem of the beam using DQM. Fig. 8 shows the distribution of the boundary line between the elastic region and the plastic region of the beam when subjected to different loads. The legend represents the load coefficients. In finite element analysis, the calculation is very time-consuming because there are 100 Gaussian points on the beam. In addition, the calculation result is limited by the load step size. When the load step size becomes a little large, the calculation result will not be converged. However, the DQM used in this paper directly solved the differential equation of the elastoplastic equilibrium of the beam to obtain the displacement of each discrete point on the beam, and it only requires a few grid points to quickly achieve a sufficiently accurate result.
|
Fig.8 Distribution of the elastic-plastic region on the cantilever beam |
Hence, the utilization of DQM is not limited by the load step size and does not need to be solved iteratively, so the calculation accuracy and efficiency are much better than those of FEM. DQM is especially suitable for the case where the analytical solution of the deflection cannot be obtained by direct integration. If the bending stiffness (such as cross-section height h(x) or elastic modulus E(x)) of a beam with variable stiffness varies according to some special functions (such as linear, parabolic, and simple exponential functions) along the length of the beam, the basic equations of the elastic and plastic deformation of the beam can be solved by direct integration to obtain its accurate analytical solution.
5 DiscussThe above method for elastic-plastic analysis of variable stiffness beams based on an ideal elastic-plastic material model can be further extended to other elastic-plastic material models, such as linear hardening materials. For the variable stiffness beam composed of linear hardening materials, the approximate differential equations of the deflection curve in the elastic and plastic regions were the same with those in Eqs.(3) and (11). The ys(x) of the boundary position between elastic and plastic zones on a given section can be calculated by Eq.(12). For Eq.(12), s1(x) relates to the hardening parameters of material. The elastic and elastic-plastic bending problems of axially variable stiffness beams composed of linear hardening materials can be further studied by using the same method as mentioned above.
6 ConclusionsIt was assumed that the height of the beam of rectangular section, the elastic modulus of the material, and the yield strength are arbitrary functions about the axial coordinate of the beam. The elastic and elastic-plastic bending problems of beams with variable stiffness were studied on the basis of plane bending. The analytical solutions of elastic and elastic-plastic deformations of variable stiffness beams with section height and elastic modulus that varied according to special functions were given. DQM was used to analyze the deformations when the bending stiffness of the beams varied arbitrarily along the axis direction of the beam. The research showed that by reasonably adjusting the variation of the bending stiffness of the beam along the length direction of the beam, the variable section and material non-uniformity could be fully utilized to reduce the maximum deflection of the beam. In addition, the change of beam section height had a greater effect on deflection than that of elastic modulus. The distribution of elastic and plastic zones along the length and height of the variable stiffness beams was only related to the external load, yield strength, and beam section height, but not the change of the elastic modulus of materials. The comparison between the results of DQM and the FEM solutions has shown that the DQM is correct and effective in elastic and elastic-plastic analysis of variable stiffness beams. The research results provide certain reference and conditions for the elastic-plastic analysis and design of axially variable stiffness beams in practical engineering.
| [1] |
Hu Qiping, Li Zhenning. Broken line converting method for bending analysis of heterogeneous beam with variable cross-section. Engineering Mechanics, 2000, 17(5): 113-114. DOI:10.3969/j.issn.1000-4750.2000.05.018 (  0) 0) |
| [2] |
Wang J, Chen J K, Liao S. An explicit solution of the large deformation of a cantilever beam under point load at the free tip. Journal of Computational and Applied Mathematics, 2008, 212(2): 320-330. DOI:10.1016/j.cam.2006.12.009 (  0) 0) |
| [3] |
Li X J, Zhu P Y, Liu Y L. Computerized solution of statically indeterminate beams with varying flexural rigidity under complex load. Engineering Mechanics, 2003, 20(4): 116-121. (in Chinese) DOI:10.3969/j.issn.1000-4750.2003.04.020 (  0) 0) |
| [4] |
Zhong Z, Yu T. Analytical bending solution of functionally graded cantilever-beam. Journal of Tongji University (Natural Science), 2006, 34(4): 443-447. (in Chinese) DOI:10.3321/j.issn:0253-374X.2006.04.004 (  0) 0) |
| [5] |
Lü C F, Chen W Q, Zhong Z. Two-dimensional thermoelasticity solution for functionally graded thick beams. Science in China Series G: Physics, Mechanics and Astronomy, 2006, 49(4): 451-460. DOI:10.1007/s11433-006-0451-2 (  0) 0) |
| [6] |
Yang Q, Zheng B L, Zhang K, et al. Analytical solution of a bilayer functionally graded cantilever beam with concentrated loads. Archive of Applied Mechanics, 2013, 83(3): 455-466. DOI:10.1007/s00419-012-0693-6 (  0) 0) |
| [7] |
Lü C F, Chen W Q, Xu R Q, et al. Semi-analytical elasticity solutions for bi-directional functionally graded beams. International Journal of Solids and Structures, 2008, 45(1): 258-275. DOI:10.1016/j.ijsolstr.2007.07.018 (  0) 0) |
| [8] |
Benatta M A, Tounsi A, Mechab I, et al. Mathematical solution for bending of short hybrid composite beams with variable fibers spacing. Applied Mathematics and Computation, 2009, 212(2): 337-348. DOI:10.1016/j.amc.2009.02.030 (  0) 0) |
| [9] |
Zhang Jing-hua, Gong Y, Li S R. Bending of functionally graded beam with variable cross-sections by differential quadrature method. Journal of Gansu Sciences, 2010, 22(1): 14-17. DOI:10.16468/j.cnki.issn1004-0366.2010.01.029 (  0) 0) |
| [10] |
Fertis D G, Taneja R. Inelastic analysis of variable stiffness members. Mathematical and Computer Modelling, 1990, 14: 942-946. DOI:10.1016/0895-7177(90)90318-H (  0) 0) |
| [11] |
Gunes R, Aydin M, Apalak M K, et al. The elasto-plastic impact analysis of functionally graded circular plates under low-velocities. Composite Structures, 2011, 93(2): 860-869. DOI:10.1016/j.compstruct.2010.07.008 (  0) 0) |
| [12] |
Jang S K, Bert C W, Striz A G. Application of differential quadrature to static analysis of structural components. International Journal for Numerical Methods in Engineering, 2010, 28(3): 561-577. DOI:10.1002/nme.1620280306 (  0) 0) |
| [13] |
Shu C, Ding H, Yeo K S. Local radial basis function-based differential quadrature method and its application to solve two-dimensional incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering, 2003, 192(7-8): 941-954. DOI:10.1016/S0045-7825(02)00618-7 (  0) 0) |
| [14] |
Sadeghian H, Rezazadeh G, Osterberg P M. Application of the generalized differential quadrature method to the study of pull-in phenomena of MEMS switches. Journal of Microelectromechanical Systems, 2007, 16(6): 1334-1340. DOI:10.1109/JMEMS.2007.909237 (  0) 0) |
| [15] |
Boresi A P, Schmidt R J, Sidebottom O M. Advanced Mechanics of Materials. New York: Wiley, 1985.
(  0) 0) |
| [16] |
Kimiaeifar A, Thomsen O T. Series solution for large deflections of a cantilever beam with variable flexural rigidity. Meccanica, 2012, 47(7): 1787-1796. (  0) 0) |
| [17] |
Karami G, Malekzadeh P. A new differential quadrature methodology for beam analysis and the associated differential quadrature element method. Computer Methods in Applied Mechanics and Engineering, 2002, 191(32): 3509-3526. DOI:10.1016/S0045-7825(02)00289-X (  0) 0) |
| [18] |
Yu T X, Zhang L C. The Theory of Plastic Bending and Application. Beijing: Science Press, 1992. (in Chinese)
(  0) 0) |
| [19] |
Xu Y P, Yu T T, Zhou D. Two-dimensional elasticity solution for bending of functionally graded beams with variable thickness. Meccanica, 2014, 49(10): 2479-2489. DOI:10.1007/s11012-014-9958-1 (  0) 0) |
 2021, Vol. 28
2021, Vol. 28


