2. Department of Civil Engineering, The University of Hong Kong, Hong Kong 999077, China
A city cluster is composed of an area of space, natural environment, and a social economy with one or two megacities as the core of the regional economy (Fig. 1). These cities constitute a relatively complete cluster with the accessibility of integrated modern transport networks, and their inner relationship is developed between individuals with the development of information network.
|
Fig.1 Sketch map of a city cluster |
Road traffic safety is the status of being able to control personal injury or property damage to an acceptable level during traffic activities. This serves as a methodological foundation for traffic projects in city clusters and has important theoretical value and practical significance. Existing models to evaluate road traffic safety in city clusters mainly concern traffic management. Most are based on the signal types used to compute the location of traffics, and its output is an analysis of various indices that reflect traffic features. Some scholars focused on analyzing the influence of geometric design characteristics on traffic management. Lam et al.[1] proposed a traffic assignment model considering the uncertainties of the imbalance between supply and demand. In order to ensure the safety of vehicles and pedestrians at intersections, Falk and Montgomery[2] investigated the psychophysiological characteristics of road users. Batrakova and Gredasova[3] showed that the number of accidents is closely related to environment, traffic, road users, and vehicle. Oguchi[4]summarized the road inference factors in Japan such as road facilities, regulations, drivers' education levels, vehicle safety standards, and emergency medical care, and analyzed their relationship with each other. Oleinik[5] stated that enforcement of traffic law is an approach to enhance road safety. Batishcheva and Ganichev[6] focused on studying driver behavior while driving and established the relationship between the elements of road conditions and the indicators of the driving status. Eusofe and Evdorides[7]presented how fund factor affects the traffic safety. Batishcheva and Ganichev[8] developed a morphological model for evaluating the potential reliability of personality factors of drivers and pedestrians and considered human factor ranks first among causes of road accidents. Van Haperen et al.[9] also observed human behavior concerning road safety, and they collected the naturalistic data of road users who were uninformed of their participation. They pointed out the relationship between human factor and road traffic safety, and thought the road user behavior can deeply affect road safety.
However, the above studies just evaluated traffic safety based on given operational states, whereas robust features were seldom considered, and the impacts of disturbances on traffic safety were ignored. Other scholars used instrumental variable analysis and multiple methods in the evaluation of traffic safety. Szeto and Gazis[10] first used the methodology of the discrete-time and the extended Kalman filter to estimate the densities and the control of critical traffic links. On this basis, many scholars developed lots of methods to evaluate road safety. Khan and Ritchie[11] used the artificial neural networks in a modular architecture to assist in detecting different types of operational problems on signalized urban arterials, and they evaluated road safety by pattern recognition. Pan et al.[12] introduced the deep belief network (DBN) as an alternative to the traditional regression models for crash modeling, and they developed the global road safety performance function to estimate road safety. Dobromirov et al.[13] used statistical data on road traffic accidents (RTAs) from 2013 to 2015 to evaluate the safety of a road. Wang et al.[14] proposed a combined usage of microscopic traffic simulation and Extreme Value Theory (EVT) for road safety evaluation. Li et al.[15] sought to examine the relationship between level of service (LOS) and safety by looking into types of crashes on approaches to signalized intersections. Others used quantitative and qualitative methods to analyze almost all factors of road safety[16-23]. Although the studies of road traffic have been focused mainly on safety level, the number of traffic accidents and their causes, particularly the problem of safety level determination in a city cluster, still has not been solved. Safety level determination usually plays an important role in countermeasures for city cluster development. But they are not fully manifested in China's urban agglomeration features.
Therefore, after considering the shortcomings of the above models, this paper presents an Order Exponential Evaluation Model (OEEM), a new comprehensive evaluation model for road traffic safety in city clusters. In this model, city cluster road traffic safety can be determined by the stochastic variables of accident risk and consequence. According to dynamic traffic information, the evaluation model can identify and warn risk and aid in strategic decision-making.
The outline of the remainder of this paper is as follows. Section 2 introduces an evaluation index system for city cluster road traffic safety that considers all factors influencing traffic safety status. Section 3 gives mathematical formulae for a comprehensive evaluation model based on order exponential function and the evaluation index system. Section 4 presents a numerical example illustrating the application of the proposed method, and Section 5 includes discussion and concluding remarks.
2 Evaluation Index SystemRoad traffic system in a city cluster is a large system involving many factors, so it is scarcely possible to cover the entire system. The index system reveals the layout and structure of a road traffic system to indicate its functional level, which includes all aspects of impact factors. The evaluation index system is the premise for the diagnosis of traffic safety, identification of dangerous points, and safety control and management of the city cluster's road traffic system, which differs from a general safety management system. The evaluation index includes the starting point of the evaluation and the specificity of the evaluation purpose. Road traffic generally has three elements: people, vehicles, and roads (including the surroundings of roads). When establishing an evaluation index system, detailed traffic accident reports and traffic disasters with the actual conditions of specific road sections should be collected, especially those concerning the environment, vehicle technical status, and driver information.
The choice of evaluation index is very important in the evaluation of road traffic network in a city cluster. Road traffic is subjected to traffic regulations and is the interaction of human, vehicles, and road infrastructure. Kong[18] shows that most traffic accidents are caused by human errors. Therefore, human are the key element and the weakest link in the system.
The indices for the entire road traffic system are as follows. First, human are the main body and play a leading role in controlling road traffic system. It is generally agreed that the direct cause of a traffic accident is an error of a driver's observation, judgment, operation, and so on. Second, vehicles as transportation tools are an important part of the road transportation system, and are closely related to traffic safety. To a certain extent, vehicles with a good technical condition can prevent drivers from making mistakes and reduce accident loss. Roads, as the infrastructure on which the road traffic system operates, play an important role in traffic safety as well. Although most statistics show that people and vehicles are responsible for accidents, difficult road conditions are a factor that cannot be ignored. Finally, the complexity of the traffic environment also influences road safety, as it distracts driver's attention and affects their judgment. It is also highly possible that in emergencies drivers are unable to notice the surrounding environment, which results in danger.
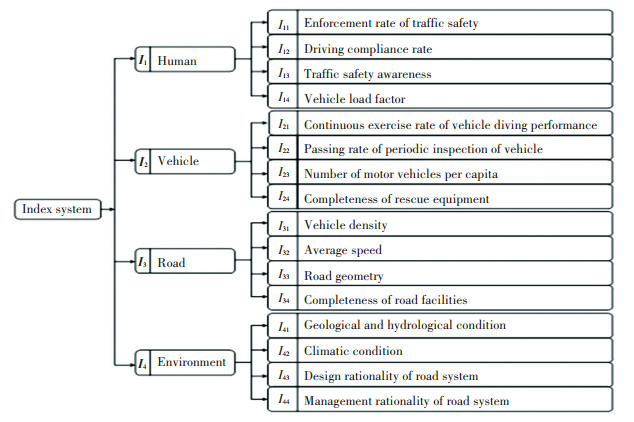
Based on the above analysis, an index system was established for city cluster road traffic safety considering human, vehicle, road, and environment (Fig. 2).
|
Fig.2 Evaluation index system of city cluster road traffic safety |
In Fig. 2, I1 is human; I2 is vehicle; I3 is road; I4 is environment; I11 is the enforcement rate of traffic safety; I12 is the driving compliance rate; I13 is traffic safety awareness; I14 is the vehicle load factor; I21 is the continuous exercise rate of vehicle driving performance; I22 is the passing rate of periodic inspection of vehicles; I23 is the number of motor vehicles per capita; I24 is the completeness of rescue equipment; I31 is the vehicle density; I32 is the average speed; I33 is the road geometry; I34 is the completeness of the road facilities; I41 is the geological and hydrological condition; I42 is the climatic condition; I43 is the design rationality of the road system; and I44 is the management rationality of the road system.
The system in Fig. 2 can be used for analyzing the interaction of "human-vehicle-road-environment" system and it also can be used for studying their mutual influence to help develop methods of optimization for the road environment and traffic and to obtain solutions meeting the requirements of safe and comfortable movement.
3 Comprehensive Evaluation ModelThis paper provides a complex analytical framework for the evaluation of city cluster road traffic safety, and the assessment model of traffic safety conditions is useful in the prevention of future traffic accidents. However, this assessment model is difficult to conduct, because too many aspects need to be considered. Order exponential function can approximate some indices, so it was adopted to assess traffic safety, in which various parameters, such as geometric conditions, traffic volume, average speed, and average accident rate, can be included reasonably. In this section, the definition of order exponents and evaluation matrices of road traffic safety are first introduced, and then a comprehensive evaluation model of city cluster road traffic safety is proposed.
3.1 Order Exponential FunctionThe aim of the proposed method is to define the types of accidents that are remarkably influenced by appropriate road traffic in a city cluster. For this reason, the most affected accident types and causes have been evaluated based on the effects of the adequateness of city cluster road traffic safety on the given type and cause. The numerical evaluation has been based on the following steps. To achieve reasonable decision-making, the order exponent function theory was applied to quantify the effects of various factors on the traffic safety in a city cluster. The proposed comprehensive evaluation model was based on the definitions of several evaluation matrices and their corresponding order exponents function.
3.1.1 Evaluation matrix of road traffic safetyThe evaluation matrix of road traffic safety shows the quantitative result of human activity evaluation in the traffic network of a city cluster. According to the indicators in Fig. 2, the evaluation matrix of the index Ii (i=1, 2, 3, 4) is defined by Eq.(1):
| $ \mathit{\boldsymbol{M}}({\mathit{\boldsymbol{I}}_i}) = \left[ {{\mathit{\boldsymbol{I}}_i}\left| {\begin{array}{*{20}{c}} {{I_{i1}}}&{{I_{i2}}}&{{I_{i3}}}&{{I_{i4}}}\\ {{w_{i1}}}&{{w_{i2}}}&{{w_{i3}}}&{{w_{i4}}}\\ {{a_{i1}}}&{{a_{i2}}}&{{a_{i3}}}&{{a_{i4}}}\\ {{r_{i1}}}&{{r_{i2}}}&{{r_{i3}}}&{{r_{i4}}} \end{array}} \right.} \right] $ | (1) |
where M(Ii) is the evaluation matrix of index Ii, Iij is the evaluation index as shown in Fig. 1, and j=1, 2, 3, 4.wij is the weight coefficient of index Iij, aij is the investigation value of index Iij, and rij is the standardized value of index Iij.
3.1.2 Order exponential function of road traffic safetyAccording to Eq.(1), the order exponent function of index Ii is defined as Eq.(2):
| $ f({\mathit{\boldsymbol{I}}_i}) = \sum\limits_{j = 1}^4 {{w_{ij}}{r_{ij}}} $ | (2) |
where f(Ii) is the order exponent function of index Ii.
3.1.3 Comprehensive order exponential function of road traffic safetyFor an overall assessment of city cluster road traffic safety, a comprehensive order exponent function should be calculated by integrating previous order exponents, as is shown by Eq.(3):
| $ \mathit{\boldsymbol{F}} = f({\mathit{\boldsymbol{I}}_1})\mathit{\boldsymbol{\vec i}} + f({\mathit{\boldsymbol{I}}_2})\mathit{\boldsymbol{\vec j}} + f({\mathit{\boldsymbol{I}}_3})\mathit{\boldsymbol{\vec k}} + f({\mathit{\boldsymbol{I}}_4})\mathit{\boldsymbol{\vec l}} $ | (3) |
where F is the comprehensive order exponent function of road traffic safety.
The value of the comprehensive order exponent function of road traffic safety can then be obtained with Eq.(4):
| $ |\mathit{\boldsymbol{F}}| = \sqrt {{{[f({\mathit{\boldsymbol{I}}_1})]}^2} + {{[f({\mathit{\boldsymbol{I}}_2})]}^2} + {{[f({\mathit{\boldsymbol{I}}_3})]}^2} + {{[f({\mathit{\boldsymbol{I}}_4})]}^2}} $ | (4) |
This paper presents OEEM, a method of traffic safety evaluation in a city cluster based on an analysis of the statistical data on road traffic accidents. The calculation process using order function is as follows.
Step 1: Determine the quantitative value of the evaluation index of city cluster road traffic safety. The evaluation matrices M(Ii)should be quantified respectively according to Eq.(2).
Step 2: Determine the weight coefficient of the evaluation index of city cluster road traffic safety. The weight coefficient of the evaluation index was determined by the relevant comparative method that can avoid subjective and partial expert opinion in determining weight coefficients and take full advantage of information on its own monitoring data. This method is as follows:
| $ {q_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{I}}_i}{\kern 1pt} {\kern 1pt} {\rm{has}}{\kern 1pt} {\kern 1pt} {\rm{advantages}}{\kern 1pt} {\kern 1pt} {\rm{over}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{I}}_j}}\\ {0.5,}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{I}}_i}{\kern 1pt} {\kern 1pt} {\rm{is}}{\kern 1pt} {\kern 1pt} {\rm{equivalent}}{\kern 1pt} {\kern 1pt} {\rm{to}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{I}}_j}}\\ {0,}&{{\rm{if}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{I}}_j}{\kern 1pt} {\kern 1pt} {\rm{has}}{\kern 1pt} {\kern 1pt} {\rm{advantages}}{\kern 1pt} {\kern 1pt} {\rm{over}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{I}}_i}} \end{array}} \right. $ |
The weight coefficient of the index Iij (Fig. 1) is defined by Eq.(5):
| $ {w_{ij}} = [\sum\limits_{j = 1}^n {{q_{ij}}} ] \cdot {[\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{q_{ij}}} } ]^{ - 1}} $ | (5) |
where qii=0.5, qij+qji=1. The weight vector of the evaluation index for human activity was calculated according to Eq.(5).
Step 3: Standardize the values of the measurement index of city cluster road traffic safety. After calculation, various indicators with different dimensions were obtained. To perform further calculation, commensurability must be conducted among these indicators to transform them into standard pattern, as shown in Eq.(6):
| $ {r_{ij}} = \left( {{a_{ij}} - \frac{1}{m}\sum\limits_{i = 1}^m {{a_{ij}}} } \right)/\sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{a_{ij}} - \frac{1}{m}\sum\limits_{i = 1}^m {{a_{ij}}} } \right)}^2}} } $ | (6) |
Step 4: Calculate the quantitative value of order exponent of city cluster road traffic safety. Based on Eq.(2), the value of the order exponential function f(Ii) was obtained.
Step 5: Calculate the comprehensive order exponent of city cluster road traffic safety. According to Eqs. (3)-(4), the value of the comprehensive order exponential function |F| was obtained, which presents the safety status of city cluster road traffic. When the value was smaller, the safety status was better in the monitoring period.
Step 6: Determine the levels of city cluster road traffic safety. To evaluate city cluster road traffic safety in an intuitionist way, the results were classified into various levels according to the value of the comprehensive order exponential function |F|. On the basis of previous studies[24], geometrical and physical conditions, traffic volume, average speed, and accident rate were considered in the determination of the safety levels, which were divided into very safe, safe, general, unsafe, and very unsafe (Table 1). The safety interval was obtained by the mean of overall point 2.
| Table 1 Interval definition of road traffic safety levels |
4 Case Analysis
In this section, the proposed model and method are applied to a case analysis based on three Chinese city clusters: Jing-Jin-Ji (city cluster A1), the Pearl River Delta (city cluster A2), and the Yangtze River Delta (city cluster A3). Detailed data of the three city clusters are given in Table 2. The data in Table 2 are from References Academy of Transportation and Highway Sciences 2013, 2014, 2015, 2016[25-28].
| Table 2 Road accidents in city clusters in China from 2013 to 2016 |
The road traffic safety in city cluster A1, city cluster A2, and city cluster A3 was evaluated by our team. Detailed data are given in Table 3.
| Table 3 Investigation value of the evaluation indicators |
4.1 Algorithm of OEEM
After the completion of Steps 1 to 3 in Section 4, four basic evaluation matrices were obtained. Eqs.(7)-(10) show the calculated evaluation matrices of city cluster A1.
| $ \mathit{\boldsymbol{M}}({\mathit{\boldsymbol{I}}_1}) = \left[ {{\mathit{\boldsymbol{I}}_1}\left| {\begin{array}{*{20}{c}} {{I_{11}}}&{{I_{12}}}&{{I_{13}}}&{{I_{14}}}\\ {0.2501}&{0.2438}&{0.2599}&{0.2462}\\ {0.8800}&{0.9200}&{0.8100}&{0.7500}\\ {0.8800}&{0.9200}&{0.8100}&{0.7500} \end{array}} \right.} \right] $ | (7) |
| $ \mathit{\boldsymbol{M}}({\mathit{\boldsymbol{I}}_2}) = \left[ {{\mathit{\boldsymbol{I}}_2}\left| {\begin{array}{*{20}{c}} {{I_{21}}}&{{I_{22}}}&{{I_{23}}}&{{I_{24}}}\\ {0.2439}&{0.2561}&{0.2572}&{0.2428}\\ {0.8200}&{0.9200}&{0.3300}&{0.7500}\\ {0.8200}&{0.9200}&{0.2191}&{0.7500} \end{array}} \right.} \right] $ | (8) |
| $ \mathit{\boldsymbol{M}}({\mathit{\boldsymbol{I}}_3}) = \left[ {{\mathit{\boldsymbol{I}}_3}\left| {\begin{array}{*{20}{c}} {{I_{31}}}&{{I_{32}}}&{{I_{33}}}&{{I_{34}}}\\ {0.2424}&{0.2468}&{0.2526}&{0.2582}\\ {2.1300}&{91.7000}&{0.8200}&{0.8700}\\ {0.1871}&{0.3750}&{0.8200}&{0.8700} \end{array}} \right.} \right] $ | (9) |
| $ \mathit{\boldsymbol{M}}({\mathit{\boldsymbol{I}}_4}) = \left[ {{\mathit{\boldsymbol{I}}_4}\left| {\begin{array}{*{20}{c}} {{I_{41}}}&{{I_{42}}}&{{I_{43}}}&{{I_{44}}}\\ {0.2464}&{0.2438}&{0.2556}&{0.2542}\\ {0.8800}&{0.6300}&{0.8500}&{0.7900}\\ {0.8800}&{0.6300}&{0.8500}&{0.7900} \end{array}} \right.} \right] $ | (10) |
The evaluation matrices of city cluster A2 and A3 were calculated by the same method. According to Step 4 in Section 4, the values of the order index can be determined by Eq.(2). The values of f(I1), f(I2), f(I3), and f(I4) for the three city clusters are given in Table 4.
| Table 4 Value of order exponent function |
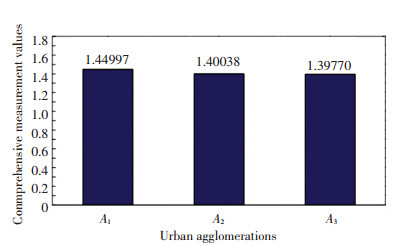
According to Step 5 in Section 4, the comprehensive order exponent can be determined by Eq.(10). The comprehensive order exponents of the three city clusters were calculated as follows: |F|(A1)=1.44997, |F|(A2)=1.40038, |F|(A3)=1.39770.
As shown by the above values, city cluster A1 is the safest of the three city clusters, and the other two are almost in the same safety condition according to calculation by Matlab2014b (Fig. 3). According to Table 1, all three city clusters should be considered safe, and the safety level of A1 is higher than A2 and A3.
|
Fig.3 Degree of danger in each city cluster |
4.2 Algorithm of the Ideal Model
As is shown by the close degree, the relation degree point of all alternatives can be determined to select the best set of feasible alternatives. An algorithm of multiple-attribute decision-making problems with an ideal approach is given as follows.
Step 1: Standardize the decision-making matrix of city cluster road traffic safety.
Step 2: Determine the weight coefficient of the decision-making index of city cluster road traffic safety with Eq.(5).
Step 3: Determine the close degree of city cluster road traffic safety by Eq.(11):
| $ {\delta _{ij}} = \frac{{{{({\mathit{\boldsymbol{P}}^*} - {{[{r_{i1}},{r_{i2}} \cdots ,{r_{im}}]}^{\rm{T}}})}^{\rm{T}}} \cdot ({\mathit{\boldsymbol{P}}^*} - {\mathit{\boldsymbol{P}}_*})}}{{\sum\limits_{j = 1}^m {{{(r_j^ + - r_j^ - )}^2}} }} $ | (11) |
where P*=[r1+, r2+, …, rm+]T, if rj+=max{rij, 1≤i≤n}; P*=[r1-, r2-, …, rm-]T, if rj-=min{rij, 1≤i≤n}. The calculated values are given in Table 5.
| Table 5 Calculated value of city clusters by the ideal model |
Step 4: Determine the comprehensive close degree of decision index of city cluster road traffic safety by Eq.(12):
| $ {\delta _i} = \sum\limits_{j = 1}^{16} {{w_j}} \cdot {\delta _{ij}} $ | (12) |
Therefore, the comprehensive close degrees of the three city clusters are δ1=0.5947, δ2=0.5458, δ3=0.5349, respectively.
The priority principle of the ideal decision-making model shows that the priority relationship of the ranking of the three city clusters is A1>A2>A3. Thus, city cluster A1 is the best investment object.
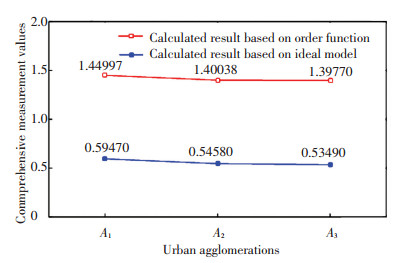
4.3 Comparative Analysis of the Two Models' Calculation ResultsBased on the case analysis in Sections 4.1 and 4.2, the calculation results of two decision-making models were calculated by Matlab2014b. The results of comparison are given in Fig. 4.
|
Fig.4 Comprehensive evaluation values of city clusters by two kinds of models |
The evaluation results were in accordance with the current situation, which show that the evaluation approach can determine road traffic safety levels in a city cluster. Specifically, the road traffic safety was 1.44997 in city cluster A1, 1.40038 in city cluster A2, and 1.39770 in city cluster A3 by OEEM, while the road traffic safety was 0.59470 in city cluster A1, 0.54580 in city cluster A2, and 0.53490 in city cluster A3 by the ideal model. That is, the priority relationship of the ranking of the three city clusters was A1>A2>A3, and the validity of the two models was proved.
However, the effective errors of these models differed. The calculation error between the maximum and minimum values of OEEM was 0.0552, and the calculation error of the ideal model was 0.0598. However, in the calculating process the relative error of the proposed method was close to 0.0380, and the relative error of the ideal model was close to 0.1010. It is obvious that the curve of OEEM is smoother and steadier than that of the ideal model. Therefore, the proposed OEEM had greater evaluation accuracy than the ideal model.
5 Discussion and ConclusionsIn this study, we examined the road traffic safety of city clusters, obtained the characteristics and regular pattern of traffic development to promote sustainable development of city clusters, and proposed a new method to identify road traffic safety levels in a city cluster. First, an integrated evaluation index system was constructed, in which core factors were taken as indicators to evaluate road traffic safety levels. Second, based on the order exponent function theory, a detailed evaluation model of city cluster road traffic safety, OEEM, was presented for determination of road traffic safety levels. Finally, the proposed approach was applied to a real case.
The effectiveness of OEEM was verified by estimating safety values of three Chinese city clusters: Jing-Jin-Ji (city cluster A1), the Pearl River Delta (city cluster A2), and the Yangtze River Delta (city cluster A3). The results show that the city cluster A1 was safer than A2, and A2 was safer than A3. The safety level of the road traffic in the three city clusters was clearly observed from the overall ranking value. Meanwhile, the elements of the evaluation index were also observed from Table 5 and the cause of a city cluster's safety level was analyzed. Therefore, OEEM can help transport managers to make policy decisions on traffic construction to avoid traffic accidents and guarantee smooth traffic. The results agreed with the real number of accidents and fatalities of the three city clusters in 2016 (Table 2). Then a road safety evaluation method was designed based on the ideal model to compare with the proposed model. The ideal model obtained similar data and showed consistency with the proposed model. However, the calculation error of OEEM was 0.0552, and the calculation error of the ideal model was 0.0598. Furthermore, the relative error of the proposed method was 0.0380, while that of the ideal model was 0.1010. It verified the superiority of the proposed model.
The primary contribution of this research is that OEEM can be used to identify road traffic safety levels in a city cluster and to suggest actions for improvement. It also works for the evaluation matrix of various indices of road traffic systems with various weights. Finally, it can be used to provide in-depth assessment of city cluster road traffic safety. OEEM can overcome the impacts of disturbances on the status of traffic safety and estimate the road safety level to clearly reflect the traffic status of a whole city cluster.
The proposed scoring error analysis takes the features of city cluster road traffic system into consideration, and was validated with other performance evaluation methods such as the ideal model. Results show that the proposed approach was better because it allowed the index to incorporate multiple indicators, whereas the ideal model is commonly used to estimate decision-making problems. Based on the case analysis in Fig. 3, the validation shall place particular focus on the ability of the two methods to identify the best and worst performers for the evaluation of road traffic safety.
This approach is also applicable for different cities. For instance, a city (rather than a city cluster) with similar road traffic may have different passenger loadings due to different the environment and population density, which lead to different conclusions regarding road traffic safety levels, but framework of OEEM needs no alteration or modification. Besides estimating the road traffic safety, OEEM can be generalized and applied to other areas such as accident statistics, traffic condition assessment, and so on.
| [1] |
Lam W H K, Shao H, Sumalee A. Modeling impacts of adverse weather conditions on a road network with uncertainties in demand and supply. Transportation Research Part B, 2008, 42(10): 890-910. DOI:10.1016/j.trb.2008.02.004 (  0) 0) |
| [2] |
Falk B, Montgomery H. Developing traffic safety interventions from conceptions of risks and accidents. Transportation Research Part F, 2007, 10(5): 414-427. DOI:10.1016/j.trf.2007.04.001 (  0) 0) |
| [3] |
Batrakova A, Gredasova O. Influence of road conditions on traffic safety. Procedia Engineering, 2016, 134: 196-204. DOI:10.1016/j.proeng.2016.01.060 (  0) 0) |
| [4] |
Oguchi T. Achieving safe road traffic — the experience in Japan. IATSS Research, 2016, 39: 110-116. DOI:10.1016/j.iatssr.2016.01.003 (  0) 0) |
| [5] |
Oleinik A. Corruption on the road: a case study of Russian traffic police. IATSS Research, 2016, 40: 19-25. DOI:10.1016/j.iatssr.2015.12.001 (  0) 0) |
| [6] |
Batishcheva O, Ganichev A. Creative approaches to organization and safety of road traffic. Transportation Research Procedia, 2017, 20: 36-40. DOI:10.1016/j.trpro.2017.01.008 (  0) 0) |
| [7] |
Eusofe Z, Evdorides H. Assessment of road safety management at institutional level in Malaysia: a case study. IATSS Research, 2017, 41(4): 172-181. DOI:10.1016/j.iatssr.2017.03.002 (  0) 0) |
| [8] |
Batishcheva O, Ganichev A. Measures to improve traffic safety at road junctions. Transportation Research Procedia, 2018, 36: 37-43. DOI:10.1016/j.trpro.2018.12.040 (  0) 0) |
| [9] |
van Haperen W, Riaz M, Daniels S, et al. Observing the observation of (vulnerable) road user behaviour and traffic safety: a scoping review. Accident Analysis & Prevention, 2019, 123: 211-221. DOI:10.1016/j.aap.2018.11.021 (  0) 0) |
| [10] |
Szeto M W, Gazis D C. Application of Kalman filtering to the surveillance and control of traffic systems. Transportation Science, 1972, 6(4): 419-439. (  0) 0) |
| [11] |
Khan S I, Ritchie S G. Statistical and neural classifiers to detect traffic operational problems on urban arterials. Transportation Research, 1998, 6(5-6): 291-314. DOI:10.1016/S0968-090X(99)00005-4 (  0) 0) |
| [12] |
Pan G Y, Fu L P, Thakali L. Development of a global road safety performance function using deep neural networks. International Journal of Transportation Science and Technology, 2016, 6(3): 159-173. DOI:10.1016/j.ijtst.2017.07.004 (  0) 0) |
| [13] |
Dobromirov V, Evtiukov S, Duncheva E, et al. Methodology and results of the traffic safety evaluation on the Saint Petersburg ring road. Transportation Research Procedia, 2017, 20: 151-158. DOI:10.1016/j.trpro.2017.01.039 (  0) 0) |
| [14] |
Wang C, Xu C C, Xia J X, et al. A combined use of microscopic traffic simulation and extreme value methods for traffic safety evaluation. Transportation Research Part C: Emerging Technologies, 2018, 90: 281-291. DOI:10.1016/j.trc.2018.03.011 (  0) 0) |
| [15] |
Li J, Wang X S, Yu R J, et al. Relationship between level of service and traffic safety at signalized intersections: grouped random parameter method. Journal of Transportation Engineering, Part A: Systems, 2018, 144(6): 04018022. DOI:10.1061/JTEPBS.0000142 (  0) 0) |
| [16] |
Ahmed M, Abdel-Aty M. A data fusion framework for real-time risk assessment on freeways. Transportation Research Part C: Emerging Technologies, 2013, 26: 203-213. DOI:10.1016/j.trc.2012.09.002 (  0) 0) |
| [17] |
Vayalamkuzhi P, Amirthalingam V. Influence of geometric design characteristics on safety under heterogeneous traffic flow. Journal of Traffic and Transportation Engineering (English Edition), 2016, 3(6): 559-570. DOI:10.1016/j.jtte.2016.05.006 (  0) 0) |
| [18] |
Kong L Z. Human factor in causation of traffic accidents. China Safety Science Journal, 2013, 23(1): 28-34. (  0) 0) |
| [19] |
Chong W, Asakura Y, Iryo T. Formulating the within-day dynamic stochastic traffic assignment problem from a Bayesian perspective. Transportation Research Part B: Methodological, 2014, 59: 45-57. DOI:10.1016/j.trb.2013.11.004 (  0) 0) |
| [20] |
Bede Z, Péter T. Optimal control with the dynamic change of the structure of the road network. Transport, 2014, 29(1): 36-42. DOI:10.3846/16484142.2014.895959 (  0) 0) |
| [21] |
Čerýn J, Černá A, Linda B. Support of decision-making on economic and social sustainability of public transport. Transport, 2014, 29(1): 59-68. DOI:10.3846/16484142.2014.897645 (  0) 0) |
| [22] |
Fancello G, Carta M, Fadda P. A decision support system for road safety analysis. Transportation Research Procedia, 2015, 5: 201-210. DOI:10.1016/j.trpro.2015.01.009 (  0) 0) |
| [23] |
Lee S, Jeong B Y. Comparisons of traffic collisions between expressways and rural roads in truck drivers. Safety and Health at Work, 2016, 7: 38-42. DOI:10.1016/j.shaw.2015.11.005 (  0) 0) |
| [24] |
Hu Q, Wang H, Liu Y. Measurement Method of Road Traffic Safety Situation Monitoring. Beijing: Science Press, 2012.
(  0) 0) |
| [25] |
Research Institute of Highway Ministry of Transport.The Blue Book of Road Safety in China 2013. Beijing: China Communications Press Co., Ltd., 2013.12-12.
(  0) 0) |
| [26] |
Research Institute of Highway Ministry of Transport. The Blue Book of Road Safety in China 2014. Beijing: China Communications Press Co., Ltd., 2014.8-8.
(  0) 0) |
| [27] |
Research Institute of Highway Ministry of Transport. The Blue Book of Road Safety in China 2015. Beijing: China Communications Press Co., Ltd., 2015.15-15.
(  0) 0) |
| [28] |
Research Institute of Highway Ministry of Transport. The Blue Book of Road Safety in China 2016. Beijing: China Communications Press Co., Ltd., 2016.7-7.
(  0) 0) |
 2021, Vol. 28
2021, Vol. 28


