The channel resource assigned to a wireless transmitter becomes a waste if it stays idle, while an active transmission of data could be eavesdropped. Spectrum sharing overcomes the first problem by having the primary user (PU) of the channel resource to share it with a secondary user. The latter can then help the former in defending against eavesdropping. The secondary user is expected to be a cognitive radio (CR) equipped with spectrum sensing function that identifies spectral opportunity or unoccupied channel. CR can make use of an unused channel to send its own data. On the other hand, when the PU has data to send, CR relinquishes the channel. CR returns the favor by transmitting artificial noise to jam the eavesdropper (EA), thus protecting the secrecy of primary data. This technique is named as physical layer security[1-2], which originates from information theory. It utilizes the physics of radio signal decaying with propagation distance. As long as the artificial noise that reaches EA is strong enough, it could garble the information that EA attempts to steal.
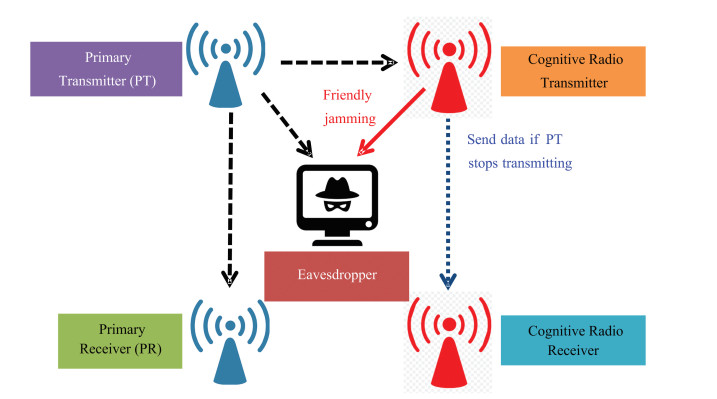
PU consists of two nodes, i.e., the primary transmitter (PT) and primary receiver (PR). CR is taken as the secondary user (SU). Conventionally, PU does not like sharing the spectral opportunity with CR, because CR's transmission could harmfully interfere with the data reception at PR. Now there is an incentive for PU, because CR helps defending against eavesdropping when PT transmits. CR sends out friendly jamming signal that is decodable by the PR, which harms only the EA but not PR. In return, CR has the benefit of sending its own data over the channel when it is unused. Such spectrum sharing scheme benefits both PU and CR. Fig. 1 illustrates the proposed model.
|
Fig.1 System model |
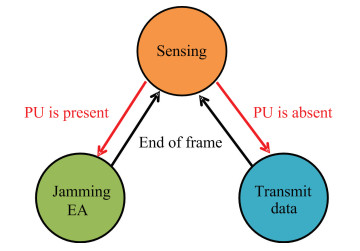
Fig. 2 shows a state transition diagram that depicts CR's operation. At first, CR senses the spectrum to identify channel occupancy. If a channel is found to be occupied (by PU), CR transits to the state of jamming EA. Otherwise, it transits to the state of transmitting its data over the unoccupied channel. Although an EA's exact location may not be known, it is assumed to be close to the PR, and that it targets only the data sent out from PT but not CR.
|
Fig.2 CR's state transition diagram |
CR's energy and time are divided between the three states depicted in Fig. 2. Suppose the duration of a data packet is T seconds. CR spends t seconds for sensing, and T-t seconds in any of the other two states (transmitting data or jamming EA). Fig. 3 illustrates the time allocation. Let τ=t/T denote the portion of time allocated for spectrum sensing.

|
Fig.3 Time spent in sensing, jamming, or transmitting data |
The scheme encourages PU to share its spectral channel with CR, since CR can protect PU from being eavesdropped. Here the benefit that the CR gets is a question. CR's throughput increases because it can transmit data when PU becomes inactive. However, jamming EA consumes energy. This may be risky for CR that has limited amount of energy. Whether it is possible to attain high throughput at low energy consumption is the topic for investigation.
Energy efficiency μ is defined as the ratio of channel throughput to energy consumption. Being highly energy efficient is critical for CR. Determining the changes of μ with respect to τ and other parameters is the way to find out how μ varies with the sensing duration and other operation parameters. Intuitively, increasing τ will increase sensing accuracy, thus the throughput should increase too, which results in higher μ. However, increasing τ also reduces the duration for sending CR's data and its throughput, implying reduced μ. These conflicting tendencies result in a maximal μ value. Let μ* denote the optimal energy efficiency, and τ* denote the value of τ that optimizes μ. This study seeks to understand how the values of μ* and τ* change under different circumstances. Therefore, a novel theoretical expression is contributed, which reveals that the (τ*, μ*) pair depends only on the following system parameters:
1) Ratio of the CR's jamming power to transmission power, PJ/PT;
2) Ratio of the CR's sensing power to transmission power, PS/PT;
3) Probability of PU being present and active (Pr1);
4) Probability of detection (PrD), which is the requirement imposed on CR by PU, with the purpose of guaranteeing sufficient protection from CR transmission;
5) Ratio of received PT signal power to noise power (SNRP);
6) Sampling rate used for sensing (fs).
In the following sections, how these parameters affect the value of (τ*, μ*) will be demonstrated. The remaining part of this paper is organized in the following manner. Section 1 describes the related works. The spectrum sensing technique is described and the problem of finding energy efficiency is formulated in Section 2. Section 3 presents the results and discussions, and Section 4 concludes this paper.
1 Related WorksThere are different ways of sharing the spectrum[3-7]. It could be shared following the use of game theory[3-5]. The users could bid for the available spectrum in an auction[3], or enforced among themselves certain rules in order to share the spectrum more efficiently[4]. In Ref. [5], the PUs compete among themselves in order to provide CRs some spectral opportunities with competitive pricing. In Ref. [6], the gain of utilizing channel fading in favor of CR transmission was analyzed, and the performance gain of using multi-antennas for spectrum sharing was presented in Ref. [7]. In contrast to these works, this study provides an incentive to PU for sharing its spectrum.
The secrecy of PU's data is an important issue[8-13]. Artificial noise was introduced in Ref. [8] to jam the EA. The idea was then expanded in Refs. [9-10]. The noise pattern was selected from the null space of the receiver's channel but not that of the EA's channel. As a result, the noise causes adverse effect to the EA's reception but not that of the legitimate receiver. Since an eavesdropper is passive, the secrecy scheme proposed in Refs. [8-10] does not assume knowing its presence or even its location. Without the knowledge of the location of EA, there is still a guaranteed minimum rate of transmission secrecy[9] and minimum secrecy capacity[10]. A 2-stage protocol is proposed in Refs. [8, 10] to get CR's help in transmitting artificial noise to jam the EA:
Stage 1: Both the PT and PR send out artificial noises. Different weighted versions of them are received by the CR and EA. Let aXY denote the channel gain between sender X and receiver Y, rA the signal received by node A. Subscripts T, R, C, and E denote PT, PR, CR, and EA, respectively.
PT transmits signal aTRx, whereas PR transmits y. CR receives the signal
| $ r_{\mathrm{C}}=\alpha_{\mathrm{TC}} \alpha_{\mathrm{TR}} x+\alpha_{\mathrm{RC}} y+n_{\mathrm{C}} $ |
EA receives the signal
| $ r_{\mathrm{E}, 1}=\alpha_{\mathrm{TE}} \alpha_{\mathrm{TR}} x+\alpha_{\mathrm{RE}} y+e_{1} $ |
Both nC and e1 are independent and identically distributed additive white Gaussian noise (AWGN) random variables.
Stage 2: CR retransmits the weighted version of the received noises while PT transmits data that will cancel out the artificial noise at the PR.
CR transmits βrC, where β is a random weight. PT transmits the signal
| $ -\beta \alpha_{\mathrm{TC}} \alpha_{\mathrm{CR}} x+z $ |
where z is the information signal to be sent by PT. PR receives signal
| $ r_{\mathrm{R}}=\alpha_{\mathrm{TR}} z+\beta \alpha_{\mathrm{CR}} \alpha_{\mathrm{RC}} y+\beta \alpha_{\mathrm{CR}} n_{\mathrm{C}}+n_{\mathrm{R}} $ |
Note that the term associated with x has vanished, i.e., PR is not affected by the artificial noise.
EA receives signal
| $ \begin{array}{c} r_{\mathrm{E}, 2}=\alpha_{\mathrm{TE}} z+\beta\left(\alpha_{\mathrm{TR}} \alpha_{\mathrm{TC}} \alpha_{\mathrm{CE}}-\beta \alpha_{\mathrm{TE}} \alpha_{\mathrm{TC}} \alpha_{\mathrm{CR}}\right) x+ \\ \beta \alpha_{\mathrm{RC}} \alpha_{\mathrm{CE}} y+\beta \alpha_{\mathrm{CE}} n_{\mathrm{C}}+e_{2} \end{array} $ |
nR and e2 are i.i.d. AWGN random variables. Note that the term associated with x is artificial noise and non-zero. The proposed scheme is effective in spite of EA's location being unknown.
In the model proposed by Lu et al.[11], the jamming signal was sent out by PT instead of CR. The latter only relayed the former's message to PR. In Refs. [12-13], the authors aimed to achieve higher secrecy performance for PU by optimizing CR's schedule and power allocation. Our objective is to achieve higher energy efficiency for CR. Xu and Li[14] have considered optimal scheduling and power allocation among multiple CRs, but not CR's energy efficiency. Yan et al.[15] have considered CR as the victim of eavesdropping. In this work, PR is the victim of eavesdropping.
Although energy efficiency has been a concern in CR networks[16-19], the issue has not been considered in the context of CR consuming energy in order to jam the EA. To attain higher energy efficiency, Pei et al.[16] optimized the times of transmitting and sensing, and the order of sensing the channels. To minimize energy consumption, Deng et al.[17] proposed an optimal schedule for spectrum sensing. Xie et al.[18] proposed an energy-efficient resource allocation method in a heterogeneous CR network architecture. The CR network structure considered in Ref. [19] is also different. It consists of a cognitive base station that allocates frequency resources to the CRs. Scheduling of such allocation was analyzed, with the objective of reaching maximum energy efficiency. Liu et al.[20] has considered the joint issue of spectrum sharing and energy efficiency of PU but not that of CR.
2 Spectrum Sensing and Energy EfficiencyIn this section, the relationship between energy efficiency and the performance of spectrum sensing is formulated. For tractable analysis, energy detector is chosen to serve the purpose of spectrum sensing. Urkowitz was the first to present the theory of energy detection[21], then Digham et al.[22] extended the theory. Ghasemi and Sousa[23] applied the theory in spectrum sensing. Now in this study, a T-second frame is considered. CR spends t seconds for sensing and the sampling rate is fs. The total number of collected energy samples N=fst. The central limit theorem applies when there is a large number of energy samples[24]. At the CR receiver, the ratio of PT signal power to noise power is denoted by SNRP. Given a target probability of detection PrD, the probability of false alarm PrF can be expressed as follows[24]:
| $ \operatorname{Pr}_{\mathrm{F}}=Q\left(\left[Q^{-1}\left(\operatorname{Pr}_{\mathrm{D}}\right) \sqrt{1+2 \mathrm{SNR}_{\mathrm{P}}}+\mathrm{SNR}_{\mathrm{P}} \sqrt{\frac{f_{s} T \tau}{2}}\right]\right) $ | (1) |
Q(·) is the standard Gaussian complementary cumulative distribution function (CDF), whereas Q-1(·) is its inverse.
Let C denote the channel capacity (normalized by channel bandwidth) of CR when PT relinquishes the channel. CR's channel capacity is assumed negligible when PT acquires the channel and is actively transmitting. At the CR receiver, the CR's transmitted signal to noise power ratio is denoted by SNRCR. C is given by
| $ C=\log _{2}\left(1+\mathrm{SNR}_{\mathrm{CR}}\right) $ | (2) |
Let Pr1 and Pr0 denote the respective probabilities of PT actively transmitting and being idle. When PT is idle, CR achieves the channel throughput[24] that is given by
| $ R=(1-\tau) \operatorname{Pr}_{0}\left(1-\operatorname{Pr}_{\mathrm{F}}\right) C $ | (3) |
where τ=t/T.
The probability of CR perceiving PT to be idle is denoted by Pr(0). The bracket in the subscript emphasizes that it is only the CR's perception, which may not be the truth. Two conditions contribute towards Pr(0): 1) PT is idle and there is no false alarm, 2) PT actively transmits but CR does not detect it[25]. Hence,
| $ \operatorname{Pr}_{(0)}=\operatorname{Pr}_{0}\left(1-\operatorname{Pr}_{\mathrm{F}}\right)+\operatorname{Pr}_{1}\left(1-\operatorname{Pr}_{\mathrm{D}}\right) $ | (4) |
Suppose CR allocates PS watts for spectrum sensing and PT watts for transmitting its data. Sensing usually consumes lower power than data transmission. Intuitively, PS increases with fs. To relate the magnitudes between PS and PT, the following simple model is proposed:
| $ P_{\mathrm{S}}=k \cdot\left(f_{s}\right) \cdot P_{\mathrm{T}} $ | (5) |
where 0 < k·(fs) < 1, k is a constant, fs is in the unit of MHz.
Here PS is assumed to increase linearly with fs in MHz.
Let ET and ES denote the respective energies CR consumes in transmitting data and sensing. Then (as in Ref. [25]),
| $ E_{\mathrm{S}}=P_{\mathrm{S}} t $ | (6) |
| $ E_{\mathrm{T}}=P_{\mathrm{T}}(T-t) \operatorname{Pr}_{(0)} $ | (7) |
Once CR senses an actively transmitting PT, the former relinquishes the channel. CR then sends out artificial noise to EA to garble its reception. It is assumed that EA is always active. Pr(1) = 1-Pr(0) denotes the probability of friendly jamming. Let PJ and EJ denote the respective power and energy consumed for jamming.
| $ E_{\mathrm{J}}=P_{\mathrm{J}}(T-t) \operatorname{Pr}_{(1)} $ | (8) |
The total energy that the CR consumes is E= ES +ET + EJ.
Being defined as the ratio of channel throughput to consumed energy[16, 25], energy efficiency is given by
| $ \mu=\frac{R}{E} $ | (9) |
After some steps, it is found that
| $ \mu=\frac{C / T}{\frac{P_{\mathrm{S}}}{\tau^{-1}-1}+\frac{\left(P_{\mathrm{T}}-P_{\mathrm{J}}\right) \operatorname{Pr}_{1}\left(1-\operatorname{Pr}_{\mathrm{D}}\right)+P_{\mathrm{J}}}{\operatorname{Pr}_{0}\left(1-\operatorname{Pr}_{\mathrm{F}}\right)}+P_{\mathrm{T}}-P_{\mathrm{J}}} $ | (10) |
For maximum μ,
| $ \begin{array}{l} \frac{{\left[ {{{\Pr }_1}\left( {1 - {{\Pr }_{\rm{D}}}} \right)\left( {\frac{{{P_{\rm{J}}}}}{{{P_{\rm{T}}}}} - 1} \right) + \frac{{{P_{\rm{J}}}}}{{{P_{\rm{T}}}}}} \right]}}{{\left( {1 - {{\Pr }_1}} \right){{[1 - Q(A + B\sqrt \tau )]}^2}(2\sqrt {{\rm{ \mathsf{ π} }}\tau } )}} \cdot \\ \frac{B}{{\exp \left[ {{{(A + B\sqrt \tau )}^2}/2} \right]}} - \frac{{\frac{{{P_{\rm{S}}}}}{{{P_{\rm{T}}}}}}}{{{{(1 - \tau )}^2}}} = 0 \end{array} $ | (11) |
where
Eq. (11) is a novel expression that allows to find the τ value that optimizes μ(i.e., τ*). It reveals that the optimal value depends only on the following parameters:
| $ \frac{P_{\mathrm{J}}}{P_{\mathrm{T}}}, \frac{P_{\mathrm{S}}}{P_{\mathrm{T}}}, \operatorname{Pr}_{1}, \operatorname{Pr}_{\mathrm{D}}, \mathrm{SNR}_{\mathrm{P}}, f_{s} $ |
Note that Eq. (11) does not depend on SNRCR, i.e., SNRCR does not affect the choice of τ, despite the fact that a strong CR signal will result in high μ*(i.e., the maximum value of μ). By using numerical method, Eq. (11) can be solved. Subsequently, the sets of (τ*, μ*) values that vary with these parameters will be determined.
3 Results and DiscussionsHere the relationships between the (τ*, μ*) pair and the parameters of
| Table 1 List of symbols |
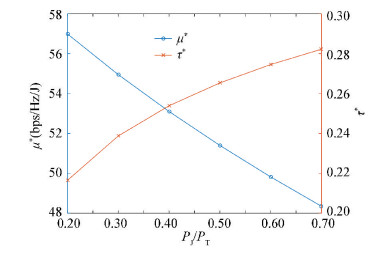
First, the changes of (τ*, μ*) with respect to PJ/PT are investigated, which vary from 0.2 to 0.7, while PT remains at 1 W.
From Fig. 4, it can be observed that 1) μ* decreases linearly with the ratio PJ/PT; as more power being consumed for jamming EA, the optimal energy efficiency naturally reduces; 2) τ* increases only a little with PJ/PT, which shows that τ* is nearly independent of PJ/PT.
|
Fig.4 μ* and τ* vs. PJ/PT |
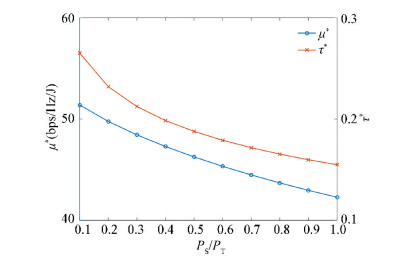
Now the changes of (τ*, μ*) are investigated with respect to PS/PT, which varies from 0.1 to 1, while PT remains at 1 W.
From Fig. 5, it can be observed that 1) μ* decreases with the ratio PS/PT; as more power is consumed for sensing, the optimal energy efficiency is reduced; 2) τ* also decreases with PS/PT; as more power is allocated for spectrum sensing, smaller duration of sensing is needed.
|
Fig.5 μ* and τ* vs. PS/PT |
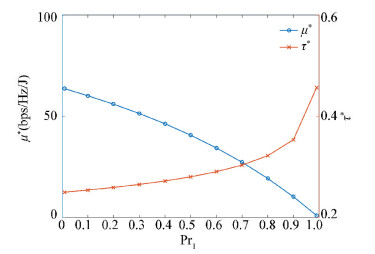
Next, the change of (τ*, μ*) is investigated with respect to Pr1, which varies from 0.01 to 0.99.
From Fig. 6, it can be observed that 1) μ* decreases significantly with Pr1; when it becomes more likely for PU to be present and active, there is less chance for the CR to transmit its data, resulting in lower optimal energy efficiency; 2) τ* increases with Pr1; when it is more probable for PT to be transmitting, CR needs to allocate a larger portion of a frame for accurately sensing the presence and activity of PU.
|
Fig.6 μ* and τ* vs. Pr1 |
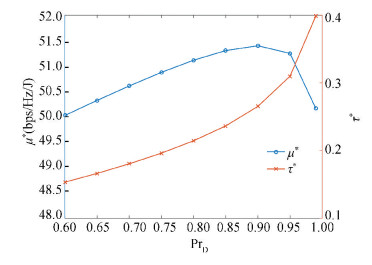
τ* and μ* change with the target PrD, which varies from 0.6 to 0.99. Fig. 7 shows the result.
|
Fig.7 μ* and τ* vs. PrD |
From Fig. 7, it can be observed that 1) μ* initially increases and later decreases with PrD, both in a very small extent, which means that PrD does not have any significant impact on μ* as long as τ* varies accordingly; 2) τ* increases with PrD; a more demanding PrD requires higher τ* in order to attain the maximal energy efficiency μ*.
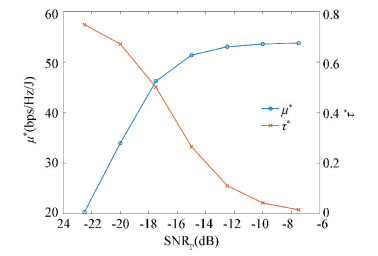
How τ* and μ* change with the SNRP measured at the CR is also assessed. Fig. 8 shows the result.
|
Fig.8 μ* and τ* vs. SNRP |
From Fig. 8, the following trends can be observed:
1) μ* increases with SNRP, but the rate of increment slows down for SNRP > -15 dB. Higher SNRP makes detection more accurate. CR can make more accurate judgment on PT's activity. This translates into higher throughput and higher μ*.
2) τ* decreases with SNRP. When the signal from PT is weak (e.g., SNRP = -22.5 dB), the CR requires large sensing duration to achieve the target detection accuracy. Given the same target detection accuracy, only short sensing duration is required when PT's signal is powerful.
Next, how the changes in sampling rate fs affect τ* and μ* are evaluated. Fig. 9 records the result.

|
Fig.9 μ* and τ* vs. fs |
The following trends are observed in Fig. 9:
1) μ* increases little with fs, whereas τ* decreases with fs.
2) The result shows that increasing the sampling rate does not significantly improve the optimal energy efficiency, other than requiring a shorter sensing duration to reach the same detection accuracy. Based on this, this study argues that a high sampling rate may not be necessary.
All the findings under the given circumstances are summarized as follows:
1) τ* and μ* are functions of
2) μ* decreases with PJ/PT, PS/PT, Pr1, but increases with SNRP. On the other hand, PrD and fs have little effect on μ*;
3) τ* decreases with PS/PT, SNRP, fs, but increases with Pr1 and PrD. On the other hand, PJ/PT has little effect on τ*.
4 ConclusionsThis study proposes a spectrum sharing model that counters eavesdropping. The CR jams an eavesdropper in return for the opportunity of spectrum access. CR's energy consumption in friendly jamming and data transmission becomes a concern. Attaining the optimal energy efficiency of CR (μ*) is the main objective of the study here. The study's primary contribution is a novel mathematical expression that allows us to find the (τ*, μ*) pair of values in the given scenario. Following that, the relationships between the (τ*, μ*) pair and six different important system parameters have been analyzed. It has been found that a strong PT's signal allows a short sensing duration and it improves μ*, but there is a limit on the amount of improvement. Increasing the sampling rate of CR may not be worthy since it does not improve μ* significantly. A more demanding target probability of detection requires a larger sensing duration, but it has insignificant impact on μ*. In this work, the security threat of eavesdropping is considered. Our future work will consider the security threat of hostile jamming. A possible solution is to require CR to relay PT's data to PR, creating a diversity of information.
| [1] |
Wyner A D. The wire-tap channel. Bell System Technical Journal, 1975, 54(8): 1355-1387. DOI:10.1002/j.1538-7305.1975.tb02040.x (  0) 0) |
| [2] |
Poor H V, Schaefer R F. Wireless physical layer security. PNAS, 2017, 114(1): 19-26. DOI:10.1073/pnas.1618130114 (  0) 0) |
| [3] |
Huang J W, Berry R A, Honig M L. Auction-based spectrum sharing. Mobile Networks and Applications, 2006, 11(3): 405-418. DOI:10.1007/s11036-006-5192-y (  0) 0) |
| [4] |
Etkin R, Parekh A, Tse D. Spectrum sharing for unlicensed bands. IEEE Journal on Selected Areas in Communications, 2007, 25(3): 517-528. DOI:10.1109/JSAC.2007.070402 (  0) 0) |
| [5] |
Niyato D, Hossain E. Competitive pricing for spectrum sharing in cognitive radio networks: dynamic game, inefficiency of Nash equilibrium, and collusion. IEEE Journal on Selected Areas in Communications, 2008, 26(1): 192-202. DOI:10.1109/JSAC.2008.080117 (  0) 0) |
| [6] |
Ghasemi A, Sousa E S. Fundamental limits of spectrum-sharing in fading environments. IEEE Transactions on Wireless Communications, 2007, 6(2): 649-658. DOI:10.1109/TWC.2007.05447 (  0) 0) |
| [7] |
Zhang R, Liang Y C. Exploiting multi-antennas for opportunistic spectrum sharing in cognitive radio networks. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1): 88-102. DOI:10.1109/JSTSP.2007.914894 (  0) 0) |
| [8] |
Negi R, Goel S. Secret communication using artificial noise. Proceedings of 2005 IEEE 62nd Vehicular Technology Conference (VTC-2005-Fall). Piscataway: IEEE, 2005, 1906-1910. DOI:10.1109/VETECF.2005.1558439 (  0) 0) |
| [9] |
Goel S, Negi R. Secret communication in presence of colluding eavesdroppers. Proceedings of MILCOM 2005 - 2005 IEEE Military Communications Conference. Piscataway: IEEE, 2005, 1501-1506. DOI:10.1109/MILCOM.2005.1605889 (  0) 0) |
| [10] |
Goel S, Negi R. Guaranteeing secrecy using artificial noise. IEEE Transactions on Wireless Communications, 2008, 7(6): 2180-2189. DOI:10.1109/TWC.2008.060848 (  0) 0) |
| [11] |
Lu W D, Gu K C, Jia M, et al. Joint resource optimization for secure transmission in cooperative CR networks. EURASIP Journal on Wireless Communications and Networking, 2017, 193(2017): 1-8. DOI:10.1186/s13638-017-0981-5 (  0) 0) |
| [12] |
Xu D, Li Q. Improving physical-layer security for primary users in cognitive radio networks. IET Communications, 2017, 11(15): 2303-2310. DOI:10.1049/iet-com.2017.0323 (  0) 0) |
| [13] |
Li Q, Xu D. Minimizing secrecy outage probability for primary users in cognitive radio networks. AEU - International Journal of Electronics and Communications, 2018, 83: 353-358. DOI:10.1016/j.aeue.2017.10.006 (  0) 0) |
| [14] |
Xu D, Li Q. Resource allocation for cognitive radio with primary user secrecy outage constraint. IEEE Systems Journal, 2018, 12(1): 893-904. DOI:10.1109/JSYST.2016.2585654 (  0) 0) |
| [15] |
Yan P S, Zou Y L, Zhu J. Secrecy outage performance of transmit antenna selection for cognitive radio systems. IET Communications, 2017, 11(13): 1998-2004. DOI:10.1049/iet-com.2016.1321 (  0) 0) |
| [16] |
Pei Y Y, Liang Y C, Teh K C. Energy-efficient design of sequential channel sensing in cognitive radio networks: optimal sensing strategy, power allocation, and sensing order. IEEE Journal on Selected Areas in Communications, 2011, 29(8): 1648-1659. DOI:10.1109/JSAC.2011.110914 (  0) 0) |
| [17] |
Deng R L, Chen J M, Yuen C, et al. Energy-efficient cooperative spectrum sensing by optimal scheduling in sensor-aided cognitive radio networks. IEEE Transactions on Vehicular Technology, 2012, 61(2): 716-725. DOI:10.1109/TVT.2011.2179323 (  0) 0) |
| [18] |
Xie R C, Yu F R, Ji H, et al. Energy-efficient resource allocation for heterogeneous cognitive radio networks with femtocells. IEEE Transactions on Wireless Communications, 2012, 11(11): 3910-3920. DOI:10.1109/TWC.2012.092112.111510 (  0) 0) |
| [19] |
Bayhan S, Alagoz F. Scheduling in centralized cognitive radio networks for energy efficiency. IEEE Transactions on Vehicular Technology, 2013, 62(2): 582-595. DOI:10.1109/TVT.2012.2225650 (  0) 0) |
| [20] |
Liu X Y, Zheng K C, Fu L Y, et al. Energy efficiency of secure cognitive radio networks with cooperative spectrum sharing. IEEE Transactions on Mobile Computing, 2019, 18(2): 305-318. DOI:10.1109/TMC.2018.2836902 (  0) 0) |
| [21] |
Urkowitz H. Energy detection of unknown deterministic signals. Proceedings of the IEEE, 1967, 55(4): 523-531. DOI:10.1109/PROC.1967.5573 (  0) 0) |
| [22] |
Digham F F, Alouini M-S, Simon M K. On the energy detection of unknown signals over fading channels. Proceedings of IEEE International Conference on Communications, 2003, 3575-3579. DOI:10.1109/ICC.2003.1204119 (  0) 0) |
| [23] |
Ghasemi A, Sousa E S. Opportunistic spectrum access in fading channels through collaborative sensing. Journal of Communications, 2007, 2(2): 71-82. DOI:10.4304/jcm.2.2.71-82 (  0) 0) |
| [24] |
Liang Y C, Zeng Y H, Peh E C Y, et al. Sensing-throughput tradeoff for cognitive radio networks. IEEE Transactions on Wireless Communications, 2008, 7(4): 1326-1337. DOI:10.1109/TWC.2008.060869 (  0) 0) |
| [25] |
Althunibat S, Granelli F. On results' reporting of cooperative spectrum sensing in cognitive radio networks. Telecommunication Systems, 2016, 62: 569-580. DOI:10.1007/s11235-015-0095-5 (  0) 0) |
 2021, Vol. 28
2021, Vol. 28


