2. Key Laboratory of Communication Network and Information Processing in Fujian Province, Xiamen 361024, Fujian, China;
3. Photonics Labs., Department of Electrical and Computer Engineering, Concordia University, Montreal QC H3G 1M8, Canada
It is hoped that the ultrashort pulses excited by semiconductor lasers are tunable and pulse frequencies far exceed the direct modulation limit[1-3]. Ultrashort pulses can be widely used in optical switches, optical interconnection[4], photoelectric sampling[5], material fabrication, and optical coherence tomography[6]. Semiconductor mode-locked lasers (SLLs), especially those with quantum dot structure, have maintained a sustained growth momentum, and have become a research hot spot in the past decade.
Quantum dot mode-locked lasers (QD MLLs) usually have two types of structures: one is two section type, the other is single-section type. The two-section structure has two parts: gain and saturation absorber. For two-section mode-locked semiconductor lasers, mode-locking can be obtained using various external cavity structures, such as basic mirror optical feedback[7-10], photoelectric feedback[11] in the saturated absorption region, hybrid mode modulation[12], non-impact cavity structure[13] in the position of saturable absorber in the cavity, controlling the temperature of the laser, and working at low temperature[14]. For single-section mode-locked semiconductor lasers, the results of material growth and device development are reported in Refs. [15-18]. Compared with two-section devices, there is less work on external modulation of one-section devices, and the method is relatively simple, mainly focusing on optical feedback[19-20].
Travelling-wave (TW) model and delayed differential equation (DDE) model are two popular methods to analyze the propagation dynamics of the electromagnetic waves in semiconductor lasers and feedback systems[21-23]. Rossetti et al.[24] proposed a TDTW model for the analysis of two-section QD MLLs in 2011, and then the model was modified and successfully applied to the study of the one-section QD MLLs[25], QD Fabry-Perot lasers[26], and QD DFB lasers[27].
The TDTW model can describe the dynamic behavior of the device more accurately by solving the one-dimensional wave equation and carrier rate equation in the cavity in time domain. In DDE model, a unidirectional annular cavity is assumed. By introducing appropriate approximation, the delay differential equation is derived from the fundamental wave equation. Compared with TW model, the computational complexity is greatly reduced. There are plenty of experimental results about optical feedback in QD MLLs, but only a few theoretical studies are reported. In practical experiments, long optical fiber is often used to provide optical feedback, so the study of long external cavity has greater value. However, the TDTW model studies the long external cavity, which means a sharp increase in the amount of calculation. Therefore, DDE model is commonly used in optical feedback research[23, 28]. There are few reports on optical feedback of TDTW model.
To depict the dynamic behavior of the device more accurately, this paper studied and analyzed the Rossi's TDTW model, and obtained a new model for the study of optical feedback in single section QD MLLs. This new model overcomes the problem that the calculation of TDTW model increases greatly when the optical feedback of long external cavity is introduced. The pulse trains of QD MLLs with and without optical feedback were simulated. In addition, the influence of round-trip time and local modulation intensity on the period of the optical pulse were studied.
1 Theoretical ModelThe block diagram of optical feedback system is given in Fig. 1, and the reflectivity at three boundaries is noted. In the figure, the rectangle on the left represents QD MLL and the rightmost rectangle represents Bragg grating with a central wave number of β0. When the length of the external cavity is much larger than that of the grating, the length of the grating is ignored. The cavity length of QD MLL is L and the external cavity length is Lext and the loss caused by each optical element of external cavity is rext. Fig. 2 shows an equivalent structure for Fig. 1, in which optical feedback cavity is modelled by an effective reflectivity reff.

|
Fig.1 Structure of QD MLL with an external cavity |

|
Fig.2 Equivalent structure of QD MLL with an external cavity |
The coupled wave equation was used to display the spatial-temporal behavior of the electromagnetic field including the feedback from external cavity as follows[24]:
| $ \begin{array}{l} \frac{\partial E^{+}}{\partial z}+\frac{1}{v_{g}} \frac{\partial E^{+}}{\partial t}=-\frac{\alpha_{i}}{2} E^{+}-{\rm{j}} P^{+}(z, t)+ \\ \ \ \ \ \ \ \ \ S^{+}(z, t)-r_{\text {ext }}\left(1-r_{L}^{2}\right) \cdot \mathrm{AT} \cdot E^{-}(L, t-\tau) \end{array} $ | (1a) |
| $ \begin{gathered} -\frac{\partial E^{-}}{\partial z}+\frac{1}{v_{g}} \frac{\partial E^{-}}{\partial t}=-\frac{\alpha_{i}}{2} E^{-}-\mathrm{j} P^{-}(z, t)+ \\ \ \ \ \ S^{-}(z, t)+r_{\mathrm{ext}}\left(1-r_{L}^{2}\right) \cdot \mathrm{AT} \cdot E^{+}(L, t-\tau) \end{gathered} $ | (1b) |
where E±(z, t) are slowly varying forward (+) and backward (-) traveling mode field amplitudes, vg is group-velocity, αi is the intrinsic waveguide loss, and P±(z, t) is the modified polarization for each forward (+)/backward (-) propagation, respectively. In this paper, the imaginary number unit is represented by j. S±(z, t) is spontaneous emission noise, t is the transmission time, and z is the position of transmission, respectively. Take optical feedback as an injection term, where τ is the roundtrip time. The term AT was used to take into account the optical feedback intensity regulating factor related to transmission loss, which is one if the loss in transmission is ignored.
Since the length of the QD laser is negligible compared with that of the outer cavity, the difference of feedback in different positions of the internal cavity is ignored. So Eq. (1) can be modified into
| $ \begin{gathered} \frac{\partial E^{+}}{\partial z}+\frac{1}{v_{g}} \frac{\partial E^{+}}{\partial t}=-\frac{\alpha_{i}}{2} E^{+}-\mathrm{j} P^{+}(z, t)+ \\ S^{+}(z, t)-f \cdot E^{-}(z, t-\tau) \end{gathered} $ | (2a) |
| $ \begin{gathered} -\frac{\partial E^{-}}{\partial z}+\frac{1}{v_{g}} \frac{\partial E^{-}}{\partial t}=-\frac{\alpha_{i}}{2} E^{-}-\mathrm{j} P^{-}(z, t)+ \\ S^{-}(z, t)+f \cdot E^{+}(z, t-\tau) \end{gathered} $ | (2b) |
where f=rext(1-rL2)·AT is used.
Based on mode-locking behavior of periodic pulses, E(z, t) must be periodically distributed in the time domain. Let Tint be the period of the QD laser without feedback. When τ is equal to an integer multiple of Tint, there is f·E±(z, t-τ)=f·E±(z, t). When τ is not equal to an integer multiple of Tint, there is τ=nTint+δ, where n is an integer, and
| $ \begin{gathered} f \cdot E^{\pm}(z, t-\tau)=f \cdot E^{\pm}(z, t- \\ \left.n T_{\mathrm{int}}-\delta\right)=f \cdot E^{\pm}(z, t-\delta) \end{gathered} $ |
Based on the aforementioned analysis, Eq. (2) is transformed into frequency domain, and the following expression is obtained:
| $ \begin{gathered} \frac{\partial E^{+}(z, \omega)}{\partial z}=\left(k(z, \omega)-\mathrm{j} \frac{\omega}{v_{g}}\right) E^{+}(z, \omega)- \\ f \cdot \mathrm{e}^{-\mathrm{j} \omega \delta} E^{-}(z, \omega)+S^{+}(z, \omega) \end{gathered} $ | (3a) |
| $ \begin{gathered} -\frac{\partial E^{-}(z, \omega)}{\partial z}=\left(k(z, \omega)-\mathrm{j} \frac{\omega}{v_{g}}\right) E^{-}(z, \omega)+ \\ f \cdot \mathrm{e}^{-\mathrm{j} \omega \delta} E^{+}(z, \omega)+S^{-}(z, \omega) \end{gathered} $ | (3b) |
where
| $ \frac{\partial}{\partial z}\left[\begin{array}{l} E^{+}(z, \omega) \\ -E^{-}(z, \omega) \end{array}\right]=\left[\boldsymbol{M}_{\delta}+\boldsymbol{M}_{g}\right]\left[\begin{array}{l} E^{+}(z, \omega) \\ E^{-}(z, \omega) \end{array}\right] $ | (4) |
where matrices Mδ and Mg are expressed respectively as
| $ \boldsymbol{M}_{\delta}=\left[\begin{array}{cc} k(z, \omega)-\mathrm{j} \frac{\omega}{v_{g}} & 0 \\ 0 & k(z, \omega)-\mathrm{j} \frac{\omega}{v_{g}} \end{array}\right] $ | (5a) |
| $ \boldsymbol{M}_{g}=\left[\begin{array}{lc} 0 & -f \cdot \mathrm{e}^{-\mathrm{j} \omega \delta} \\ f \cdot \mathrm{e}^{-\mathrm{j} \omega \delta} & 0 \end{array}\right] $ | (5b) |
In Eq.(5b), when δ is small enough, the first order Taylor expansion of fe-jωδ at ω0 which is f(1-jδω0) can be used, and Eq. (5b) can be given by
| $ \boldsymbol{M}_{g}=\left[\begin{array}{l} 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -f \cdot\left(1-\mathrm{j} \delta \omega_{0}\right) \\ f \cdot\left(1-\mathrm{j} \delta \omega_{0}\right) \ \ \ \ \ 0 \end{array}\right] $ | (5c) |
For a given small step Δz, Eq. (4) is simplified into
| $ \begin{array}{l} {\left[\begin{array}{c} E^{+}(z+\Delta z, \omega) \\ E^{-}(z, \omega) \end{array}\right]=\exp \left[\boldsymbol{M}_{\delta} \Delta z\right] \exp \left[\boldsymbol{M}_{g} \Delta z\right]} \\ \ \ \ \ \ \ \ \ \ \ \ \ {\left[\begin{array}{c} E^{+}(z, \omega) \\ E^{-}(z+\Delta z, \omega) \end{array}\right]} \end{array} $ | (6) |
The numerical solution of Eq. (6) can be approximated as
| $ \begin{array}{l} {\left[\begin{array}{c} E^{+}(z+\Delta z, \omega+\Delta \omega) \\ E^{-}(z, \omega+\Delta \omega) \end{array}\right]=} \\ \ \ \ \ {\left[\begin{array}{ll} \operatorname{sech}(\gamma \Delta z) \mathrm{e}^{k(z, \omega) \Delta z} & \operatorname{jtanh}(\gamma \Delta z) \mathrm{e}^{k(z, \omega) \Delta z} \\ \mathrm{j} \tanh (\gamma \triangle z) \mathrm{e}^{-k(z, \omega) \Delta z} & \operatorname{sech}(\gamma \Delta z) \mathrm{e}^{-k(z, \omega) \Delta z} \end{array}\right]\cdot} \\ \ \ \ \ {\left[\begin{array}{c} E^{+}(z, \omega) \\ E^{-}(z+\Delta z, \omega) \end{array}\right]} \end{array} $ | (7) |
where γ=jf(1-jδω0), and when Δz is small enough, ek(z, ω)△z≈1-k(z, ω)Δz is obtained. Now adding the spontaneous emission noise with a step of Δz, Eq. (7) is rewritten as
| $ \begin{aligned} E^{+}&(z+\Delta z, t+\Delta t)=\operatorname{sech}(\gamma \Delta z)\left(E^{+}(z, t)-\right. \\ &\left.\frac{\alpha_{i}}{2} E^{+}(z, t) \Delta z-\mathrm{j} P^{+}(z, t) \Delta z\right)+ \\ &\operatorname{jtanh}(\gamma \Delta z)\left(E^{-}(z+\Delta z, t)-\frac{\alpha_{i}}{2} E^{-}(z+\right. \\ &\left.\Delta z, t) \Delta z-\mathrm{j} P^{-}(z+\Delta z, t) \Delta z\right)+S^{+}(z, t) \Delta z \end{aligned} $ | (8a) |
| $ \begin{aligned} E^{-}&(z-\Delta z, t+\Delta t)= \operatorname{jtanh}(\gamma \Delta z)\left(E^{+}(z-\Delta z, t)-\right.\\ &\left.\frac{\alpha_{i}}{2} E^{+}(z-\Delta z, t) \Delta z-\mathrm{j} P^{+}(z-\Delta z, t) \Delta z\right)+\\ &\operatorname{sech}(\gamma \Delta z)\left(E^{-}(z, t)-\frac{\alpha_{i}}{2} E^{-}(z, t) \Delta z-\right.\\ &\left.\mathrm{j} P^{-}(z, t) \Delta z\right)+S^{-}(z, t) \Delta z \end{aligned} $ | (8b) |
The boundary conditions for Eq. (8) are as follows:
| $ E^{+}(0, t)=r_{r} E^{-}(0, t) $ | (9a) |
| $ E^{+}(L, t)=r_{\text {eff }} E^{-}(L, t) $ | (9b) |
As shown in Fig. 2, the effective reflectivity
Optical feedback makes the local optical intensity modulated, which in turn modulates the gain[30]. So each QD population's contribution to the whole effective polarization is defined as follows (see Appendix):
| $ \begin{array}{l} p_{i \text{GS}}^{\pm}(z, t)=\frac{\mathrm{j}}{\hbar} \frac{\omega_{0}}{2 {\rm{ \mathsf{ π}}} c \eta} \frac{\Gamma_{x y}}{h_{\mathrm{W}}} N_{D} A_{\mathrm{GS}} D_{\mathrm{GS}}\left(2 \rho_{i \mathrm{GS}}-1\right) \cdot \\ \ \ \ \ I_{i \mathrm{GS}}^{\pm}(z, t) \cdot \\ \frac{G_{i}}{1+\varepsilon_{1}\left(\left|E^{+}\right|^{2}+\left|E^{-}\right|^{2}\right)+2 \varepsilon_{2}\left|E^{+}\right|\left|E^{-}\right| \cos \left(2 \beta_{0} \Delta z+\varphi\right)} \end{array} $ | (10) |
where Γxy is the field confinement factor in the QD laser, ND is the QD surface density, AGS is the coefficient of the interband transition matrix element containing the GS (ground state) transition, DGS is the degeneracy of GS QD states, hW is the quantum well (QW) width, ρiGS is the carrier occupation probability, ε1 and ε2 refer to the local intensity modulation intensity coefficients caused by the optical feedback intensity and grating structure respectively, β0 is the central wave numbers in Bragg grating, φ is the relative phase difference between E+ and E-. In this paper, φ=0 and β0 =ω0/c are set.
The detailed expressions for Iim±(z, t) and P±(z, t) can be found in Ref. [24]:
| $ \begin{aligned} &I_{i m}^{\pm}(z, t)=\mathrm{e}^{\mathrm{j}\left(\mathtt{\varpi}_{i m}-\omega_{0}\right) \Delta t} \mathrm{e}^{-\Gamma \Delta t} I_{i m}^{\pm}(z, t-\Delta t)+ \\ &\ \ \ \ \frac{1}{2} \Delta t\left[E^{\pm}(z, t)+\mathrm{e}^{\mathrm{j}\left(\mathtt{\varpi}_{i m}-\omega_{0}\right) \Delta t} \mathrm{e}^{-\Gamma \Delta t} E^{\pm}(z, t-\Delta t)\right] \end{aligned} $ | (11a) |
and
| $ P^{\pm}(z, t)=\sum\limits_{i=1}^{N} \sum\limits_{m=\mathrm{GS}, \mathrm{ES}} p_{i m}^{\pm}(z, t) $ | (11b) |
The carrier density rate equations in the feedback system are given in Ref. [25]:
| $ \frac{\mathrm{d} N_{\mathrm{SCH}}}{\mathrm{d} t}=\eta_{i} \frac{J}{e} \Delta z W-\frac{N_{\mathrm{SCH}}}{\tau_{r}^{\mathrm{SCH}}}-\frac{N_{\mathrm{SCH}}}{\tau_{c}^{W}} $ | (12a) |
| $ \begin{aligned} \frac{\mathrm{d} N_{W}}{\mathrm{~d} t} &=\frac{N_{\mathrm{SCH}}}{\tau_{c}^{W}}-\frac{N_{W}}{\tau_{r}^{W}}-\\ & \sum\limits_{i=1}^{N} \frac{G_{i}}{\tau_{c}} N_{W}\left(1-f_{i}\right)+\sum\limits_{i=1}^{N} \frac{N_{i \mathrm{GS}}}{\tau_{e}^{i}} \end{aligned} $ | (12b) |
| $ \begin{aligned} \frac{\mathrm{d} N_{i \mathrm{GS}}}{\mathrm{d} t}&=\frac{G_{i}}{\tau_{c}} N_{W}\left(1-f_{i}\right)-\frac{N_{i \mathrm{GS}}}{\tau_{e}^{i}}-\frac{N_{i\mathrm{GS}}}{\tau_{s}}- \\ &\frac{\mathrm{j} \Delta z}{\hbar \omega_{i}}\left[\left(E^{+} p_{i \mathrm{GS}}^{+*}-E^{-*} p_{i \mathrm{GS}}^{+}\right)+\right. \\ &\left.\left(E^{-} p_{i \mathrm{GS}}^{-*}-E^{-*} p_{i \mathrm{GS}}^{-}\right)\right] \end{aligned} $ | (12c) |
The time dynamics of the feedback system can be presented by solving Eqs. (8)-(12) iteratively.
According to Ref. [25], the self-focusing effect leading to mode locking can be expressed in our model as follows:
| $ E^{+}(L, t)=\left(1-\frac{s_{0}}{1+\left|E^{+}(L, t)\right|^{2} / I_{\mathrm{sat}}}\right) E^{+}(L, t) $ | (13) |
where |E+(L, t)|2 is the laser intensity under normalized conditions, s0 is the unsaturated loss, and Isat is saturation intensity of the QD laser. The values of s0 and Isat used in the paper are 0.35 and 0.16 W, respectively.
2 Results and DiscussionThe time-domain dynamic of the one section QD MLLs was studied by using the model. The calculated results were compared with the test data in Ref.[31], and the simulation model parameters are given in Table 1.
| Table 1 Simulation Parameters |
A comparison between the measured curve and the calculated curve is depicted in Fig. 3 for the QD MLL without optical feedback. It can be seen from the figure that the simulated data are in good agreement with experimental data. The periodic time is 20 ps, the pulse width (FWHM) of simulation results is 200 fs, and the FWHM of the experiment results is 295 fs. The disagreement between simulation and experimental data can be attributed to the influence of group velocity, which is not considered.
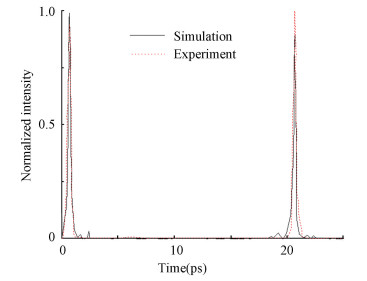
|
Fig.3 Optical pulse trains without optical feedback |
Fig. 4 shows the simulation result with optical feedback. In Ref. [31], 8 fiber Bragg gratings with the same frequency interval were used to carry out optical feedback experiments. The experimental results showed that when the QD MLL with a pulse period of 20 ps was introduced into the external cavity, and the periodic pulse of 2.29 ps was obtained. In this paper, let parameter δ=0 and ε1=ε2=2.3, the periodic time is 2.3 ps, which is consistent with the experimental data.
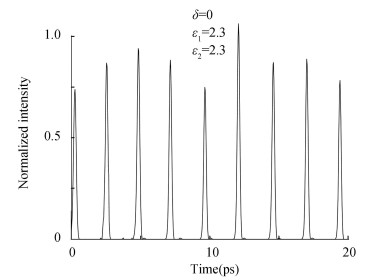
|
Fig.4 Optical pulse trains with optical feedback |
Figs. 5 (a)-(c) depict optical intensity pulse while τ is not an integral multiple of Tint, and δ= 10-14, 1.4×10-14, and 10-13 s were considered. It can be seen that with the increase of offsets, the pulses are more distorted. This may be due to the competition between the feedback pulse sequence and the laser generated pulse sequence with the increase of offset, resulting in the increase of noise and pulse distortion. Compared with Fig. 3 and Fig. 4, the period of the pulse is the shortest when τ=nTint. The studies in Fig. 4 and Fig. 5 show that optical feedback can cause stable or unstable pulse effects. When τ=nTint, the pulse propagation in the outer cavity matches the pulse in the QDMLL perfectly, forming resonance and obtaining stable pulse effect. At this time, the period of the pulse is the shortest and the frequency of the pulse increased the most. This frequency pulling caused by feedback has been verified in the experiment[3, 7-8]. The DDE model was used to study the optical feedback in Ref. [23], and the conclusion of frequency pulling caused by optical feedback was also obtained. When δ=10-13, the pulse propagation in the outer cavity and the pulse in the QD MLL could not form resonance, resulting in the instability of the pulse.

|
Fig.5 Optical intensity pulse trains with different δ |
Fig. 6 shows the impact of local optical intensity modulated coefficient ε1 and ε2, where two cases were considered: ε1=ε2 =2.1 and 2.5. With the increase of ε1 and ε2, the pulse period was shortened more. The gain modulation effect caused by optical feedback was studied as shown in Fig. 6. It is considered that the optical feedback will cause the inhomogeneous distribution of photons in the direction of propagation, which makes the carriers almost completely confined in the quantum dots, and further inhibit the carriers diffusion along the waveguide, thus suppressing the gain. The larger the ε1 and ε2 are, the stronger the suppression effect is, and the shorter the pulse period caused by feedback is.
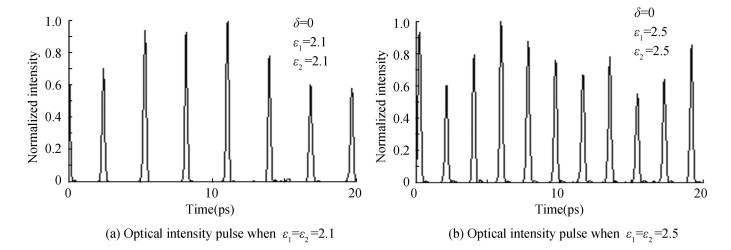
|
Fig.6 Optical intensity pulse trains with different ε1 and ε2 |
3 Conclusions
A TDTW model of single-section QD mode-locked lasers with optical feedback has been proposed. The influence of external cavity round trip time on the pulse sequence was researched. Further, the influence of local light intensity modulation caused by feedback on pulse period was studied. The simulated pulse was consistent with experimental results. The optical feedback term was introduced into the TDTW model, and the improved model based on reasonable assumptions solved the problem that the cavity length is too long and the calculation is huge when the finite difference method is used to numerically solve the propagation equation of spatiotemporal field dynamics in the cavity. Compared with other optical feedback models[23, 28], it does not need to assume the geometry of the laser cavity, but takes into account the QD optical susceptibility, distribution dynamics in the QD states, and spontaneous emission noise. Because the general expression of TDTW model with optical feedback is given, the proposed optical feedback model of QD MLLs can be extended to model other types of semiconductor lasers under optical feedback conditions.
AppendixDerivation of the electric polarization expression Eq. (10)
The electric polarization expression is written as[24]
| $ \begin{aligned} -\mathrm{j} & \frac{\omega_{0}}{2 c \eta \varepsilon_{0}} \Gamma_{x y} P^{\pm}(z, t)=\\ & \sum\limits_{i=1}^{N} g_{i \mathrm{GS}}^{\pm}(z, t)\left(2 \rho_{\mathrm{GS}}-1\right) I_{i \mathrm{GS}}^{\pm}(z, t) \end{aligned} $ | (A.1) |
The local optical intensity is strongly modulated by feedback, and then the gain is modulated by parameter ε1 and ε2. Therefore, the gain giGS±(z, t) is written as[30]
| $ \begin{aligned} &g_{i \mathrm{GS}}^{\pm}(z, t)= \\ &\frac{g_{0, i \mathrm{GS}}^{\pm}(z, t)}{1+\varepsilon_{1}\left(\left|E^{+}\right|^{2}+\left|E^{-}\right|^{2}\right)+2 \varepsilon_{2}\left|E^{+}\right|\left|E^{-}\right| \cos \left(2 \beta_{0} z+\varphi\right)} \end{aligned} $ | (A.2) |
Here, g0, iGS±(z, t) is the gain without optical feedback, which is given in Ref. [24]. The total forward/backward polarization is obtained by summation over N groups of QDs:
| $ P^{\pm}(z, t)=\sum\limits_{i=1}^{N} p_{i\mathrm{GS}}^{\pm}(z, t) $ | (A.3) |
Combining (A.1)-(A.3), piGS±(z, t) is obtained for a step of Δz in light propagation direction:
| $ \begin{aligned} &p_{i\mathrm{GS}}^{\pm}(z, t)=\frac{\mathrm{j}}{\hbar} \frac{\omega_{0}}{2 {\rm{ \mathsf{ π}}} c \eta} \frac{\Gamma_{x y}}{h_{W}} N_{D} A_{\mathrm{GS}} D_{\mathrm{GS}}\left(2 \rho_{i \mathrm{CS}}-1\right) \cdot I_{i \mathrm{GS}}^{\pm}(z, t) \cdot \\ &\frac{G_{i}}{1+\varepsilon_{1}\left(\left|E^{+}\right|^{2}+\left|E^{-}\right|^{2}\right)+2 \varepsilon_{2}\left|E^{+}\right|\left|E^{-}\right| \cos \left(2 \beta_{0} \Delta z+\varphi\right)} \end{aligned} $ | (A.4) |
| [1] |
Qiao W C, Chu H W, Zhao S Z, et al. Passive mode-locking characteristics from the Nd: Gd0.19Y0.81VO4 laser at 1.34 um. Optics & Laser Technology, 2016, 82: 101-103. DOI:10.1016/j.optlastec.2016.03.014 (  0) 0) |
| [2] |
Wang F H, Pistore V, Riesch M, et al. Ultrafast response of harmonic modelocked THz lasers. Light: Science & Applications, 2020, 9(1): 51. DOI:10.1038/s41377-020-0288-x (  0) 0) |
| [3] |
Nikiforov O, Jaurigue L, Drzewietzki L, et al. Experimental demonstration of change of dynamical properties of a passively mode-locked semiconductor laser subject to dual optical feedback by dual full delay-range tuning. Optics Express, 2016, 24(13): 14301-14310. DOI:10.1364/OE.24.014301 (  0) 0) |
| [4] |
Keeler G A, Nelson B E, Agarwal D, et al. The benefits of ultrashort optical pulses in optically interconnected systems. IEEE Journal of Selected Topics in Quantum Electronics, 2013, 9(2): 477-485. DOI:10.1109/JSTQE.2003.813317 (  0) 0) |
| [5] |
Gao F, Luo S, Ji H M, et al. Ultrashort pulse and high power mode-locked laser with chirped InAs/InP quantum dot active layers. IEEE Photonics Technology Letters, 2016, 28(13): 1481-1484. DOI:10.1109/LPT.2016.2561302 (  0) 0) |
| [6] |
Žemaitis A, Gečys P, Barkauskas M, et al. Highly-efficient laser ablation of copper by bursts of ultrashort tuneable (fs-ps) pulses. Scientific Reports, 2019, 9(1): 12280. DOI:10.1038/s41598-019-48779-w (  0) 0) |
| [7] |
Raghunathan R, Grillot F, Mee J K, et al. Tuning the external optical feedback-sensitivity of a passively mode-locked quantum dot laser. Applied Physics Letters, 2014, 105: 041112-1-041112-5. DOI:10.1063/1.4891576 (  0) 0) |
| [8] |
Rauch S, Drzewietzki L, Klehr A, et al. Experimental study of the timing jitter of a passively mode-locked external-cavity semiconductor laser subject to repetition rate transitions and optical feedback. IEEE Journal of Quantum Electronics, 2015, 51(4): 1300107. DOI:10.1109/JQE.2015.2402431 (  0) 0) |
| [9] |
Balzer J C, Pilny R H, Döpke B, et al. Passively mode-locked diode laser with optimized dispersion management. IEEE Journal of Selected Topics in Quantum Electronics, 2015, 21(6): 1101008. DOI:10.1109/JSTQE.2015.2418225 (  0) 0) |
| [10] |
Arkhipov R M, Arkhipov M V, Babushkin I. Self-starting stable coherent mode-locking in a two-section laser. Optics Communications, 2016, 361: 73-78. DOI:10.1016/j.optcom.2015.10.030 (  0) 0) |
| [11] |
Drzewietzki L, Breuer S, Elsaber W. Timing phase noise reduction of mode-locked quantum-dot lasers by time-delayed optoelectronic feedback. Electronics Letters, 2013, 49(8): 557-559. DOI:10.1049/el.2013.0763 (  0) 0) |
| [12] |
Habruseva T, Arsenijevic D, Kleinert M, et al. Optimum phase noise reduction and repetition rate tuning in quantum-dot mode-locked lasers. Applied Physics Letters, 2014, 104: 02112-1-02112-4. DOI:10.1063/1.4861604 (  0) 0) |
| [13] |
Simos H, Simos C, Mesaritakis C, et al. Amplitude and timing noise in a noncolliding passively mode-locked quantum dot laser. IEEE Photonics Technology Letters, 2015, 27(5): 506-509. DOI:10.1109/LPT.2014.2383433 (  0) 0) |
| [14] |
Finch P, Hutchings M D, Blood P, et al. Improving the optical bandwidth of passively mode-locked InAs quantum dot lasers. IEEE Journal of Selected Topics in Quantum Electronics, 2015, 21(6): 1101407. DOI:10.1109/JSTQE.2015.2416675 (  0) 0) |
| [15] |
Gosset C, Merghem K, Martinez A, et al. Subpicosecond pulse generation at 134 GHz using a quantum-dash-based Fabry-Perot laser emitting at 1.56 μm.. Applied Physics Letters, 2006, 88(24): 241105.1-241105.3. DOI:10.1063/1.2213007 (  0) 0) |
| [16] |
Klaime K, Piron R, Paranthoen C, et al. 20 GHz to 83 GHz single section InAs/InP quantum dot mode-locked lasers grown on (001) misoriented substrate. Proceedings of the 2012 International Conference on Indium Phosphide and Related Materials. Piscataway: IEEE, 2012, 181-184. DOI:10.1109/ICIPRM.2012.6403352 (  0) 0) |
| [17] |
Klaime K, Calo C, Piron R, et al. 23 and 39 GHz low phase noise monosection InAs/InP (113)B quantum dots mode-locked lasers. Optics Express, 2013, 21(23): 29000-29005. DOI:10.1364/OE.21.029000 (  0) 0) |
| [18] |
Lu Z G, Liu J R, Poole P J, et al. Ultra-high repetition rate InAs/InP quantum dot mode-locked lasers. Optics Communications, 2011, 284: 2323-2326. DOI:10.1016/j.optcom.2010.11.083 (  0) 0) |
| [19] |
Jiao Z J, Liu J R, Lu Z G, et al. A-band InAs/InP quantum dot semiconductor mode-locked laser emitting 403-GHz repetition rate pulses. IEEE Photonics Technology Letters, 2011, 23(9): 543-545. DOI:10.1109/LPT.2011.2114340 (  0) 0) |
| [20] |
Jiao Z J, Liu J R, Lu Z G, et al. Tunable terahertz beat signal generation from an InAs/InP quantum-dot mode-locked laser combined with external-cavity. IEEE Photonics Technology Letters, 2012, 24(6): 518-520. DOI:10.1109/LPT.2011.2182642 (  0) 0) |
| [21] |
Vizzino A, Gioannini M, Montrosset I. Dynamic simulation of clock recovery with self-pulsating three-section distributed-feedback lasers. IEEE Journal of Quantum Electronics, 2002, 38(12): 1580-1586. DOI:10.1109/JQE.2002.805102 (  0) 0) |
| [22] |
Rebrova N, Huyet G, Rachinskii D, et al. Optically injected mode-locked laser. Physical Review, 2011, 83(6Pt 2): 066202. DOI:10.1103/PhysRevE.83.066202 (  0) 0) |
| [23] |
Otto C, Ludge K, Vladimirov A G, et al. Delay-induced dynamics and jitter reduction of passively mode-locked semiconductor lasers subject to optical feedback. New Journal of Physics, 2012, 14(11): 113033. DOI:10.1088/1367-2630/14/11/113033 (  0) 0) |
| [24] |
Rossetti M, Bardella P, Montrosset I. Time-domain travellingwave model for quantum dot passively mode-locked lasers. IEEE Journal of Quantum Electronics, 2011, 47(2): 139-150. DOI:10.1109/JQE.2010.2055550 (  0) 0) |
| [25] |
Jiao Z J, Zhang R, Zhang X P, et al. Modeling of single-section quantum dot mode-locked lasers: impact of group velocity dispersion and self phase modulation. IEEE Journal of Quantum Electronics, 2013, 49(12): 1008-1015. DOI:10.1109/JQE.2013.2285115 (  0) 0) |
| [26] |
Gioannini M, Rossetti M. Time-domain traveling wave model of quantum dot DFB lasers. IEEE Journal of Selected Topics in Quantum Electronics, 2011, 17(5): 1318-1326. DOI:10.1109/JSTQE.2011.2128857 (  0) 0) |
| [27] |
Gioannini M, Bardella P, Montrosset I. Time-domain traveling-wave analysis of the multimode dynamics of quantum dot fabry-perot lasers. IEEE Journal of Selected Topics in Quantum Electronics, 2015, 21(6): 1900811. DOI:10.1109/JSTQE.2015.2425537 (  0) 0) |
| [28] |
Jaurigue L, Krauskopf B, Lüdge K. Multipulse dynamics of a passively mode-locked semiconductor laser with delayed optical feedback. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2017, 27: 114301. DOI:10.1063/1.5006743 (  0) 0) |
| [29] |
Kakiuchida H, Ohtsubo J. Characteristics of a semiconductor laser with external feedback. IEEE Journal of Quantum Electronics, 1994, 30(9): 2087-2097. DOI:10.1109/3.309866 (  0) 0) |
| [30] |
Jones D J, Zhang L M, Carroll J E, et al. Dynamics of monolithic passively mode-locked semiconductor laser. IEEE Journal of Quantum Electronics, 1995, 31(6): 1051-1058. DOI:10.1109/3.387042 (  0) 0) |
| [31] |
Lu Z G, Liu J R, Poole P J, et al. Ultra-high repetition rate InAs/InP quantum dot mode-locked lasers. Optics Communications, 2011, 284: 2323-2326. DOI:10.1016/j.optcom.2010.11.083 (  0) 0) |
 2021, Vol. 28
2021, Vol. 28


