The hyperspectral imagery (HSI) is composed of hundreds of narrow bands with high spectral resolution, which captures signatures of different substances measured by surface reflectance. However, the low spatial resolution would lead to the mixed components in HSIs. As a result, unmixing techniques are developed to acquire the spectrum and its spatial distribution of each material from the highly mixed data.
Deep autoencoders are emerging as a popular approach for unsupervised unmixing due to its strong capacity for low-level feature interpretation. The hierarchical structure of the network can learn the latent distribution of the input and extract representative features effectively. Several researches have investigated autoencoder models for linear unmixing. The autoencoder cascade is an instructive work which marginalized denoising autoencoder is concatenated with a nonnegative autoencoder[1]. To handle the problems with outliers, ASNSA adopts local outlier factor to detect the outlier samples[2], while DAEN utilizes the variational autoencoder to perform blind unmixing for HSIs[3]. Endnet develops a novel unmixing scheme with sparsity and smoothness constraints to improve consistency[4]. uDAs incorporates the denoising process into the network by imposing a denoising constraint[5]. However, these network models are usually impacted by noise since the correlation of the spatial and spectral information is not simultaneously taken into consideration.
HSIs exhibit local consistency spatially, and incorporating spatial information can improve the robustness of the unmixing methods. Hypergraph is often taken as an effective manifold structure to represent spatial-spectral relationships among pixels[6-7]. In this paper, a robust 3D convolutional autoencoder (R3dCAE) unmixing framework was developed with spatial constraint. Here a deep denoising 3-dimensional convolutional autoencoder was designed to cope with the high noise disturbance. Furthermore, a non-negative sparse autoencoder was attached subsequently. To fully exploit the latent spatial contextual information, a hypergraph structure was constructed to preserve local consistency of abundances. l2, 1-norm regularizer was also imposed to improve the sparsity of the solution. Hidden endmembers and abundances can be obtained properly by training the network with the denoised data.
1 R3dCAE Model for Hyperspectral UnmixingThe proposed R3dCAE model concatenated a denoising 3D convolutional autoencoder (denoising 3D CAE) with a non-negative sparse autoencoder (NNSAE) network (Fig. 1). In the proposed method, a set of corrupted data was used to train the denoising 3D CAE to recover original signals. Furthermore, an NNSAE was attached which incorporates the non-negative and sparsity constraints as well as a hypergraph regularizer for accurate estimation of endmembers and abundances.

|
Fig.1 The block diagram of the proposed deep network for HSI unmixing |
1.1 Denoising Autoencoder
The denoising autoencoder attempts to recover the clean data from the noisy input using the coupled encoder-decoder network. The encoder projects the data x into low-dimensional embedding z = fθ(x)=σ(We x + be), and the decoder retrieves the original data
| $ \min \limits_{\theta, \theta^{\prime}} J\left(\theta, \theta^{\prime}\right)=\frac{1}{n} \sum\limits_{i=1}^{n} \frac{1}{2}\left\|g_{\theta^{\prime}}\left(f_{\theta}\left(\tilde{\boldsymbol{x}}_{i}\right)\right)-\boldsymbol{x}_{i}\right\|_{2}^{2} $ | (1) |
Here masking noise of factor ν was adopted in the sample process, i.e., a fraction ν of the elements of x was randomly chosen to be 0. The denoising autoencoder can be interpreted as to define and learn a low-dimensional manifold for high dimensional input and capture the main variations in the data[8]. Representative high-order features can be extracted by nonlinear data transformation.
1.2 Deep 3D Denoising Convolutional AutoencoderTo reduce the negative impact by noise disturbance, here a denoising 3D convolutional autoencoder was constructed, and the volumetric representation of the corrupted data was fed into the network directly.
The HSI data is a third order tensor containing multiple channels to store spectral signatures, and the high spectral and spatial correlation makes it difficult for quantitative analysis of HSIs. Therefore, here a 3D convolution network capable of exploiting the spectral-spatial correlation in HSI was constructed. Principle and robust features from spatial context and spectral signature can be extracted automatically using 3D convolution layers and 3D pooling layers[9].
In the proposed network, the encoder was constructed with 6 convolutional layers and 3 maxpooling layers, and the decoder was designed with 6 deconvolution layers and 3 unpooling layers inversely. ReLU was chosen as the activation function[10]. Table 1 shows the structure of proposed R3dCAE network for the input synthetic data Y ∈
| Table 1 Structure of proposed R3dCAE network for hyperspectral unmixing |
1.3 NNSAE with Hypergraph Structure
In the linear model, HSI data can be expressed as
| $ \boldsymbol{Y}=\boldsymbol{A} \boldsymbol{X}+\boldsymbol{N} $ | (2) |
where Y ∈
Autoencoders are unsupervised network models to transform data into low-dimension representations and learn efficient features. Generally, a simple three-layer autoencoder learns the latent representations by the encoder and then recovers the input by the decoder. Consequently, the unmixing problem can be expressed by the autoencoder model. In the unmixing autoencoder, the latent representation X can be acquired from the input Y in the encoding part X =f (Y) =σ(W· Y), and the number of hidden units is specified as the number of endmembers. In the decoding part g (X) = AX, the weight matrix A is regarded as the set of endmembers, and the output of the encoder X from hidden layer serves as the abundances associated with the endmembers.
Meanwhile, in the proposed work, a hypergraph structure was constructed to exploit spatial contextual information. A hypergraph is an extended undirected graph where the edges can hold any number of vertices. Let vertex set V={v1, v2, ..., vN} be a finite set with N elements. The set E={e1, e2, ..., eM} is the edge set with M edges defined on V, and each edge ej is a subset of V. Define G=(V, E) as a hypergraph on V such that
| $ {\mathop \cup_{j=1}\limits^{M}} e_{j}=V, e_{j} \neq \varnothing, j=1,2, \cdots, M $ | (3) |
The edge ej in a hypergraph G=(V, E) can be associated with a positive weight w(ej). Denote W s as the diagonal weight matrix with diagonal entries w(ej), j=1, 2, …, M. The degree of vertex v is the summed weights of associated edges, defined as d(v)=Σ{e∈E|v∈e}w(e), while the degree of edge e is the cardinality of the set e, defined as δ(e)=|e|. The laplacian matrix is defined as[11]
| $ \boldsymbol{L}_{H}=\boldsymbol{D}_{v}-\boldsymbol{H} \boldsymbol{W}_{s}\left(\boldsymbol{D}_{e}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} $ | (4) |
where H is the incidence matrix, D v and D e are the diagonal matrices with the diagonal entries (Dv)ii=d(vi), (De)jj=δ(ej), respectively, and W s is the weight matrix. The incidence matrix H ∈
In order to represent the relationship among pixels, a k-uniform hypergraph structure was constructed in the HSI with each edge containing K vertices. The spectrum yi∈ Y was deemed as one vertex vi in set V. The edge ei with respect to vi was generated by including vi and its K neighbors in the square local region with side length d. For simplicity, K was set equal to d. The attached weight which described the similarity of pixels in spectral domains was calculated by
| $ w\left(e_{i}\right)=\sum\limits_{y_{j} \in e_{i}} \exp \left(-\frac{\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|_{2}^{2}}{\sigma^{2}}\right) $ | (5) |
where exp(·) denotes the exponential function, and
| $ J_{H G}(X)=\mathop \Sigma\limits_{e \in E} \mathop \Sigma\limits_{\{i, j\} \in e}\frac{w(e)}{\delta(e)}|| \boldsymbol{x}_{i}-\boldsymbol{x}_{j}||_{F}^{2}=\operatorname{Tr}\left(\boldsymbol{X} \boldsymbol{L}_{H} \boldsymbol{X}^{\mathrm{T}}\right) $ | (6) |
The network learned the weights and representations that reconstructed the data by minimizing the reconstruction error as well as the hypergraph regularizer. Furthermore, a l2, 1-norm penalty was imposed on W to encourage small number of nonzero lines of W and promote row sparsity[12]. Therefore, the cost function was defined as
| $ \begin{aligned} &J(\boldsymbol{A}, \boldsymbol{W})=\frac{1}{2}\|\boldsymbol{A} \sigma(\boldsymbol{W} \boldsymbol{Y})-\boldsymbol{Y}\|_{2}^{2}+ \\ &\ \ \ \ \ \ \ \ \lambda_{H G} \operatorname{Tr}\left(\boldsymbol{\sigma}(\boldsymbol{W} \boldsymbol{Y}) \boldsymbol{L}_{H} \sigma(\boldsymbol{W} \boldsymbol{Y})^{\mathrm{T}}\right)+\gamma\|\boldsymbol{W}\|_{2,1} \end{aligned} $ | (7) |
In the implementation the block-coordinate descent scheme was adopted for optimization. Each time one matrix was updated while other variables were fixed. The updating rule for matrix A is given as
| $ \boldsymbol{A}=\max (\boldsymbol{A}-\alpha \nabla \boldsymbol{A}, 0) $ | (8) |
| $ \nabla \boldsymbol{A}=(\boldsymbol{A} \boldsymbol{X}-\boldsymbol{Y}) \boldsymbol{X}^{\mathrm{T}}, \boldsymbol{X}=\sigma(\boldsymbol{W} \boldsymbol{Y}) $ | (9) |
The learning rate α was determined following the Armijo rule[5]. W was estimated by back propagation as
| $ \boldsymbol{W}^{k+1}=\boldsymbol{W}^{k}-\beta \nabla \boldsymbol{W}^{k} $ | (10) |
where
| $ \begin{aligned} \nabla \boldsymbol{W}^{k}&=\left(\boldsymbol{A}^{\mathrm{T}}(\boldsymbol{A} \boldsymbol{X}-\boldsymbol{Y})+2 {\lambda}_{H G} \boldsymbol{X} \boldsymbol{L}_{H}\right) \cdot \sigma^{-1}(\boldsymbol{Y})+ \\ &\gamma \operatorname{diag}\left(\left(\boldsymbol{W}.^{2} * {\bf{1}}_{L}\right) .{ }^{1 / 2}\right) \boldsymbol{W} \end{aligned} $ | (11) |
In the training process, the matrices of A and X were initialized by VCA[13] and FCLS[14] algorithms and iteratively updated until convergence is approached.
2 Experimental Results and AnalysisIn this section, experiments were designed on both synthetic and real-world data to illustrate the unmixing performance. Parameters for the proposed network were set as follows: ν=0.3, α=1, β=10-3, γ=λHG=10-6, K=5. Results of MVSA[15], RCoNMF[16], MVCNMF[17], SGSNMF[18], uDAS[5] were also given for comparative purposes. For quantitative comparison, unmixing results were evaluated with spectral angle distance (SAD) in angles and root-mean-square error (RMSE).
2.1 Unmixing Experiments on Synthetic DataThe synthetic image data containing 26×26 pixels was linearly generated from 5 endmembers selected from signatures in USGS spectral library[19]. The image space was partitioned into several blocks containing pure pixels, and a low-pass filter was applied to construct the abundances. Then the abundances were normalized to satisfy sum-to-one constraint. After generating the synthetic data with endmembers and abundances, the scene was finally contaminated with i.i.d. Gaussian noise.
Table 2 and Table 3 show the unmixing performance of different algorithms for synthetic data, given in mean SAD and RMSE values, respectively, with 30 parallel tests. From Table 2, it can be observed that the proposed R3dCAE achieved lower spectral discrepancy for endmember extraction under different noise disturbances. In the R3dCAE framework, noises can be removed from the observed spectra, so that the non-negative autoencoder was able to obtain endmembers and abundances with higher accuracy by incorporating the sparsity constraint and the hypergraph regularizer. uDAS can have a comparable performance for endmember abstraction as it adopted the denoising constraint in the network. Unsatisfactory results by methods of MVSA, RCoNMF, MVCNMF, and SGSNMF at low SNR indicate that they were highly sensitive to the noise. On the other hand, the results in Table 3 show that R3dCAE yielded lower RMSE values in abundance estimation, which also demonstrate its superiority over comparative methods in hyperspectral unmixing tasks.
| Table 2 SAD (in angles) comparison at different noise levels |
| Table 3 RMSE comparison at different noise levels |
For illustrative purposes, Fig. 2 shows the comparison between the ground truth signatures and endmembers obtained by proposed R3dCAE framework when SNR=20dB, which reveals a good match for endmember extraction. Fig. 3 shows a graphical comparison of estimated abundances by different unmixing methods. Abundance maps by R3dCAE exhibit spatial consistency and contain less noisy pixels due to the introduction of hypergraph structure.
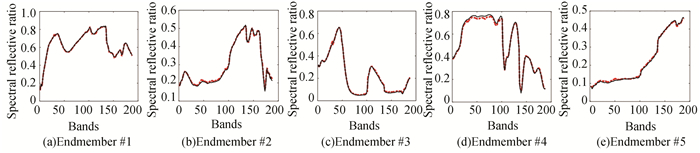
|
Fig.2 Endmembers by the proposed R3dCAE(black), compared with ground truth signatures (red) with SNR=20 dB |
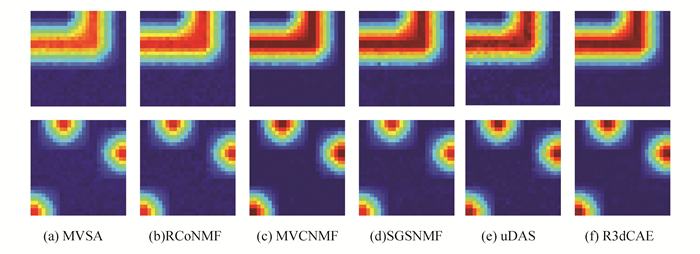
|
Fig.3 Estimated abundance maps of Endmember #1(Top Row) and #3(Bottom Row) on synthetic data by the proposed R3dCAE, compared with methods of MVSA, RCoNMF, MVCNMF, SGSNMF, and uDAS with SNR=20 dB |
In summary, the experimental results reveal that proposed R3dCAE outperformed other unmixing techniques. This is because the deep denoising network architecture can hierarchically extract robust and effective local features in spectral and spatial dimensions with 3D operations, and reconstruct high-quality denoised data. Additionally, incorporating spatial information by hypergraph structure in the NNSAE improves the unmixing performances. The l2, 1-norm regularizer was also introduced for sparsity enhancement of solution. However, it is worth noting that the proposed R3dCAE method does not rely on a specific model for noise generation. The Gaussian process can model the major part of the additive noise, including the thermal noise and quantization noise in HSI data[20], and the experiments reveal the effectiveness of proposed framework for images with Gaussian noise. For HSIs contaminated by signal dependent noise and pattern noise, R3dCAE model may yield inferior results compared with methods by modeling the signal noise strictly. In addition, a proper parameter λHG should be selected elaborately to achieve the optimal unmixing performance. The presence of outliers would also bring negative impact on accurate endmembers and abundances estimation.
2.2 Unmixing Experiments on Real DataThe well-known AVIRIS Cuprite dataset was adopted to validate the unmixing performance of the proposed algorithm in this experiment. The scene consisted of 224 spectral bands ranging from 0.4 μm to 2.5 μm, with nominal spectral resolution of 10 nm. Here a 250×191 pixel subset of the scene was utilized as it contains representative mineral spectral signatures for unmixing. Low SNR and water vapor absorption bands were removed and the remaining bands were employed to study the unmixing performances of different methods.
To compare the capacity for endmember extraction on real Cuprite data, Table 4 shows the SAD values of endmembers obtained by considered unmixing algorithms on different minerals. It is observed that the proposed unmixing autoencoder network R3dCAE yielded lower spectral discrepancy overall, which suggests that it has a strong capacity for extracting endmembers in the mixed hyperspectral data. Fig. 4 also illustrates the fractional distribution of abundances acquired by R3dCAE, and the abundance maps exhibit good discriminability and present condensation appearance for different materials. On the other hand, methods of MVC-NMF and SGSNMF can achieve good unmixing performances, while the unsatisfactory results by MVSA and RCoNMF indicate that those methods are insufficient to identify all endmembers present in the data.
| Table 4 Results obtained by different unmixing algorithms for AVIRIS Cuprite dataset |

|
Fig.4 Estimated abundance maps of the AVIRIS Cuprite data by the proposed framework(Top row: Alunite, Andradite, Buddingtonite, Dumortierite, Kaolinite-1, and Kaolinite-2;Bottom row: Muscovite, Montmorillonite, Nontronite, Pyrope, Sphene, and Chalcedony) |
3 Conclusions
In hyperspectral unmixing problems, the noise disturbance would bring negative impact on the estimation of endmembers and abundances in practical application. To cope with high noise disturbance in HSI data, a robust 3D convolutional autoencoder unmixing framework was proposed for hyperspectral unmixing problem in this paper. A denoising 3-dimensional convolutional autoencoder was designed to retrieve original spectral signatures, and a restrictive non-negative sparse autoencoder with spatial constraint was followed for endmember extraction and abundance estimation. The encoding and decoding processes by 3D convolutional operations make it possible to extract joint spectral-spatial information hierarchically for clean data retrieval. Then the non-negative autoencoder was attached subsequently with sparsity constraint. Furthermore, the spatial-contextual information was exploited to improve the robustness of the network and the hypergraph structure was constructed in the unmixing scheme to preserve the spatial consistency of abundances. Comparative experiments were conducted on synthetic data and real data, which reveals the superiority of proposed network architecture for hyperspectral unmixing.
| [1] |
Guo R, Wang W, Qi H R. Hyperspectral image unmixing using autoencoder cascade. Proceedings of the 2015 7th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS). Piscataway: IEEE, 2015, 1-4. DOI:10.1109/whispers.2015.8075378 (  0) 0) |
| [2] |
Su Y C, Marinoni A, Li J, et al. Nonnegative sparse autoencoder for robust endmember extraction from remotely sensed hyperspectral images. Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Piscataway: IEEE, 2017, 205-208. DOI:10.1109/igarss.2017.8126930 (  0) 0) |
| [3] |
Su Y C, Li J, Plaza A, et al. Deep Auto-Encoder Network for Hyperspectral Image Unmixing. IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Piscataway: IEEE, 2018, 6400-6403. DOI:10.1109/igarss.2018.8519571 (  0) 0) |
| [4] |
Ozkan S, Kaya B, Akar G B. Endnet: sparse autoencoder network for endmember extraction and hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(1): 482-496. DOI:10.1109/tgrs.2018.2856929 (  0) 0) |
| [5] |
Qu Y, Qi H R. uDAS: an untied denoising autoencoder with sparsity for spectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(3): 1698-1712. DOI:10.1109/tgrs.2018.2868690 (  0) 0) |
| [6] |
Jia P Y, Zhang M, Shen Y. Hypergraph learning and reweighted l1-norm minimization for hyperspectral unmixing. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(6): 1898-1904. DOI:10.1109/jstars.2019.2916058 (  0) 0) |
| [7] |
Wang W H, Qian Y T, Tang Y Y. Hypergraph-regularized sparse NMF for hyperspectral unmixing. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(2): 681-694. DOI:10.1109/jstars.2015.2508448 (  0) 0) |
| [8] |
Vincent P, Larochelle H, Bengio Y, et al. Extracting and composing robust features with denoising autoencoders. Proceedings of the 25th International Conference on Machine Learning (ICML 2008). Eqaila, Kuwait: ACM, 2008, 1096-1103. DOI:10.1145/1390156.1390294 (  0) 0) |
| [9] |
Ji J Y, Mei S H, Hou J H, et al. Learning sensor-specific features for hyperspectral images via 3-dimensional convolutional autoencoder. Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Piscataway: IEEE, 2017, 1820-1823. DOI:10.1109/igarss.2017.8127329 (  0) 0) |
| [10] |
Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (AISTATS). Ft Lauderdale, 2011, 315-323. (  0) 0) |
| [11] |
Zhang Z H, Bai L, Liang Y H, et al. Joint hypergraph learning and sparse regression for feature selection. Pattern Recognition, 2017, 63: 291-309. DOI:10.1016/j.patcog.2016.06.009 (  0) 0) |
| [12] |
Iordache M-D, Bioucas-Dias J M, Plaza A. Collaborative sparse regression for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 341-354. DOI:10.1109/tgrs.2013.2240001 (  0) 0) |
| [13] |
Nascimento J M P, Dias J M B. Vertex component analysis: a fast algorithm to unmix hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 898-910. DOI:10.1109/tgrs.2005.844293 (  0) 0) |
| [14] |
Heinz D C, Chang C I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 529-545. DOI:10.1109/36.911111 (  0) 0) |
| [15] |
Li J, Agathos A, Zaharie D, et al. Minimum volume simplex analysis: a fast algorithm for linear hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(9): 5067-5082. DOI:10.1109/tgrs.2015.2417162 (  0) 0) |
| [16] |
Li J, Bioucas-Dias J M, Plaza A, et al. Robust collaborative nonnegative matrix factorization for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6076-6090. DOI:10.1109/tgrs.2016.2580702 (  0) 0) |
| [17] |
Miao L D, Qi H R. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 765-777. DOI:10.1109/tgrs.2006.888466 (  0) 0) |
| [18] |
Wang X Y, Zhong Y F, Zhang L P, et al. Spatial group sparsity regularized nonnegative matrix factorization for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11): 6287-6304. DOI:10.1109/tgrs.2017.2724944 (  0) 0) |
| [19] |
Bioucas-Dias J M, Plaza A, Dobigeon N, et al. Hyperspectral unmixing overview: geometrical, statistical, and sparse regression-based approaches. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(2): 354-379. DOI:10.1109/JSTARS.2012.2194696 (  0) 0) |
| [20] |
Landgrebe D A, Malaret E. Noise in remote-sensing systems: the effect on classification error. IEEE Transactions on Geoscience and Remote Sensing, 1986, GE-24(2): 294-300. DOI:10.1109/tgrs.1986.289648 (  0) 0) |
 2021, Vol. 28
2021, Vol. 28


