Rethinking about the Formulae of the Relationship between Euler Angles and Texture
0 Introduction
The orientation distribution function sections(ODFs) are analyzed by the formulae of the Euler angles and texture when the EBSD micro-texture and the X-ray macro-texture characterizations are carried out, and the textures in materials are obtained[1-4]. Whether these formulae are correct or not depends on the accuracy and reliability of texture characterizations. The formulae for cubic, orthorhombic, and hexagonal crystal structures given by Roe are listed as Eqs. (1)-(6)[3-4]:
Cubic crystal structure:
|
$
H: K: L=(-\sin \theta \cos \varphi):(\sin \theta \sin \varphi): \cos \theta
$
|
(1) |
|
$
\begin{aligned}
&U: V: W=(\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi): \\
&\quad(-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi):(\sin \theta \cos \psi)
\end{aligned}
$
|
(2) |
Orthorhombic crystal structure:
|
$
H: K: L=(-a \sin \theta \cos \varphi):(b \sin \theta \sin \varphi):(c \cos \theta)
$
|
(3) |
|
$
\begin{aligned}
U: V: W=&[(\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi) / a]: \\
&[(-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi) / b]: \\
&[\sin \theta \cos \psi / c]
\end{aligned}
$
|
(4) |
Hexagonal crystal structure:
|
$
\left(\begin{array}{l}
H \\
K \\
i \\
L
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
-\sin \theta \cos \varphi \\
\sin \theta \sin \varphi \\
\cos \theta
\end{array}\right)
$
|
(5) |
|
$
\left(\begin{array}{l}
U \\
V \\
T \\
W
\end{array}\right)=\left(\begin{array}{ccc}
\frac{1}{\sqrt{3}} & -\frac{1}{3} & 0 \\
0 & \frac{2}{3} & 0 \\
-\frac{1}{\sqrt{3}} & -\frac{1}{3} & 0 \\
0 & 0 & \frac{a}{c}
\end{array}\right) \cdot\left(\begin{array}{c}
\cos \theta \cos \psi \cos \varphi-\sin \psi \sin \varphi \\
-\cos \theta \cos \psi \sin \varphi-\sin \psi \cos \varphi \\
\sin \theta \cos \psi
\end{array}\right)
$
|
(6) |
The formulae for cubic, orthorhombic, and hexagonal crystal structures given by Bunge are listed as Eqs. (7)-(12)[3-4]:
Cubic crystal structure:
|
$
H: K: L=\left(\sin \theta \sin \varphi_{1}\right):\left(-\sin \theta \cos \varphi_{1}\right): \cos \theta
$
|
(7) |
|
$
\begin{aligned}
U: V: W=&\left(\cos \varphi_{2} \cos \varphi_{1}-\sin \varphi_{2} \sin \varphi_{1} \cos \theta\right):\\
&\left(\cos \varphi_{2} \sin \varphi_{1}+\sin \varphi_{2} \cos \varphi_{1} \cos \theta\right):\left(\sin \varphi_{2} \sin \theta\right)
\end{aligned}
$
|
(8) |
Orthorhombic crystal structure:
|
$
\begin{aligned}
H: K: L=&\left(a \sin \theta \sin \varphi_{1}\right):\left(-b \sin \theta \cos \varphi_{1}\right): \\
&(c \cos \theta)
\end{aligned}
$
|
(9) |
|
$
\begin{aligned}
U: V: W=&\left[\left(\cos \varphi_{2} \cos \varphi_{1}-\sin \varphi_{2} \sin \varphi_{1} \cos \theta\right) / a\right]: \\
&\left[\left(\cos \varphi_{2} \sin \varphi_{1}+\sin \varphi_{2} \cos \varphi_{1} \cos \theta\right) / b\right]: \\
&\left[\left(\sin \varphi_{2} \sin \theta\right) / c\right]
\end{aligned}
$
|
(10) |
Hexagonal crystal structure:
|
$
\left(\begin{array}{c}
H \\
K \\
i \\
L
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
\sin \theta \sin \varphi_{1} \\
-\sin \theta \cos \varphi_{1} \\
\cos \theta
\end{array}\right)
$
|
(11) |
|
$
\begin{aligned}
\left(\begin{array}{c}
U \\
V \\
t \\
W
\end{array}\right) &=\left(\begin{array}{ccc}
\frac{1}{\sqrt{3}} & -\frac{1}{3} & 0 \\
0 & \frac{2}{3} & 0 \\
-\frac{1}{\sqrt{3}} & -\frac{1}{3} & 0 \\
0 & 0 & \frac{a}{c}
\end{array}\right) \cdot \\
&\left(\begin{array}{c}
-\cos \theta \sin \varphi_{1} \sin \varphi_{2}+\cos \varphi_{1} \cos \varphi_{2} \\
\cos \theta \cos \varphi_{1} \sin \varphi_{2}+\sin \varphi_{1} \cos \varphi_{2} \\
\sin \theta \sin \varphi_{2}
\end{array}\right)
\end{aligned}
$
|
(12) |
Eqs. (1) and (2) for the cubic crystal structure given by Roe are calculated as follows:
|
$
\begin{aligned}
H U+& K V+L W=-\sin \theta \cos \varphi(\cos \psi \cos \theta \cos \varphi-\\
&\sin \psi \sin \varphi)+\sin \theta \sin \varphi(-\cos \psi \cos \theta \sin \varphi-\\
&\sin \psi \cos \varphi)+\cos \theta \sin \theta \cos \psi=0
\end{aligned}
$
|
This meets the condition that ND is perpendicular to RD. Let
|
$
h_{c}=-\sin \theta \cos \varphi ; k_{c}=\sin \theta \sin \varphi ; l_{c}=\cos \theta
$
|
|
$
u_{c}=\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi
$
|
|
$
v_{c}=-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi
$
|
|
$
w_{c}=\sin \theta \cos \psi
$
|
|
$
\therefore h_{c} u_{c}+k_{c} v_{c}+l_{c} w_{c}=0
$
|
The formula of the crystal plane angle in the orthorhombic crystal structure is written as Eq. (13):
|
$
\cos \phi=\frac{\frac{h_{1} h_{2}}{a^{2}}+\frac{k_{1} k_{2}}{b^{2}}+\frac{l_{1} l_{2}}{c^{2}}}{\sqrt{\left(\frac{h_{1}^{2}}{a^{2}}+\frac{k_{1}^{2}}{b^{2}}+\frac{l_{1}^{2}}{c^{2}}\right)\left(\frac{h_{2}^{2}}{a^{2}}+\frac{k_{2}^{2}}{b^{2}}+\frac{l_{2}^{2}}{c^{2}}\right)}}
$
|
(13) |
Eqs. (3) and (4) for orthogonal crystal structure given by Roe are substituted into the numerator of the Eq. (13), as listed below:
|
$
\frac{H U}{a^{2}}+\frac{K V}{b^{2}}+\frac{L W}{c^{2}}=\frac{h_{c} u_{c}}{a^{2}}+\frac{k_{c} v_{c}}{b^{2}}+\frac{l_{c} w_{c}}{c^{2}} \neq 0
$
|
The formula of the angle between the two crystal planes for hexagonal crystal structure is listed as Eq. (14):
|
$
\cos \phi=\frac{h_{1} h_{2}+k_{1} k_{2}+\frac{1}{2}\left(h_{1} k_{2}+h_{2} k_{1}\right)+\frac{3 a^{2}}{4 c^{2}} l_{1} l_{2}}{\sqrt{\left(h_{1}^{2}+k_{1}^{2}+h_{1} k_{1}+\frac{3 a^{2}}{4 c^{2}} l_{1}^{2}\right)\left(h_{2}^{2}+k_{2}^{2}+h_{2} k_{2}+\frac{3 a^{2}}{4 c^{2}} l_{2}^{2}\right)}}
$
|
(14) |
Eqs. (5) and (6) for hexagonal crystal structure given by Roe are also substituted into the numerator of the Eq. (14), as listed below:
|
$
\begin{aligned}
H U+K V+& \frac{1}{2}(H V+U K)+\frac{3 a^{2}}{4 c^{2}} L W=\\
& \frac{1}{2}\left(h_{c} u_{c}+k_{c} v_{c}\right)+\frac{3 a^{2}}{4 c^{2}} l_{c} w_{c} \neq 0
\end{aligned}
$
|
Only when $\frac{{3{\mathit{a}^2}}}{{4{\mathit{c}^2}}} = \frac{1}{2}$,
|
$
\begin{gathered}
\frac{1}{2}\left(h_{c} u_{c}+k_{c} v_{c}\right)+\frac{3 a^{2}}{4 c^{2}} l_{c} w_{c}=\frac{1}{2}\left(h_{c} u_{c}+\right. \\
\left.k_{c} v_{c}+l_{c} w_{c}\right)=0
\end{gathered}
$
|
It does not satisfy the definition that ND is perpendicular to RD in orthogonal and hexagonal crystal structure according to Roe's formulae, neither does Bunge's.
In this paper, according to the calculation conditions proposed by Roe and Bunge, the formulae of Euler angles and texture types are deduced independently. Some differences among these formulae will be found and explained.
1 Recalculation of the Formulae of the Euler Angles and the Texture According to the Roe Notations
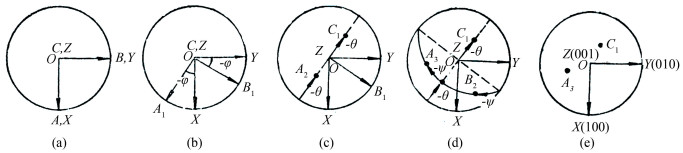
In order to describe the spatial orientation of each grain in the plate texture specimen, it is necessary to specify two rectangular coordinate systems. A Cartesian coordinate system O-ABC is used to represent the specimen coordinate system, and OA, OB, and OC are usually used to represent RD, TD, and ND of the rolling surface, respectively. The other Cartesian coordinate system O-XYZ is fixed on the grain, indicating the crystal coordinate system. In cube crystal structure, OX, OY, and OZ coincide with [100], [010], and [001] directions, respectively. In this way, the normal, rolling, and transverse orientations of the grain in the crystal space can be completely expressed by Euler angles. The Euler angles refer to three rotations which, when performed in the correct sequence, transform the specimen coordinate system into the crystal coordinate system - in other words, specify the orientation. There are several different conventions for expressing the Euler angles[5-6]. The most commonly used are those formulated by Roe, as shown in Fig. 1. The rotations are[5]
1) φ about the normal direction OC, transforming the transverse direction OB into OB1 and the rolling direction OA into OA1;
2) θ about the axis OB1 (in its new orientation), transforming the normal direction OC into OC1 and the rolling direction OA1 into OA2;
3) ψ about OC1 (in its new orientation), transforming the transverse direction OB1 into OB2 and the rolling direction OA2 into OA3;
φ, θ, and ψ are the Euler angles (Roe notation). The effect of the operation sequence of these three rotations can be followed in Fig. 1[4].
According to Roe notation, the coordinates of A1 and B1 in O-XYZ crystal coordinate system are shown as
|
$
A_{1}=(\cos \varphi,-\sin \varphi, 0)
$
|
|
$
B_{1}=(\sin \varphi, \cos \varphi, 0)
$
|
The coordinates of A2 and C1 in O-A1B1C specimen coordinate system are shown as
|
$
A_{2}=(\cos \theta, 0, \sin \theta)
$
|
|
$
C_{1}=(-\sin \theta, 0, \cos \theta)
$
|
The coordinates of A2 and C1 in O-XYZ crystal coordinate system are shown as
|
$
A_{2}=(\cos \theta \cos \varphi,-\cos \theta \sin \varphi, \sin \theta)
$
|
|
$
C_{1}=(-\sin \theta \cos \varphi, \sin \theta \sin \varphi, \cos \theta)
$
|
The coordinates of A3 and B2 in O-A2B1C1 specimen coordinate system are shown as
|
$
A_{3}=(\cos \psi,-\sin \psi, 0)
$
|
|
$
B_{2}=(\sin \psi, \cos \psi, 0)
$
|
The coordinates of A3 and B2 in O-XYZ crystal coordinate system are shown as
|
$
A_{3 x}=\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi
$
|
|
$
A_{3 y}=-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi
$
|
|
$
A_{3 z}=\cos \psi \sin \theta
$
|
|
$
B_{2 x}=\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi
$
|
|
$
B_{2 y}=-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi
$
|
|
$
B_{2 z}=\sin \psi \sin \theta
$
|
Because OA3, OB2, and OC1 indicate the rolling direction RD[UVW], transverse direction TD [RST], and normal direction ND [HKL] of the rolling surface, respectively, so the coordinates of C1, A3, and B2 in O-XYZ crystal coordinate system represent the indices [HKL], [UVW], and [RST] of ND, RD, and TD, respectively. The formulae of the texture and the Euler angles in the cubic crystal structure are listed as follows:
|
$
H=-\sin \theta \cos \varphi
$
|
|
$
K=\sin \theta \sin \varphi
$
|
|
$
U=\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi
$
|
|
$
V=-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi
$
|
|
$
W=\sin \theta \cos \psi
$
|
|
$
R=\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi
$
|
|
$
S=-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi
$
|
|
$
T=\sin \psi \sin \theta
$
|
The formulae of ND, RD, and TD in the cubic crystal structure can be abbreviated as Eq. (15), (16), and (17), respectively.
|
$
H: K: L=(-\sin \theta \cos \varphi):(\sin \theta \sin \varphi): \cos \theta
$
|
(15) |
|
$
\begin{aligned}
U: V: W=&(\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi):\\
&(-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi): \\
&(\sin \theta \cos \psi)
\end{aligned}
$
|
(16) |
|
$
\begin{aligned}
R: S: & T=(\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi): \\
&(-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi): \\
&(\sin \psi \sin \theta)
\end{aligned}
$
|
(17) |
Compared with the above Eqs. (1) and (2) given by Roe, it is found that Eqs. (15) and (16) are exactly the same as Eqs. (1) and (2).
ND and TD vector dot products are calculated as below:
|
$
\begin{aligned}
H R+& K S+L T=\\
&(-\sin \theta \cos \varphi)(\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi)+\\
&(\sin \theta \sin \varphi)(-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi)+\\
& \cos \theta(\sin \psi \sin \theta)=-\sin \theta \cos \theta \sin \psi \cos ^{2} \varphi-\\
& \sin \theta \sin \varphi \cos \varphi \cos \psi-\sin \theta \cos \theta \sin \psi \sin ^{2} \varphi+\\
& \sin \theta \sin \varphi \cos \varphi \cos \psi+\cos \theta \sin \psi \sin \theta=\\
&-\sin \theta \cos \theta \sin \psi\left(\cos ^{2} \varphi+\sin ^{2} \varphi\right)+\\
& \cos \theta \sin \psi \sin \theta=0
\end{aligned}
$
|
|
$
\therefore H R+K S+L T=0
$
|
In the same way,
|
$
U R+V S+W T=0, H U+K V+L W=0
$
|
Therefore, the formulae of Euler angles and the texture in cubic crystal structure meet the conditions that ND, RD, and TD are perpendicular to each other.
The unit lengths of X, Y, and Z axes in the tetragonal crystal structure are a, a, and c, respectively. The miller indices of ND, RD, and TD in the tetragonal crystal structure are depended on ND (hc, kc, lc), RD (uc, vc, wc), and TD (rc, sc, tc) in cubic crystal structure. They are multiplied by the unit length a, a, and c, respectively. The miller indices of ND, RD, and TD in the tetragonal crystal structure are listed as ND (ahc, akc, clc), RD (auc, avc, cwc), and TD (arc, asc, ctc). The expressions of the Euler angles and texture type in the tetragonal crystal structure are shown in Eqs. (18)-(20).
|
$
H: K: L=(-a \sin \theta \cos \varphi):(a \sin \theta \sin \varphi):(c \cos \theta)
$
|
(18) |
|
$
\begin{aligned}
U: V: W=&[a(\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi)]: \\
&[a(-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi)]: \\
&(c \sin \theta \cos \psi)
\end{aligned}
$
|
(19) |
|
$
\begin{aligned}
R: S: T=&[a(\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi)]: \\
&[a(-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi)]: \\
&(c \sin \psi \sin \theta)
\end{aligned}
$
|
(20) |
In the same way, the miller indices of ND, RD, and TD in the orthorhombic crystal structure are listed as (ahc, bkc, clc), (auc, bvc, cwc), and (arc, bsc, ctc), respectively. The expressions of the Euler angles and texture type in the orthorhombic crystal structure are shown in Eqs. (21)-(23):
|
$
H: K: L=(-a \sin \theta \cos \varphi):(b \sin \theta \sin \varphi):(c \cos \theta)
$
|
(21) |
|
$
\begin{aligned}
U: V: W=&[a(\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi)]: \\
&[b(-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi)]: \\
&(c \sin \theta \cos \psi)
\end{aligned}
$
|
(22) |
|
$
\begin{aligned}
R: S: T=&[a(\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi)]: \\
&[b(-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi)]: \\
&(c \sin \psi \sin \theta)
\end{aligned}
$
|
(23) |
There are some differences between Eqs. (21)-(22) and Eqs. (9)-(10) given by Roe.
The miller indices Eqs. (21)-(23) of ND, RD, and TD in the orthorhombic crystal structure are substituted into the numerator of Eq. (5), then the following equations are obtained:
|
$
\begin{gathered}
\frac{H U}{a^{2}}+\frac{K V}{b^{2}}+\frac{L W}{c^{2}}=a^{2}\left(h_{c} u_{c}\right) / a^{2}+b^{2}\left(k_{c} v_{c}\right) / b^{2}+ \\
c^{2}\left(l_{c} w_{c}\right) / c^{2}=h_{c} u_{c}+k_{c} v_{c}+l_{c} w_{c}=0
\end{gathered}
$
|
|
$
\begin{gathered}
\frac{H R}{a^{2}}+\frac{K S}{b^{2}}+\frac{L T}{c^{2}}=a^{2}\left(h_{c} r_{c}\right) / a^{2}+b^{2}\left(k_{c} s_{c}\right) / b^{2}+ \\
c^{2}\left(l_{c} t_{c}\right) / c^{2}=h_{c} r_{c}+k_{c} s_{c}+l_{c} t_{c}=0
\end{gathered}
$
|
|
$
\begin{gathered}
\frac{U R}{a^{2}}+\frac{V S}{b^{2}}+\frac{W T}{c^{2}}=a^{2}\left(u_{c} r_{c}\right) / a^{2}+b^{2}\left(v_{c} s_{c}\right) / b^{2}+ \\
c^{2}\left(w_{c} t_{c}\right) / c^{2}=u_{c} r_{c}+v_{c} s_{c}+w_{c} t_{c}=0
\end{gathered}
$
|
Therefore, the formulae of Euler angles and texture in orthorhombic crystal structure meet the conditions that ND, RD, and TD are perpendicular to each other, so does the tetragonal crystal structure.
In three axes coordinate system of hexagonal structure, OX axis is perpendicular to crystal plane (1010), OY axis is perpendicular to crystal plane (1210), OZ is perpendicular to crystal plane (0001), and the O-ABC specimen coordinate system coincides with the O-XYZ crystal coordinate system at the initial position. OA, OB, and OC represent RD, TD and ND of the specimen, respectively. The O-ABC specimen coordinate axes rotate 3 times according to the Roe notation. It is assumed that the unit cell constants of hexagonal structure are equal to a and c, respectively. The coordinates of A3, B2, and C1 can be obtained from the results of cubic structure after 3 times rotation according to the Roe notation. The transformation formulae between the coordinates (x, y, z) of any point in the O-XYZ crystal coordinate system and the corresponding point coordinates (U, V, W) of three axes coordinate system in hexagonal crystal structure are listed as follows:
|
$
U=\frac{2 a x}{\sqrt{3}}
$
|
(24) |
|
$
V=a y+\frac{a x}{\sqrt{3}}
$
|
(25) |
In hexagonal crystal system, the three indices (h, k, l) of crystal plane are not consistent with the normal direction indices [u, v, w] of the same crystal plane. However, the four indices (h, k, i, l) of a crystal plane are consistent with the normal direction indices [u, v, t, w]. The three indices [U, V, W] can be changed into the four indices [u, v, t, w] as follows:
Here, x is replaced by ax, y by by, and z by cz.
|
$
u=U-\frac{1}{2} V
$
|
(27) |
|
$
v=V-\frac{1}{2} U
$
|
(28) |
|
$
t=-\frac{1}{2}(U+V)
$
|
(29) |
Eqs. (24), (25), and (26) are substituted into Eqs. (27), (28), (29), and (30), respectively. The general expressions of ND, RD, and TD in hexagonal crystal structure are obtained as Eqs. (31)-(34):
|
$
u=\frac{\sqrt{3}}{2} a x-\frac{1}{2} a y
$
|
(31) |
|
$
t=-\frac{\sqrt{3}}{2} a x-\frac{1}{2} a y
$
|
(33) |
|
$
\left(\begin{array}{c}
u \\
v \\
t \\
w
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & 1
\end{array}\right)\left(\begin{array}{c}
a x \\
a y \\
c z
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)
$
|
(35) |
The $\left( {\begin{array}{*{20}{c}}
x\\
\mathit{y}\\
\mathit{z}
\end{array}} \right) $ in Eq. (35) are replaced by $\left( {\begin{array}{*{20}{c}}
{{\mathit{h}_\mathit{c}}}\\
{{\mathit{k}_\mathit{c}}}\\
{{l_c}}
\end{array}} \right) $,
$\left( {\begin{array}{*{20}{c}}
{{u_c}}\\
{{v_c}}\\
{{w_c}}
\end{array}} \right) $, and $\left( {\begin{array}{*{20}{c}}
{{r_c}}\\
{{s_c}}\\
{{t_c}}
\end{array}} \right) $ direction indices of ND, RD, and TD in cubic crystal structure, respectively, which are expressed by Eqs. (15)-(17). The complete matrix of ND, RD, and TD in hexagonal crystal structures can be obtained in turn, as shown in Eqs. (36)-(38).
The complete matrix is then transformed into
|
$
\begin{aligned}
\mathrm{ND}:\left(\begin{array}{c}
H \\
K \\
i \\
L
\end{array}\right) &=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
h_{c} \\
k_{c} \\
l_{c}
\end{array}\right)=\\
&\left(\begin{array}{cccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
-\sin \theta \cos \varphi \\
\sin \theta \sin \varphi \\
\cos \theta
\end{array}\right)
\end{aligned}
$
|
(36) |
|
$
\begin{aligned}
&\mathrm{RD}:\left(\begin{array}{c}
U \\
V \\
t \\
W
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
u_{c} \\
v_{c} \\
w_{c}
\end{array}\right)= \\
&\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0\\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
\cos \psi \cos \theta \cos \varphi-\sin \psi \sin \varphi \\
-\cos \psi \cos \theta \sin \varphi-\sin \psi \cos \varphi \\
\sin \theta \cos \psi
\end{array}\right)
\end{aligned}
$
|
(37) |
|
$
\begin{aligned}
&\mathrm{TD}:\left(\begin{array}{c}
R \\
S \\
m \\
T
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
r_{c} \\
s_{c} \\
t_{c}
\end{array}\right)=\\
&\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
\sin \psi \cos \theta \cos \varphi+\cos \psi \sin \varphi \\
-\sin \psi \cos \theta \sin \varphi+\cos \psi \cos \varphi \\
\sin \theta \sin \psi
\end{array}\right)
\end{aligned}
$
|
(38) |
The direction indices of the ND and RD in Eqs. (36) and (37) are substituted into the numerator of the hexagonal crystal plane angle Eq. (14) as below:
|
$
\begin{aligned}
H U+&K V+\frac{1}{2}(H V+U K)+\frac{3 a^{2}}{4 c^{2}} L W= \\
&a\left(\frac{\sqrt{3}}{2} h_{c}-\frac{1}{2} k_{c}\right) a\left(\frac{\sqrt{3}}{2} u_{c}-\frac{1}{2} v_{c}\right)+a^{2} k_{c} v_{c}+ \\
&\frac{1}{2}\left\{a^{2}\left(\frac{\sqrt{3}}{2} h_{c}-\frac{1}{2} k_{c}\right) v_{c}+a^{2}\left(\frac{\sqrt{3}}{2} u_{c}-\frac{1}{2} v_{c}\right) k_{c}\right\}+ \\
&\frac{3 a^{2}}{4 c^{2}} c^{2} l_{c} w_{c}=\frac{3}{4} a^{2}\left(h_{c} u_{c}+k_{c} v_{c}+l_{c} w_{c}\right)=0
\end{aligned}
$
|
Thus, ND is always perpendicular to RD in Eqs. (36)-(37). In the same way, it is easy to verify that ND, RD, and TD are perpendicular to each other in Eqs. (36)-(38). There are some differences between Eq. (37) and Eq. (12) provided by Roe.
2 Recalculation of Formulae between Euler Angles and the Texture According to Bunge Notations
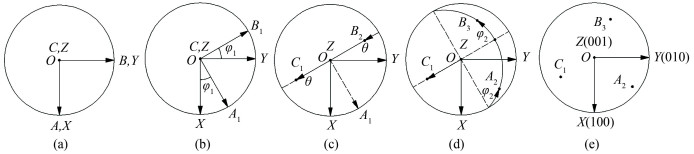
Besides expressing the Euler angles according to Roe notations, there is another expression of the Euler angles according to Bunge notations, as shown in Fig. 2. The rotations are[5-6]
1) φ1 about the normal direction OC, transforming the transverse direction OB into OB1 and the rolling direction OA into OA1;
2) θ about the axis OA1 (in its new orientation), transforming the normal direction OC into OC1 and transverse direction OB1 into OB2;
3) φ2 about OC1 (in its new orientation), transforming the transverse direction OB2 into OB3 and the rolling direction OA1 into OA2;
φ1, θ, and φ2 are the Euler angles (Bunge notations). The effect of the operation sequence of these three rotations can be followed in Fig. 2.
The coordinates of A1, B1, and C in O-XYZ crystal coordinate system are shown as
|
$
\boldsymbol{g}_{\varphi_{1}}=\left(\begin{array}{ccc}
\cos \varphi_{1} & \sin \varphi_{1} & 0 \\
-\sin \varphi_{1} & \cos \varphi_{1} & 0 \\
0 & 0 & 1
\end{array}\right)
$
|
The coordinates of A1, B2, and C1 in O-A1B1C specimen coordinate system are shown as
|
$
\boldsymbol{g}_{\theta}=\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & \sin \theta \\
0 & -\sin \theta & \cos \theta
\end{array}\right)
$
|
The coordinates of A1, B2, and C1 in O-XYZ crystal coordinate system are shown as
|
$
A_{1 x}=\cos \varphi_{1}, A_{1 y}=\sin \varphi_{1}, A_{1 z}=0
$
|
|
$
B_{2 x}=-\cos \theta \sin \varphi_{1}, B_{2 y}=\cos \theta \cos \varphi_{1}, B_{2 z}=\sin \theta
$
|
|
$
C_{1 x}=\sin \theta \sin \varphi_{1}, C_{1 y}=-\sin \theta \cos \varphi_{1}, C_{1 z}=\cos \theta
$
|
The coordinates of A2, B3, and C1 in O-A1B2C1 specimen coordinate system are shown as
|
$
\boldsymbol{g}_{\varphi_{2}}=\left(\begin{array}{ccc}
\cos \varphi_{2} & \sin \varphi_{2} & 0 \\
-\sin \varphi_{2} & \cos \varphi_{2} & 0 \\
0 & 0 & 1
\end{array}\right)
$
|
The coordinates of A2, B3, and C1 in O-XYZ crystal coordinate system are shown as
|
$
A_{2 x}=\cos \varphi_{2} \cos \varphi_{1}-\sin \varphi_{2} \sin \varphi_{1} \cos \theta
$
|
|
$
A_{2 y}=\cos \varphi_{2} \sin \varphi_{1}+\sin \varphi_{2} \cos \varphi_{1} \cos \theta
$
|
|
$
A_{2 z}=\sin \varphi_{2} \sin \theta
$
|
|
$
B_{3 x}=-\sin \varphi_{2} \cos \varphi_{1}-\cos \varphi_{2} \cos \theta \sin \varphi_{1}
$
|
|
$
B_{3 y}=-\sin \varphi_{2} \sin \varphi_{1}+\cos \varphi_{2} \cos \theta \cos \varphi_{1}
$
|
|
$
B_{3 z}=\cos \varphi_{2} \sin \theta
$
|
|
$
C_{1 x}=\sin \theta \sin \varphi_{1}, C_{1 y}=-\sin \theta \cos \varphi_{1}, C_{1 z}=\cos \theta
$
|
In this case, OC1 is ND of the specimen, OA2 is RD, and OB3 is TD. The formulae of the texture dependent on Euler angle (φ1, θ, φ2) is highly similar to these provided by Roe. It is quite easy to obtain all formulae for cubic, tetragonal, orthorhombic, hexagonal, and other crystal structures by Bunge notations. These formulae are shown as follows:
For cubic crystal structure,
|
$
\begin{aligned}
&\ \ \ \ \text { ND: } \\
&H: K: L=\left(\sin \theta \sin \varphi_{1}\right):\left(-\sin \theta \cos \varphi_{1}\right): \cos \theta
\end{aligned}
$
|
(39) |
|
$
\begin{aligned}
&\ \ \ \ \mathrm{RD}: \\
&U: V: W=\left(\cos \varphi_{2} \cos \varphi_{1}-\sin \varphi_{2} \sin \varphi_{1} \cos \theta\right): \\
&\qquad\left(\cos \varphi_{2} \sin \varphi_{1}+\sin \varphi_{2} \cos \varphi_{1} \cos \theta\right): \\
&\qquad\left(\sin \varphi_{2} \sin \theta\right)
\end{aligned}
$
|
(40) |
|
$
\begin{aligned}
&\ \ \ \ \mathrm{TD}: \\
& R: S: T=\left(-\sin \varphi_{2} \cos \varphi_{1}-\cos \varphi_{2} \cos \theta \sin \varphi_{1}\right): \\
&\qquad\left(-\sin \varphi_{2} \sin \varphi_{1}+\cos \varphi_{2} \cos \theta \cos \varphi_{1}\right): \\
&\qquad\left(\cos \varphi_{2} \sin \theta\right)
\end{aligned}
$
|
(41) |
For tetragonal crystal structure,
|
$
\begin{aligned}
&\ \ \ \ \text { ND: } \\
&H: K: L=\left(a \sin \theta \sin \varphi_{1}\right):\left(-a \sin \theta \cos \varphi_{1}\right):(c \cos \theta)
\end{aligned}
$
|
(42) |
|
$
\begin{aligned}
& \ \ \ \ \mathrm{RD}: \\
& U: V: W=\left[a\left(\cos \varphi_{2} \cos \varphi_{1}-\sin \varphi_{2} \sin \varphi_{1} \cos \theta\right)\right]: \\
&\ \ \ \ \ \ \ \ \left[a\left(\cos \varphi_{2} \sin \varphi_{1}+\sin \varphi_{2} \cos \varphi_{1} \cos \theta\right)\right]: \\
&\ \ \ \ \ \ \ \ \left[c\left(\sin \varphi_{2} \sin \theta\right)\right]
\end{aligned}
$
|
(43) |
|
$
\begin{aligned}
&\ \ \ \ \mathrm{TD}: \\
&R: S: T=\left[a\left(-\sin \varphi_{2} \cos \varphi_{1}-\cos \varphi_{2} \cos \theta \sin \varphi_{1}\right)\right]: \\
&\qquad\left[a\left(-\sin \varphi_{2} \sin \varphi_{1}+\cos \varphi_{2} \cos \theta \cos \varphi_{1}\right)\right]: \\
&\qquad\left[c\left(\cos \varphi_{2} \sin \theta\right)\right]
\end{aligned}
$
|
(44) |
For orthorhombic crystal structure,
|
$
\begin{aligned}
&\ \ \ \ \mathrm{ND}: \\
&H: K: L=\left(a \sin \theta \sin \varphi_{1}\right):\left(-b \sin \theta \cos \varphi_{1}\right):(c \cos \theta)
\end{aligned}
$
|
(45) |
|
$
\begin{aligned}
&\quad\mathrm{RD}: \\
&U: V: W=\left[a\left(\cos \varphi_{2} \cos \varphi_{1}-\sin \varphi_{2} \sin \varphi_{1} \cos \theta\right)\right]: \\
&\qquad\left[b\left(\cos \varphi_{2} \sin \varphi_{1}+\sin \varphi_{2} \cos \varphi_{1} \cos \theta\right)\right]: \\
&\qquad\left[c\left(\sin \varphi_{2} \sin \theta\right)\right]
\end{aligned}
$
|
(46) |
|
$
\begin{aligned}
&\ \ \ \ \mathrm{TD}: \\
&R: S: T=\left[a\left(-\sin \varphi_{2} \cos \varphi_{1}-\cos \varphi_{2} \cos \theta \sin \varphi_{1}\right)\right]: \\
&\qquad\left[b\left(-\sin \varphi_{2} \sin \varphi_{1}+\cos \varphi_{2} \cos \theta \cos \varphi_{1}\right)\right]: \\
&\qquad\left[c\left(\cos \varphi_{2} \sin \theta\right)\right]
\end{aligned}
$
|
(47) |
For hexagonal crystal structure,
|
$
\mathrm{ND}:\left(\begin{array}{c}
H \\
K \\
i \\
L
\end{array}\right)=\left(\begin{array}{cccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\left(\begin{array}{c}
\sin \theta \sin \varphi_{1} \\
-\sin \theta \cos \varphi_{1} \\
\cos \theta
\end{array}\right)
$
|
(48) |
|
$
\begin{aligned}
\mathrm{RD}:\ \ &\left(\begin{array}{c}
U \\
V \\
t \\
W
\end{array}\right)=\left(\begin{array}{cccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\cdot\\
&\left(\begin{array}{c}
-\cos \theta \sin \varphi_{1} \sin \varphi_{2}+\cos \varphi_{1} \cos \varphi_{2} \\
\cos \theta \cos \varphi_{1} \sin \varphi_{2}+\sin \varphi_{1} \cos \varphi_{2} \\
\sin \theta \sin \varphi_{2}
\end{array}\right)
\end{aligned}
$
|
(49) |
|
$
\begin{aligned}
\mathrm{TD}:\ \ &\left(\begin{array}{c}
R \\
S \\
m \\
T
\end{array}\right)=\left(\begin{array}{ccc}
\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 1 & 0 \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 \\
0 & 0 & \frac{c}{a}
\end{array}\right)\cdot \\
&\left(\begin{array}{ccc}
-\cos \theta \sin \varphi_{1} \cos \varphi_{2} -\cos \varphi_{1} \sin \varphi_{2} \\
\cos \theta \cos \varphi_{1} \cos \varphi_{2} -\sin \varphi_{1} \sin \varphi_{2} \\
\sin \theta \cos \varphi_{2}
\end{array}\right)
\end{aligned}
$
|
(50) |
It has been proved that ND, RD, and TD are perpendicular to each other in Eqs. (39)-(46) by the method used in Roe notation. There are some differences among the formulae in orthorhombic and hexagonal crystal structures compared with Eqs. (9)-(12) provided by Bunge.
3 Discussion
The relationships between the texture and Euler angles is actually the coordinate transformation between the crystallographic coordinate and the specimen appearance coordinate according to certain rules. Frankly speaking, this mathematical derivation is not complicated. For the cubic crystal system, the formulae deduced by this paper are exactly the same as those of the Roe and Bunge. For the orthorhombic and hexagonal crystal systems, the trigonometric function parts of the formulae deduced by the authors is exactly the same as those of the Roe and Bunge except for the coefficient parts in the formulae. At expression formulae of the texture deduced in this paper, ND, RD, and TD are uniformly expressed as crystal plane indices. When calculating the standard pole figures of the common textures of hexagonal crystal system materials, ND and RD are calculated according to the crystal plane indices[7-8]. When designing the pole figure measurement software for the characterization of hexagonal crystal system texture, ND and RD are also used as the crystal plane indices. Nevertheless, the expression of ND and RD may be inconsistent in the textural formulae deduced by Roe and Bunge, where ND is used as the crystal plane indices, and RD may be used as the crystal direction indices. For cubic crystal system, the angle between crystal plane and crystal direction is the same, but for other crystal systems, the formula of angle between crystal plane index and crystal direction index has not been deduced. Therefore, for orthorhombic and hexagonal crystal systems, the traditional formulae deduced by Roe and Bunge may still be correct, but in the practice of material texture characterizations, it is easy to bring confusion to users.
4 Conclusions
The formulae deduced in this paper are inspired by the notations of Roe and Bunge. In the formulae of a texture, ND, RD, and TD are uniformly used as the crystal plane indices, so they are suitable for the corresponding formulae of crystal plane angles, which brings convenience to texture characterizations.
In the traditional formulae deduced by Roe and Bunge, ND is used as the crystal plane indices, and RD and TD may be used as the crystal direction indices, which may cause the differences among the formulae derived by the authors and by Roe and Bunge.
During the teaching of crystal orientation characterizations and the design of commercial software for material texture characterizations, users should pay attention to the differences among the formulae.
 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 0)
0) 2021, Vol. 28
2021, Vol. 28


