Slinger is a kind of rotary atomizer that accelerates the liquid to a high relative speed to the air by mechanical rotation and produces a fine liquid spray. It is usually used in the combustion chamber of small aircraft engines. The shape of the orifice on a slinger is usually round or slot, and the geometric parameters of the orifice play an important role in the slinger atomization.
Dahm investigated the slinger with various orifices. The geometric parameters of the orifices are shown in Table 1[1-3]. The liquid leaves the slinger orifice in two regimes: film mode and stream mode. The film mode indicates the liquid leaves the orifice along its circumference and forms a liquid film, while the stream mode indicates the liquid leaves the orifice on the side of the orifice that is opposite to the slinger rotation direction and forms a liquid column. The film mode performs in two breakup ways: subcritical breakup and supercritical breakup. After leaving the orifice, the liquid film first aggregates into a liquid column and then breaks into droplets, which is termed subcritical breakup; if the liquid film breaks into droplets directly after leaving the orifice, it is termed supercritical breakup. The breakup modes of the film are related to the Weber number Weh with the liquid film thickness h as the characteristic length. The smaller the Weh, the more likely the liquid film performs subcritical breakup. The slinger's liquid spray SMD is related to Wet, with t as the characteristic length. t is determined by the liquid regimes when it leaves the orifice. When the liquid leaves the orifice in film-supercritical regime, t is equivalent to the thickness of the liquid film; when the liquid performs film-subcritical regime, t is equivalent to the diameter of the liquid column that is aggregated by the liquid film; when the liquid performs stream mode, t is equivalent to the diameter of the orifice.
Carmen found the liquid breakup distance after leaving the orifice to increase with the increases in the liquid flowrate, and decrease with the increases in the slinger rotary speed[4-7]. The distribution range of the diameter of the droplets in the liquid spray increases with the increases in the liquid flowrate, and decreases with the increases in the slinger rotary speed. The liquid breakup distance and the spray SMD decrease with the increases in the diameter of the orifice.
Choi found the liquid in the slinger performs irregular breakup when the rotary speed is low or the liquid flowrate is high, which will produce large droplets and deteriorate the atomization performance[8-11]. The spatial distribution of the liquid spray depends on the diameter of the orifice. The orifice with a larger diameter can produce a more uniform and wider distributed liquid spray. If the slinger works in a lateral airflow, whose flow direction is parallel to the axis of the slinger, the velocity of the airflow will affect the atomization of the slinger. When the velocity of the lateral airflow is less than 50 m/s, the liquid spray SMD decreases with the increases in the slinger rotary speed. However, if the velocity of the lateral airflow is more than 100 m/s, the spray SMD will not change significantly with the change of slinger rotary speed.
Ye[12] presented a three-dimensional numerical simulation to study the liquid regimes near the orifice of the slinger. He found the liquid flowrates of each orifices are different in a short time and the total liquid flowrate of the slinger varies with time as well. Chakraborty[13] found the Coriolis force cannot be ignored when the slinger's rotary speed is high, and the liquid will leave the orifice from the orifice side that is opposite to the rotary direction. Based on Dahm's research[1-3], Rezayat[14] found when the rotary speed of slinger is up to 4000 r/min, and the liquid performs subcritical breakup; when the rotary speed is more than 5000 r/min, a phenomenon of liquid jet bifurcation is observed; when the rotary speed is up to 10000 r/min, the liquid performs supercritical breakup.
The existing researches on how the parameters of the orifice affect the atomization of the slinger are mainly qualitative results obtained from theoretical analysis or experimental research. This paper will present quantitative research and explore how the geometric parameters of the orifice affect the atomization of the slinger.
1 Test ApparatusFig. 1 is a diagram of the test rig. A motor drives the slinger with a rotary speed range of 0-24 kr/min and the minimum adjustment unit is 6 r/min.
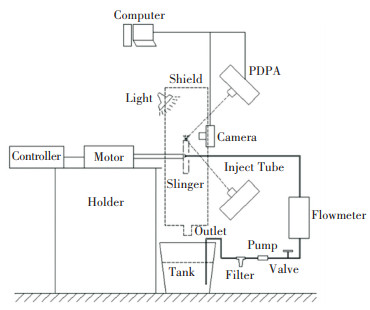
|
Fig.1 Diagram of the test rig |
A transparent shield surrounds the slinger and is used to collect the liquid thrown out from the test slinger and return it to the liquid tank. The liquid in the tank is driven by a pump. It passes through the filter, pump, valve, and mass flowmeter, and then is ejected from the inject tube and finally hits on the wall of the test slinger to start a new liquid recycle. The minimum measuring unit of the mass flowmeter is 0.1 g/s, and the measuring range corresponds to 0-40 g/s.
The measurement equipment includes a high-speed camera and aphase of doppler particle analyzer (PDPA). The high-speed camera is used to capture the liquid regime near the slinger, and the maximum shooting frequency corresponds to 2500 fps. The PDPA is used to measure the diameter of the droplets in the liquid spray, from which SMD and the RR (Rosin-Rammler) distribution index n can be calculated. The spray SMD is used to evaluate the size of the droplets. The smaller the SMD, the smaller the droplets. n is used to evaluate the uniformity of the liquid spray. The larger the n, the more uniform the liquid spray. The minimum measuring unit corresponds to the laser wavelength of the PDPA and is about 0.5 mm. The measuring error of the PDPA is related to the types of the measurement particles when measuring liquid spray. The relative error for measuring the diameter of the droplet is 0.5%, while that for the quantity of the droplets is 1%[15].
Water is used as the main test liquid. Adding sulfonic acid in the water will change its surface tension, which can be used to explore the effect of the liquid surface tension on the atomization performance. The property of liquid solutions is shown in Table 2.
| Table 2 Property of liquid solutions |
The structure of the test slinger is shown in Fig. 2. The radius R of the slinger is 50 mm. The serial number and the shape parameters of the test orifices are shown in Fig. 3. The radial length l of orifice A-F is 3 mm, the shape of orifice A-C is round, and orifice D-E is a slot. The perimeters of orifice B and D are the same, and orifice C, E, and F have the same perimeter likewise. Besides, two orifice Bl and Dl with the same shape parameters as orifice B and D respectively are added, and their the radial length l are 6 mm.

|
Fig.2 Schematic diagram of the slinger |
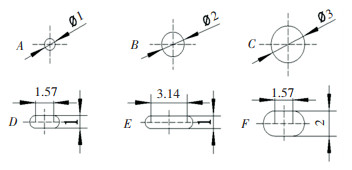
|
Fig.3 Chart of orifices shape and size(Unit: mm) |
2 Theoretical Analysis
High-speed photography found three liquid regimes exist near the orifice. Except for film mode and stream mode found by Dahm[1-3], the full mode will be formed when the liquid fills the orifice. The three liquid regimes are shown in Fig. 4.

|
Fig.4 Liquid regimes in the orifice |
Weber number Wet is the most important parameter to predict the liquid atomization, and the characteristic length t of Wet is different when the liquid leaves the orifice in various regimes. However, it was found through experiments that when the rotary speed of the slinger is larger than 3 kr/min, the three liquid regimes all perform turbulent breakup. That means the liquid film or stream is severely torn by the air to form multiple fragments with a diameter approximating to the thickness h of the liquid film in the orifice. According to Dahm's research[1-3], there is
| $ h\left( R \right) = {\left( {\frac{{3{\mu _L}m}}{{{\rm{ \mathsf{ π} }}d\rho _L^2{\omega ^2}R}}} \right)^{\frac{1}{3}}} $ | (1) |
where μL denotes dynamic viscosity of the liquid and is 0.001 Pa·s, m denotes mass flowrate of the liquid, ρL denotes the density of the liquid and is 1000 kg/m3, ω denotes the rotary speed of the liquid, and d denotes the diameter of the orifice. When the orifice is a slot, there is
| $ d = P/{\rm{ \mathsf{ π} }} $ | (2) |
where P denotes the perimeter of the orifice.
In most cases, the liquid regimes perform turbulent breakup as shown in Fig. 5. Therefore Weh with h as the characteristic length has the highest correlation coefficient with the liquid spray, and that was proved by the experiment results.
| $ W{e_h}{\rm{ = }}{\rho _G}{u^2}h/\sigma $ | (3) |
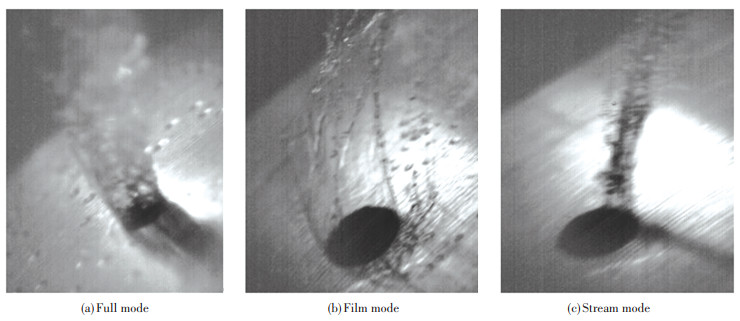
|
Fig.5 Regimes of turbulent breakup |
where ρG is the density of gas and is 1.29 kg/m3, and u is the velocity at the edge of the slinger. The following equation is obtained:
| $ u = \omega R $ | (4) |
Substituting Eqs.(1), (4) and the values of other parameters into Eq.(3):
| $ W{e_h} = 8.62 \times {10^{ - 6}}{\left( {m{\omega ^4}/d{\sigma ^3}} \right)^{\frac{1}{3}}} $ | (5) |
Therefore, Weh~
The radial position of the point where the liquid is thrown from the slinger completely broke into droplets corresponding to the working condition of the slinger. That means the radial position where the spray SMD is the minimum changes with the slinger working condition. In previous researches, the parameters of the liquid spray are usually measured at a fixed point and the effect of the changes in the minimun SMD position cannot be considered. In the experiment of this paper, the liquid spray parameters at a series of radial positions were firstly measured, then the parameters where the liquid SMD was the minimum were selected and analyzed, hence the effect of the change in the minimum SMD position was eliminated.
Liquid spray SMD and distribution index n are the two main parameters to evaluate the atomization performance. Fig. 6 shows the liquid spray SMD from various orifices versus Weh. The test data are discretely distributed corresponding to Weh, thus it is impossible to compare SMD quantitatively. First, the fitting formulas between SMD and Weh of each orifice were calculated, then the fitting formulas were compared with each other, and the quantitative comparisons can be achieved.
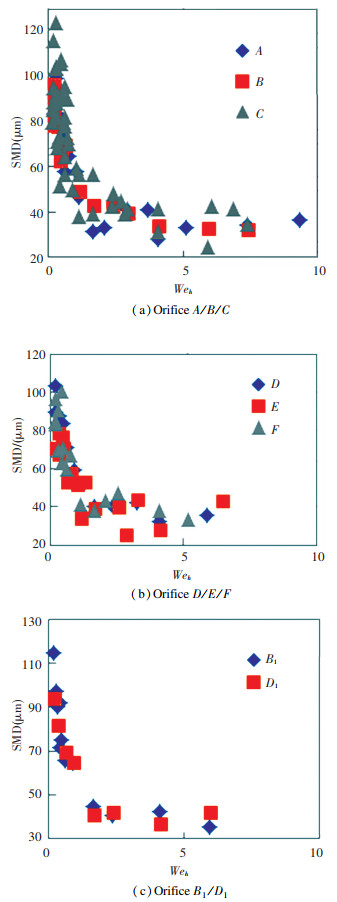
|
Fig.6 Relationship between SMD and Weh of various orifices |
Exponential, linearity, logarithmic, power, and polynomial functions were used to fit the relationship between SMD/n and Weh. The formula with the highest relative coefficient was selected as the fitting formula and used to represent the atomization performance of the orifice. Table 3 is the table of fitting formula about SMD and Weh, and Table 4 is the table of fitting formula about n and Weh. The relative coefficients of the SMD fitting formulas are higher than those of n, which means the analysis of SMD is reliable, while the analysis of n is only reliable to a certain extent.
| Table 3 Fitting formulas of spray SMD |
| Table 4 Fitting formulas of n |
4 Analysis and Discussion 4.1 Change Rules of SMD 4.1.1 Effect of diameter of round orifice
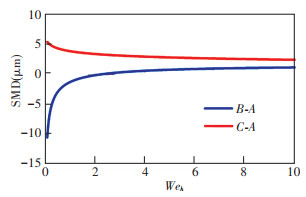
In the legend of Fig. 7, B-A corresponds to SMD of orifice B minus SMD of orifice A, which is 55.809Weh-0.305-57.068Weh-0.334. The other expressions in the legend show the same meaning. From Fig. 8, it is found the orifice C with the largest diameter of 3 mm exhibits the maximum SMD. When Weh < 2.158, orifice B with a diameter of 2 mm exhibits the minimum SMD. When Weh>2.158, orifice A with a diameter of 1 mm exhibits the minimum SMD. The conclusion is different from previous research which predicts increases in diameter of orifice will reduce the spray SMD. According to the experiment results in this paper, within a certain range of Weh, an optimal diameter exists with which the orifice exhibits the minimum spray SMD. Different ranges of Weh correspond to different optimal diameters; when Weh < 2.158, the optimal diameter is 2 mm; when Weh>2.158, the optimal diameter is 1 mm. Hence, the diameter of the orifice should be determined by the working condition of the slinger when designing a slinger. Adopting a diameter as large as possible is not always beneficial to atomization.
|
Fig.7 Curves of the effect of round orifice diameter on SMD |
|
Fig.8 Curves of the effect of shape parameters of slot orifice on SMD |
4.1.2 Effect of shape parameters of slot orifice
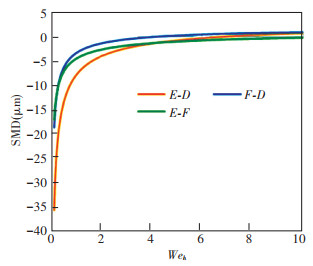
Orifice D and E have the same width but different axial lengths, orifice D and F have the same axial length but different widths, and orifice E and F have the same perimeter. As shown in Fig. 8, in most cases, orifice E exhibits smaller SMD than orifice D, and only when Weh>6.853, the SMD of orifice D is smaller. Compare orifice D with F; when Weh < 4.184, the SMD of orifice F is smaller; when Weh>4.184, orifice D exhibits smaller SMD. The SMD of orifice E is always smaller than that of orifice F.
Previous research shows that an increase in the axial length of a slot orifice can reduce the spray SMD within a large range of Weh, but increases in the width of a slot orifice have little effect on spray SMD. When the perimeters of the slot orifices are the same, the one whose axial length is larger exhibits a smaller SMD. When Weh is large enough, orifice D with a smaller perimeter exhibits the smallest SMD. Therefore, lengthening the slot orifice is beneficial to atomization when Weh is not very large, but widening the slot orifice is not recommended.
4.1.3 Effect of shapes of orificesWhen the perimeters of the orifices are the same, the d in Eq.(1) of each orifice is the same likewise. Fig. 9 shows the comparison curves of SMD between the orifices with the same perimeters. When Weh < 2.620, the spray SMD of slot orifice D is larger than that of round orifice B; when Weh>2.620, orifice D exhibits a smaller SMD than orifice B. Compare slot orifice E/F with round orifice C; the SMD of E/F is always smaller than that of orifice C. The results mean that when Weh is the same, the slot orifice performs smaller SMD than round orifice in most cases. Only when the perimeter and Weh are both small, the round orifice's SMD is smaller.

|
Fig.9 Curves of the effect of orifice shapes on SMD |
4.1.4 Effect of radial length of the orifice
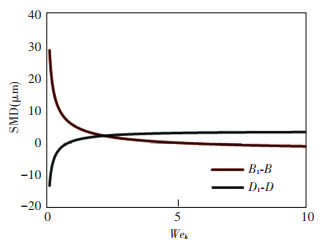
Fig. 10 is the comparison curves of SMD between the orifices with different radial lengths but the same shape parameters. The radial length of Bl and Dl is 6 mm, while that of B and D is 3 mm. When Weh < 5.748, the SMD of round orifice Bl is larger than that of orifice B; when Weh>5.748, the SMD of orifice Bl is smaller than that of orifice B, but the values of SMD of both orifices are very close. In slot orifices, when Weh < 0.769, orifice Dl exhibits a smaller SMD than orifice D; when Weh>0.769, the SMD of orifice Dl is larger than that of orifice D. When Weh is the same, the SMD of orifice Dl is larger than that of orifice D by about 5 μ m. Consequently, increases in the radial length of an orifice will cause an increase in SMD in most cases, especially in slot orifice.
|
Fig.10 Curves of the effect of radial length l of the orifice on SMD |
4.1.5 Effect of surface tension
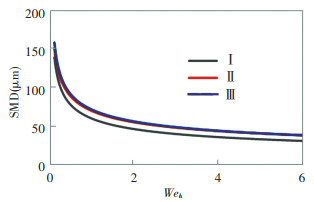
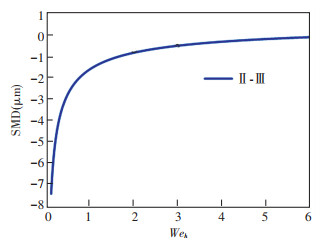
Fig. 11 shows curves of the relationship between SMD and Weh when the surface tension is different, and the values of the test solutions' surface tension are shown in Table 2. When Weh is the same, the SMD of Solution Ⅰ is the minimum, while those of Solution Ⅱ and Ⅲ are nearly the same. From Fig. 12, it is found the SMD of Solution Ⅱ is smaller than Solution Ⅲ. Consequently, when Weh keeps the same, SMD increases with decreases in surface tension. It is found from Eq.(5) that Weh~σ-1. If Weh keeps the same when σ decreases, other parameters such as rotary speed or flowrate should decrease too, and the spray SMD may increase.
|
Fig.11 Curves of the effect of surface tension on SMD (orifice C) |
|
Fig.12 Comparison curve between Solution Ⅱ and Solution Ⅲ (orifice C) |
4.2 Change Rules of n 4.2.1 Effect of the diameter of round orifice
As shown in Fig. 13, in most cases, n increases with increases in diameter of round orifice. Only when 1.16 < Weh < 3, n of orifice B is smaller than that of orifice A; or when 1.15 < Weh < 2.74, n of orifice C is smaller than that of orifice A. When Weh < 1.33, n of orifice C is smaller than that of orifice B. The results show that increases in the diameter of the round orifice can improve the uniformity of the liquid spray in most cases.

|
Fig.13 Curves of the effect of diameter of the round orifice on n |
4.2.2 Effect of shape parameters of slot orifice
As shown in Fig. 14, orifice E exhibits the maximum n, and n of orifice D is larger than that of orifice F. Only when Weh < 0.59, n of orifice D is larger than that of orifice E; when Weh < 0.63, n of orifice F is larger than that of orifice E; when Weh < 0.85, n of orifice F is larger than orifice D. Consequently, lengthening the slot orifice is beneficial to increase the uniformity of the spray, but widening the slot orifice will cause a less uniform spray.

|
Fig.14 Curves of the effect of shape parameters of slot orifice on n |
4.2.3 Effect of shapes of orifices
Fig. 15 is the spray distribution index comparison curves between the round orifice and the slot orifice with the same perimeter. If the perimeter of the orifice is 2π (orifice B and D), when Weh < 3.51, n of the round orifice is larger; when Weh>3.51, n of slot orifice is larger, but the difference between the values of n of both orifices are less than 0.1. If the perimeter of the orifice is 3π (orifice C/E/F), n of orifice E is larger than that of orifice C, and only when Weh < 0.91, orifice C performs a larger n. n of orifice F is always smaller than that of orifice C.

|
Fig.15 Curves of the effect of orifice shape on n |
The projection length of the orifice D in the axis direction of slinger is longer than that of orifice B, and that of orifice E is longer than that of orifice C, but the axis projection length of orifice F is shorter than that of orifice C. Consequently, it can be considered that when the perimeters of the orifices are the same, the orifice with a longer axis projection length performs a more uniform spray. Only when Weh is very small, the round orifice performs a more uniform spray.
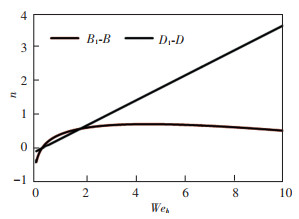
4.2.4 Effect of radial length of the orificeFig. 16 shows spray distribution index comparison curves between orifices with different radial lengths but the same shape parameters. In most cases, n of the orifice with a longer radial length is larger, especially in slot orifices. Only when Weh < 0.33, n of orifice B is larger than that of orifice Bl; when Weh < 0.34, n of orifice D is larger than that of orifice Dl. Consequently, with the orifice in the radial direction lengthened, the uniformity of the spray becomes obviously better, especially in slot orifices.
|
Fig.16 Curves of the effect of orifice radial length on n |
4.2.5 Effect of surface tension
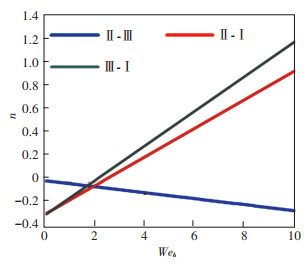
As shown in Fig. 17, when the liquid surface tension decreases, n increases at the same Weh. Only when Weh < 1.97, n of Solution Ⅲ is smaller than that of Solution Ⅰ; when Weh < 2.32, n of Solution Ⅱ is smaller than that of Solution Ⅰ; when Weh < 0.33, n of Solution Ⅲ is smaller than that of Solution Ⅱ. Consequently, when Weh keeps the same, the uniformity of the spray becomes better as the liquid surface tension decreases. Only when Weh is small, the uniformity of the spray does not optimize as the surface tension decreases.
|
Fig.17 Curves of the effect of surface tension on n (orifice C) |
5 Summary and Discussion
In a certain range of Weh, an optimal diameter exists when the round orifice produces the smallest liquid spray. Under the same Weh, increases in the axial length of a slot orifice decrease the spray SMD. In most cases, the spray SMD of slot orifice is smaller than that of the round orifice; increases in the radial length of orifice cause the spray SMD to be larger, especially in slot orifice; when the liquid surface tension decreases, the spray SMD increases.
Under the same Weh, enlarging the round orifice will improve the uniformity of spray in most cases. Increases in the axial length of the orifice will improve the uniformity of the spray likewise, but if the axial length is too long, the spray uniformity becomes worse. When the equivalent diameters of the orifices are the same, the orifice with a longer axial projection length will produce a more uniform spray. Increasing the radial length of the orifice improves the spray uniformity significantly; the bigger the liquid surface tension, the worse the spray uniformity.
In conclusion, the parameters of the orifice should be determined according to the range of Weh of the slinger's actual work condition. Usually, the slot orifice performs a better spray than round orifice with the same perimeter. Increases in the radial length of the orifice cause the spray SMD to be larger, but the spray uniformity becomes better at the same time. To a certain extent, increases in the axial length of slot orifice improve the liquid spray, but if the axial length is too large, the uniformity of the spray will become worse.
| [1] |
Dahm W J A, Patel P R, Lerg B H. Experimental visualizations of liquid breakup regimes in fuel slinger atomization. Atomization and Sprays, 2006, 16(8): 933-944. DOI:10.1615/AtomizSpr.v16.i8.50 (  0) 0) |
| [2] |
Dahm W J A, Patel P R, Lerg B H. Fundamental analysis of liquid atomization by fuel slingers in small gas turbines. Proceedings of the 32nd AIAA Fluid Dynamics Conference and Exhibit. Reston, VA: AIAA, 2002. 2002- 3183. DOI: 10.2514/6.2002-3183.
(  0) 0) |
| [3] |
Dahm W J A, Patel P R, Lerg B H. Analysis of liquid breakup regimes in fuel slinger atomization. Atomization and Sprays, 2006, 16(8): 933-944. DOI:10.1615/AtomizSpr.v16.i8.50 (  0) 0) |
| [4] |
Sescu C, Kucinschi B R, Afjeh A A, et al. Experimental test rig with results on liquid atomization by slinger injectors. Journal of Engineering for Gas Turbines and Power, 2011, 133(11): 45051-45054. DOI:10.1115/1.4003790 (  0) 0) |
| [5] |
Carmen S, Bogdan K, Abdollah A. Computational analysis of a slinger atomizer. Proceedings of the 46th AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit. Reston, VA: AIAA, 2010. AIAA 2010-6581. DOI: 10.2514/6.2010-6581.
(  0) 0) |
| [6] |
Sescu C, Kucinschi B R, Masiulaniec C K, et al. Experimental test rig with results on atomization by slinger injectors. Proceedings of the 4th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston, VA: AIAA, 2008: AIAA 2008-4771.
(  0) 0) |
| [7] |
Sescu C, Kucinschi B, Afjeh A, et al. Parametricstudy of liquid atomization by slinger injectors. Proceedings of the 45th AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit. Reston, VA: AIAA, 2009. AIAA 2009-4829. DOI: 10.2514/6.2009-4829.
(  0) 0) |
| [8] |
Choi S M, Jang S H. Spray behavior of the rotary atomizer with in-line injection orifices. Atomization and Sprays, 2010, 20(10): 863-875. DOI:10.1615/AtomizSpr.v20.i10.30 (  0) 0) |
| [9] |
Choi S M, Jang S H, Lee D H, et al. Spray characteristics of the rotating fuel injection system of a micro-jet engine. Journal of Mechanical Science and Technology, 2010, 24(2): 551-558. DOI:10.1007/s12206-009-1206-6 (  0) 0) |
| [10] |
Choi S M, Yun S, Jeong H J, et al. Spatial drop behavior of a rotary atomizer in a cross flow. Atomization and Sprays, 2012, 22(12): 1077-1095. DOI:10.1615/AtomizSpr.2013007146 (  0) 0) |
| [11] |
Choi S M, Yun S, Jeong H J, et al. Spray incross flow of a rotary atomizer. Atomization and Sprays, 2012, 22(2): 143-161. DOI:10.1615/AtomizSpr.2012005049 (  0) 0) |
| [12] |
Ye Y L, Jin J, Liu R, et al. Non-uniform flow characteristics of direct-connected fuel slinger. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(8): 1560-1568. DOI:10.13700/j.bh.1001-5965.2018.0693 (  0) 0) |
| [13] |
Chakraborty A, Sahu S. Liquid atomization in a high-speed slinger atomizer. Proceedings of the ASME Gas Turbine India Conference GTINDIA 2019. New York: ASME, 2019. 1-10. DOI: 10.1115/GTINDIA2019-2626.
(  0) 0) |
| [14] |
Rezayat S, Farshchi M, Karimi H, et al. Spray characterization of a slinger injector using a high-speed imaging technique. Journal of Propulsion and Power, 2018, 34(2): 469-481. DOI:10.2514/1.B36498 (  0) 0) |
| [15] |
Jia W D, Li P P, Qiu B J, et al. Application of phase doppler's particle analyzer in reek spray nozzle's characteristic experiment. China Rural Power and Hydropower, 2008, 9: 70-75. (in Chinese) (  0) 0) |
 2022, Vol. 29
2022, Vol. 29







