Nowdays, distributed power generation systems are developing rapidly with the ever-increasing demand on renewable energy[1]. Because of the remarkable fluctuation of renewable energy, such as wind power and hydropower, distributed power system may encounter the degradation of efficiency and controllability[2], and the high-order switching harmonics caused by PWM strategy applied in converters for power transmission may deteriorate the grid-side current[3-4].
To efficiently attenuate the current ripple resulted from the grid-side inverter, a filter is usually connected in series between the inverter and the grid. Different from the L-type filter with an equal inductance, the LCL-type filter can obtain better harmonic attenuation[5]. Due to its lower cost and smaller size, LCL filters can acquired more attention in current harmonic suppression[6-7], whereas a drawback related to LCL filters is the resonance issue. The converter-side damping strategies can alter the equivalent impedance to ensure the controllability of power systems, which consist of inherent-damping methods, passive damping methods and active damping methods. An appropriate design may offer inherent damping for LCL-type power systems, whereas this strategy requires extremely strict matching of system digital delay and sampling position[8-10]. The passive damping methods are convenient to employment and have acquired a wide application in industrial fields. This type of methods can achieve better harmonic attenuation even under complex grid voltage disturbance at the expense of power loss[11-12]. Compared with passive damping, active damping can be more flexible and have no additional power loss[13]. However, additional sensors for state feedback may complicate the control configuration and decrease reliability.
State space regulation is prominent enough in the LCL-type control which enables the arrangement of the dominant dynamics and resonant dynamics[14]. This can be designed by choosing pole locations, by dead-beat strategies as well as by calculating the optimal cost function or with Bessel functions. Based on the direct pole placement, the regulation parameters could be achieved as the analytical expression incorporating characteristics of LCL-type systems. Meanwhile, to eliminate additional measurements in contrast with conventional controllers, several state estimation strategies are developed.
Currently, many power control strategies based on synchronous transformation are widely applied in grid-tied converters[15], which require the amplitude and phase information of grid-side voltage acquired by the PLL. For three-phase systems, the most common method is the synchronous reference frame PLL (SRF-PLL). SRF-PLL is an ideal algorithm of high quality that can work in high bandwidth and obtain great phase-locked response[16]. With regard to the grid voltage disturbance, the injection harmonics from q axis may deteriorate the ability of PLL, even leading to the instability.
In Refs. [17-19], the decoupled double SRF-PLL (DDSRF-PLL) method is proposed to attenuate the harmonic components and accurately extract the positive sequence component of grid voltage. Eventually, the target of grid-side controller design is to ensure the smooth power transmission between converters and the grid. Aimed at improving dynamic performance of power reference tracking, an enhanced power regulator is developed for single phase power converters in Refs. [20-21]. In three phase power systems, the coupling between d axis components and q axis components will affect the robustness of power controllers, a decoupling parallel control strategy is proposed in Ref. [22] to diminish the coupling power disturbance.
The current control performance has a great influence on the power control performance. Nevertheless, in the LCL-type grid-oriented inverter, the PI controller associated with current combined with active damping is not effective. Although the state space control methods work well, but additional capacitive voltage sensors and grid-side current sensors are required, increasing control costs and making the system structure more complex. The innovations in this article are as follows:
1) Combining the state space controller with the state space observer, the full-order closed-loop control of the state variables is realized when only the inverter side current sensors are applied. Meanwhile, the sampling noise attenuation isrealized through the reasonable observer pole locations, which improves the current closed-loop performance.
2) The corresponding control parameter design method is deduced, and the control parameter design expression is simplified compared with the expression of the previous papers.
This paper is organized as follows. Firstly, the system model of grid-tied converters with LCL filters is illustrated in Section 1. Then, Section 2 describes the design of current regulator. A state space regulator related to current control for three-phase distributed generation system is developed according to continuous switching-cycle-averaged model of converters, whose phase angle is captured by SRF-PLL with loop filter. Taking the three-order characteristics of LCL-type converters into consideration, this paper proposes an extended Luenberger state observer to implement the observation of capacitor voltage and grid-side current based on the measurement of converter-side current, which can diminish extra sensors and act as the low pass filters. Next, Section 3 presents the design of power controller. A stable closed loop control strategy of reactive and active power is developed according to instantaneous power calculation principles, whose references are given by tracking differentiator for reduction of impact on the grid. Finally, simulation results are displayed in Section 4 and Section 5 summarizes the conclusions of this paper.
1 System ModelThe voltage source inverter (VSI) is linked to the grid through a grid-connected transformer or the PCC node. So as to effectively attenuate the current harmonics generated by the switching voltage, a set of LCL-type filters are usually connected between the grid-side inverter and the PCC node. Fig. 1 shows the structure of converters with LCL filters, where the converter-side currents are defined as ia′, ib′, ic′ respectively, and the grid voltages are defined as uga, ugb, ugc, which all can be measured directly. The converter-side voltages are defined as ua′, ub′, uc′, which could be derived by the reference voltages. Grid-tied currents ia, ib, ic and capacitor voltages ua, ub, uc are the state variables estimated.
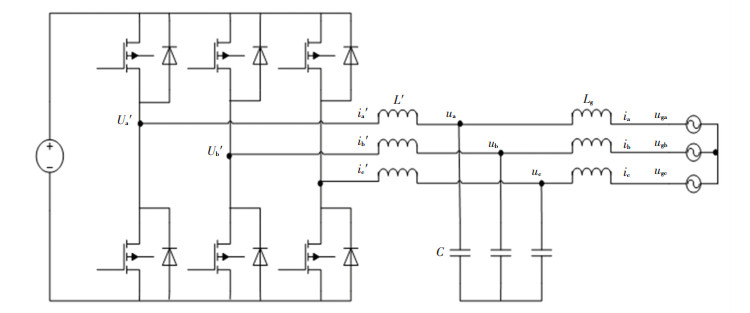
|
Fig.1 Configuration of grid side converters with LCL filters |
The series inductors L′ and the parallel capacitors C satisfies the following assumptions.
1) The inductance of series inductors and the capacitance of parallel capacitors are equal, respectively;
2) No mutual inductance exists between the three-phase series inductors.
1.1 State-Space Model for LCL FilterTo simplify the analysis dimensions of this model, complex space vectors in synchronous coordinates are applied; for instance, the grid voltage vector is expressed as ug=ugd+jugq, where ugq=0. The state vector is selected as x=[ig uc ic]T, where uc is the capacitor voltage ucd+jucq, and ig is the grid-tied current igd+jigq, while ic is the inverter-tied current icd+jicq, respectively. Meanwhile, the converter side voltage is uc′=ucd′+jucq′, where ucd′ and ucq′ are d axis and q axis converter side voltage, respectively. Dynamics of grid-side current ig in the state space form can be derived as
| $ \begin{aligned} \frac{\mathrm{d} \boldsymbol{x}}{\mathrm{d} t}=&\underbrace{\left[\begin{array}{ccc} -\frac{R_{\mathrm{s}}}{L_{\mathrm{g}}}-\mathrm{j} \omega_{\mathrm{e}} & \frac{1}{L_{\mathrm{g}}} & 0 \\ -\frac{1}{C} & -\mathrm{j} \omega_{\mathrm{e}} & \frac{1}{C} \\ 0 & -\frac{1}{L^{\prime}} & -\mathrm{j} \omega_{\mathrm{e}} \end{array}\right]}_{A} \boldsymbol{x}+\underbrace{\left[\begin{array}{c} 0 \\ 0 \\ \frac{1}{L^{\prime}} \end{array}\right]}_{B_{\mathrm{c}}} u_{\mathrm{c}}^{\prime}+\\ &\underbrace{\left[\begin{array}{c} -\frac{1}{L_{\mathrm{g}}} \\ 0 \\ 0 \end{array}\right]}_{B_{\mathrm{g}}} u_{\mathrm{g}}\\ &\ \ \ \ \ \ \ \ \boldsymbol{i}_{\mathrm{g}}=\underbrace{\left[\begin{array}{lll} 1 & 0 & 0 \end{array}\right] \boldsymbol{x}}_{C_{\mathrm{g}}} \end{aligned} $ | (1) |
As can be seen in Fig. 1, the inverter-side inductance is defined as L′, the capacitance is defined as C. Besides, Rs and Lg are grid-side value of resistors and inductors respectively, where ωe is the grid angular frequency.
The transfer function from the converter voltage to the grid current can be calculated as follows:
| $ \boldsymbol{G}_{\mathrm{c}}(s)=\frac{i_{\mathrm{g}}(s)}{u_{\mathrm{c}}^{\prime}(s)}=\boldsymbol{C}_{\mathrm{g}}(s \boldsymbol{I}-\boldsymbol{A})^{-1} \boldsymbol{B}_{\mathrm{c}} $ | (2) |
At the same time, for the capacitor terminal voltage uc, the control matrix is Cu=[0 1 0]; for the converter current ic, the output matrix is Cc=[0 0 1]. In the following analysis, the sampling delay is considered and SVPWM is assumed as the linear model, whose delay Td=3Ts/2 is taken into consideration in Eq.(3).
| $ u_{\mathrm{c}}^{\prime}(t)=u_{\mathrm{cref}}^{\prime}\left(t-T_{\mathrm{d}}\right) $ | (3) |
where ucref′ represents the converter side voltage reference.
1.2 Resonance IssuesThe filter parameters are designed according to classical LCL filter design principles associated with current ripple and reactive power restriction. The simulation system specifications are given in Table 1. The Bode diagram of open loop function Gc(s) is displayed in Fig. 2 where the resonant frequency is 4.6 kHz. Near the resonant frequency, the open-loop gain of Gc(s) is greater than 0, and the phase angle will convert from -90° to -270° which may be responsible for the instability of the converter systems.
| Table 1 Simulation parameters |
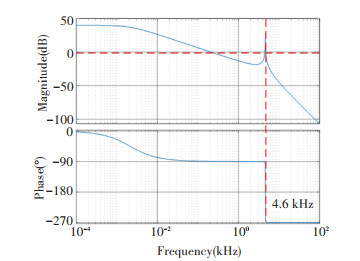
|
Fig.2 Bode diagram of open loop converter systems with LCL filters |
2 Current Control Design
The current regulation diagram is displayed in Fig. 3. As shown in Fig. 3, the converter voltage references are calculated by the state space PI controller equipped with a four-order extended state observer which can provide the estimated capacitor voltages and grid currents, respectively. Although the converter current ic can be measured directly, the estimate
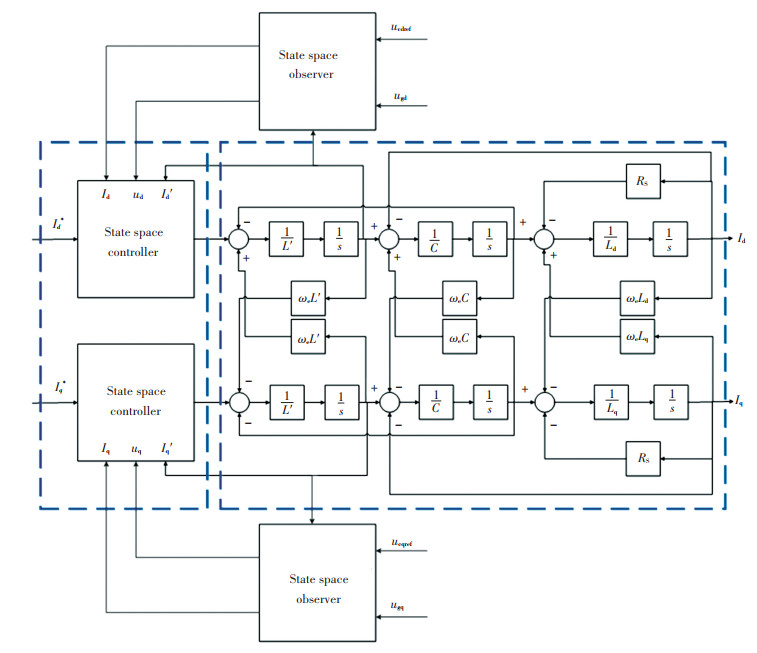
|
Fig.3 Diagram of state space PI control with extended Luenberger state observers |
The feedback control on grid currents as well as on capacitor voltages and converter currents are implemented based on state space control strategies. In comparison with conventional PI control, control degrees of freedom (DOFs) are improved and better parameters can be obtained through flexible parameter design.
2.1 State-Space PI ControllerIn order to simplify the analysis process, the influence of the grid angular frequency ωe coupling is temporarily ignored, then the dq axis relationship between grid current and converter-side voltage can be analyzed independently. Based on the q axis model, the design of state space PI controller is analyzed. The state space model of q axis is defined as
| $ \begin{aligned} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{q}}}{\mathrm{d} t}=&\underbrace{\left[\begin{array}{ccc} -\frac{R_{\mathrm{s}}}{L_{\mathrm{g}}} & \frac{1}{L_{\mathrm{g}}} & 0 \\ -\frac{1}{C} & 0 & \frac{1}{C} \\ 0 & -\frac{1}{L^{\prime}} & 0 \end{array}\right]}_{A_{\mathrm{q}}} \boldsymbol{X}_{\mathrm{q}}+\underbrace{\left[\begin{array}{c} 0 \\ \frac{1}{L^{\prime}} \end{array}\right]}_{B_{\mathrm{q}}} u_{\mathrm{cq}}^{\prime}+\\ &\underbrace{\left[\begin{array}{c} -\frac{1}{L_{\mathrm{g}}} \\ 0 \\ 0 \end{array}\right]}_{B_{\mathrm{gq}}} u_{\mathrm{gq}}\\ &\ \ \ \ \ \ \ \ \boldsymbol{i}_{\mathrm{g}}=\underbrace{\left[\begin{array}{lll} 1 & 0 & 0 \end{array}\right] \boldsymbol{x}}_{C_{\mathrm{g}}} \end{aligned} $ | (4) |
To suppress the steady-state error of current response, a state variable related to error integration is combined with previous model, which is defined as
| $ X_{\mathrm{Iq}}=\int\left(i_{\mathrm{gq}}^{*}-i_{\mathrm{gq}}\right) \mathrm{d} t $ | (5) |
where igq* is the current reference.
According to the above definition, the q axis current state space controller can be designed as follows:
| $ \begin{gathered} u_{\mathrm{q}}^{\prime}=k_{\mathrm{tq}} i_{\mathrm{gq}}^{*}+k_{\mathrm{iq}} X_{\mathrm{Iq}}-K_{\mathrm{q}} X_{\mathrm{q}} \\ \boldsymbol{K}_{\mathrm{q}}=\left[\begin{array}{lll} k_{1 \mathrm{q}} & k_{2 \mathrm{q}} & k_{3 \mathrm{q}} \end{array}\right] \\ i_{\mathrm{gq}}=C_{\mathrm{g}} X_{\mathrm{q}} \end{gathered} $ | (6) |
where ktq and kiq are the tracking parameter and the integration parameter respectively when k1q, k2q, k3q are defined as the state feedback gain.
Therefore, the q axis current model equipped with state space strategies can be derived as
| $ \begin{array}{c} {\left[\begin{array}{c} \dot{X}_{\mathrm{q}} \\ \dot{X}_{\mathrm{Iq}} \end{array}\right]=} \underbrace{\left[\begin{array}{cc} A_{\mathrm{q}}-B_{\mathrm{q}} K_{\mathrm{q}} & B_{\mathrm{q}} k_{\mathrm{iq}} \\ -C_{\mathrm{g}} \end{array}\right]}_{\tilde{A}_{\mathrm{q}}}\left[\begin{array}{c} X_{\mathrm{q}} \\ X_{\mathrm{Iq}} \end{array}\right]+\\ \underbrace{\left[\begin{array}{c} B_{\mathrm{q}} k_{\mathrm{tq}} \\ 1 \end{array}\right] i_{\mathrm{gq}}^{*}+\left[\begin{array}{c} B_{\mathrm{gq}} u_{\mathrm{gq}} \\ 0 \end{array}\right]}_{\tilde{B}_{\mathrm{q}}} \\ \boldsymbol{i}_{\mathrm{gq}}=\underbrace{\left[\begin{array}{ll} C_{\mathrm{g}} & 0 \end{array}\right]}_{\tilde{C}_{\mathrm{g}}}\left[\begin{array}{c} X_{\mathrm{q}} \\ X_{\mathrm{Iq}} \end{array}\right] \end{array} $ | (7) |
Then, the transfer function for grid current from converter-side voltage is expressed as
| $ G_{\mathrm{q}}(s)=\frac{i_{\mathrm{q}}(s)}{i_{\mathrm{q}}^{*}(s)}=\widetilde{C}_{\mathrm{g}}\left(s I-\tilde{A}_{\mathrm{q}}\right)^{-1} \tilde{B}_{\mathrm{q}} $ | (8) |
The dynamic characteristics of the q axis current regulation are configured by the polynomial equations approach, and the pole selection can be performed by the following classic equation:
| $ N_{\mathrm{eq}}(s)=\left(s^{2}+2 \xi_{1} \omega_{1} s+\omega_{1}^{2}\right)\left(s^{2}+2 \xi_{2} \omega_{2} s+\omega_{2}^{2}\right) $ | (9) |
where ξ1 is the passband damping ratio, ω1 is the passband bandwidth, ξ2 is the resonance damping ratio, and ω2 is the resonance frequency.
As shown in Eq.(9), the system can realize the decoupling of the passband characteristics and the attenuation characteristics of high frequency where the gains are selected properly. Meanwhile, the suppression of the high-frequency resonance and the selection of the resonance frequency can be implemented. Compared with the current loop controller design based on PI controller, the state space methods have higher efficiency and flexibility.
After equivalent calculation, the coefficients of the state space method can be determined as
| $ k_{3 \mathrm{q}}=2 L^{\prime}\left(\xi_{1} \omega_{1}+\xi_{2} \omega_{2}\right)-L^{\prime} R_{\mathrm{s}} C $ | (10a) |
| $ k_{2 \mathrm{q}}=L^{\prime} C\left(\omega_{1}^{2}+\omega_{2}^{2}+4 \xi_{1} \omega_{1} \xi_{2} \omega_{2}\right)-\frac{L^{\prime}}{L_{\mathrm{q}}}-1-\frac{R_{\mathrm{s}} C k_{3 \mathrm{q}}}{L_{\mathrm{q}}} $ | (10b) |
| $ k_{1 \mathrm{q}}=-k_{3 \mathrm{q}}-R_{\mathrm{s}} k_{2 \mathrm{q}}+L^{\prime} L_{\mathrm{q}} C\left(2 \xi_{1} \omega_{1} \omega_{2}^{2}+2 \xi_{2} \omega_{2} \omega_{1}^{2}\right) $ | (10c) |
| $ k_{\mathrm{iq}}=\omega_{1}^{2} \omega_{2}^{2} L^{\prime} L_{\mathrm{q}} C $ | (10d) |
| $ k_{\mathrm{tq}}=\frac{k_{\mathrm{iq}}}{a} $ | (10e) |
In Eq.(10e), a is the zero location of the closed-loop system, which is usually selected near the cutoff frequency, which can be adjusted to enhance the dynamic performance of the system. Similarly, the d axis current loop coefficients can be calculated.
2.2 State-Space ObserverRegardless of the state space controller or the PI controller combined with the active damping method, additional voltage sensors or current sensors are required to access the state feedbacks, which inevitably raise the design cost and complexity of the control structure, and reduce the feasibility. Hence, this paper adopts converter side current sampling and grid-side voltage sampling strategies where capacitor terminal voltages and currents injected into the grid can be obtained through the extended Luenberger state observer[23-24].
Ignoring the dq axis coupling, the inverter current ic and the grid voltage ug can be obtained by measurement, and the inverter side voltage uc′ is calculated by Eq.(3). Taking the q axis as an example, the Luenberger state observer can be established as
| $ \begin{array}{ccc} \begin{aligned} \frac{\mathrm{d} \hat{\boldsymbol{X}}_{\mathrm{q}}}{\mathrm{d} t}=&\underbrace{\left[\begin{array}{ccc} -\frac{R_{\mathrm{s}}}{L_{\mathrm{q}}} & \frac{1}{L_{\mathrm{q}}} & 0 \\ -\frac{1}{C} & 0 & \frac{1}{C} \\ 0 & -\frac{1}{L^{\prime}} & 0 \end{array}\right]}_{A_{\mathrm{q}}} \hat{\boldsymbol{X}}_{\mathrm{q}}+\underbrace{\left[\begin{array}{c} 0 \\ 0 \\ \frac{1}{L^{\prime}} \end{array}\right]}_{B_{\mathrm{q}}} u_{\mathrm{gq}}+\\ &L_{\mathrm{cq}}\left(i_{\mathrm{cq}}^{\prime}-\hat{l}{}_{\mathrm{cq}}^{\prime}\right)\\ \end{aligned}\\ \hat{\boldsymbol{l}}{}_{\mathrm{cq}}^{\prime}=\underbrace{\left[\begin{array}{lll} 0 & 0 & 1 \end{array}\right]}_{C_{\mathrm{c}}} \hat{\boldsymbol{X}}_{\mathrm{q}}\\ \boldsymbol{L}_{\mathrm{cq}}=\left[\begin{array}{lll} l_{1 \mathrm{q}} & l_{2 \mathrm{q}} & l_{3 \mathrm{q}} \end{array}\right]^{\mathrm{T}} \end{array} $ | (11) |
where Lcq is the observer gain vector and
| $ \widetilde{\boldsymbol{X}}_{\mathrm{q}}=\boldsymbol{X}_{\mathrm{q}}-\hat{\boldsymbol{X}}_{\mathrm{q}} $ | (12) |
Based on the error equation, the error convergence equation can be expressed as
| $ \frac{\mathrm{d} \widetilde{\boldsymbol{X}}_{\mathrm{q}}}{\mathrm{d} t}=\left(\boldsymbol{A}_{\mathrm{q}}-\boldsymbol{L}_{\mathrm{cq}} \boldsymbol{C}_{\mathrm{c}}\right) \widetilde{\boldsymbol{X}}_{\mathrm{q}} $ | (13) |
Then, the characteristic polynomial of the error matrix can be configured as follows:
| $ \begin{gathered} \operatorname{det}\left[s \boldsymbol{I}-\left(\boldsymbol{A}_{\mathrm{q}}-\boldsymbol{L}_{\mathrm{cq}} \boldsymbol{C}_{\mathrm{q}}\right)\right]=\left(s+\omega_{\mathrm{o1}}\right)\left(s^{2}+\right. \\ \left.2 \xi_{\mathrm{o} 2} \omega_{\mathrm{o} 2} s+\omega_{\mathrm{o} 2}^{2}\right) \end{gathered} $ | (14) |
where ωo1 determines the first-order pole, ξo2 and ωo2 determine the complex poles associated with resonance, and the gains of the q axis observer can be calculated as follows:
| $ \begin{gathered} l_{3 \mathrm{q}}=2 \xi_{\mathrm{o2} } \omega_{\mathrm{o} 2}+\omega_{\mathrm{o} 1}-\frac{R_{\mathrm{s}}}{L_{\mathrm{g}}} \\ l_{2 \mathrm{q}}=\frac{L^{\prime} L_{\mathrm{g}}+1-L_{\mathrm{g}} C\left(2 \xi_{\mathrm{o} 2} \omega_{\mathrm{o} 2} \omega_{\mathrm{o} 1}+\omega_{\mathrm{o} 2}^{2}\right)+l_{3 \mathrm{q}} R_{\mathrm{s}} C}{L^{\prime} L_{\mathrm{g}} C} \\ l_{1 \mathrm{q}}=\frac{C}{L^{\prime}}\left(\omega_{\mathrm{o1}} \omega_{\mathrm{o} 2}^{2}+\frac{L^{\prime}}{L_{\mathrm{g}}} l_{2 \mathrm{q}} R_{\mathrm{s}}-\frac{l_{3 \mathrm{q}}}{L_{\mathrm{g}} C}-\frac{L^{\prime} R_{\mathrm{s}}}{L_{\mathrm{g}} C}\right) \end{gathered} $ | (15) |
However, high observation poles need to be configured when the observation error is expected to be eliminated completely, resulting in the enlargement of noise sensitivity in state observers. According to the above state observervation model, the observed inverter current is chosen as the feedback variable for closed loop PI control. The improvement of observer dimensions and DOFs may help the promotion of dynamic characteristics in observation.
Aimed at removing the steady error, an extra state variable related to error integration is added into the state space vector, which can be expressed as
| $ \hat{X}_{\mathrm{Iq}}=\int\left(i_{\mathrm{cq}}^{\prime}-\hat{l}{}_{\mathrm{cq}}^{\prime}\right) \mathrm{d} t $ | (16) |
Then the associated vectors can be defined as
| $ \boldsymbol{L}_{\mathrm{otq}}=\left[\begin{array}{lll} 0 & 0 & l_{\mathrm{tq}} \end{array}\right]^{\mathrm{T}} $ | (17) |
| $ \boldsymbol{L}_{\mathrm{iq}}=\left[\begin{array}{lll} 0 & 0 & l_{\mathrm{iq}} \end{array}\right]^{\mathrm{T}} $ | (18) |
where ltq represents the reference gain and liq represents the integral gain. The dynamics of the improved observer with the extend state can be derived as
| $ \begin{aligned} \left[\begin{array}{l} \dot{\hat{X}}_{\mathrm{q}} \\ \dot{\hat{X}}_{\mathrm{Iq}} \end{array}\right]=&\underbrace{\left[\begin{array}{cc} A_{\mathrm{q}}-L_{\mathrm{opq}} C_{\mathrm{q} 1} & L_{\mathrm{iq}} \\ -C_{\mathrm{q} 1} & 0 \end{array}\right]}_{\hat{A}_{\mathrm{q}}}\left[\begin{array}{l} \hat{X}_{\mathrm{q}} \\ \hat{X}_{\mathrm{Iq}} \end{array}\right]+\underbrace{\left[\begin{array}{c} L_{\mathrm{otq}} \\ 1 \end{array}\right]}_{\hat{L}_{\mathrm{q}}} i_{\mathrm{cq}}^{\prime}+\\ &\left[\begin{array}{c} B_{\mathrm{q}} \\ 0 \end{array}\right] u_{\mathrm{q}}^{\prime}\\ &\ \ \ \ \ \ \hat{l}{}_{\mathrm{cq}}^{\prime}=\underbrace{\left[\begin{array}{cc} C_{\mathrm{q} 1} & 0 \end{array}\right]}_{\hat{C}_{\mathrm{q}}}\left[\begin{array}{l} \hat{X}_{\mathrm{q}} \\ \hat{X}_{\mathrm{Iq}} \end{array}\right] \end{aligned} $ | (19) |
In this observation model, the q axis converter voltages and grid voltages are given as the feedforward variables. From Eq.(19), the transfer function of the state space observer with the extended integration state can be expressed as
| $ G_{\mathrm{oq}}(s)=\frac{\hat{l}{}_{\mathrm{q}}^{\prime}(s)}{i_{\mathrm{q}}^{\prime}(s)}=\hat{C}_{\mathrm{q}}\left(s I-\hat{A}_{\mathrm{q}}\right)^{-1} \hat{L}_{\mathrm{q}} $ | (20) |
This detailed closed loop function is considerably complicated. Hence, when ignoring the imperceptible effect of capacitance in low frequency signals, the observation can be simplified as
| $ G_{\mathrm{oq}}(s)=\frac{L^{\prime}\left(l_{\mathrm{tq}} s+l_{\mathrm{iq}}\right)}{\left(L^{\prime}+L_{\mathrm{q}}\right) s^{2}+\left(L^{\prime} l_{\mathrm{tq}}+R_{\mathrm{s}}\right) s+L^{\prime} l_{\mathrm{iq}}} $ | (21) |
Eventually, the observer parameters can be tuned as Eqs.(22) and (23) according to the required passband damping ratio ξo and the above observation passband ωo.
| $ l_{\mathrm{tq}}=\frac{2\left(L^{\prime}+L_{\mathrm{q}}\right) \xi_{\mathrm{o}} \omega_{\mathrm{o}}-R_{\mathrm{s}}}{L^{\prime}} $ | (22) |
| $ l_{\mathrm{iq}}=\frac{\left(L^{\prime}+L_{\mathrm{q}}\right) \omega_{\mathrm{o}}^{2}}{L^{\prime}} $ | (23) |
In the same way, the gains of the d axis observer can be obtained. In the actual system design, the poles of the observer are generally selected to be 2 to 6 times the poles of the controller, and the cutoff frequency of the observer should not exceed the Nyquist frequency.
3 Power Control DesignWhen finishing designing the inner current regulation, the structure of power loop can be shown as Fig. 4. All in all, the bandwidth of outer loop should be less than that of inner loop. In this section, the PLL technology capturing the phase angle of grid voltage vectors and power regulation methods are discussed.
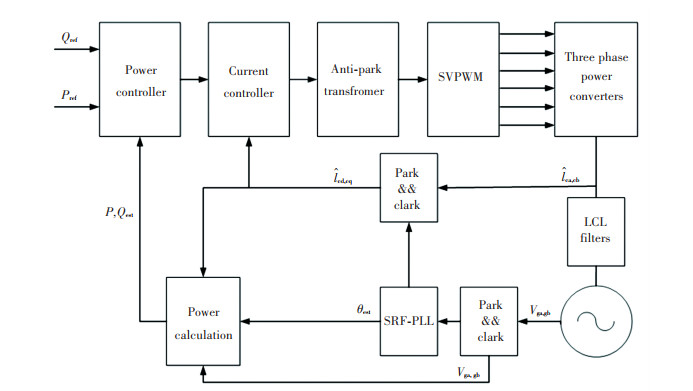
|
Fig.4 Diagram of power closed-loop control |
3.1 SRF-PLL with Loop Filter
In three-phase grid-oriented converters, the most commonly used phase-locked loop is SRF-PLL, as shown in Fig. 5, and a loop filter is introduced before the PI regulator to filter out the corresponding harmonics in fundamental grid voltages ugq or corresponding negative sequence components for the elimination of the impact of grid voltages on SRF-PLL extraction phase angle. This method is called SRF-PLL based on loop filter.
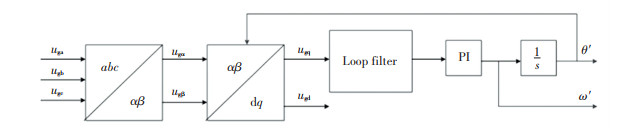
|
Fig.5 The diagram of SRF-PLL with the loop filter |
It is revealed that three-phase grid voltages are transformed to the synchronous rotating voltages, where the d axis and q axis grid-tied voltages are
| $ \left\{\begin{array}{l} u_{\mathrm{gd}}=V_{\mathrm{m}} \cos \left(\theta-\theta^{\prime}\right) \\ u_{\mathrm{gq}}=V_{\mathrm{m}} \sin \left(\theta-\theta^{\prime}\right) \end{array}\right. $ | (24) |
In Eq.(24), θ′ is the phase angle extracted by SRF-PLL. When the real angle θ is close to the estimated one, Eq.(24) can be expressed as
| $ \left\{\begin{array}{l} u_{\mathrm{gd}} \approx V_{\mathrm{m}} \\ u_{\mathrm{gq}} \approx V_{\mathrm{m}}\left(\theta-\theta^{\prime}\right) \end{array}\right. $ | (25) |
Therefore, ugd represents the observed grid voltage magnitude while ugq reflects the error between grid voltage real angle and estimated one. Based on the illustration in Fig. 5, the transfer equation of PLL can be expressed as
| $ G_{\mathrm{pl}}(s)=\frac{\theta^{\prime}(s)}{\theta(s)}=\frac{s k_{\mathrm{pl}} V_{\mathrm{m}}+k_{\mathrm{il}} V_{\mathrm{m}}}{s^{2}+s k_{\mathrm{pl}} V_{\mathrm{m}}+k_{\mathrm{il}} V_{\mathrm{m}}} $ | (26) |
When the controller gains are selected as Eqs. (27) and (28), the system can be equivalent to Eq.(29).
| $ k_{\mathrm{il}}=\frac{\omega_{\mathrm{p}}^{2}}{V_{\mathrm{m}}} $ | (27) |
| $ k_{\mathrm{pl}}=\frac{2 \xi_{\mathrm{p}} \omega_{\mathrm{p}}}{V_{\mathrm{m}}} $ | (28) |
| $ G_{\mathrm{pl}}(s)=\frac{2 \xi_{\mathrm{p}} \omega_{\mathrm{p}} s+\omega_{\mathrm{p}}^{2}}{s^{2}+2 \xi_{\mathrm{p}} \omega_{\mathrm{p}} s+\omega_{\mathrm{p}}^{2}} $ | (29) |
where ξp is the damping ratio and ωp is the bandwidth of SRF-PLL. ξp is usually selected as 0.707 and the cutoff frequency ωp is often designed 5 to 10 times the fundamental frequency of grid.
3.2 Power Controller DesignIn the dq coordinates, active power and reactive power injecting into grid can be derived according to instantaneous power calculation principles:
| $ \left\{\begin{array}{l} P_{\mathrm{s}}=\frac{3}{2}\left(u_{\mathrm{gd}} i_{\mathrm{gd}}+u_{\mathrm{gq}} i_{\mathrm{gq}}\right) \\ Q_{\mathrm{s}}=\frac{3}{2}\left(u_{\mathrm{gq}} i_{\mathrm{gd}}-u_{\mathrm{gd}} i_{\mathrm{gq}}\right) \end{array}\right. $ | (30) |
In the case of ugq=0, the power calculation can be simplified as follows:
| $ \left\{\begin{array}{l} P_{\mathrm{s}}=\frac{3}{2} u_{\mathrm{gd}} i_{\mathrm{gd}} \\ Q_{\mathrm{s}}=-\frac{3}{2} u_{\mathrm{gd}} i_{\mathrm{gq}} \end{array}\right. $ | (31) |
In this paper, PI controller is used to implement closed-loop power tracking control on the grid side. The PI parameters are characterized according to the requirement of power dynamics.
4 Simulation ResultsSimulations were used to verify the proposed current control methods and power control methods. Specifications of the simulations are presented in Table 1, where the amplitude and frequency of grid-side voltage was selected as the corresponding constants.
4.1 ValidationIn contrast with the performance of state space PI controller, a conventional PI current regulator with active damping is developed. The PI parameters are tuned based on classic system design principles, where the bandwidth corresponds with that of the proposed controller and the active damping ratio is selected in constrained conditions. Meanwhile, the LCL filter parameters selected by classic parameter design methods are applied in the simulation system.
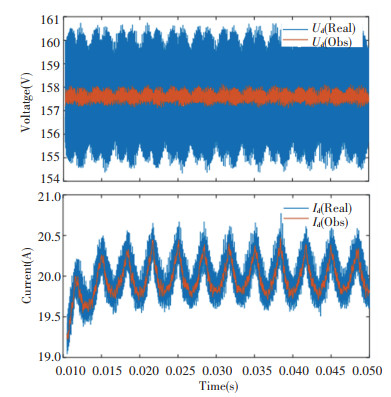
The observation efficiency of the state space observer is displayed in the following section, in which only capacitor voltages and grid currents are discussed due to inverter currents measured directly by sensors. As can be seen in Fig. 6, the observer observes the actual voltages and currents quickly and accurately respectively and attenuates the disturbing harmonics acting as low pass filters where the percentage of diminished noise components exceeds 80%.
|
Fig.6 Comparison between measured d q axis voltages as well as currents and observed voltages and currents |
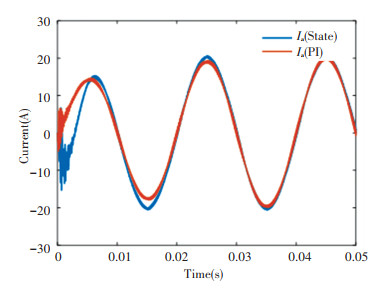
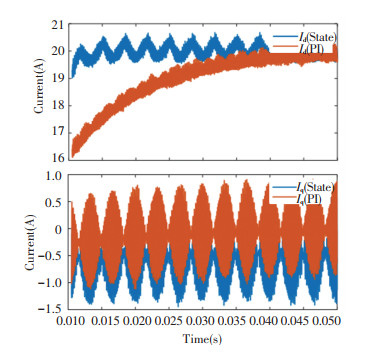
Next, the dynamic responses of grid currents using the two controllers are compared under the step of 20 A in the reference igd* of the grid current. Fig. 7 shows that there may be fewer low-order harmonic components in grid currents when using the state space strategies(THDc=1.94%), compared with those from the PI controller with active damping(THDc=2.03%). Generally, the simulation findings show that the proposed strategies have superior capabilities to eliminate harmonics. In Fig. 8, current ripples of d axis currents and q axis currents from the two controllers are presented, respectively. The DOFs of the regulation structure are higher in the state space controllers than that in conventional PI control with active damping, resulting in more prominent dynamic characteristics and resonance suppression.
|
Fig.7 Comparison of phase currents from state-space PI control and conventional PI with active damping |
|
Fig.8 Comparison of dq axis currents from state-space PI control and conventional PI with active damping |
4.2 Parameter Errors
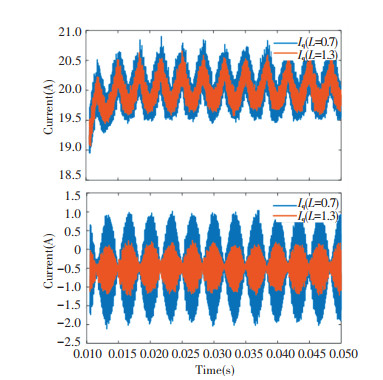
Besides, the effect of the varying grid inductance was examined in this paper. The corresponding cases of the parameter deviations ΔLg/Lg=0.3 and ΔLg/Lg= -0.3 were simulated, and the findings are displayed in Fig. 9. The findings reveal that the grid inductance fluctuation has little influence on the d axis current ripple, whose current fluctuation is less than 1% while the q axis current may be influenced more seriously, whose current fluctuation is more than 50%. Overall, the power regulation system maintains its stability when the parameter varies, and the larger inductance may decrease the resonance frequency, contributing to better harmonic attenuation.
|
Fig.9 Simulated grid-current step response with parameter errors ΔLg/Lg =0.3 and ΔLg/Lg=-0.3 |
4.3 SRF-PLL Response
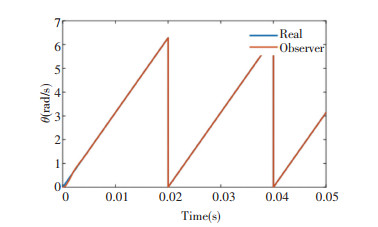
Simulations were implemented to demonstrate the effectiveness of the proposed power control method. The PLL bandwidth was set up as 1000 rad/s and the PLL damping ratio was 0.707. As shown in Fig. 10, the SRF-PLL with the loop filter achieves fast and accurate phase tracking, which can meet the actual requirements, where the fundamental frequency of grid was selected as 50 Hz.
|
Fig.10 The tracking performance of SRF-PLL with loop filter |
4.4 Power Tracking Response
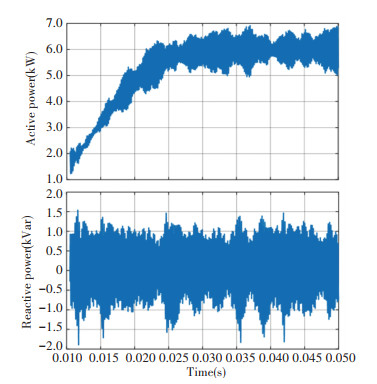
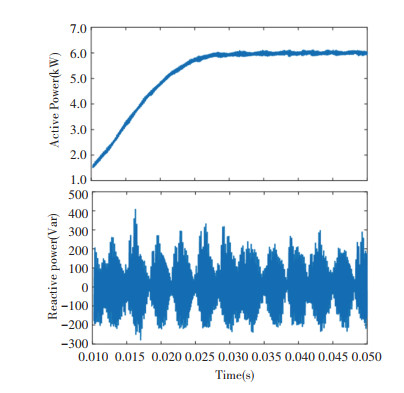
Aimed to verify power closed loop regulation performance, the reference of active powerPref and reactive power Qref were set as 6 kW and 0 kVar, respectively. The tracking differentiator was employed to smooth the references, eliminating the impact on the grid. Fig. 11 reflects the power responses using PI current controllers with active damping, where the chattering magnitude of active power and reactive power steady responses is nearly 1000. Fig. 12 shows the responses with state space controllers based on the extended Luenberger observation, in which both active power and reactive power achieve stable tracking without remarkable power error, whose magnitude is less than 200. Compared with responses in Fig. 11, less fluctuation and more excellent power closed loop performance are acquired when state space current control strategies are applied. Fig. 12 reveals that noise elimination from state space observer plays a more active role than filters after power calculation without state space observers.
|
Fig.11 Active power and reactive power response with PI controller based on active dampingwhen active power reference was set as 6 kW |
|
Fig.12 Active power and reactive power response with state space controller based on the extended Luenberger observer when active power reference was set as 6 kW |
Fig. 13 Displays the current responses under above power conditions with state space control schemes and conventional PI schemes, respectively. In each graph, the current is 0.5 times the actual value while the grid voltage is 0.2 times the actual one. In terms of phase angle tracking, the current responses of the two methods have almost same phase angle compared with that of the phase A grid voltage. However, the proposed methods in this paper are much superior to PI methods in the harmonic suppression regardless of high order ones or low order ones whose current THD are 2.31% and 6.4%, respectively. Besides, to achieve similar responses just like the ones from state space controllers, considerably small active damping parallel visual resistance is employed in conventional PI systems, which inevitably gives rise to the amplification of noise, degrading the stability.

|
Fig.13 Phase current response with state space controller based on the extended Luenberger observer and PI controller with active damping(the blue represents the grid voltage and the red represents the current response) |
Next, the reactive power reference was set as -2 kW at 0.05 s. Fig. 14 and Fig. 15 present the active and reactive power responses using the above two methods, respectively. Contrast with the active power in Fig. 14 whose oscillation problems may become more serious due to the coupling between active power and reactive power, the active power in Fig. 15 may be slightly affected by the increase of reactive power. Besides, reactive power harmonics in Fig. 15 using proposed methods are much smaller than those in Fig. 14, contributing to the improvement of system stability and dynamic characteristics.
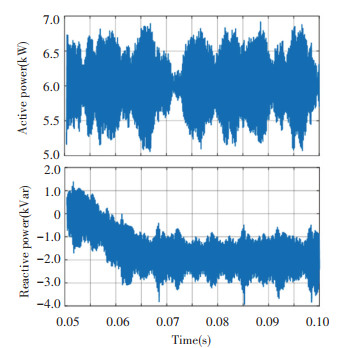
|
Fig.14 Active power and reactive power response with PI controller based on active damping when reactive power reference was set as -2 kW |
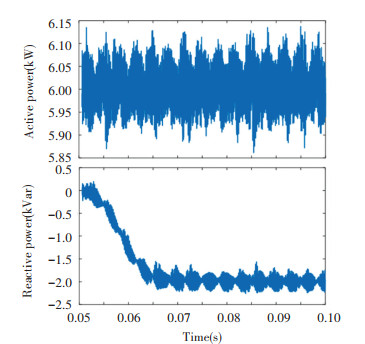
|
Fig.15 Active power and reactive power response with state space controller based on the extended Luenberger observer when reactive power reference was set as -2 kW |
5 Conclusions
Currently, the grid-connected inverter technology with LCL filter is an important research direction of distributed power generation and new energy power generation. The main contribution of this article are as follows:
1) Aimed at overcoming poor current response caused by simplified methods neglecting the capacitors, this paper proposes a state space PI current regulation strategy based on the mathematical model of LCL-type grid-tied converters, which combines the state space methods' disturbance-rejecting ability and the high efficiency of integrated control, bringing about the high precision control of grid current.
2) To avoid the application of current or voltage sensors, which may decrease the reliability and increase the cost, an extended Luenberger state observer for full-order observation of state variables is proposed whose parameters are designed by the polynomial equations approach, improving the design efficiency of the converter systems. Besides, the state observer also functions as the filter which strengthens systems' ability to anti-interference.
Combined with the theoretical analysis above, a set of 6 kW simulation system was constructed and the effectiveness of the proposed methods is demonstrated eventually.
| [1] |
Lawrence R, Middlekauff S. The new guy on the block. IEEE Industry Applications Magazine, 2015, 11(1): 54-59. DOI:10.1109/MIA.2005.1380328 (  0) 0) |
| [2] |
Blaabjerg F, Chen Z, Kjaer S B. Power electronics as efficient interface in dispersed power generation systems. IEEE Transactions on Power Electronics, 2004, 19(5): 1184-1194. DOI:10.1109/TPEL.2004.833453 (  0) 0) |
| [3] |
Blaabjerg F, Teodorescu R, Liserre M, et al. Overview of control and grid synchronization for distributed power generation systems. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1398-1409. DOI:10.1109/TIE.2006.881997 (  0) 0) |
| [4] |
Wang X F, Blaabjerg F, Wu W M. Modeling and analysis of harmonic stability in an ac power-electronics-based power system. IEEE Transactions on Power Electronics, 2014, 29(12): 6421-6432. DOI:10.1109/TPEL.2014.2306432 (  0) 0) |
| [5] |
Wu W M, He Y B, Blaabjerg F. An LLCL power filter for single phase grid-tied inverter. IEEE Transactions on Power Electronics, 2012, 27(2): 782-789. DOI:10.1109/TPEL.2011.2161337 (  0) 0) |
| [6] |
Wu W M, Sun Y J, Lin Z, et al. A modified LLCL filter with the reduced conducted EMI noise. IEEE Transactions on Power Electronics, 2014, 29(7): 3393-3402. DOI:10.1109/EPE.2013.6634408 (  0) 0) |
| [7] |
Alemi P, Bae C-J, Lee D-C. Resonance suppression scheme based on PR control for single-phase grid-connected inverters with LLCL filters. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 459-467. DOI:10.1109/JESTPE.2015.2464699 (  0) 0) |
| [8] |
Tang Y, Loh P C, Wang P, et al. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters. IEEE Transactions on Power Electronics, 2012, 27(3): 1433-1443. DOI:10.1109/TPEL.2011.2162342 (  0) 0) |
| [9] |
Yin J J, Duan S X, Liu B Y. Stability analysis of grid-connected inverter with LCL filter adopting a digital single-loop controller with inherent damping characteristic. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1104-1112. DOI:10.1109/TⅡ.2012.2222424 (  0) 0) |
| [10] |
Parker S G, McGrath B P, Holmes D G. Regions of active damping control for LCL filters. IEEE Transactions on Industry Applications, 2014, 50(1): 424-432. DOI:10.1109/TIA.2013.2266892 (  0) 0) |
| [11] |
Wu W M, He Y B, Tang T H, et al. A new design method for the passive damped LCL- and LLCL-filter based single-phase grid-tied inverter. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4339-4350. DOI:10.1109/TIE.2012.2217725 (  0) 0) |
| [12] |
Wu W M, Sun Y J, Huang M, et al. A robust passive damping method for LLCL-filter-based grid-tied inverters to minimize the effect of grid harmonic voltages. IEEE Transactions on Power Electronics, 2014, 29(7): 3279-3289. DOI:10.1109/TPEL.2013.2279191 (  0) 0) |
| [13] |
Hanif M, Khadkikar V, Xiao W D, et al. Two degrees of freedom active damping technique for filter-based grid connected PV systems. IEEE Transactions on Industrial Electronics, 2014, 61(6): 2795-2803. DOI:10.1109/TIE.2013.2274416 (  0) 0) |
| [14] |
Dannehl J, Liserre M, Fuchs F W. Filter-based active damping of voltage source inverters with LCL filters. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3623-3633. DOI:10.1109/TIE.2010.2081952 (  0) 0) |
| [15] |
Carugati I, Maestri S, Donato P G, et al. Variable sampling period filter PLL for distorted three-phase systems. IEEE Transactions on Power Electronics, 2012, 27(1): 321-330. DOI:10.1109/TPEL.2011.2149542 (  0) 0) |
| [16] |
Golestan S, Monfared M, Freijedo F D. Design-oriented study of advanced synchronous reference frame phase-locked loops. IEEE Transactions on Power Electronics, 2013, 28(2): 765-778. DOI:10.1109/TPEL.2012.2204276 (  0) 0) |
| [17] |
Rodriguez P, Pou J, Bergas J, et al. Decoupled double synchronous reference frame PLL for power converters control. IEEE Transactions on Power Electronics, 2007, 22(2): 584-592. DOI:10.1109/TPEL.2006.890000 (  0) 0) |
| [18] |
Achlerkar P D, Panigrahi B K. New perspectives on stability of decoupled double synchronous reference frame PLL. IEEE Transactions on Power Electronics, 2022, 37(1): 285-302. DOI:10.1109/TPEL.2021.3099162 (  0) 0) |
| [19] |
Wang Z, Zheng Y, Cheng M, et al. Unified control for a wind turbine-superconducting magnetic energy storage hybrid system based on current source converters. IEEE Transactions on Magnetics, 2012, 48(11): 3973-3976. DOI:10.1109/TMAG.2012.2201213 (  0) 0) |
| [20] |
Bojoi R I, Limongi L R, Roiu D, et al. Enhanced power quality control strategy for single-phase inverters in distributed generation systems. IEEE Transactions on Power Electronics, 2011, 26(3): 798-806. DOI:10.1109/TPEL.2010.2103572 (  0) 0) |
| [21] |
Chen L, Nian H, Xu Y Y. Improved model predictive direct power control of grid side converter in weak grid using kalman filter and DSOGI. Chinese Journal of Electrical Engineering, 2019, 5(4): 22-32. DOI:10.23919/CJEE.2019.000024 (  0) 0) |
| [22] |
Xu S G, Wang J P, Xu J P. A current decoupling parallel control strategy of single-phase Inverter with voltage and current dual closed loop feedback. IEEE Transactions on Industrial Electronics, 2013, 60(4): 1306-1313. DOI:10.1109/ECCE.2010.5618256 (  0) 0) |
| [23] |
Franklin G F, Powell J D, Emami-Naeini A. Feedback control of dynamic systems. Upper Saddle River, NJ, USA: Prentice-Hall, 2002. 840-840.
(  0) 0) |
| [24] |
Kukkola J, Hinkkanen M. Observer-based state-space current control for a three-phase grid-connected converter equipped with an LCL filter. IEEE Transactions on Industry Applications, 2014, 50(4): 2700-2709. DOI:10.1109/TIA.2013.2295461 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


