2. Anhui Domain Compute Co., Ltd, Hefei 230000, China
The kinematics characteristics of a suspension system represent the relationship among the vertical travel of the wheel and the wheel alignment parameters (camber angle, toe angle, kingpin inclination angle, and caster angle), wheel spacing, as well as the height of the vehicle roll center[1]. These parameters remarkably affect the handling and stability of a vehicle[2]. Optimizing the coordinates of suspension hard-points is effective to improve kinematics performance.
Extensive research into the optimization of coordinates of hard-points of vehicle suspension has been conducted. Excessive computational efforts are required when all the coordinates are considered design variables due to the high number of coordinates of hard-points. To address this issue, sensitivity analysis is usually used to select the most significant coordinates affecting the kinematics parameters of the vehicle, e.g., wheel alignment parameters, sideslip of tire, tread, wheelbase, roll center height, Ackerman rate, and minimum turning diameter[3]. However, the selection of coordinates as design variables is usually an arbitrary process to a certain extent because the influence of each coordinate of hard-point on different kinematics parameters varies greatly.
In addition to this issue, conflicting objectives also cause difficulties in the multiobjective optimization of the values of coordinates. In a multiobjective evolutionary algorithm (e.g., sequential approximation optimization, NSGA-II, IP-GA, and grey family design algorithm), multiple optimization objectives are separated in the entire optimization process and are minimized or maximized at the same time to obtain a solution repository[4-7], well-known as a Pareto front[8]. The number of solutions in Pareto front increases with the increase in the number of objective functions. In this event, selecting the best solution is very challenging due to the large number of solutions available[9]. To this end, few approaches, such as the kε-optimality method, the greedy reduction algorithm, and the adjoint sensitivity approach, have been proposed in previous studies to find an optimal solution in a Pareto front[10-12]. However, these methods are extremely subjective.
In summary, two significant issues exist in previous studies on the kinematics optimization of vehicle suspension as follows: a) influence of a hard-point coordinate on different wheel alignment parameters is diverse, thus selecting a group of hard-point coordinates with the greatest influences on the overall suspension kinematics performance as design variables is difficult; b) In multiobjective optimization, objective methods to select the optimal solution from the Pareto front are limited.
These issues can be solved through the use of single-objective optimization. Specifically, the sensitivities of a design variable to different wheel alignment parameters can be converted into a single comprehensive sensitivity index, which facilitates the screening of design variables. Similarly, by means of the transformation of a multiobjective optimization function into a single-objective function, the optimal solution can be solved directly. Thus, selecting the optimal solution from the Pareto front is unnecessary.
Previous methods of transforming multiobjective optimization into single-objective optimization include the weighted sum method, the main objective method, and the stratified sequencing method[13-15]. However, these approaches lack objectivity in selecting weights of sub-objectives in the transformation process. The optimization results of the weighted sum method will be biased toward the subobjectives with larger orders of magnitude. The main objective method considers only the most important subobjective during optimization. The stratified sequencing method follows the idea of optimizing relatively important subobjectives first. Therefore, the results can be undesirable in situations, where multiple subobjectives have similar importance.
Grey relational analysis (GRA) is an important multivariate statistical analysis method for evaluating multiple conflicting indicators in the field of decision making. It transforms multiobjective responses into a single indicator, i.e., grey relational grade (GRG), through the comparison between the performance sequence and the ideal reference sequence[16]. In addition, the improved entropy weight method (IEWM) based on information theory can reflect the uncertain performance information of random variables. It can be used as an unbiased and objective method to determine the weight of each performance index in GRG. Therefore, the present study bridges the research gap of previous studies by proposing the GRA-IEWM method, which eliminates the subjectivity in the selection of design variables and multiobjective optimization.
The remainder of the paper is organized as follows: In Section 1, the system dynamics model of McPherson suspension is developed, and its accuracy is validated through field test. Section 2 selects design variables based on the objective method, namely, IEWM-GRA. In Section 3, the approximate model between the objective functions and the hard-point coordinates is formulated using support vector regression (SVR) and fruit fly optimization algorithm (FOA) at first. Then, a single-objective optimization function toward the improvement of suspension kinematics performance is formulated using the IEWM-GRA method again. In Section 4, comparisons among the IEWM-GRA method, the original coordinate scheme, and the traditional multiobjective optimization method are made in terms of kinematic performance. Section 5 concludes the findings and points out possible research directions in the future.
1 Development and Validation of Full Vehicle ModelAs the basis of the research, the dynamics model of the front MacPherson suspension was developed initially on the basis of the parameters of an A0 class vehicle, which was accomplished by the ADAMS/Car. The system consisted of a knuckle, tie rod, spring, shock absorber, lower control arm, and tire.
The original hard-point coordinates of the left front MacPherson suspension are listed in Table 1. The left and right suspension hard-point coordinates are symmetrical around the longitudinal axis of the vehicle. Thus, the hard-point coordinates of the right front MacPherson suspension are omitted.
| Table 1 Original hard-point coordinates of the left front MacPherson suspension |
A multibody dynamic model of the entire vehicle was developed to validate the accuracy of the MacPherson suspension (Fig. 1). The full vehicle model consists of MacPherson front suspensions, torsion beam rear suspension, steering system, tires, powertrain, and body. The accuracy of the vehicle model was verified through the pylon course slalom test, steering-returnability test and ride comfort test of the actual vehicle (Fig. 2). The parameters of the vehicle model and the detailed comparisons, which have been documented in the previous work, were omitted for brevity[17]. The previous results showed good reliability of the vehicle model; thus, it was used for subsequent optimization and analysis.

|
Fig.1 Multibody dynamics model of the A0 class vehicle |

|
Fig.2 Pylon course slalom test |
2 Selections of Suspension Design Variables by Using IEWM-GRA 2.1 Sensitivity Analysis of Suspension Hard-Point Coordinates
If all the suspension hard-point coordinates are considered design variables, then excessive computational efforts are required in the optimization process. To solve this issue, sensitivity analysis should be carried out to select the coordinates with the greatest impact on wheel alignment parameters. With respect to the left front suspension, the previous research revealed that the locations of the tie rod outer point, the tie rod inner point, the lower control arm outer point, the lower control arm front point, and the shock absorber upper point are important factors that affect the kinematics characteristics[18]. Thus, these alternative coordinates were selected for sensitivity analysis performed in ADAMS/Insight. Two levels were set for each coordinate, i.e., the minimum and maximum value of variation range of the coordinate. Then, the L214 (215) test matrix was selected. For each test, the parallel wheel travel test was performed in the ADAMS/Car by using the following excitation function:
| $ S=50 \times \sin (360 \times t) $ | (1) |
where S stands for the vertical position of the wheel (mm), and t is time (s). A total of 100 simulation steps were found.
The results of the sensitivity analysis are shown in Table 2. This finding indicates that each coordinate has various effects on the front wheel alignment parameters. Thus, selecting the design variables directly is difficult.
| Table 2 Sensitivity of suspension hard-point coordinate |
2.2 Formulation of Single-Objective Optimization Function Using IEWM-GRA
The problem of selecting design variables can be addressed through the IEWM-GRA method. GRA is a method to deal with problems with uncertainties, few data, and poor information. Its basic idea is to judge the correlation of two sequences in accordance with the similarity of geometric shapes of sequence curves. It transforms discrete observations of system factors into piecewise continuous polylines. Then, in accordance with the geometric characteristics of polylines, a model to test the degree of correlation is developed. When the geometry of the polylines is similar, the degree of association between the sequences is great, and vice versa[19].
In GRA, GRG is an important index to evaluate the multiple responses. GRG reasonably determines the relationship and similarity between two different sequences by using the geometric similarity of sequence curves in the system. However, one issue associated with the GRG in previous studies is the calculation of weight of each performance index. The commonly used methods for determining weight are the Delphi method[20], the analytic hierarchy process[21], and the fuzzy comprehensive evaluation method[22]. The first two methods rely on experts' knowledge to subjectively determine the weight of each subobjective. However, the fuzzy evaluation method tends to overemphasize the importance of extreme values, thereby causing the losses of effective information.
Entropy weight method (EWM) is an objective method based on information theory, where entropy is an index to measure the disorder of the system. A larger entropy represents a greater variety of responses. However, in the entropy weight method, if all entropy values approach 1, then a small difference in entropy value may cause a large change in the entropy weight of an index, thus the weights of some indicators are inconsistent with their importance[23]. IEWM can overcome the drawback of EWM and provide an objective and accurate approach to calculate the weight of each performance index in GRG by modifying the formula of entropy weight[24].
Thus, through the integrated use of GRA and IEWM, the sensitivities of a design variable to different wheel alignment parameters can be converted into a single comprehensive sensitivity index, which facilitates the screening of alternative design variables.
A multiobjective decision making problem is assumed to have n alternatives and m evaluation indices. Normalization of the response variables was performed initially; it can either be minimization (cost attribute) or maximization (benefit attribute). The maximization attribute is normalized as follows[25]:
| $ x_{i}^{*}(j)=\frac{x_{i}(j)-\min {\rm x}_{i}(j)}{\max x_{i}(j)-\min {\rm x}_{i}(j)} $ | (2) |
The minimization attribute is normalized as
| $ x_{i}^{*}(j)=\frac{\max x_{i}(j)-x_{i}(j)}{\max x_{i}(j)-\min {\rm x}_{i}(j)} $ | (3) |
where i = 1, 2, ..., n, j = 1, 2, ..., m. xi*(j) denotes the original value, and max xi(j) and min xi(j) are the largest and smallest value of the j-th index, respectively.
Xi={xi*(j), i=1, 2, …, n} refers to the compared sequence, and X0={x0*(j), j=1, 2, …, m} indicates a reference sequence, which represents an ideal comparison standard. For the larger-the-better problem, X0 consists of the maximum sensitivity value of each index, which can be determined from Table 2. The grey relational coefficient of the Xi and X0 at index j can be derived from Eq. (4):
| $ \xi_{i}(j)=\frac{\min \limits_{i} \min \limits_{j} \Delta x_{i}^{*}(j)+\rho \max \limits_{i} \max \limits_{j} \Delta x_{i}^{*}(j)}{\Delta x_{i}^{*}(j)+\rho \max \limits_{i} \max \limits_{j} \Delta x_{i}^{*}(j)} $ | (4) |
where ξi(j) denotes the grey relational coefficient, Δxi*(j)=x*0(j)-xi*(j), ρ is the distinguishing coefficient, which is 0.5 [26].
GRG is calculated by the following equation:
| $ \gamma_{i}=\frac{1}{m} \sum\limits_{j=1}^{m} \lambda_{j} \xi_{i}(j) $ | (5) |
where γi denotes GRG, λj represents the weight assigned to each index j. Parameter λj is determined using IEWM. The general steps for the implementation of the IEWM are as follows:
Step 1. Raw data standardization. The original data matrix Z is defined as follows:
| $ \boldsymbol{Z}=\left[\begin{array}{ccc} x_{1}(1) & \cdots & x_{1}(m) \\ \vdots & & \vdots \\ x_{n}(1) & \cdots & x_{n}(m) \end{array}\right] $ | (6) |
Normalization of the original data matrix is obtained as follows[27]:
| $ r_{i j}=\frac{x_{i}(j)}{\sum\limits_{i=1}^{n} x_{i}(j)} $ | (7) |
where rij represents the normalized value of the j-th evaluation index on the i-th alternative.
Step 2. Define the entropy of IEWM
The entropy Hj of the j-th index is calculated by the following equation:
| $ H_{j}=-\frac{1}{\ln n} \sum\limits_{i=1}^{n} r_{i j} \ln r_{i j} $ | (8) |
when rij is zero, lnrij is zero.
Step 3. Evaluate the indicator weight of IEWM
The weight λj of the j-th evaluation index is determined as follows:
| $ \lambda_{j}= \begin{cases}\left(1-\bar{H}^{35.35}\right) w_{0 j}+\bar{H}^{35.35} w_{1 j}, & H_{j}<1 \\ 0, & H_{j}=1\end{cases} $ | (9) |
| $ w_{0 j}=\frac{1-H_{j}}{\sum\limits_{j=1}^{m}\left(1-H_{j}\right)} $ | (10) |
| $ w_{1 j}=\frac{1+\bar{H}-H_{j}}{\sum\limits_{j=1, H_{j} \neq 1}^{m}\left(1+\bar{H}-H_{j}\right)} $ | (11) |
where
GRG was used as the comprehensive sensitivity index, in which IEWM was used to determine the weight of sensitivity of each wheel alignment parameter. The weight of each wheel alignment parameter is shown in Table 3, and the GRG values of alternative design variables are shown in Table 4.
| Table 3 Weight of sensitivity of wheel alignment parameter using IEWM |
| Table 4 Grey relational coefficient and GRG |
According to the results of Table 4, the following nine hard-point coordinates with the highest GRGs were selected as design variables: control arm front z, control arm outer x, control arm outer y, control arm outer z, damper upper x, damper upper y, steering rod inner z, steering rod outer x, and steering rod outer z. These coordinates are denoted as x1, x2, …, x9.
3 Formulation of Single-Objective Optimization Function of Suspension Kinematics Performance 3.1 Approximate Model between Objective Functions and Hard-Point CoordinatesDeveloping an approximate model between design variables and optimization objectives is the basis for subsequent optimization process. SVR is a machine learning approach based on structural risk minimization[28]. Compared with the traditional approximation methods, such as the response surface method and the Kriging model, SVR not only has good generalization ability, but can also effectively solve the dimension disaster problem. Thus, SVR was used for the development of the approximate model.
In SVR, penalty factor and kernel function parameter are two important training parameters that affect the performance of regression[29]. Traditional methods for SVR parameter optimization mainly include trial-and-error and cross-validation[30-31]. These methods have large errors and high calculation cost, and only local optimization can be achieved. FOA is a metaheuristic algorithm proposed and popular in recent years; it is characterized by a simple mechanism, few control parameters, fast convergence, and strong global search capability[32]. FOA was used to optimize the parameters of the SVR approximate model to improve its accuracy and efficiency. The flowchart of the FOA-SVR method is illustrated in Fig. 3.

|
Fig.3 Flowchart of FOA-SVR method |
The FOA-SVR model should be developed by fitting the data of the parallel wheel travel test. In ADAMS/insight, DOE screening (two-level) method was used to design the parallel wheel travel test. For the nine design hard-point coordinates, 512(29) sets of the simulation data of all tests were derived. Among them, 412 sets of data were randomly selected as the training set, and 100 sets of data as the test set. The values of C and γ of the SVR approximate model, which were optimized by FOA, are shown in Table 5.
| Table 5 Optimal value of C and γ |
FOA-SVR approximate models between the variation of the front wheel alignment parameters, and the coordinates of suspension hard-points were formulated using the following excitation function:
| $ y_{1}(\boldsymbol{X})=\sum\limits_{i=1}^{l_{1}}\left(\alpha_{i}^{*}-\alpha_{i}\right) K\left(\boldsymbol{x}_{i}, \boldsymbol{X}\right)+b_{1} $ | (12) |
| $ y_{2}(\boldsymbol{X})=\sum\limits_{i=1}^{l_{2}}\left(\alpha_{i}^{*}-\alpha_{i}\right) K\left(\boldsymbol{x}_{i}, \boldsymbol{X}\right)+b_{2} $ | (13) |
| $ y_{3}(\boldsymbol{X})=\sum\limits_{i=1}^{l_{3}}\left(\alpha_{i}^{*}-\alpha_{i}\right) K\left(\boldsymbol{x}_{i}, \boldsymbol{X}\right)+b_{3} $ | (14) |
| $ y_{4}(\boldsymbol{X})=\sum\limits_{i=1}^{l_{4}}\left(\alpha_{i}^{*}-\alpha_{i}\right) K\left(\boldsymbol{x}_{i}, \boldsymbol{X}\right)+b_{4} $ | (15) |
where y1(X), …, y4(X) represent the variation of the toe angle, camber angle, caster angle, and kingpin inclination angle during wheel travel. ld(d=1, 2, 3, 4) denotes the number of support vectors. bs(s=1, 2, 3, 4) is the bias term. K(xi, X) refers to the Gaussian kernel function. X is the hard-point coordinate vector, X=[x1, x2, …, x9]T.
To verify the reliability of the FOA-SVR models, 100 sets of test data were substituted. The comparisons between the predicted values and the true values are shown in Fig. 4. Several goodness-of-fit and accuracy indices are used to evaluate the model (Table 6).
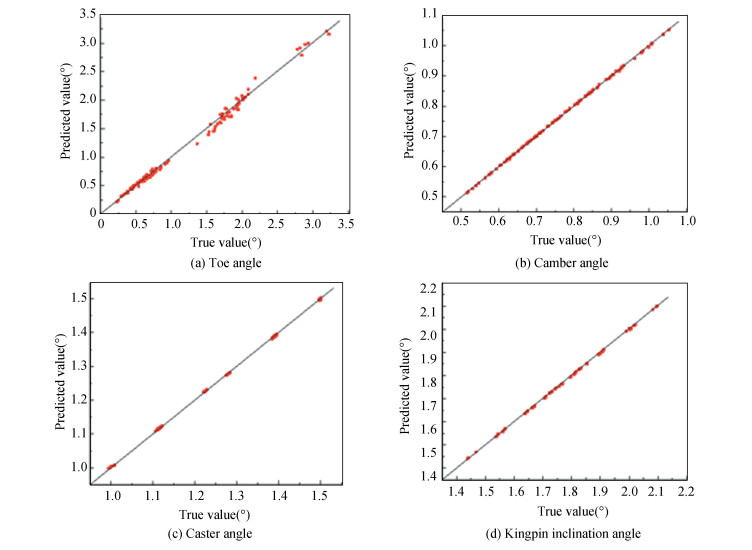
|
Fig.4 Comparison between the predicted value and true value of the FOA-SVR model: (a) variation of toe angle; (b) variation of camber angle; (c) variation of caster angle; (d) variation of kingpin inclination angle |
| Table 6 Performance of the FOA-SVR model |
As shown in Table 6, the MAPE (Mean Absolute Percentage Error) values of y1(X), y2(X)…, y4(X) are 2.91%, 0.24%, 0.11%, and 0.13%. The MSE (Mean Square Error) of each model is lower than 0.001. Therefore, the models have good accuracies. The R2 of the models is higher than 0.99, ensuring a desirable goodness-of-fit.
3.2 Single-Objective Optimization Function for Suspension Kinematics CharacteristicsMultiobjective optimization functions for suspension kinematics characteristics was determined using the FOA-SVR approximate models as follows:
| $ \left\{\begin{array}{l} \min y_{1}(\boldsymbol{X}) \\ \min y_{2}(\boldsymbol{X}) \\ \min y_{3}(\boldsymbol{X}) \\ \min y_{4}(\boldsymbol{X}) \\ \text { s.t. } x_{k}^{\min } \leqslant x_{k} \leqslant x_{k}^{\max }, k=1,2, \cdots, 9 \end{array}\right. $ | (16) |
where xkmin and xkmax denote the lower and upper limits of hard-point coordinate xk, respectively.
The multiobjective optimization function is transformed into a single-objective optimization function by applying the GRG as follows:
| $ \left\{\begin{array}{l} -\max \frac{1}{m} \sum\limits_{j=1}^{m} \lambda_{j} \frac{\min \limits_{i} \min \limits_{j} \Delta y_{i}(j)+\rho \max \limits_{i} \max \limits_{j} \Delta y_{i}(j)}{\Delta y_{i}(j)+\rho \max \limits_{i} \max \limits_{j} \Delta y_{i}(j)} \\ \text { s.t. } x_{k}^{\min } \leqslant x_{k} \leqslant x_{k}^{\max }, k=1,2, \cdots, 9 \end{array}\right. $ | (17) |
where Δyi(j)=y0(j)-yi(j), i=1, 2, ..., n, j=1, 2, ..., m. y0(j) denotes the minimum value of the j-th objective function, yi(j)=yj(X). The weight of the j-th objective function, λj, is calculated by IEWM, as shown in Table 7.
| Table 7 Weight of variation of front wheel alignment parameters by using IEWM |
4 Analysis of Optimization Results 4.1 Solution of the IEWM-GRA Optimization Method
After the formulation of the single-objective optimization function, an optimization algorithm should be determined to solve the function. Differential evolution (DE) is a stochastic evolutionary algorithm based on population difference[33]. The basic idea is to generate the initial species randomly within the feasible range, cross and mutate the initial population, and select the population according to the survival rule of the biologically fittest. DE has been widely applied for its easy implementation, good convergence, and strong global optimization ability. In the DE algorithm, crossover factor CR and mutation scaling factor F are two critical parameters to determine the convergence speed and population diversity. Evidently, the traditional DE algorithm uses fixed F and CR, which are selected from previous experience and adjusted on the basis of the time-consuming trial-and-error. However, for better convergence, these parameters should be changed during evolution. An efficient DE-variant self-adaptive differential evolution (jDE) algorithm, which has self-adapted F and CR during the search process, was used to solve the single-objective optimization function[34].
In Eq. (17), y0(j) is obtained by the jDE algorithm. Then, the jDE algorithm was applied again to solve the single-objective optimization problem. The fitness value curve is shown in Fig. 5. The figure illustrated that the fitness value reaches the optimum when the iterations exceed 110. The optimal values of the nine design variables derived by the jDE algorithm are [4.492, -2.916, -702.483, 11.770, 29.500, 595.000, 93.889, 130.079, 81.322]. The left and right suspension hard-point coordinates are symmetrical around the longitudinal axis of the vehicle. Thus, the optimal hard-point coordinates of the front right suspension can be obtained accordingly.
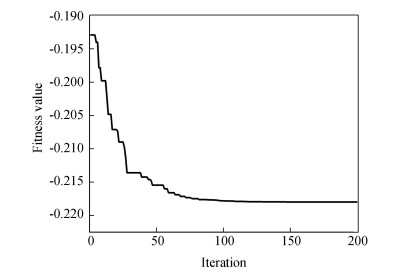
|
Fig.5 Fitness valve curve of the jDE algorithm |
4.2 Solution of the IEWM-GRA Optimization Method
To evaluate the effectiveness of the IEWM-GRA optimization method, it was compared with the traditional multiobjective optimization method and the original coordinate scheme (the hard-point coordinates are shown in Table 1).
In the traditional multiobjective optimization, in accordance with the sensitivity analysis results of Table 2, nine hard-point coordinates (control arm front x, control arm outer x, control arm outer y, control arm outer z, damper upper x, damper upper y, steering rod inner x, steering rod outer x, and steering rod outer z) with relatively high sensitivities were selected as design variables[18]. On the basis of the data of orthogonal tests in Adams/Insight, an approximate model of front wheel alignment parameters and hard-point coordinates was developed using the response surface method[35]. Then, the multiobjective optimization functions were formulated. Subsequently, optimization functions were solved using the GA algorithm. The algorithm stops when a precision is satisfied or the number of iterations reaches 1000. The nondominated Pareto front was then obtained with 1000 iterations, consuming approximately 15 min for a typical-performance computer. The computation time is three to four times that of the IEWM-GRA optimization method. Finally, a solution was selected from nondominated Pareto solution set by using the direct weighting method[17], which is also a subjective method. The optimal coordinates are [13.550, -3.007, -699.593, -11.790, 29.571, -594.942, 100.73, 127.546, 80.765].
The parallel wheel travel test was carried out in the ADAMS/Car with the suspension parameters, which are derived from the three methods. The changes in front wheel alignment parameters with wheel travel are illustrated in Fig. 6. Specific variation values of front wheel alignment parameters are given in Table 8.
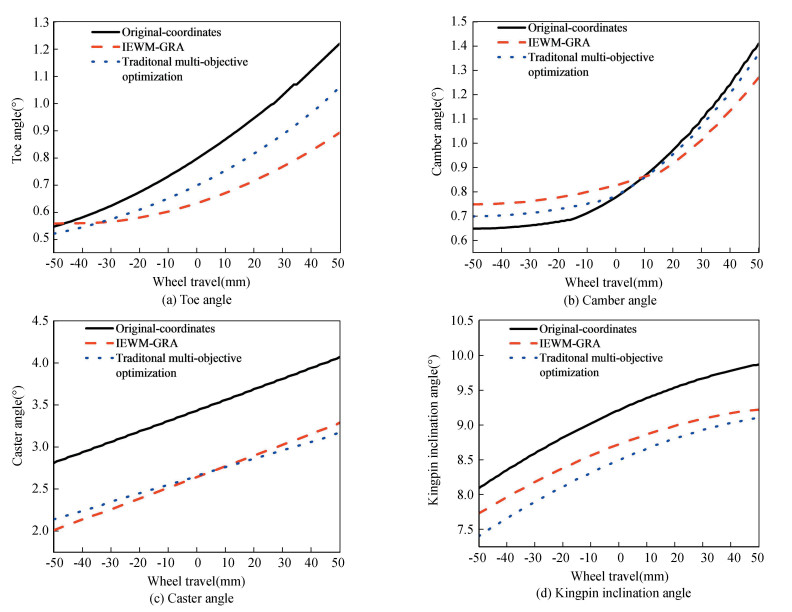
|
Fig.6 Changes of front wheel alignment parameters based on three methods |
| Table 8 Comparisons among three methods |
Evidently, Fig. 6 and Table 8 show that compared with the original coordinate scheme, the reductions of variations of the toe angle, camber angle, caster angle, and kingpin inclination angle using IEWM-GRA method reach 50.21%, 31.43%, 1.94%, and 15.91%, respectively. The IEWM-GRA method also outperforms the traditional multiobjective optimization method in terms of variations of toe angle, camber angle, and kingpin inclination angle, with reductions up to 37.3%, 21.7%, and 12.1%, respectively. However, an increase (21.9%) in the variation range of the caster angle is also observed (These reduction ratios can be calculated from Table 8). This phenomenon can be explained by the proposed IEWM-GRA method that ensures the ideal overall results. However, a subfunction may not achieve its best value. Generally, the IEWM-GRA method improves the kinematics performance of the vehicle suspension and enhances the computational efficiency of the optimization process effectively.
5 ConclusionsAn important issue associated with the traditional multiobjective optimization of suspension geometric design is the lack of objectivity. In addition, the search performance of the optimization algorithm deteriorates sharply as the number of optimization objectives increases. Concerning these issues, a method is proposed to convert multiobjective optimization into single-objective optimization in geometric design of a MacPherson suspension system through the integrated use of GRA and an IEWM. The following conclusions can be drawn:
1) GRA is a desirable index reflecting the complicated interrelationships among the designated performance characteristics. However, IEWM is an objective and reasonable method to determine the weights in GRG. The integrated use of the two approaches eliminates the subjectivity and improves the efficiency of multiobjective optimization of vehicle suspension.
2) The FOA-SVR method has made considerable fitting results with many independent variables and show good accordance with the true values. The MAPE between the results of ADAMS simulation and those of the SVR relationship models is less than 3%, and the R2 is greater than 0.99.
3) The iteration steps of the IEWM-GRA method and the traditional multiobjective optimization method are 110 and 1000, respectively. The computing time of the latter method is three to four times of the former one.
4) The single-objective optimization using the IEWM-GRA method outperforms the original coordinate scheme comprehensively, with reductions of variations of toe angle, camber angle, caster angle, and kingpin inclination angle reaching 50.21%, 31.43%, 1.94%, and 15.91%, respectively. Despite a larger variation range of caster angle, the EWM-GRA method also exhibits better kinematic performance than the traditional multiobjective optimization method.
5) As a demonstration of the IEWM-GRA method, this study focuses only on four important optimization objectives. The influences of the hard-point coordinates on other kinematics parameters (sideslip of tire, tread, wheelbase, roll center height, Ackerman rate, and minimum turning diameter) should also be considered in future studies to further verify the effectiveness of the proposed method in solving problems with higher complexity.
AcknowledgmentsThe assistance from engineers at Anhui Jianghuai Automobile Co., Ltd. in providing the model parameters is greatly appreciated. The authors also appreciate the valuable suggestions from Professor Guoqiang Mao of Xidian University to improve the quality of the paper.
| [1] |
Yang S J, Bao Y, Liu Y, et al. Kinematic analysis of the double wishbone suspension in ADAMS. Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific). Piscataway: IEEE, 2014, 4704149. DOI:10.1109/ITEC-AP.2014.6941253 (  0) 0) |
| [2] |
Wu J L, Luo Z, Zhang Y Q, et al. An interval uncertain optimization method for vehicle suspensions using Chebyshev metamodels. Applied Mathematical Modelling, 2014, 38(15-16): 3706-3723. DOI:10.1016/j.apm.2014.02.012 (  0) 0) |
| [3] |
Gao J, Yang X J, Niu Z R. Robust optimization and sensitivity analysis of hardpoints on suspension characteristics and full vehicle handling performance. Journal of Jiangsu University, 2014, 35(3): 249-256. DOI:10.3969/j.issn.1671-7775.2014.03.001 (  0) 0) |
| [4] |
Mahmoodi-Kaleibar M, Javanshir I, Asadi K, et al. Optimization of suspension system of off-road vehicle for vehicle performance improvement. Journal of Central South University, 2013, 20(4): 902-910. DOI:10.1007/s11771-013-1564-1 (  0) 0) |
| [5] |
Park K, Heo S J, Kang D O, et al. Robust design optimization of suspension system considering steering pull reduction. International Journal of Automotive Technology, 2013, 14(6): 927-933. DOI:10.1007/s12239-013-0102-3 (  0) 0) |
| [6] |
Nagarkar M P, Patil G J V, Patil R N Z. Optimization of nonlinear quarter car suspension-seat-driver model. Journal of Advanced Research, 2016, 7(6): 991-1007. DOI:10.1016/j.jare.2016.04.003 (  0) 0) |
| [7] |
Yarmohammadisatri S, Shojaeefard M H, Khalkhali A. A family base optimization of a developed nonlinear vehicle suspension model using gray family design algorithm. Nonlinear Dynamics, 2017, 90(1): 649-669. DOI:10.1007/s11071-017-3686-8 (  0) 0) |
| [8] |
Nariman-Zadeh N, Salehpour M, Jamali A, et al. Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm MUGA. Engineering Applications of Artificial Intelligence, 2010, 23(4): 543-551. DOI:10.1016/j.engappai.2009.08.008 (  0) 0) |
| [9] |
Papaioannou G, Koulocheris D. An approach for minimizing the number of objective functions in the optimization of vehicle suspension systems. Journal of Sound and Vibration, 2018, 435: 149-169. DOI:10.1016/j.jsv.2018.08.009 (  0) 0) |
| [10] |
Gobbi M, Haque I, Papalambros P Y, et al. Optimization and integration of ground vehicle systems. Vehicle System Dynamics, 2005, 43(6-7): 437-453. DOI:10.1080/00423110500158841 (  0) 0) |
| [11] |
Venkat V, Jacobson S H, Stori J A. A post-optimality analysis algorithm for multi-objective optimization. Computational Optimization and Applications, 2004, 28(3): 357-372. DOI:10.1023/B:COAP.0000033968.55439.8b (  0) 0) |
| [12] |
Zhu Y, Dopico D, Sandu C, et al. Dynamic response optimization of complex multibody systems in a penalty formulation using adjoint sensitivity. Journal of Computational and Nonlinear Dynamics, 2015, 10(3): 031009. DOI:10.1115/1.4029601 (  0) 0) |
| [13] |
Marler R T, Arora J S. The weighted sum method for multi-objective optimization: new insights. Structural and Multidisciplinary Optimization, 2010, 41(6): 853-862. DOI:10.1007/s00158-009-0460-7 (  0) 0) |
| [14] |
Zhang L, Wu W M, Huang X W. A dynamic optimization model for adjacent signalized intersection control systems based on the stratified sequencing method. Journal of Highway and Transportation Research and Development, 2016, 10(1): 85-91. DOI:10.3969/j.issn.1002-0268.2015.09.020 (  0) 0) |
| [15] |
Liu Y, Ren H X, Ding H X, et al. Position optimization of trench bottom structure based on the main object method. Chinese Journal of Engineering, 2016, 38(3): 314-319. DOI:10.13374/j.issn2095-9389.2016.03.003 (  0) 0) |
| [16] |
Liu S, Lin Y. Introduction to Grey System Theory. In: Grey Systems. Understanding Complex Systems. Berlin: Springer, 2010, 68: 1-18. DOI: 10.1007/978-3-642-16158-2_1.
(  0) 0) |
| [17] |
Shi Q, Peng C W, Chen Y K, et al. Robust kinematics design of MacPherson suspension based on a double-loop multi-objective particle swarm optimization algorithm. Proceedings of the Institution of Mechanical Engineers. Part D: Journal of Automobile Engineering, 2019, 223(12): 3263-3278. DOI:10.1177/0954407018821556 (  0) 0) |
| [18] |
Wang X T, Zhao Y F, Jiao B. Simulation analysis and optimization design of double-wishbone independent suspension. Applied Mechanics and Materials, 2014, 541: 519-523. DOI:10.4028/www.scientific.net/AMM.541-542.519 (  0) 0) |
| [19] |
Wang P, Meng P, Zhai J Y, et al. A hybrid method using experiment design and grey relational analysis for multiple criteria decision making problems. Knowledge-Based System, 2013, 53: 100-107. DOI:10.1016/j.knosys.2013.08.025 (  0) 0) |
| [20] |
Yang X J, Zeng L, Zhang R. Cloud delphi method. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2012, 20(1): 77-97. DOI:10.1142/s0218488512500055 (  0) 0) |
| [21] |
Ahmed F, Kilic K. Fuzzy analytic hierarchy process: a performance analysis of various algorithms. Fuzzy Sets and Systems, 2019, 362: 110-128. DOI:10.1142/10.1016/j.fss.2018.08.009 (  0) 0) |
| [22] |
Pei Q T, Li H B, Liu Y Q, et al. A grey evaluation model for predicting rockburst proneness based on combination weight and its application. Rock and Soil Mechanics, 2014, 35(S1): 49-56. DOI:10.16285/j.rsm.2014.s1.005 (  0) 0) |
| [23] |
Zhou H C, Zhang G H, Wang G L. Multi objective decision making approach based on entropy weights for reservoir flood control operation. Journal of Hydraulic Engineering, 2017, 38(1): 100-106. DOI:10.3321/j.issn:0559-9350.2007.01.015 (  0) 0) |
| [24] |
Ouyang S, Liu Z W, Li Q, et al. A new improved entropy method and its application in power quality evaluation. Advanced Materials Research, 2013, 706-708: 1726-1733. DOI:10.4028/www.scientific.net/amr.706-708.1726 (  0) 0) |
| [25] |
Misal N D, Sadaiah M. Multi-objective optimization of photochemical machining of inconel 601 using grey relational analysis. Materials Today: Proceedings, 2018, 5(2): 5591-5600. DOI:10.1016/j.matpr.2017.12.150 (  0) 0) |
| [26] |
Duran E, Duran U B, Akay D, et al. Grey relational analysis between Turkey's macroeconomic indicators and domestic savings. Grey Systems: Theory and Application, 2017, 7(1): 45-59. DOI:10.1108/GS-10-2016-0039 (  0) 0) |
| [27] |
Hafezalkotob A, Hafezalkotob A. Extended MULTIMOORA method based on Shannon entropy weight for materials selection. Journal of Industrial Engineering International, 2016, 12(1): 1-13. DOI:10.1007/s40092-015-0123-9 (  0) 0) |
| [28] |
Ghanizadeh A R, Abbaslou H, Amlashi A T, et al. Modeling of bentonite/sepiolite plastic concrete compressive strength using artificial neural network and support vector machine. Frontiers of Structural and Civil Engineering, 2019, 13(1): 215-239. DOI:10.1007/s11709-018-0489-z (  0) 0) |
| [29] |
Wang J Z, Hou R, Wang C, et al. Improved v-support vector regression model based on variable selection and brain storm optimization for stock price forecasting. Applied Soft Computing, 2016, 49: 164-178. DOI:10.1016/j.asoc.2016.07.024 (  0) 0) |
| [30] |
Akande K O, Owolabi T O, Olatunji S O, et al. A hybrid particle swarm optimization and support vector regression model for modelling permeability prediction of hydrocarbon reservoir. Journal of Petroleum Science and Engineering, 2017, 150: 43-53. DOI:10.1016/j.petrol.2016.11.033 (  0) 0) |
| [31] |
Karasuyama M, Nakano R. Optimizing SVR hyperparameters via fast cross-validation using AOSVR. 2007 International Joint Conference on Neural Networks. Piscataway: IEEE, Proceedings of the 2007.1186-1191. DOI: 10.1109/IJCNN.2007.4371126.
(  0) 0) |
| [32] |
Kanarachos S, Griffin J, Fitzpatrick M E. Efficient truss optimization using the contrast-based fruit fly optimization algorithm. Computers and Structures, 2017, 182: 137-148. DOI:10.1016/j.compstruc.2016.11.005 (  0) 0) |
| [33] |
Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/a:1008202821328 (  0) 0) |
| [34] |
Fister I, Iglesias A, Galvez A, et al. Novelty search for global optimization. Applied Mathematics and Computation, 2019, 347: 865-881. DOI:10.1016/j.amc.2018.11.052 (  0) 0) |
| [35] |
Bezerra M A, Santelli R E, Oliveira E P, et al. Response surface methodology RSM as a tool for optimization in analytical chemistry. Talanta, 2008, 76(5): 965-977. DOI:10.1016/j.talanta.2008.05.019 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


