Slinger is a mechanical atomizing device and mainly used in the combustion chamber of small and microturbine engines in virtue of simple structure and lightweight. The liquid leaves the slinger orifice in various regimes and the liquid regimes will affect the atomization performance of the slinger.
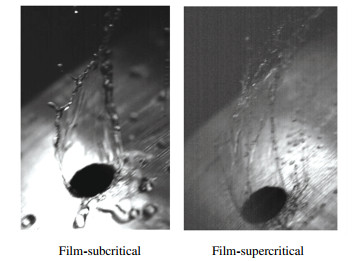
Dahm et al.[1-3] investigated the liquid breakup regimes of the slinger. The liquid leaves the orifice of the slinger in two modes: film mode and stream mode. If the liquid leaves the slinger along the circumference of the orifice and forms a film, it is termed film mode; if the liquid accumulates on the side of the orifice opposite to the slinger rotation direction when leaving, it is termed stream mode. Likewise, the breakup regime of the film mode is divided into two kinds: subcritical breakup and supercritical breakup. Subcritical breakup means the liquid leaves the orifice in the film regime and then aggregates into a liquid column under liquid surface tension. Supercritical breakup means the liquid film breaks into fragments directly by aerodynamic force when leaving the orifice. Ro is the ratio of centrifugal force to Coriolis force and is used to estimate the liquid regime when it leaves the orifice. The larger the Ro, the more likely it is to form stream mode. The breakup regime of film mode is correlated to the Weber number corresponding to the liquid film. The larger the Weber number, the more likely the liquid film performs supercritical breakup. The spray Sauter Mean Diameter (SMD) is correlated to the Weber number with a characteristic length determined by the liquid breakup regimes. The characteristic length of the film-subcritical regime is the diameter of the liquid column aggregated by the liquid film, while that of film-supercritical regime is the thickness of the film and that of the stream mode is the orifice diameter.
Besides, most of the existing research is focused on the liquid spray characteristics of the slinger.Morishita[4] studied the atomization characteristics of three slingers with different structures. He found the rotary speed of the slinger is the most important factor that affects the atomization, and presented the relationship formula between spray SMD and rotary speed. Choi et al.[5-9] investigated the spray spatial distribution and how the crossflow affected the atomization when the slinger was in a crossflow whose velocity direction is parallel to the axis of the slinger. Sescu et al.[10-13] studied the liquid regimes in the orifice of slinger by numerical simulation, and used Phase Doppler Particle Analyzer (PDPA) to measure the spray SMD at different rotary speeds. Jones[14] designed a new type of slinger that uses a swirl nozzle to replace the traditional orifice and found the atomization performance became worse. Kottala[15] performed a numerical simulation on the slinger, which is mainly focused on the primary and secondary breakup of the liquid near the orifice. Ye et al.[16] studied the liquid regimes of in and out the slinger by three-dimensional numerical simulation, and found the total liquid flowrate of the slinger varies significantly with the time and the liquid flowrates in each orifice are different in a short time. Chakraborty and Sahu[17] studied the liquid regimes in the orifice of slinger when the rotary speed is high. The results show that the Coriolis force cannot be ignored in most cases and the liquid will accumulate on the side opposite to the rotary direction when leaving the orifice. Rezayat et al.[18] studied the liquid breakup regimes of the slinger, and found when the rotary speed is up to 4000 r/min, the liquid performs subcritical breakup; when the rotary speed is more than 5000 r/min, a phenomenon of liquid jet bifurcation is observed; when the rotary speed is up to 10000 r/min, the liquid performs supercritical breakup.
Among all the research about the slinger atomization of past scholars, Werner J. A. Dahm's research is very valuable and has been cited in many papers. Though Dahm et al.[1-3] carried out a detailed and deep study on liquid breakup regimes and atomization of a slinger, the effect of the liquid surface tension on the liquid regimes is not involved, and the conclusions presented in the papers have not been verified by reliable experimental data. This paper will perform theoretical analysis and experimental research on the slinger to verify, correct, and extend Dahm's conclusions.
1 Effect of Structure TensionIf the shape of the slinger orifice is not round, such as square, slot, etc., the liquid surface tension will drive the liquid to accumulate on the corners of the orifice for their small curvature radius[1-3]. However, if the orifice is round whose curvature radius is the same everywhere, how the liquid surface tension affects the liquid regime needs to be studied.
1.1 Liquid Regime in the Orifice (Excluding Coriolis Force)In Fig. 1, R1 denotes the inner diameter of the slinger and R0 denotes the outer diameter. The orifice of the slinger is round, and d, l denote its diameter and length respectively, where l= R0-R1. ω denotes the rotary speed of the slinger. According to the research of Dahm et al.[3], the liquid will form a film in a very short distance after entering the orifice, as shown in Fig. 2, in which x, y denote the coordinate axes; R denotes the distance from the calculation point to the slinger axis; h(R) is the thickness of the liquid film that has a distance of R away from the axis, which in most cases is very small; a denotes the centrifugal acceleration, where a=ω2R.
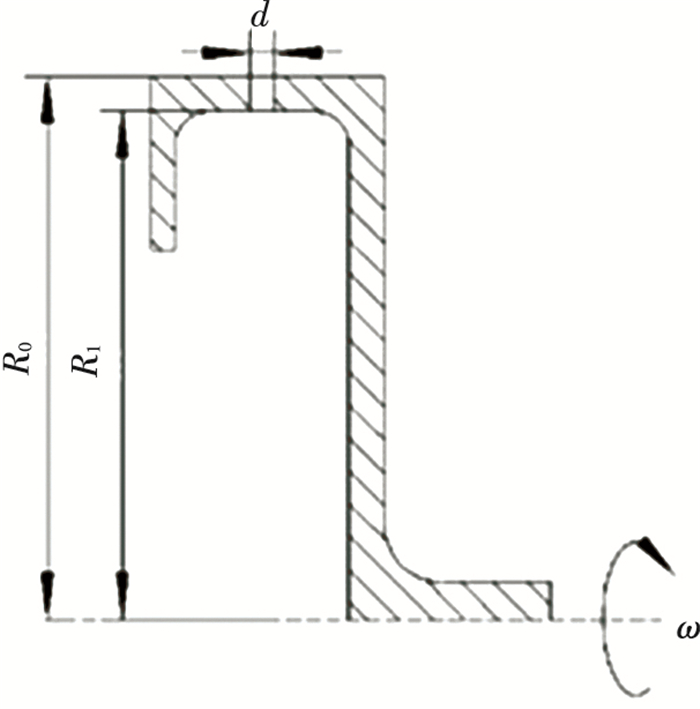
|
Fig.1 Schematic diagram of the slinger[3] |

|
Fig.2 Schematic diagram of the liquid on the inner wall of the orifice (axis in the picture denotes the slinger axis)[3] |
The Reynolds number of the liquid filmis Re=(ρLuaveh)/μL, where ρL denotes liquid density, uave denotes the average velocity of the liquid in the film in the x-axis direction, and μL denotes liquid dynamic viscosity. For h is very small and Re is usually less than 1000, the liquid can be regarded as a laminar flow. The velocity of the liquid in y-axis direction can be neglected when the liquid film becomes stabilized. Dahm et al.[3] found
| $ u(y)=-\frac{\rho_{L} \omega^{2} R}{2 \mu_{L}} y^{2}+\frac{\rho_{L} \omega^{2} R h(R)}{\mu_{L}} y $ | (1) |
where u denotes the velocity of the liquid in the x-direction, ω denotes the rotary speed of the slinger.
The overall liquid massflowrate of the slinger is M, the number of the orifices on the slinger is N, and the mass flowrate corresponding to a single orifice is m=M/N. The thickness of the film is calculated as
| $ h(R)=\left(\frac{3 \mu_{L} m}{{\rm{ \mathsf{ π} }} d \rho_{L}^{2} \omega^{2} R}\right)^{\frac{1}{3}} $ | (2) |
The R of the orifice can be regarded as constant for
Substituting Eq.(1) into Eq.(2), the following equation is obtained:
| $ u(y)=-\frac{\rho_{L} \omega^{2} R}{2 \mu_{L}} y^{2}+\left(\frac{3 \rho_{L} m \omega^{4} R^{2}}{{\rm{ \mathsf{ π} }} d \mu_{L}^{2}}\right)^{\frac{1}{3}} y $ | (3) |
The average velocity of the liquid in the x-direction is calculated by Eq.(3):
| $ u_{\text {ave }}=\left(\frac{\omega^{2} R m^{2}}{3 \mu_{L} \rho_{L} {\rm{ \mathsf{ π} }}^{2} d^{2}}\right)^{\frac{1}{3}} $ | (4) |
Assume c is the ratio of film thickness to orifice diameter, then
| $ c=\frac{2 h}{d}=\left(\frac{24 \mu_{L} m}{{\rm{ \mathsf{ π} }} d^{4} \rho_{L}^{2} \omega^{2} R}\right)^{\frac{1}{3}} $ | (5) |
Based on the practical application of the slinger in turbine engines[19], the value of the parameters in the previous formula is shown as follows:
In Table 1, σ denotes liquid surface tension, ρa denotes air density. The maximum rotary speed of the slinger ωmax is inversely proportional to the slinger radius R, where R=5 cm, ωmax=40000 r/min; or R=1 cm, ωmax=100000 r/min.
| Table 1 Parameters value |
The fuel is kerosene when the slinger practically works, but in the experiment, it is dangerous to atomize kerosene, thus water is usually used instead. The parameters of the two liquids are shown in Table 2.
| Table 2 Liquids parameters |
With reference to Table 1, Table 2, and the actual working conditions of the slinger, the thickness of the liquid film in the orifice is usually much smaller than the diameter of the orifice, and the range of c can be estimated as follows:
| $ 0.003 \leqslant c \leqslant 0.1 $ | (6) |
According to the research of Dahm et al.[1-3], after entering the orifice, the liquid will form a regime as shown in Fig. 3 in a short radial distance. Then the liquid will flow to the side of the orifice reverse to the slinger rotary direction due to Coriolis force and finally form a liquid regime as shown in Fig. 4. When the liquid regime changes from Fig. 3 to Fig. 4, the change of the surface energy is Wσ as the surface area of the liquid changes; the change of the wall adhesion work is Wsv as the area of the wall covered by the liquid changes.
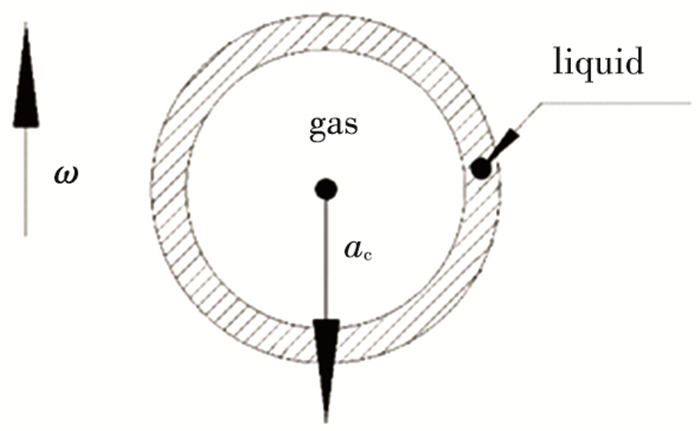
|
Fig.3 Schematic diagram of liquid lateral movement in the orifice (ω denotes rotation direction) |
The liquid area in Fig. 4 is a sector with a central angle θ, and is equivalent to the liquid area in Fig. 3.
| $ \theta-\sin \theta=2 {\rm{ \mathsf{ π} }}\left(2 c-c^{2}\right) $ | (7) |

|
Fig.4 Schematic diagram of liquid distribution in steady state under Coriolis force (ω denotes rotation direction) |
According to Eq.(6), the high-order terms in Eq.(7) can be ignored:
| $ \theta-\sin \theta \approx 4 {\rm{ \mathsf{ π} }} c $ | (8) |
Since Eq.(7) cannot be solved directly, the equation is firstly solved numerically, and then an approximate alternative solution of the equation is found by curve fitting. In the range of Eq.(6), 1000 points is equally divided, and Eq.(7) is numerically solved at each point.
Fig. 5 is the fitting curve of Eq.(7), and the fitting formula is
| $ \theta=4.608 c^{0.35} $ | (9) |
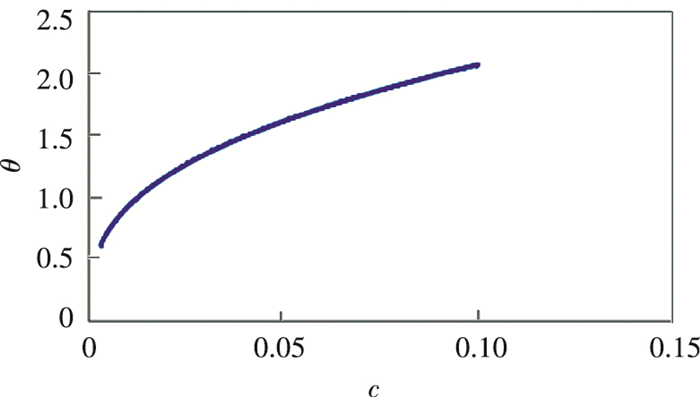
|
Fig.5 Fitting curve of Eq.(7) |
The correlation coefficient is 0.9998, thus Eq.(9) can be used to replace Eq.(7).
According to Eq.(6) and (7),
| $ 0.613 \leqslant \theta \leqslant 2.071 $ | (10) |
From Fig. 3 to Fig. 4, the change of surface energy is
| $ W_{\sigma}=2 \sigma r\left[{\rm{ \mathsf{ π} }}(1-c)-\sin \frac{\theta}{2}\right] $ | (11) |
As shown in Fig. 6, the contact angle of liquid and wall is α, where 0 < α < π. When the wall covered by liquid changes to be covered by gas, it is necessary to overcome the wall adhesion. Per unit area wall covered by liquid changes to be covered by saturated vapor, and the adhesion work is[20]
| $ W_{s v}{}^{\prime}=\sigma(1+\cos \alpha) $ | (12) |
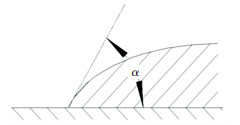
|
Fig.6 Diagram of the contact angle between liquid and wall |
As the air near the wall in the orifice can be considered as saturated vapor of the liquid, with reference to Fig. 3-4 and Eq.(12), the following equation is obtained:
| $ W_{s v}=\sigma r(1+\cos \alpha)(2 {\rm{ \mathsf{ π} }}-\theta) $ | (13) |
where Wσ is positive work, Wsv is negative work, and the total work of the surface tension σ is
| $ W=\sigma d\left[{\rm{ \mathsf{ π} }}(1-c)-\sin \frac{\theta}{2}\right]-\frac{\sigma d}{2}(1+\cos \alpha)(2 {\rm{ \mathsf{ π} }}-\theta) $ | (14) |
Differentiating Eq.(14) by σ, the following equation is obtained:
| $ \frac{\partial W}{\partial \sigma}=r\left(\left(r \theta-2 \sin \frac{\theta}{2}\right)-2 {\rm{ \mathsf{ π} }}(\cos \alpha+c)+\theta \cos \alpha\right) $ | (15) |
Perform Taylor series expansionon sinθ, then
| $ \sin \theta=\theta-\frac{1}{3 !} \theta^{3}+\frac{1}{5 !} \theta^{5}+o\left(\theta^{5}\right) $ | (16) |
In Eq.(16), the larger the θ, the larger the o(θ5). Combine them with Eq.(10), then
| $ \frac{o\left(\theta^{5}\right)}{\sin \theta} \leqslant 0.035 $ | (17) |
Therefore, the 5th-order Taylor series can be used to replace sinθ. Substituting Eq.(16) into Eq.(8), the following equation is obtained:
| $ \frac{1}{6} \theta^{3}-\frac{1}{120} \theta^{5} \approx 4 {\rm{ \mathsf{ π} }} c $ | (18) |
Substituting sin(θ/2) into Eq.(15) with a 5th-order Taylor series and referring to Eq.(18), Eq.(19) is obtained:
| $ \frac{\partial W}{\partial \sigma}=-r\left(\left({\rm{ \mathsf{ π} }} c-\frac{1}{640} \theta^{5}\right)+(2 {\rm{ \mathsf{ π} }}-\theta) \cos \alpha\right) $ | (19) |
By reference to Eq.(6), (8), (9), and (10) and numerical calculation, the following inequality is obtained:
| $ {\rm{ \mathsf{ π} }} c-\frac{1}{640} \theta^{5}>0 $ | (20) |
The larger the c, the larger the
When α≤90°, which is equivalent to cos α≥0, it is obvious ∂W/∂σ < 0. In this case, as the surface tension increases, the liquid in the orifice becomes more difficult to accumulate on one side of the orifice.
When α>90°, which is equivalent to cos α < 0, if ∂W/∂σ>0,
| $ \cos \alpha<\frac{{\rm{ \mathsf{ π} }} c-\frac{1}{640} \theta^{5}}{\theta-2 {\rm{ \mathsf{ π} }}} $ | (21) |
cosα will reach the maximum as c reaches its maximum. Combine it with Eq.(6) and (10), the following is obtained:
| $ \cos \alpha<-0.06 $ | (22) |
When α>93.5°, ∂W/∂σ>0. In this case, as the surface tension increases, it becomes easier for the liquid in the orifice to accumulate on one side of the orifice.
In summary, there is a critical angle α0, where
| $ \cos \alpha_{0}=\frac{{\rm{ \mathsf{ π} }} c-\frac{1}{640} \theta^{5}}{\theta-2 {\rm{ \mathsf{ π} }}}>90^{\circ} $ | (23) |
If α < α0, the surface tension of the liquid inhibits the liquid from accumulating on one side of the orifice, and the smaller the α, the greater the effect of surface tension. If α=α0, liquid surface tension exerts no effect on liquid aggregation. If α>α0, the surface tension will promote the liquid to accumulate on one side of the orifice, and the larger the α, the greater the effect of surface tension. With reference to Eqs.(2), (9), and (23), it is found that the value of α0 is related to c, and the larger the c, the larger the α0, which means increases in liquid flowrate or decreases in diameter of the orifice or rotary speed will extend the range of the contact angle in which the surface tension will inhibit the liquid lateral movement in the orifice.
2 Experimental Investigation 2.1 Test ApparatusAs shown in Fig. 7, the test slinger is driven by a motor mounted on a bracket and controlled by a frequency regulator. The rotary speed of the motor was in the range of 0-24000 r/min, and the minimum adjustment unit was 6 r/min. A transparent shield surrounded the test slinger to collect and return the liquid into the liquid tank. The liquid in the tank was driven by a pump, and sequentially passed through filter, pump, valve, mass flowmeter, and inlet pipe, then hit on the wall of the test slinger, which was thrown out and started a new cycle. A fine-turning valve was used to adjust the liquid flowrate precisely. The measuring range of the mass flowmeter was 0-40 g/s and the minimum measurement unit corresponded to 0.1 g/s. A high-speed camera was used to capture the liquid regime and the maximum capture frequency was 2500 fps. The spray SMD was measured by a PDPA. The measurement error of PDPA was related to the types of measured particles when liquid spray was being measured, and the relative error of particle size measurement was 0.5%[21], which is too little to be shown in the chart of this paper.

|
Fig.7 Diagram of test apparatus |
The structure of the test slinger is shown in Fig. 1. There was only one orifice on the slinger to prevent mutual interference between the liquids from plurality orifices. The parameters of the test slinger are shown in Table 3.
| Table 3 Parameter of test slinger(mm) |
2.2 Liquid Regime in Orifice
Fig. 8 is the pictures of the liquid regimes in the orifice. Besides film mode (Ⅱ) and stream mode (Ⅲ) found by Dahm et al.[3], the liquid may fill the orifice if the rotary speed is low or the liquid flowrate is large, which is termed full mode (Ⅰ).

|
Fig.8 Liquid regimes in the orifice (rotary direction is anticlockwise) |
Fig. 9 is the breakup mode of liquid film. As shown in Fig. 8 and Fig. 9, different liquid regimes can be distinguished clearly except a few middle states. In the experiment, multiple pictures were taken for the liquid regime at every state in order to eliminate manual errors.
|
Fig.9 Liquid regimes in the orifice |
Ro is the ratio of centrifugal force to Coriolis force on the liquid in the orifice:
| $ R_{\mathrm{o}}=R \omega / u_{\text {ave }} $ | (24) |
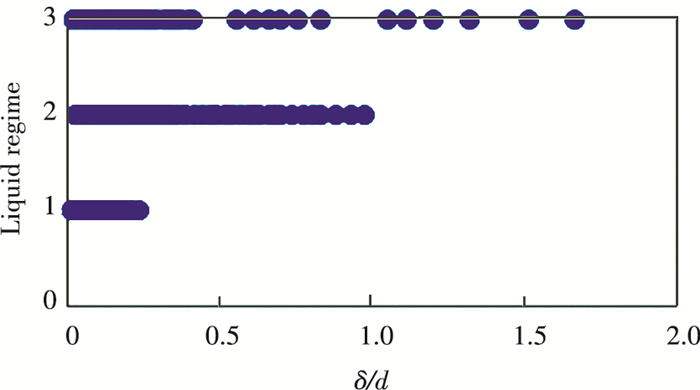
δ is the liquid lateral displacement driven by Coriolis force when the liquid is entering or leaving the orifice. Dahm believe δ/d can be used to estimate whether the liquid regime is film mode or stream mode.
| $ \delta / d \approx 0.5(l / d)(l / R) R_{\mathrm{o}} $ | (25) |
The lager the δ/d, the more likely the liquid performs stream mode. Conversely, the smaller the δ/d, the more likely it performs film mode[3].
Fig. 10 is the relationship between liquid regimes and δ/d. Theoretically, δ≤d, if δ/d>1, the liquid regime must be stream mode. When δ/d < 0.24, the three liquid regimes all appear. In full mode, the orifice is filled with the liquid, indicating it is reasonable that δ/d is small. But neither the appearance of the stream mode when δ/d is small nor the existence of the film mode when δ/d is close to 1 can be explained by the theory of Dahm et al.[3].
|
Fig.10 Relationship between liquid regimes and δ/d (On the ordinate, 1 denotes full mode, 2 denotes film mode, 3 denotes stream mode) |
The effects of liquid viscosity and surface tension were not considered in Eq.(25). During the transition from Fig. 3 to Fig. 4, the liquid viscosity prevents the liquid from flowing to one side of the orifice to form stream mode. The liquid surface tension will inhibit the liquid lateral flow if the contact angle α < 90°. In most cases, the contact angle between the liquid and the slinger is smaller than 90°, therefore under the combined effect of liquid viscosity and surface tension, the liquid can keep the film mode even when δ/d is close to 1.
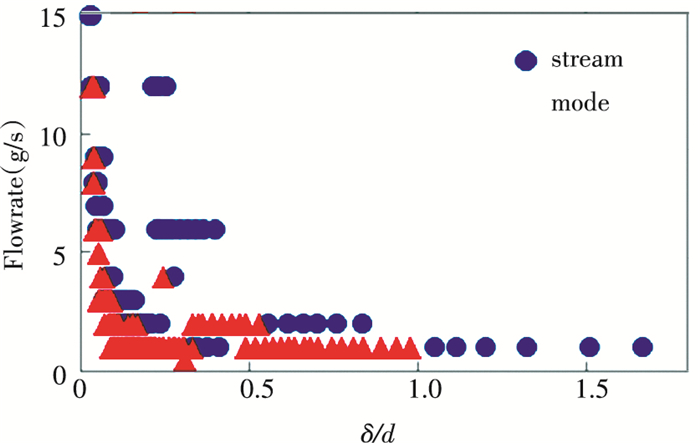
Fig. 11 is the relationship between m and δ/d of stream mode and film mode. When the liquid performs stream mode, the larger the m, the smaller the δ/d when the stream mode first appears. Once the stream mode appears, increases in rotary speed will not change the liquid regime, and if m > 12 g/s, increases in δ/d will not change the liquid regime either. In the same orifice, δ/d corresponding to stream mode is larger than that of film mode, and once the liquid regime changes from film mode to stream mode, the liquid regime will keep stream mode with increases in δ/d. When m < 6 g/s, film mode and stream mode appear alternatively with increases in δ/d, which means the δ/d corresponding to film mode and stream mode are different in different orifices, and δ/d cannot be used to estimate the liquid regime in various orifices.
|
Fig.11 Liquid regimes verses m and δ/d |
The film mode appears onlywhen m≤12 g/s. If m > 12 g/s, film mode disappears and only full mode or stream mode occurs. When δ/d is small, the liquid regime performs full mode; as δ/d increases, the liquid regime switches from full mode to stream mode directly without going through film mode, even when δ/d is very small.
Besides, it is found the liquid regime will change from film mode to stream mode suddenly under certain conditions, as shown in Fig. 12. The rotary speed only increases by 60 r/min, and the liquid regime switches from film mode to stream mode without any intermediate state.

|
Fig.12 Change from film mode to stream mode without transition state (d =3 mm, m =3 g/s, the rotary direction is anticlockwise) |
For the phenomena above cannot be explained by the theories of Dahm et al.[2-3], two hypotheses are presented to provide a reasonable explanation.
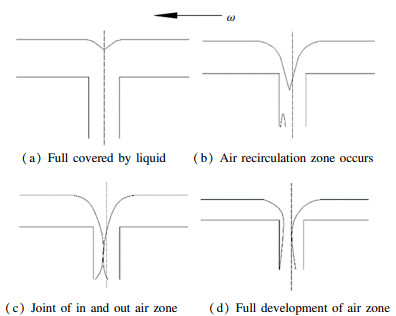
2.2.1 Drain Pool HypothesisWhen the liquid flowrate entering the orifice is greater than the maximum flowrate at which the orifice can pass through, a liquid film will be formed in the slinger and cover the entrance of the orifice, as shown in picture (a) of Fig. 13. The process of the liquid passing through the orifice can be regarded as a drained pool.
|
Fig.13 Schematic diagram of the drain pool hypothesis (ω denotes rotation direction) |
The liquid in the orifice will be accelerated by centrifugal force. According to the conservation of mass, an air recirculation zone may form at the exit of the orifice.Besides centrifugal force, the liquid in the orifice is also affected by the Coriolis force. Fig. 14 is the liquid radial speed distribution at the exit of the orifice calculated by numerical simulation. A cylinder zone with a diameter of 1 mm and a height of 3 mm is created to simulate the fluid zone of the orifice, the boundary condition of the inlet is mass flow inlet and the mass flowrate is 4 g/s. The boundary condition of outlet is pressure outlet and the relative pressure is 0. The fluid zone rotates around the axis of the slinger, and the rotary speed equals the rotary speed of slinger. The turbulent mode is k-ε, the mesh number is 0.1 million, and the calculation state is steady.
|
Fig.14 Liquid radial speed distribution at the exit of the orifice (m =4 g/s, ω denotes rotation direction) |
According to the results, it is found that the liquid part with low velocity is concentrated on the same side as the rotation direction, where the air is most likely to return and form an air recirculation zone.At the same time, a vortex appears on the liquid film surface inner the slinger, as shown in picture (b) of Fig. 13. As the rotary speed increases, the vortex and the air recirculation zone become larger and larger, and are eventually connected, as shown in picture (c)-(d) of Fig. 13.
The liquid regimes corresponding to each figure of Fig. 13 is as follows: full mode corresponds to picture (a), stream mode corresponds to others, and as the rotary speed increases, the liquid accumulation of stream mode is increasing. The above information provides a reasonable explanation for the phenomenon that the liquid regime changes from full mode to stream mode directly, and even when δ/d is very small, stream mode can also be formed.
2.2.2 Tangential Relative Slip HypothesisThe rotary speed of the liquid in the cavity of the slinger is not exactly equivalent to the slinger rotary speed. There is a tangential relative slip between the liquid and the wall of the slinger. Assume k is the tangential slip ratio, where
| $ k=\left(V_{\theta}-v_{\theta}\right) / V_{\theta}=\left(\omega R-v_{\theta}\right) / \omega R $ | (26) |
where Vθ denotes the tangential velocity of the slinger and vθ denotes the tangential velocity of the liquid. The research of Ahmed suggests that the tangential relative slip ratio between the liquid and the rotary atomizer is about 18%-40%[22].
When the tangential relative slip velocity between the liquid and the wall in the slinger is low, the liquid flows closely on the wall of the orifice after entering the orifice under the combined effect of Coanda effect, surface tension, viscous and centrifugal force, and forms the liquid regime as shown in Fig. 3 within a short radial distance. However, when the tangential relative slip velocity reaches a certain level, the liquid will enter the orifice in the form of a parabola, as shown in Fig. 15. Then the liquid hits on the side of the orifice opposite to the slinger rotation direction, therefore the liquid regime outside the orifice will change from film mode to stream mode suddenly.
|
Fig.15 Schematic diagram of liquid regime entering the orifice (the thick line indicates the liquid, the thin line indicates the wall, ω denotes rotation direction) |
2.3 Subcritical and Supercritical Breakup
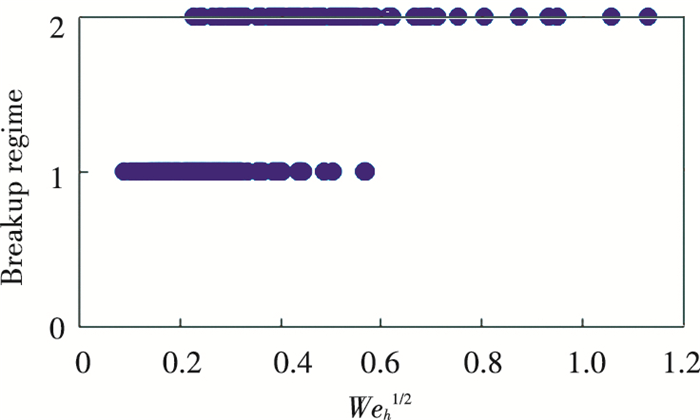
Dahm et al.[1-3] considered the breakup regimes of film mode are related to Weber number corresponding to the film, and the decision parameter is T, where
| $ T \sim \sqrt{\rho_{G} u_{c}^{2} h / \sigma}=W e_{h}^{\frac{1}{2}} $ | (27) |
where uc denotes the tangential velocity at the edge of the slinger. The smaller the T, the more likely the film performs subcritical breakup; the larger the T, the more likely the liquid performs supercritical breakup.
From Fig. 16, it is found when
|
Fig.16 Relationship between breakup regime and Weber number (On the ordinate, 1 denotes subcritical, 2 denotes supercritical) |
2.4 Spray SMD
Oht denotes Ohnesorge number, and Wet denotes Weber number, where
| $ O h_{t}=\mu_{L} / \sqrt{\rho_{L} \sigma t} $ | (28) |
| $ W e_{t}=\rho_{G} u_{c}^{2} t / \sigma $ | (29) |
where t denotes characteristic length and is related to the liquid breakup regime. According to the research of Dahm et al.[3], when the liquid performs film-supercritical breakup, t=h; when the liquid performs film-subcritical breakup, t=d', and d' denotes the diameter of the liquid column aggregated by the liquid film, where
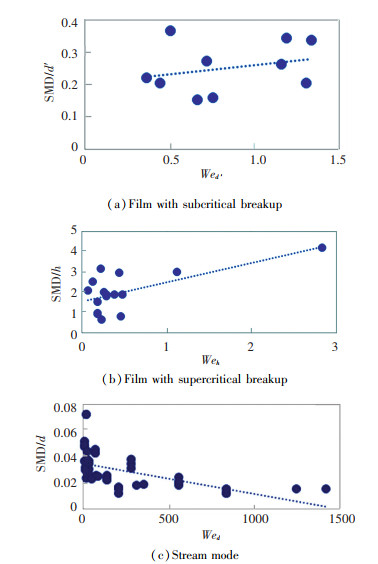
Dahm et al. analyzed the experimental data from the perspective of Morishita's research[3-4]. The results show that the correlation coefficient of SMD/d~Wed or SMD/d'~Wed' is 0.81, and one of SMD/h~Weh is only 0.46. This indicates the liquid performs film-subcritical breakup or stream mode in Morishita ' s experiment, and film-supercritical breakup hardly appears. But the theoretical results of the research of Dahm et al.[1-3] indicate the liquid in Morishita ' s experiment mainly performs film-supercritical breakup. He considered the data of spray SMD was inaccurate because the samples of the spray were collected on a silicon oil film on a glass plate and then were photographed to measure the size of the droplets[4]. The method cannot get the spray SMD accurately. However, according to the research in Section 2.2 of this paper, the liquid in Morishita ' s experiment performed stream mode in most cases, and the conclusion of Dahm ' s research on the liquid regimes about Morishita ' s experiment is right.
Fig. 17 is the correlation between spray SMD and Weber numbers corresponding to various liquid breakup regimes based on the experimental data in this paper. The correlation coefficient of film-subcritical is 0.081, film-supercritical is 0.434, stream mode is 0.323, all of which show a bad correspondence between spray SMD and Weber number. The liquid breakup regime only affects the primary breakup of the liquid, and in the process of the secondary breakup, a lot of tiny droplets are produced when the large droplets are split into small droplets by aerodynamics force, and little correlation exists between these tiny droplets and the liquid breakup regimes. These tiny droplets make the correlation between the spray SMD and liquid breakup regime worse, therefore the correlation coefficients are poor in Fig. 17.
|
Fig.17 Correlation between spray SMD and Wet corresponding to various liquid breakup regimes |
The measurement method of Morishita ignored the tiny droplets[4]. The spray SMD measured by PDPA in this paper is smaller than Morishita's under the same operating condition. The size of bigger droplets in the spray is affected by the primary breakup, that is affected by liquid breakup regimes. Morishita summed up the spray SMD by measuring the size of bigger droplets, therefore the spray SMD coincidentally shows good correlation to the Weber number corresponding to stream mode.
Though the liquid breakup regime only affects the primary breakup, the spray SMD is affected by Weber number. Fig. 18 shows the fitting curve between spray SMD and Weh, where
| $ \mathrm{SMD}=64.5 W e_{h}^{-0.304} $ |

|
Fig.18 Correlation between spray SMD and Weh of slinger |
The correlation coefficient is 0.897. Compared with Wed and Wed', the correlation coefficient of Eq.(30) is the largest, which indicates the characteristic length of the liquid corresponds to the thickness of the film calculated by Eq.(2) in most cases.
The liquid breakup regime in the experiment of this paper is mainly stream mode. Fig. 19 shows two common breakup regimes of stream mode. In Fig. 19(a), although the liquid has accumulated on one side of the orifice, it re-opens into a liquid film under the action of air after leaving the orifice and then performs primary breakup. In Fig. 19(b), the tangential speed of the liquid is very high, and the liquid stream will be torn into lots of fragments violently by aerodynamic force after leaving the orifice. The characteristic lengths of both breakup regimes are close to h, therefore the correlation between spray SMD and Weh is the best.
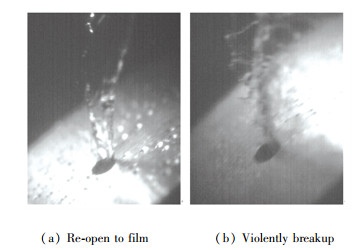
|
Fig.19 Breakup regimes of steam mode (rotary direction is anticlockwise) |
3 Conclusions
A theoretical analysis was performed on slinger, which shows the liquid surface tension and the contact angle α between liquid and slinger wall play an important role in liquid regimes. If the orifice is round whose curvature radius is the same everywhere, there is a critical angle α0>90°; if α < α0, the liquid surface tension will inhibit the liquid from flowing to one side of the orifice driven by Coriolis force; if α>α0, the liquid surface tension will promote the liquid to flow to the side.
Three liquid regimes appeared in the orifice: full mode, film mode, and stream mode, and δ/d could not be used to estimate the liquid regime accurately. The reason may be that when liquid flowrate is large enough, the process of the liquid passing through the orifice is just like a drained pool, the air outside the orifice returns from the same side of the orifice as the rotation direction, and the liquid regime changes from full mode to stream mode directly. If the flowrate is low, a tangential relative slip exists between the liquid and the wall in the slinger. When the slip velocity is large enough, the liquid may enter the orifice in a parabola form, and the liquid regime outside the orifice changes from film mode to stream mode within a little increase in rotary speed.
When the decision parameter
The liquid breakup regimes could affect the primary breakup of the liquid, but a lot of tiny droplets were produced in the secondary breakup with little correlation to the liquid breakup regime. Therefore, the correlation between SMD/t and Wet was poor.
On the whole, the spray SMD has a power relationship with Weh, and the correlation coefficient is close to 0.9.
| [1] |
Dahm W J A, Patel P R, Lerg B H. Experimental visualizations of liquid breakup regimes in fuel slinger atomization. Atomization and Sprays, 2006, 16(8): 933-944. DOI:10.1615/AtomizSpr.v16.i8.50 (  0) 0) |
| [2] |
Dahm W J A, Patel P R, Lerg B H. Fundamental analysis of liquid atomization by fuel slingers in small gas turbines. Proceedings of the 32nd AIAA Fluid Dynamics Conference and Exhibit. Reston, VA: AIAA, 2002. AIAA 2002-3138. DOI: 10.2514/6.2002-3183.
(  0) 0) |
| [3] |
Dahm W J A, Patel P R, Lerg B H. Analysis of liquid breakup regimes in fuel slinger atomization. Atomization and Sprays, 2006, 16(8): 945-962. DOI:10.1615/AtomizSpr.v16.i8.60 (  0) 0) |
| [4] |
Morishita T. A development of the fuel atomizing device utilizing high rotational speed. ASME 1981 International Gas Turbine Conference and Products Show. New York: ASME, 1980. 1-6. DOI: 10.1115/81-GT-180.
(  0) 0) |
| [5] |
Choi S M, Jang S H. Spray behavior of the rotary atomizer with in-line injection orifices. Atomization and Sprays, 2010, 20(10): 863-875. DOI:10.1615/AtomizSpr.v20.i10.30 (  0) 0) |
| [6] |
Choi S M, Jang S H, Lee D H, et al. Spray characteristics of the rotating fuel injection system of a micro-jet engine. Journal of Mechanical Science and Technology, 2010, 24(2): 551-558. DOI:10.1007/s12206-009-1206-6 (  0) 0) |
| [7] |
Lee J, Choi Y, Yoonet S, et al. Spray characteristics of an air-driven rotary atomizer with a double-layer cup for use in an industrial oil burner. Atomization and Sprays, 2010, 20(7): 639-652. DOI:10.1615/AtomizSpr.v20.i7.50 (  0) 0) |
| [8] |
Jang S H, Choi S M. Atomization characteristics of the high speed rotating injection system with single column orifice. Journal of ILASS-Korea, 2009, 14(3): 97-102. (  0) 0) |
| [9] |
Choi H, Lee D, Youet G, et al. Spray characteristics of the rotary atomizer for the slinger combustor. Journal of ILASS-Korea, 2008, 13(3): 149-155. (  0) 0) |
| [10] |
Sescu C, Kucinschi B R, Afjeh A A, et al. Experimental test rig with results on liquid atomization by slinger injectors. Journal of Engineering for Gas Turbines and Power, 2011, 133(11): 114505. DOI:10.1115/1.4003790 (  0) 0) |
| [11] |
Sescu C, Kucinschi B R, Sescu A. Computational analysis of a slinger atomizer. Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston, VA: AIAA, 2010. AIAA 2010-6581. DOI: 10.2514/6.2010-6581.
(  0) 0) |
| [12] |
Sescu C, Kucinschi B, Masiulaniec K, et al. Experimental test rig with results on atomization by slinger injectors. Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston, VA: AIAA, 2012. AIAA 2008-4771. DOI: doi:10.2514/6.2008-4771.
(  0) 0) |
| [13] |
Sescu C, Kucinschi B, Afjeh A, et al. Parametric study of liquid atomization by slinger injectors. Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston, VA: AIAA, 2009. AIAA 2009-4829. DOI: 10.2514/6.2009-4829.
(  0) 0) |
| [14] |
Jones N S. A Parametric Study of Micro Atomizing Nozzles on a Rotary Fuel Slinger. Toledo: University of Toledo, 2014.
(  0) 0) |
| [15] |
Kottala S. Numerical Simulation of Slinger Atomization and Comparison with Other Investigator's Experimental Results. Toledo: The University of Toledo, 2011.
(  0) 0) |
| [16] |
Ye Y L, Jin J, Liu R, et al. Non-uniform flow characteristics of direct-connected fuel slinger. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(8): 1560-1568. DOI:10.13700/j.bh.1001-5965.2018.0693 (  0) 0) |
| [17] |
Chakraborty A, Sahu S. Liquid Atomization in a High-Speed Slinger Atomizer. Proceedings of the ASME 2019 Gas Turbine India Conference GTINDIA2019. New York: ASME, 2019. 1-10. DOI: 10.1115/GTINDIA2019-2616.
(  0) 0) |
| [18] |
Rezayat S, Farshchi M, Karimi H, et al. Spray characterization of a slinger injector using a high-speed imaging technique. Journal of Propulsion and Power, 2018, 34(2): 469-481. DOI:10.2514/1.B36498 (  0) 0) |
| [19] |
Domnick J, Thieme M. Atomization characteristics of high-speed rotary bell atomizers. Atomization and Sprays, 2006, 16(8): 857-874. DOI:10.1615/AtomizSpr.v16.i8.10 (  0) 0) |
| [20] |
Guo L J. Dynamics of Two-Phase and Mutiphase Flow. Xi'an: Xi'an Jiaotong University Press, 2002: 144-145.
(  0) 0) |
| [21] |
Jia W D, Li P P, Qiu B J, et al. Application of PDPA in the experimental study of atomization characteristics of nozzles. China Rural Water Conservancy and Hydropower, 2008(09): 70-72. (in Chinese) (  0) 0) |
| [22] |
Ahmed M, Youssef M S. Influence of spinning cup and disk atomizer configurations on droplet size and velocity characteristics. Chemical Engineering Science, 2014, 107: 149-157. DOI:10.1016/j.ces.2013.12.004 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


