2. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
China holds the biggest coal yield in the world, while the coal quality varies significantly. Low quality coal is regarded as containing more impurities and these useless organic or inorganic matters influence the forming process of ash and cinder during combustion. The ash content of the normal coal usually reaches 20%-30% while that of the low-quality coal reaches more than 40%[1]. Unburned coal and ash with flue gas flow along heating surfaces, some of which would stick on surfaces and form deposition[2].
Impacting of ash particles sometimes results in severe erosion of re-heater and super-heater, even crack of the tube wall. Fly-ash deposition always influences flow pattern of the gas and causes more resistance, then the thermal efficiency of the whole boiler would decline definitely[3].
The fly-ash deposition in coal-fired boilers has been studied over the years. Recently, more and more scholars start to study fly-ash deposition phenomenon with development of numerical technique, namely CFD technique. The chemical composition, temperature, diameter and shape of particles, impacting surface, turbulent diffusion and characteristics of different geometry of impacting surfaces are main factors which cause important influence on deposited phenomenon. Three aspects, namely trajectory of particle, deposition equation and growth of deposition layer are key processes which are usually considered in the simulation of the fly-ash deposition.
Venturini et al.[4] proposed a cloud model to show the influence of turbulent diffusion to trajectory of particles. This model calculates the complete trajectory of particle and precisely shows movement behavior of particles before they deposit on the surface compared with the usual used model: the DRW model. However, more internal memory of computer and time-consumption limit its expanded usage. Weber et al.[5] focused on relative error, boundary and turbulent diffusion to get a precise result.
Walsh et al.[6] developed a kind of criterion to judge deposition, namely the critical viscosity model which is easy to operate and already broadly used in depositing and slagging phenomenon in pulverized coal furnace and heat exchanger of gasifier[7]. Nevertheless, several parameters which imply complexity of chemical composition and importance in precisely calculating results of viscosity of coal ash are not considered in critical viscosity model. Recently, some scholars revised the original critical viscosity to predict the deposition phenomenon.
Sreedharan and Tafti[8] considered the deposition phenomenon of softened particles with modified critical viscosity model. The high-temperature condition was chosen in the numerical process and final results were validated by experimental data. Losurdo et al.[9], based on JKR theory, set up a kind of inertial collision model for visco-elastic particles to study deposition phenomenon. Mueller et al.[10] combined transportation of particles and thermochemical theory to simulate deposition phenomenon of melted ash which contains much alkali metal. Ai and Kuhlman[11] established relationship between temperature of coal ash and Young modulus of ash particles based on experimental data, and adopted original critical viscosity model to simulate deposition behavior of coal ash in high temperature. Fan et al.[12] simulated the sintering process of fly-ash with numerical method. He used viscosity model of Walsh to calculate sticking efficiency of imputing fly-ash particles, and adopted thermal conductive model of Richards to calculate the deposition-layer thermal problem. Random-walk model is here for particle's tracking. Finally, Fan et al.[12] described the deposition height, deposition mass and deposition porosity in his paper. However, his results were not verified with experimental data, so the rationality of the model is unknown.
As for low-temperature environment, critical viscosity model is no more suitable for simulating deposition. However, another kind of deposition model was developed based on force analysis, namely the inertial collision deposition model. Pan et al.[13] regarded deposited ash as a kind of special prose style free from parallelism, based on dynamics model of prose style free from parallelism, to set up a new kind of mechanism of inertial collision model. Abd-Elhady[14] simulated impacting process of particles hitting on deposition layer, and calculated critical impacting velocity.
Geometry of deposition layer is another key point.Richards et al.[15] promoted a modified deposition model to describe sticking and growing behavior of particles, which adopts impacting efficiency and fly-ash diameter and composition distribution to predict particles-deposit growing. This model not only defines the discipline of the deposition for single particle, but also determined the thermal conductivity, surface emissivity and phase composition of the deposition. Results of this model fit those of the experiment well. Wacławiak and Kalisz[16] simulated unsteady deposition of fly-ash in boiler with Fluent and extra User Defined Function code. Process of deposition was mirrored by dynamic mesh technique of Fluent. Average diameter, velocity and impact angle were considered in UDF code. Finally, simulated results were compared with experimental results and fit each other well. Pérez et al.[17] also used Fluent to simulate deposition process, and the transversal spacing of the tube bundle was varied in his research. However, the validated experiment data is absent.
Huang et al.[18] and Zhao et al.[19] described their model of sticking of ash particles, forming deposits in pulverized coal combustion. They experimentally studied the phenomenon in a 25 kW down-fired rig. In Ref. [18], the authors linked theoretical studies of velocity profiles, namely velocity magnitudes and impaction angles, around a bare tube with observed deposit shapes. This way they correlated the general equation using Stokes number with the deposit heights, incorporated a correcting parameter. Their later research[19] continued the previous discussion and fully described the deposit forming model. They used a 3D adhesive discrete model (DEM), which correlates deposit flux with kinetics parameters of the ash particles and focuses on structure of the deposit in detail. However, this complex model relies on mechanical properties of ash particles, as the authors use Young modules and Poisson's ratio of the particles, and its surface energy[18-19]. Although the assumed parameters may be questionable as obtained in laboratory studies, where different Reynolds numbers are present, and for a single tube arrangement, this model uses a sophisticated and modern tool to predict the deposit formation.
Deposition process has been studied for a long time, but accurate validation of growing geometry of deposition between experiment and simulation, distribution characteristics of deposited particles are not detailedly studied in recent years. To further understand those two main subjects, a preliminary study on a drop tube furnace is necessary and it will facilitate investigation on industrial facilities. In detail, the influence of various forces and velocities will be investigated through dynamic mesh technique modelling in this work.
1 Experimental SetupAsh deposition experimental system is shown in Fig. 1, which is well equipped to control the particle concentration, the temperature, the velocity and the composition of the flue gas. The whole system is constituted of heating furnace, air distribution section, feeding section, deposition-ash sampling probe, image catching section and fume exhaust section.
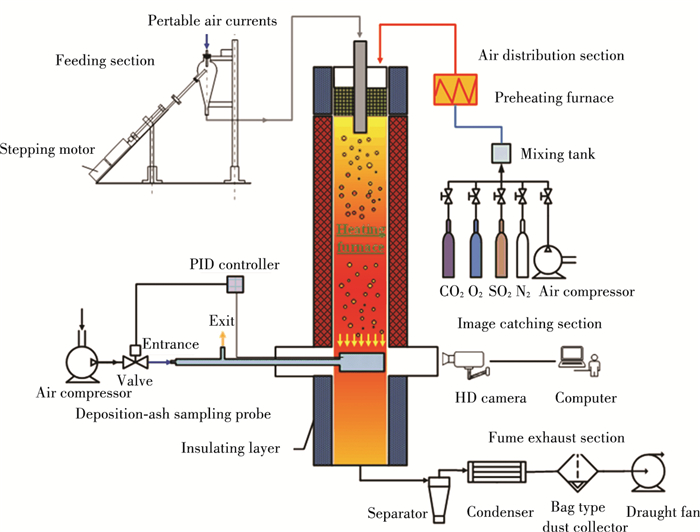
|
Fig.1 System diagram of hot test setup for flying ash deposition and schematic diagram of depositing ash sampling probe |
The patented deposition-ash sampling probe utilized in the data processing is shown in Fig. 2. When the sampling probe is inserted horizontally into the high-temperature gas, the section controls its surface temperature the same as the setting level all the time. Air compressor sends cold air to the probe through an inlet of the drive pipe, and an outlet-air of the drive pipe is controlled by a valve controller. The changing rate of flow of cold air is used to control the temperature on the surface of the probe. It is possible to obtain up to ±5 ℃ temperature variation when the design temperature is 550 ℃ as shown in Fig. 3. The periodic fluctuation of the temperature in Fig. 3 is due to the control algorithm of the surface temperature of the probe. The internal control algorithm of the flow rate of the cold air is based on PID algorithm, which generates overshoot and oscillation.
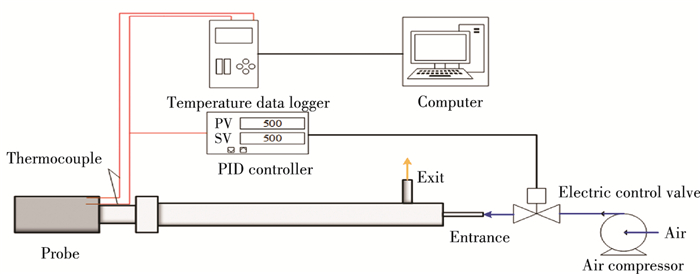
|
Fig.2 Patented deposition ash sampling probe |

|
Fig.3 Curve of varying temperature of ash deposit sampling probe |
Image catching section is shown in Fig. 4. The whole deposition process will be collected as video by an AONI camera in front of the observation window. The AONI A3000 auto-focus micro-shot camera has 1.2 million pixels for a precise video collection. The final video file will be converted to images at different time by the Image-Pro Plus6.0 software.
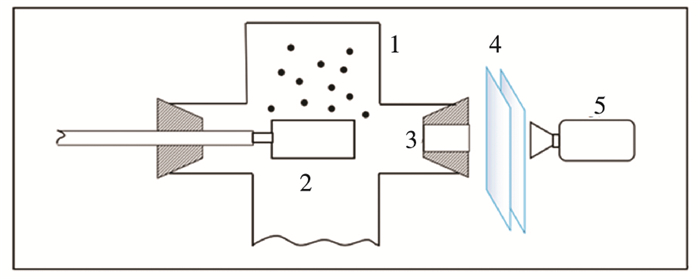
|
1.Quartz tube furnace 2. Ash deposition probe 3. Window 4. Quartz glass slice 5. Camera Fig.4 Schematic diagram of image collection on ash deposition online |
The whole experimental procedure includes: 1) collecting ash from the bag filter from a 135 MW lignite-fired fluidized bed boiler; 2)burning out the ash in a Muffle-furnace at 850 ℃ in atmosphere for 4 h to guarantee its components constant; 3) sieving the ash and measure its size distribution using Malvern laser particle size analyzer; 4) pouring the ash into the micro-feeder above the drop tube furnace; 5) setting the furnace temperature as 850 ℃ and the probe temperature as 550 ℃, then start the feeder; 6) recording the ash deposition growth along with time. The coal ash comes from the Jin-Cheng anthracite, the range of diameters is between 0 and 2.36 mm. Details of the distribution of particle diameter is shown in Fig. 5. The vertical axis represents the mass fraction, and the horizontal axis means the particle diameter.

|
Fig.5 Diameter distribution of the ash |
The ultimate and proximate analysis of the coal sample, and chemical compositions analysis of coal ash can be found in Tables 1 and 2, respectively.
| Table 1 Ultimate and proximate analysis of the coal sample |
| Table 2 Chemical-compositions analysis of ash sample from original coal sample |
The post-process under different time is shown in Fig. 6. The total length between the deposition peak and its corresponding farthest point on the edge of the tube has been recorded, and the deposition height is calculated by subtracting the diameter from the total length. This measurement method is also utilized in the simulation result.

|
Fig.6 Post-processing of the images on ash deposit when velocity of inlet-2 equals to 2.05 m/s |
In this paper, the physical properties like diameter have been considered in the deposition model based on the assumption of force analysis of the single particle. The simulation results show reasonable distribution of the ash deposition compared with experimental data. The chemical properties of the ash particles have been analyzed but not included into the deposition model. The geometry and final height of the ash deposition obtained through the processed images are also shown in Fig. 6.
2 Modeling Process 2.1 Deposition ModelWacławiak and Kalisz[16] set up a deposition criterion based on the normal elastic bounce force Fs, n, Van der Waals' force Fvw and gravity FG, the criterion is shown as Eq.(1):
| $ \boldsymbol{F}_{\mathrm{s}, \mathrm{n}} <\left(\boldsymbol{F}_{\mathrm{vw}}+\boldsymbol{F}_{G}\right) $ | (1) |
The ash particles will deposit on the surface when Fs, n is less than the sum of Fvw and FG. Meanwhile, Fs, n can be expressed as Eq.(2). Such equation is based on experiments and presented in previous research[20-21].
| $ \boldsymbol{F}_{\mathrm{s}, \mathrm{n}}=K d_{\mathrm{p}}^{2} w_{\mathrm{p}}^{1.2} $ | (2) |
K is proportional constant and its unit is kg/(m2.2s0.8); wp represents normal velocity of the particel and its unit is m/s; dp is particle diameter and its unit is m.
The coefficients and exponents are found by trail-and-error method. Eq.(2) represents the normal elastic bounce force. The assumption is taken when the particle is hitting on the surface in normal direction. Regarding the parameter, normal velocity of the particle is considered, which means the angle of repose of the ash deposition would influence the normal direction of the particle as the formation of the ash deposition changes during the simulation. In other words, the change of the angle of repose of the ash particles is considered in our model.
Fig. 7 shows analytical forces when a particle impacts on the probe surface.

|
Fig.7 Particle impacting process diagram |
In order to correlate typical range of diameters and velocities observed in commercial solid fuel fired boilers in deposits, Tomeczek and Wacławiak[22] set up a relationship between K and particle diameter as follows in Eq.(3):
| $ K\left(d_{\mathrm{p}}\right)=G\left(\frac{d_{\mathrm{p}}}{d_{\mathrm{ref}}}\right)^{n} $ | (3) |
G is a constant with kg/(m2.2s0.8) as its unit, dref represents reference diameter with m as its unit, and n is exponent constant. G, dref and n are determined by the deposition situation.
Fvw is expressed as Eq.(4):
| $ \boldsymbol{F}_{\mathrm{vw}}=\frac{B d_{\mathrm{p}}}{6 \delta^{2}} $ | (4) |
B is Hamaker constant with the value of 1.0×1017 kg·m2/s2; δ is the distance between particle and deposition surface with a value of 0.5dp with the unit of m.
For Eq.(4), the Van der Waals' force, only relative distance is included, the direction is not considered.
FG is shown as Eq.(5):
| $ \boldsymbol{F}_{G}=\frac{1}{6} \pi d_{\mathrm{p}}^{3} \rho_{\mathrm{p}} g $ | (5) |
dp is particle diameter with m as its unit; ρp is particle density with kg/m3 as its unit; g is gravitational constant with m/s2 as its unit.
2.2 Simulation MethodsThe drop tube furnace with the length of 1.4 m and 50 mm ID is shown in Fig. 8. The 22 mm OD probe is placed at 160 mm height from the bottom of the tube. Ash is injected through an 8 mm ID inlet above the furnace.

|
Fig.8 Structure diagram of hot test setup for fly-ash deposition and the mesh of the computed domain |
A 2D geometry and mesh is shown in Fig. 8. Probe surface is divided into 40 parts, and the numerical arrangement is shown in Fig. 8. The middle ash inlet is defined as inlet-1, and the other 2 inlets are defined as inlet-2. The ash-carried air flow velocity of inlet-1 is 3.48 m/s and the temperature is 576 K. Velocity of inlet-2 has 3 settings: 1.11 m/s, 1.58 m/s and 2.05 m/s, while the temperature is always 793 K. Outlet of tube is connected to atmosphere. The turbulence k-ε model is chosen with default parameters. DPM model is used to predict the interaction between gas and particles, and the DPM sources would be updated every 10 flow iterations. Rosin-Rammler distribution is selected and the detail information of coal ash sample is presented in Table 3.
| Table 3 Parameters of particle size and properties of coal ash sample |
An algorithm of calculation is presented in Fig. 9. A steady state solution is achieved when software accuracy of flow and energy balances for each iteration keeps under or oscillates near the setting residual. It means the current grid and time step is appropriate to get a converged result.
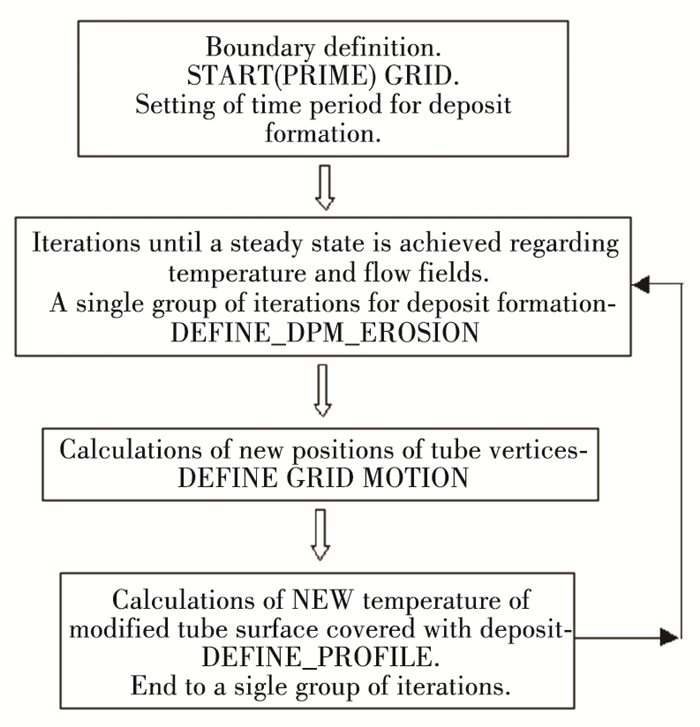
|
Fig.9 Calculation algorithm for ash deposit formation used in Fluent code |
A UDF code for predicting the deposition behavior and describing the deposition process with dynamic mesh technique was used in this case. Fluent enables dynamic meshing in a few modes. The most general one: 2 faces will be dragged after a single node moves independently. Such method was used in this presented modeling. A schematic view of this movement is shown in Fig. 10. It also presents the main disadvantage of restricting a single node movement, and shows when a node is shifted too far, the neighboring faces dragged by the node will overlap. This leads to an interruption and a fatal error, so movements must be tailored to fit mesh size. It is obvious that bigger faces are better for that dynamic meshing. However, coarse mesh is a defect for prediction of flow pattern. Researchers must find a compromise between those two aspects.

|
Fig.10 Schematic of moving single node with dynamic meshing method |
3 Results 3.1 Deposition under Different Inlet Velocities
It should be stressed that in numerical prediction of deposition formation and growth, it is difficult to link micro-scale of individual fate of a single ash particle (with diameter of microns) hitting a tube surface and later the deposit with macro-scale of growth in millimeters. This can be done by applying simplified equations which would be easy for numerical utilization. Normal elastic bounce force Fs, n is quite difficult to be measured in reality. However, many tries proved it is possible to find values fitting the simulated process. In this paper, G = 2.0, dp=1.2×10-4 and n=1.2. Some of our former similar work can be found in Refs.[16] and [22].
The most important question is how the ash deposition is predicted. Basically, this means the deposition height and shape. Verification between experiments of the 3 cases (velocity in inlet-2 equals to 1.1 m/s, 1.58 m/s and 2.05 m/s) and simulations have been done, and the comparisons of deposition heights are shown in Fig. 11. Tendency of increasing deposited height on probe in simulation and experiment is shown in Fig. 11(a), (b) and (c). As can be seen, the whole tendency is agreed with each other before 15 min. In experimental data, growing height increases linearly, which is different from none-linear increasing of simulated data after 15 min. The final deposition height is almost the same between experiment and simulation at 30 min. Fig. 11(d) shows deposition geometry at different time (1 min, 2 min, 7 min, 20 min and 25 min) with dynamic mesh technique.
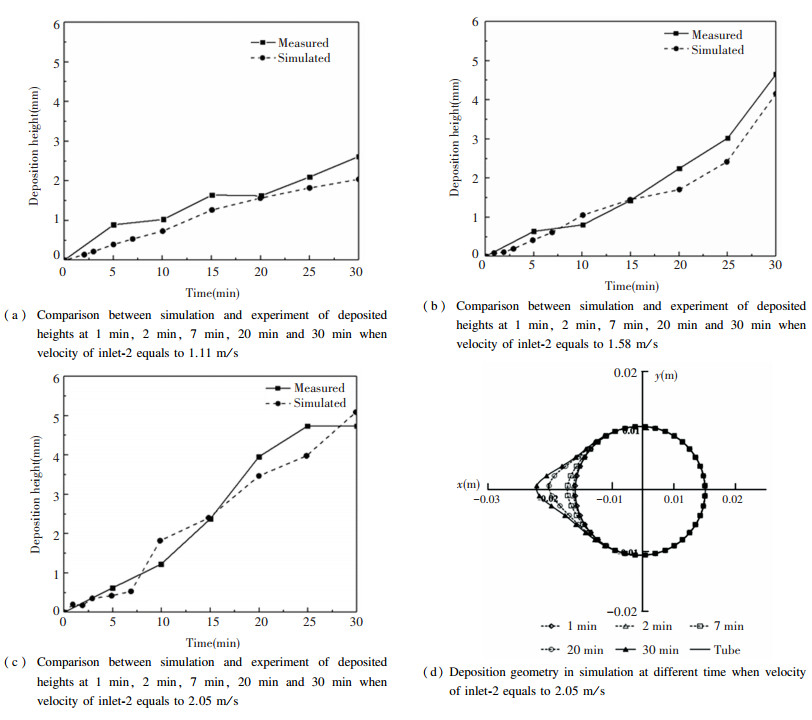
|
Fig.11 Verification between simulation and experiment |
Experimental images at 1 min, 5 min and 25 min are displayed in Fig. 12(a), (b), and (c).

|
Fig.12 Deposition geometry change as time increases |
Deposition geometry in simulation has a well symmetric feature as the existence of symmetric recirculation flows around probe. However, an asymmetric deposition geometry on experimental image was detected as deposition time increased due to unexpected experimental error.
It is difficult to analyze properties of impacted and deposited particles during the experiment process. Nevertheless, numerical method can solve this problem as single particle behavior is captured during the simulation. The probe surface was divided into 40 parts with individual memories in Fluent, then UDF code is used to cope with impacted or deposited particles on the probe surfaces and collect relative parameters.
First of all, mean diameter distribution of impacted and deposited particles are discussed. The size distribution of particles has a very important influence on inertial impaction and eddy impaction[20]. In this case, different sizes of particles have different FG which is a main factor of the deposition probability.
Impacted particles on the probe has a larger mean diameter distribution than deposited particles. Particles impacted at upside of the probe surface displayed a uniform distribution. Smaller size of particles would impact at upside than downside. Recirculation phenomenon in the down-stream side may be a reasonable explanation for this impacting condition. A number of ash particles flowing around the probe impact on the wall and rebound from it. Smaller particles have less energy to rebound longer distance than larger-size particles and may hardly reach the downside of the probe. Different flow velocity in inlet-2 does not have a significant influence on impacting behavior.
As for deposited particles, distribution of smaller-size particles than impacted particles is shown in Figs. 13-14. Almost no particles stick at the downside of the probe, which agrees with experimental results. Deposition confined to the upside of the probe shrunk with increasing velocity in inlet-2. Larger magnitude of velocity around the probe shows a strong ability of blowing out the side-deposition layer. Meanwhile, smaller size particles would more likely deposit as side velocity increased.
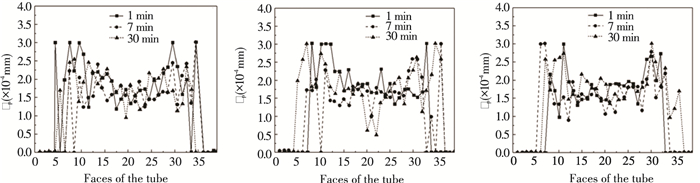
|
Fig.13 Calculated average diameter of hitting particles in 3 cases of various inlet-2 velocity |
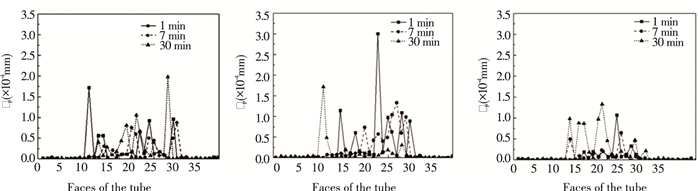
|
Fig.14 Calculated average diameter of sticking particles in 3 cases of various inlet-2 velocity |
The normal velocity of ash particles is an important parameter for normal elastic bounce force Fs, n. The distribution of the average normal velocity of hitting particles (wp) is shown in Fig. 15. A similar Gaussian distribution is detected on the upside of the probe. Particles impacted on the middle get a larger possibility to stick on the probe than those impacted on the side. In the whole deposition process, normal velocity distribution on the upside of the probe does not change a lot under condition 1 and condition 3. However, a typical decrease occurs under condition 2 with velocity in inlet-2 of 2.05 m/s. As deposition time increases, a typical change of deposition geometry was detected in Fig. 14 which influences the normal velocity distribution. In other words, it means the steep deposition geometry decreases normal impacting velocity. Deposition geometry in condition 1 and condition 2 could not be steeper than condition 3 as normal velocity distribution does not change obviously as time increases in Fig. 15.

|
Fig.15 Calculated average normal velocity of hitting particles in 3 cases of various inlet-2 velocity |
Deposition geometry has an important influence on deposition process. Steep geometry decreases normal impacting velocity and makes the following deposited tendency slow down. Deposition geometry has a different rate under different conditions which could be detected through accretion rate in Fig. 16. Accretion rate on surface (outside surface of probe and deposition surface) in five classifications (1 min, 2 min, 3 min, 5 min, 7 min, 25 min) are presented. It is obvious that extreme accretion rate means maximum deposition. Extreme accretion rate would take more time as velocity in inlet-2 increased. It means steady deposition behavior postponed as velocity in inlet-2 increased.
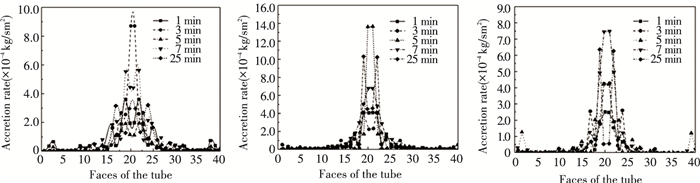
|
Fig.16 Accretion rate at different position of probe in 3 cases of various inlet-2 velocity |
3.2 Deposition under Different Probe Diameters
Different diameters impact the deposition behavior dramatically since the attacking rate of the ash varies due to changing attacking areas. In the meantime, flow field would also be intrinsically influenced by the narrowing/enlarging aisles between the tube and the furnace wall which also affect the formation of ash deposition.
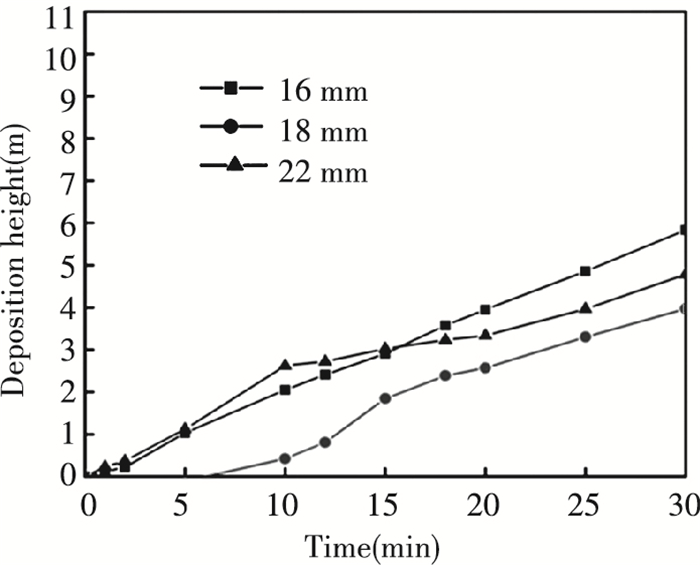
In this section, the ash deposition of different tube diameters including 16 mm, 18 mm and 22 mm with inlet-2 velocity equaling to 2.05 m/s are compared.
The interesting phenomenon is that the final deposition height of 16 mm case is the largest, and both 18 mm and 22 mm cases are lower. Larger tube diameters mean larger attacking areas, so the deposition area increases accordingly on the tube surface which decreases the deposition height accumulation along the flow direction. It is also easy to find in Fig. 17 that 18 mm case and 22 mm case have turning points which indicate increased flow velocity near the tube induced by the narrowed flow path of aisles blows out the ash deposition during its deposition processes, meaning as the diameter increases, the space between the probe and the wall, and the space between probes are shrinking, which accelerates the flow air. The increasing velocity of the flow field near the probes has a significant flushing effect to the edge of the deposition ash, which results in the decrease of the height of the deposition.
|
Fig.17 Deposition height under different tube diameters (16 mm, 18 mm and 22 mm) with inlet-2 velocity equaling to 2.05 m/s |
3.3 Deposition on Two Tubes under Horizontal and Vertical Arrangement
In industrial applications, multiple tubes arrangement is usually used to make the ash deposition behavior more complicated. In this section, the deposition on two tubes under horizontal and vertical arrangements is studied. The tube diameters and inlet-2 velocity are 22 mm and 2.05 m/s, respectively.
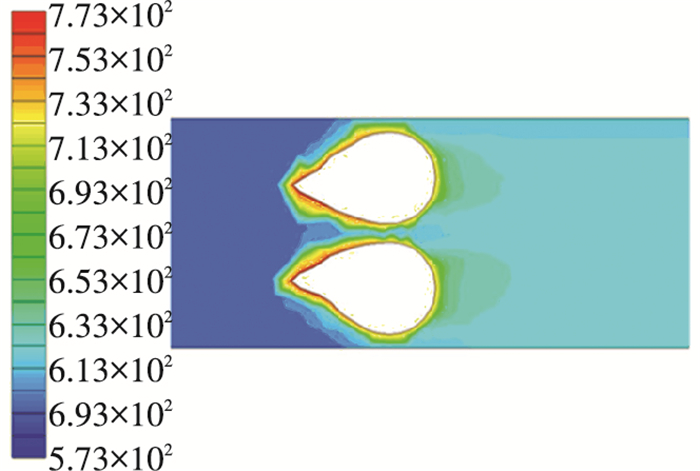
For horizontal arrangement case, Fig. 18 shows the temperature contour at 30 min. The deposition on two tubes are almost the same due to the symmetric arrangement, and the air flow between two deposition piles pushes the deposition height peak of each tube directing to the furnace wall.
|
Fig.18 Deposition geometry at 30 min in horizontal arrangement |
In Fig. 18(a), the growing process is different from that of single tube. The deposition geometry is no more symmetric which has been explained before. Through Fig. 19(b), the final deposition at 30 min is about twice larger than that of single tube under same inlet-2 velocity and diameter. The horizontal arrangement of multiple tubes definitely intensifies the deposition tendency compared with single tube case.

|
Fig.19 Deposition geometry and height at various time in horizontal arrangement |
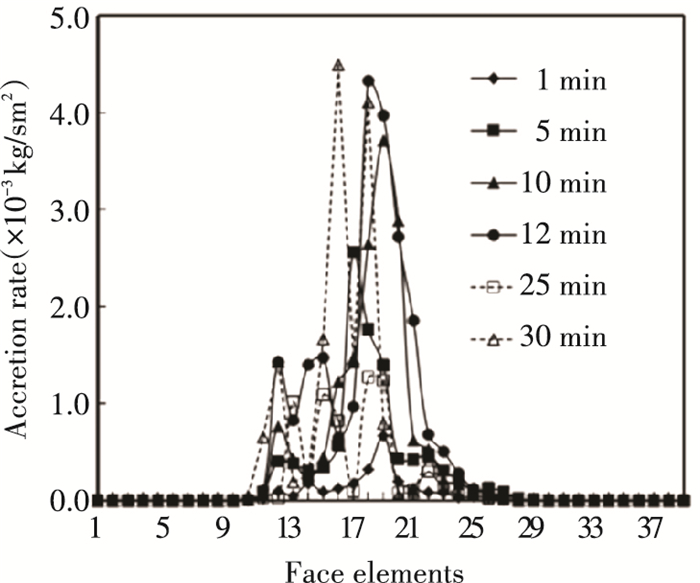
In Fig. 20, the accretion rate of one of the two tubes at various time implies that from 1 min to 30 min, the accretion rate keeps increasing. However, the peak rate tends to move to the left side which corresponds to wall side after 10 min, meaning that the moving trend proves formation of the final deposition geometry in Fig. 18.
|
Fig.20 Deposition accretion rate at various time |
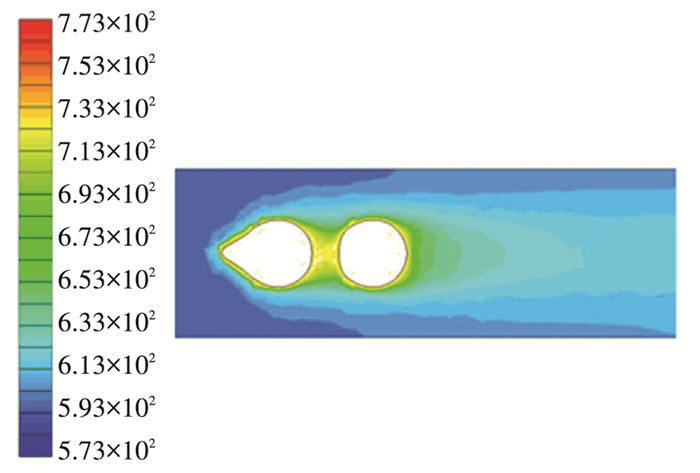
For vertical arrangement case, the final deposition geometry of two tubes is shown in Fig. 21. The deposition mostly attached on the tube towards the inlet flow, and the surface of the tube behind is clear. The deposition geometry is the same as the single tube case. However, in Fig. 22(a) and (b), the deposition height is about 1.5 mm larger than single tube.
|
Fig.21 Deposition geometry at 30 min in vertical arrangement |
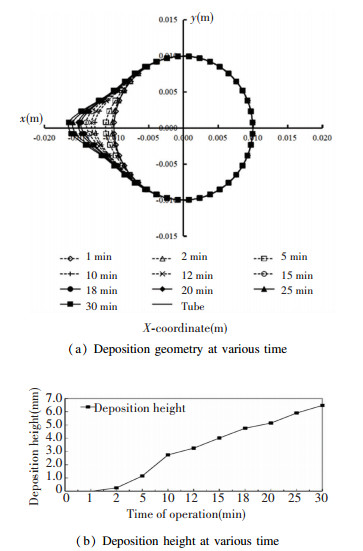
|
Fig.22 Deposition geometry and height at various time in vertical arrangement |
In Fig. 23, the accretion rate reveals that the deposition process declines after 10 min, the peak position oscillates and finally fixes at the center after 25 min.
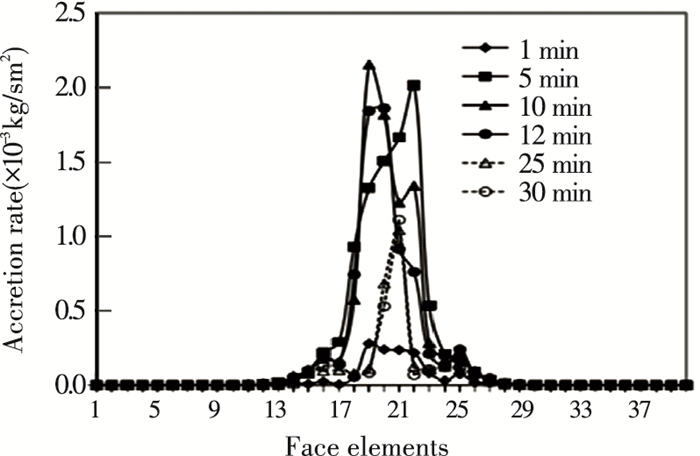
|
Fig.23 Deposition accretion rate at various time |
Through comparing the results of horizontal and vertical arrangements, the developed simulation method can effectively predict the deposition tendency of double tubes arrangements and could probably be useful for multi-tubes prediction. Specifically, the horizontal arrangement intrinsically makes the deposition easier to grow and more likely, even trigger damage in industrial facilities in reality.
4 ConclusionsNumerical research of predicting has been studied in this paper.
The dynamic mesh technique is used to predict the growth of ash deposition in a drop tube furnace and describe the whole formation process of ash deposition, along with several important parameters of impacting and sticking particles implying the feature of deposition behavior.
Particle size has an important influence on deposition behavior. Impacted particles have larger size distribution than deposited particles. A typical smaller size distribution occurs when velocity in inlet-2 equals to 2.05 m/s.
Particle normal impacted velocity plays an important role due to elastic bounce force term. Gaussian distribution was detected in the upside of the probe and 2 extreme velocities occurred at the side of the probe which verified rebound phenomenon of particles at side walls.
Deposited geometry was influenced by side velocity (velocity in inlet-2). Large velocity has an obvious effect to change the shape of deposition and postpone the steady time.
Validation between experiment and simulation has been done and displayed agreeable results between each other.
Then, the tube diameter effect mentioned shows that smaller tube diameter may trigger higher deposition height. Finally, the different arrangements of multiple tubes have been studied. It shows the horizontal arrangement causes the deposition to be heavier than vertical arrangement.
| [1] |
Cen K F. The Prevention Principle and Calculation of Dust, Slag, Wear and Corrosion of Boiler and Heat Exchanger. Beijing: Scientific Press, 1994: 1-24.
(  0) 0) |
| [2] |
Wang B. Monitoring and Soot Blowing Optimization of Coal-fired Boilers. Shanghai: Shanghai Jiao Tong University, 2012. 1-6.
(  0) 0) |
| [3] |
Yu H M. Study on the Online Monitoring of Ash Fouling on Heating Surface of Power Station Boiler. Beijing: North China Electric Power University. 2006. 1-9.
(  0) 0) |
| [4] |
Venturini P, Borello D, Hanjalić K, et al. Modelling of particles deposition in an environment relevant to solid fuel boilers. Applied Thermal Engineering, 2012, 49: 131-138. DOI:10.1016/j.applthermaleng.2011.08.030 (  0) 0) |
| [5] |
Weber R, Schaffel-Mancini N, Mancini M, et al. Fly ash deposition modelling: requirements for accurate predictions of particle impaction on tubes using RANS-based computational fluid dynamics. Fuel, 2013, 108: 586-596. DOI:10.1016/j.fuel.2012.11.006 (  0) 0) |
| [6] |
Walsh P M, Sayre A N, Loehden D O, et al. Deposition of bituminous coal ash on an isolated heat exchanger tube: effects of coal properties on deposit growth. Progress in Energy and Combustion Science, 1990, 16(4): 327-345. DOI:10.1016/0360-1285(90)90042-2 (  0) 0) |
| [7] |
Wang X H, Zhao D Q, He L B. Numerical research in deposition process of coal ash residue. Advances in Mechanics, 2005, 35(3): 417-426. (  0) 0) |
| [8] |
Sreedharan S S, Tafti D K. Composition dependent model for the prediction of syngas ash deposition in turbine gas hotpath. International Journal of Heat and Fluid Flow, 2011, 32(1): 201-211. DOI:10.1016/j.ijheatfluidflow.2010.10.006 (  0) 0) |
| [9] |
Losurdo M, Spliethoff H, Kiel J. Ash deposition modeling using a visco-elastic approach. Fuel, 2012, 102: 145-155. DOI:10.1016/j.fuel.2012.04.047 (  0) 0) |
| [10] |
Mueller C, Selenius M, Theis M, et al. Deposition behaviour of molten alkali-rich fly ashes-development of a submodel for CFD applications. Proceedings of the Combustion Institute, 2005, 30(2): 2991-2998. DOI:10.1016/j.proci.2004.08.116 (  0) 0) |
| [11] |
Ai W G, Kuhlman J M. Simulation of coal ash particle deposition experiments. Energy Fuels, 2011, 25(2): 708-718. DOI:10.1021/ef101294f (  0) 0) |
| [12] |
Fan J R, Zha X D, Sun P, et al. Simulation of ash deposit in a pulverized coal-fired boiler. Fuel, 2001, 80(5): 645-654. DOI:10.1016/S0016-2361(00)00134-4 (  0) 0) |
| [13] |
Pan Y D, Si F Q, Xu Z G. Fouling model on heated surface of utility boiler. Chinese Journal of Electrical Engineering, 2010, 30(8): 63-67. (  0) 0) |
| [14] |
Abd-Elhady M S. Gas-side Particulate Fouling in Biomass Gasifiers. Eindhoven: Technische Universiteit Eindhoven, 2005. 41-61.
(  0) 0) |
| [15] |
Richards G H, Slater P N, Harb J N. Simulation of ash deposit growth in a pulverized coal-fired pilot scale reactor. Energy & Fuels, 1993, 7(6): 774-781. DOI:10.1021/ef00042a012 (  0) 0) |
| [16] |
Wacławiak K, Kalisz S. A practical numerical approach for prediction of particulate fouling in PC boilers. Fuel, 2012, 97: 38-48. DOI:10.1016/j.fuel.2012.02.007 (  0) 0) |
| [17] |
Pérez M G, Vakkilainen E, Hyppänen T. 2D dynamic mesh model for deposit shape prediction in boiler banks of recovery boilers with different tube spacing arrangements. Fuel, 2015, 158: 139-151. DOI:10.1016/j.fuel.2015.04.074 (  0) 0) |
| [18] |
Huang Q, Li S Q, Shao Y C, et al. Dynamic evolution of impaction and sticking behaviors of fly ash particle in pulverized coal combustion. Proceedings of the Combustion Institute, 2019, 37(4): 4419-4426. DOI:10.1016/j.proci.2018.06.035 (  0) 0) |
| [19] |
Zhao Y Q, Huang Q, Yao Q, et al. Prediction and validation of ash sticking probablity under fouling conditions in pulverized coal combustion. Proceedings of the Combustion Institute, 2021, 38(4): 5311-5318. DOI:10.1016/j.proci.2020.06.053 (  0) 0) |
| [20] |
Tekenov Z T. Adhesion of Powdery Materials. Frunze: Ilim Press, 1985.
(  0) 0) |
| [21] |
Pronobis M. Weitere Erkenntnisse zum Einfluß der Verschmutzung auf den Warmeaustausch in Konvektiven Kesselrohrbündeln. VGB Kraftwerkstechnik, VGB Kraftwerkstechnik, 1989, 69(11): 1067-1074. (  0) 0) |
| [22] |
Tomeczek J, Wacławiak K. Two-dimensional modelling of deposits formation on platen super-heaters in pulverized coal boilers. Fuel, 2009, 88(8): 1466-1471. DOI:10.1016/j.fuel.2009.02.023 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


