2. School of Automotive and Traffic Engineering, Hefei University of Technology, Hefei 230009, China
Lithium-ion batteries can provide high energy efficiency and power density. They also have some other characteristics, such as smaller mass density (which can withstand high or low temperature working environment), fast charging speed, long durability, very little self discharge, no generation of hydrogen, and so on. Therefore, they are more suitable for the field of new energy vehicles. But inaccurate evaluation of their state-of-health (SOH)/state-of-charge (SOC) may result in some faults, such as overcharge, over discharge, uncertain failure, and safety hazards[1]. SOH is one of the main factors of lithium-ion batteries. Shen et al.[2] proposes a co-estimation scheme of SOC, SOH, and state of function for lithium-ion batteries in electric vehicles. SOH is also used to compute SOC of lithium-ion batteries. Therefore, it is essential for lithium-ion batteries to obtain an accuracy value of SOH. The value of SOH can be affected by many aspects, for example, the aging mechanism of lithium-ion batteries and the difficulty of real-time measurement. It is more complex and difficult than SOC estimation[3]. To estimate the SOH of batteries, now there are three main ways: the first is to utilize the direct current internal resistance (DCR) of lithium-ion batteries to estimate SOH; the second is to use the model of batteries for the estimation of SOH; the third is to employ some control or identification algorithms to calculate SOH.
Direct current internal resistance is often utilized to estimate SOH of batteries. Thus it is meaningful to discover the relationship between the internal resistance and other parameters. Many researchers have looked into this question deeply. Zhang et al.[4] used Extended Kalman Filter algorithm to find the relationship between the battery SOC and the internal resistance. Remmlinger et al.[5] made use of linear least squares algorithm to calculate an equivalent internal resistance by a battery equivalent circuit model, which considers the influence of battery temperature to improve the robustness and accuracy for SOH estimation results. Hung et al.[6] developed a real-time estimation system of SOH by dynamic impedance of lithium-ion batteries. What they have in common is that they use the internal resistance method to estimate SOH. However, it is difficult to make clear of the relationship between SOH and internal resistance. Particularly, in the case of considering a serious affection of battery temperature, the relationship between them will become more complex. In addition, this approach is only fit for a same type of battery. It is impossible to estimate SOH only by adopting internal resistance. Leijen et al.[7] described the knowledge about effective battery capacitance. It is considered to be the local slope of the voltage v.s. charge curve derived from a third order polynomial relationship between these parameters. This maximum effective capacitance will be considered as a sign that the battery module is at the end of its life or will have a catastrophic failure. Besides internal resistance, open circuit voltage is also linked with the SOH inextricably. Therefore, only one parameter cannot accurately indicate the SOH well.
The lithium-ion batteries model is often used for the estimation of SOH.Weng et al.[8] developed a model parameterization and adaptation framework utilizing the simple structure of support vector regression representation with determined support vectors, so that the model parameters can be estimated in real-time and extended to nonlinear dynamic systems with the given properties.
It is most often for SOH estimation to adopt aging mechanism model[9]. The aging mechanism model analyzes microscopic physical and electrochemical processes of lithium-ion batteries, with special focuse on the aging process. At present, there are two ways to make clear of the aging mechanism, i.e., destructive and non-destructive. The former can accurately reflect internal aging of the battery, and simulate internal mechanism. In view of large computer workload, complex model, and time consumption, it is difficult for the former to achieve application in engineering practice. To obtain the aging mechanism model, the latter focuses on looking for the appropriate aging characteristic and establishes a relationship between some parameters and the aging degree of lithium-ion batteries. Even though the latter way shows worse in accuracy of SOH estimation, it requires smaller quantity of computation in practical operation. Based on the model of equivalent circuit, Bi et al.[10] proposes an SOH dynamic estimation approach by genetic resampling particle filter, in which the complexity and nonlinearity of battery system are taken into account. Hua et al.[11] proposed a nonlinear predictive filter to estimate SOH. Based on charge curve of batteries, Li et al.[12] proposed a universal capacity model to estimate SOH. Narayanrao et al.[13] described a stress-SOH curve of lithium-ion batteries based on fatigue strength model of metal material. By analyzing diffusion process in the spherical particle model, a lumped parameter is employed as the mechanical stress during the cycle. But the model of lithium-ion batteries cannot reveal the chemical reaction precisely because of complexity and nonlinearity. It is not the best choice to adopt the model to estimate the SOH.
With regard to the use of control algorithm, Zou et al.[14] proposed a model predictive control method for battery charging control, achieving the best tradeoff between the the time of charging and battery SOH. Zhang et al.[15] described a way to estimate the SOH of lithium-ion batteries through identifying the bulk capacitance of its equivalent circuit model. This algorithm is discussed to derive the attenuation factor of the bulk capacitance in different cycles. Chen et al.[16] developed a genetic algorithm to estimate the SOH, in which the temperature of batteries is taken into account. Wu et al.[17] adopted group method of data handling to make clear of the differential geometric properties and battery SOH. This SOH can be estimated by the group method with the properties of input voltage curve. Due to large amount of calculation, the algorithm is difficult to use in actual engineering. Zenati et al.[18] applied fuzzy logic system to estimate SOH. Liu et al.[19] proposed a comprehensive predictive method that combines two health factors related to SOH, i.e., battery capacity and time interval of equal discharging voltage difference series. Chaoui et al.[20] presented a nonlinear autoregression with exogenous inputs architecture of the dynamically driven recurrent networks for SOC and SOH estimation. Lin et al.[21] proposed a probabilistic neural network to estimate the SOH of Lithium-ion batteries. But all of the above need large amount of calculation, thus they are not fit to be applied in engineering practice.
There are still many problems aboutthe estimation of SOH for batteries[22], such as the lack of approaches to analyze aging process simply and effectively. As for the non-linear time variant characteristic of the SOH of lithium-ion batteries, it is difficult to be measured directly and accurately. But in engineering practice, battery engineers can estimate the SOH more accurately by experimental results of key parameters. If the estimation approach of battery engineers is extracted to identify the SOH, it will be a better way to solve this problem. In this paper, an internal combustion engine (ICE) map approach is used to indicate the SOH as maritime positioning principle in ancient navigation. Temperature translation is proposed to translate the DCR/open circuit voltage (OCV) of different temperature into a nominal value at 25 ℃. Nominal SOH is proposed to indicate a unified value for different temperature conditions. SOH map is proposed to illustrate a triangular relationship which contains nominal DCR, nominal OCV, and nominal SOH, in which nominal SOH can be checked. According to experimental validation, it can be concluded that SOH map is a better candidate approach for estimating SOH in practical applications.
The structure of this paper is as follows. After a simple explanation for SOH of batteries in Section 1, this humanlike cross-location approach is introduced in Section 2. The cross-location approach is applied into the estimation of SOH in Section 3. The experimental results are interpreted in Section 4. Some concluding remarks are given in Section 5.
1 State of HealthLithium-ion batteries system is a key part of powertrain for battery electric vehicle, which is composed of lots of lithium-ion cells. Battery management system, whose functions include estimation of SOH and SOC at real-time, is utilized to control these cells. As illustrated in Fig. 1, SOC indicates actual charge of batteries, which is applied to some limits of output power and current. SOH is a key parameter for estimation of SOC, which indicates actual capacity of lithium-ion batteries.

|
Fig.1 Relationship between SOH and SOC for lithium-ion batteries |
On the other hand, SOH can indicate battery aging. The accurate estimation of SOH is beneficial to reduce estimation error of SOC. It is necessary for estimation of battery capacity to set up a battery capacity aging model. Due to battery aging, OCV and DCR change together. There is a close relationship between SOC and SOH, which affects the results of estimation[23]. As illustrated in Fig. 1, the initial capacity of lithium-ion batteries decides maximal value of actual capacity. The actual capacity is from the SOH of lithium-ion batteries, which decides maximal value of actual charge. The SOC of lithium-ion batteries equals to the actual charge. The SOH indicates the rest of capacity for batteries. The rest of range for electric vehicle is computed by the SOC of batteries.
The actual capacity is not easy to be obtained in engineering practice. In fact, the service life of batteries is often applied to the SOH.
Note 1.There is a different characteristic between SOH and SOC. Under the range of operating temperature in a single life cycle, the SOC does fluctuate with the change of environmental temperature, but the SOH hardly changes. Based on the above characteristic of batteries, it may be assumed that the SOH does not change with environmental temperature in a single life cycle. That is to say, in a single life cycle of batteries, the SOH can be considered as a same value under different environmental temperature.
2 Cross-Location ApproachWith regard to a complicated system, its important performance is usually decided by two or more key parameters. Just like sailing in ocean, if location information of steamship cannot be corrected at real-time, it is easy to deviate from target route. Because there is no global position system in ancient times, ancient people invented a cross-location approach to compute a geographical location of steamship during the course of navigation, which made use of clock, sundials, and compass as illustrated in Fig. 2.

|
Fig.2 Cross-location approach of steamship in the ocean |
Based on Fig. 2, it can be seen that both the longitude and the latitude are utilized to indicate a coordinate of current position of steamship during the course of navigation, which is named as human-like cross-location in this paper. Now, lots of battery engineers also use multiple parameters to identify the performance of lithium-ion batteries, which is a same approach with the navigation location of ancient people in reality. Therefore, the cross-location approach may be utilized to estimate the SOH of batteries, which is a multiple-input single-output algorithm in fact.
Note 2.The same logic as the location of steamship may be applied into the estimation of SOH. The location of steamship is decided by the longitude and the latitude. The SOH of batteries may be indicated through the DCR and OCV. The position of steamship is not measured directly in ancient times, which can be computed by human-like cross-location approach. The SOH cannot be measured directly, but cross-location approach can be employed to identify it.
3 SOH Map AlgorithmSome characteristics of lithium-ion batteries are going to change with the attenuation of battery life, such as direct current internal resistance and open circuit voltage. As illustrated in Fig. 3, there is a relationship curve among DCR, OCV, capacity, and cycle life in lithium-ion batteries. The capacity is measured under 1 C discharge/charge at 25 ℃. The DCR and the OCV are measured under the condition of 50% SOC at 25 ℃.

|
Fig.3 Relationship between cycle life, capacity, DCR, and OCV |
It can be seen from Fig. 3 that cycle life is almost inversely proportional to capacity, so that cycle life is used to indicate the SOH of batteries. There is a greater change of the DCR with the increase of cycle life. Within about 100 cycles, the DCR decreases obviously. After about 100 cycles, the DCR increases gradually as the increase of cycle life of lithium-ion batteries. As for the OCV, it is inversely proportional to cycle life before 250 cycles, and there is a little change after 250 cycles. According to the above-mentioned data, it can be concluded that both DCR and OCV are strongly associated with the SOH. Therefore, there is a better way to employ DCR and OCV to estimate the SOH.
3.1 Definition of Nominal SOHIn general, SOH can be defined by capacity, internal resistance, cycle life, and so on. In this section, the cycle life is employed to indicate the SOH of batteries as illustrated in Fig. 3.
Environmental temperature is an important parameter of batteries. Even if the batteries are not operated, ultra temperature can make it attenuate. If environmental temperature does not change within operating temperature range, it can be assumed that the SOH will not change during operation as well. During the practical application, the environmental temperature changes slightly with time, and the real SOH does not change. Therefore, an estimated value at some certain temperature can be used to indicate the SOH at different temperature. Based on this assumption, a nominal SOH is utilized to describe the SOH of batteries under different environmental temperature. In this study, 25 ℃ is used as the environmental temperature of nominal SOH25 as expressed in Eq.(1):
| $ {\rm{SO}}{{\rm{H}}_{25}} = \frac{{{C_{{\rm{aged}}25}}}}{{{C_{{\rm{rated}}}}}} \times 100{\rm{\% }} $ | (1) |
In Eq.(1), Crated is the rated cycle life of batteries at the beginning of use, Caged25 is the aged cycle life at 25 ℃ for current state of lithium-ion batteries.
Note 3.In summary, it can be seen that the SOH does not change in a single cycle at operating temperature. Therefore, some characteristics of linear interval can be utilized to estimate the cycle number of the SOH, and this cycle number can be employed as a nominal SOH around the current cycle of batteries. In this paper, SOH25 is employed as a nominal cycle of the SOH around the current cycle, whose performance parameters for DCR and OCV may be measured or computed in the linear interval of lithium-ion batteries.
3.2 Cross-Location of SOHAs for the SOC estimation, SOH is an important parameter, and vice versa. Both the SOH and the SOC impact each other during the estimation. The impact between the SOC and the SOH is going to continue with all cycles till the end of life. Therefore, both the SOC and the SOH are becoming coupling parameters. In this section, a estimation approach of SOH is going to be introduced without the use of SOC.
In Eq.(2), the direct current internal resistance is related with the SOC, the SOH, and environmental temperature.
| $ {\rm{DCR}} = f({\rm{ Temp, SOC}}, {\rm{SOH}}) $ | (2) |
In Eq.(3), the OCV is associated with the SOC, the SOH, and environmental temperature.
| $ {\rm{OCV}} = g({\rm{ Temp }}, {\rm{SOC}}, {\rm{SOH}}) $ | (3) |
According to the analysis of lots of data for lithium-ion batteries, at a certain environmental temperature, the DCR may be determined by the SOC and the SOH as shown in Eq.(4):
| $ {\rm{DCR}} = {f_T}({\rm{SOC}}, {\rm{SOH}}) $ | (4) |
Under a certain environmental temperature, the OCV may be determined by the SOC and the SOH as shown in Eq.(5).
| $ {\rm{OCV}} = {g_T}({\rm{SOC}}, {\rm{SOH}}) $ | (5) |
Reorganize Eq.(6) and Eq.(7) as follows:
| $ {\rm{SOC}} = R\left[ {f_T^{ - 1}({\rm{DCR}}), {\rm{SOH}}} \right] $ | (6) |
| $ {\rm{SOC}} = V\left[ {f_T^{ - 1}({\rm{DCV}}), {\rm{SOH}}} \right] $ | (7) |
Combine Eq.(6) and Eq.(7) as follows:
| $ R\left[ {f_T^{ - 1}({\rm{DCR}}), {\rm{SOH}}} \right] = V\left[ {g_T^{ - 1}({\rm{OCV}}), {\rm{SOH}}} \right] $ | (8) |
Arrange Eq.(8) as follows:
| $ {\rm{SOH}} = H({\rm{DCR}}, {\rm{OCV}}) $ | (9) |
Eq.(9) shows the interrelation of battery parameters. A cross-location approach is used to estimate the SOH of battery only according to the DCR and the OCV. The approach does not need accurate estimation of the SOC, which can avoid the influence of SOC estimation error.
As is known, an efficient map of ICE makes use of speed and torque to illustrate the efficiency. As formulated in Eq.(9), the SOH of lithium-ion battery may also be illustrated by the DCR and the OCV, which is named by SOH map. But, there is a difference between the ICE map and the SOH map. The ICE map is not affected by the environmental temperature. In SOH map, the value of SOH becomes larger as environmental temperature increases. For convenient application in practical engineering, a nominal SOH map is proposed in this paper, which is under the condition of 25 ℃ environmental temperature. Similarly, for the DCR and the OCV under different environmental temperature, their numerical value may also be translated into DCR25 and OCV25 at 25 ℃.
Put DCR25 and OCV25 into Eq.(9), the nominal SOH SOH25 at 25 ℃ environmental temperature is as follows:
| $ {\rm{SO}}{{\rm{H}}_{25}} = H\left( {{\rm{DC}}{{\rm{R}}_{25}}, {\rm{OC}}{{\rm{V}}_{25}}} \right) $ | (10) |
Till now, the nominal SOH25 has been built, which is composed of the DCR25 and OCV25 as illustrated in Fig. 4. In other words, the human-like cross-location approach is applied into the SOH estimation of lithium-ion batteries.
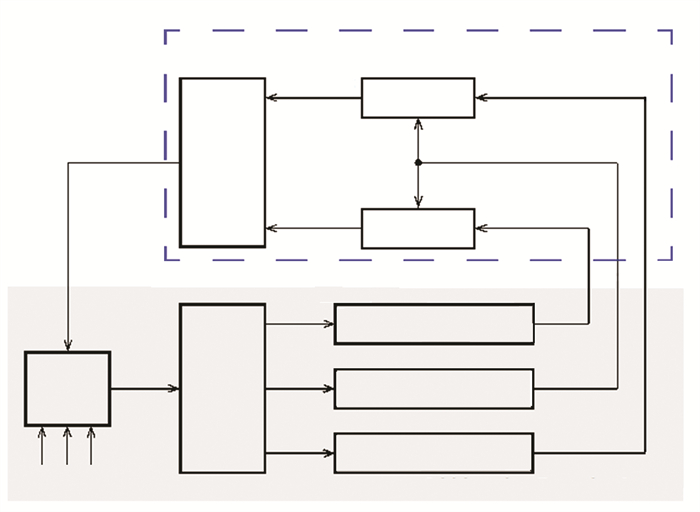
|
Fig.4 Cross-location approach for estimation of SOH |
Comparison of Fig. 4 and Fig. 2 shows that the OCV is similar to the longitude, and the DCR to the latitude. The OCV is measured by sensors and transformed into nominal value by OCV25 map. The DCR is computed by some variables and transformed into nominal value by DCR25 map.
Note 4.Similarly to ICE map, an SOH map is set up to show the relationship among the SOH, the OCV, and DCR. According to the nominal DCR25 and OCV25, the nominal SOH25 may be looked up from the SOH map.
3.3 Measurement of ParametersA lithium-ion batteries system is composed of lots of batteries. In Fig. 5, there is only a cell from the whole batteries system. In general, a passive equalization approach is utilized to manipulate voltage balancing among all cells of lithium-ion batteries system, whose circuits are illustrated in Fig. 5.
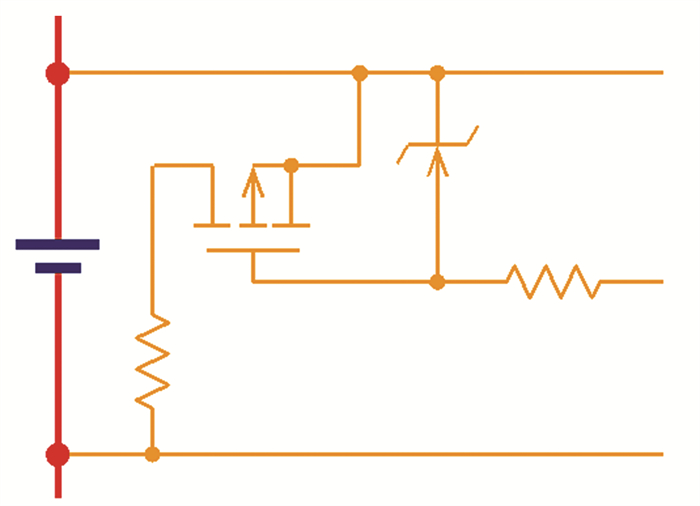
|
Fig.5 Passive equalization circuit of battery management system to measure the DCR and the OCV |
As shown in Fig. 5, the OCV U0 and the load voltage U1 may be measured and obtained by voltage sensor chip, e.x.LTC6811. The DCR may be computed by Eq.(11):
| $ {R_0} = \frac{{\left( {{U_0} - {U_1}} \right) \cdot {R_1}}}{{{U_1}}} $ | (11) |
Note 5. With respect to cells of power battery system, the OCV may be measured by voltage sensor, and the DCR may be computed as Eq.(11). The SOH map, which may be easily applied into engineering practice, consists of the OCV and the DCR.
4 Experimental ValidationA lithium-ion battery of LiNi(1-2x)CoxMnxO2(NCM) is used for validation of human-like cross-location approach in a test bench from Fig. 6. Some key parameters of NCM are going to be listed in the table of battery parameters. According to the experimental results, some maps including OCV, DCR, and SOH are illustrated in more details below.

|
Fig.6 Test bench of lithium-ion batteries |
4.1 Battery Parameters
There are many kinds of lithium-ion batteries, e.g., LFP, LMO, LCO, NCA, and NCM. In this paper, NCM battery is used for experimental validation of SOH estimation by humanlike cross-identification algorithm. Some parameters of NCM battery are listed in Table 1.
| Table 1 Lithium-ion battery parameters for NCM |
As listed in Table 1, nominal voltage of NCM battery is 3.68 V, operation voltage range is from 2.7 V to 4.15 V. In reality, specific density of mass is 169 Wh/kg, which is larger than 160 Wh/kg. Specific density of volume is larger than 300 Wh/L. Under the condition of 25 ℃ and 50% SOC, its direct current internal resistance is about 0.8 m, which is less than 1 m. Under the condition of 25 ℃, continuous discharge rate is larger than 1.5 C, peak discharge rate of 50% SOC is larger than 4 C for 5 s, peak discharge rate of 50% SOC is larger than 3 C for 30 s. Under the condition of 25 ℃, continuous charge rate is larger than 1 C, 5 s peak charge rate is larger than 2.5 C, 30 s peak charge rate is larger than 1.5 C. Operating temperature range is between -40 ℃ and +60 ℃. Cycle life is larger than 3200 and calendar life is about 15 years. It is obvious that an energy battery can be used for experimental validation.
Based on the application of human-like cross-location approach for SOH estimation, NCM battery can be used in some test scenarios, and the parameters are listed in Table 1. In the following table, temperature transformation is illustrated, which translates DCR/OCV under different temperature into an equivalent value at 25 ℃. Then, according to the performance curve of battery, the SOH map is illustrated.
4.2 Temperature Transformation of DCRUnder the condition of same SOH, the DCR of lithium-ion batteries changes with the environmental temperature. Therefore, nominal DCR curves may be built under different environmental temperature, in which an equivalent DCR at 25 ℃ is looked up. With regard to the DCR of batteries in Fig. 7, the relationship between the equivalent value and the measured is illustrated under the same environmental temperature.
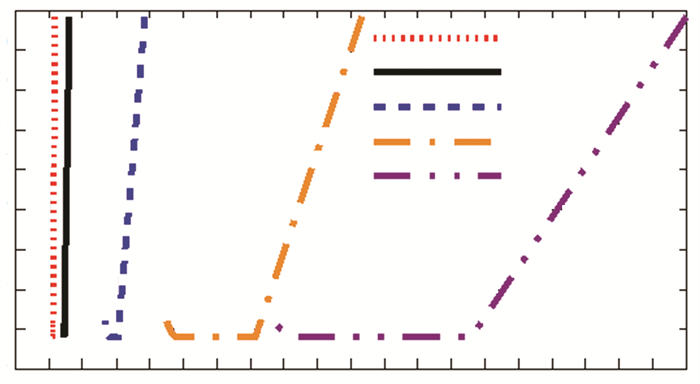
|
Fig.7 Relationship between 25 ℃ equivalent value and the measured for the DCR |
As illustrated in Fig. 7, for the DCR of batteries, the relationship between the equivalent value and the measured value is proportional under the same environmental temperature. While the environmental temperature is above 0 ℃, the relationship curve of battery DCR is linear. When the environmental temperature is below 0 ℃, the relationship curve of battery DCR is piecewise linear. At 25 ℃, the slope of equivalent DCR curve is one. At -25 ℃, the slope of equivalent DCR curve is zero when the measured DCR is less than 6.9 m.
4.3 Temperature Transformation of OCVUnder the same SOH, the OCV of lithium-ion battery changes with the environmental temperature. Therefore, nominal OCV curves may be built under different environmental temperature, in which an equivalent value of OCV at 25 ℃ may be decided by the measured value. For the OCV of batteries in Fig. 8, the relationship between equivalent value and the measured is illustrated under the same environmental temperature.
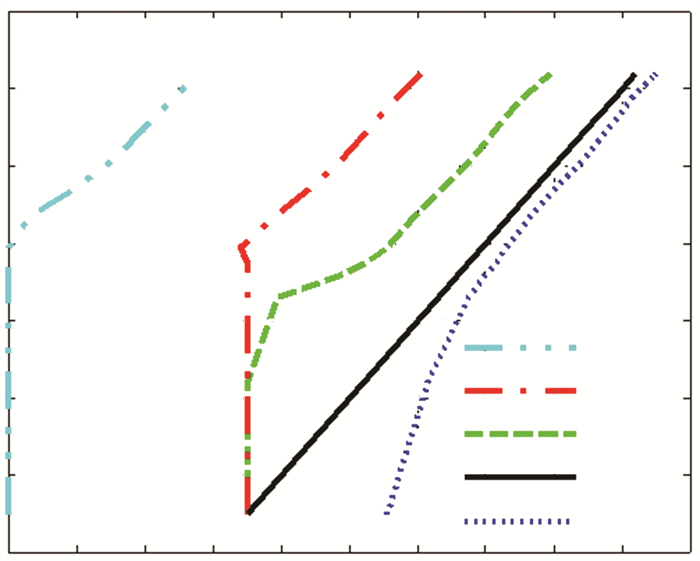
|
Fig.8 Relationship between 25 ℃ equivalent value and the measured for the OCV |
As indicated in Fig. 8, for the OCV of battery, the relationship between the equivalent value and the measured is not proportional under the same environmental temperature.
When the environmental temperature is at 25 ℃, the relationship of battery OCV is linear and its slope is one. When the environmental temperature is at 40 ℃, the relationship of battery OCV is nonlinear, and the measured value is larger than the equivalent. When the environmental temperature is lower than 25 ℃, the relationship of battery OCV is also nonlinear, and the measured value is less than the equivalent. When the environmental temperature is at -25 ℃, the measured value of OCV is as low as about 2 V.
4.4 SOH MapTill now, for NCM lithium-ion battery, the different temperature DCR/OCV can be translated into a same temperature (25 ℃) value, and the individual relationship among DCR, OCV, and SOH is discovered. Therefore, the SOH map may be built from the aforementioned relationship as illustrated in Fig. 9.

|
Fig.9 SOH map of NCM lithium-ion batteries |
Based on Fig. 9, the coordinate axis X is the OCV, the coordinate axis Y is the DCR, and the contour lines indicate nominal SOH of batteries.
It can be seen that the left blue dotted line represents a specified voltage that indicates the SOC as 0%, and the right red chain line represents another specified voltage that indicates the SOC as 100%.
From Fig. 9, it can be seen that the DCR increases with the attenuation of NCM lithium-ion battery. In reality, the SOH decreases with the attenuation of NCM lithium-ion battery. Besides, the OCV also decreases with the attenuation of NCM lithium-ion battery.
As for the DCR in the SOH map, there are two performance characteristics.One is that the DCR increases as the decrease of the SOH at a same OCV; another is that the DCR decreases as the increase of the OCV at a same SOH.
As for the OCV, there is a performance characteristic. A turning point of relationship curve between the OCV and the DCR is at 3.7 V. When the OCV is larger than 3.7 V, the slope between the OCV and the DCR is small and similar linear. When the OCV is less than 3.7 V, the slope between the OCV and the DCR is large and nonlinear.
With regard to the SOH as illustrated in Fig. 9, all SOH curves do not intersect each other; conversely, they are parallel to each other approximately. Comparison of the SOH map with the ICE map shows that the OCV corresponds to the engine speed, the DCR corresponds to the engine torque, and the SOH corresponds to the engine efficiency.
Note 6. Between the SOH map and the ICE map, there are two characteristics. One is that a DCR only matches an OCV at the same SOH of lithium-ion batteries, and a engine speed can match two engine torques under the same engine efficiency. The other is that many compositions of the DCR and the OCV map out a same SOH, which is the same as ICE map. The SOH map may be employed to estimate the SOH for batteries in practical application.
5 ConclusionsIt is difficult for lithium-ion batteries to estimate the SOH by rule and line in engineering practice. The direct current internal resistance and the OVC are two key performance parameters of batteries, and they are usually regarded as the state variables of cross location.
Under a same SOH for batteries, different environmental temperature correspond different values of the DCR and the OCV. But when the environmental temperature recovers the initial value, both the DCR and the OCV can recover the initial value. Therefore, a temperature translation approach can be utilized to translate the DCR/OCV of different temperature into a nominal value at 25 ℃.
Compared with some well-developed machine learning methods, SOH map greatly simplifies the whole operation process from the structure, and can consider the influence of OCV, DCR, and temperature at the same time, and estimate SOH accurately and quickly.
As is known, it is a better approach for ICE if the ICE map is used for illustration of its efficiency performance. Similarly, an SOH map is utilized to illustrate the SOH for batteries. Compared with the two maps, OCV corresponds to the engine speed, the DCR corresponds to the engine torque, and SOH corresponds to the engine efficiency. There are two common characteristics in the SOH map and the ICE map. One is that a DCR only matches an OCV at the same SOH for batteries, and an engine speed can match two engine torques under the same engine efficiency. The other is that many compositions of the DCR and the OCV map out a same SOH, which is the same as ICE map. From the above-mentioned characteristics, a conclusion can be drawn that the SOH map is a better method to estimate the SOH of batteries in engineering practice.
Further work regarding this topic includes: 1) calibrating the DCR map, OCV map, and SOH map through repeated experiments; and 2) applying SOH map to estimate the SOH of the battery in a real electric vehicle.
| [1] |
Hu X S, Cao D P, Egardt B. Condition monitoring in advanced battery management systems: moving horizon estimation using a reduced electrochemical model. IEEE Transactions on Mechatronics, 2018, 23(1): 167-178. DOI:10.1109/TMECH.2017.2675920 (  0) 0) |
| [2] |
Shen P, Ouyang M G, Lu L G, et al. The co-estimation of state of charge, state of health and state of function for lithium-ion batteries in electric vehicles. IEEE Transactions on Vehicular Technology, 2018, 61(1): 92-103. DOI:10.1109/TVT.2017 (  0) 0) |
| [3] |
Yuan H F, Dung L R. Off-line state-of-health estimation for high power lithium-ion batteries using three-point impedance extraction method. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2019-2032. DOI:10.1109/TVT.2016.2572163 (  0) 0) |
| [4] |
Zhang F, Rehman M M U, Wang H J, et al. State-of-charge estimation based on microcontroller implemented sigma-point Kalman filter in a modular cell balancing system for Lithium-Ion battery packs. Control and Modeling for Power Electronics, 2015, 66(3): 1-7. DOI:10.1109/COMPEL.2015.7236525 (  0) 0) |
| [5] |
Remmlinger J, Buchholz M, Meiler M, et al. State-of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation. Journal of Power Sources, 2011, 196(12): 5356-5357. DOI:10.1016/j.jpowsour.2010.08.035 (  0) 0) |
| [6] |
Hung M H, Lin C H, Lee L C, et al. State-of-charge and state-of-health estimation for lithium-ion batteries based on dynamic impedance technique. Journal of Power Sources, 2014, 268(4): 861-873. DOI:10.1016/j.jpowsour.2014.06.083 (  0) 0) |
| [7] |
Leijen P, Alistair S R D, Kularatna N. Use of effective-capacitance variation as a measure of state-of-health in a series-connected automotive battery pack. IEEE Transactions on Vehicular Technology, 2018, 67(3): 1961-1968. (  0) 0) |
| [8] |
Weng C H, Sun J, Peng H E. Model parametrization and adaptation based on the invariance of support vectors with applications to battery state-of-health monitoring. IEEE Transactions on Vehicular Technology, 2015, 64(9): 3908-3917. DOI:10.1109/TVT.2014.2364554 (  0) 0) |
| [9] |
Zhang J L, Tong W, Sun Y N, et al. Summarization of estimation methods of the state of health of lithium batteries. Journal of Power Supply, 2017, 15(2): 128-134. DOI:10.13234/j.issn.2095-2805.2017.2.128 (  0) 0) |
| [10] |
Bi J, Zhang T, Yu H Y, et al. State-of-health estimation of lithium-ion battery packs in electric vehicles based on genetic resampling particle filter. Applied Energy, 2016, 182(2): 558-568. DOI:10.1016/j.apenergy.2016.08.138 (  0) 0) |
| [11] |
Hua Y, Cordoba-Arenas A, Warner N, et al. A multi time scale state of charge and state of health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. Journal of Power Sources, 2015, 280(2): 293-312. DOI:10.1016/j.jpowsour.2015.01.112 (  0) 0) |
| [12] |
Li X, Jiang J C, Wang L Y, et al. A capacity model based on charging process for state of health estimation of lithium-ion batteries. Applied Energy, 2016, 177(2): 537-543. DOI:10.1016/j.apenergy.2016.05.109 (  0) 0) |
| [13] |
Narayanrao R, Joglekar M M, Inguva S. A phenomenological degradation model for cyclic aging of lithium ion cell materials. Journal of the Electrochemical Society, 2012, 160(1): 125-137. DOI:10.1149/2.013302jes (  0) 0) |
| [14] |
Zou C F, Manzie C, Nesic D. Model predictive control for lithium-ion battery optimal charging. IEEE Transactions on Mechatronics, 2018, 23(2): 947-957. DOI:10.1109/TMECH.2018.2798930 (  0) 0) |
| [15] |
Zhang C H, Zhang Y, Li Y. A novel battery state-of-health estimation method for hybrid electric vehicles. IEEE Transactions on Mechatronics, 2015, 20(5): 2604-2612. DOI:10.1109/TMECH.2014.2371919 (  0) 0) |
| [16] |
Chen Z, Mi C C, Fu Y H, et al. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. Journal of Power Sources, 2013, 240(3): 184-192. DOI:10.1016/j.jpowsour.2013.03.158 (  0) 0) |
| [17] |
Wu J, Wang Y, Zhang X, et al. A novel state of health estimation method of Li-ion battery using group method of data handling. Journal of Power Sources, 2016, 327(31): 457-464. DOI:10.1016/j.jpowsour.2016.07.065 (  0) 0) |
| [18] |
Zenati A, Desprez P, Razik H. Estimation of the SOC and the SOH of li-ion batteries, by combining impedance measurements with the fuzzy logic inference. Proceedings of the IECON 2010-Conference on IEEE Industrial Electronics Society. Piscataway: IEEE, 2011. 11726423. DOI: 10.1109/IECON.2010.5675408.
(  0) 0) |
| [19] |
Liu D T, Xie W, Liao H T, et a. An integrated probabilistic approach to lithium-ion battery remaining useful life estimation. IEEE Transactions on Instrumentation and Measurement, 2015, 64(3): 660-670. DOI:10.1109/TIM.2014.2348613 (  0) 0) |
| [20] |
Chaoui H, Ibe-Ekeocha C C. State of charge and state of health estimation for lithium batteries using recurrent neural networks. IEEE Transactions on Vehicular Technology, 2017, 66(9): 8773-8783. DOI:10.1109/TVT.2017.2715333 (  0) 0) |
| [21] |
Lin H T, Liang T J, Chen S M. Estimation of battery state of health using probabilistic neural network. IEEE Transactions on Industrial Informatics, 2013, 9(2): 679-685. DOI:10.1109/TⅡ.2012.2222650 (  0) 0) |
| [22] |
Zou Y, Hu X S, Ma H M, et al. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. Journal of Power Sources, 2015, 273(31): 793-803. DOI:10.1016/j.jpowsour.2014.09.146 (  0) 0) |
| [23] |
Andre D, Appel C, Soczka-Guth T, et al. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. Journal of Power Sources, 2013, 224(5): 20-27. DOI:10.1016/j.jpowsour.2012.10.001 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


