2. Laboratory of Electromagnetic Processes of Materials, Northeastern University, Shenyang 110004, China
Recently, many people investigated a model for transport phenomena called the totally asymmetric simple exclusion process (TASEP) with applications to study surface growth[1], protein synthesis[2], molecular motors[3], vehicular traffic[4], etc. The TASEP model is a simplified version of ASEP, where particles are allowed to move stochastically and independently along a particular direction (generally, from left to right). Because of its conceptual simplicity, TASEP and its extension models are applied in vehicular traffic modeling, such as various updates and lattice geometries applied on a one-dimensional single lane TASEP[5-12].
Kolomeisky[5] and Liu et al.[6] studied TASEP with open boundary conditions with one defect site by different updated rules, random rule, and updated rule, respectively. Based on Ref. [5], Shaw et al.[2] investigated arbitrary size particles in TASEP with a single defect site, indicating the steady phase diagrams are identical to that in standard TASEP with shifts of phase boundaries. Subsequently, Liu et al.[7] and Xiao et al.[8] explored TASEP models with a range of consecutive defect sites by random and parallel updated rules. The results show that the steady state diagrams are more complex. More recently, two refined mean field methods have been employed to examine the influence of a single defect site near the lattice boundary on the steady state properties[9]. Both methods can describe TASEP with stronger molecular interactions better, and the obtained results agree with simulations.
TASEP with ramps can be used to depict vehicular traffic. At present, many studies are focused on the TASEP with ramps. Some important results have been obtained[10-12], such as zone inhomogeneity and on-ramp on TASEP. The existence of the MC/MC, MC/LD and MC/HD phases in the steady phase diagram resulted from the different relationship between hopping rate p and on-ramp rate q[10].
More recently, many researchers have focused on traffic management strategies because these policies are vital for lightening traffic congestions and improving traffic flows at bottlenecks. A junction can be defined as a place where traffic alters different lines, directions, or joints. However, it always becomes system's bottleneck due to the low efficiency of traffic flow in all directions. A junction of two parallel lanes merged into a single lane has been studied by TASEP model[13]. An improved domain wall method has been introduced to discuss the first-order phase boundaries due to the density correlations. Afterward, a multi-input multi-output junction was investigated by TASEP with the parallel updated rule[14], displaying the potential applications of a junction.
Nevertheless, in reality, vehicles' different road priority in traffic (or bandwidth requirements in internet traffic) results in unequal injection rates. Therefore, the influence of unequal entrance rates with junction[15] on the traffic has been explored, implying that the stationary-state phases depended on the entrance rate of the first sub-lane. Based on this model, the influences of hopping rates on the system have also been obtained[16], namely, the phase diagram structure qualitatively varied with different hopping rate. Consequently, they were extensively investigated by TASEP[17-25]. Traffic management policies always control the entrance (α) or exit (β) rate of particles (vehicles) according to the lane state, for instance, the lane density[18-22]. In the light of the lattice density, the variation of input rate was introduced by Woelki[22] with the TASEP approach. This method is understood as a type of ramp metering in vehicular traffic[26-27].
However, in reality, there are many road network nodes in the traffic system, which will become bottlenecks if the control strategy is weak. We explore the system through the TASEP model with the exit feedback control strategy to improve traffic flows at road network nodes. This paper considers a feedback control strategy for a single lane TASEP model and investigates how the exit control strategy affects the traffic flow rate. All possible input rates at which the system achieves maximum possible current under feedback will be shown.
1 Model DescriptionIn this section, TASEP with open boundaries under exit control feedback policy will be described, as illustrated in Fig. 1.
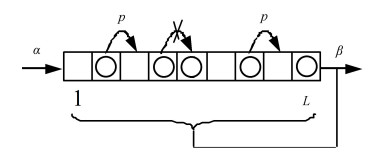
|
Fig.1 Graphic view of TASEP with open boundaries under the exit control feedback policy |
The system contains L sites in one dimensional lattice, and there are only two states, occupied and empty, for each site. A particle which is at site i will attempt to go to site i+1 with rate p, only the site i+1 is vacant. Note that the particle will remain at site i, if site i+1 is occupied. In addition, particles can enter and exit the system from the left boundary (empty) and the right boundary (occupied) with rates α and β, respectively[28]. Importantly, the leaving rate β is defined as the average over the occupancy probability of all L sites (ρi) as follows:
| $ \beta = \frac{1}{L}\sum\limits_{i = 1}^L p {\rho _i} $ | (1) |
Obviously, the system will reduce to the normal TASEP when the exit control feedback policy is canceled. All kinetic properties can be given by exact solutions[29], and the system characteristics are as follows.
For low density (LD) phase, the entrance rate dominates its kinetic when α and β satisfy α < β, α < p/2. The particle current J, the particle densities of the left boundary ρ1, the bulk ρbulk and the right boundary ρL are
| $ \begin{array}{l} J = \alpha \left( {1 - \frac{\alpha }{p}} \right), {\rho _1} = \frac{\alpha }{p}, {\rho _{{\rm{bulk}}}} = \frac{\alpha }{p}\\ \;\;\;\;{\rho _L} = \alpha \left( {1 - \frac{\alpha }{p}} \right)/\beta \end{array} $ | (2) |
For the high density (HD) phase, the kinetics depends on the exiting process as β < α, β < p/2. Meanwhile, the particle current and densities are given by
| $ \begin{array}{l} J = \beta \left( {1 - \frac{\beta }{p}} \right), {\rho _1} = 1 - \beta \left( {1 - \frac{\beta }{p}} \right)/\alpha , \\ \;\;{\rho _{{\rm{bulk }}}} = 1 - \frac{\beta }{p}, {\rho _L} = 1 - \frac{\beta }{p} \end{array} $ | (3) |
At last, the maximum current (MC) phase is related to the large entrance and exit rates α>p/2, β>p/2. Therefore, we can describe the particle current and densities as
| $ J = \frac{p}{4}, {\rho _1} = 1 - \frac{p}{{4\alpha }}, {\rho _{{\rm{bulk }}}} = \frac{1}{2}, {\rho _L} = \frac{p}{{4\beta }} $ | (4) |
The assumption that the sensors on various sections of the road are able to measure the average occupancy of sites is applied in our study. Clearly, the control feedback policy was used to lead to the system achieving maximum flow rate whenever possible. According to Eqs. (2)-(4), the recurrence relationship for the average occupancies of each steady phase can be obtained by using mean field approximation as follows:
| $ {\rho _1} = 1 - \frac{J}{\alpha }, {\rho _{i + 1}} = 1 - \frac{1}{p} \cdot \frac{J}{{{\rho _i}}}, {\rho _L} = \frac{J}{\beta } $ | (5) |
Therefore, Eq. (5) can be used to simplify Eq. (1). We note that the grand total ρi exists in any phase, ρbulk dominates over the values at the endpoints, and the limit average densities converge to ρbulk. As L is large enough, it yields
| $ \begin{array}{l} \beta = \frac{1}{L}\sum\limits_{i = 1}^L p {\rho _i} = \frac{1}{L}\left( {p{\rho _1} + \sum\limits_{i = 2}^{L - 1} p {\rho _i} + p{\rho _L}} \right) = \\ \;\;\;\;\frac{1}{L}\left[ {p\left( {1 - \frac{J}{\alpha }} \right) + \sum\limits_{i = 1}^{L - 2} p \left( {1 - \frac{1}{p} \cdot \frac{J}{{{\rho _i}}}} \right) + p\left( {\frac{J}{\beta }} \right)} \right]\\ \;\;\;\;{\rm{ = }}\\ \;\;\;\;\frac{1}{L}\left[ {Lp + \frac{1}{p}\left( {\frac{J}{\beta } - \frac{J}{\alpha } - 1} \right) - \sum\limits_{i = 1}^{L - 2} {\frac{J}{{{\rho _i}}}} } \right] = \\ \;\;\;\;p - \frac{J}{{{\rho _{{\rm{bulk }}}}}} \end{array} $ | (6) |
According to Eq. (2), J/ρbulk=p-α is obtained when the system is in the LD phase, implying that
| $ \beta = \alpha $ | (7) |
While according to Eq. (3), we can obtain J/ρbulk=β when the system lies in the HD phase, indicating that
| $ \beta = p/2 $ | (8) |
At last, when the system is in the MC phase, J/ρbulk=p/2 is obtained according to Eq. (4), which again leads to
| $ \beta = p/2 $ | (9) |
Therefore, the effect of exit control policy is a collapse of the phase transition diagram Fig. 2(a) onto the phase transition line as shown in Fig. 2(b). Obviously, J is independent of β and adjusted based on α. The current of the system will be in one of the two possible phases under the control policy as follows:
| $ \alpha < \frac{p}{2}, J \to \alpha \left( {1 - \frac{\alpha }{p}} \right) $ | (10) |
| $ \alpha > \frac{p}{2}, J \to \frac{p}{4} $ | (11) |
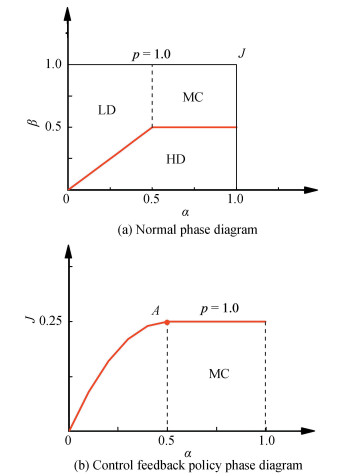
|
Fig.2 Exit control feedback policy changes the phase diagram by collapsing the phase diagram on the red line |
According to Eqs. (10) and (11), the exit control feedback strategy leads to the system operating at the MC phase even in the HD phase. This behavior is summarized in Table 1. In addition, the coordinate of the Point A in Fig. 2(b) is defined as the phase transformation point, and it depends on the hopping rate p, namely, A (α= p/2, J= p/4), as illustrated in Fig. 3. Evidently, the left boundary of the MC phase will move towards right with the growth of p; meanwhile, J increases. The current and the entrance rate for Point A satisfy J=α/2.
| Table 1 Effect of exit control feedback policy on one dimensional TASEP |
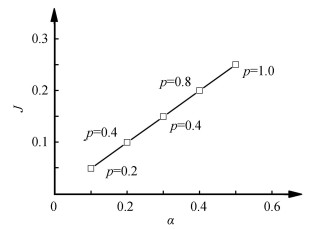
|
Fig.3 Relationship of Point A coordinate with different hopping rates p |
When the density of the system is obtained and equal to 0.6, according to J/ρbulk=β, β= p/2.4 is obtained. At this time, the parameters p is given as 0.6, and the exit rate can be calculated and β= 0.25. According to Eq. (3), the density and current of the system can be obtained as 0.67 and 0.134, respectively. Clearly, the theoretical results are approximately equal to our real value. The error is caused by the fact that the correlation between neighboring particles was ignored.
3 ConclusionsThe investigation in this paper presents the effect of the exit control feedback policy for TASEP on one-dimensional single lane. According to the exit control feedback strategy, the leaving rate β can be rewritten as β= p-J/ρbulk. When the system is in the free flow (the LD phase), the entrance rate satisfies α < p/2, and the exit rate reduces its value. Importantly, the exit rate maintains itself at β= p/2 to achieve the system's maximum flow rate for all other phases.
Additionally, the phase transformation Point A can be described by the coordinate (α= p/2, J= p/4). It is decided by the hopping rate p, and the current and the entrance rate for Point A satisfy J=α/2. Note that J grows with the increase of p.
The results indicate that our study model can be employed to control the traffic flow of the highway system. When the density of the highway system reaches high density, the traffic flow decreases sharply. At this time, the speed of vehicles can be adjusted to control the exit rate, thus leading to the traffic flow being in the maximum current and reducing the clogging time.
| [1] |
Meakin P, Ramanlal P, Sander L M, et al. Ballistic deposition on surfaces. Physics Review A, 2008, 34: 5091-5103. DOI:10.1103/PhysRevA.34.5091 (  0) 0) |
| [2] |
Shaw L B, Kolomeisky A B, Lee K H. Local inhomogeneity in asymmetric simple exclusion processes with extended objects. Journal of Physics A: Mathematical and General, 2003, 37(6): 2105-2113. DOI:10.1088/0305-4470/37/6/010 (  0) 0) |
| [3] |
Klumpp S, Lipowsky R. Traffic of molecular motors through tube-like compart-ments. Journal of Statistical Physics, 2003, 113: 233-268. DOI:10.1023/A:1025778922620 (  0) 0) |
| [4] |
Liu Y N, Xiao W C, Dong D, et al. The effect of single on-ramp with constrained resources on the density of asymmetric simple exclusion processes. Renewable and Sustainable Energy Reviews, 2016, 62: 815-820. DOI:10.1016/j.rser.2016.05.038 (  0) 0) |
| [5] |
Kolomeisky A B. Asymmetric simple exclusion model with local inhomogeneity. Journal of Physics A, 1998, 31(4): 1153. DOI:10.1088/0305-4470/31/4/006 (  0) 0) |
| [6] |
Liu M Z, Wang R L, Jiang R, et al. Defect-induced transitions in synchronous asymmetric exclusion processes. Physics Letters A, 2009, 373(2): 195-200. DOI:10.1016/j.physleta.2008.11.011 (  0) 0) |
| [7] |
Liu M Z, Wang R L, Hu M B, et al. Synchronous asymmetric exclusion processes with an extended defect. Physics Letters A, 2010, 374(13-14): 1407-1413. DOI:10.1016/j.physleta.2010.01.001 (  0) 0) |
| [8] |
Xiao S, Cai J J, Liu F. Zone inhomogeneity with the random asymmetric simple exclusion process in a one-lane system. Chinese Physics B, 2009, 18(11): 4613-4621. (  0) 0) |
| [9] |
Dong J J, Zia R K P, Schmittmann B. Understanding the edge effect in TASEP with mean-field theoretic approaches. Journal of Physics A: Mathematical and Theoretical, 2008, 42: 015002. DOI:10.1088/1751-8113/42/1/015002 (  0) 0) |
| [10] |
Xiao S, Bai J Y. Investigation of asymmetric simple exclusion processes with zoned inhomogeneity and on-ramp. Modern Physics B, 2013, 27(9): 1350062. DOI:10.1142/S0217984913500620 (  0) 0) |
| [11] |
Parmeggiani A, Franosch T, Frey E. Phase coexistence in driven one-dimensional transport. Physical Review Letter, 2003, 90(8): 086601. DOI:10.1103/PhysRevLett.90.086601 (  0) 0) |
| [12] |
Qiu K, Yang X Q, Zhang W, et al. Density profiles in the totally asymmetric exclusion processes with both local inhomogeneity and Langmuir kinetics. Physica A: Statistical Mechanics and its Applications, 2007, 373: 1-10. DOI:10.1016/j.physa.2006.06.015 (  0) 0) |
| [13] |
Pronina E, Kolomeisky A B. Theoretical investigation of totally asymmetric exclusion processes on lattices with junctions. Journal of Statistical Mechanics: Theory and Experiment, 2005, 7: 07010. DOI:10.1088/1742-5468/2005/07/P07010 (  0) 0) |
| [14] |
Liu M Z, Wang R L. Asymmetric exclusion processes on m-input n-output junctions with parallel update. Physica A: Statistical Mechanics and its Applications, 2009, 388(19): 4068-4074. DOI:10.1016/j.physa.2009.05.048 (  0) 0) |
| [15] |
Xiao S, Liu M.Z, Wang J J, et al. Effect of unequal injection rates on asymmetric exclusion processes with junction. Chinese Physics B, 2011, 20(6): 060509. DOI:10.1088/1674-1056/20/6/060509 (  0) 0) |
| [16] |
Xiao S, Cai J J, Liu F, et al. Effect of unequal injection rates and different hopping rates on asymmetric exclusion processes with junction. Chinese Physics B, 2010, 19(9): 090202. DOI:10.1088/1674-1056/19/9/090202 (  0) 0) |
| [17] |
Imai T, Nishinari K. Optimal information provision for maximizing flow in a forked lattice. Physical Review E, 2015, 91(6): 062818. DOI:10.1103/PhysRevE.91.062818 (  0) 0) |
| [18] |
Mitra M K, Chatterjee S. Boundary induced phase transition with stochastic entrance and exit. Journal of Statistic Mechanics: Theory and Experiment, 2014, P10019. DOI:10.1088/1742-5468/2014/10/P10019 (  0) 0) |
| [19] |
Woelki M. Density-feedback control in traffic and transport far from equilibrium. Physical Review E, 2013, 87(6): 062818. DOI:10.1103/PhysRevE.87.062818 (  0) 0) |
| [20] |
Xiao S, Chen X Y, Liang R Q, et al. Impact of effective injection rates on density and phase diagram at the branching point. International Journal of Modern Physics B, 2018, 32(26): 1850291. DOI:10.1142/S0217979218502910 (  0) 0) |
| [21] |
Xiao S, Chen X Y, Liang R Q, et al. Off-ramp on boundary of totally asymmetric simple exclusion process with different hopping rates. Proceedings of the 2018 IEEE International Conference on Automation, Electronics and Electrical Engineering (AUTEEE). Piscataway: IEEE, 2018. 350-353. DOI: 10.1109/AUTEEE.2018.8720778.
(  0) 0) |
| [22] |
Woelki M. Density-feedback control in traffic and transport far from equilibrium. Physics Review E, 2013, 87(6): 062818. DOI:10.1103/PhysRevE.87.062818 (  0) 0) |
| [23] |
Nagatani T. Traffic jam at adjustable tollgates controlled by line length. Physica A: Statistical Mechanics and its Applications, 2016, 442: 131-136. DOI:10.1016/j.physa.2015.09.051 (  0) 0) |
| [24] |
Popkov V, Salerno M, Schütz G M. Asymmetric simple exclusion process with periodic boundary driving. Physical Review E-Statistical, Nonlinear, and Soft Matter Physics, 2008, 78(1): 011122. DOI:10.1103/physreve.78.011122 (  0) 0) |
| [25] |
Arita C, Foulaadvand M E, Santen L. Signal optimization in urban transport: a totally asymmetric simple exclusion process with traffic lights. Physical Review E, 2017, 95(3-1): 032108. DOI:10.1103/PhysRevE.95.032108 (  0) 0) |
| [26] |
Gomes G, Horowitz R. Optimal freeway ramp metering using the asymmetric cell transmission model. Transportation Research Part C-Emerging Technologies, 2006, 14(4): 244-262. DOI:10.1016/j.trc.2006.08.001 (  0) 0) |
| [27] |
Papageorgiou M, Kotsialos A. 2000 Freeway ramp metering: an overview. IEEE Transactions on Intelligent Transportation Systems, 2002, 3(4): 228-239. DOI:10.1109/TITS.2002.806803 (  0) 0) |
| [28] |
Spitzer F. Interaction of Markov processes. Advances in Mathematics, 1970, 5(2): 246-290. DOI:10.1016/0001-8708(70)90034-4 (  0) 0) |
| [29] |
Ebrahim Foulaadvand M, Chaaboki S, Saalehi M. Characteristics of the asymmetric simple exclusion process in the presence of quenched spatial disorder. Physical Review E-Statistical, Nonlinear, and Soft Matter Physics, 2007, 75(1): 011127. DOI:10.1103/PhysRevE.75.011127 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


