Cylindrical roller bearings(CRBs) are used for fast operations because of their low-friction torque characteristics. They have the capacity to sustain large radial loads and a few thrust loads at moderate speeds and are being used in several industries like the aerospace, automobiles, and marines. If equipped with few lubrication holes, a special retainer and a specially contoured raceway and roller profiles, it can operate satisfactorily even under the high-speed and high-load conditions for applications in aerospace industry. There are many different causes of rolling bearing failure, for example, the fatigue, wear, running marks, corrosion/erosion, over-hitting, and overload. However, fatigue is often considered the classic failure mode of rolling bearings, which is related with the dynamic capacity of the bearing. To have a minimum variation of the objective function (e.g., fatigue life of the bearing), in case of presence of manufacturing tolerances in the design variables, the optimization must be a robust design. The robust design also ensures that the design is still feasible, i.e., the dimensions obtained after robust optimization are such that even if there is variation in their value during manufacturing, the resulting variation in the objective function will be within a desirable range. In the present study, a robust design optimization method has been used, which is based on the flexible physical programming approach. Flexibility of robust design optimization means that the designer is allowed to specify the various levels of each design variable as well as of the objective function.
Messac and Ismail Yahaya[1] came forth with a methodology for the robust design optimization, the methodology being dependent on a flexible physical programming approach and ensuring that the objective function varies by minimum possible value in case of uncertainties or variations in design variables as per designer's choice. Chen et al.[2] examined how effective the physical programming approach is in ensuring that the design outcome does turn out to be a robust one and established that the physical programming approach is superior over the other conventional methods. Giassi et al.[3] used robust design techniques to develop a multi-disciplinary optimization method for use in concurrent engineering. The Taguchi's design[4] model was mainly based on the loss function. With this model, the quality indeed got improved, but there were several inefficiencies in the method, and for problems with non-linearity of higher orders, it would often give less than satisfactory results. Hence, for the present study, the robust design has been achieved using flexible programming approach, which treats each objective function and its desired tolerance, and the design variables and their maximum possible tolerances independently, while expresses designer preference, hence eliminating all the above stated deficiencies.
Changsen[5] examined the rolling bearings to explain their load distribution, deformation, kinematics, geometry, and stresses, hence calculating the dynamic load rating, static load rating, life and Elasto-hydrodynamic lubricant film thickness. Harris[6] analyzed the rolling element bearings comprehensively. Seireg[7] studied the use of different methods of optimization in designing the mechanical devices, and also analyzed a few of its illustrative examples. Deb et al.[8] developed the NSGA-Ⅱ algorithm, which is implemented in the current study. NSGA-Ⅱ algorithm possesses less computational complexity, gives better convergence and better spread for Pareto optimal fronts as compared with its contemporaries. Branke et al.[9] studied multi-objective evolutionary algorithm, but in the modified form, which can concentrate the search on knee regions. Hirani[10] optimized the hydrodynamic bearings to minimize the power loss, temperature rise, and oil feed flow.
Link et al.[11] performed optimization on a suction muffler and bearing to reduce the bearing power losses and enhance the suction muffler energy efficiency using the genetic algorithm (GA). Saruhan et al.[12] developed a method for optimum design of tilting pad bearings, which is based on GA. Hirani and Suh[13] performed the optimization of fluid-film steadily loaded journal bearings to minimize the power loss and oil flow. Wang[14] studied the usefulness of parallel optimization for the lubrication analysis with the help of GA. Kim et al.[15] developed a method for identification of bearing parameters, which was based on the scheme of global optimization making use of measured unbalance response of rotor-bearing system. Gupta et al.[16] performed single and multi-objective optimization of ball bearings taking the dynamic capacity, static capacity, and elasto-hydrodynamic minimum film thickness as the objective functions. The study also deals with sensitivity analysis of various design variables to observe their impact on the objective functions. Xie et al.[17] did a study on grease lubricated ball bearing's Elasto-hydrodynamic lubrication and performed a numerical calculation on it. Tiwari et al.[18] performed the optimization of dynamic capacity for a tapered roller bearing and then carried out a sensitivity analysis to find out the effect of design variables on dynamic capacity. Solanki et al.[19] performed bearing design optimization to maximize its load carrying capacity with respect to clearance, and to minimize the film thickness and temperature rise. Panda et al.[20] took help of the particle-swarm optimization (PSO) algorithm for a radial ball bearing to maximize its fatigue life. Dragoni[21] performed optimization of tapered roller bearings to maximize its static load capacity taking the internal dimensions as design variables. Tiwari and Chandran[22] performed the multi-objective optimization of CRBs taking the dynamic capacity, Elasto-hydrodynamic minimum film thickness, and the maximum temperature as objective functions. The study also deals with comparison of life of the customary and optimized bearings. Dewangan et al.[23] performed bearing optimization to minimize the power loss using GA. Kim et al.[24] utilized a micro-genetic algorithm to optimize an angular contact ball bearing, thereby enhancing the values of its radial and axial stiffness. Tudose et al.[25] did a study to find out the optimal bench bearing arrangement in order to maximize its life. Kalyan and Tiwari[26] performed the multi-objective optimization of needle roller bearings taking dynamic capacity and elasto-hydrodynamic minimum film thickness as the objective functions. The study also deals with sensitivity analysis to find out the variations in the two objective functions with specific variation in design variables. Verma and Tiwari[27] performed robust single-objective optimization of tapered roller bearing taking dynamic capacity as objective function. It gives a robust optimal design by taking variability into account. Salunkhe et al.[28] utilized different optimization techniques to find out the usefulness of the modified design of rolling contact bearing. In addition to the above mentioned literature, standard texts[29-30] have also been referred to to get a basic understanding of bearings and optimization algorithms. Hardly any study has yet been done on the robust optimization of rolling bearings, as there are always some manufacturing tolerances in the bearing design drawing. With these objectives in mind, the robust design optimization of CRBs is done using the NSGA-Ⅱ algorithm in this study.
In the present paper, a constrained non-linear robust optimization problem for the design of CRB has been proposed and a detailed description of the procedure to solve it is described. The problem consists of nine design variables, four of which are basic design variables and the remaining are constrain parameters. The basic design variables are basic geometries of the bearing that directly affect the dynamic capacity. The five constraint parameters are used to restrict the feasible design space. The dynamic capacity is optimized, while due to the tolerances in the bearing dimensions, its variation has been minimized and the tolerances have been taken from the bearing catalogues which help in finding the upper and lower bounds of the design variables. The main work has been done on the mathematical problem formulation of the robust optimization. Constraints based on geometry and strength criterion have been formulated. A total of nineteen constraints for deterministic optimization and twenty-one constraints for robust optimization have been included. The design problem has been optimized by real-coded GA and the dynamic capacity obtained after optimization is more than that available in the standard catalogue.
Hence, in the present section, in addition to the brief introduction, a summary of the related works done previously on bearing design has also been stated and motivation for the present work is derived. In Section 1, the geometrical aspects of CRBs, on which the present study is focused, have been explained in brief. Besides, mathematical formulations have been derived based on studies done previously in similar fields, i.e., the robust optimization, and the single and multi-objective optimizations of rolling-element bearings. The section has been further divided into sub-sections that deal individually with the formulations of objective functions, constraints, and variable bounds required for the optimization algorithm. In Section 2, implementation of NSGA-Ⅱ to rolling element bearing using different parameters in the optimization algorithm NSGA-Ⅱ have been discussed. In Section 3, the results obtained have been discussed quantitatively and qualitatively, and in Section 4 conclusions have been made regarding the nature of obtained results.
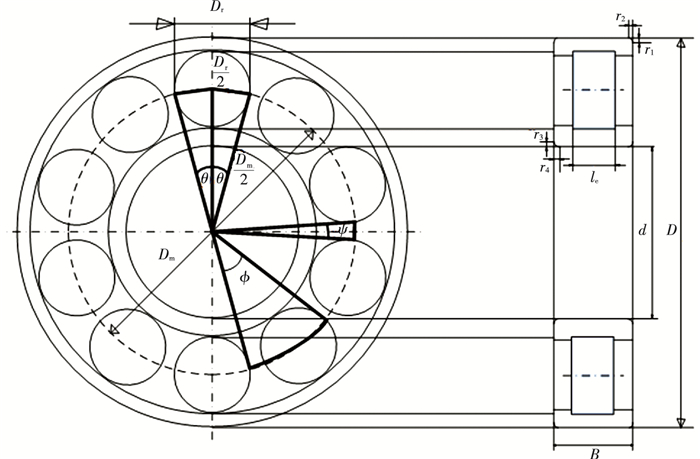
1 Geometrical Aspects and Problems Formulation for Robust Optimization of CRBsCRB is identified using standard boundary dimensions, namely, the outer diameter (D), bore diameter (d), and bearing width (B). To avoid sharp edges, chamfering is provided on the faces of both raceways. As shown in Fig. 1, the chamfering dimensions for the roller bearing are the outer ring chamfer height r1, the outer ring chamfer width r2, the inner ring chamfer height r3, and the inner ring chamfer width r4. The minimum value of these chamfering radii is provided in the bearing catalogues. The internal geometry of CRB is described well using the following: roller diameter Dr, pitch diameter Dm, number of rollers Z, and effective roller length le. For the present problem, the boundary dimensions and minimum chamfer radius are consulted from the SKF general catalogue[31].
|
Fig.1 Typical CRB cross-section |
In the current study, a robust optimization (which is non-linear in nature) will be performed for CRBs, for which an evolutionary algorithm NSGA-Ⅱ has been chosen because of its elite-preserving strategy, explicit diversity-preserving mechanism, and overall ability to preserve a better solution spread. First, a brief on solving a deterministic optimization is provided.
A deterministic optimization problem comprises 3 parts: objectives, constraints, and variable bounds.
1) Objectives:
Minimize/Maximize
| $ f(\boldsymbol{x}) $ | (1) |
where x refers to the design variable vector to be optimized and f is the objective function. Here, the design variable vector x consists of the variables to be used for the deterministic optimization, which in case of CRB is given as
| $ \mathit{\boldsymbol{x}} = {\left[ {{D_{\rm{m}}}{D_{\rm{r}}}Z{l_{\rm{e}}}{K_{D\min }}{K_{D\max }}\varepsilon \;e\;\beta } \right]^{\rm{T}}} $ | (2) |
where KDmax is the maximum roller diameter limiter, KDmin is the minimum roller diameter limiter, ε is the parameter for the outer ring strength consideration, e is the parameter for mobility condition and β is the parameter for the effective length of the roller. The parameters Dm, Dr, Z and le represent the bearing internal geometry. The remaining five parameters give the bearing a feasible design space in the form of constraints to make the dimensions obtained from optimization possible for manufacture. The range of values needs to be input for each of these nine variables, out of which a set of variables is obtained that gives the optimum objective function. The range for each of these variables will be discussed in Section 1.3.
2) Constraints:
Subject to
| $ g_j(\boldsymbol{x}, \boldsymbol{p}) \geqslant 0, j=1, 2, \cdots \cdots, J $ | (3) |
where p refers to vector of those parameters in the constraints that are not present in the objective function:
| $ \boldsymbol{p}=\left[\begin{array}{lll} D & d & B \end{array}\right]^{\mathrm{T}} $ | (4) |
whose value remains constant during optimization, but may undergo variations during manufacturing, hence their variation must be considered, which will be discussed in the robust optimization; g refers to the design constraints for deterministic optimization; j is the number of design constraints used in deterministic optimization.
The values for these parameters will be discussed in Section 1.3.
3) Variable Bounds:
| $ \boldsymbol{x}_l^{(\mathrm{L})} \leqslant \boldsymbol{x}_l \leqslant \boldsymbol{x}_l^{(\mathrm{U})}, l=1, 2, \cdots \cdots, L $ | (5) |
Decision variable xl is the l-th element of the design variable vector x, and will take a value within the lower and upper bounds xl(L) and xl(U), respectively; superscript (L) refers to lower limit and superscript (U) refers to upper limit. The procedure to solve robust optimization is explained as follows.
As has been explained in the work by Messac and Ismail Yahaya[1] on the robust design using physical programming approach, certain modifications need to be made in the objective function, constraints, and variable bounds in order to make the design robust. The new objective functions, constraints, and design space are formulated as follows. Hence, the physical programming problem model can be expressed as
a) Objective function:
| $ \min \limits_x\{f(\boldsymbol{x})+\Delta f(\boldsymbol{x}, \Delta \boldsymbol{x})\} $ | (6) |
The only change from Eq.(1) in the case of deterministic optimization is the inclusion of term Δf, which comprises terms from the vector Δx; although the design variable vector to be used for optimization is still x only. It must be noted that Δ may be the variation in design variable, constraint or objective function. The vector Δx comprises
| $ \Delta \boldsymbol{x}=\left[\begin{array}{lll} \Delta D_{\mathrm{m}} & \Delta D_{\mathrm{r}} & \Delta l_{\mathrm{e}} \end{array}\right]^{\mathrm{T}} $ | (7) |
where ΔDm is the bearing pitch diameter tolerance, ΔDr is the roller diameter tolerance, and Δle is the roller length tolerance. The value of each of these tolerances has to be input by the user. Decision of the value for each of these tolerances will be discussed in Section 1.3.
b) Subject to the constraints
| $ \begin{gathered} g_j(\boldsymbol{x}, \boldsymbol{p}) \geqslant \Delta g_j(\boldsymbol{x}, \boldsymbol{p}, \Delta \boldsymbol{x}, \Delta \boldsymbol{p}) \\ j=1, 2, \cdots \cdots, J \end{gathered} $ | (8) |
The change from Eq.(3) in the case of deterministic optimization is the inclusion of term Δg, which comprises of terms from the vector Δx and Δp. The vector Δp comprises
| $ \Delta \boldsymbol{p}=\left[\begin{array}{lll} \Delta D & \Delta d & \Delta B \end{array}\right]^{\mathrm{T}} $ | (9) |
where ΔD is the bearing outer diameter tolerance, Δd is the bearing bore diameter tolerance, and ΔB is the bearing width tolerance. Here the value for each of these tolerances must be input by the user as well. Decision of the value for each of these tolerances is discussed in Section 1.3.
The constraints from Eq. (9) can be further stated as
| $ \begin{gathered} h_k(\boldsymbol{x}, \boldsymbol{p})=g_k(\boldsymbol{x}, \boldsymbol{p})-\Delta g_k(\boldsymbol{x}, \boldsymbol{p}, \Delta \boldsymbol{x}, \Delta \boldsymbol{p}) \\ k=1, 2, \ldots, K \end{gathered} $ | (10) |
where K is the number of robust design constraints used in robust optimization. Eq.(10) must be written in the inequality form as
| $ h_k(\boldsymbol{x}, \boldsymbol{p}) \geqslant 0 $ | (11) |
where h is the design constraint in inequality form. It must be noted that the number of deterministic optimization constraints is different from the number of robust design constraints. Hence, they must be represented by different values of "J" and "K", respectively. Eqs.(8) and (10) show the conversion of each deterministic optimization constraint to the robust optimization constraint. For Eq. (8), only the deterministic constraint is utilized, hence "j" is used for this equation. While for Eq. (10), it is already converted to robust design constraint, hence it is shown by "k", where k is the number of robust design constraints used. But it must be noted that for all those constraints that are getting converted from deterministic to robust, the values of "J" and "K" are the same, although here the values differ for "j" and "k" due to the addition of two new constraints in the robust optimization prescribing the bounds of variation in the objective function. The presence of these two extra constraints in case of the robust optimization shall be explained in details in Section 1.2.
The bounds for design variables undergoing manufacturing variations will change from those in Eq.(5) and the new variable bounds are given as
| $ x_l^{(\mathrm{L})}+\Delta x_l \leqslant x_l \leqslant x_l^{(\mathrm{U})}-\Delta x_l, l=1, 2, \cdots \cdots, L $ | (12) |
where L is the number of design variables x. To find out the variation in objective function, as seen in Eq.(6), it can be calculated as
| $ \Delta f(\boldsymbol{x}, \Delta \boldsymbol{x})=\sqrt{\sum\limits_{l=1}^L\left(\frac{\partial f}{\partial x_l} \Delta x_l\right)^2}, j=1, 2, \cdots \cdots, J $ | (13) |
Similarly, the changes made in constraints of deterministic optimization to convert it to a robust optimization as seen in Eq.(8) are as follows:
| $ \Delta g_j(\boldsymbol{x}, \boldsymbol{p}, \Delta \boldsymbol{x}, \Delta \boldsymbol{p})=\sum\limits_{l=1}^L\left|\frac{\partial g_j}{\partial x_l} \Delta x_l\right|+\sum\limits_{m=1}^M\left|\frac{\partial g_j}{\partial p_m} \Delta p_m\right| $ | (14) |
where M is the number of parameters p.
1.1 Objective FunctionsThe function to maximize/minimize is designed here. The dynamic capacity Cd is optimized, which is defined as "constant radial load that can be endured by a group of evidently similar bearings for a rating life of one million revolutions of the inner ring for a static load and fixed outer ring". The expression for dynamic capacity of CRB is mathematically defined as[6]
| $C_{\mathrm{d}}=b_{\mathrm{m}} f_{\mathrm{c}}\left(i l_{\mathrm{e}}\right)^{\frac{7}{9}} Z^{\frac{3}{4}} D_{\mathrm{r}}^{\frac{29}{27}} $ | (15) |
with
| $ f_{\mathrm{c}}=207.9 \lambda \nu \gamma^{\frac{2}{9}} \frac{(1-\gamma)^{\frac{29}{27}}}{(1+\gamma)^{\frac{1}{4}}}\left[1+\left\{1.04\left(\frac{1-\gamma}{1+\gamma}\right)^{\frac{143}{108}}\right\}^{\frac{9}{2}}\right]^{-\frac{2}{9}} $ |
and
| $ \gamma=\frac{D_{\mathrm{r}}}{D_{\mathrm{m}}} $ | (16) |
where bm(=1.36) is a component in Cd to take into account the latest developments in technology, λ(=0.61) is the reduction component for the discrepancies that may occur during the manufacturing and mounting of roller bearing, ν(=1.36) is a component to justify the edge loading and i is number of rows of roller[32]. For the fatigue life calculation, an equivalent radial load is obtained based on actual applied radial and axial loads on the bearing, and the dynamic capacity obtained from Eq. (15) is used in conjunction with the equivalent radial load for the life estimation.
It should be noted that Cd of the bearing depends on material properties as can be seen by the presence of terms like contact stress σ and maximum contact stress for line contact σmaxl in the constraints for optimization of Cd and several other geometrical parameters. For the deterministic design optimization, the aim is to maximize Cd and the expression can be mathematically written as
| $ \max [f(\boldsymbol{x})]=\max \left[C_{\mathrm{d}}\right]=\min \left[-C_{\mathrm{d}}\right] $ | (17) |
Since the robust optimization is performed, the objective is modified according to Eq. (6) as
| $ \min \{f+\Delta f\}, f=-C_{\mathrm{d}} $ | (18) |
As is already known, the variation in the objective function will only be due to the design variables that do have a tolerance and are present in the mathematical formula for the objective function. Therefore, in case of Cd, the variation is not due to the bearing outer diameter D, bore diameter d or width B. Using Eq. (13) and (18), there is
| $ \begin{aligned} & \Delta f=\sqrt{\left(\frac{\partial f}{\partial D_{\mathrm{r}}} \Delta D_{\mathrm{r}}\right)^2+\left(\frac{\partial f}{\partial D_{\mathrm{m}}} \Delta D_{\mathrm{m}}\right)^2+\left(\frac{\partial f}{\partial l_{\mathrm{e}}} \Delta l_{\mathrm{e}}\right)^2}= \\ & \sqrt{\left(\frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{r}}} \Delta D_{\mathrm{r}}\right)^2+\left(\frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{m}}} \Delta D_{\mathrm{m}}\right)^2+\left(\frac{\partial C_{\mathrm{d}}}{\partial l_{\mathrm{e}}} \Delta l_{\mathrm{e}}\right)^2} \\ & \end{aligned} $ | (19) |
Here, only positive sign is taken so as to find out the magnitude of variation in objective function to reduce this magnitude to a minimum possible value using Eq.(18) and make it lie within a desirable range with the constraints in the form of Eq.(11). Detailed explanation of how to obtain
| $ \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{r}}} \Delta D_{\mathrm{r}}, \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{m}}} \Delta D_{\mathrm{m}}, \frac{\partial C_{\mathrm{d}}}{\partial l_{\mathrm{e}}} \Delta l_{\mathrm{e}} $ |
has been given in Appendix A.
Hence, with Eqs. (20)-(22), the revised values of objective function due to tolerances in design variables can be obtained. Then Cd can be maximized and the variation in its magnitude can be minimized with NSGA-Ⅱ algorithm[8, 28].
| $ \begin{array}{l} \frac{{\partial {C_{\rm{d}}}}}{{\partial {D_{\rm{r}}}}}\Delta {D_{\rm{r}}} = {C_{\rm{d}}}\left\{ {\left( {\frac{{35}}{{27}} \cdot \frac{{\Delta {D_{\rm{r}}}}}{{{D_{\rm{r}}}}}} \right) - \left( {\frac{{29}}{{27}} \cdot \frac{{\Delta {D_{\rm{r}}}}}{{{D_{\rm{m}}} - {D_{\rm{r}}}}}} \right)} \right.\\ \left. { - \left( {\frac{1}{4} \cdot \frac{{\Delta {D_{\rm{r}}}}}{{{D_{\rm{m}}} + {D_{\rm{r}}}}}} \right) - \frac{2}{9} \times \frac{{143}}{{24}}\left( {1 - \frac{1}{K}} \right)\left( { - \frac{{\Delta {D_{\rm{r}}}}}{{{D_{\rm{m}}} - {D_{\rm{r}}}}} - \frac{{\Delta {D_{\rm{r}}}}}{{{D_{\rm{m}}} + {D_{\rm{r}}}}}} \right)} \right\} \end{array} $ | (20) |
| $ \begin{aligned} \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{m}}} \Delta D_{\mathrm{m}}= & C_{\mathrm{d}}\left[-\left(\frac{6}{27} \cdot \frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}}\right)+\left(\frac{29}{27}\right)\left(\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}-D_{\mathrm{r}}}-\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}}\right)-\left(\frac{1}{4}\right) \right.\\ &\left. \left(\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}+D_{\mathrm{r}}}-\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}}\right)-\frac{2}{9} .\right. \\ & \left.\frac{143}{24}\left(1-\frac{1}{K}\right)\left\{\left(\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}-D_{\mathrm{r}}}-\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}}\right)-\left(\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}+D_{\mathrm{r}}}-\frac{\Delta D_{\mathrm{m}}}{D_{\mathrm{m}}}\right)\right\}\right] \end{aligned} $ | (21) |
| $ \frac{\partial C_{\mathrm{d}}}{\partial l_{\mathrm{e}}} \Delta l_{\mathrm{e}}=C_{\mathrm{d}} \frac{7}{9} \cdot \frac{\Delta l_{\mathrm{e}}}{l_{\mathrm{e}}} $ | (22) |
The constraints affecting the optimization are defined here. Conversion of the constraints from deterministic optimization to robust optimization is also discussed. Constraints help in defining a feasible domain of values for design parameters and variation in the objective function. For the deterministic optimization[26], 19 constraints are taken. But since the robust optimization is performed, two more constraints are in the present optimization problem. They have been explained as follows. The complete list of constraints used in deterministic as well as robust optimization is given in Table B1 of Appendix B. All the constraints are explained for deterministic optimization.
1) Constraints 1 and 2:
The pitch diameter of the bearing must lie between the bearing inner diameter and bearing outer diameter, thereby ensuring enough chamfering space for the inner and outer rings' sharp corners, as given in Table B1 of Appendix B. The values of r1min and r3min are given as input. Decision of their values is discussed in Section 1.3.
2) Constraints 3 and 4:
The range of values that can be taken for mean diameter of the roller is based on strength as well as geometric considerations, while its lower limit came with the aid of contact stress expression, and the upper limit came with bearing geometry. It must have a minimum value such that the roller can endure the contact stress arising due to external loads. The contact stresses have been explained in details in Constraint 14. The maximum value for roller Dr is limited by boundary dimensions, i.e., bearing outer diameter D and inner diameter d; and it can be calculated by taking into consideration the radii for chamfering of the inner and outer ring corners, so that chamfered corners can be obtained. Therefore, from Ref. [6], the range of values for Dr can be taken as given in Table B1 of Appendix B. Qmax is the maximum normal load acting between the roller and the raceway, and σCmax is the maximum contact stress on the roller. Qmax can be found out using the Stribeck's expression[6], which is given in Table B1 of Appendix B. Fr is the radial load acting on the roller, α (= 00) is the angle between the cylindrical roller and the outer raceway. For Constraint 3, the maximum contact stress σCmax is taken as the safe contact stress σCsafe. The values for the parameters σCmax and σCsafe need to be input. Decision of their values and Fr is discussed in Section 1.3.
3) Constraints 5 and 6:
For the number of rollers, the lower limit is calculated from the bearing pitch diameter's lower limit and the roller mean diameter's upper limit. Similarly, the upper limit is calculated from the bearing pitch diameter's upper limit and roller mean diameter's lower limit. Hence, as indicated in Ref. [6], the range of values for Z is listed in Table B1 of Appendix B.
4) Constraints 7 and 8:
The factors KDmin and KDmax decide the feasible lower and upper limits for the diameter of rolling element as given in Table B1 of Appendix B. The limits to these parameters have been chosen based on the parametric study by using initial optimization runs as Ref. [33].
5) Constraints 9 and 10:
In order to take care of the running mobility of bearings, the difference between the pitch diameter and bearing average diameter must not exceed a certain specified value(Table B1 of Appendix B). Possible choices for the parameter have been chosen from the parametric study[33].
6) Constraint 11:
The bearing ring thickness at the bottom of the outer raceway must exceed or be equal to εDr, where ε is an unknown constraint constant[22], as given in Table B1 of Appendix B.
7) Constraint 12:
The outer ring thickness must be sufficiently large to allow for the corners to be chamfered (Table B1 of Appendix B).
8) Constraint 13:
It is observed that the stresses developed in the inner ring are always greater than those in the outer ring. That is why there must also be a constraint for the thickness of ring. In CRBs, the design for inner ring must be such that it has greater endurance for stresses than the outer ring since the former has to take more stresses because of its convex curvature (Table B1 of Appendix B).
9) Constraint 14:
Ref.[6] accords to the ISO standards. The value for this maximum contact stress shall vary only if the bearing is a ball bearing in place of roller bearing, or else it shall always be the same for all roller bearings, as per the ISO standards (Table B1 of Appendix B).
10) Constraint 15:
Similarly, the outer ring must also not be stressed beyond the permissible value, as has been shown in Table B1 of Appendix B.
11) Constraint 16:
In roller bearings, to make sure that the rollers are able to roll effortlessly on the inner and outer ring raceways, and not collide among themselves, they must be suitably spaced. In standard bearings, there must at least be an angular spacing of one degree between two rollers. The constraint is explained in Table B1 of Appendix B.
Considering Fig. 1, let the angular gap between two consecutive rollers (i.e., angle subtended between the ending of one roller and beginning of immediately next roller) be ψ. Let the angle subtended between the endings of two consecutive rollers be ϕ. Let 2θ be the angle subtended by each of the roller at the center of bearing bore (i.e., angle subtended between the ending and beginning of the same roller). Hence, as can be seen in Fig. 1, there is
| $ \psi=\varphi-2 \theta $ | (23) |
| $ \varphi=\frac{2 \pi}{Z} $ | (24) |
and
| $ \theta=\arcsin \left(\frac{D_{\mathrm{r}} / 2}{D_{\mathrm{m}} / 2}\right)=\arcsin \left(\frac{D_{\mathrm{r}}}{D_{\mathrm{m}}}\right) $ | (25) |
Hence, using Eqs. (23), (24) and (25), there is
| $ \begin{aligned} \psi= & \left\{\frac{2 \pi}{Z}-2 \arcsin \left(\frac{D_{\mathrm{r}}}{D_{\mathrm{m}}}\right)\right\}= \\ & \left\{\frac{2 \pi}{Z}-2 \arcsin \left(\frac{D_{\mathrm{r}}}{D_{\mathrm{m}}}\right)\right\} \cdot \frac{180}{\pi}(\mathrm{deg}) \end{aligned} $ | (26) |
To maintain the angular spacing to always be at least 1°,
| $ \psi \geqslant 1^{\circ} $ | (27) |
Hence, using Eqs. (26) and (27), there is
| $ \left\{\frac{2 \pi}{Z}-2 \arcsin \left(\frac{D_{\mathrm{r}}}{D_{\mathrm{m}}}\right)\right\} \times \frac{180}{\pi} \geqslant 1 $ | (28) |
Now, Eq. (28) is written as
| $ 2 \pi-2 Z \arcsin \left(\frac{D_{\mathrm{r}}}{D_{\mathrm{m}}}\right)-Z \frac{\pi}{180} \geqslant 0 $ | (29) |
12) Constraints 17 and 18:
In the roller bearing design, the roller length also plays an important role, hence its constraining must also be done with utmost care. In the present case, le is considered analogous to Dr. le and B put a check on the upper limit of le (i.e., le < βB). Moreover, the overall roller length must not exceed a constraint value so that it does not extend from the chamfering of the rings. The same can be seen in Table B1 of Appendix B. The limits to these parameters have been chosen based on the parametric study by using initial optimization runs as in Ref. [33].
13) Constraint 19:
Thickness of the outer ring must be sufficient to ensure the occurrence of the maximum dynamic shear stress at the center of the ring even for the most adverse case. The maximum dynamic shear stress must arise at thrice the Zstatic (Table B1 of Appendix B). Zstatic is the depth of occurrence of maximum static shear stress.
14) Constraint 20 & 21:
This constraint is not applicable for deterministic optimization and applies only for robust optimization. In physical programming for the robust design, the designer needs to specify the preference of variation in the objective function due to variation in input variables. Different ranges for percentage variations are prescribed in the objective function Cd for different CRBs. The reason for prescribing different ranges is elaborated in Section 3. The objective function variations at the design variable tolerance values shall always be within this range and towards the lower limit since the objective function variation is minimized, as can be seen in Eqs. (18) and (19). As is known, each design variable tolerance value input in this study is the maximum possible tolerance for the particular design variable for that CRB, hence the objective function variation corresponding to all those design variable tolerance inputs collectively will also be the most possible for that CRB and objective function. The total objective function variation is directly proportional to each design variable tolerance, as can be seen in Eqs. (13) and (19). Hence, the variation in that objective function for that CRB due to tolerances in the design variables (which shall always be less than the tolerances input by us) shall never be greater than the upper limit of the range of percentage variation prescribed in the constraints. The prescribed ranges of variation in the objective function for each of the CRBs are mentioned in Table 1. The detailed reason behind choosing different values for percentage variation in the objective function for different CRBs is expounded in Section 3. For CRB NU202, as can be seen in Table 1, a 1.2%-1.5% variation is prescribed in the objective function Cd. Hence,
| $ 0.012 \leqslant \frac{\Delta C_{\mathrm{d}}}{C_{\mathrm{d}}} \leqslant 0.015 $ | (30) |
| Table 1 Prescribed ranges of variation in objective function for each of the CRBs |
For CRB NU202, to express the constraint in the form as given in Table B1 of Appendix B, there is
| $ \left(\frac{\Delta C_{\mathrm{d}}}{C_{\mathrm{d}}}\right)_{\text {Lower }}=0.012, \left(\frac{\Delta C_{\mathrm{d}}}{C_{\mathrm{d}}}\right)_{\text {Upper }}=0.015 $ |
As is known, the above constraint is only to define robustness, hence no modification is needed as done previously for conversion from the deterministic optimization to the robust optimization. To express it in the form as given in Eq. (11), it is
| $ h_{20}(\boldsymbol{x})=\frac{\Delta C_{\mathrm{d}}}{C_{\mathrm{d}}}-0.012 \geqslant 0 $ | (31) |
| $ h_{21}(\boldsymbol{x})=-\frac{\Delta C_{\mathrm{d}}}{C_{\mathrm{d}}}+0.015 \geqslant 0 $ | (32) |
As has been studied by Messac and Ismail Yahaya[1], the constraints used in the deterministic optimization have been modified in a suitable manner to use it for the robust optimization using Eqs.(8), (10), and (14). All the conversions are in Table B1 of Appendix B (along with their derivations given below the table).
1.3 Bounds for Design VariablesDecision of the range for design variables are present in the vector
| $ \boldsymbol{x}=\left[\begin{array}{lllllllll} D_{\mathrm{m}} & D_{\mathrm{r}} & Z & l_{\mathrm{e}} & K_{D \min } & K_{D \max } & \varepsilon & e & \beta \end{array}\right]^{\mathrm{T}} $ |
which can be used as input for any CRB in case of deterministic optimization and the robust optimization. But before this, it must be known how to decide D, d, B, r1min, r2min, r3min, and r4min, Cd and the limiting speed to be input for each bearing. The value for each of these parameters has been taken from Ref.[31] and listed in Table 2. These parameters are used in deciding the range for the basic design variables Dm, Dr, Z and le. The bounds help to define a more concise feasible search space to be used in GAs for faster convergence of the solution. To find the bounds in the case of deterministic optimization for basic design variables for CRB NU202, inputs are boundary dimensions (Table 2), the radial load equals to 10% of Cd(Table 2), the speed of shaft equals to the limiting speed for NU202, i.e., 26000 r/min (Table 2), and the maximum contact stress is as mentioned in Table 3 for the type of bearing (i.e. roller or ball). As is known, the rated life (or L10) for CRB is mathematically given as
| $ L_{10}=\left(\frac{C_{\mathrm{d}}}{F_{\mathrm{r}}}\right)^{\frac{10}{3}} $ | (33) |
| Table 2 Standard CRB parameters used for the design |
| Table 3 Material properties of the bearing steel |
where L10 is in millions of revolutions, Cd is in N and Fr (radial load) is in N. Hence, it is preferred to take a lower value of the radial load in order to achieve greater rated life for CRB considering the fact that the aim of this paper is to maximize the fatigue life. Hence, the radial load is chosen as 10% of Cd. However, a different value for the radial load may also be chosen for the present study, while considering the fact that it should be small enough to give a good rated life. It must be noted that the speed of shaft equal to the limiting speed is taken for each of the bearing, as it is unsafe to operate any bearing beyond its limiting speed. The bounds of the basic design variables in case of deterministic optimization have been calculated with the help of the constraints used in the deterministic optimization.
The detailed explanation for how to obtain the bounds for each of the basic design parameters from the constraints (Table B1 of Appendix B) is given in Appendix C. The bounds for these variables shall remain the same even in case of robust optimization when they are used for the deterministic optimization[22], because the variable bounds differ for any CRB for the robust and deterministic optimization only for those variables which have certain tolerances during manufacturing. The bounds for these design variables would also be the same irrespective of the type of CRB.
The bounds for the design variables of the CRB NU202 have been mentioned for the deterministic optimization in Table C1 of Appendix C.
The values of tolerances for the basic design variables and bearing boundary dimensions for each of the CRB have been mentioned in Table D1 of Appendix D. Detailed explanation of how to determine the tolerances for each dimension of the CRBs has been given in Appendix D. While in the case of bearing boundary dimension, the tolerances are always taken as negative. In case of basic design variables, the tolerances may be taken as negative and positive. The input for tolerances in bearing boundary dimensions is taken as negative because they have been conventionally accepted as negative values only. But it must be noted that robust design constraints and the robust design objective function treat negative and positive tolerances (whether of basic design variables or bearing boundary dimensions) in the same manner, as can be seen from Eq.(20) and Eqs.(B.8)-(B.109) in Appendix B.
With the help of robust optimization, a set of design variables shall be achieved, which, even if in the worst case, varies by a value equal to the tolerances (Table D1 in Appendix D). The variation in that objective function for that CRB shall never be greater than the upper limit of the range of percentage variation prescribed in Constraints 20 and 21. To convert the range of bounds for basic design parameters from the deterministic optimization to the robust optimization, Eq. (12) can be used. The pitch diameter Dm for CRB NU202 is considered. For the deterministic optimization and referring to Table C1 in Appendix C, there is
| $ 15.6 \leqslant D_{\mathrm{m}} \leqslant 33.8 $ | (34) |
As is given in Table D1 of Appendix D, the variation in the pitch diameter ΔDm (mm) for CRB NU202 is
| $ \mid \Delta D_{\mathrm{m}} \mathrm{I}=0.010 \Rightarrow \Delta D_{\mathrm{m}}=\pm 0.010 $ | (35) |
Hence, with Eqs. (34) and (35), for the robust optimization, the range for pitch diameter is
| $ 15.6+\Delta D_{\mathrm{m}} \leqslant D_{\mathrm{m}} \leqslant 33.8-\Delta D_{\mathrm{m}} $ | (36) |
Although the positive and negative tolerances are treated the same by the robust design constraints and objective functions, different values of optimized design variables and optimized objective functions are obtained on taking a design variable tolerance as negative or positive. This is due to the fact that the sign of design variable tolerance will cause the new robust design bounds of basic design variables to be different, even if the tolerance magnitude remains the same. Hence, although the final optimized objective functions and design variables for the cases of positive and negative tolerances shall have very close values, the probability of them being exactly the same is very low.
However, the final optimized objective functions as well as design variables are not at all affected by the sign of tolerances in bearing boundary dimensions and only affected by their magnitude.
Consider negative tolerances for basic design variables:
Using Eq. (12) and data for CRB NU202 basic design variables from Table C1 and design variable tolerances from Table D1 of Appendix D for ΔDm=-0.010, there is
| $ \begin{gathered} 15.6-0.010 \leqslant D_{\mathrm{m}} \leqslant 33.8+0.010 \Rightarrow \\ 15.59 \leqslant D_{\mathrm{m}} \leqslant 33.81 \end{gathered} $ | (37) |
For ΔDr=-0.008, there is
| $ \begin{gathered} 0.2659-0.008 \leqslant D_{\mathrm{m}} \leqslant 9.1+0.008 \Rightarrow \\ 0.2579 \leqslant D_{\mathrm{m}} \leqslant 9.108 \end{gathered} $ | (38) |
For Δle=-0.120, there is
| $ \begin{gathered} 0.0106-0.120 \leqslant l_{\mathrm{e}} \leqslant 9.35+0.120 \Rightarrow \\ -0.1094 \leqslant l_{\mathrm{e}} \leqslant 9.47 \end{gathered} $ | (39) |
Neglecting the negative value, there is
| $ 0 \leqslant l_{\mathrm{e}} \leqslant 9.47 $ | (40) |
Hence, the bounds for the basic design variables are obtained for the robust optimization of CRB NU202 for negative tolerances in this way. Similarly, the bounds for the robust optimization for the other CRBs are obtained as well, for both negative and positive tolerances. The bounds for the design variables of CRB NU202 have been mentioned for the robust optimization for negative tolerances in Table 4.
| Table 4 Bounds of design variables for NU 202 for the robust optimization for negative tolerances |
Since the bounds for the design variables KDmin, KDmax, ε, e and β remain the same irrespective of the type of optimization (whether deterministic or robust) and the type of CRBs, the bounds for the basic design variables Dm, Dr and le for the robust optimization of each of the CRBs for the prescribed maximum positive and negative tolerances (Table D1 of Appendix D) have been mentioned in Table C2 of Appendix C. It must be noted that the bounds for the design variable Z remain the same irrespective of the type of optimization (whether deterministic or robust), but they do vary with the type of CRB being considered.
1.4 Constraint HandlingConstrained optimization problems involve inequality and/or equality constraints. Solving such problems using GA requires a constraint handling method. There are several ways to handle constraints, but owing to the simplicity and ease of operation, both the penalty function[34] and penalty parameter-less[35] approaches are frequently applied, although the method best suited for optimization algorithms working with population is the penalty parameter-less method. The aforesaid method incurs a summation of penalty terms 〈gj(X)〉 and 〈hk(X)〉 corresponding to the constraint violation function CV(X). It calculates the overall normalized constraint violation of the solution X as follows:
| $ C_V(X)=\sum\limits_{j=1}^{21}\left\langle g_j(X)\right\rangle $ | (41) |
A flow chart of NSGA-Ⅱ[8, 29] is shown in Fig. 2, which gives the procedure for solving the present optimization problem. It must be noted that although the different multi-objective optimization GAs work on slightly different paths of approach when dealing with a multi-objective optimization problem, they behave in exactly the same manner when dealing with a single objective optimization problem as the objective function. Hence, whenever a multi-objective optimization GA is used for solving single-objective optimization problems, the usual entire procedure, i.e., initialization, evaluation, selection, reproduction, re-evaluation, and so on, stays the same, as it would be for a simple real-coded GA. But what makes NSGA-Ⅱ the best multi-objective optimization algorithm is its low computational complexity and diversity preservation. It also has the advantage of elitism, which is also the advantage of the most other multi-objective optimization procedure. So, when NSGA-Ⅱ is used for single objective optimization, the benefits it brings along are low computational complexity and diversity preservation, which are not present in the other potential single-objective optimization methods, namely, evolution strategies, evolutionary programming, genetic programming, etc. This is the reason why NSGA-Ⅱ is used but not any other available multi-objective optimization methods in place of the other available potential single-objective optimization methods.

|
Fig.2 Flowchart of NSGA-Ⅱ algorithm |
In the present problem of CRB, nine design variables have been considered and encoded in real-coded chromosomes, thereafter appropriate modifications are made to the NSGA-Ⅱ code to take the number of rollers Z as integer value. Table 3 lists the material properties like Young's modulus, Poisson's ratio and acceptable contact stress σCsafe. For the bearing, the alloy steel 52100 grade bearing steel is chosen as the material due to its features of high wear resistance, rolling fatigue strength, cost-effectiveness, and long working life. These values are used as inputs to decide the range for the basic design variables Dm, Dr, Z, and le for the deterministic optimization (Appendix C), and also as inputs for the optimization constraints (Table B1 of Appendix B).
The bounds for the design variables of the CRB NU202 are mentioned for the deterministic optimization in Table D1. With Eq. (12), the bounds of the basic design variables Dm, Dr and le for deterministic optimization (Table D1) along with data for design variable tolerances from Table D1 are taken as inputs to decide the range for the basic design variables for the robust optimization in the similar manner as that in Eqs. (37) - (40). The values of tolerances for the basic design variables Dm, Dr, and le, and bearing boundary dimensions for each of the CRB mentioned in Table D1 are taken as inputs for robust optimization constraints, as listed in Table B1 of Appendix B.
The bounds for the design variables of the CRB NU202 are mentioned for the robust optimization for negative tolerances in Table 4. The bounds for the basic design variables Dm, Dr, and le for the robust optimization for each of the CRBs for the prescribed maximum positive and negative tolerances (Table D1 of Appendix D) are mentioned in Table C2 of Appendix C.
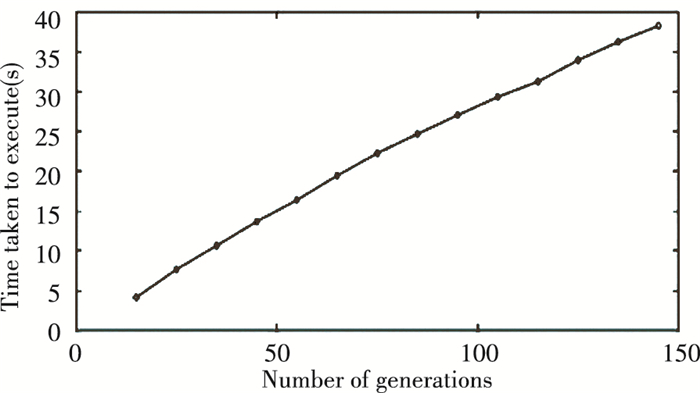
3 Results and ObservationsThe results obtained after the robust optimization of NU202 for negative tolerances (Table D1 of Appendix D) and prescribed variation of 1.2%-1.5% in the objective function (Table 1) for the population size 1000 and different values of number of generations are given in Table 5. In the case of the CRB NU202, for a population size of 1000, the number of generations used for obtaining the final solution is 125. The reason for using this value for the number of generations corresponding to population size 1000 is the convergence of values of the objective function towards a higher magnitude and different design variables towards a particular value as the chosen value of number of generation approaches (Table 5). Convergence of the different design variables and the objective function towards increasing value of number of generations can be seen in Figs. 3, 4 and 5. Even higher values of number of generations can be used for the given population size, but it is a futile exercise, as the results obtained are almost the same as those obtained now, and it is also computationally exhaustive (Table 5 and Fig. 6) because the execution time keeps on increasing by increasing number of generations. Hence, to minimize the execution time as much as possible, a minimum possible number of generations are kept and these values are strictly stuck to. It must be noted that for a different value of population size, the value for the number of generations at which convergence occurs might be different. After finalizing the population size and the number of generations for each run, GA parameters (mutation probability, crossover probability, mutation index, crossover index and random seed) are chosen. The lower value of GA parameters gives the maximum spread of solution points and hence diverse results. Therefore, lower values are chosen for GA parameters for the present study[26]. As mentioned earlier, a random seed has also been used as the GA parameter and used to generate initial population for each run. GA parameter variations and their favoured values have been given in Table 6. Similarly, NSGA-Ⅱ can be implemented for other standard CRBs for the negative as well as positive tolerances for any prescribed range of variation in the objective function with the data from Tables 2, 3, 6, 7 and 8. A certain value is used for population size and the number of generations for the robust optimization of Cd. In this study, a population size of 1000 is kept and the number of generations is varied up to the point of convergence in design variables and objective functions. The final optimized dimensions for the robust optimization of Cd for each of the CRB are mentioned in Table 2. The negative as well as positive tolerances after prescribing suitable ranges of variation in the objective function have been provided in Table 7.
| Table 5 Robust optimization results for Cd of CRB NU202 for different values of number of generations |

|
Fig.3 Convergence of Dm(mm), Dr (mm), Z and le (mm) with number of generations for robust optimization of CRB NU202 for negative tolerances |
|
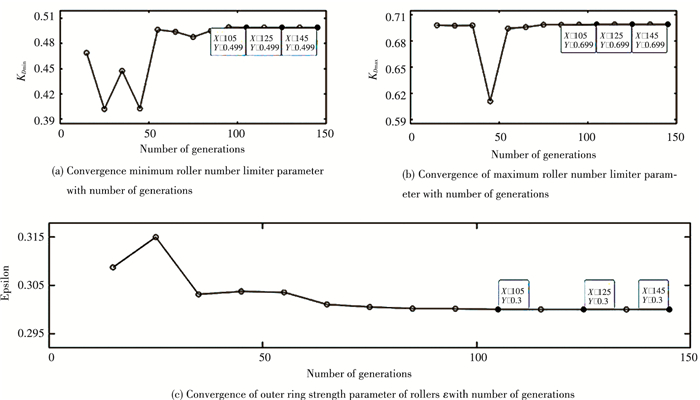
Fig.4 Convergence of KDmin, KDmax and ε with number of generations for robust optimization of CRB NU202 for negative tolerances |

|
Fig.5 Convergence of e, β and Cd(N) with number of generations for robust optimization of CRB NU202 for negative tolerances |
|
Fig.6 Increase in execution time with number of generations for robust optimization of CRB NU202 for negative tolerances |
| Table 6 GA parameter variations and favoured values |
| Table 7 Robust optimization results for dynamic capacity of different CRBs for negative and positive tolerances |
| Table 8 Robust optimization results for Cd of CRB NU202 for negative tolerances and different values of prescribed variation in objective function |
It can be seen from Table 8 that when NSGA-Ⅱ is implemented for the robust optimization of Cd for NU202 for negative tolerances, and different ranges of variation are prescribed in the objective function and using data from Tables 1, 2, 3 and 4. The final optimized values of design variables and objective functions have decreased from the previously prescribed range of variation 1.2%-1.5%. This is because while the tolerances input for CRB NU202 remains the same, an increase in prescribed range of variation demands a decrease in one or all of the basic design parameters Dm, Dr, and le, as can be seen in Eqs. (20)-(22). Due to this decrease in these basic design parameters, Cd has decreased. Although a highly flexible design of the bearing is preferred (i.e., acceptability of high percentages of variations in the objective function), the importance of a high value of the dynamic capacity cannot be ignored. Hence, a balance needs to be maintained between the flexibility in design and load carrying capacity. Hence, by observing the results from Table 8, the final range of variation was prescribed to be 1.2%-1.5% for the robust optimization of Cd for NU202 for negative tolerances, considering the fact that the final optimized objective function after performing the robust optimization for any objective for any CRB using positive/negative tolerance must be comparable to the value obtained on the deterministic optimization for that objective function for that CRB[22]. For example, Ref. [22] proposes that for NU202, for single objective optimization of Cd, (Cd)optimum=22160 N. From Table 8, an optimized value 22081 N is obtained for the robust optimization of Cd for NU202 for negative tolerances, which lies near the above value and is only for prescribed range of variation 1.2%-1.5%. Hence, 1.2%-1.5% is chosen as the prescribed range of variation.
Similarly, different ranges of variation in the objective function can be prescribed for the robust optimization of Cd for each of the CRB mentioned in Table 2, for both negative and positive tolerances. The prescribed ranges of variation in the objective function for each of the CRBs have been mentioned in Table 1. Now, after deciding a prescribed range of variation of 1.2%-1.5% for the robust optimization of Cd for NU202 for negative tolerances, NSGA-Ⅱ can be implemented for the robust optimization of Cd for NU202 for positive tolerances, prescribing the same range of variation in the objective function as the case of negative tolerance and using data from Tables 1, 2, 3 and 4. Now, the bounds of basic design variables Dm, Dr, and le have changed from the case of negative tolerance for NU202 (Table C2 of Appendix C). Hence, although the final optimized values of design variables and objective functions are very close to the case of negative tolerance for NU202, they are surely different as can be seen in Table 9. But the idea of still using the same prescribed range of variation as negative tolerance in case of positive tolerance does turn out to be useful, as the optimized value of Cd=21990 N (Table 9) is still comparable to the value (Cd)optimum=22160 N[22]. Hence, the same range of variation is prescribed in the objective function for the robust optimization of Cd for each of the CRB for negative and positive tolerances.
| Table 9 Robust optimization results for Cd of CRB NU202 for negative and positive tolerances for a prescribed variation of 1.2%-1.5% in objective function |
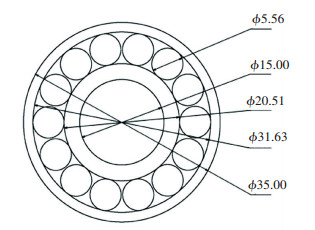
To check whether the optimized dimensions are geometrically feasible or not, NU202 bearing is drawn for dimensions obtained using the robust optimization of Cd of NU202 for negative tolerances, as given in Table 9, which uses a solid modelling software and is shown in Fig. 7, where the cross-sectional view of the optimized bearing NU-202 is shown. From the figures, it can be inferred that no interference is there between the dimensions.
|
Fig.7 Radial dimensions of optimized bearing for robust optimization of NU202 with Cd as objective function |
The objective function variations of the design variable tolerance values input in this study shall always be within the range prescribed by us in Constraints 20 and 21.
The problem that the objective function Cd varies with each of the basic design variable Dm, Dr and le undergoing manufacturing tolerances is investigated. Hence, using results from Table 9 for the negative tolerances of CRB NU202 and Eqs. (20) - (22), there is
| $ \begin{aligned} & \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{r}}}=0.191 C_{\mathrm{d}} \\ & \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{m}}}=0.00495 C_{\mathrm{d}} \\ & \frac{\partial C_{\mathrm{d}}}{\partial l_{\mathrm{e}}}=0.0988 C_{\mathrm{d}} \end{aligned} $ | (42) |
Hence, the change rate of Cd with each of the design variables Dm, Dr and le is positive. It means that for a positive tolerance in any of the dimensions Dm, Dr and le during the manufacturing of bearings, the objective function Cd will increase, while a negative tolerance in the same will cause a decrease in the Cd. The objective function Cd also changes at the maximum rate for Dr and it is least affected by the changes in Dm. Although a positive tolerance for the design variables Dm, Dr, and le does not seem to be a problem, it causes an increase in the objective function Cd, which is good for the bearing. But in that case, if the final optimized dimensions are obtained using the robust optimization and only the deterministic optimization is performed, the tolerances may cause the final manufactured dimensions to be violating one or more than one of the Constraints 1-19.
The total percentage variation in the objective function Cd are due to the tolerances in each of the design variables Dm, Dr, and le. Hence, using the results from Eq. (42) and with the data from Table D1 for the negative tolerances of CRB NU202, there is
| $ \begin{aligned} & \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{r}}} \Delta D_{\mathrm{r}}=-1.91 \times 10^{-3} C_{\mathrm{d}} \\ & \frac{\partial C_{\mathrm{d}}}{\partial D_{\mathrm{m}}} \Delta D_{\mathrm{m}}=-0.0396 \times 10^{-3} C_{\mathrm{d}} \\ & \frac{\partial C_{\mathrm{d}}}{\partial l_{\mathrm{e}}} \Delta l_{\mathrm{e}}=-11.856 \times 10^{-3} C_{\mathrm{d}} \end{aligned} $ | (43) |
Hence, with the results obtained in Eq. (43), there is
| $ \frac{\Delta C_{\mathrm{d}}}{C_{\mathrm{d}}}=-1.2009 \times 10^{-2} \simeq-1.2 \% $ | (44) |
The negative sign in Eq. (44) has been mentioned to show that the net variation in Cd of the CRB NU202 for negative tolerances in the design variables Dm, Dr, and le will be negative. As is observed above, with Eq. (43), a negative tolerance in the design variables Dm, Dr, and le will cause a decrease in the Cd.
As is mentioned, the objective function variation magnitudes at the design variable tolerance values input for any CRB for any objective function shall always be within the range prescribed in this study for the CRBs in Table 1 and towards the lower limit that has been observed in Eq. (44). From Table 1, the prescribed range of variation for CRB NU202 for robust optimization of Cd is 1.2%-1.5% and a net variation of 1.2% is obtained in the objective function Cd, as can be seen in Eq. (44).
But it must be insured that the optimum results obtained for the robust optimization satisfies each of the constraints. To this end, the values for the left side of each of the robust optimization constraints are calculated, which is given in Table B1 of Appendix B, corresponding to the results obtained for the robust optimization of NU202 for negative tolerances and prescribed variation in the objective function as mentioned in Table 9. The obtained values for left side corresponding to each constraint have been mentioned in Appendix E, where all the values are greater than zero, hence it is certain that the optimum solution obtained for robust optimization of NU202 for negative tolerances and prescribed variation in the objective function does satisfy all the constraints. Hence, it can be concluded that the results in Table 7 obtained on robust optimization of each of the CRBs for negative and positive tolerances and prescribed variation in the objective function do satisfy the 21 robust optimization constraints, as mentioned in Table B1.
Consider Constraint 1 and the value of its left side in Appendix E. The value of left side for Constraint 1 is 10.4498, which indicates that if only Constraint 1 needs to be followed to find out the value of Dm, it (obtained through optimization) can be still decreased by 10.4498 mm. Similarly, the value of left side for Constraint 2 is 7.7112, which means that if only Constraint 2 needs to be followed to find out the value of Dm, it (obtained through optimization) can still be increased by 7.7112 mm. But in order to determine the value of optimum Dm, both Constraints 1 and 2 have to be followed in addition to several other constraints out of the total 21 available constraints. Hence, the optimum value is obtained for Dm. The condition that each of the constraint contains Dm as a design variable has been satisfied. It must be noted that each of the nine design variables considered in this study may be the only design variable in a constraint, or it may be present as one of the several design variables in a constraint.
Similarly, consider Constraint 7, the value of its left side in Appendix E is 1.0961, which indicates that if only Constraint 7 has to be followed to find out the optimum values of the design variables Dr and KDmin, both values (obtained through optimization) can still be changed simultaneously or individually, such that the value of the expression
| $ \left\{2 D_{\mathrm{r}}-K_{D \min }(D-d)-K_{D \min }(|\Delta D|+|\Delta d|)\right\} $ |
does not decrease by more than 1.0961 mm. But in order to determine the value of optimum Dr and KDmin in addition to Constraint 7, several other constraints out of total 21 constraints have to be followed. Hence, the optimum value for each of the design variables, Dr and KDmin are obtained. The condition that each of the constraint contains Dr and KDmin as the design variable(s) in combined form or separately has been satisfied.
For any of the constraint (whether consisting of just one design variable or a set of design variables), the nearer the value of LHS to zero is, the more critical the constraint would be. This criticality of a constraint can be seen in reference to all the constraints or in reference to only those constraints, sharing at least one common design variable. Consider the criticality of a constraint in reference to all the constraints. For the set of design variables present in this most critical constraint, the convergence to a stable value shall occur more quickly than convergence to a stable value for the set of design variables present in less critical constraints. The explanation for it has been given in the next paragraph. Consider the criticality of a constraint in reference to the constraints sharing at least one common design variable. Then out of all the constraints consisting of a design variable, the final optimized value for that design variable shall depend on the constraint that is most critical for that design variable.
In Appendix E for Constraints 11 and 16, the value of left-hand side corresponding to the optimum results for the robust optimization of NU202 for negative tolerances, as given in Table 9, lies very close to 0, which indicates that these are the most critical constraints (in reference to all the constraints). Being a critical constraint means that for each run, these constraints will limit the range of design variables (out of the range that has been input) to optimize the objective function. Hence, the algorithm will keep only those populations as favourable parent populations in further generations, which do satisfy these constraints (i.e., the most critical ones). Hence, for the design variables that are present in these critical constraints, parent populations are carried forward for many generations. Hence for those design variables, the convergence to a stable value can be said to have occurred very quickly, i.e., in the initial generations itself. Hence, in the present case of robust optimization of the dynamic capacity of NU202 for negative tolerances (Table 9) and also for the robust optimization of each of the CRBs for positive/negative tolerance (Table 7), design variables Dm, Dr, ε and Z present in Constraints 11 and 16 shall converge to a stable value more quickly than the other design variables.
As can be observed in the final results for the optimization of Cd for CRB NU202 (Tables 7 and 9), while some of the design variables like le, KDmin, KDmax, ε, e and β are converging to the boundary values of their prescribed range, the others like Dm, Dr and Z converge to a value lying somewhere between the bounds of prescribed range. First of all, the point of convergence of basic design variables, Dm, Dr, Z and le representing the bearing internal geometry are discussed. As can be seen in Section 1.3, the upper and lower bounds for these basic design variables for robust optimization have been derived from the bounds for these design variables for the deterministic optimization, which themselves are based on a few of the constraints from Table B1 of Appendix B, as can be seen in Appendix C. As has been mentioned previously, if the criticality of a constraint is considered in reference to the constraints having at least one common design variable, out of all the constraints consisting of a design variable, the final optimized value for that design variable shall depend on the constraint that is most critical for that design variable. Hence, for any of the basic design variables, convergence to a boundary value of the prescribed range shall occur, only if the critical constraint for that design variable is the same as the constraint that had been used to find its upper and lower bound for the deterministic optimization in Appendix C. The point of convergence of the remaining five design variables are discussed, namely, KDmin, KDmax, ε, e, and β that give the bearing a feasible design space in the form of constraints, as given in Table B1 of Appendix B.
To understand the convergence of KDmin and KDmax, consider Constraints 7 and 8, as can be seen in Table B1 of Appendix B.
| $ K_{D \min } \frac{D-d}{2} \leqslant D_{\mathrm{r}} \leqslant K_{D \max } \frac{D-d}{2} $ | (45) |
As can be seen in Eq. (43), the change rate of Cd with respect to the design variable Dr is positive, which means that in order to maximize Cd (which is the purpose of this study), Dr must also be high. As can be seen in Eq. (45), in order to make the search space for Dr corresponding to Constraints 7 and 8, it only consists of higher values for Dr. The upper and lower bounds for this constraint must also be high, for which high values of KDmin and KDmax are required. Hence, the optimization algorithm tries to obtain values for these design variables KDmin and KDmax as high as possible, while always takes into consideration the fact that the values to which the design variables Dr, KDmin and KDmax are constrained through this constraint do not violate any of the remaining 19 constraints. The optimization algorithm succeeds in increasing the values for these design variables, KDmin and KDmax, up to the maximum possible value (i.e., the upper bound of prescribed range) without violating any of the remaining 19 constraints, i.e., the values to which KDmin and KDmax converge to are the upper bounds for their prescribed range.
To understand the convergence of e, consider Constraints 9 and 10, as can be seen in Table B1 of Appendix B.
| $ (0.5-e)(D+d) \leqslant D_{\mathrm{m}} \leqslant(0.5+e)(D+d) $ | (46) |
With the help of Eq.(43), Dm must also be high in order to maximize dynamic capacity. As can be seen in Eq. (46), a high value of e will give a higher value for the upper bound for search space of Dm corresponding to Constraints 9 and 10. As can be seen in Eq. (46), a higher value of e shall cause the lower bound for the search space of Dm corresponding to Constraints 9 and 10 to be lower, which is not a problem, as the optimization algorithm can still look for higher values for Dm. Hence, a highest possible value for e is searched for, such that the values to which Dm and e are constrained through this constraint do not violate any of the remaining 19 constraints. Hence, the value to which the design variable e converges to is the upper bound for its prescribed range.
To understand the convergence of ε, consider Constraint 11, as can be seen in Table B1 of Appendix B.
| $ \begin{gathered} 0.5\left(D-D_{\mathrm{m}}-D_{\mathrm{r}}\right)-\varepsilon D_{\mathrm{r}} \geqslant 0 \Rightarrow \\ D_{\mathrm{m}}+(1+2 \varepsilon) D_{\mathrm{r}} \leqslant D \end{gathered} $ | (47) |
As can be seen in Eq.(47), a smaller value of ε will increase the upper bound for search space of both Dm and Dr, corresponding to Constraint 11, to an even higher value. Hence, the optimization algorithm converges the design variable ε to the least possible value (i.e., lower bound for its prescribed range), meanwhile ensures that the values to which the design variables Dm, Dr and e are constrained through this constraint do not violate any of the remaining 20 constraints.
To understand the convergence of β, consider Constraint 17, as can be seen in Table B1 of Appendix B.
| $ \beta B-l_{\mathrm{e}} \geqslant 0 \text { or } l_{\mathrm{e}} \leqslant \beta B $ | (48) |
As can be seen in Eq. (43), Cd can be maximized by increasing le. As can be seen in Eq. (48), a higher value of β is well suited to make the upper bound of the search space for le higher. Hence, the value of the design variable β is increased as much as possible, while always takes care of the fact that the values to which the design variables le and β are constrained through this constraint do not violate any of the remaining 20 constraints. Hence, the design variable β converges to the upper bound of its prescribed range.
4 ConclusionsThe present study is primarily focused on having an optimum design of cylindrical bearing that not only gives us the maximum load carrying capacity but also remains least affected by the possible practical error that can occur in the form of tolerances during its manufacturing. The study presented some mathematical formulations that make it easier to achieve the objective of having a robust design. The formulations have shown that in order to achieve the robustness, adjustments need to be made in all three components of any optimization process, i.e., the objective function, constraints and variable bounds. Hence, based on the results of the present study, the following conclusions can be drawn:
1) It is possible to optimize a bearing design in such a manner that its variations due to tolerances in design variables (whose maximum value has been prescribed by us in both positive and negative direction) are never greater than the upper limit of the range of percentage variation prescribed for it during manufacturing. This is possible to be manufactured, as solid modelling software can be used to draw such a bearing with geometrical parameters as obtained by the robust optimization.
2) The change rate for the objective function Cd corresponding to each of the design variables Dm, Dr and le undergoing variations during manufacturing is positive.
3) Out of all the parameters, which have been given tolerance and affect the objective function, the roller diameter has the maximum effect on dynamic capacity and the mean diameter has the least.
In this work, the robust design of CRBs has been carried out with a single objective function, namely, the dynamic capacity Cd. However, bearings may have different application requirements, so a multi-objective optimization of robust design for CRBs can be carried out by considering simultaneously and in pairs of objective functions as Cd, maximum bearing temperature Tmax, and the elasto-hydrodynamic minimum film thickness hmin as objective functions. Apart from this, the vibration performance and fatigue life of a rolling element bearing can be significantly affected by variable compliances of the inherent bearings, the rotor, and housing compliances, and these can be considered as a future work.
AppendicesNote: The electronic version of Appendix A, B, C, D, E is available at http://hit.alljournals.cn/jhit_cn/ch/reader/view_abstract.aspx?file_no=202211070000001&edit_id=20221107103135001&flag=2.
| [1] |
Messac A, Ismail Yahaya A. Multi objective robust design using physical programming. Structural and Multi-disciplinary Optimization, 2002, 23: 357-371. DOI:10.1007/s00158-002-0913-0 (  0) 0) |
| [2] |
Chen W, Sahai A, Messac A, et al. Exploring the effectiveness of physical programming in robust design. ASME Journal of Mechanical Design, 122(2): 1-28. DOI:10.1115/1.533565 (  0) 0) |
| [3] |
Giassi A, Bennis F, Maisonneuve J J. Multidisciplinary design optimization and robust design approaches applied to concurrent design. Structural and Multi-disciplinary Optimization, 2004, 28: 356-371. DOI:10.1007/s00158-004-0417-9 (  0) 0) |
| [4] |
Tshibangu W-M A. Taguchi method or compromise programming as robust design optimization tool: the case of a flexible manufacturing system. Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO). Piscataway: IEEE, 2015. 15662165.
(  0) 0) |
| [5] |
Changsen W. Analysis of Rolling Element Bearings. New York: John Wiley & Sons, 1991.
(  0) 0) |
| [6] |
Harris T A. Rolling Bearing Analysis. New York: John Wiley and Sons, 2001.
(  0) 0) |
| [7] |
Seireg A. A survey of optimization of mechanical design. ASME Journal of Engineering for Industry, 1972, 94: 495-499. DOI:10.1115/1.3428181 (  0) 0) |
| [8] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi objective genetic algorithm: NSGA-Ⅱ. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 (  0) 0) |
| [9] |
Branke J, Deb K, Dierolf H, et al. Finding knees in multi-objective optimization. Proceedings of the International Conference on Parallel Problem Solving from Nature PPSN. Berlin, Heidelberg: Springer, 2004. 722-731.
(  0) 0) |
| [10] |
Hirani H. Multi objective optimization of a journal bearing using the pareto optimality concept. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2004, 218(4): 323-336. DOI:10.1243/1350650041762668 (  0) 0) |
| [11] |
Link R, Possamai F C, Pereira E L L. Muffler and bearing optimization applying Genetic algorithm. International Journal of Rotating Machinery, 2004, 10: 301-307. DOI:10.1155/S1023621X04000314 (  0) 0) |
| [12] |
Saruhan H, Rouch K E, Roso C A. Design optimization of tilting-pad journal bearing using a genetic algorithm. International Journal of Rotating Machinery, 2004, 10(4): 301-307. DOI:10.1155/S1023621X04000314 (  0) 0) |
| [13] |
Hirani H, Suh N P. Journal bearing design using multi-objective genetic algorithm and axiomatic design approaches. Tribology International, 2005, 38: 481-491. DOI:10.1016/j.triboint.2004.10.008 (  0) 0) |
| [14] |
Wang N Z. A parallel computing application of the genetic algorithm for lubrication optimization. Tribology Letters, 2005, 18: 105-112. DOI:10.1007/s11249-004-1763-x (  0) 0) |
| [15] |
Kim Y H, Yang B S, Tan A C C. Bearing parameter identification of rotor-bearing system using clustering-based hybrid evolutionary algorithm. Structural and Multi-disciplinary Optimization, 2007, 33: 493-506. DOI:10.1007/s00158-006-0055-5 (  0) 0) |
| [16] |
Gupta S, Tiwari R, Nair S B. Multi-objective design optimization of rolling bearings using genetic algorithms. Mechanism and Machine Theory, 2007, 42(10): 1418-1443. DOI:10.1016/j.mechmachtheory.2006.10.002 (  0) 0) |
| [17] |
Xie X P, Peng C L, Chen S L. Numerical analysis of influence of solid particles on elasto hydrodynamicline contacts under grease lubrication. Journal of South China University of Technology (Natural Science Edition), 2012, 40(7): 51-56. DOI:10.3969/j.issn.1000-565X.2012.07.009 (  0) 0) |
| [18] |
Tiwari R, Sunil K K, Reddy R S. An optimal design methodology of tapered roller bearings. International Journal for Computational Methods in Engineering Science and Mechanics, 2012, 13(2): 108-127. DOI:10.1080/15502287.2011.654375 (  0) 0) |
| [19] |
Solanki A, Patel P, Parmar B. Design formulation and optimum load carrying capacity of hydrodynamic journal bearing by using genetic algorithm. International Journal for Research in Applied Science and Engineering Technology, 2014, 2: 132-138. (  0) 0) |
| [20] |
Panda S, Panda S N, Nanda P, et al. Comparative study on optimum design of rolling element bearing. Tribology International, 2015, 92: 595-604. DOI:10.1016/j.triboint.2015.07.034 (  0) 0) |
| [21] |
Dragoni E. Optimal design of paired tapered roller bearings under centered radial and axial static loads. Mechanics and Industry, 2015, 16: 604-615. DOI:10.1051/meca/2015032 (  0) 0) |
| [22] |
Tiwari R, Chandran R M P. Multitude of objectives based optimum designs of cylindrical roller bearings with evolutionary methods. ASME Journal of Tribology, 2015, 137(4): 041504-041504. DOI:10.1115/1.4030166 (  0) 0) |
| [23] |
Dewangan V K, Rajput L, Sharma A. Design optimization of plain journal bearing to minimize the power loss using genetic algorithm. International Journal for Research in Applied Science and Engineering Technology, 2016, 4: 687-693. DOI:10.22214/ijraset.2016 (  0) 0) |
| [24] |
Kim S W, Kang K, Yoon K, et al. Design optimization of an angular contact ball bearing for the main shaft of a grinder. Mechanism and Machine Theory, 2016, 104: 287-302. DOI:10.1016/j.mechmachtheory.2016.06.006 (  0) 0) |
| [25] |
Tudose L, Şerdean F M, Tudose C. Optimal design under uncertainty of bearing arrangements. Mechanism and Machine Theory, 2016, 98: 164-179. DOI:10.1016/j.mechmachtheory.2015.12.008 (  0) 0) |
| [26] |
Kalyan M, Tiwari R. Multi-objective optimization of needle roller bearings based on fatigue and wear using evolutionary algorithm. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2016, 230(2): 170-185. DOI:10.1177/1350650115594639 (  0) 0) |
| [27] |
Verma S K, Tiwari R. Robust optimum design of tapered roller bearings based on maximization of fatigue life using evolutionary algorithm. Mechanism and Machine Theory, 2020, 152: 103894. DOI:10.1016/j.mechmachtheory.2020.103894 (  0) 0) |
| [28] |
Salunkhe A V, Agashe U C, Hatwalane S. A review on design optimization of rolling contact bearings. International Journal of Current Engineering and Technology, 2017, 7(3): 983-986. (  0) 0) |
| [29] |
Deb K. Multi-Objective Optimization Using Evolutionary Algorithms. New York: John Wiley & Sons, 2001.
(  0) 0) |
| [30] |
Harris T A, Kotzalas M N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis. Boca Raton, Florida: CRC Press, 2006.
(  0) 0) |
| [31] |
SKF. General Catalogue. Paderborn, Germany: Media Print, 2005. (  0) 0) |
| [32] |
Bureau of Indian Standards. IS3824. Rolling Bearings: Dynamic Load Ratings and Rating Life. New Delhi: Bureau of Indian Standards, 2003.
(  0) 0) |
| [33] |
Rao B R, Tiwari R. Optimum design of rolling element bearings using genetic algorithms. Mechanisms and Machine Theory, 2007, 42(2): 233-250. DOI:10.1016/j.mechmachtheory.2006.02.004 (  0) 0) |
| [34] |
Hoffmeister F, Sprave J. Problem-Independent Handling of Constraints by Use of Metric Penalty Functions. http://ls11-www.cs.tu-dortmund.de/~joe/papers/ep96a.pdf, 2021-05-08.
(  0) 0) |
| [35] |
Deb K. An efficient constraint handling method for genetic algorithms. Computer Methods in Applied Mechanics and Engineering, 2002, 186: 311-338. DOI:10.1016/S0045-7825(99)00389-8 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29

 ,
Twinkle Mandawat
,
Twinkle Mandawat