2. Jiangsu Key Laboratory of Urban ITS, Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, School of Transportation, Southeast University, Nanjing 210008, China
Urban transit system, the backbone for the sustainable urban development, has been widely recognized as an efficient scheme to ameliorate various transportation problem in many countries, such as traffic congestion, air pollution, fuel consumption, economic loss and crashes. However, as the transit operation costs increase, the transit ticket revenue in most cities cannot offset the operation cost, which leads to the contradiction between supply and demand[1-4]. If a reasonable assessment cannot be made, it is difficult for transport authorities to provide a rational amount of subsidy. Therefore, it is necessary to study how to keep the balance between the regular operation cost of transit enterprises and the continuous investment on infrastructures from transport authorities.
The public transit fare system is mainly divided into two categories: flat and differentiated. Currently, most cities have implemented flat fare structures because of their simplicity and low cost[5]. However, such scheme overcharges the passengers with short distance and undercharges the passengers with long distance, which gives rise to inequity and poor financial performance[5-6]. As smart payment and global positioning system (GPS) technologies have been widely implemented in most cities, differentiated fare structure becomes more reasonable and feasible for transit operators in practice[7]. According to previous research[8-9], different types of differentiated fares strategies are summarized as follows: time-based, distance-based (including mileage-and station-based), and service-based (related with mode or speed). These different fare types are termed as fare structures, while the specific charging pattern is named as fare pattern for a particular fare structure: the distance-based fare[10].
Among these three fare structures, distance-based fare strategy has been relatively fare to passengers, which is beneficial for attracting transit ridership[6, 11-12] and is widely used in many urban cities (Singapore and Melbourne) or urban rail system[13]. However, traditional distance-based fare pattern cannot give full play to its own advantages as a result of the elasticity of short trips and the amount of long trips in real world[14]. Passengers usually choose the travel path with lower generalized travel cost when developing a travel strategy. This travel choice behaviour would attract higher amount of passengers into the hot transit line or path, which may lead to severe congestion and lower level of service in hot transit lines or paths. In order to overcome this drawback and make better use of the distance-based fare structure, this paper proposes an Euclidean distance-based fare structure with nonlinear fare patterns.
As shown in Fig. 1, the red line represents the Euclidean distance from the boarding node and alighting node. The black lines, including solid and dashed lines, are actual bus travel trajectory, which is used to calculate the actual bus travel distance. In this newly distance-based fare structure, the transit fare is not a function of the actual travel distance, but the Euclidean distance. Therefore, passengers would no longer concern the fare for route choice and freely choose the paths with higher efficiency, which leads to a much even distribution of passenger flow and wise use of the transit network system. This structure is termed as nonlinear distance-based fare, which is a nonlinear increasing function.

|
Fig.1 Illustration of Euclidean distance |
This paper aims to analyze the nonlinear distance-based fare structure with Euclidean distance in the urban transit network. The contributions of this work are twofold. First, Euclidean distance is adopted to reformulate the distance-based transit fare structure that is certificated to be nonlinear and non-additive. Second, a principal-agent game is introduced into the bi-level programming for exploring the relationship of different stakeholders.
In Section 1, the transit fare structure design problem involving basic notation, transit fare structure expression and path-based stochastic transit assignment (STA) is briefly introduced. Then, Section 2 introduces the principle-agent game into the bi-level programming model for the optimal distance-based transit fare problem. Subsequently, a GA is adopted as the solution algorithm in Section 3. In Section 4, the proposed model and solution algorithm are verified by a small transit network. Finally, the discussion and concluding remarks are given.
1 Transit Fare Structure Design Problem 1.1 Network RepresentationA strongly connected transit network is denoted by G=(N, L), where N and L are the set of transit stations and transit lines, respectively, as shown in Fig. 2(a). It is assumed that a transit line is a set of transit vehicles and stops on the fixed path connecting the same links and stations between two terminals, such as L1: O, N2, N3, D or L2: O, N1, N3, D. Transit link refers to any link portion of a transit line connecting two consecutive stations, such as

|
Fig.2 Illustration of the transit network by using lines (a) and route sections (b) respectively |
1.2 Transit Fare Structure
As discussed in Section 0, this paper mainly focuses on distance-based fare structure involving three representative charging structure: mileage-based, station-based and Euclidean distance-based fare and compares them with flat fare structure.
Let τf be the ticket price of flat fare. τm0 and τm are termed as fixed and variable components of mileage-based fare, respectively; τst0 and τst represent fixed and variable components of station-based fare, respectively; τd0 and τd denote fixed and variable components of Euclidean distance-based fare, respectively. Thus the different type of distance-based fare patterns can be calculated by
| $ \tau_{s, k}= \begin{cases}\tau_{\mathrm{f}}, & {\rm { Flatfare }} \\ \tau_{\mathrm{m}}^0+\tau_{\mathrm{m}} \cdot l(i, j), & {\rm { Mileage-basedfare }} \\ \tau_{\mathrm{st}}^0+\tau_{\mathrm{st}} \cdot \operatorname{ceil}\left(\frac{|j-i|}{n_{\mathrm{st}}}\right) & , {\rm { Station-based\; fare }} \\ \tau_{\mathrm{d}}^0+\tau_{\mathrm{d}} \cdot|d(i, j)|, & {\rm { Euclidean \;distance-based\; fare }} \end{cases} $ | (1) |
where τs, k is the fare on section s of path k; ceil(·) represents the minimum positive integer larger than itself; nst represents base number of stations of station-based fare. l(i, j) represents the distance traveled on bus line from node i to j, d(i, j) represents the Euclidean distance between node i and node j. Note that according to the distance-based fare structure in Singapore, the range of flat fare is from 0 to 5, and fixed and variable components of other differentiated fare structures are from 0 to 3 and from 0 to 2, respectively.
Transit fares charged based on sections mean that passengers would be charged twice when boarding and alighting. Therefore, the node i and node j in Eq. (1) only denote the boarding node and alighting node of one section, respectively. All the passengers should tap their cards twice (boarding and alighting), because in the first time, fare system only records the passengers' boarding station and in the second time, the number of stations or mileage between node i and j is calculated. Thus the total path fare τk can be obtained by the sum of the fare of each sections on this path:
| $ \tau_k=\sum\limits_{s \in S_k} \tau_{s, k} $ | (2) |
Considering the fixed component of fare structure functions, the total path fare τk is nonlinear and non-additive, which means that the overall charged fare of path k connecting one OD directly is not the sum of all the section fares along this path. Consequently, a set of candidate paths is needed in the first place and then the total path fares could be calculated.
For the simplicity of description, this paper adopts the following assumptions:
a) The transit market is assumed to be monopolistic. All the transit lines are owned and operated by one transit enterprise. How to determine the fare structure is controlled by this transit operator under the regulation and the control of government;
b) The subsidy from the government is defined as a function of regulation cost CR, which is a predetermined constant given by government based on the analysis of the operation cost per person of the previous year. The profit rate is also predetermined by transit authorities;
c) At transfer stations, it is assumed that passengers have the freedom to choose and wait for the expected vehicle to minimize their total travel cost, rather than boarding the first arriving vehicle.
d) The transit network is supposed to be uncongested, and no passenger capacity is considered for transit vehicle.
According to Eq. (2), the path fare τk is obtained by the sum of section fares of path k. However, due to the existence of fixed and variable components in nonlinear fare structure as shown in Eq. (1), the fare directly charged from the boarding node and to the alighting node is not the sum of section fares, which makes path fare non-additive. For example, as shown in Fig. 1, fares of the two sections are calculated in terms of Eq. (2) based on their respective Euclidean distance. Thus, the path fare τk equals to the sum of these two section fares, which is not the same as the fare directly charged between the two nodes because of the fixed components of fare function and the non-additive of Euclidean distance. Consequently, the path-based transit assignment is adopted in this paper.
1.3 Path-Based STA with Nonlinear Fare StructureAs aforementioned, the path representation based on route section is infeasible in this model, because the variance of mileage and stations that different lines contain in a section makes it unpractical when station-based or mileage-based transit fare are taken into consideration. But this variance has no impact on flat and nonlinear fare structure because they only consider the boarding and alighting stations of one section regardless of the transit lines passengers have used.
Thus, in order to keep an equivalent condition among different fare structures, this paper will adopt the path representation in the form of transfer nodes sequence connected by transit lines. Before transit assignment, a candidate path set is firstly generated with the information of transfer nodes and transit lines. It is assumed that the path set is known and fixed[16], ranked in a descending order of time-related travel cost.
The generalized travel cost for each section s of path k connecting OD pair w consists of three parts: in-vehicle travel time ts, kw, waiting time ws, kw, and transit fare τs, kw. The first two parts are time-dependent attributes that can be converted as a monetary attribute shown in the latter one. The passengers' perceived travel time is assumed to follow Gumbel distribution. Let ξs, kw be the random error term associated with users' perception error on path travel time following independent and identical distributed Gumbel variable[17]. Thus, the passengers' path travel cost ckw is defined as
| $ c_k^w=\sum\limits_{w \in W} \sum\limits_{k \in K} \sum\limits_{s \in S}\left(t_{s, k}^w+w_{s, k}^w+\lambda \tau_{s, k}^w+\xi_{s, k}^w\right) $ | (3) |
where λ is the passenger's value of time (VOT), converting transit fare into time-units. The path choice probability is presented by the following logit formula[17]:
| $ P_k^w=\frac{\exp \left(-\theta c_k^w\right)}{\sum\limits_{k \in K} \exp \left(-\theta c_k^w\right)} $ | (4) |
where θ is the dispersion parameter, which is positively associated with passengers' perception of the path travel time.
The transit fare structure has also vital impacts on the passenger demand. Let qw be the total passenger demand between OD pair w and it thus can be expressed as a continuous and monotonically decreasing function of the expected minimum disutility Sw:
| $ q_w=D_w\left(S_w\right) $ | (5) |
where the expected minimum disutility Sw can be measured as
| $ S_w=E\left[\min\limits _{k \in K}\left\{c_k^w\right\}\right]=-\frac{1}{\theta} \ln \sum\limits_{k \in K} \exp \left(-\theta c_k^w\right) $ | (6) |
As mentioned above, it is assumed that the demand function is termed as continuous and monotonically decreasing function. A linear form of demand function is adopted as follows[18]:
| $ q_w=q_w^0-\beta S_w $ | (7) |
where let the maximum OD demand be qw0, and β denotes the sensitivity to the expected minimum travel cost. Thus, the passenger flow hkw on path k between OD pair w can be calculated by
| $ h_k^w=q_w P_k^w $ | (8) |
In practice, the decision process of transit fare pattern involves three stakeholders, namely, transport authority, transit enterprise, and passenger[19]. Passengers expect high-quality services from the transit enterprises supervised by transport authorities. Therefore, it is a three-party game, in which one game is between authority and enterprise pursing maximization of social welfare and financial interest, respectively, and the other is leader-follower game exploring the reaction of passengers to the transit fare strategies and subsiding policies.
2.1 Principal-Agent GameResearch works commonly use total operator revenue[18], user benefit[20], total passengers' demand[21] or total social welfare[13, 22] as the assessment index of transit authorities and operators. However, previous studies usually consider the single stakeholder in the transit fare design and ignore the game between transport authorities and transit operators. In order to describe the relationship between the enterprise and authority, a principal-agent game is introduced, where the urban transport authority and transit enterprise act as the principal and agent, respectively[13].
This scenario is selected for two reasons. One is the different objectives from the transport authority and transit operator. Transport authority intends to achieve maximization of social welfare and transit enterprise inclines to maximize the profit including the ticket revenue and financial subsidy. The other reason is asymmetric information. The transit company actually masters most important information incorporating the operation cost, total passenger demand and ticket revenue, while the authority cannot observe the transit operation data directly. Accordingly, the principal-agent game is proposed to describe the interaction between the transport authority and transit enterprise based on the characteristics above.
The transit enterprise's profit can be defined as follows:
| $ \begin{aligned} \text { Profit }= & \sum\limits_{w \in W} \sum\limits_{k \in K} \tau_k^w h_k^w- \\ & {\left[\sum\limits_{l \in L}\left(C_0+C_1 \cdot T_l \cdot N_l\right)+\sum\limits_{w \in W} \sum\limits_{k \in K} C_3 h_k^w\right] } \end{aligned} $ | (9) |
where the first term is the revenue of the transit enterprise by charging. The second part represents the operation cost including fixed cost C0, operation cost C1 and flow related cost C3. Tl is the itinerary travel time of line l, Nl is the number of itineraries of line l in an hour.
As for the transportation authorities, their objective is to reach the maximization of social welfare including a financial balance between transit enterprises and passengers. Specifically, on the one hand, they regulate an upper bound of the ticket price to keep the fare in a low level to make it acceptable for most citizens and a lower bound considering the operation cost, i.e.:
| $ \tau_{\min } \leqslant \tau \leqslant \tau_{\max } $ | (10) |
In practice, on the other hand, due to the policy of low price ticket, financial subsidy is a common solution to keep the transit enterprises operating and developing[1]. Therefore, it is necessary to decide subsidy by depending on the transit enterprises' operation performance to at least maintain the operation and motivate the transit enterprise to offer service of higher quality. Thus, the maximization of social welfare could be reached at the same time because the policy of subsidizing could benefit both of the transit enterprises and passengers. According to the newly enacted Urban Transit Regulation, its mathematical expression is as follows:
| $ S=\sum\limits_{w \in W}\left[C_{\mathrm{R}}(1+r)-\bar{\tau}\right] \cdot q_w(\tau) $ | (11) |
where CR is the regulation cost in the target year, which is provided by the transportation authority; r is the regulation profit rate for public transport industry, which is set by transport authority to maintain the sustainable development of transport enterprises; τ is the average fare and qw(τ) is the total passenger demand of the entire transit system, both of which are given by the lower-level problem.
2.2 Bi-Level Programming ModelBi-level programming model has been regarded as the effective scheme to solve Mathematical Programming with Equilibrium Constraints (MPEC) in the field of transportation network[23-24]. There are much literature on the development of bi-level model to solve the transit fare pattern design problem[9, 13, 22]. From the above discussion, the optimal distance-based transit fare design incorporating the principle-agent game can be expressed mathematically by the following bi-level programming model:
Upper level
| $ \begin{gathered} \max\limits _\tau Z(\tau, q(\tau), h(\tau))=\sum\limits_{w \in W} \sum\limits_{k \in K} \tau_k^w h_k^w- \\ {\left[\sum\limits_{l \in L}\left(C_0+C_1 \cdot T_l \cdot N_l\right)+\sum\limits_{w \in W} \sum\limits_{k \in K} C_3 h_k^w\right]+} \\ \sum\limits_{w \in W}\left[C_{\mathrm{R}}(1+r)-\bar{\tau}\right] \cdot q_w(\tau) \end{gathered} $ | (12) |
which subjects to
| $ q_w=\sum\limits_{k \in K} h_k^w $ | (13) |
| $ \tau_{\min } \leqslant \tau \leqslant \tau_{\max } $ | (14) |
Lower level
| $ {\rm{Eqs}}. \;(3)-(8) $ |
It is noted that the passengers will make their route choice in response and ridership will be calculated at the lower level accordingly when the fare strategy and level of service are provided at the upper level.
3 Solution AlgorithmThe proposed bi-level programming model is acknowledged to be an NP-hard problem[25]. Due to the complexity of the proposed bi-level model, it is difficult to adopt an exact algorithm. Thus a heuristic GA is employed as solution method for this model[23].
It is of considerable importance to illustrate the GA structure. First, the initial population composed of a group of chromosomes is randomly generated, in which each chromosome represents a corresponding fare pattern τs, k. The fixed and variable components are expressed as two genes in one chromosome. A transit assignment problem at the lower level is solved to obtain the corresponding equilibrium path flow hkw and demand qw with the generated population at the upper level. The equilibrium flow is in turn delivered into the upper level to update the chromosome fitness Z(τ, q, h). This process is repeated and terminated until a stop criterion is satisfied. The stop criterion is usually based on whether the number of iteration reaches the maximum or objective fitness gets the optimum.
4 Numerical Example 4.1 Data DescrpitionTo numerically validate the proposed methodology, one example transit network involving 9 nodes (Fig. 3) is adopted in this paper. This example transit network comprises one OD pair (i.e. N1-N9), 9 nodes (from N1 to N9) and five transit lines (from L1 to L5).
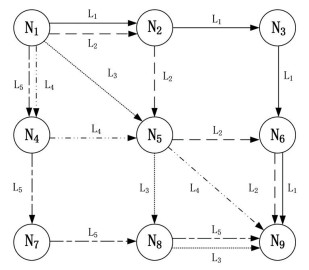
|
Fig.3 Structure of the example network using lines |
Furthermore, it is assumed that the potential OD demand (Passenger/h) is 1000. The value of parameters β, λ and θ are set to be 7.0, 0.3 and 0.9, respectively. The other example transit network information is presented in Table 1. For the flat fare scheme, the range of flat fare is from 0 to 3. As for the nonlinear fare structure, the fixed and variable components are from 0 to 3.0 and from 0 to 0.2, respectively. For example, the initial generation of fare pattern could be τd, 10=2.85, τd, 1=0.09, τd, 20=2.82, τd, 2=0.02, ……, τd, 500=2.54, τd, 50=0.07. In the initial generation of GA procedure, there are 50 chromosomes randomly generated for each fare structures. The parameters used in the GA for the numerical test are shown in Table 2. The maximum number of iterations is set to be 50. It is noted that "¥" denotes the Chinese Yuan (RMB) in this paper and ¥1 is about $0.15 USD at market exchange rates. The programs designed in this paper were all coded in MATLAB and run on the computer with the Inter Core i7-3770/3.4 GHz, 8 GB Ram.
| Table 1 Basic description for the example transit network |
| Table 2 GA parameters |
4.2 Result Analysis
According to the predetermined network data and GA parameters, the optimal results including financial performance and transit assignment can be obtained and analyzed separately. The optimal financial performance of four comparable fare structures is firstly depicted in Table 3 and Fig. 3.
| Table 3 Computational results for different fare structure |
Nonlinear distance-based transit fare structure performs a better economic management among these four charging schemes, whereas flat transit fare structure presents worse financial problem, which also has been demonstrated in some literature[26-27]. As demonstrated in Fig. 3, the flat fare regime gets the lowest profits (-302 ¥/h) and requires the highest amount of subsidy (780 ¥/h). On the contrary, the nonlinear distance-based transit fare structure is guaranteed to generate the maximum profits and revenue, while providing the lowest subsidy for the transport authority. From Table 3, it is evident that the optimal average fare and average total travel cost of flat fare structure are lower than others, while the potential passenger demand of flat fare structure is larger. It shows that lower fare level clearly attracts more passengers to travel by transit, but the transit ticket revenue cannot offset the operation cost and a large amount of subsidy is still required.
The transit assignment was solved, and the top eight most commonly used paths were then selected to analyze the passenger flows distribution of four fare structures. It is obvious from Table 4 that path 1 attracts the largest number of passengers among all used paths as a result of the minimal travel time, waiting time and fares. Passengers prefer path 2 in addition to path 1 because this path may have no transfer with higher departure frequency and lower fixed cost.
| Table 4 The most common eight paths |
Furthermore, path 1 can be taken as an example to compare the path flow transferring proportion of four fare structure demonstrated in Table 5. The proportion of passenger flow of path 1 under the flat fare structure of total demand is relatively greater than any others, which could be attributed to the lower average fare level. Thus, passengers are more sensitive to the time-related cost than fares. As for the nonlinear distance-based fare, the passenger flow on the most attractive path is released and assigned to other paths.
| Table 5 Passenger proportion of path 1 of total demand |
As depicted in Table 6, a comparison of two average fare structures was made between mileage-based fare commonly applied in practice and nonlinear distance-based fare. The average fare of path 1 in nonlinear distance-based fare regime is greater than that of mileage-based fare because the trajectory of buses travel in path 1 is nearly linear as described in Fig. 4. The optimal nonlinear distance-based fare level is greater than mileage-based fare. However, the average fare of paths is not nearly linear. In other words, they are zig-zag and lower than those in mileage-based fare regime. Therefore, those paths apart from path 1 would attract more passengers and achieve greater revenue.
| Table 6 Average fare of each path |

|
Fig.4 Optimal financial performance of four fare structures |
5 Discussion and Conclusions
This paper proposes a new nonlinear transit fare structure based on Euclidean distance to optimize transit network performance. Regarding the non-additivity of nonlinear transit fare pattern, the path-based STA with elastic demand is adopted to evaluate the specific transit fare pattern. A bi-level programming model is further developed for solving the optimal transit fare structure design problem. Because the aim of transport authority is to maximize social welfare and transit enterprise prefers the maximization of profit such as the ticket revenue and financial subsidy, their objectives are obviously conflicting. Considering the relationship between the authority and enterprise, a principal-agent game is also incorporated into the proposed bi-level programming model to balance their conflicting objectives.
The results show that the proposed model and algorithm are feasible and efficient by the numerical example. It is clearly demonstrated that the nonlinear distance-based transit fare structure has a better financial performance and trip distribution than flat fare. Ultimately, the proposed transit fare structure alleviates the gathering of passengers, reduces the huge subsidy of transport authority, and improves the revenue of transit enterprise.
This paper only presents some initial steps in conducting the research on optimal nonlinear distance-based transit fare design problem from theoretical perspective. Further work is required to further extend these models to consider more practical issues such as multi-mode transit networks, multi-objective problem, transfer discounts or continuous values-of-time and to adopt the other methodologies to solve the proposed model precisely. Although the numerical results cannot be implemented in the transit system management immediately, it indeed provides a method, an idea and a direction for further transit system optimization in the future.
| [1] |
Tirachini A, Hensher D A, Rose J M. Multimodal pricing and optimal design of urban public transport: the interplay between traffic congestion and bus crowding. Transportation Research Part B, 2014, 61: 33-54. DOI:10.1016/j.trb.2014.01.003 (  0) 0) |
| [2] |
May A D, Kelly C, Shepherd S. The principles of integration in urban transport strategies. Transport Policy, 2006, 13(4): 319-327. DOI:10.1016/j.tranpol.2005.12.005 (  0) 0) |
| [3] |
Borndörfer R, Karbstein M, Pfetsch M E. Models for fare planning in public transport. Discrete Applied Mathematics, 2012, 160(18): 2591-2605. DOI:10.1016/j.dam.2012.02.027 (  0) 0) |
| [4] |
Litman T. Evaluating Public Transit Benefits and Costs. Victoria: Victoria Transport Policy Institute, 2011, 65. (  0) 0) |
| [5] |
Kholodov Y, Jenelius E, Cats O, et al. Public transport fare elasticities from smartcard data: evidence from a natural experiment. Transport Policy, 2021, 105: 35-43. DOI:10.1016/j.tranpol.2021.03.001 (  0) 0) |
| [6] |
Brown A E. Fair fares? How flat and variable fares affect transit equity in Los Angeles. Case Studies on Transport Policy, 2018, 6(4): 765-773. DOI:10.1016/j.cstp.2018.09.011 (  0) 0) |
| [7] |
Jang W. Travel time and transfer analysis using transit smart card data. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2144(1): 142-149. DOI:10.3141/2144-16 (  0) 0) |
| [8] |
Fleishman D, Shaw N, Joshi A, et al. TCRP Report 10: Fare Policies, Structures, and Technologies. https://www.trb.org/publications/tcrp/tcrp_rpt_10-a.pdf. .
(  0) 0) |
| [9] |
Guo Q W, Sun Y S, Schonfeld P, et al. Time-dependent transit fare optimization with elastic and spatially distributed demand. Transportation Research Part A: Policy and Practice, 2021, 148: 353-378. DOI:10.1016/j.tra.2021.04.002 (  0) 0) |
| [10] |
Liu Z Y, Meng Q, Wang S A. Speed-based toll design for cordon-based congestion pricing scheme. Transportation Research Part C: Emerging Technologies, 2013, 31: 83-98. DOI:10.1016/j.trc.2013.02.012 (  0) 0) |
| [11] |
Tsai F M, Chien S I, Spasovic L N. Optimizing distance-based fares and headway of an intercity transportation system with elastic demand and trip length differentiation. Transportation Research Record: Journal of the Transportation Research Board, 2008, 2089(1): 101-109. DOI:10.3141/2089-13 (  0) 0) |
| [12] |
Zhou J P, Zhang M, Zhu P Y. The equity and spatial implications of transit fare. Transportation Research Part A Policy & Practice, 2019, 121: 309-324. DOI:10.1016/j.tra.2019.01.015 (  0) 0) |
| [13] |
Wang Q, Schonfeld P, Deng L B. Profit maximization model with fare structures and subsidy constraints for urban rail transit. Journal of Advanced Transportation, 2021, 2021: 6659384. DOI:10.1155/2021/6659384 (  0) 0) |
| [14] |
Ling J H. Transit fare differentials: a theoretical analysis. Journal of Advanced Transportation, 1998, 32(3): 297-314. DOI:10.1002/atr.5670320304 (  0) 0) |
| [15] |
de Cea J, Fernández E. Transit assignment for congested public transport systems: an equilibrium model. Transportation Science, 1993, 27(2): 133-147. DOI:10.1287/trsc.27.2.133 (  0) 0) |
| [16] |
Wu J H, Florian M, Marcotte P. Transit equilibrium assignment a model and solution algorithms. Transportation Science, 1994, 28(3): 193-203. DOI:10.1287/trsc.28.3.193 (  0) 0) |
| [17] |
Sheffi Y. Urban Transportation Networks. Englewood Cliffs: Prentice-Hall, 1985.
(  0) 0) |
| [18] |
Schmcker J D, Bell M G H, Kurauchi F, et al. A Game Theoretic Approach to the Determination of Hyperpaths in Transportation Networks. Boston, MA: Springer, 2009. DOI: 10.1007/978-1-4419-0820-9_1.
(  0) 0) |
| [19] |
Lam W H K, Zhou J. Optimal fare structure for transit networks with elastic demand. Transportation Research Record: Journal of the Transportation Research Board, 2000, 1733(1): 8-14. DOI:10.3141/1733-02 (  0) 0) |
| [20] |
Kocur G, Hendrickson C. Design of local bus service with demand equilibrium. Transportation Science, 1982, 16(2): 149-170. DOI:10.1287/trsc.16.2.149 (  0) 0) |
| [21] |
Yook D, Heaslip K. Determining appropriate fare levels for distance-based fare structure: considering users' behaviors in a time-expanded network. Transportation Research Record: Journal of the Transportation Research Board, 2014, 2415: 127-135. DOI:10.3141/2415-14 (  0) 0) |
| [22] |
Li Z C, Lam W H K, Wong S C. The optimal transit fare structure under different market regimes with uncertainty in the network. Networks and Spatial Economics, 2009, 9(2): 191-216. DOI:10.1007/s11067-007-9058-z (  0) 0) |
| [23] |
Sun X, Liu Z Y, Thompson R G, et al. A multi-objective model for cordon-based congestion pricing schemes with nonlinear distance tolls. Journal of Central South University, 2016, 23(5): 1273-1282. DOI:10.1007/s11771-016-0377-4 (  0) 0) |
| [24] |
Liu Z Y, Wang S A, Meng Q. Optimal joint distance and time toll for cordon-based congestion pricing. Transportation Research Part B: Methodological, 2014, 69: 81-97. DOI:10.1016/j.trb.2014.08.005 (  0) 0) |
| [25] |
Ben-Ayed O, Boyce D E, Blair Ⅲ C E. A general bilevel linear programming formulation of the network design problem. Transportation Research Part B: Methodological, 1988, 22(4): 311-318. DOI:10.1016/0191-2615(88)90006-9 (  0) 0) |
| [26] |
Daskin M S, Schofer J L, Haghani A E. A quadratic programming model for designing and evaluating distance-based and zone fares for urban transit. Transportation Research Part B: Methodological, 1988, 22(1): 25-44. DOI:10.1016/0191-2615(88)90032-X (  0) 0) |
| [27] |
Ling J H. Transit fare differentials: a theoretical analysis. Journal of Advanced Transportation, 1998, 32(3): 297-341. DOI:10.1002/atr.5670320304 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


