Amorphous alloys are generally prepared by rapidly cooling metallic liquids. Because of their unique structural feature, amorphous alloys owe some better thermodynamic and mechanical properties compared with crystals[1]. However, due to such a rapid cooling rate, it is difficult to obtain the details of the microstructure using the common experimental equipment and predict the microstructure with the universal equilibrium phase diagram. As a result, molecular dynamics simulation is used to study the rapid cooling process of preparing amorphous alloys. Since the cooling rate has great influence on the final structure, in order to obtain the similar structure with the experiment, the time scale of simulation is required to be the same as that in the experiment. However, the time scale in the simulation is several orders of magnitude smaller than that in the experiment. Generally, the cooling rate of the amorphous materials prepared in the experiment is 105-106 K/s. At the cooling rate in this range, the crystallization will be dynamically inhibited and the amorphous structure will be finally obtained[2-6]. In the classical molecular dynamics simulation, the system can contain tens of thousands or even hundreds of thousands of atoms, which can well describe the characteristics of the amorphous structure. However, the time step is a femtosecond, and the slowest cooling rate can reach 109 K/s, which is several orders of magnitude higher than the cooling rate in the experiments. Therefore, the structure cannot relax completely under the simulated cooling condition. In the process of rapid cooling for the preparation of amorphous alloys, α relaxation occurs at high temperature, generally within one picosecond[7], which could be detected at the quenching rate of 1010-1011 K/s. However, when the temperature falls below the glass transition temperature (Tg), the relaxation can be detected on the experimental time scale and cannot be captured at any simulated cooling rate. Due to the high glass forming ability and other excellent mechanical properties, the Zr-based amorphous alloys have been the research hotspot and a lot of simulation studies have been done on the Zr-Cu and Zr-Cu-Al systems[8]. The local structure in the Zr54 Cu46 alloy was characterized through Honeycutt-Andersen by Kelton[9]. The icosahedral structures matched well with the chemical and topological order of the supercooled liquid[9-12]. The basic short-range structure of icosahedral structures in Zr50Cu50, Zr36Cu64, Zr65Cu35, and Zr35Cu65 amorphous alloys were found by conducting classical molecular dynamics[13-19]. Wong[20] used classical molecular dynamics to simulate the atomic structure of ZrxCu90-xAl10 (x=20, 30, 40, 50, 60, 70) and found that content of Zr(Cu) had great influence on obtaining icosahedral structures. Nath[21] reported that the influence of Zr content on the toughness and strength of ZrCuAl alloy was studied by using classical molecular dynamics simulation.Recently, annealing close to Tg has been demonstrated to effectively reduce the influence of the high cooling rates in MD simulations[22-24]. By reducing the effective uniform cooling rates to as low as 2.8×107 K/s, Zhang et al.[22, 24] confirmed significant energetic stability and well-developed short-range icosahedral and Bergman-type medium-range order in the Cu64.5 Zr35.5 alloy. The studies of the Zr55Cu35Al10 ternary alloy on structural evolution and energy landscape during glass transition have been carried out in our previous work[35-36]. Therefore, in this paper, the cooling rate will be reduced by adding isothermal annealing near Tg on the Zr55Cu35Al10 ternary alloy[25-26] during the continuous cooling process, and the effects of different cooling rates on the short and medium-range structure and energy landscape of the obtained amorphous samples will be studied.
1 Computational Method 1.1 Simulation Method1) Continuous cooling: The study was carried out using classic molecular dynamics simulations with embedded atom method potentials[27]. In this work, a Zr55Cu35Al10 system containing 8768 Zr atoms, 5632 Cu atoms, and 1600 Al atoms was heated up to 2000 K first, then kept at 2000 K for 10 ns. Then the system was cooled to 300 K at the speed of 5.00×1011 K/s, 5.00×010 K/s, and 5.00×109 K/s, respectively.
2) Continuous cooling + isothermal annealing: The initial configuration was heated up to 2000 K and then kept at 2000 K for 10 ns, then quenched to 700 K slightly below the Tg (about 730 K reported in the previous work[35]) at the speed of 1010 K/s and isothermal at 700 K for 170 ns and 2000 ns respectively, and then cooled to 300 K at the speed of 1010 K/s to obtain the required structure. The time of the whole cooling process was 340 ns and 2170 ns respectively and the average cooling rate was 5.00×109 K/s and 7.80×108 K/s respectively.
1.2 Structure AnalysisThe common way to study medium-range structure is to analyze the coordination polyhedron connection mode[28-33]. The connection modes of coordination polyhedron mainly include the connection of sharing one atom (point connection), sharing two atoms (line connection), sharing three atoms, and sharing four atoms (face connection). In this paper, the medium-range structure will be described by analyzing the four coordination polyhedron connections.
1.3 Energy AnalysisThe cluster formation energy for an N-atom cluster is defined as
| $ E_{{\mathrm{p}}, C}=1 / N \sum\limits_{i=1}^N\left(E_{{\mathrm{p}}, i}-E_{{\mathrm{ref}}, \alpha}\right) $ | (1) |
Ep, i represents the potential energy (PE) of the th atom and Eref, α represents the reference energy of the type α atom[34-35]. The reference energy is the crystal chemical PE (hcp Zr, fcc Cu and fcc Al). The effective radius for an N-atoms cluster is as follows:
| $ r_{\rm {eff }}=1 /(N-1) \sum\limits_{i=1}^{N-1}\left(d_{{\mathrm{c}}, i}\right) $ | (2) |
dc, i represents the distance between the central atom and the shell atom.
2 Results and Discussion 2.1 Potential EnergyPE is an important index to evaluate the stability of amorphous structure, which is closely related to the cooling process. Fig. 1 shows the PE of the sample at 300 K with different cooling rates. PE is obtained by calculating the average value of the PE data of the last 50 ps at 300 K. By comparing the PE of the two samples quenched with the same average cooling rate of 5.00×109 K/s, it is found that although the cooling time is the same, the PE of the sample experiencing isothermal annealing at 700 K decreases obviously. Comparison of the PE of the two samples experiencing isothermal annealing at 700 K shows that the rate of two continuous cooling stages is the same, while the potential energy of the samples with long isothermal annealing time is significantly lower than that of the sample with short isothermal time. Therefore, more stable amorphous structure can be obtained by adding isothermal annealing at a temperature slightly lower than Tg and prolonging isothermal annealing time. For continuous cooling samples, it is found that the cooling rate is basically linear with the logarithm of the potential energy. By linear fitting and extending the line, the effective uniform cooling rate of the samples with isothermal annealing is 1.85×109 K/s and 2.93×108 K/s, which are roughly one third of their corresponding average cooling rates (5.00×109 K/s and 7.80×108 K/s).
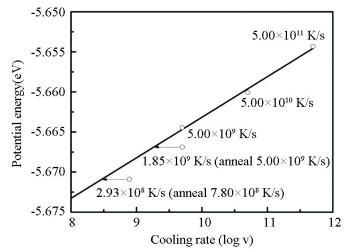
|
Fig.1 Change of the potential energy of the Zr55Cu35Al10 alloy at 300 K as a function of the cooling rate |
2.2 Pair Distribution Function
Fig. 2 and Fig. 3 show the total and partial pair distribution functions (PDFs). In the total PDF curves, the attenuation of the peak well reflects the structural characteristics of the amorphous alloy. It can be seen that the cooling rate has impact on the final structure of the samples. At lower cooling rate, the peak strength of the first peak becomes greater and the peak position shifts to the right. The splitting of the second peak experiences little change while the peak strength of the main peak increases and the peak position shifts to the left. For the partial pair distribution function, the biggest difference exists in the second peak of Zr-Zr and Cu-Cu atomic pairs, in which peak strength increases significantly with the decrease of the cooling rate. The enhancement and leftwing deviation of the main peak in the second peak are mainly related to the Cu-centered medium range structure. Near r=5 Å, the peak strength of the second peak of Zr-Cu, Cu-Cu, and Cu-Al atomic pair increases significantly with the decrease of the cooling rate. The weak enhancement of the splitting of the second peak is related to the Zr-centered medium-range structure. Near r=6 Å, the splitting of the second peak of Zr-Zr, Zr-Cu, and Zr-Al atoms becomes more obvious with the decrease of the cooling rate.
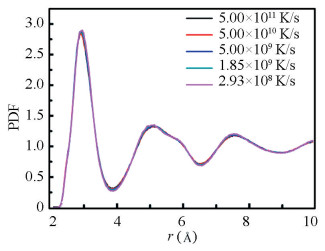
|
Fig.2 The total PDFs of the Zr55Cu35Al10 alloy at 300 K at different cooling rates |

|
Fig.3 The partial PDFs of the Zr55Cu35Al10 alloy at 300 K at different cooling rates |
2.3 Coordination Polyhedron
In order to analyze the influence of different cooling rates on the amorphous structure, the structures obtained at 300 K was compared with the effective uniform cooing rate of 5.00×1011 K/s and 2.93×108 K/s. Fig. 4 shows the distribution of the fraction of coordination polyhedron with different coordination numbers (CNs). For the Zr-centered coordination polyhedron, the fraction of the coordination polyhedron with high CNs in the structure obtained at low cooling rate is relatively large, especially for CN=15, 16. The energy distribution of the different coordination polyhedron is presented in Fig. 5. It is found that the energy of the Zr-centered coordination polyhedron firstly decreases and then increases. The lowest cluster energy belongs to the coordination polyhedron with CN=16. It follows that the Zr-centered polyhedron with high CN have lower energy and are structurally more stable. For the Cu and Al-centered coordination polyhedron, the fraction of the coordination polyhedron (CN=12) significantly increases. Thus it can be seen that the formation of the Cu and Al-centered polyhedron with CN=12 is the preference during the cooling process. By calculating the energy distribution of these polyhedron, it is found that the energy of the Cu and Al-centered polyhedron present the same change trend as the Zr-centered polyhedron, decreasing firstly and then increasing. The difference is that when CN increases to 12, the energy decreases significantly, reaching the lowest energy. The significant decrease of the energy is related to the effective radius of the coordination polyhedron. Fig. 6 shows the change of the effective radius of coordination polyhedron. It can be seen that at low cooling rate, the effective radius of the Zr-centered coordination polyhedron is smaller, and the stacking of the coordination polyhedron is more compact. However, as the CN increases, the effective radius gap becomes smaller and smaller, indicating that the cooling rate has little influence on the effective radius of the Zr-centered coordination polyhedron with high CNs. For the coordination polyhedron centered on Cu atom and Al atom, when CN=12, effective radius decreases obviously at low cooling rate. In other words, the central atoms of the coordination polyhedron with CN=12 formed at a low cooling rate are more strongly connected to the shell atoms. In a word, the short-range structure of the coordination polyhedron formed at low cooling rate has a closer packing with lower energy.

|
Fig.4 The fraction of the different kinds of Zr, Cu, and Al-centered coordination polyhedron with different coordination numbers of the Zr55Cu35Al10 alloy at 300 K at different cooling rates |
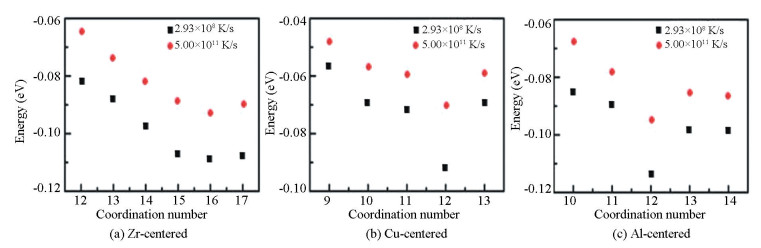
|
Fig.5 The energy of the different kinds of Zr, Cu, and Al-centered coordination polyhedron with different coordination numbers of the Zr55Cu35Al10 alloy at 300 K at different cooling rates |
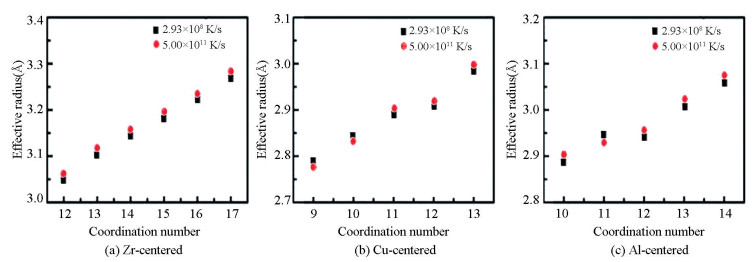
|
Fig.6 The effective radius of the different kinds of Zr, Cu, and Al-centered coordination polyhedron with different coordination numbers of the Zr55Cu35Al10 alloy at 300 K at different cooling rates |
2.4 Medium-Range Structure
Fig. 7 shows the PDF for Zr55Cu35Al10 metallic glass at 300 K and the decomposed PDF for the second nearest neighbor peak with the effective uniform cooing rate of 5.00×1011 K/s and 2.93×108 K/s. It can be seen from the figure that the main peak of the sub-neighbor peak of the amorphous structure obtained at low cooling rate enhances, while the splitting of the second peak presents no obvious change. As can be seen from the figure, the main peak of the sub-neighbor peak is mainly derived from the coordination polyhedron connection sharing three atoms, followed by the connection with two shared atoms. The splitting of the second peak is mainly derived from the connection sharing one atom, followed by the connection sharing two atoms. In the structure obtained at low cooling rate, the number of the coordination polyhedron connection sharing three atoms is large, leading to the formation of the stronger main peak in the sub-neighbor peak obtained at low cooling rate. However, under the two cooling modes, there is no significant change in the fraction distribution of connections sharing one atom and two atoms at the splitting position. As a result, the splitting of the second peak shows little change.
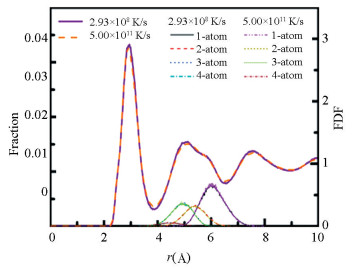
|
Fig.7 PDF for Zr55Cu35Al10 metallic glass at 300 K and the decomposed PDF for second nearest neighbor atoms via 1-atom (sharing one atom), 2-atom (sharing two atoms), 3-atom (sharing three atoms), and 4-atom (sharing four atoms) coordination polyhedron connections at different cooling rates |
It can be seen from Fig. 8 that the number of coordination polyhedron connection sharing one atom is the largest in all structures obtained at all cooling rates while the number of coordination polyhedron connection sharing four atoms is the least. As the cooling rate decreases and the relaxation time increases, it tends not to form coordination polyhedron connections sharing one atom and four atoms. There is a significant increase in the number of face connection sharing three atoms and a corresponding decrease in the number of the line connection sharing two atoms. The number of more tightly bonded face connection increases to improve the density and stability of the system. Calculating the energies of the medium-range structures with different connection modes (Fig. 9), it is found that the energy of the coordination polyhedron connection sharing three atoms is the lowest among the four connection modes, while the energy of the connection sharing two atoms is the highest. Although the connection sharing four atoms is also tightly bonded, it presents low stability with high cluster energy. Therefore, from the perspective of energy and structure, the medium-range structure transforms towards the coordination polyhedron connection sharing three atoms with the lowest cluster energy and tightly bonded structure at low cooling rate.
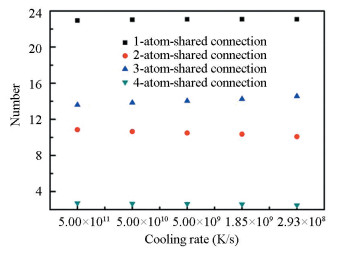
|
Fig.8 The average number of the coordination polyhedron connections with the number of shared atoms from one to four at different cooling rates |

|
Fig.9 The energy of the coordination polyhedron connections with the number of shared atoms from one to four at different cooling rates |
3 Conclusions
In this paper, the effects of different cooling rates on the structure and energy of Zr55Cu35Al10 alloy were studied by molecular dynamics simulations. The main conclusions are as follows: 1) More stable amorphous structure can be obtained by adding isothermal annealing at a temperature slightly lower than Tg and prolonging isothermal annealing time. 2) At low cooling rate, it is more likely to form Zr-centered coordination polyhedron with high CN and Cu, Al-centered coordination polyhedron with CN=12. 3) With the decrease of the cooling rate, the medium-range structure transforms towards the coordination polyhedron connection sharing three atoms with the lowest cluster energy and tightly bonded structure.
| [1] |
Todd R H, Allen D K, Alting L. Manufacturing Processes Reference Guide. South Norwalk, CT: Industrial Press Inc., 1994: 99-125.
(  0) 0) |
| [2] |
Jun W K, Willens R H, Duwez P O L. Non-crystalline structure in solidified gold-silicon alloys. Nature, 1960, 187(4740): 869. DOI:10.1038/187869b0 (  0) 0) |
| [3] |
Greer A L. Confusion by design. Nature, 1993, 366(6453): 303. DOI:10.1038/366303a0 (  0) 0) |
| [4] |
Inoue A, Takeuchi A. Recent development and application products of bulk glassy alloys. Acta Materialia, 2011, 59(6): 2243-2267. DOI:10.1016/j.actamat.2010.11.027 (  0) 0) |
| [5] |
Schroers J. Processing of bulk metallic glass. Advanced Materials, 2010, 22(14): 1566-1597. DOI:10.1002/adma.200902776 (  0) 0) |
| [6] |
Chen M. A brief overview of bulk metallic glasses. NPG Asia Materials, 2011, 3(9): 82. DOI:10.1038/asiamat.2011.30 (  0) 0) |
| [7] |
Angell C A, Ngai K L, McKenna G B, et al. Relaxation in glass forming liquids and amorphous solids. Journal of Applied Physics, 2000, 88(6): 3113-3157. DOI:10.1063/1.1286035 (  0) 0) |
| [8] |
Wu W F, Li Y. Bulk metallic glass formation near intermetallic composition through liquid quenching. Applied Physics Letters, 2009, 95(1): 011906. DOI:10.1063/1.3168411 (  0) 0) |
| [9] |
Wessels V, Gangopadhyay A K, Sahu K K, et al. Rapid chemical and topological ordering in supercooled liquid Cu46Zr54. Physical Review B, 2011, 83(9): 094116. DOI:10.1103/physrevb.83.094116 (  0) 0) |
| [10] |
Mauro N A, Bendert J C, Vogt A J, et al. High energy x-ray scattering studies of the local order in liquid Al. The Journal of Chemical Physics, 2011, 135(4): 044502. DOI:10.1063/1.3609925 (  0) 0) |
| [11] |
Kim T H, Kelton K F. Structural study of supercooled liquid transition metals. The Journal of Chemical Physics, 2007, 126(5): 054513. DOI:10.1063/1.2431173 (  0) 0) |
| [12] |
Lee G W, Gangopadhyay A K, Kelton K F, et al. Difference in icosahedral short-range order in early and late transition metal liquids. Physical Review Letters, 2004, 93(3): 037802. DOI:10.1103/PhysRevLett.93.037802 (  0) 0) |
| [13] |
Soklaski R, Nussinov Z, Markow Z, et al. Connectivity of icosahedral network and a dramatically growing static length scale in Cu-Zr binary metallic glasses. Physical Review B, 2013, 87(18): 184203. DOI:10.1103/PhysRevB.87.184203 (  0) 0) |
| [14] |
Sha Z D, Zhang Y W, Feng Y P, et al. Molecular dynamics studies of short to medium range order in Cu64Zr36 metallic glass. Journal of Alloys and Compounds, 2011, 509(33): 8319-8322. DOI:10.1016/j.jallcom.2011.05.071 (  0) 0) |
| [15] |
Almyras G A, Matenoglou G M, Komninou P, et al. On the deposition mechanisms and the formation of glassy Cu-Zr thin films. Journal of Applied Physics, 2010, 107(8): 084313. DOI:10.1063/1.3366715 (  0) 0) |
| [16] |
Li M, Wang C Z, Hao S G, et al. Structural heterogeneity and medium-range order in ZrxCu100-x metallic glasses. Physical Review B, 2009, 80(18): 184201. DOI:10.1103/PhysRevB.80.184201 (  0) 0) |
| [17] |
Ding J, Cheng Y Q, Ma E. Full icosahedra dominate local order in Cu64Zr34 metallic glass and supercooled liquid. Acta Materialia, 2014, 69: 343-354. DOI:10.1016/j.actamat.2014.02.005 (  0) 0) |
| [18] |
Zemp J, Celino M, Schönfeld B, et al. Icosahedral superclusters in Cu64Zr36 metallic glass. Physical Review B, 2014, 90(14): 144108. DOI:10.1103/PhysRevB.90.144108 (  0) 0) |
| [19] |
Wu Z W, Li F X, Huo C W, et al. Critical scaling of icosahedral medium-range order in CuZr metallic glass-forming liquids. Scientific Reports, 2016, 6: 35967. DOI:10.1038/srep35967 (  0) 0) |
| [20] |
Wang C C, Wong C H. Structural properties of ZrxCu90-xAl10 metallic glasses investigated by molecular dynamics simulations. Journal of Alloys and Compounds, 2012, 510(1): 107-113. DOI:10.1016/j.jallcom.2011.07.110 (  0) 0) |
| [21] |
Nath S K D. Formation, microstructure and mechanical properties of ternary ZrxCu90-xAl10 metallic glasses. Journal of Non-Crystalline Solids, 2015, 409: 95-105. DOI:10.1016/j.jnoncrysol.2014.11.004 (  0) 0) |
| [22] |
Zhang F, Mendelev M I, Zhang Y, et al. Effects of sub-Tg annealing on Cu64.5Zr35.5 glasses: a molecular dynamics study. Applied Physics Letters, 2014, 104(6): 061905. DOI:10.1063/1.4864652 (  0) 0) |
| [23] |
Ward L, Miracle D, Windl W, et al. Structural evolution and kinetics in Cu-Zr metallic liquids from molecular dynamics simulations. Physical Review B, 2013, 88(13): 134205. DOI:10.1103/physrevb.88.134205 (  0) 0) |
| [24] |
Zhang Y, Zhang F, Wang C Z, et al. Cooling rates dependence of medium-range order development in Cu64.5Zr35.5 metallic glass. Physical Review B, 2015, 91(6): 064105. DOI:10.1103/physrevb.91.064105 (  0) 0) |
| [25] |
Zhang Y, Wang C Z, Mendelev M I, et al. Diffusion in a Cu-Zr metallic glass studied by microsecond-scale molecular dynamics simulations. Physical Review B, 2015, 91(18): 180201. DOI:10.1103/PhysRevB.91.180201 (  0) 0) |
| [26] |
Sun Y, Zhang Y, Zhang F, et al. Cooling rate dependence of structural order in Al90Sm10 metallic glass. Journal of Applied Physics, 2016, 120(1): 015901. DOI:10.1063/1.4955223 (  0) 0) |
| [27] |
Cheng Y Q, Ma E, Sheng H W. Atomic level structure in multicomponent bulk metallic glass. Physical Review Letters, 2009, 102(24): 245501. DOI:10.1103/PhysRevLett.102.245501 (  0) 0) |
| [28] |
Bennett C H. Serially deposited amorphous aggregates of hard spheres. Journal of Applied Physics, 1972, 43(6): 2727-2734. DOI:10.1063/1.1661585 (  0) 0) |
| [29] |
Lee M, Lee C M, Lee K R, et al. Networked interpenetrating connections of icosahedra: effects on shear transformations in metallic glass. Acta Materialia, 2011, 59(1): 159-170. DOI:10.1016/j.actamat.2010.09.020 (  0) 0) |
| [30] |
Pan S P, Qin J Y, Wang W M, et al. Origin of splitting of the second peak in the pair-distribution function for metallic glasses. Physical Review B, 2011, 84(9): 092201. DOI:10.1103/PhysRevB.84.092201 (  0) 0) |
| [31] |
Luo W K, Sheng H W, Ma E. Pair correlation functions and structural building schemes in amorphous alloys. Applied Physics Letters, 2006, 89(13): 131927. DOI:10.1063/1.2356473 (  0) 0) |
| [32] |
van de Waal B W. On the origin of second-peak splitting in the static structure factor of metallic glasses. Journal of Non-Crystalline Solids, 1995, 189(1-2): 118-128. DOI:10.1016/0022-3093(95)00208-1 (  0) 0) |
| [33] |
Ding J, Ma E, Asta M, et al. Second-nearest-neighbor correlations from connection of atomic packing motifs in metallic glasses and liquids. Scientific Reports, 2015, 5: 17429. DOI:10.1038/srep17429 (  0) 0) |
| [34] |
Wu S Q, Wang C Z, Hao S G, et al. Energetics of local clusters in Cu64.5Zr35.5 metallic liquid and glass. Applied Physics Letters, 2010, 97(2): 021901. DOI:10.1063/1.3464164 (  0) 0) |
| [35] |
Zhao J F, Inoue A, Liu C T, et al. Structural evolution and energy landscape of the clusters in Zr55Cu35Al10 metallic liquid and glass. Scripta Materialia, 2016, 117: 64-67. DOI:10.1016/j.scriptamat.2016.02.023 (  0) 0) |
| [36] |
Zhao J F, Xie X X, Xu Y, et al. Structural evolution and energy landscape of Zr55Cu35Al10 ternary alloy during glass transition. Journal of Alloys and Compounds, 2020, 825: 154109. DOI:10.1016/j.jallcom.2020.154109 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


