2. State Key Laboratory of Advanced Welding and Joining, Harbin Institute of Technology, Harbin 150001, China
Thermoelectric(TE) materials provide an alternative mechanism for power generation and solid-state cooling by converting thermal energy (waste heat) into electrical energy mutually and reversibly. The reserves of fossil fuels (gas, oil, and coal) are limited and would last up to 2042 (gas and oil) and 2112 (coal)[1]. According to the data published by the International Energy Agency, European Environmental Agency and Energy Information Administration, 87% of energy in the world comes from burning fossil fuels[2]. Approximately 17% of energy out of 87% is used for useful work, and the remaining 70% is wasted in the form of heat[3-6]. With the passage of time, fossil fuels are gradually depleted and more energy is lost as heat. This has compelled researchers to focus on harnessing unused energy (wasted energy), which can bring sustainability as well as extend the depletion period of the reserves.
Fabrication of thermoelectric generators (TEGs) has become an area of attention in the field of energy harvesting for small and large sorts of applications, depending on size, materials used and power delivered. Thermoelectric generators are normally divided into two types, micro-TEGs and large bulk-TEGs[7-8]. Micro-TEGs can generate electrical power in the range of microwatts to milliwatts, while the bulk-TEGs can provide the output power from several to hundreds of watts. Thermoelectric generators are used in high, medium and low-power applications including aerospace, automobiles, industrial electronics, medical wearable, and wireless sensor network[9-12].
The energy conversion efficiency of TEGs, also known as thermoelectric conversion efficiency, is expressed as[13-14]:
| $ \eta_{\max }=\frac{T_{\mathrm{h}}-T_{\mathrm{c}}}{T_{\mathrm{h}}} \times \frac{\sqrt{1+\overline{z T}}-1}{\sqrt{1+\overline{z T}}+\frac{T_{\mathrm{c}}}{T_{\mathrm{h}}}} $ | (1) |
where Th and Tc are the temperatures at the hot end and cold end, respectively. MzT is the thermoelectric figure of merit and can be expressed as:
| $ z T=\frac{\alpha^2 \sigma}{\kappa} T $ | (2) |
where T is the absolute temperature in Kelvin, κ is total thermal conductivity, σ is electrical conductivity, α is the Seebeck coefficient and α2α is the power factor. According to the different temperature ranges for practical applications, TE materials are broadly divided into three families. Typical TE materials and their operating temperature ranges are presented in Table 1[15-21].
| Table 1 Typical thermoelectric materials and their operating temperature ranges |
zT ≥ 3 is the target value of more advanced TE materials[22]. However, the zT values for TE materials reported previously are still lower than the target value. To improve the zTs, it is necessary to increase the numerator (α2σ) and decrease the denominator (κ) values in Eq. (2). In Eq.(2), α and σ can be mathematically expressed as:
| $ \alpha=\frac{8 \pi^2 k_B^2 m^* T}{3 e h^2}\left(\frac{\pi}{3 n}\right)^{2 / 3} $ | (3) |
and
| $ \sigma=\frac{n e^2 \tau}{m^*} $ | (4) |
where kB is the Boltzmann constant, h is the plank constant, m* is the effective mass of the charge carrier, n is the charge carrier concentration, e is a charge on carrier, and τ is the relaxation time. From the right-hand side of Eqs. (3) and (4), it is clear that α and σ are inverse parameters of each other with respect to n and m*. Therefore, this task is quite challenging to decouple these intertwined parameters and optimize the ultimate MzT values. In Eq. (2), κ is the totality of the electronic part (κe) and phonon part (κl). Therefore, Eq. (2) can be rewritten as:
| $ M_{ \mathrm{zT}}=\frac{\alpha^2 \sigma}{\kappa_e+\kappa_l} T $ | (5) |
where
| $ \kappa_e=L \sigma T $ | (6) |
and
| $ \kappa_l=\frac{v C l_{\mathrm{ph}}}{3} $ | (7) |
where L is the Lorenz number, v is the phonon velocity, C is the specific heat capacity and lph is the phonons mean free path (MFP). According to Eq. (6), κe is directly proportional to σ, which means high σ values cause high κe values. For instance, metals show high values of both κe and σ because the dominant part of heat conduction in metals is electrons. Generally, we use different L for metals and semiconductors, where L=2.44 × 10-8 W·Ω/K2 for most metals (degenerate limit) and L=1.5 ×10-8 W·Ω/K2 for non-degenerate semiconductors[23]. Phonons (quantized lattice vibrations) are the leading carriers of heat in non-metallic crystalline materials. The quantum theory of lattice vibration and the phonon concept were established for understanding heat conduction in crystalline solids. The speed of propagation of acoustic phonons in the lattice is known as phonon velocity. The velocity of phonon is determined as the group velocity, which can be mathematically expressed as Vgr=∂ω/∂K[24]. ω is the frequency of the acoustic wave and K is the wave vector of the vibration associated with its wavelength by K=2π/λ. At low values of K, phonons with longer wavelengths can propagate for large distances in the lattice. However, this behavior fails at large values of K. MFP of phonon is the average distance between the guest atoms. Thermal conductivity is contingent on how far phonons are portable between scattering events (their MFP). In non-metallic materials, κ results from the collective contributions of phonons with wide-ranging MFP. Recently, the MFP of the phonon can be experimentally measured[25]. Fang et al.[26] theoretically calculated κ for intrinsic and doped silicon carbide (SiC). Because of the low n of the intrinsic semiconductor, κe can be ignored. However, for semiconductors with high doping concentration, κe of electrons cannot be ignored, and there thermal conductivity is mainly affected by phonon scattering of electrons and ionization impurity scattering. To be more specific, it is quite challenging to improve the MzT values due to the robust combination between α, σ and κe as α is contrariwise to n, whereas σ and κe are directly proportional to n.
It is clear that κl can be suppressed by reducing the MFP of the phonon. Geometrical effects, such as atomic-scale point defects, mesoscale grain boundaries, artificial induced nanoscale dislocations, nanostructuring, etc., limit the MFP of phonons. In this article, we review some basic approaches using which phonons scattering can be enhanced and the MzT values are improved in TE materials.
1 Atomic-scale Point Defects Approach 1.1 Elemental Doping or Alloying ApproachThis approach can be accomplished via elemental doping/alloying in the host compound. The thermal resistance of pristine compounds increases by introducing point defects in its crystals. Elemental doping/alloying introduces mass fluctuations and field strains in the matrix of the host compounds, which are caused by differences in their atomic masses and ionic sizes, respectively.
Theoretically, κl can be calculated as follows[27-29]:
| $ \frac{k_{l, \text { Alloy }}}{k_{l, \mathrm{Parent}}}=\frac{\arctan (u)}{u} $ | (8) |
| $ u^2=\frac{\pi^2 \theta_D \mathit{\Omega}}{h v^2} k_{l, \text { Parent }} \mathit{\Gamma} $ | (9) |
where h, θD and Ω are Planck's constant, Debye temperature, and volume per atom, respectively.
In Eq.(9), v is the average sound velocity and can be expressed as:
| $ v=\left[\frac{1}{3}\left(\frac{1}{v_l^3}+\frac{2}{v_t^3}\right)\right]^{-1 / 3} $ | (10) |
where vl and vt denote longitudinal and shear sound velocities.
Γ is the scattering parameter and contains three parts i.e., mass difference, strain field and binding force difference. If the binding force difference is not taken into consideration, the scattering parameters of the mass difference (ΓM) and strain field (ΓS) can be written as[30]:
| $ \mathit{\Gamma}_M=\sum\limits_{i=1}^n \mathit{\Gamma}_{M i} $ | (11) |
| $ \mathit{\Gamma}_S=\sum\limits_{i=1}^n \mathit{\Gamma}_{S i} $ | (12) |
where
| $ \mathit{\Gamma}_{M i}=x_i\left[\left(M_i-M\right) / M\right]^2 $ | (13) |
| $ \mathit{\Gamma}_{S i}=x_i\left\{\varepsilon\left[\left(\delta-\delta_{i \mathrm{sub}}\right) / \delta\right]^2\right\} $ | (14) |
Among them, Mi is the atomic weight of the ith substitution atom, M is the atomic weight of the original atom, δisub is the atomic radius of the ith substitution atom, δ is the atomic radius of the original atom and xi is the ratio of ith substitution atom.
In Eq.(14), ε is a material-related parameter that is given by:
| $ \varepsilon=\frac{2}{9}\left[6.4 \gamma \frac{1+r}{1-r}\right]^2 $ | (15) |
where γ is the Gruneisen parameter
| $ \gamma=\frac{3}{2}\left(\frac{1+V_p}{2-3 V_p}\right) $ | (16) |
Vp=r is the Poisson ratio and can be expressed as:
| $ V_P=\frac{1-2\left(V_t / V_l\right)^2}{2-2\left(V_t / V_l\right)^2} $ | (17) |
Therefore, the total scattering parameter Γtotal is:
| $ \mathit{\Gamma}_{\text {total }}=\mathit{\Gamma}_M+\mathit{\Gamma}_S=\sum\limits_{i=1}^n \mathit{\Gamma}_{M i}+\sum\limits_{i=1}^n \mathit{\Gamma}_{S i} $ | (18) |
Enhancing phonons scattering by point defects requires large field strains and large mass fluctuations. However, due to the creation of perturbations in the periodic potential, particularly with large strains affecting the mobility (μ) of the charge carriers (Fig. 1(a)), it is necessary to choose the doping/alloying element that has a smaller size difference from the host atom. In other words, to decouple κl and μ with respect to point defects, it is necessary to choose the doping/alloying component that has a larger mass variance and almost similar ionic size compared with the host atom (Fig. 1(b)). Liu[31] et al. proposed that in p-type (Nb, Ta) FeSb and n-type (Zr, Hf) NiSn alloys, lanthanide contraction paved the best way to suppress κl to the minimum while maintaining μ unaffected, as shown in Fig. 1(c) and (d). For example, the atomic radii of Hf and Zr are nearly similar, i.e. 208 pm and 206 pm, respectively, but there are large differences in atomic mass. Also, Nb and Ta have large differences in atomic mass, but possess nearly similar atomic radii, i.e. 198 pm and 200 pm, respectively. The large difference in atomic masses and nearly similar atomic radii in the above mentioned alloys results in a large scattering of phonons and very less perturbation in periodicity of potential, respectively.
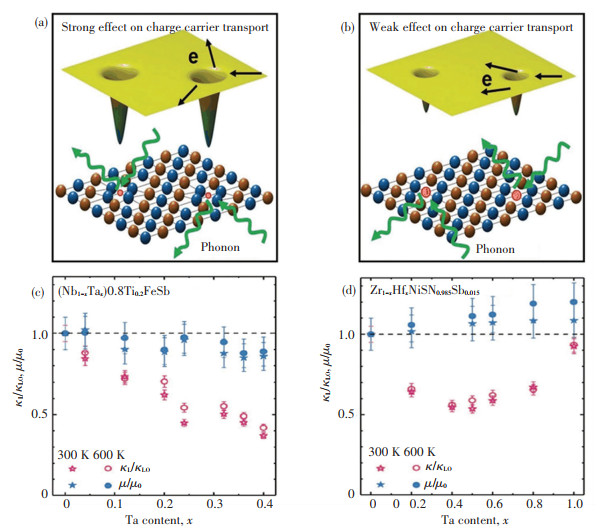
|
Fig.1 (a) More considerable radius difference between host atoms (blue and brown yellow) and alloyed atoms (red) generates more substantial perturbation to the periodic potential and thus deteriorates the charge carrier transport; (b) schematic depicts that weak effect on charge carrier transport can be realized if there are more minor radius differences between host atoms and alloying atoms; (c) and (d) displays the effects of Ta and Hf elements on κL and mobility μ of NbFeSb, and ZrNiSn, respectively. μo and κLo represent mobility and the lattice thermal conductivity for the pure compound, respectively. (Reproduced with permission[31], Copyright © 2018, John Wiley and Sons) |
The use of various elements to introduce point defects in Bi2 Te3-based TE materials has been reported, such as In, Cl, Fe, Ag, Br, Cu, Sn and Ga [32-40]. An enhancement in MzT values was attributed to the reduction of κl and improvement of electronic transport properties. The reduction in κl was due to the enhanced phonons scattering caused by point defects. A MzT value of ~0.74 at 373 K was reported in n-type (Bi0.99Ag0.04)2(Te0.96Se0.04)3 prepared by mechanical alloying (MA) and spark plasma sintering (SPS)[35]. κl was reduced, while an opposite trend for α2σ was observed. Ag doping introduced point defects in the crystal structure and phonon scattering was enhanced. Improved MzT of ~0.8 and ~0.65 at 300 K were reported in 1 at% Cr intercalated and substituted Bi2Te3, respectively[37]. Cr either by substitution or intercalation resulted in point defects in the matrix, which scattered high-frequency phonons and κl was reduced. At 300 K a MzT ~1.09 was achieved in polycrystalline 1.0 at% Fe-doped Bi0.48Sb1.52Te3[40]. Fe doping has been shown effective in enhancing the α2σ due to the optimization of n. Also, κl was suppressed by strong phonon scattering initiating from the atomic mass variance among Fe, Bi, and/or Sb. Lee et al. reported a high MzT ~1.2 at 320 K in 0.5 at% In-doped Bi0.4Sb1.6Te3 polycrystal[38]. As a result of the control amount of In or Ga doping, the κl was suppressed by strong point-defect phonon scattering. Nearly comparable power factors were observed in doped and undoped samples because of the resemblance of the density of states near the valence-band maximum.
In the 1950s, Ioffe proposed that forming solid solutions is an effective strategy for improving TE performance[41]. The compounds with the same crystalline and bonding nature can form a solid solution to suppress κl. For example, in Bi2Te3-Sb2Te3 and PbTe-PbSe solid solutions, κl was suppressed to 0.909 and 1.0 W/(m·K) from 2.0 and 1.538 W/(m·K), respectively. Korkosz et al. reported a MzT value of ~2.0 at 800 K in the pseudoternary Na-doped (PbTe)0.86(PbSe)0.07(PbS)0.07[42]. They ascribed this high MzT to the very low κl. The atomic mass variation and atomic size differences among the Te, Se and S elements introduced more point defects in the crystal structure of PbTe, hence the phonon scattering was enhanced. This approach has been extensively employed in inorganic TE materials including the metal-based chalcogenides[43-47], half-Heusler (HH) compounds[48-54], Zintl phase compounds[55-57], selenides[58-59], silicides[60-61], etc.
Alloying of SnS witha similar crystal structure and bonding nature to SnSe leads to phonon scattering owing to atomic mass fluctuations and large dissimilarities in atomic radii between S and Se elements[62-63]. MzT of 0.64 and 1.0 at 823 K were obtained. κl was decreased from ~0.57 to ~0.36 W/(m·K) and from 0.59 to 0.32 W/(m·K) at 823 K. Alloying strategy is also used to increase the bandgap and boost the inferior TE performance of materials. For example, Ag2Te material shows low κ and high μ value, but the MzT value in its pristine form is only 0.6. The low performance of this material is because of the nearly intrinsic conduction due to the small bandgap. A MzT of ~1.0 was realized by increasing the bandgap of Ag2Te when it is alloyed with PbTe[64]. The deleterious effects of minority carriers were reduced by increasing the bandgap, and the electronic transport properties were enhanced. Alloying in bulk materials also makes it conceivable to direct the convergence of several valleys. High valley degeneracy leads to a high effective mass and then α. Ioffe et al. obtained a convergence of 12 valleys in Pb0.98Na0.02Te1-xSex alloys, which led to a high MzT ~1.8 at 850 K[41].
1.2 Vacancy Engineering ApproachThe effect on TE properties of defects formed caused by introducing vacancies in the matrix are also notable[65-69]. Vacancies introduce missing atoms and missing interatomic linkages in the matrix and enhance phonon scattering. Asfandiyar et al. introduced artificial Sn vacancies in the SnS and SnSe-SnS samples, which broke translation symmetry and boosted phonon scattering[63]. Consequently, κ was suppressed compared with their pristine counterparts. All the vacancy-containing samples showed inferior κl to the pure SnSe sample as depicted in Fig. 2(a). Sn vacancies introduced strong phonons scattering and as a result, κl was suppressed. Also, charge carrier density increases by introducing vacancies in the matrix. In fact, introducing artificial vacancies resembles hole-doping in the matrix. Fermi level shifts into the valence band due to an upsurge in the hole concentration as shown in Fig. 2(b). For example, the n value of 0.6 × 1019 cm-3 in pure SnSe was increased to 1.07 × 1019 cm-3 upon introducing vacancies (Sn0.95Se). zTs of ~1.0 and ~2.1 at elevated temperatures were reported in Sn0.985S0.25Se0.75 and Sn0.95Se, respectively[63, 65]. They attributed the high MzT to the low κl and enhanced α2σ resulting from Sn vacancies.
|
Fig.2 (a) Lattice thermal conductivity of pure and vacancy-containing samples. Vacancy containing samples witnessed low κl values resulting from enhanced mid-frequency phonons scattering; (b) n of pure and vacancy-containing samples, confirming that n increased with the introduction of vacancies in the SnSe compound((a) and (b) Reproduced with permission[65], Copyright © 2018, ACS publications); (c) HAADF-STEM image of Eu2Zn0.98Sb2 and (d) κl of Eu2Zn1-xSb2 (x = 0, 0.01, 0.02, and 0.04). The pink-filled circles represent Eu atoms while the blue-filled circles represent Sb atoms (Reproduced with permission[67], Copyright © 2019, PANS) |
Cu vacancies are easy to form in the CuAgSe and change from stoichiometric to non-stoichiometric compounds[68]. Cu vacancies significantly tune n and lead to high electrical conductivity in the CuAgSe. Also, Cu vacancies act as point defects, when scattered phonons and κ was simultaneously suppressed. High TE performance can be witnessed in the off-stoichiometric InSe-based thermoelectric materials[70-75]. The TE properties were tuned by deficiency of Se elements. The performance of Bi2O2Se was improved upon introducing Bi vacancies in the system[76]. Introducing Ag defects (Ag vacancies) in the Ag1-xGaTe2, the performance was improved approximately two times compared with its stoichiometric counterpart (AgGaTe2)[77].
Zintl compounds are deliberated to be potential TE materials for use at the medium-ranging temperatures. Chen et al. prepared Eu2Zn1-xSb2 bulks by high-energy ball milling and hot pressing[67]. This 2-1-2-type Zintl phase compound has a 50% intrinsic Zn vacancy, which induces an ultralow κl (see Fig. 2(c) and 2(d)). Due to the smaller atomic number, Zn appeared darker, while Eu and Sb showed bright columns due to their more enormous atomic masses as shown in Fig. 2(c). It is obvious that half the sites in this crystal structure are occupied by Zn atoms (yellow filled circles). In contrast, half sites are unoccupied (yellow open circles), which validates 50% intrinsic Zn vacancy. A MzT ~0.6 at 700 K was achieved in the Eu2ZnSb2 compound. With increasing extrinsic Zn vacancy, κl was further reduced and the electrical properties were optimized, giving rise to an improved MzT ~1.0 at 823 K for Eu2Zn0.98Sb2.
2 Nanostructuring ApproachThe TE performance of materials can be effectively manipulated by nanostructure engineering. This approach can lead to reduction in κl, which results from enhanced phonon scattering at the interfaces while also through quantum confinement effects for an increase in α. A particular nanostructure can effectively manipulate the TE performance of inorganic materials. Dimensionality can play a crucial role in reducing κl. For example, strong phonon scattering can be witnessed in low-dimensional materials due to a large number of interfaces compared with their bulk counterparts. In the following sections, a brief discussion has been made on one, two and three-dimensional nanostructure materials.
2.1 One Dimensional (1D) NanostructureThe electronic density of states is concentrated at certain energies if the diameter of one-dimensional material such as nanotubes or nanowires is sufficiently small.Decreasing the diameter of nanowires to a few quantum states causes a split in energy bands, which leads to a decrease in the κl without affecting the electrical transport properties. To date, there are few research studies on the TE performance of 1D materials.
Harman method (resistance measurements by DC and AC methods)was used in obtaining the MzT values of isolated nanowires. Also, the suspended micro-chips technique was used to measure the TE properties[78]. Chen et al. reported a MzT value of ~0.9 at 353 K for Bi2Te3 nanowire arrays using the electrodeposition technique[79]. Also, it was reported that the MzT value might decrease with time due to oxidizing the nanowire surface. A MzT ~0.82 was attained in Bi2Te3 wire of size 200 nm[80]. A high MzT of ~1.0 and ~0.6 were reported in silicon 20 nm and 10 nm wide nanowires, respectively[81]. This value is 100 times higher compared with its bulk silicon counterpart (bulk silicon MzT ~0.01 at 300 K). The enhancement in MzT of these nanowires can be attributed to the reduction in κl when the diameters are small enough as shown in Fig. 3.

|
Fig.3 (a) High-resolution image of 20 nm wide Si nanowires; (b) κ, presented as κbulk/κnanowire. The inset displays the area of the device containing the nanowires before (top) and after (bottom) the XeF2 etches to eradicate the nanowire. The yellow dashed frame represents nanowires. (Reproduced with permission[81], Copyright © 2008, Springer Nature) |
2.2 Two Dimensional (2D) Nanostructure
In 1993, Kim and co-workers suggested that MzT could be optimized to its maximum values by forming thin films (quantum-well superlattices) of certain materials[75]. They calculated MzT for Bi2Te3 thin films. The calculated MzT was 13 times higher than that of its bulk counterpart. This higher MzT in thin films was attributed to the reduced κl resulting from enhanced phonons scattering between layers. Venkatasubramanian et al. obtained a MzT of ~2.0 at 300 K in Bi2Te3 and Sb2Te3 layered thin films[82]. The prepared films using organic chemical vapor deposition were c-oriented. In 2001, the above MzT was further enhanced to ~2.4 at the same measured temperature by optimizing the phonon scattering in the thin film[83].
Besides, other two-dimensional materials, including PbTe/Pb0.93Eu0.07Te[73], PbTe/PbSe0.2Te0.8[84], and Si0.85Ge0.15[85] have been widely studied, and their performance has been improved. The enhancement in MzT of these films has generally been ascribed to the reduced κl. Lee and co-workers examined the κ of Si/Ge superlattices with periods between 30 to 300 Å[85]. They found that κ of these superlattices is lower than that of Si/Ge alloys. With decreasing superlattices period (30 < L < 70 Å), a decreasing trend in the room-temperature κ along the in-plane direction was experimentally observed. However, superlattices with comparatively long periods (L> 130 Å) show lower κ than those of short-period samples. This unforeseen low κ in longer period samples was credited to the robust interruption of the lattice vibrations by prolonged defects formed throughout lattice-mismatched development. In 2000, the TE performance of Si/Ge superlattices was re-investigated[86]. The results for κ were similar to those of Lee's work, as depicted in Fig. 4. Both results show an increasing trend in κ with increasing temperature. A similar tendency in κ was also observed in GeTe/Bi2Te3 superlattices. Tong et al. have suggested two possible mechanisms for this abnormal result[87]. 1) κ is affected by thermal boundary resistance i.e., the low-temperature thermal boundary resistance of samples becomes bigger and increases with increasing frequency and 2) considers the factor of κe in the partially coherent regime, which is based on the wave-particle duality of phonons. A single-element thin-film superlattice SiGe/Si coolers were prepared[88]. The two-fold improvement in the TE performance was accredited to the reduced κ.

|
Fig.4 (a) κ of Si/Ge superlattices. Each symbol is labeled by a superlattice period L measured in Å; (b) κ of undoped Si/Ge superlattices. (Reproduced with permission[85-86], Copyright © 1997, AIP Publishing and Copyright © 2000, Elsevier) |
2.3 Three-Dimensional (3D) Nanostructure
Nanostructuring of 3D bulk materials leads to high density of grains, nanoscale precipitate secondary phases, lattice defects and distortions. κl can be suppressed over a wide temperature range by strengthening all wavelength phonon scattering. Dresselhaus and coworkers have exposed that the bulk materials containing nanoparticle inclusions show better TE performance than those without nanoparticle inclusions[89].
Bi2Te3 bulk nanostructure was prepared by MA followed by SPS and their TE performance was studied. A high MzT value of ~1.3 at 373 K was obtained for nanostructured bulk Bi0.5 Sb1.5 Te3 sample[90]. Mehta et al. prepared nanostructured (BiSb)2(TeSe)3 bulks samples using microwave technique and reported a MzT of ~1.1[91]. A MzT of ~1.16 at 420 K was reported in a nanostructured Bi2Te3 bulk sample synthesized by a wet chemical method followed by SPS[92]. A MzT of ~1.4 at 373 K was achieved in a nanostructured BixSb2-xTe3 bulk sample prepared by high-energy ball milling and hot pressing[93]. Xie and co-workers subjected the Bi0.52Sb1.48Te3 sample to annealing followed by SPS and enhanced the MzT to ~1.56 at 300 K[94]. At 320 K a highest MzT ~1.86 was reported in Bi0.5Sb1.5Te3 compounds[95]. This enhancement in zT value was attributed to the low κl resulting from enhanced midfrequency phonons scattering by nanoscale dislocation arrays, as depicted in Fig. 5(a).
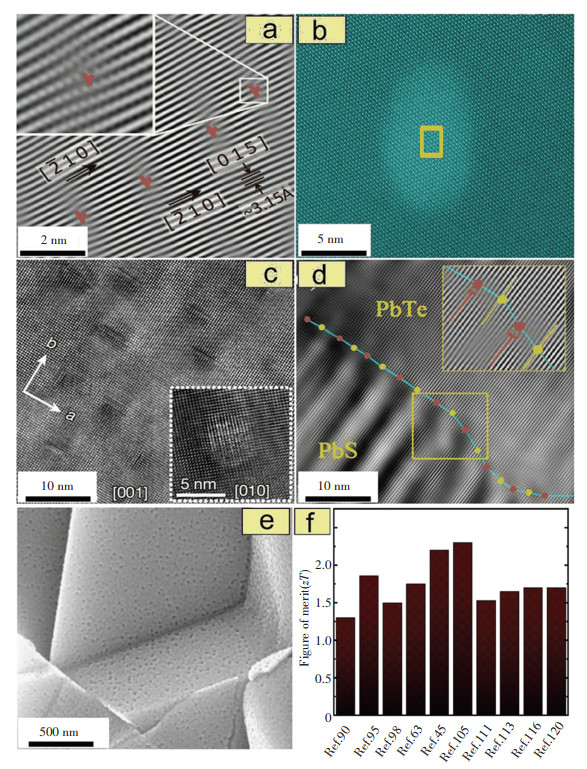
|
Fig.5 (a) FFT image of the Bi0.5Sb1.5Te3 sample. Inset shows nanoscale dislocations (Reproduced with permission[95], Copyright © 2015, Science); (b) HAADF-STEM image of the 0.7 at% Ag-doped Sn0.985S0.25Se0.75, depicting spherical nanoscale-precipitate in the matrix, reveals continuous lattice between matrix and precipitate (Reproduced with permission[63], Copyright © 2020, Elsevier); (c) High-magnification image of the PbTe-SrTe lattice. Inset shows a coherent interface between the nanoprecipitate and matrix (Reproduced with permission[45], Copyright © 2012, Springer Nature); (d) HRTEM image, display PbS/PbTe coherent interface with interfacial dislocation (Reproduced with permission[104], Copyright © 2015, John Wiley and Sons); (e) High-magnification FESEM image of the AgSbTe2 bulk, and depicting nanopores inside the grains (Reproduced with permission[113], Copyright © 2011, Springer); (f) Improved peak MzT values of the nanostructured bulk materials |
Nanoscale precipitate secondary phases can be introduced by the formation of the solid solution to enhance TE performance. There are two kinds of precipitates (coherent and incoherent precipitates) formed in a solid solution matrix. The coherent nanoscale precipitates scatter long wavelength phonons. Unlike coherent precipitates, incoherent nanoscale precipitates have a large disparity with the matrix and scatter short wavelength phonons. Li et al. theoretically investigated phonon transport across coherent and incoherent interfaces[96]. The simulation results indicated that the phonon defect scattering becomes stronger with decreasing phonon wavelength. For phonons with shorter wavelength, they observed a strong phonon scattering across incoherent interfaces. Our previous work reported a high MzT value of ~1.75 at 823 K for SnS-SnSe solid solutions[63]. This high MzT was ascribed to the very low value of κ. The existence of AgSnSe2 nanoscale coherent precipitates within the grains contributes to an impressively low κl. (Fig. 5(b)). A MzT of ~0.6 at 750 K was obtained in SnSe[97]. The low κl was due to the formation of secondary phases (AgSnSe2). At 773 K a MzT ~1.33 was achieved in Ag and Na co-doped SnSe possessing Ag8SnSe6 secondary phases. The low κ was credited to the nanoscale precipitate secondary phases (Ag6SnSe8). The effect of nanostructuring on κl is related to phonon mean free path (MFP). Luo et al. calculated frequency-dependent phonon MFP using Callaway's model[98]. Their calculations suggested point defects and Umklapp scattering mostly affect high-frequency phonons, whereas low-frequency phonons were affected by electron-phonon coupling. The calculated MFP due to nanoscale coherent precipitate was somewhat longer than that of electron-phonon coupling but shorter than those of the point defects and the Umklapp scattering, signifying that nanoprecipitate scattered generally the low-to-middle frequency (long wavelength) phonons. Zhao and co-workers reported a high MzT of ~1.5 at 793 K through Ag and Ge co-doping[99]. A MzT ~1.2 at 773 K was achieved by suppressing κl via introducing PbSe secondary phases in the SnSe matrix[97, 100]. Besides, SnTe and ZnSe secondary phases have been used to suppress the κl in SnSe polycrystals[101-102].
In 2004, Kanatzidis and his research team successfully introduced AgSbTe2 nanodots into PbTe[103]. They achieved a high MzT due to the low κ via enhancing the phonons scattering. Two years later, Biswas and co-workers achieved a peak MzT ~2.2 in PbTe endotaxially nanostructured with SrTe as shown in Fig. 5(c)[45]. A zT of ~2.3 was reported in Na-doped (PbTe)0.8(PbS)0.2[104-105]. This high MzT was credited to the very low κl arising from coherent precipitate with interfacial dislocations depicting in Fig. 5(d). The binary PbTe-PbS and PbSe-PbS compounds have been extensively studied and advanced to a state of remarkably high TE performance[106-109].Besides, the performance of pseudo-ternary Pb(TeSeS) was investigated[42, 104, 110].This ternary system has shown high MzT over a wide-ranging temperature. Also, a MzT ~1.2 at 423 K was achieved in TAGS (AgSbTe2 mixed with SiGe compounds). Zhang and co-workers prepared composites in situ with Sb2Te or Ag2Te embedded in the AgSbTe2 matrix and obtained a MzT value of ~1.53[111]. They ascribed this high MzT to the reduced κ resultant from nanodomain boundaries phonon scattering. A high MzT of ~1.59 at 573 K was obtained in AgSbTe2 ternary alloy[112].This ternary alloy was produced by MA and SPS techniques. The high MzT value has been accredited to the large α at room temperature and extremely low value of κ. This MzT value was further enhanced to ~1.65.Du et al. introduced nanoscale pores (5-10 nm) to the bulk AgSbTe2 shown in Fig. 5(e), which were in situ created throughout a melt-spinning SPS synthesis process[113].
CoSb3-based TE materials are up-and-coming applicants for power generation applications in the medium temperature range. The same material system can realize high performance for n-type and p-type materials. The cage-like open structure can be found in these materials. Up on filling these cages with the foreign atoms, the phonons scattering can be enhanced. At 800 K a MzT ~1.43 was attained in the In0.2Ce0.5Co4Sb12 bulk sample[114]. The enhancement in MzT was attributed to the reduced κ resulting from in situ InSb nanoislands phonons scattering. A MzT of ~1.5 at 850 K was realized in (GaSb)0.2-Yb0.26Co4Sb12 nanocomposite possessing GaSb nanoinclusions[115].The reduced κ was accredited to the GaSb nanoinclusions, which intensified phonons scattering. The research on the single-filled skutterudites was gradually developed into a multiple-filled skutterudites system so as to further reduce κl. It was shown both experimentally and theoretically that filling the cage with multiple guest atoms is more effective to reduce κl. For example, the MzT value of ~1.0 for the single-filled CoSb3-based material was enhanced to ~2.0 using multiple atoms filling. Shi et al. synthesized CoSb3 using Ba, La and Yb cofillers[116]. They obtained a very high MzT ~1.7 at 850 K, which was attributed to the enhanced α2σ along with reduced κl. Dissimilar rattling frequencies of the manifold guest's atomic filling in the cages of CoSb3 resulted in the strong scattering of nearly all wavelength phonons, making κl near to the theoretical minimum. Magnesium silicide (Mg2Si) and its solid solutions have been explored by Nicolaou in 1976[17]. Also, these materials are promising in the medium range of temperature. A MzT ~1.2 at 750 K was realized for Mg2.16(Si0.3Sn0.7)0.98Sb0.02[117]. κl was reduced due to Mg2Sn-rich nanoscale precipitates distributed in the matrix. Bellanger and the research group produced bulk nanostructured Mg2Si0.4Sn0.6 materials composed of nanograins with sizes below 200 nm and excellently dispersed Sn-rich nanoparticles[118]. All the samples were prepared by MA and SPS. It was suggested that the most effective way to suppress κ is to synthesize samples with nanoscale grain sizes instead of nanoparticles. Consequently, an ultra-low κ of less than 1.2 W/(m·K) was realized at ~300 K in samples with nanoscale grain sizes. A very high MzT value of ~1.7 at 673 K was achieved in Bi and Cr co-doped Mg2Si0.3Sn0.7[119]. Elemental Cr and Sn-rich nanoprecipitates embedded in the matrix were observed. The Cr-containing sample showed a 15% reduction in κl compared with the only Bi-doped sample while retaining comparable values of α2σ. Fig. 5(f) shows the improved MzT values via nanostructuring in bulks materials.
The preferred strategy to realize developments in thermoelectric is the recent example of phonon-liquid electron-crystal (PLEC). κl can be reduced even underneath glasses as phonon scattering becomes stronger by the liquid-like fluctuating sublattice[120-121]. Superionic conductors have been developed as a class of favorable applicants to obtain very low κ because these materials show long-range liquid-like ionic performance[122-124]. Cu3SbSe3 shows distinctive liquid-like sublattice and has risen as a low-cost promising candidate with intrinsic ultralow κ. Wang and co-workers experimentally measured the temperature-dependent Raman spectra combined with a theoretical approach on Cu3SbSe3 and Cu3SbSe4 bulks and clarified their different phonon manners[125]. As Cu3SbSe4 validates a classical κ, whereas Cu3SbSe3 exhibits a liquid-like κ of ~0.7-1.0 W/(m·K) at room temperature[126]. Therefore, these compounds offer an exceptional prospect to vigorously analyze the thermal structure and phonon scattering evolution from definite solid vibration to continuous superionic diffusion. The results revealed the activation of superionic conversion for both structurally inequivalent Cu atoms in Cu3SbSe3, which resulted in a mutual broadband phonon scattering. Also, the results showed that phonon quasiparticles were intensely scattered across the superionic transition besides the diffusion channels, whereas the liquid-like diffusion of Cu was excessively sluggish to entirely downfall the transmission of all transverse phonon modes of Cu3SbSe3.
3 SummaryIn the present review, we have discussed in detail the improvement in the thermoelectric figure of merit (MzT) of the thermoelectric materials at bulk (3D) and nanoscale (1D and 2D). Reducing the thermal transport properties of thermoelectric materials, particularly the lattice part (κl), is a crucial zone that can enable larger MzT. Point-defect engineering and nanostructuring are the two typical approaches to suppress the lattice thermal conductivity. To decouple the interrelated lattice thermal conductivity and mobility, it is suggested to dope/alloy the pure compounds with nearly similar atomic size but different atomic mass dopants. Another effective point defects approach is introducing intentional vacancies in the pure compounds. The lattice thermal conductivity and power factor can be simultaneously optimized due to enhancing phonon scattering and increasing carrier concentration, respectively. Careful tailoring of nanostructures, including dimension, shape and interface, is an effective way to boost the thermoelectric performance. Fabrications of 1D-nanostructure, 2D-nanostructure and 3D-nanostructure materials made it possible to suppress the thermal conductivity and increase the Seebeck coefficient due to enhancing phonons scattering at the interfaces and quantum confinement effect, respectively.
| [1] |
Shafiee S, Topal E. When will fossil fuel reserves be diminished?. Energy Policy, 2009, 37: 181-189. DOI:10.1016/j.enpol.2008.08.016 (  0) 0) |
| [2] |
World energy consumption. https://en.wikipedia.org/wiki/.
(  0) 0) |
| [3] |
Tan G, Zhao L D, Kanatzidis M G. Rationally designing high-performance bulk thermoelectric materials. Chemistry Review, 2016, 116: 12123-12149. DOI:10.1021/acs.chemrev.6b00255 (  0) 0) |
| [4] |
Yang L, Chen Z G, Dargusch M S, et al. High performance thermoelectric materials: Progress and their applications. Advanced Energy Materials, 2018, 8: 1701797. DOI:10.1002/aenm.201701797 (  0) 0) |
| [5] |
Liu W D, Chen Z G, Zou J. Eco-friendly higher manganese silicide thermoelectric materials: progress and future challenges. Advanced Energy Materials, 2018, 8: 1800056. DOI:10.1002/aenm.201800056 (  0) 0) |
| [6] |
Patil D S, Arakerimath R R, Walke P V. Thermoelectric materials and heat exchangers for power generation-A review. Renewable and Sustainable Energy Reviews, 2018, 95: 1-22. DOI:10.1016/j.rser.2018.07.003 (  0) 0) |
| [7] |
Siddique A R M, Mahmud S, Heyst B V. A review of the state of the science on wearable thermoelectric power generators (TEGs) and their existing challenges. Renewable and Sustainable Energy Reviews, 2017, 73: 730-744. DOI:10.1016/j.rser.2017.01.177 (  0) 0) |
| [8] |
Yuan Z C, Tang X B, Xu Z H, et al. Screen-printed radial structure micro radioisotope thermoelectric generator. Applied Energy, 2018, 225: 746-754. DOI:10.1016/j.apenergy.2018.05.073 (  0) 0) |
| [9] |
Mustafavi S A, Mahmoudi M. Modeling and fabricating a prototype of a thermoelectric generator system of heat energy recovery from hot exhaust gases and evaluating the effects of important system parameters. Applied Thermal Engineering, 2018, 132: 624-636. DOI:10.1016/j.applthermaleng.2018.01.018 (  0) 0) |
| [10] |
Solbrekken G, Yazawa K, Cohen B. Thermal management of portable electronic equipment using thermoelectric energy conversion. IEEE Cat. No. 04CH37543, Las Vegas, 2004, 1: 276-283. DOI: 10.1109/ITHERM.2004.1319185.
(  0) 0) |
| [11] |
Amar A B, Kouki A, Cao H. Power approaches for implantable medical devices. Sensors, 2015, 15: 28889-28914. DOI:10.3390/s151128889 (  0) 0) |
| [12] |
Duong T P, Lee J W. Experimental results of high-efficiency resonant coupling wireless power transfer using a variable coupling method. IEEE Microwave and Wireless Components Letters, 2011, 21: 442-444. DOI:10.1109/LMWC.2011.2160163 (  0) 0) |
| [13] |
Kim H S, Liu W S, Chen G, et al. Relationship between thermoelectric figure of merit and energy conversion efficiency. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112: 8205-8210. DOI:10.1073/pnas.1510231112 (  0) 0) |
| [14] |
Snyder G J, Snyder A H. Figure of merit ZT of a thermoelectric device defined from materials properties. Energy and Environmental Science, 2017, 10: 2280-2283. DOI:10.1039/C7EE02007D (  0) 0) |
| [15] |
Koumoto K, Funahashi R, Guilmeau E, et al. Thermoelectric ceramics for energy harvesting. Journal of American Ceramic Society, 2013, 96: 1-23. DOI:10.1111/jace.12076 (  0) 0) |
| [16] |
Funahashi R. Thermoelectric Energy Conversion: Theories and Mechanisms, Materials, Devices, and Applications. 1st Edition. Cambridge: Woodhead Publishing/Elsevier, 2021.
(  0) 0) |
| [17] |
Freer R, Ekren D, Ghosh T, et al. Key properties of inorganic thermoelectric materials〞tables (version 1). Journal of Physics Energy, 2022, 4: 022002. DOI:10.1088/2515-7655/ac49dc (  0) 0) |
| [18] |
Jood P, Chetty R, Ohta M. Structural stability enables high thermoelectric performance in room temperature Ag2Se. Journal of Materials Chemistry A, 2020, 8: 13024-13037. DOI:10.1039/D0TA02614J (  0) 0) |
| [19] |
Zhang Q, Liao B L, Lan Y C, et al. High thermoelectric performance by resonant dopant indium in nanostructured SnTe. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110: 13261-13266. DOI:10.1073/pnas.1305735110 (  0) 0) |
| [20] |
Wang X Y, Yao H H, Yin L, et al. Band modulation and strain fluctuation for realizing high average zT in GeTe. Advanced Energy Materials, 2022, 12: 2201043. DOI:10.1002/aenm.202201043 (  0) 0) |
| [21] |
Zhang Z W, Yan Y R, Li X F, et al. A dual role by incorporation of magnesium in YbZn2Sb2 zintl phase for enhanced thermoelectric performance. Advanced Energy Materials, 2020, 10: 2001229. DOI:10.1002/aenm.202001229 (  0) 0) |
| [22] |
Jaziri N, Boughamoura A, Müller J, et al. A comprehensive review of thermoelectric generators: technologies and common applications. Energy Reports, 2020, 6: 264-287. DOI:10.1016/j.egyr.2019.12.011 (  0) 0) |
| [23] |
Kim H S, Gibbs Z M, Tang Y L, et al. Characterization of Lorenz number with Seebeck coefficient measurement. APL Materials, 2015, 3: 041506. DOI:10.1063/1.4908244 (  0) 0) |
| [24] |
Misra P K. Physics of Condensed Matter. Pittsburg: Academic Press, 2010: 44.
(  0) 0) |
| [25] |
Regner K T, Sellan D P, Su Z H, et al. Broadband phonon mean free path contributions to thermal conductivity measured using frequency domain thermoreflectance. Nature Communications, 2013, 4: 1640. DOI:10.1038/ncomms2630 (  0) 0) |
| [26] |
Fang X Y, Wang K, Hou Z L, et al. Electronic scattering leads to anomalous thermal conductivity of n-type cubic silicon carbide in the high-temperature region. Journal of Physics: Condensed Matter, 2012, 24: 4458022012. DOI:10.1088/0953-8984/24/44/445802 (  0) 0) |
| [27] |
Yang J, Meisner G P. Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds. Applied Physics Letters, 2004, 85: 1140. DOI:10.1063/1.1783022 (  0) 0) |
| [28] |
Xiao Y, Chang C, Pei Y L, et al. Origin of low thermal conductivity in SnSe. Physical Review B, 2016, 94: 125203. DOI:10.1103/PhysRevB.94.125203 (  0) 0) |
| [29] |
Mao J, Kim H S, Shuai J, et al. Thermoelectric properties of materials near the band crossing line in Mg2Sn-Mg2Ge-Mg2Si system. Acta Materialia, 2016, 103: 633-642. DOI:10.1016/j.actamat.2015.11.006 (  0) 0) |
| [30] |
Klemens P G. The scattering of low-frequency lattice waves by static imperfections. Proceedings of the Physical Society. Section A, 1955, 68: 1113. DOI:10.1088/0370-1298/68/12/303 (  0) 0) |
| [31] |
Liu Y T, Fu C G, Xia K Y, et al. Lanthanide contraction as a design factor for high-performance half-heusler thermoelectric materials. Advanced Materials, 2018, 30: 1800881. DOI:10.1002/adma.201800881 (  0) 0) |
| [32] |
Kulbachinskii V A, Kytin V G, Tarasov P M, et al. Anomalous increase of the thermopower and thermoelectric figure of merit in Ga-doped p-(Bi0.5Sb0.5)2Te3 single crystals. Physics of Solid State, 2010, 52: 1830-1835. DOI:10.1134/S1063783410090076 (  0) 0) |
| [33] |
Fuccillo M, Jia S, Charles M E, et al. Thermoelectric properties of Bi2Te2Se compensated by native defects and Sn doping. Journal of Electronic Materials, 2013, 42: 1246-1253. DOI:10.1007/s11664-013-2577-0 (  0) 0) |
| [34] |
Chung D U, Hogan T, Brazis P, et al. CsBi4Te6: a high-performance thermoelectric material for low-temperature applications. Science, 2000, 287: 1024. DOI:10.1126/science.287.5455.1024 (  0) 0) |
| [35] |
Zhang X, Ma X Y, Lu Q M., et al. Thermoelectric properties of Ag-doped n-type (Bi2-x AgxTe3)0.96- (Bi2Se3)0.04 pseudobinary alloys. Journal of Electronic Materials, 2011, 40: 773-777. DOI:10.1007/s11664-011-1568-2 (  0) 0) |
| [36] |
Kulbachinskii V, Kytin V G, Kudryashov A A, et al. Influence of Sn on the thermoelectric properties of BixSb1-x)2Te3 single crystals. Journal of Solid State Chemistry, 2012, 193: 83-88. DOI:10.1016/j.jssc.2012.03.061 (  0) 0) |
| [37] |
Han M K, Ryu H, Kim S J. Effect of chromium doping on the thermoelectric properties of Bi2Te3:CrxBi2Te3 and CrxBi2-x Te3. Journal of Electronic Materials, 2013, 42: 2758-2763. DOI:10.1007/s11664-013-2670-4 (  0) 0) |
| [38] |
Lee K H, Hwang S, Ryu B, et al. Enhancement of the thermoelectric performance of Bi0.4Sb1.6Te3 alloys by In and Ga doping. Journal of Electronic Materials, 2013, 42: 1617-1621. DOI:10.1007/s11664-012-2356-3 (  0) 0) |
| [39] |
Kitagawa H, Matsuura T, Kato T, et al. Thermoelectric properties of Cu-doped n-type Bi2Te2.85Se0.15 prepared by liquid phase growth using a sliding boat. Journal of Electronic Materials, 2015, 44(1870): 1875. DOI:10.1007/s11664-014-3578-3 (  0) 0) |
| [40] |
Mun H, Lee K H, Kim S J, et al. Fe-doping effect on thermoelectric properties of p-type Bi0.48Sb1.52Te3. Materials, 2015, 8: 959-965. DOI:10.3390/ma8030959 (  0) 0) |
| [41] |
Ioffe A F. Semiconductor Thermoelements, and Thermoelectric Cooling. London: Infosearch, 1957.
(  0) 0) |
| [42] |
Korkosz R J, Chasapis T C, Lo S H, et al. High ZT in p-type (PbTe)1-2x(PbSe)x(PbS)x thermoelectric materials. Journal of the American Chemical Society, 2014, 136: 3225-3237. DOI:10.1021/ja4121583 (  0) 0) |
| [43] |
Pei Y Z, Shi X Y, Lalonde A, et al. Convergence of electronic bands for high performance bulk thermoelectrics. Nature, 2011, 473: 66-69. DOI:10.1038/nature09996 (  0) 0) |
| [44] |
Xu Z J, Wu H J, Zhu T J, et al. Attaining high mid-temperature performance in (Bi, Sb)2Te3 thermoelectric materials via synergistic optimization. NPG Asia Materials, 2016, 8: e302. DOI:10.1038/am.2016.134 (  0) 0) |
| [45] |
Biswas K, He J Q, Blum I D, et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature, 2012, 489: 414-418. DOI:10.1038/nature11439 (  0) 0) |
| [46] |
Ang R, Khan A U, Tsujii N, et al. Thermoelectricity generation and electron-magnon scattering in a natural chalcopyrite mineral from a deep-sea hydrothermal vent. Angewandte. Chemie, International Edition, 2015, 54: 13101-13105. DOI:10.1002/anie.201505517 (  0) 0) |
| [47] |
Hazan E, Ben-Yehuda O, Madar N, et al. Functional graded germanium-lead chalcogenide-based thermoelectric module for renewable energy applications. Advanced Energy Materials, 2015, 5: 1500272. DOI:10.1002/aenm.201500272 (  0) 0) |
| [48] |
Xie H H, Wang H, Pei Y Z, et al. Beneficial contribution of alloy disorder to electron and phonon transport in half-Heusler thermoelectric materials. Advanced Functional Materials, 2013, 23: 5123-5130. DOI:10.1002/adfm.201300663 (  0) 0) |
| [49] |
Fu C G, Bai S Q, Liu Y T, et al. Realizing high figure of merit in heavy-band p- type half-Heusler thermoelectric materials. Nature Communications, 2015, 6: 8144. DOI:10.1038/ncomms9144 (  0) 0) |
| [50] |
Makongo J P A, Misra D K, Zhou X Y, et al. Simultaneous large enhancements in thermopower and electrical conductivity of bulk nanostructured half-Heusler alloys. Journal of the American Chemical Society, 2011, 133: 18843-18852. DOI:10.1021/ja206491j (  0) 0) |
| [51] |
Kim K S, Kim Y M, Mun H, et al. Direct observation of inherent atomic-scale defect disorders responsible for high-performance Ti1-xHfxNiSn1-ySby half-heusler thermoelectric alloys. Advanced Materials, 2017, 29: 1702091. DOI:10.1002/adma.201702091 (  0) 0) |
| [52] |
Page A, Van der Ven A, Poudeu P F P, et al. Origins of phase separation in thermoelectric (Ti, Zr, Hf)NiSn half-Heusler alloys from first principles. Journal of Materials Chemistry A, 2016, 4: 13949-13956. DOI:10.1039/C6TA04957E (  0) 0) |
| [53] |
Fu C G, Zhu T J, Liu Y T, et al. Band engineering of high performance p-type FeNbSb based half-Heusler thermoelectric materials for figure of merit zT>1. Energy and Environmental Science, 2015, 8: 216-220. DOI:10.1039/C4EE03042G (  0) 0) |
| [54] |
Liu Y T, Xie H H, Fu C G, et al. Demonstration of a phonon-glass electron-crystal strategy in (Hf, Zr)NiSn half-Heusler thermoelectric materials by alloying. Journal of Materials Chemistry, A. Materials for Energy and Sustainability, 2015, 3: 22716-22722. DOI:10.1039/c5ta04418a (  0) 0) |
| [55] |
Shuai J, Geng H Y, Lan Y C, et al. Higher thermoelectric performance of Zintl phases (Eu0.5Yb0.5)1-xCaxMg2Bi2 by band engineering and strain fluctuation. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113: E4125-E4132. DOI:10.1073/pnas.1608794113 (  0) 0) |
| [56] |
Tamaki H, Sato H K, Kanno T. Isotropic conduction network and defect chemistry in Mg3+δSb2-based layered zintl compounds with high thermoelectric performance. Advanced Materials, 2016, 28: 10182-10187. DOI:10.1002/adma.201603955 (  0) 0) |
| [57] |
Zhang J, Song L R, Pedersen S H, et al. Discovery of high-performance low-cost n-type Mg3Sb2-based thermoelectric materials with multi-valley conduction bands. Nature Communications, 2017, 8: 13901. DOI:10.1038/ncomms13901 (  0) 0) |
| [58] |
Zhao L D, Tan G J, Hao S Q, et al. Ultrahigh power factor and thermoelectric performance in hole-doped single-crystal SnSe. Science, 2016, 351: 141-144. DOI:10.1126/science.aad3749 (  0) 0) |
| [59] |
Peng K L, Lu X, Zhan H, et al. Broad temperature plateau for high ZTs in heavily doped p-type SnSe single crystals. Energy and Environmental Science, 2016, 9: 454-460. DOI:10.1039/C5EE03366G (  0) 0) |
| [60] |
Jiang G Y, He J, Zhu T J, et al. High performance Mg2(Si, Sn) solid solutions: a point defect chemistry approach to enhancing thermoelectric properties. Advanced Functional Materials, 2014, 24: 3776-3781. DOI:10.1002/adfm.201400123 (  0) 0) |
| [61] |
Chen Z, Girard S N, Meng F, et al. Approaching the minimum thermal conductivity in Rhenium-substituted higher manganese silicides. Advanced Energy Materials, 2014, 4: 1400452. DOI:10.1002/aenm.201400452 (  0) 0) |
| [62] |
Asfandiyar, Wei T R, Li Z L, et al. Thermoelectric SnS and SnS-SnSe solid solutions prepared by mechanical alloying and spark plasma sintering: anisotropic thermoelectric properties. Scientific Reports, 2017, 7: 43262-43269. DOI:10.1038/srep43262 (  0) 0) |
| [63] |
Asfandiyar, Cai B W, Zhuang H L, et al. Polycrystalline SnSe-Sn1-vS solid solutions: vacancy engineering and nanostructuring leading to high thermoelectric performance. Nano Energy, 2020, 69: 104393. DOI:10.1016/j.nanoen.2019.104393 (  0) 0) |
| [64] |
Pei Y Z, Heinza N A, Snyder G J. Alloying to increase the band gap for improving thermoelectric properties of Ag2Te. Journal of Materials Chemistry, 2011, 21: 18256-18260. DOI:10.1039/C1JM13888J (  0) 0) |
| [65] |
Wei W, Chang C, Yang T, et al. Achieving high thermoelectric figure of merit in polycrystalline SnSe via introducing Sn vacancies. Journal of the American Chemical Society, 2018, 140: 499-505. DOI:10.1021/jacs.7b11875 (  0) 0) |
| [66] |
Jiang Q H, Yan H X, Khaliq J, et al. Enhancement of thermoelectric properties by atomic-scale percolation in digenite CuxS. Journal of Materials Chemistry A, 2014, 2: 9486-9489. DOI:10.1039/C4TA01250J (  0) 0) |
| [67] |
Chen C, Xue W H, Li S, et al. Zintl-phase Eu2ZnSb2: a promising thermoelectric material with ultralow thermal conductivity. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116: 2831-2836. DOI:10.1073/pnas.1819157116 (  0) 0) |
| [68] |
Wang X B, Qiu P F, Zhang T S, et al. Compound defects and thermoelectric properties in ternary CuAgSe-based materials. Journal of Materials Chemistry A, 2015, 3: 13662-13670. DOI:10.1039/C5TA02721G (  0) 0) |
| [69] |
Asfandiyar, Cai B W, Zhao L D, et al. High thermoelectric figure of merit ZT>1 in SnS polycrystals. Journal of Materiomics, 2020, 6: 77-85. DOI:10.1016/j.jmat.2019.12.003 (  0) 0) |
| [70] |
Rhyee J S, Lee K H, Lee S M, et al. Peierls distortion as a route to high thermoelectric performance in In4Se3-δ crystals. Nature, 2009, 459: 965-968. DOI:10.1038/nature08088 (  0) 0) |
| [71] |
Rhyee J S, Kim J H. Chemical potential tuning and enhancement of thermoelectric properties in indium selenides. Materials, 2015, 8: 1283-1324. DOI:10.3390/ma8031283 (  0) 0) |
| [72] |
Ahn K, Cho E, Rhyee J S, et al. Effect of cationic substitution on the thermoelectric properties of In4-xMxSe2.95compounds (M=Na, Ca, Zn, Ga, Sn, Pb; x=0.1). Applied Physics Letters, 2011, 99: 102110. DOI:10.1063/1.3637053 (  0) 0) |
| [73] |
Rhyee J S, Ahn K, Lee K H, et al. Enhancement of the thermoelectric figure-of-merit in a wide temperature range In4Se3-xCl0.03 bulk crystals. Advanced Materials, 2011, 23: 2191-2194. DOI:10.1002/adma.201004739 (  0) 0) |
| [74] |
Zhu G, Lan Y C, Wang H Y, et al. Effect of selenium deficiency on the thermoelectric properties of n- type In4Se3-x compounds. Physical Review B, Condensed Matter, 2011, 83: 115201. DOI:10.1103/PhysRevB.83.115201 (  0) 0) |
| [75] |
Kim J H, Kim M J, Oh S, et al. Thermoelectric properties of Se-deficient and Pb-/Sn-codoped In4Pb0.01Sn0.03Se3-x polycrystalline compounds. Journal of Alloys and Compounds, 2014, 615: 933-936. DOI:10.1016/j.jallcom.2014.06.196 (  0) 0) |
| [76] |
Zhan B, Liu Y C, Tan X, et al. Enhanced thermoelectric properties of Bi2O2Se ceramics by Bi deficiencies. Journal of the American Ceramic Society, 2015, 98: 2465-2469. DOI:10.1111/jace.13619 (  0) 0) |
| [77] |
Yusufu A, Kurosaki K, Kosuga A, et al. Thermoelectric properties of Ag1-x GaTe2 with chalcopyrite structure. Applied Physics Letters, 2011, 99: 061902. DOI:10.1063/1.3617458 (  0) 0) |
| [78] |
Zhou J H, Jin C G, Seol J H, et al. Thermoelectric properties of individual electrodeposited bismuth telluride nanowires. Applied Physics Letters, 2005, 87: 133109. DOI:10.1063/1.2058217 (  0) 0) |
| [79] |
Chen C L, Chen Y Y, Lin S J, et al. Fabrication and characterization of electrodeposited bismuth telluride films and nanowires. The Journal of Physical Chemistry C, 2010, 114: 3385-3389. DOI:10.1021/jp909926z (  0) 0) |
| [80] |
Menke E J, Brown M A, Li Q, et al. Bismuth telluride (Bi2Te3) nanowires: synthesis by cyclic electrodeposition/stripping, thinning by electrooxidation, and electrical power generation. Lengmuir, 2006, 22(25): 10564-10574. DOI:10.1021/la061275g (  0) 0) |
| [81] |
Boukai A I, Bunimovich Y, Kheli J T, et al. Silicon nanowires as efficient thermoelectric materials. Nature, 2008, 451: 168-171. DOI:10.1038/nature06458 (  0) 0) |
| [82] |
Venkatasubramanian R, Colpitts T, Watko E, et al. MOCVD of Bi2Te3, Sb2Te3 and their superlattice structures for thin-film thermoelectric applications. Journal of Crystal Growth, 1997, 170: 817-821. DOI:10.1016/S0022-0248(96)00656-2 (  0) 0) |
| [83] |
Venkatasubramanian R, Siivola E, Colpitts T, et al. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature, 2001, 413: 597-602. DOI:10.1038/35098012 (  0) 0) |
| [84] |
Beyer H, Nurnus J, Bçttner H, et al. High thermoelectric figure of merit ZT in PbTe and Bi2Te3-based superlattices by a reduction of the thermal conductivity. Physica E: Low-dimensional Systems and Nanostructures, 2002, 13: 965-968. DOI:10.1016/S1386-9477(02)00246-1 (  0) 0) |
| [85] |
Lee S M, Cahill D G, Venkatasubramanian R. Thermal conductivity of Si-Ge superlattices. Applied Physics Letters, 1997, 70: 2957-2959. DOI:10.1063/1.118755 (  0) 0) |
| [86] |
Borca-Tasciuca T, Liu W L, Liu J L, et al. Thermal conductivity of symmetrically strained Si/Ge superlattices. Superlattices and Microstructures, 2000, 28: 199-206. DOI:10.1006/spmi.2000.0900 (  0) 0) |
| [87] |
Tong H, Lan F, Liu Y J, et al. Positive dependence of thermal conductivity on temperature in GeTe/Bi2Te3 superlattices: the contribution of electronic and particle wave lattice thermal conductivity. Journal of Physics D: Applied Physics, 2017, 50: 355102. DOI:10.1088/1361-6463/aa7c94 (  0) 0) |
| [88] |
Zeng G, Shakouri A, Bounty C L, et al. SiGe micro-cooler. Electronics Letters, 1999, 35: 2146-2147. DOI:10.1049/EL:19991435 (  0) 0) |
| [89] |
Dresselhaus M S, Chen G, Tang M Y, et al. New directions for low-dimensional thermoelectric materials. Advanced Materials, 2007, 19: 1043-1053. DOI:10.1002/adma.200600527 (  0) 0) |
| [90] |
Ma Y, Hao Q, Poudel B, et al. Enhanced thermoelectric figure-of-merit in p- type nanostructured bismuth antimony tellurium alloys made from elemental chunks. Nano Letters, 2008, 8: 2580-2584. DOI:10.1021/nl8009928 (  0) 0) |
| [91] |
Mehta R J, Zhang Y L, Karthik C, et al. A new class of doped nanobulk high-figure-of-merit thermoelectrics by scalable bottom-up assembly. Nature Materials, 2012, 11: 233-240. DOI:10.1038/nmat3213 (  0) 0) |
| [92] |
Wu F, Song H Z, Gao F, et al. Effects of different morphologies of Bi2Te3 nanopowders on thermoelectric properties. Journal of Electronic Materials, 2013, 42: 1140-1145. DOI:10.1007/s11664-013-2541-z (  0) 0) |
| [93] |
Poudel B, Hao Q, Ma Y, et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science, 2008, 320: 634-638. DOI:10.1126/science.1156446 (  0) 0) |
| [94] |
Xie W J, Tang X F, Yan Y G, et al. High thermoelectric performance BiSbTe alloy with unique low-dimensional structure. Journal of Applied Physics, 2009, 105: 113713. DOI:10.1063/1.3143104 (  0) 0) |
| [95] |
Kim S I, Lee K H, Mun H A, et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science, 2015, 348: 109-114. DOI:10.1126/science.aaa4166 (  0) 0) |
| [96] |
LiW X, Chen X, Yang S F. Phonon transport across coherent and incoherent interfaces. JOM, 2019, 71: 3885-3891. DOI:10.1007/s11837-019-03731-1 (  0) 0) |
| [97] |
Chen C L, Wang H, Chen Y Y, et al. Thermoelectric properties of p-type polycrystalline SnSe doped with Ag. Journal of Materials Chemistry A, 2014, 2: 11171-11176. DOI:10.1039/C4TA01643B (  0) 0) |
| [98] |
Luo Y B, Cai S T, Xia H, et al. High thermoelectric performance in polycrystalline SnSe via dual-doping with Ag/Na and nanostructuring with Ag8SnSe6. Advanced Energy Materials, 2019, 9: 1803072. DOI:10.1002/aenm.201803072 (  0) 0) |
| [99] |
Zhao Q, Qin B C, Wang D Y, et al. Realizing high thermoelectric performance in polycrystalline SnSe via silver doping and germanium alloying. ACS Applied Energy Materials, 2020, 3: 2049-2054. DOI:10.1021/acsaem.9b01475 (  0) 0) |
| [100] |
Lee Y K, Ahn K, Cha J, et al. Enhancing p- type thermoelectric performances of polycrystalline SnSe via tuning phase transition temperature. Journal of the American Chemical Society, 2017, 139: 10887-10896. DOI:10.1021/jacs.7b05881 (  0) 0) |
| [101] |
Guo H F, Xin H X, Qin X Y, et al. Enhanced thermoelectric performance of highly oriented polycrystalline SnSe based composites incorporated with SnTe nanoinclusions. Journal of Alloys and Compounds, 2016, 689: 87-93. DOI:10.1016/j.jallcom.2016.07.291 (  0) 0) |
| [102] |
Li J C, Li D, Qin X Y, et al. Enhanced thermoelectric performance of p-type SnSe doped with Zn. Scripta Materialia, 2017, 126: 6-10. DOI:10.1016/j.scriptamat.2016.08.009 (  0) 0) |
| [103] |
Hsu K F, Loo S, Guo F, et al. Cubic AgPbmSbTe2+m: bulk thermoelectric materials with high figure of merit. Science, 2004, 303: 818-821. DOI:10.1126/science.1092963 (  0) 0) |
| [104] |
Yamini S A, Mitchell D R, Gibbs Z M, et al. Heterogeneous distribution of sodium for high thermoelectric performance of p -type multiphase lead-chalcogenides. Advanced Energy Materials, 2015, 5: 1501047. DOI:10.1002/aenm.201501047 (  0) 0) |
| [105] |
Wu D, Zhao L D, Tong X, et al. Superior thermoelectric performance in PbTe-PbS pseudo-binary: extremely low thermal conductivity and modulated carrier concentration. Energy and Environmental Science, 2015, 8: 2056-2068. DOI:10.1039/C5EE01147G (  0) 0) |
| [106] |
Ibáñez M, Korkosz R J, Luo Z S, et al. Electron doping in bottom-up engineered thermoelectric nanomaterials through HCl-mediated ligand displacement. Journal of the American Chemical Society, 2015, 137: 4046-4049. DOI:10.1021/jacs.5b00091 (  0) 0) |
| [107] |
Androulakis J, Todorov I, He J, et al. Thermoelectrics from abundant chemical elements: high-performance nanostructured PbSe-PbS. Journal of the American Chemical Society, 2011, 133: 10920-10927. DOI:10.1021/ja203022c (  0) 0) |
| [108] |
Jaworski C M, Wiendlocha B, Jovovic V, et al. Combining alloy scattering of phonons and resonant electronic levels to reach a high thermoelectric figure of merit in PbTeSe and PbTeS alloys. Energy and Environmental Science, 2011, 4: 4155-4162. DOI:10.1039/C1EE01895G (  0) 0) |
| [109] |
Girard S N, He J Q, Zhou X Y, et al. High performance Na-doped PbTe-PbS thermoelectric materials: electronic density of states modification and shape-controlled nanostructures. Journal of the American Chemical Society, 2011, 133: 16588-16597. DOI:10.1021/ja206380h (  0) 0) |
| [110] |
Yamini S A, Wang H, Gibbs Z M, et al. Thermoelectric performance of tellurium-reduced quaternary p-type lead-chalcogenide composites. Acta Materialia, 2014, 80: 365-372. DOI:10.1016/j.actamat.2014.06.065 (  0) 0) |
| [111] |
Zhang S N, Zhu T J, Yang S H, et al. Improved thermoelectric properties of AgSbTe2 based compounds with nanoscale Ag2Te in situ precipitates. Journal of Alloys and Compounds, 2010, 499: 215-220. DOI:10.1016/j.jallcom.2010.03.170 (  0) 0) |
| [112] |
Wang H, Li J F, Zou M M, et al. Synthesis and transport property of AgSbTe2 as a promising thermoelectric compound. Applied Physics Letters, 2008, 93: 202106. DOI:10.1063/1.3029774 (  0) 0) |
| [113] |
Du B L, Li H, Xu J J, et al. Enhanced thermoelectric performance and novel nanopores in AgSbTe2 prepared by melt spinning. Journal of Solid State Chemistry, 2011, 184: 109-114. DOI:10.1016/j.jssc.2010.10.036 (  0) 0) |
| [114] |
Li H, Tang X F, Zhang Q J, et al. High performance InxCeyCo4Sb12 thermoelectric materials with in situ forming nanostructured InSb phase. Applied Physics Letters, 2009, 94: 102114. DOI:10.1063/1.3099804 (  0) 0) |
| [115] |
Xiong Z, Chen X H, Huang X Y, et al. High thermoelectric performance of Yb0.26Co4Sb12/ y GaSb nanocomposites originating from scattering electrons of low energy.. Acta Materialia, 2010, 58: 3995-4002. DOI:10.1016/j.actamat.2010.03.025 (  0) 0) |
| [116] |
Shi X, Yang J, James R S, et al. Multiple-filled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports. Journal of the American Chemical Society, 2011, 133: 7837-7846. DOI:10.1021/ja111199y (  0) 0) |
| [117] |
Yin K, Su X L, Yan Y G, et al. In situ nanostructure design leading to a high figure of merit in an eco-friendly stable Mg2Si0.70 solid solution. RSC Advances, 2016, 6: 16824-16831. DOI:10.1039/C5RA27171A (  0) 0) |
| [118] |
Bellanger P, Gorsse S, Bernard-Granger G, et al. Effect of microstructure on the thermal conductivity of nanostructured Mg2(Si, Sn) thermoelectric alloys: an experimental and modeling approach. Acta Materialia, 2015, 95: 102-110. DOI:10.1016/j.actamat.2015.05.010 (  0) 0) |
| [119] |
Goyal G K, Mukherjee S, Malik R C, et al. High thermoelectric performance in Mg2(Si0.7) by enhanced phonon scattering. ACS Applied Energy Materials, 2019, 2: 2129-2137. DOI:10.1021/acsaem.8b02148 (  0) 0) |
| [120] |
Liu H L, Shi X, Xu F F, et al. Copper ion liquid-like thermoelectrics. Nature Materials, 2012, 11: 422-425. DOI:10.1038/nmat3273 (  0) 0) |
| [121] |
Rowe D M, Pollock D D, Stockholm J G, et al. CRC Handbook of Thermoelectrics. Boca Raton: CRC Press, 1995.
(  0) 0) |
| [122] |
Tyagi K, Gathori B, Bathula S, et al. Thermoelectric and mechanical properties of spark plasma sintered Cu3SbSe3 and Cu3SbSe4: promising thermoelectric materials. Applied Physics Letters, 2014, 105: 261902. DOI:10.1063/1.4904996 (  0) 0) |
| [123] |
Niedziela J L, Bansal D, May A F, et al. Selective breakdown of phonon quasiparticles across superionic transition in CuCrSe2. Nature Physics, 2019, 15: 73-78. DOI:10.1038/s41567-018-0298-2 (  0) 0) |
| [124] |
Damay F, Petit S, Rols S, et al. Localised Ag+ vibrations at the origin of ultralow thermal conductivity in layered thermoelectric AgCrSe2. Scientific Reports, 2016, 6: 23415. DOI:10.1038/srep23415(2016) (  0) 0) |
| [125] |
Wang C, Wu Y X, Pei Y Z, et al. Dynamic disorder phonon scattering mediated by Cu atomic hopping and diffusion in Cu3SbSe3. npj Computational Materials, 2020, 6: 155. DOI:10.1038/s41524-020-00421-4 (  0) 0) |
| [126] |
Zhang Y S, Skoug E, Cain J, et al. First-principles description of anomalously low lattice thermal conductivity in thermoelectric Cu-Sb-Se ternary semiconductors. Physical Review B, 2012, 85: 054306. DOI:10.1103/PhysRevB.85.054306 (  0) 0) |
 2022, Vol. 29
2022, Vol. 29


