2. Key Laboratory of Beijing City on Preparation and Processing of Novel Polymer Materials, Beijing University of Chemical Technology, Beijing 100029, China;
3. Beijing Engineering Research Center of Advanced Elastomers, Beijing University of Chemical Technology, Beijing 100029, China
With the over consumption of fossil fuels, abundant attention has been paid to energy crisis and environmental conservation all over the world. As one of the major sources of energy consumption[1-3], the car industry has also been required to transform to a development mode of energy conservation, safety and environmental protection[4]. In recent years, high performance tires involving good wear resistance[5-7], low rolling resistance[8-10], high wet skid resistance[11-13] (the famous 'magic triangle'[14] which is challenging to balance) as well as good mechanical property[15-16] are becoming the main trend of tire industry. Among the four properties mentioned above, wear resistance is the most concerned for the following reasons: on the one hand, wear resistance has an important impact on the service life and driving safety[17-18] of automobiles, and abrasive particles are undisputed sources of air[19-22], soil[23-24] and water pollution[25-27]; on the other hand, relatively large experimental noise[28] often exists in wear resistance tests. Tread rubber composites, which are the main components[29] of tires, are closely related to the 'magic triangle' and mechanical properties of tires, making it an essential factor in the development of high performance tires.
One of the biggest obstacles to the design of tread rubber composites is the compromise of multiple target performance. Considering the complex relationship among formulation variables and target properties and mutual inhibition between different properties[30], varying one factor at a time (OFAT)[31] might not provide a satisfactory result. The research methodologies of the Design of Experiments (DoE)[32] such as orthogonal design[33-34] and uniform design[35-36] are especially suitable for systems affected by multiple factors. However, DoE-based range analysis[37] is of high uncertainty because of the absence of consideration of interactions between variables (e.g., the well-known rubber-filler interactions[38] in this study), and cannot give accurate predictions. Usually a quadratic model[39] is expected to be established for further analysis in DoE. However, it is still insufficient to describe the complicated relationship among formulation and properties of rubber composites, especially for wear resistance. What is needed is an efficient method to quickly predict and balance multiple target properties.
Machine learning (ML), as an advanced analysis method, has been widely used in medicine, chemistry[40], robotics[41], geospatial analysis[42] and other disciplines due to its unique advantages. On the one hand, compared with traditional experiment-driven material development methods and time-consuming molecular dynamics simulation methods[43-44], machine learning[45-47] as a data-driven method can effectively reduce costs, improve efficiency, and reduce the dependence on scientific intuition. On the other hand, machine learning does not require many simplifying assumptions and solving complicated mathematical equations (sometimes even high nonlinear partial differential equations) like theoretical learning[48], making it a useful tool to model different engineering problems under real-world conditions. Unfortunately, as far as the author knows, there have been few reports on the application of machine learning methods in optimization design of tread rubber composites.
In this work, a "Uniform design-Machine learning" strategy (Fig. 1) for performance prediction and multi-performance optimization of tread rubber composites was proposed. Adjustable design elements include types of natural rubber (NR), antioxidant 4020 loading and types of carbon black (CB). First, uniform design was utilized for sample collection to ensure the representativeness of the sample set, and there were a total of 21 experiments in this uniform design. Then statistical analysis as well as 6 different kinds of machine learning analysis methods were implemented and compared. Finally, validation experiments were implemented to evaluate the optimization designs from statistical analysis and machine learning analysis, and the influence of design factors on multi-performance-wear resistance (the primary optimization index), rolling resistance, wet skid resistance and tensile strength was also discussed. Our approach is general and applicable to guide the design and optimization of various materials with desired properties.

|
Fig.1 Schematic diagram of the "Uniform design-Machine learning"strategy |
1 Materials and Methods 1.1 Materials
Three different types of carbon black (CB) samples N220, N234 and N330 were purchased from Shanghai Cabot Chemical Co., Ltd. Precipitated silica VN3 (SiO2) was supplied by Qingdao Degussa Chemical Co., Ltd. Three kinds of NR samples were RSS-1# (Indonesia), YB-1# (Yunnan Rubber Products Co., Ltd., China) and Synthetic NR (Yunnan Natural Rubber Industry Group Xishuangbanna Jingyang Co., Ltd., China), respectively. Other rubber additives, including zinc oxide (ZnO), stearic acid (SA), sulphur (S), N-cyclohexyl-2-benzothiazole sulphonamide (CZ), 3-mercaptopropyl-ethoxy-bis(tridecyl-pentaethoxy-siloxane) (Si747), triethoxysilane-terminated liquid polybutadiene (TTPB), poly(1, 2-dihydro-2, 2, 4-trimethylquinoline) (RD), N-1, 3-dimethylbutyl-N'-phenyl-p-phenylenediamine (4020) were industrial grade products.
1.2 Preparation of NR Composites21 compounds were prepared according to the basic recipe (Supplementary Information(SI) Table S1) and uniform design (SI Table S2) via a two-step mixing technique. Firstly, NR, CB, Silica, Si747, TTPB paraffin wax and antioxidants were added into an internal mixer at 100 ℃. Afterwards the components were further kneaded for 5 min at 150 ℃ for the in-situ modification of silica before discharging and then cooled down to room temperature. In the second mixing step, ZnO, stearic acid, accelerator CZ and sulfur were mixed with the compound on a two-roll mill.
The scorch time and optimum cure time of the compounds were determined using a rotor-less rheometer (Beijing Huanfeng Chemical Machinery Trial Plant, Beijing, China) at 151 ℃. NR composites for DMTA (dynamic mechanical thermal analysis) and mechanical properties test were prepared by compression molding at 151 ℃ for optimum cure time + 2 min using a flat vulcanizing machine (Huzhou Dongfang Machinery Co., Ltd., China).
1.3 CharacterizationThe static mechanical properties were investigated utilizing an electronic tensile machine (CMT4104, Shenzhen SANS Testing Machine Co., Ltd., China) with a tensile rate of 500 mm/min, and the hardness was measured using a Shore A durometer. A VA3000 DMTA (01dBMetravib Co., Ltd., France) at 10 Hz in tension mode was employed to detect the dynamic mechanical properties, and the temperature varied from -80 to +80 ℃ with the heating rate of 3 ℃/min. An RPA 2000 (Alpha Technologies Co., USA) was used to test the dynamic rheological properties of the samples at 60 ℃. The strain amplitude varied from 0.1% to 200% at 1 Hz for the rubber compounds, and ranged from 0.1 to 42% at 10 Hz for the NR composites. Contact angle measurement[49-50] was carried out using the sessile drop method. The cross-linking density was tested on a MesoMR23-060H-I solid-state 1H low-field NMR spectrometer (Niumag Analytical Instrument Corp, China) with the measurement temperature of (90±0.1) ℃. The abrasion resistance of the NR composites was tested on an Akron abrasion tester (Jiangsu Mingzhu Science and Technology Development Co. Ltd., China) according to GB/T1689-1998.
1.4 Statistical AnalysisStatistical analysis, including range analysis and ANOVA are implemented via IBM SPSS Statistics 26 software.
1.5 Machine-Learning ModelsFour basic algorithms-ridge regression(RR), artificial neural networks (ANN), support vector machine regression (SVR), classification and regression tree (CART) and two integrated algorithms-gradient boosting decision tree (GBDT) and extreme gradient boosting (XGB) were used to establish the regression model. Among the four basic algorithms, ridge regression[51], also known as Tikhonov regularization[52], is an improved least-squares method (LSM) dedicated to the analysis of collinear data, which can give lower values than the variance values obtained from the LSM due to the introduction of bias as sacrifice; ANN[53-54] is a mathematical model inspired by the nervous system of human brain for information processing, which allows ANN to approximate complex data sets, but also leads to its easy fall into overfitting; SVR maps input vectors into a high-dimensional feature space to implement nonlinear regression with the aid of kernel functions[55], and usually performs better than ANN on small sample nonlinear regression problems[56]; CART[57] is a recursive partitioning method aiming at producing subsets of the data set which are as homogeneous as possible pertaining to the target variable. It is constructed by splitting subsets of the data set with all predictor variables. Starting from the whole data set, two child nodes are created repeatedly[58]. This tree-like structure makes CART more interpretable than black box models such as ANN. Different from the four basic algorithms mentioned above, both ensemble algorithms (GBDT and XGB) integrate multiple weak regressors to construct a powerful regressor. GBDT[59] adopt a serial strategy that only one CART regressor is produced each iteration along the negative gradient of the previous weak classifier. XGB[60] is an improvement of the GBDT method and is not prone to fall into overfitting due to the introduction of regularization terms. Leave-one-out (loo) cross-validation method[61] was adopted to assess the validity of various regressors in view of its advantages in making full use of small sample data and avoiding over-fitting. Briefly, this process involves dividing the dataset into 21 random segments, of which 20 were used for training and the 21st as the test set. A total of 21 iterations were implemented and the averaged prediction error was applied for the evaluation of regressors. The prediction error includes mean square error (MSE) and mean relative error (MRE), which can be described using Eqs.(1) and (2):
| $ \operatorname{MRE}=\frac{1}{n} \sum\limits_{i=1}^n\left(\frac{\left|y_i-\hat{y}_l\right|}{y_l}\right) $ | (1) |
| $ \mathrm{MSE}=\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-\hat{y}_l\right)^2 $ | (2) |
where n is sample number of test data sets; y is the target value and ŷ is the predicted value. All of the prediction and regressors-evaluation methods were implemented utilizing the Scikit-Learn Python library[45].
2 Results and Discussion 2.1 Sample PointsThe preparation and characterization of material (tread rubber composites in this work) are typically time and cost consuming, making it difficult to gain big datasets like other fields. Consequently, it is essential to obtain highly representative sample points through as few experiments as possible. In this work, uniform design (UD) which was first proposed by Fang[62] was applied to generate sample points. Compared with other DoE methodologies, uniform design determines the number of the experimental trials based only on the level of factors, hence substantially reducing experimental trials while ensuring uniform distribution of sample points in experimental region. Types of NR(A), antioxidant 4020 loading (B) and types of CB (C) were chosen as design factors. Other ingredients in the formulation included activator, antioxidant, accelerator and sulfur, whose loading was controlled to be constant (SI Table S1). Three levels were selected for each factor, resulting in a total of 21 experiments in this uniform design. Each level of factors was adopted equally possibly seven times to ensure uniformity of sampling (Fig. 2), where the sample points represented by hollow point, blue dot and yellow dot were implemented 0, 1 and 2 times, respectively. The experimental results are given in Table 1. In tire industry, rolling resistance and wet skid resistance are usually evaluated with 0 ℃ tanδ and 60 ℃ tanδ, respectively. The smaller the 60 ℃ tanδ value, the smaller the rolling resistance. The larger the 0 ℃ tanδ, the better the wet skid resistance.
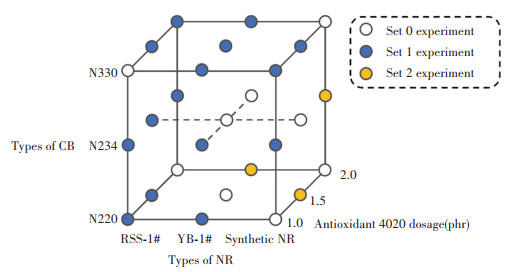
|
Fig.2 Uniform design of three formulation variables: Types of NR (A), antioxidant 4020 loading (B) and types of CB (C) |
| Table 1 Experimental values of four target performances for the 21 NR composites samples |
2.2 Statistical Analysis 2.2.1 Range Analysis
Range analysis based on uniform design is implemented to evaluate the main effect of each factor on the four target attributes. In this case, the analysis of each factor is isolated, and the interactions between factors are not taken into account. The mean value is used to evaluate the effect of different levels of a certain factor on the target performance, while the influence of different factors on the target performance is compared by the ranges of the mean value of the target performance.
For example, if only the influence of types of NR(A) on Akron abrasion is estimated, Fig. 3(a) shows that the mean value of Akron abrasion is the lowest when YB-1# is used. Similarly, for antioxidant 4020 loading (B) and types of CB (C), the levels corresponding to the lowest mean values of Akron abrasion are "2 phr antioxidant 4020" and "N330", respectively. In addition, the range (difference between the highest value and the lowest value) of mean Akron abrasion caused by antioxidant 4020 loading (B) is the highest among the three factors, indicating that antioxidant 4020 loading (B) has the greatest influence on Akron abrasion. However, the error bar shows that Akron abrasion fluctuates greatly when synthetic NR is used, making it possible to obtain an abrasion value even lower than when YB-1# is selected. This may be due to the great difference in affinity between synthetic NR and different types of CB, which seriously affects the dispersion of fillers. Therefore, the lower fluctuation limit of Akron abrasion rather than the mean value should be considered when designing NR composites with the best wear resistance. That is to say, the design derived from Fig. 3(a) that is likely to achieve the minimum Akron abrasion is "Synthetic NR (A=3), 2 phr antioxidant 4020 (B=3), N234 (C=3)". Similarly, Figs. 3(b), (c), (d) indicate that the formulation variables with the greatest influence on 0 ℃ tanδ, 60 ℃ tanδ and tensile strength are antioxidant 4020 (B), types of CB (C), antioxidant 4020 (B), respectively. Considering the fluctuation scopes of the target performance, the potential optimization design given by range analysis with high wear resistance, low rolling resistance, high wet skid resistance and high tensile strength is "Synthetic NR (A=3), 2 phr antioxidant 4020 (B=3), N330 (C=3)". It is noteworthy that whether the design is feasible is still uncertain because of the high fluctuation of range analysis, hence it is critical for multi-performance optimization of NR composites to implement an analytical method with lower uncertainty. Besides, direct prediction of target performance cannot be achieved by range analysis.
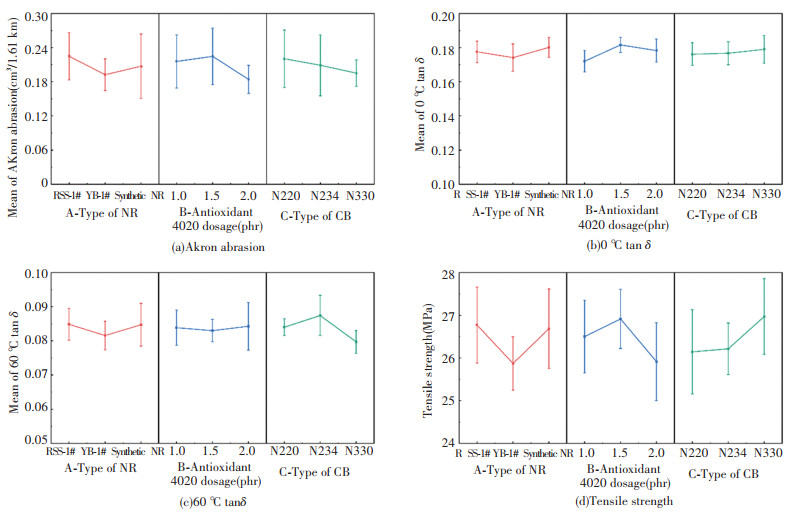
|
Fig.3 Main effect of three formulation variables on four target performances |
2.2.2 Analysis of Variance (ANOVA)
ANOVA was conducted to establish full quadratic models for the prediction of multi-performance. However, Table 2 indicates that no significant term exists in the total quadratic model on Akron abrasion (the primary target property), meaning that quadratic model is not suitable for describing the relationship between design factors and Akron abrasion due to its complexity. Similar results are also found in ANOVA of the remaining three target properties (SI Tables S3, S4, S5). Therefore, it is necessary to find a more appropriate methodology to establish regression models.
| Table 2 ANOVA of UD, response surface regression of the full quadratic model on Akron abrasion |
2.3 Machine Learning Analysis 2.3.1 Modeling
As discussed above, statistical analysis (range analysis and ANOVA) did not give satisfactory results, therefore machine learning (ML) methods are applied for further analysis in this section. Unlike range analysis, machine learning analysis lists three interaction terms -AB, AC, BC in addition to the three design factors -A, B, C as the optional inputs, thus the interaction between formulation variables is fully considered. Four different prediction models of Akron abrasion, 0 ℃ tanδ, 60 ℃ tanδ and tensile strength are established using the most appropriate modeling conditions. When screening the best modeling conditions, different inputs and algorithms were compared to achieve the minimum deviation and variance. For details, please refer to SI Figs. S1, S2 and Table S6.
Modeling conditions and prediction capabilities of prediction models for different target performance are listed in Table 3. All models show acceptable generalization capability, although the prediction error of Akron abrasion is slightly high. As mentioned earlier, the prediction of wear resistance is relatively more difficult, which just testifies the necessity of choosing Akron abrasion as the primary optimization index. Interaction terms are included in the inputs of all prediction models, demonstrating that interactions between design factors indeed have a significant impact on the target performance of tread rubber composites. Also, training effect for different prediction models are depicted in Fig. 4. The predicted values on the sample sets are basically consistent with the experimental values, which further illustrates the rationality of the obtained models.
| Table 3 Modeling conditions and prediction capabilities of prediction models for different target performance |
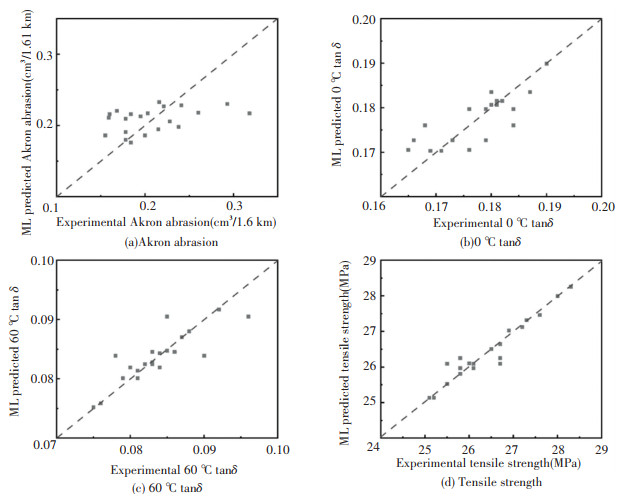
|
Fig.4 Training effect of ML models for different target performance |
The relative importance of the amount of input in each target performance prediction model is shown in Figs. 5(a), (b), (c), (d). It can be seen that the interaction term between types of NR and antioxidant 4020 loading (AB) has a significant effect on 0 ℃ tanδ, 60 ℃ tan δ and tensile strength, and the interaction term between types of NR and types of CB (AC) is the most important factor for both Akron abrasion and tensile strength, indicating that there are non negligible interactions between each formulation variables. These interactions reflect the differences in the affinities between different kinds of NR and antioxidant 4020 or different kinds of carbon black, which will be discussed in detail later.

|
Fig.5 Relative importance of inputs on different target performance |
2.3.2 Design for Multi-Performance Optimization
Considering the mutual inhibition between different properties, it is a great challenge to make full use of the potential of NR composites and realize the comprehensive optimization of multi-performance. Here is an attempt to see if this can be achieved using the established ML models. The design goal is proposed in combination with domain knowledge and material potential reflected by the variation range of each target performance in the sample set (Akron abrasion(cm3/1.61 km): 0.155-0.318, 0 ℃ tanδ: 0.165-0.190, 60 ℃ tanδ: 0.075-0.096, tensile strength(MPa): 25.1- 28.3). High performance tread materials require high wear resistance (the primary target property), high wet skid resistance, high tensile strength and low rolling resistance. Consequently, the design goal is set as "Akron abrasion < 0.185(cm3/1.61 km), 0 ℃ tanδ > 0.170, 60 ℃ tanδ < 0.080, tensile strength > 27.0 MPa".
The multi-performance optimization process based on machine learning analysis is as follows. Firstly, through traversing the unexplored space with the established prediction model of Akron abrasion, the designs with high wear resistance were screened out; Secondly, 0 ℃ tanδ, 60 ℃ tanδ and tensile strength of these selected designs were simultaneously predicted by means of their respective prediction models, and designs satisfying all the target performance requirements were considered as candidate optimization designs.
Optimization designs (designs 1-5) derived from machine learning analysis are summarized in Table 4, where samples for subsequent verification experiments (designs 2, 5, 6) are also indicated. Observing Table 4, it can be concluded that to meet the design goals, the most suitable type of CB (C) is N330, and the Akron abrasion (the primary target property) gradually decreases with the increase of antioxidant 4020 loading (B). In addition, synthetic NR (A=3) is used in most of the candidate designs, but when the loading of antioxidant is high enough, the adoption of RSS-1# (A=1) is also acceptable. It is worth mentioning that OD-1# is consistent with the results of previous range analysis, indicating that simple range analysis can also be a good guide for the optimization design of NR composites. However, since the performance prediction of unknown designs can be achieved with the aid of the established ML prediction models, machine learning analysis can obtain more candidate optimization designs and fully exploit the potential of NR composites compared with range analysis.
| Table 4 Optimization designs (designs 1-5) derived from machine learning analysis and samples for verification experiments (designs 2, 5, 6) |
2.4 Verification Experiments
To test the validity of the design, three sets of validation experiments were implemented (Table 4), in which OD-1# (also an optimization scheme of range analysis) and OD-2# are two optimization designs derived from ML analysis, while CG-3# is a randomized design as a contrast.
The values of all target properties for verification experiments are summarized in Fig. 6 and Table 5. Fig. 6(a) depicts that OD-2# possesses the highest tanδ peak value which can be attributable to a weakened filler network. In the glass transition zone, the filler network can be hardly destroyed due to the weak mobility of the molecular chains, hence the main reason for energy dissipation is the friction losses between the rubber chains[63]. A weaken filler network means less rubber chains trapped in the filler network and thereby enhances the inner friction between the rubber molecular chains, resulting in a high tanδ peak in this case. Fig. 6(b) and 6(c) are magnifications of tanδ versus temperature curves near 0 ℃ and 60 ℃, respectively. It has been widely accepted that 0 ℃ tanδ reflects the wet skid resistance and 60 ℃ tanδ reflects the rolling resistance in tire industry and the effective balance between these two performances is a very concerned problem. Evidently, CG-3# has the best wet skid resistance while OD-2# shows the lowest rolling resistance.
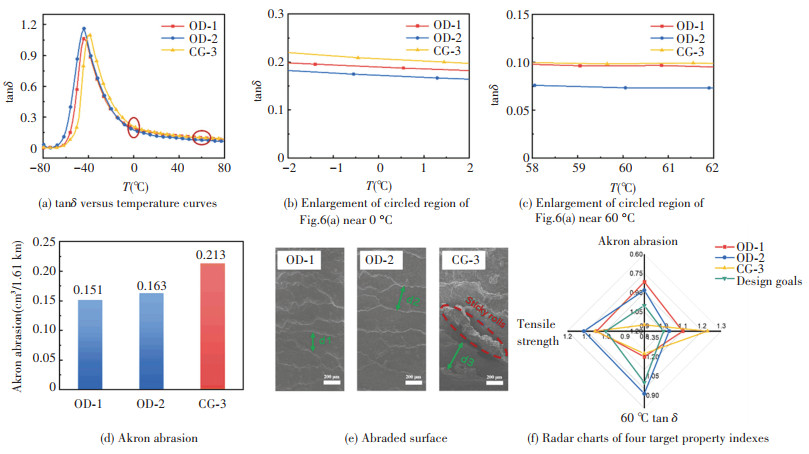
|
Fig.6 Results of verification experiments |
| Table 5 Mechanical properties of verification experiments |
Fig. 6(d) reveals that the experimental Akron abrasion values of the three verification experiments increase in the order of OD-1# < OD-2# < CG-3#, which is consistent with the prediction results of ML models (the predicted values are 0.156, 0.179, 0.223 (cm3/1.61 km), respectively). Fig. 6(e) depicts the abraded surface of the verification samples, from which it can be seen clearly that different from OD-1# and OD-2#, CG-3# with the worst wear resistance displays a larger distance between the ridges, and the abraded surface is oily and tarry. Besides, sticky rolls originating from mechano-chemical degradation are observed in CG-3# in addition to wear patterns, demonstrating that mechano-chemical degradation cannot be ignored in the abrasion of NR composites. Regarding another important target property-tensile strength, Table 5 presents that OD-2# has the highest tensile strength, followed by CG-3# and OD-1#.
To intuitively evaluate the feasibility of the designs, the verification results were normalized according to the equation below:
| $ {\rm{Target\;property\;index=Target\;property\;values/ \\ \;\;\;\;\;\;\;\;\;\;\;\;Target\;property\;design\;goals}} $ | (3) |
where target property can be Akron abrasion, 0 ℃ tanδ, tensile strength or 60 ℃ tanδ.
Fig. 6(f) portrays that OD-2# derived from ML analysis meets the optimization requirements of all target performance, especially for Akron abrasion and 60 ℃ tanδ(about 21% and 9% lower than the design targets, respectively), demonstrating the feasibility of our proposed "Uniform design-Machine learning" strategy. Another optimum design OD-1#, originating from intuitive analysis, also shows gratifying comprehensive performance, although its 60 ℃ tanδ is relatively high. In contrast, the wear resistance and rolling resistance of randomly designed CG-3# are not up to standard. To summarize, the range analysis based on uniform design does provide positive guidance for the multi-performance optimization of NR composites, but no predicted results are given, and the interaction between features is not taken into account. In contrast, ML analysis not only reduces uncertainty, but also provides all possible optimization designs by traversing the unexplored space, which greatly improves design efficiency.
Moreover, the reasons for the performance differences among the three verification samples are discussed. Table 5 illustrates that OD-2# possesses the highest hardness. Modulus at 300% and the lowest elongation at break all reflect its high cross-linking degree, which can be demonstrated by the cross-linking density of the three verification samples(Fig. 7(a)). One possible reason is that OD-2# uses RSS-1# (A=1) and the other two validation samples use synthetic NR (A=3) which does not contain non-rubber components that promote vulcanization. High cross-linking density limits the movement of rubber molecular chains, which explains why OD-2# has the lowest 0 ℃ tanδ and 60 ℃ tanδ.

|
Fig.7 Other characterizations for the further analysis of verification experiments |
Figs. 7(b), 7(c) depict that the values of storage modulus (G′) are dramatically decreased with the increasing strain, owing to the so called 'Payne effect' which is often used to evaluate the dispersion of fillers. It is noteworthy that the 'Payne effects' of the three verification samples undergo a reversal before and after vulcanization, with OD-#1 having the lowest 'Payne effect' before vulcanization while "OD-2#" having the lowest 'Payne effect' after vulcanization, due to the reaggregation of fillers during vulcanization. The low 'Payne effect' of OD-2# vulcanizate means good filler dispersion, explaining why the vulcanizate of OD-2# has the lowest tanδ (Fig. 7(d)), which also agrees with the results of DMA analysis.
Furthermore, contact angle measurement was implemented to better understand the dispersion of fillers from the perspective of the interaction between types of NR (A) and types of CB (C). The surface energies of fillers and rubber are depicted in Fig. 7(e), from which the adhesion work (Wa) and the difference of adhesion work (ΔWa) are calculated (Fig. 7(f)). Stockelhuber[49-50] proposed that Wa and ΔWa can be used as the thermodynamic predictors for filler-polymer adhesion and filler flocculation, respectively. Fig. 7(f) illustrates that Wa of N330-Synthetic NR (OD-1#) is the highest, thus OD-1# has the highest filler-interface interaction and exhibits the best filler dispersion before vulcanization. ΔWa denotes the energetic difference of a dispersed and a flocculated composite. The bigger the difference of the ΔWa is, the more the filler particles tend to flocculate. Besides, the high cross-linking density of OD-2# also limits the re-aggregation of fillers. Together, these two reasons resulted in the lowest degree of flocculation of OD-2# during vulcanization, which explains the reversal of the 'Payne effect' before and after vulcanization.
As for Akron abrasion, studies have shown that abrasion of NR composites is inseparable from mechano-chemical degradation. With the decrease in the amount of antioxidant 4020, mechanical degradation is more likely to occur, so the abraded surface of CG-3# is obviously oily, accompanied by larger ridge spacing than OD-1# and OD-2#. On the other hand, the wear resistance of OD-1# is superior to that of OD-2# due to the higher affinity between synthetic NR and N330 (refer to Wa).
3 ConclusionsTo obtain desired NR composites with high wear resistance, low rolling resistance, high tensile strength and high wet skid resistance, the research methodology of "Uniform design-Machine learning" is proposed in the present study. On the one hand, uniform design allows generation of representative sample points with as few experiments as possible, which greatly saves design costs. On the other hand, our results show that compared with statistical analysis, machine learning analysis is more suitable for establishing the performance prediction models of NR composites and can give more candidate optimization designs that meet the multi-performance optimization goals, which significantly improves the design efficiency.
Validation experiments are implemented to evaluate the feasibility of the designs. The results of validation experiments are in agreement with the predictions of ML models, showing that both OD-1# (synthetic NR, 2 phr antioxidant 4020, N330) and OD-2# (RSS-1#, 2.25 phr antioxidant 4020, N330) could effectively balance each target performance, among which OD-1# exhibited the better abrasion resistance and OD-2# possessed the lower 60 ℃ tanδ. The present study highly approves the positive role of machine learning in balancing the target properties of NR composites. It gives guidance by traversing the unexplored space with ML prediction models in selecting the optimal formulation variables satisfying multi-performance optimization objectives, which greatly reduces the design cost and improves the optimization efficiency.
Supplementary InformationThe Supporting Information including Table S1-Table S6 and Fig. S1-Fig. S2.
The three formula variables are marked in red, including Types of NR (A), Antioxidant 4020 loading (B) and Types of CB (C), and the loading of other components is controlled to be consistent for all samples.
Table S2 gave the formula of uniform design, according to which 21 different NR samples were prepared.
| Table S1 Basic recipe of NR composites |
| Table S2 Uniform design table |
| Table S3 ANOVA of UD, response surface regression of the full quadratic model on 0 ℃ tan δ |
| Table S4 ANOVA of UD, response surface regression of the full quadratic model on 60 ℃ tan δ |
| Table S5 ANOVA of UD, response surface regression of the full quadratic model on tensile strength |
| Table S6 Features corresponding to models with different numbers of features |
|
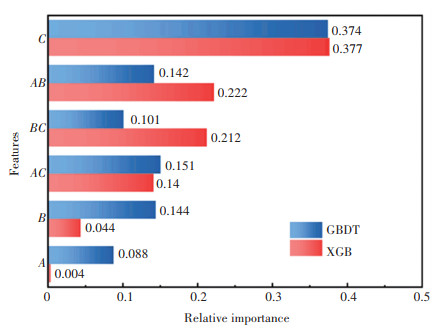
S1 Feature importance obtained from GBDT and XGB on Akron abrasion |
|
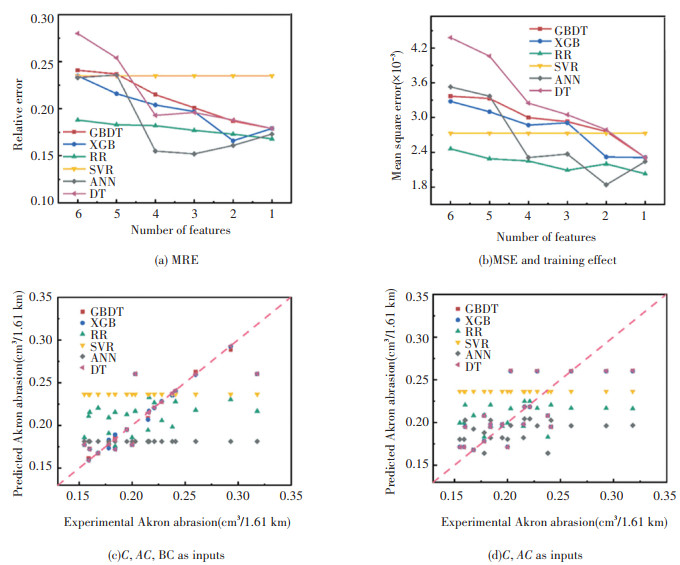
S2 Effect of different machine learning algorithms and inputs on the generalization capability |
Optional inputs include three design factors -A, B, C and three interaction terms -AB, AC, BC. Starting with all six features, the unimportant features are gradually eliminated referring to the relative importance (see SI Fig. S1) of features originated from GBDT (learning rate=0.1, n estimators=100, max depth=3) and XGB (learning rate=0.1, n estimators=200, max depth=5) algorithms until only one independent variable remains. Fig. S2(a), S2(b) indicate that if only the prediction error is minimized, it is appropriate to select ANN (hidden layer sizes=6, learning rate=0.1) or RR (α=1.0, fit intercept=True) algorithm and 2 or 3 features as independent variables. According to Table S6, when the number of features is 3 and 2, the corresponding features are "C, AC, BC" and "C, AC". Fig. S2(c) and S2(d) show the predictions of each model for the training set when using "C, AC, BC" and "C, AC" as inputs, respectively, revealing that biases are evidently smaller when "C, AC, BC" is selected. Further, by comparison, the learning effect of RR on training sets is better than that of ANN, thus it could be concluded that the most appropriate modeling conditions for Akron abrasion are: "C, AC, BC" as inputs and RR as algorithm.
| [1] |
Sommer F, Dietze V, Baum A, et al. Tire abrasion as a major source of microplastics in the environment. Aerosol and Air Quality Research, 2018, 18(8): 2014-2028. DOI:10.4209/aaqr.2018.03.0099 (  0) 0) |
| [2] |
Wagner S, Hüffer T, Klöckner P, et al. Tire wear particles in the aquatic environment-A review on generation, analysis, occurrence, fate and effects. Water Research, 2018, 139: 83-100. DOI:10.1016/j.watres.2018.03.051 (  0) 0) |
| [3] |
Wik A, Dave G. Occurrence and effects of tire wear particles in the environment-A critical review and an initial risk assessment. Environmental Pollution, 2009, 157(1): 1-11. DOI:10.1016/j.envpol.2008.09.028 (  0) 0) |
| [4] |
Hilonga A, Kim J K, Sarawade P B, et al. Synthesis of mesoporous silica with superior properties suitable for green tire. Journal of Industrial and Engineering Chemistry, 2012, 18(5): 1841-1844. DOI:10.1016/j.jiec.2012.04.015 (  0) 0) |
| [5] |
Lang A, Klüppel M. Influences of temperature and load on the dry friction behaviour of tire tread compounds in contact with rough granite. Wear, 2017, 380-381: 15-25. DOI:10.1016/j.wear.2017.02.047 (  0) 0) |
| [6] |
Liang H, Fukahori Y, Thomas A G, et al. Rubber abrasion at steady state. Wear, 2009, 266(1-2): 288-296. DOI:10.1016/j.wear.2008.07.006 (  0) 0) |
| [7] |
Liang H, Fukahori Y, Thomas A G, et al. The steady state abrasion of rubber: Why are the weakest rubber compounds so good in abrasion?. Wear, 2010, 265(5-6): 756-762. DOI:10.1016/j.wear.2009.11.015 (  0) 0) |
| [8] |
Kong L H, Li F, Wang F H, et al. In situ assembly of SiO2 nanodots/layered double hydroxide nanocomposite for the reinforcement of solution-polymerized butadiene styrene rubber/butadiene rubber. Composites Science and Technology, 2018, 158: 9-18. DOI:10.1016/j.compscitech.2018.01.036 (  0) 0) |
| [9] |
Zhang C F, Tang Z H, Guo B C, et al. Significantly improved rubber-silica interface via subtly controlling surface chemistry of silica. Composites Science and Technology, 2018, 156: 70-77. DOI:10.1016/j.compscitech.2017.12.020 (  0) 0) |
| [10] |
Zhang P, Morris M, Doshi D. Materials development for lowering rolling resistance of tires. Rubber Chemistry and Technology, 2016, 89(1): 79-116. DOI:10.5254/rct.16.83805 (  0) 0) |
| [11] |
Wang Q G, Liu J R, Cui Q D, et al. Effect of elastomer nanoparticles on improving the wet skid resistance of Sbr/Nr composites. Rubber Chemistry and Technology, 2016, 89(2): 262-271. DOI:10.5254/rct.15.84849 (  0) 0) |
| [12] |
Wang Y X, Ma J H, Zhang L Q, et al. Revisiting the correlations between wet skid resistance and viscoelasticity of rubber composites via comparing carbon black and silica fillers. Polymer Testing, 2011, 30(5): 557-562. DOI:10.1016/j.polymertesting.2011.04.009 (  0) 0) |
| [13] |
Wang Y X, Wu Y P, Li W J, et al. Influence of filler type on wet skid resistance of SSBR/BR composites: effects from roughness and micro-hardness of rubber surface. Applied Surface Science, 2011, 257(6): 2058-2065. DOI:10.1016/j.apsusc.2010.08.129 (  0) 0) |
| [14] |
Dong M J, Zhang T X, Zhang J C, et al. Mechanism analysis of Eucommia ulmoides gum reducing the rolling resistance and the application study in green tires. Polymer Testing, 2020, 106539. DOI:10.1016/j.polymertesting.2020.106539 (  0) 0) |
| [15] |
Bijarimi M, Zulkafli H, Beg M D H. Mechanical properties of industrial tyre rubber compounds. Journal of Applied Sciences (Faisalabad), 2010, 10(13): 1345-1348. DOI:10.3923/jas.2010.1345.1348 (  0) 0) |
| [16] |
Lu Y L, Liu J, Hou G Y, et al. From nano to giant? Designing carbon nanotubes for rubber reinforcement and their applications for high performance tires. Composites Science and Technology, 2016, 137: 94-101. DOI:10.1016/j.compscitech.2016.10.020 (  0) 0) |
| [17] |
Huang M, Guibert M, Thévenet J, et al. A new test method to simulate low-severity wear conditions experienced by rubber tire materials. Wear, 2018, 410-411: 72-82. DOI:10.1016/j.wear.2018.06.004 (  0) 0) |
| [18] |
Sun J T, Sun J J, Zhang P. Effects of the interaction of hardness, resilience, and fatigue properties on the abrasion properties of rubber blends. Journal of Applied Polymer Science, 2013, 130(2): 1212-1219. DOI:10.1002/app.39258 (  0) 0) |
| [19] |
Alves C A, Vicente A M P, Calvo A I, et al. Physical and chemical properties of non-exhaust particles generated from wear between pavements and tyres. Atmospheric Environment, 2020, 224: 117252. DOI:10.1016/j.atmosenv.2019.117252 (  0) 0) |
| [20] |
Gietl J K, Lawrence R, Thorpe A J, et al. Identification of brake wear particles and derivation of a quantitative tracer for brake dust at a major road. Atmospheric Environment, 2010, 44(2): 141-146. DOI:10.1016/j.atmosenv.2009.10.016 (  0) 0) |
| [21] |
Panko J M, Chu J, Kreider M L, et al. Measurement of airborne concentrations of tire and road wear particles in urban and rural areas of France, Japan, and the United States. Atmospheric Environment, 2013, 72: 192-199. DOI:10.1016/j.atmosenv.2013.01.040 (  0) 0) |
| [22] |
Thorpe A J, Harrison R M, Boulter P G, et al. Estimation of particle resuspension source strength on a major London Road. Atmospheric Environment, 2007, 41(37): 8007-8020. DOI:10.1016/j.atmosenv.2007.07.006 (  0) 0) |
| [23] |
Kreider M L, Panko J M, Mcatee B L, et al. Physical and chemical characterization of tire-related particles: comparison of particles generated using different methodologies. Science of the Total Environment, 2010, 408(3): 652-659. DOI:10.1016/j.scitotenv.2009.10.016 (  0) 0) |
| [24] |
Padoan E, Rome C, Ajmone-Marsan F. Bioaccessibility and size distribution of metals in road dust and roadside soils along a peri-urban transect. Science of the Total Environment, 2017, 601-602: 89-98. DOI:10.1016/j.scitotenv.2017.05.180 (  0) 0) |
| [25] |
Murray K E, Thomas S M, Bodour A A. Prioritizing research for trace pollutants and emerging contaminants in the freshwater environment. Environmental Pollution, 2010, 158(12): 3462-3471. DOI:10.1016/j.envpol.2010.08.009 (  0) 0) |
| [26] |
Panko J M, Kreider M L, Mcatee B L, et al. Chronic toxicity of tire and road wear particles to water- and sediment-dwelling organisms. Ecotoxicology, 2013, 22(1): 13-21. DOI:10.1007/s10646-012-0998-9 (  0) 0) |
| [27] |
Wagner S, Huffer T, Klockner P, et al. Tire wear particles in the aquatic environment-A review on generation, analysis, occurrence, fate and effects. Water Research, 2018, 139: 83-100. DOI:10.1016/j.watres.2018.03.051 (  0) 0) |
| [28] |
Vieira T, Ferreira R P, Kuchiishi A K, et al. Evaluation of friction mechanisms and wear rates on rubber tire materials by low-cost laboratory tests. Wear, 2015, 328-329: 556-562. DOI:10.1016/j.wear.2015.04.001 (  0) 0) |
| [29] |
Wu J, Chen L, Wang Y S, et al. Effect of temperature on wear performance of aircraft tire tread rubber. Polymer Testing, 2019, 79: 106037. DOI:10.1016/j.polymertesting.2019.106037 (  0) 0) |
| [30] |
Salehi M, Noordermeer J W M, Reuvekamp L A E M, et al. Parameter optimization for a laboratory friction tester to predict tire ABS braking distance using design of experiments. Materials & Design, 2020, 194: 108879. DOI:10.1016/j.matdes.2020.108879 (  0) 0) |
| [31] |
Mandenius C F, Brundin A. Bioprocess optimization using design-of-experiments methodology. Biotechnology Progress, 2008, 24(6): 1191-1203. DOI:10.1002/btpr.67 (  0) 0) |
| [32] |
Gajera B Y, Shah D A, Dave R H. Development of an amorphous nanosuspension by sonoprecipitation-formulation and process optimization using design of experiment methodology. International Journal of Pharmaceutics, 2019, 559: 348-359. DOI:10.1016/j.ijpharm.2019.01.054 (  0) 0) |
| [33] |
Kim S J, Cho Y G, Oh C S, et al. Development of a dual phase steel using orthogonal design method. Materials & Design, 2009, 30(4): 1251-1257. DOI:10.1016/j.matdes.2008.06.017 (  0) 0) |
| [34] |
Su L S, Zhang J B, Wang C J, et al. Identifying main factors of capacity fading in lithium ion cells using orthogonal design of experiments. Applied Energy, 2016, 163: 201-210. DOI:10.1016/j.apenergy.2015.11.014 (  0) 0) |
| [35] |
Li X, Li X B, Su Y H. A hybrid approach combining uniform design and support vector machine to probabilistic tunnel stability assessment. Structural Safety, 2016, 61: 22-42. DOI:10.1016/j.strusafe.2016.03.001 (  0) 0) |
| [36] |
Ping H L, Xu G H, Wu S F. System optimization of cyclohexane dehydrogenation under multiphase reaction conditions using the uniform design method. International Journal of Hydrogen Energy, 2015, 40(46): 15923-15932. DOI:10.1016/j.ijhydene.2015.09.002 (  0) 0) |
| [37] |
Xin Z X, Zhang Z X, Pal K, et al. Study of microcellular injection-molded polypropylene/waste ground rubber tire powder blend. Materials & Design, 2010, 31(1): 589-593. DOI:10.1016/j.matdes.2009.07.002 (  0) 0) |
| [38] |
Ismail H, Omar N F, Othman N. Effect of carbon black loading on curing characteristics and mechanical properties of waste tyre dust/carbon black hybrid filler filled natural rubber compounds. Journal of Applied Polymer Science, 2011, 121(2): 1143-1150. DOI:10.1002/app.33511 (  0) 0) |
| [39] |
Wang J P, Chen Y Z, Wang Y, et al. Optimization of the coagulation-flocculation process for pulp mill wastewater treatment using a combination of uniform design and response surface methodology. Water Research, 2011, 45(17): 5633-5640. DOI:10.1016/j.watres.2011.08.023 (  0) 0) |
| [40] |
Wang C S, Fu H D, Jiang L, et al. A property-oriented design strategy for high performance copper alloys via machine learning. npj Computational Materials, 2019, 5(1): 87. DOI:10.1038/s41524-019-0227-7 (  0) 0) |
| [41] |
Lesort T, Lomonaco V, Stoian A, et al. Continual learning for robotics: definition, framework, learning strategies, opportunities and challenges. Information Fusion, 2020, 58: 52-68. DOI:10.1016/j.inffus.2019.12.004 (  0) 0) |
| [42] |
Tehrany M S, Jones S, Shabani F, et al. A novel ensemble modeling approach for the spatial prediction of tropical forest fire susceptibility using logitboost machine learning classifier and multi-source geospatial data. Theoretical and Applied Climatology, 2019, 137(1-2): 637-653. DOI:10.1007/s00704-018-2628-9 (  0) 0) |
| [43] |
Liu J, Wu S Z, Zhang L Q, et al. Molecular dynamics simulation for insight into microscopic mechanism of polymer reinforcement. Physical Chemistry Chemical Physics, 2011, 13(2): 518-529. DOI:10.1039/C0CP00297F (  0) 0) |
| [44] |
Liu J, Zhang L Q, Cao D P, et al. Static, rheological and mechanical properties of polymer nanocomposites studied by computer modeling and simulation. Physical Chemistry Chemical Physics, 2009, 11(48): 11365-11384. DOI:10.1039/B913511A (  0) 0) |
| [45] |
Kailkhura B, Gallagher B, Kim S, et al. Reliable and explainable machine learning methods for accelerated material discovery. arXiv: Computational Physics, 2019, 5: 108. DOI:10.1038/s41524-019-0248-2 (  0) 0) |
| [46] |
Raccuglia P, Elbert K C, Adler P D F, et al. Machine-learning-assisted materials discovery using failed experiments. Nature, 2016, 533(7601): 73-76. DOI:10.1038/nature17439 (  0) 0) |
| [47] |
Yuan R H, Liu Z, Balachandran P V, et al. Accelerated discovery of large electrostrains in BaTiO3‐based piezoelectrics using active learning. Advanced Materials, 2018, 30(7): 1702884. DOI:10.1002/adma.201702884 (  0) 0) |
| [48] |
Fukahori Y, Gabriel P, Liang H, et al. A new generalized philosophy and theory for rubber friction and wear. Wear, 2020, 446-447: 203166. DOI:10.1016/j.wear.2019.203166 (  0) 0) |
| [49] |
Stockelhuber K W, Das A, Jurk R, et al. Contribution of physico-chemical properties of interfaces on dispersibility, adhesion and flocculation of filler particles in rubber. Polymer, 2010, 51(9): 1954-1963. DOI:10.1016/j.polymer.2010.03.013 (  0) 0) |
| [50] |
Stockelhuber K W, Svistkov A S, Pelevin A, et al. Impact of filler surface modification on large scale mechanics of styrene butadiene/silica rubber composites. Macromolecules, 2011, 44(11): 4366-4381. DOI:10.1021/ma1026077 (  0) 0) |
| [51] |
Toğaçar M, Ergen B, Cömert Z. Application of breast cancer diagnosis based on a combination of convolutional neural networks, ridge regression and linear discriminant analysis using invasive breast cancer images processed with autoencoders. Medical Hypotheses, 2020, 135: 109503. DOI:10.1016/j.mehy.2019.109503 (  0) 0) |
| [52] |
Mao F, Zhao X F, Ma P M, et al. Revision of biological indices for aquatic systems: a ridge-regression solution. Ecological Indicators, 2019, 106: 105478. DOI:10.1016/j.ecolind.2019.105478 (  0) 0) |
| [53] |
Marugán A P, Márquez F P G, Perez J M P, et al. A survey of artificial neural network in wind energy systems. Applied Energy, 2018, 228: 1822-1836. DOI:10.1016/j.apenergy.2018.07.084 (  0) 0) |
| [54] |
Zhao Z T, Lou Y, Chen Y F, et al. Prediction of interfacial interactions related with membrane fouling in a membrane bioreactor based on radial basis function artificial neural network (ANN). Bioresource Technology, 2019, 282: 262-268. (  0) 0) |
| [55] |
Koschwitz D, van Treeck J F C. Data-driven heating and cooling load predictions for non-residential buildings based on support vector machine regression and NARX Recurrent Neural Network: a comparative study on district scale. Energy, 2018, 165: 134-142. DOI:10.1016/j.energy.2018.09.068 (  0) 0) |
| [56] |
Min J H, Lee Y C. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Systems with Applications, 2005, 28(4): 603-614. DOI:10.1016/j.eswa.2004.12.008 (  0) 0) |
| [57] |
Yeo B, Grant D. Predicting service industry performance using decision tree analysis. International Journal of Information Management, 2018, 38(1): 288-300. DOI:10.1016/j.ijinfomgt.2017.10.002 (  0) 0) |
| [58] |
Ture M, Tokatli F, Kurt I. Using Kaplan-Meier analysis together with decision tree methods (C&RT, CHAID, QUEST, C4.5 and ID3) in determining recurrence-free survival of breast cancer patients. Expert Systems with Applications, 2009, 36(2): 2017-2026. DOI:10.1016/j.eswa.2007.12.002 (  0) 0) |
| [59] |
Huan J, Li H, Li M B, et al. Prediction of dissolved oxygen in aquaculture based on gradient boosting decision tree and long short-term memory network: A study of Chang Zhou Fishery Demonstration Base, China. Computers and Electronics in Agriculture, 2020, 175: 105530. DOI:10.1016/j.compag.2020.105530 (  0) 0) |
| [60] |
Pathy A, Meher S, Balasubramanian P. Predicting algal biochar yield using eXtreme Gradient Boosting (XGB) algorithm of machine learning methods. Algal Research, 2020, 50: 102006. DOI:10.1016/j.algal.2020.102006 (  0) 0) |
| [61] |
Wong T T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognition, 2015, 48(9): 2839-2846. DOI:10.1016/j.patcog.2015.03.009 (  0) 0) |
| [62] |
Fang K, Lin D K J, Winker P, et al. Uniform design: theory and application. Technometrics, 2000, 42(3): 237-248. DOI:10.1080/00401706.2000.10486045 (  0) 0) |
| [63] |
Kong L H, Li F, Wang F H, et al. High-performing multi-walled carbon nanotubes/silica nanocomposites for elastomer application. Composites Science and Technology, 2018, 162: 23-32. DOI:10.1016/j.compscitech.2018.04.008 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30


