With the continuous improvement of high-speed train (HST) mileage and speed, its fault diagnosis technology is urgently needed. Thus, researching on fault diagnosis of HST is of theoretical and practical significance.
The fault diagnosis technology have been investigated for high-speed trains in recent years. Among these, many research has been done on the traction system of trains such as the traction rectifier[1], three-phase inverter[2], and the traction motor[3]. For the brake system, a support vector machine (SVM) framework is proposed in Ref. [4] to realize the fault detection of the train braking system. The research on the fault diagnosis of other train components includes the gear[5], suspension system[6], and the bogie[7-9]. However, these studies only paid attention to the fault diagnosis of train components but not the fault diagnosis of the train running state with complex nonlinear characteristics.
Many research has been done on the fault diagnosis for dynamics of HST. Among these, an adaptive compensation algorithm is proposed in Ref. [10], which regards the whole train as a single particle model to realize the fault-tolerant control of HST under the failure of the actuator. Further, the train is regarded as a multi-particle model, and the coupling force between adjacent cars is considered for fault diagnosis[11]. In addition, based on an adaptive algorithm and a neutral network, the speed and position of the vehicles are tracked[12-13]. However, these studies only considered actuator failures but not concurrent actuators and sensor failures. Moreover, these studies only considered the fault-tolerant control with faults having known bound but not the estimation of specific faults.
As fault estimation is the final process of fault diagnosis and can be the basis for active fault-tolerant control, the fault estimation is extremely important for HST. Further, the operating noise of HST not only affects the safety of passengers, but also causes engineering fatigue damage to train equipment. Therefore, it is of realistic significance for fault estimation of HST with operating noise. As is known to all, the UKF filter algorithm has high accuracy for fault estimation of the system with noise. Some UKF-based method have been proposed for fault estimation of HST. Aiming at the fault estimation of the suspension systems of HST, a Kalman filtering-like fault estimation algorithm have been proposed[14]. For fault detection and fault estimation of the induction motor of HST, nonlinear Kalman filtering methods have been investigated[15]. However, these studies only performed state or failure estimations on structure component but not the dynamics of HST, and the noise in their research is just an idealized random model, which has little practical significance.
So far, there are some difficulties in UKF-based fault estimation for dynamics of HST. The one is the uncertainty in the system, such as the measurement uncertainties, the other one is the change in system noise. Generally speaking, the train operating noise mainly consists of mechanical noise, electrical noise and aerodynamic excitation noise. Mechanical noise is mainly caused by friction between wheels and rails, electrical noise is mainly caused by arc discharge generated by pantograph lifting, and aerodynamic excitation noise is mainly caused by eddy currents on the surface of the train body. With the increase of train speed, aerodynamic noise has become the main noise source of the train. However, aerodynamic noise is not strictly white noise, and sometimes has the unknown statistics. For some actual systems with process and measurement uncertainties, strong tracking algorithm and adaptive algorithm have been proposed in Refs. [16] and [17], respectively. To implement an accurate fault estimation for Satellite Attitude Control Systems (ACSs) with unknown noise, adaptive algorithm have been proposed in our former study[18]. However, for systems with uncertainties and unknown noise together, the investigation still needs to be improved.
For these reasons, this paper proposes an adaptive robust unscented Kalman filter (ARUKF) algorithm, which considers the measurement uncertainty and statistical unknown noise to implement fault estimation for dynamics of HST. An augmented state space system is established that considers both actuator and sensor failures. Aerodynamic noise is applied to the leading and trailing cars. The noise of the middle car is assumed to be mechanical noise, and all of the noise is closer to the actual operating noise of the train. In addition, the measurement uncertainty is considered, and a robust lower bound is introduced to reduce its influence on the filtering accuracy. An adaptive algorithm is proposed based on moving windows to implement an unbiased estimation of the noise with unknown statistics. Compared with the aforementioned algorithm, the improvement of this algorithm is as follows. Firstly, the algorithm considers both actuator and sensor failures, as well as measurement uncertainty which extends the fault estimation for dynamics of HST. Secondly, the robust algorithm is introduced into the update of the UKF algorithm to ensure the filtering accuracy. Finally, an adaptive algorithm based on moving window is proposed to decrease the influence of the unknown statistics of the noise on filtering, which widens the applied scope of the UKF-based algorithm for dynamics of HST.
The context of this paper is organized as follows. In Section 1, a multi-particle dynamics model of HST with measurement uncertainty and unknown statistical noise is established, the actuator and sensor faults are given. In Section 2, a robust lower bound is proposed to decrease the influence of measurement uncertainty on filtering accuracy. In Section 3, an ARUKF algorithm is proposed based on moving windows for implementing an unbiased estimation of the time-vary noise with unknown statistics. In Section 4, the effectiveness of the algorithm is analyzed by simulation. Finally, conclusions are drawn.
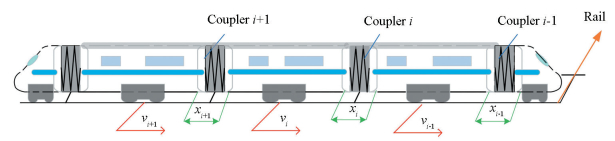
1 System Modeling for Dynamics of HSTIn this section, considering rolling mechanical resistance and air resistance, the HST model is simplified to a multi-particle model as shown in Fig. 1, which is a five-car model.
|
Fig.1 Force diagram of HST model consisting of 5-cars |
In Fig. 1, mi, xi, vi, and ui donate the mass of ith car, the relative distance between i car and i+1 car, the speed of i car, and the effort of i car, respectively. The dynamic characteristic of the couplers connecting every two adjacent cars can be simplified as a spring model. The spring model is given as
| $f\left(\boldsymbol{x}_i\right)=k \boldsymbol{x}_i+d \dot{\boldsymbol{x}}_i$ | (1) |
where k and d are spring and damping constants.
As the train speed increases, the aerodynamic drag become the major resistance, and is only considered on the first car in this paper. The rolling resistance and aerodynamic drag are given as
| $\boldsymbol{R}_r=\varepsilon_0+\varepsilon_v \boldsymbol{v}$ | (2) |
| $\boldsymbol{R}_a=\varepsilon_a \boldsymbol{v}^2$ | (3) |
where ε0, εv and εa are Davis formula coefficients.
Regarding each car as a mass point for dynamic analysis, considering the mechanical resistance and air resistance of each car during operation, the dynamic characteristics of the train running direction can be described as the following multi-particle dynamic model.
| $\left\{\begin{array}{l}\dot{\boldsymbol{x}}_i=\boldsymbol{v}_i-\boldsymbol{v}_{i+1}+\boldsymbol{\mu}_i(t), i=1, 2, \cdots, n-1 \\ m_1 \dot{\boldsymbol{v}}_1=\boldsymbol{u}_1-k \boldsymbol{x}_1-d \dot{\boldsymbol{x}}_1-\left(\varepsilon_0+\varepsilon_v v_1\right) m_1- \\ \qquad \varepsilon_a\left(\sum\limits_{i=1}^n m_i\right) \boldsymbol{v}_1^2+\delta_1(t) \\ m_i \dot{\boldsymbol{v}}_i=\boldsymbol{u}_i+k\left(\boldsymbol{x}_{i-1}-\boldsymbol{x}_i\right)-d\left(\dot{\boldsymbol{x}}_{i-1}-\dot{\boldsymbol{x}}_i\right)- \\ \qquad \left(\varepsilon_0+\varepsilon_v \boldsymbol{v}_i\right) m_i+\delta_i(t), i=2, 3, \cdots, n-1 \\ m_n \dot{\boldsymbol{v}}_n=\boldsymbol{u}_n+k \boldsymbol{x}_{n-1}+d \dot{\boldsymbol{x}}_{n-1}-\left(\varepsilon_0+\varepsilon_v \boldsymbol{v}_n\right) \boldsymbol{m}_n+ \\ \qquad \delta_n(t)\end{array}\right.$ | (4) |
Define the cruising speed of HST as vr, the relative displacement between every adjacent cars as xie, the speed of each car as vie at the equilibrium state, respectively. Obviously, xie and vie satisfy that xie=0, vie= vr. Further, defining the traction force of the i car as uie in the cruising mode at the equilibrium state which is attained as
| $\boldsymbol{u}_1^{\mathrm{e}}=\varepsilon_0 \boldsymbol{m}_1+\varepsilon_v \boldsymbol{m}_1 \boldsymbol{v}_r+\varepsilon_a \sum\limits_{i=1}^n m_i \boldsymbol{v}_r^2$ | (5) |
| $\boldsymbol{u}_i^{\mathrm{e}}=\varepsilon_0 \boldsymbol{m}_i+\varepsilon_v \boldsymbol{m}_i \boldsymbol{v}_r, i=2, \cdots, n$ | (6) |
then take Taylor expansion of the train dynamic Eq.(4) near the cruising speed vr, the following equation is otainted as
| $\left\{\begin{array}{l}\dot{\hat{\boldsymbol{x}}}_i=\hat{\boldsymbol{v}}_i-\hat{\boldsymbol{v}}_{i+1}+\mu_i(t), i=1, 2, \cdots, n-1 \\ m_1 \dot{\hat{\boldsymbol{v}}}_1=\hat{\boldsymbol{u}}_1-k \hat{\boldsymbol{x}}_1-d\left(\hat{\boldsymbol{v}}_1-\hat{\boldsymbol{v}}_2\right)-\varepsilon_v \hat{\boldsymbol{v}}_1 m_1- \\ \quad 2 \varepsilon_a \sum\limits_{i=1}^n m_1 \boldsymbol{v}_r \hat{\boldsymbol{v}}_1-\varepsilon_a \sum\limits_{i=1}^n m_i \hat{\boldsymbol{v}}_i^2+\delta_1(t) \\ m_i \dot{\hat{\boldsymbol{v}}}_i=\hat{\boldsymbol{u}}_i+k\left(\hat{\boldsymbol{x}}_{i-1}-\hat{\boldsymbol{x}}_i\right)-d\left(\hat{\boldsymbol{v}}_{i-1}-2 \hat{\boldsymbol{v}}_i+\hat{\boldsymbol{v}}_{i+1}\right)- \\ \quad \varepsilon_v \hat{\boldsymbol{v}}_i m_i+\delta_i(t), i=2, 3, \cdots, n-1 \\ m_n \dot{\hat{\boldsymbol{v}}}_n=\hat{\boldsymbol{u}}_n+k \hat{\boldsymbol{x}}_{n-1}+d\left(\hat{\boldsymbol{v}}_{n-1}-\hat{\boldsymbol{v}}_n\right)-\varepsilon_v \hat{\boldsymbol{v}}_n m_n+\delta_n(t)\end{array}\right.$ | (7) |
where
Define ψ(t)=
| $\left\{\begin{array}{l}\dot{\psi}(t)=\boldsymbol{A} \boldsymbol{\psi}(t)+\boldsymbol{E}_{\xi} p(\boldsymbol{\psi}(t))+B \boldsymbol{u}(t)+ \\ \qquad \boldsymbol{F}_a \boldsymbol{f}^a(t)+\boldsymbol{w}(t) \\ \boldsymbol{y}=\boldsymbol{C} \psi(t)+\boldsymbol{F}_s \boldsymbol{f}^{s}(t)+\Delta \boldsymbol{E}(t)+\boldsymbol{v}(t)\end{array}\right.$ | (8) |
where ψ(t) is state vector, u(t) is input vector,
| $\boldsymbol{A}=\left[\begin{array}{cc}0 & \boldsymbol{A}_{11} \\ \boldsymbol{A}_{21} & \boldsymbol{A}_{22}\end{array}\right], \boldsymbol{A}_{11}=\left[\begin{array}{cccc}1 & -1 & \cdots & 0 \\ \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & 1 & -1\end{array}\right]$ |
| $\boldsymbol{A}_{21}=\left[\begin{array}{ccc}\frac{-k}{m_1} & \cdots & 0 \\ \frac{k}{m_2} & \ddots & \vdots \\ \vdots & \ddots & \frac{-k}{m_4} \\ 0 & \cdots & \frac{k}{m_5}\end{array}\right]$ |
| $\boldsymbol{A}_{22}=\left[\begin{array}{cccc}U_1 & \frac{d}{m_1} & \cdots & 0 \\ \frac{d}{m_2} & \ddots & \ddots & \vdots \\ \vdots & \ddots & U_{n-1} & \frac{d}{m_{n-1}} \\ 0 & \cdots & \frac{d}{m_n} & U_n\end{array}\right]$ |
| $U_i=\left\{\begin{array}{l}-a_1-\frac{d}{m_1}-2 \sum\limits_{i=1}^n \frac{m_i}{m_1} \varepsilon_a v_r, i=1 \\ -\varepsilon_v-\frac{d}{m_i}, i=2, \cdots, n\end{array}\right.$ |
| $\boldsymbol{B}=\left[\begin{array}{l}0 \\ \boldsymbol{I}_n\end{array}\right], \boldsymbol{E}_{\xi}=\left[\begin{array}{lll}0_{1 \times(n-1)} & 1 & 0_{1 \times(n-1)}\end{array}\right]$ |
| $P(\psi(t))=-\varepsilon_a \frac{\sum\limits_{i=1}^n m_i}{m_1} \hat{v}_1^2=\psi_n^2, \boldsymbol{F}_a=\left[\begin{array}{ll}F_{a c} & F_{a d}\end{array}\right]$ |
Remark 1 Some investigations have found that when the train speed reaches 200 km/h, aerodynamic noise becomes the main noise of the train, and it is not strictly random white noise. In this paper, the process and measurement noise are regarded as the time-varying noise. Moreover, the air noise of the first car and the trailing car are the largest.
According to the former study[19], this paper introduces three types of common faults, and all of these faults occurring during the trains' running can be summarized as actuator-like faults and sensor-like faults.
In summary, the actuator-like faults includes the actuator fault and the train structure failure. The actuator fault is the fault signal coupled with the input signal of the actuator, and its fault distribution matrix has the same direction, i.e., its distribution matrix is the same as the corresponding column vector of the input matrix B. Assuming that a fault occurs in the ith controller of the system, the fault signal and its corresponding distribution matrix can be described as
| $\boldsymbol{f}_a^c(t)=\zeta_i(t), \boldsymbol{F}_{a c, i}=\boldsymbol{B}_i$ | (9) |
where Bi denotes the ith column of B, ζi(t) is an arbitrary time-varying signal.
The train structure failure is the fault signal appearing at the p-th coupler caused by the strain of the coupler, and its essence is the change of the spring coefficient k of the train coupler, and the direction of the change of the fault signal distribution matrix is the same as that of the system matrix A, which can be described as follows:
| $\boldsymbol{f}_a^d(t)=\boldsymbol{x}_p(t), \boldsymbol{F}_{a d, p}=\Delta \boldsymbol{A}_p$ | (10) |
where ΔAp denotes the change in the pth column of matrix A, and xp(t) denotes the pth element of the state vector x(t).
The sensor fault-like mode is the fault of the sensor measurement, and can be modeled as an additive signal term in the signal measurement equation as follows:
| $\boldsymbol{y}(t)=\boldsymbol{C} \boldsymbol{x}(t)+\boldsymbol{F}_s \boldsymbol{f}_s(t)$ | (11) |
where Fs is a column vector whose elements are all zeros except for the one in the sth position, and fs(t) is an arbitrary time-varying signal.
In order to obtain a discrete time system model, defining n=2n-1+q+r, choosing the sampling interval σ as σ=tk+1-tk, assuming the sampling interval σ sufficiently small, the following equation is obtained[20-21]:
| $\boldsymbol{f}_{a, k} \approx \boldsymbol{f}_{a, k-1}, \boldsymbol{f}_{s, k} \approx \boldsymbol{f}_{s, k-1}$ | (12) |
Based on Eq. (12), using the Euler discretization method, the continuous time system model (8) is transformed into a discrete time system one as
| $\left\{\begin{array}{l}\bar{\boldsymbol{\psi}}_k=f\left(\bar{\boldsymbol{\psi}}_{k-1}, \boldsymbol{u}_{k-1}\right)+\bar{\boldsymbol{w}}_{k-1} \\ \boldsymbol{y}_k=\bar{\boldsymbol{C}}\bar{\boldsymbol{\psi}}_k+\Delta \boldsymbol{E}_k+\boldsymbol{v}_k\end{array}\right.$ | (13) |
where
| $\bar{\boldsymbol{\psi}}_k=\left[\begin{array}{lll}\boldsymbol{\psi}_k & \boldsymbol{f}_k^a & \boldsymbol{f}_k^s \end{array}\right]^{\mathrm{T}} \in \boldsymbol{R}^{\bar{n}}$ |
| $f\left(\bar{\boldsymbol{\psi}}_{k-1}, \boldsymbol{u}_{k-1}\right)=\bar{\boldsymbol{A}} \bar{\boldsymbol{\psi}}_{k-1}+\eta\left(\bar{\boldsymbol{\psi}}_{k-1}, \boldsymbol{u}_{k-1}\right)$ |
| $\bar{\boldsymbol{A}}=\left[\begin{array}{ccc}\boldsymbol{I}_n+{\sigma \boldsymbol { A }} & {\sigma} \boldsymbol{F}_a & 0 \\ 0 & \boldsymbol{I} & 0 \\ 0 & 0 & \boldsymbol{I}\end{array}\right]$ |
| $\eta\left(\bar{\boldsymbol{\psi}}_{k-1}, \boldsymbol{u}_{k-1}\right)=\left[\begin{array}{c}\sigma \bar{p}\left(\boldsymbol{\psi}_{k-1}, \boldsymbol{u}_{k-1}\right) \\ 0 \\ 0\end{array}\right]$ |
| $\begin{gathered}\bar{p}\left(\boldsymbol{\psi}_{k-1}, \boldsymbol{u}_{k-1}\right)=p\left(\boldsymbol{\psi}_{k-1}\right)+\boldsymbol{B} \boldsymbol{u}_{k-1} \\ \bar{\boldsymbol{C}}=\left[\begin{array}{lll}\boldsymbol{C} & 0 & \boldsymbol{F}_s\end{array}\right]\end{gathered}$ |
ΔEk satisfies that
| $\Delta \boldsymbol{E}_k=\boldsymbol{M} \boldsymbol{F}_k \boldsymbol{N}, \boldsymbol{F}_k^{\mathrm{T}} \boldsymbol{F}_k \leqslant \boldsymbol{I}$ | (14) |
wk, vk satisfies that
| $\begin{gathered}E\left(\boldsymbol{w}_k\right)=E\left(\boldsymbol{v}_k\right)=0 \\ E\left\{\left[\begin{array}{l}\boldsymbol{w}_k \\ \boldsymbol{v}_k\end{array}\right]\left[\begin{array}{ll}\boldsymbol{w}_k^{\mathrm{T}} & \boldsymbol{v}_k^{\mathrm{T}}\end{array}\right]\right\}=\left[\begin{array}{cc}\boldsymbol{Q}_k & 0 \\ 0 & \boldsymbol{R}_k\end{array}\right]\end{gathered}$ |
E(·) denotes solving the mathematical expectation.
Additionally, the real covariance of wk-1 satisfies that E(wk-1wk-1T)=Qk-1= diag(Qk-1, Q1, k-1), diag(·) denotes generating diagonal matrix.
2 RUKF AlgorithmIn this section, an RUKF algorithm is used to realize the fault estimation of HST with measurement uncertainties. Assume that the statistics of Qk and Rk are known, according to the Kalman filtering theory, the predicted and the update process are expressed as
| $\hat{\bar{\psi}}_{k / k-1}=f\left(\hat{\bar{\psi}}_{k-1}\right)$ | (16) |
| $\hat{\bar{\psi}}_k=\hat{\bar{\psi}}_{k / k-1}+K_k\left(y_k-\bar{C} \hat{\bar{\psi}}_{k / k-1}\right)$ | (17) |
Define
| $\tilde{\bar{\psi}}_{k / k-1}=\bar{\psi}_k-\hat{\bar{\psi}}_{k / k-1}$ | (18) |
then the following equation is obtained as
| $\begin{aligned} \tilde{\bar{\psi}}_{k / k-1}= & f\left(\bar{\psi}_{k-1}\right)+\bar{w}_{k-1}-f\left(\hat{\bar{\psi}}_{k-1}\right)= \\ & f\left(\hat{\bar{\psi}}_{k-1}\right)+T_k\left(\bar{\psi}_{k-1}-\hat{\bar{\psi}}_{k-1}\right)+ \\ & \Delta\left(\tilde{\bar{\psi}}_{k-1}\right)^2+\bar{w}_{k-1}-f\left(\hat{\bar{\psi}}_{k-1}\right)= \\ & T_k \bar{\psi}_{k-1}+\Delta\left(\tilde{\bar{\psi}}_{k-1}\right)^2+\bar{w}_{k-1}\end{aligned}$ | (19) |
where
| $\varSigma_{k / k-1} \leqslant \boldsymbol{P}_{k / k-1}$ | (20) |
then
| $\begin{aligned} & \boldsymbol{P}_{k / k-1}=E\left(\tilde{\bar{\psi}}_{k / k-1} \tilde{\bar{\psi}}_{k / k-1}^{\mathrm{T}}\right)= \\ & \quad\left(\boldsymbol{T}_k+\Delta \boldsymbol{T}_k\right) \boldsymbol{P}_{k-1}\left(\boldsymbol{T}_{\mathrm{k}}+\Delta \boldsymbol{T}_k\right)^{\mathrm{T}}+\bar{\boldsymbol{Q}}_k\end{aligned}$ | (21) |
Define
| $\tilde{\bar{\psi}}_k=\bar{\psi}_k-\hat{\bar{\psi}}_k$ | (22) |
then
| $\tilde{\bar{\psi}}_{k / k-1}=\bar{\psi}_k-\hat{\bar{\psi}}_{k / k-1}-\boldsymbol{K}_k\left(\boldsymbol{y}_k-\bar{\boldsymbol{C}} \hat{\bar{\psi}}_{k / k-1}\right)$ | (23) |
Further, there is
| $\begin{gathered}\tilde{\bar{\psi}}_k=\tilde{\bar{\psi}}_{k / k-1}-\boldsymbol{K}_k\left(\bar{\boldsymbol{C}}{\tilde{\bar{\psi}}_{k / k-1}}+\Delta \boldsymbol{E}_k+\boldsymbol{v}_k\right)= \\ {\left[\left(\boldsymbol{I}-\boldsymbol{K}_k \bar{\boldsymbol{C}}\right) \tilde{\bar{\psi}}_{k / k-1}-\boldsymbol{K}_k \Delta \boldsymbol{E}_k\right]-\boldsymbol{K}_k \boldsymbol{v}_k}\end{gathered}$ | (24) |
As uncertainties ΔEk exists in Eq. (24), it is hard to calculate covariance matrix Σk of
Lemma 1 For known matrices χ1, χ2, χ3 and χ4, χ4 satisfies that χ4Tχ4≤I. If a positive scalar α and a symmetric positive definite matrix U exist which satisfy
| $\alpha^{-1} \boldsymbol{I}-\boldsymbol{\chi}_3 \boldsymbol{U} \boldsymbol{\chi}_3^{\mathrm{T}}>0$ | (25) |
then the following inequality holds:
| $\begin{array}{r}\left(\boldsymbol{\chi}_1+\boldsymbol{\chi}_2 \boldsymbol{\chi}_4 \boldsymbol{\chi}_3\right) \boldsymbol{U}\left(\boldsymbol{\chi}_1+\boldsymbol{\chi}_2 \boldsymbol{\chi}_4 \boldsymbol{\chi}_3\right)^{\mathrm{T}} \leqslant \\ \boldsymbol{\chi}_1\left(\boldsymbol{U}^{-1}-\alpha \boldsymbol{\chi}_3^{\mathrm{T}} \boldsymbol{\chi}_3\right)^{-1} \boldsymbol{\chi}_1^{\mathrm{T}}+\alpha^{-1} \boldsymbol{\chi}_2 \boldsymbol{\chi}_2^{\mathrm{T}}\end{array}$ | (26) |
Based on Eq. (24) and Lemma 1, Theorem 1 is proposed.
Theorem 1 If a positive constant γ exists which satisfies
| $\gamma^2 \boldsymbol{I}-\boldsymbol{N} \boldsymbol{N}^{\mathrm{T}}>0$ | (27) |
the estimation error
| $\begin{aligned} & \boldsymbol{P}_k=\left(\boldsymbol{I}-\gamma^{-2} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right)^{-1}\left(\boldsymbol{K}_k \bar{\boldsymbol{C}}-\boldsymbol{I}\right) \boldsymbol{P}_{k / k-1}\left(\boldsymbol{K}_k \bar{\boldsymbol{C}}-\boldsymbol{I}\right)^{\mathrm{T}}+ \\ & \quad \boldsymbol{\gamma}^2 \boldsymbol{K}_k \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}} \boldsymbol{K}_k^{\mathrm{T}}+\boldsymbol{K}_k \boldsymbol{R}_k \boldsymbol{K}_k^{\mathrm{T}}\end{aligned}$ | (28) |
with gain
| $\boldsymbol{K}_k=\frac{\boldsymbol{P}_{k / k-1} \bar{\boldsymbol{C}}^{\mathrm{T}}}{\bar{\boldsymbol{C}} \boldsymbol{P}_{k / k-1} \bar{\boldsymbol{C}}^{\mathrm{T}}+\boldsymbol{N}_M+\left(\boldsymbol{I}-\gamma^{-2} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right) \boldsymbol{R}_k}$ | (29) |
which makes
| $\mathrm{E}\left(\tilde{\bar{\boldsymbol{\psi}}}_k \tilde{\bar{\boldsymbol{\psi}}}_k^{\mathrm{T}}\right)=\boldsymbol{\varSigma}_k \leqslant \boldsymbol{P}_k$ | (30) |
In Eq. (30), NM=γ2NNT-NTNMMT.
Proof. From Eq. (24), the following equation is obtained:
| $\tilde{\bar{\psi}}_k=-\left(\boldsymbol{K}_k \bar{\boldsymbol{C}}-\boldsymbol{I}\right) \tilde{\bar{\psi}}_{k / k-1}-\boldsymbol{K}_k \Delta \boldsymbol{E}_k-\boldsymbol{K}_k \boldsymbol{v}_k$ | (31) |
As vk is independent of
| $\begin{aligned} & \boldsymbol{\varSigma}_k=E\left(\tilde{\bar{\boldsymbol{\psi}}}_k \tilde{\bar{\boldsymbol{\psi}}}_k^{\mathrm{T}}\right)= \\ & \left.\boldsymbol{E}<\left\{\left(\boldsymbol{K}_k \bar{\boldsymbol{C}}-\boldsymbol{I}\right) \tilde{\bar{\psi}}_{k / k-1}+\boldsymbol{K}_k \boldsymbol{M} \boldsymbol{F}_k \boldsymbol{N}\right]-\boldsymbol{K}_k \boldsymbol{v}_k\right\} \cdot \\ & \left\{-\left[\left(\boldsymbol{K}_k \bar{C}-\boldsymbol{I}\right) \tilde{\bar{\psi}}_{k / k-1}-\boldsymbol{K}_k \boldsymbol{M} \boldsymbol{F}_k \boldsymbol{N}\right]-\boldsymbol{K}_k \boldsymbol{v}_k\right\}^{\mathrm{T}}>= \\ & {\left[\left(\boldsymbol{K}_k \bar{\boldsymbol{C}}-\boldsymbol{I}\right) \tilde{\bar{\psi}}_{k / k-1}+\boldsymbol{K}_k \boldsymbol{M} \boldsymbol{F}_k \boldsymbol{N}\right] \cdot} \\ & {\left[\left(\boldsymbol{K}_k \bar{\boldsymbol{C}}-{\boldsymbol{I}}\right) \tilde{\bar{\psi}}_{k / k-1}+\boldsymbol{K}_k \boldsymbol{M} \boldsymbol{F}_k \boldsymbol{N}\right]^{\mathrm{T}}+\boldsymbol{K}_k \boldsymbol{R}_k \boldsymbol{K}_k^{\mathrm{T}}} \end{aligned}$ | (32) |
Combining Eq.(26) and Eq.(32) in Lemma 1, it is obtained that
| $\begin{aligned} & \varSigma_k \leqslant \lambda\left(\boldsymbol{I}-\boldsymbol{K}_k \bar{\boldsymbol{C}}\right) \varSigma_{k / k-1}\left(\boldsymbol{I}-\boldsymbol{K}_k \bar{\boldsymbol{C}}\right)^{\mathrm{T}}+ \\ & \quad \gamma^2 \boldsymbol{K}_k \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}} \boldsymbol{K}_k^{\mathrm{T}}+\boldsymbol{K}_k \boldsymbol{R}_k \boldsymbol{K}_k^{\mathrm{T}}\end{aligned}$ | (33) |
where
| $\lambda=\left(\boldsymbol{I}-\gamma^{-2} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right)^{-1}$ | (34) |
Substitute Pk=Σk into Eq. (33), Eq. (28) is obtained; let
| $\boldsymbol{K}_k=\frac{\boldsymbol{P}_{k / k-1} \bar{\boldsymbol{C}}^{\mathrm{T}}}{\bar{\boldsymbol{C}}\boldsymbol{P}_{k / k-1} \bar{\boldsymbol{C}}^{\mathrm{T}}+\lambda^{-1} \gamma^2 \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}}+\lambda^{-1} \boldsymbol{R}_k}$ | (35) |
Substituting Eq. (34) into Eq. (35), Eq. (29) is established.
So Theorem 1 is proved.
According to the aforementioned discussion, RUKF for fault estimation of HST based on the augmented system (13) is expressed as the following steps.
Step 1 The initial value of the state estimate
| $\left\{\begin{array}{l}\xi_{i, k-1}=\hat{\bar{\psi}}_{k-1}, i=0 \\ \xi_{i, k-1}=\hat{\bar{\psi}}_{k-1}+a\left(\sqrt{(n+1) \boldsymbol{P}_{k-1}}\right)_i , \\ \quad i=1, 2, \cdots, \bar{n} \\ \xi_{i, k-1}=\hat{\bar{\psi}}_{k-1}-a\left(\sqrt{(n+1) \boldsymbol{P}_{k-1}}\right)_i, \\ \quad i=\bar{n}+1, \bar{n}+2, \cdots, 2 \bar{n}\end{array}\right.$ | (36) |
where a is the adjustment parameter.
Step 2 Each of sigma points is transformed by the process model f( ) as
| $\xi_{i, k / k-1}=f\left(\xi_{i, k-1}\right)$ | (37) |
The state prediction and its corresponding covariance are updated as
| $\hat{\bar{\psi}}_{k / k-1}=\sum\limits_{i=0}^{2 \bar{n}} \omega_i \xi_{i, k / k-1}$ | (38) |
| $\begin{aligned} P_{k / k-1}= & \sum\limits_{i=0}^{2 \bar{n}} \omega_i\left(\xi_{i, k / k-1}-\hat{\bar{\psi}}_{k / k-1}\right)\left(\xi_{i, k / k-1}-\hat{\bar{\psi}}_{k / k-1}\right)^{\mathrm{T}}+ \\ & \boldsymbol{\bar{Q}}_{k-1}\end{aligned}$ | (39) |
Step 3 Update. The state estimation value is obtained by Eq. (16). Its corresponding covariance is obtained by Eq. (28). Additionally, Kk is obtained by Eq. (29).
Step 4 Repeat Steps 1-3 from the obtained
Step 5 The estimation of actuator fault
| $\hat{\boldsymbol{f}}_k^a=\left[\begin{array}{lll}0 & \boldsymbol{I} & 0\end{array}\right] \hat{\bar{\psi}}_k, \hat{\boldsymbol{f}}_k^s=\left[\begin{array}{lll}0 & 0 & \boldsymbol{I}\end{array}\right] \hat{\bar{\psi}}_k$ | (40) |
According to Lemma 1, Eq. (21) can be transformed into
| $\boldsymbol{P}_{k / k-1}=\boldsymbol{T}_k\left(\boldsymbol{P}_{k-1}^{-1}-\gamma^{-2} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{L}\right)^{-1} \boldsymbol{T}_k^{\mathrm{T}}+\gamma^2 \boldsymbol{K}_k \boldsymbol{D}_k \boldsymbol{D}_k^{\mathrm{T}} \boldsymbol{K}_k^{\mathrm{T}}+\bar{\boldsymbol{Q}}_k$ | (41) |
However, in Step 2, the predicted covariance Pk/k-1 is obtained by Eq. (39) instead of Eq. (41) considering that for term ΔTk, the constant matrix Dk and L are selected by experience.
Remark 2 Similar to the deduction in Ref. [22], for system (8) and its corresponding error system (21), let Dk=0, if the following inequalities are satisfied:
| $\gamma^2 \boldsymbol{I}-\boldsymbol{L} \boldsymbol{P}_k \boldsymbol{L}^{\mathrm{T}}>0$ | (42) |
| $\left\{\begin{array}{l}\operatorname{det}\left(\boldsymbol{I}-\boldsymbol{K}_k \bar{\boldsymbol{C}}\right) \neq 0 \\ \operatorname{det}\left(\boldsymbol{T}_k\right) \neq 0 \\ \operatorname{det}(\boldsymbol{L}) \neq 0\end{array}\right.$ | (43) |
where det(·) denotes solving the determinant of a square matrix.
Then the following inequality is obtained as
| $\frac{\sum\limits_{k=0}^{n}{{{\left\| {{{\bar{\psi }}}_{k}} \right\|}^{2}}}}{\left\| {{{\bar{\psi }}}_{0}} \right\|_{P_{0}^{-1}}^{2}+\sum\limits_{k=1}^{n}{\left( \left\| {{\bar{\boldsymbol{w}}}_{k}} \right\|_{Q_{k}^{-1}}^{2}+\left\| {{\boldsymbol{v}}_{k}} \right\|_{R_{k}^{-1}}^{2} \right)}}{{\gamma }^{2}}$ | (44) |
where
In Section 3, for systems with known noise statistics, a robust algorithm based on system (8) for fault estimation of dynamics of HST is proposed. However, as mentioned above, for systems with unknown noise, the UKF-based filtering method may lose its estimation accuracy as the statistics of the noise are unknown. Therefore, in this section, an adaptive filtering algorithm based on moving window is proposed to implement the unbiased estimation of the time-varying noise so that a unbiased fault estimation for dynamics of HST based on system (13) is implemented.
If X1, X2, …, XN are independent identically distributed random variables, and their corresponding empirical distribution function satisfy
| $F_n(x)=\frac{1}{n} \sum\limits_{i=1}^n \boldsymbol{I}_{X_i \leqslant x}$ | (45) |
where IXi≤x defines the characteristic function.
Considering system (13), define the innovation as
| $\boldsymbol{e}_k=\boldsymbol{y}_k-\hat{\boldsymbol{y}}_{k / k-1}$ | (46) |
where
Theorem 2 For 1≤j≤N, assume that in the interval of N, the process and measurement noise are constant or with tiny change, then for the augmented system (13), Qk-1 and Rk have the unbiased estimators as follows:
| $\begin{array}{l} \hat{\bar{\boldsymbol{Q}}}_{k-1}=\frac{1}{N} \sum\limits_{j=1}^N\left[\boldsymbol{P}_{k-j}+\hat{\boldsymbol{K}}_{k-j} \boldsymbol{e}_{k-j} \boldsymbol{e}_{k-j}^{\mathrm{T}} \hat{\boldsymbol{K}}_{k-j}^{\mathrm{T}}-\right.\\ \qquad \qquad \sum\limits_{i=0}^{2 \bar{n}} \omega_i\left(\xi_{i, k-j / k-1-j}-\hat{\bar{\psi}}_{k-j / k-1-j}\right) \cdot \\ \qquad \qquad \left.\left(\xi_{i, k-j / k-1-j}-\hat{\bar{\psi}}_{k-j / k-1-j}\right)^{\mathrm{T}}\right]\end{array}$ | (47) |
| $\begin{aligned} \hat{\boldsymbol{R}}_k= & \frac{1}{N} \sum\limits_{j=1}^N\left(\boldsymbol{e}_{k-j} \boldsymbol{e}_{k-j}^{\mathrm{T}}-\bar{\boldsymbol{C}}\left(1-\mu^{-1} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right) \boldsymbol{P}_{k-j / k-1-j} \bar{\boldsymbol{C}}^{\mathrm{T}}-\right. \\ & \left.\mu \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}}\right)\end{aligned}$ | (48) |
where
| $\hat{K}_{k-j}=\frac{\boldsymbol{P}_{k-j / k-j-1} \bar{\boldsymbol{C}}^{\mathrm{T}}}{\bar{\boldsymbol{C}} \boldsymbol{P}_{k-j / k-j-1} \bar{\boldsymbol{C}}^{\mathrm{T}}+\boldsymbol{N}_M+\left(\boldsymbol{I}-\gamma^{-2} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right) \hat{\boldsymbol{R}}_k}$ | (49) |
ek-j is the innovation which satisfies Eq. (46), N is the length of the moving window.
Proof From Eq. (43) it is known that
| $E\left(\boldsymbol{e}_k \boldsymbol{e}_k^{\mathrm{T}}\right)=E\left[\left(\boldsymbol{y}_k-\hat{\boldsymbol{y}}_{k / k-1}\right)\left(\boldsymbol{y}_k-\hat{\boldsymbol{y}}_{k / k-1}\right)^{\mathrm{T}}\right]$ | (50) |
In the moving window with the width of N, i.e., in time domain of (tk-N, tk), j=1, 2, …, N. Assume the statistic of the noise has tiny change, then the following equation is obtained as
| $\bar{\boldsymbol{Q}}_{k-1}=\bar{\boldsymbol{Q}}_{k-1-j}, \boldsymbol{R}_k=\boldsymbol{R}_{k-j}$ | (51) |
From Eq. (11), the following equation is obtained as
| $\hat{\bar{\psi}}_{k-j}-\hat{\bar{\psi}}_{k-j / k-1-j}=\boldsymbol{K}_{k-j}\left(\boldsymbol{y}_{k-j}-\hat{\boldsymbol{y}}_{k-j / k-1-j}\right)$ | (52) |
Considering the orthogonality of
| $\begin{array}{l} \boldsymbol{P}_{k-j / k-j-1}-\boldsymbol{P}_k=E\left[\left(\tilde{\bar{\boldsymbol{\psi}}}_{k-j}-\tilde{\bar{\boldsymbol{\psi}}}_{k-j / k-1-j}\right) \cdot\right. \\ \quad \left.\left(\tilde{\bar{\boldsymbol{\psi}}}_{k-j}-\tilde{\bar{\boldsymbol{\psi}}}_{k-j / k-1-j}\right)^{\mathrm{T}}\right]=E\left[\left(\hat{\bar{\psi}}_{k-j}-\hat{\bar{\boldsymbol{\psi}}}_{k-j / k-1-j}\right) \cdot\right. \\ \quad \left.\left(\hat{\bar{\boldsymbol{\psi}}}_{k-j}-\hat{\bar{\boldsymbol{\psi}}}_{k-j / k-1-j}\right)^{\mathrm{T}}\right]=E\left\{\left[\boldsymbol{K}_{k-j}\left(\boldsymbol{y}_{k-j}-\hat{\boldsymbol{y}}_{k-j / k-1-j}\right)\right] \cdot\right. \\ \quad \left.\left[\boldsymbol{K}_{k-j}\left(\boldsymbol{y}_{k-j}-\hat{\boldsymbol{y}}_{k-j / k-1-j}\right)\right]\right\}=\boldsymbol{K}_{k-j} \boldsymbol{e}_{k-j} \boldsymbol{e}_{k-j}^{\mathrm{T}} \boldsymbol{K}_{k-j}^{\mathrm{T}} \end{array}$ | (53) |
Combining Eqs. (52) and (53), the following equation is obtained as
| $\begin{aligned} E & \left\{\frac{1}{N} \sum\limits_{j=1}^N\left[\boldsymbol{K}_{k-j} \boldsymbol{e}_{k-j} \boldsymbol{e}_{k-j}^{\mathrm{T}} \boldsymbol{K}_{k-j}^{\mathrm{T}}\right]\right\}= \\ & \frac{1}{N} \sum\limits_{j=1}^N\left(\boldsymbol{P}_{k-j / k-1-j}-\boldsymbol{P}_{k-j}\right)= \\ & \frac{1}{N} \sum\limits_{j=1}^N\left[\sum\limits_{i=0}^{2 \bar{n}} \omega_i\left({\xi}_{i, k-j / k-1-j}-\hat{\bar{\psi}}_{k-j / k-1-j}\right) \cdot\right. \\ & \left.\left(\xi_{i, k-j / k-1-j}-\hat{\bar{\psi}}_{k-j / k-1-j}\right)^{\mathrm{T}}-\boldsymbol{P}_{k-j}+\bar{\boldsymbol{Q}}_{k-1-j}\right]= \\ & \frac{1}{N} \sum\limits_{j=1}^N\left[\sum\limits_{i=0}^{2 \bar{n}} \omega_i\left(\xi_{i, k-j / k-1-j}-\hat{\bar{\psi}}_{k-j / k-1-j}\right) \cdot\right. \\ & \left.\left(\boldsymbol{\xi}_{\boldsymbol{i, k-j / k-1-j}}-\hat{\bar{\boldsymbol{\psi}}}_{\boldsymbol{k-j / k-1-j}}\right)^{\bf{T}}-\boldsymbol{P}_{k-j}\right]+\bar{\boldsymbol{Q}}_{k-1}\end{aligned}$ | (54) |
solving the expectation for the Eq. (47), then it is equivalent to Eq. (54).
Similarly,
| $\begin{array} {l} E\left[\frac{1}{N} \sum\limits_{j=1}^N\left(\boldsymbol{e}_{k-j} \boldsymbol{e}_{k-j}^{\mathrm{T}}\right)\right]= \\ \quad \frac{1}{N} \sum\limits_{j=1}^N\left[\left(\boldsymbol{y}_{k-j}-\hat{\boldsymbol{y}}_{k-j / k-j-1}\right)\left(\boldsymbol{y}_{k-j}-\hat{\boldsymbol{y}}_{k-j / k-j-1}\right)^{\mathrm{T}}\right]= \\ \quad \frac{1}{N} \sum\limits_{j=1}^N\left[\left(\bar{\boldsymbol{C}}{\tilde{\bar{\psi}}_{k-j / k-j-1}}+\Delta \boldsymbol{E}_{k-j}\right) \times\right. \\ \quad \left.\left(\bar{\boldsymbol{C}} \tilde{\bar{\psi}}_{k-j / k-j-1}+\Delta \boldsymbol{E}_{k-j}\right)^{\mathrm{T}}+\boldsymbol{R}_{k-j}\right] \end{array}$ | (55) |
Further, from Lemma 1 and Eq. (13), it is obtained that
| $\begin{aligned} & \left(\bar{\boldsymbol{C}} \tilde{\bar{\psi}}_{k-j / k-j-1}+\Delta \boldsymbol{E}_{k-j}\right)\left(\bar{\boldsymbol{C}}{\tilde{\bar{\psi}}_{k-j / k-j-1}}+\Delta \boldsymbol{E}_{k-j}\right)^{\mathrm{T}} \leqslant \\ & \bar{\boldsymbol{C}}\left(1-\mu^{-1} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right) \boldsymbol{P}_{k-j / k-1-j} \bar{\boldsymbol{C}}^{\mathrm{T}}+\mu \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}}\end{aligned}$ | (56) |
Minimize the inequality (56), then the following equation is obtained as
| $\begin{array} {l} E\left[\frac{1}{N} \sum\limits_{j=1}^N\left(\boldsymbol{e}_{k-j} \boldsymbol{e}_{k-j}^{\mathrm{T}}\right)\right]= \\ \qquad \frac{1}{N} \sum\limits_{j=1}^N\left[\bar{\boldsymbol{C}}\left(1-\mu^{-1} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right) \boldsymbol{P}_{k-j / k-1-j} \bar{\boldsymbol{C}}^{\mathrm{T}}+\right. \\ \qquad \left.\mu \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}}\right]+\boldsymbol{R}_k\end{array}$ | (57) |
Solving the expectation for the Eq. (48), then it is equivalent to Eq. (57).
So Theorem 2 is proved.
Therefore, the fault estimation steps of the ARUKF algorithm based on moving window are as follows:
Step 1 The initial value of the state estimate value and its covariance is given. The sigma points are selected by Eq. (36).
Step 2 Prediction. ξi, k/k-1 and
| $\begin{array}{l} \boldsymbol{P}_{k / k-1}=\sum\limits_{i=0}^{2 \bar{n}} \omega_i\left(\xi_{i, k / k-1}-\hat{\bar{\psi}}_{k / k-1}\right)\left(\xi_{i, k / k-1}-\hat{\bar{\psi}}_{k / k-1}\right)^{\mathrm{T}}+ \\ \qquad\qquad \hat{\bar{\boldsymbol{Q}}}_{k-1} \end{array}$ | (58) |
Step 3 Update the state estimation and its covariance are as follows:
| $\hat{\bar{\psi}}_k=\hat{\bar{\psi}}_{k / k-1}+\hat{\boldsymbol{K}}_k\left(y_k-\bar{\boldsymbol{C}}{\hat{\bar{\psi}}_{k / k-1}}\right)$ | (59) |
| $\begin{array}{l}\boldsymbol{P}_k=\left(\boldsymbol{I}-\gamma^{-2} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N}\right)^{-1}\left(\hat{\boldsymbol{K}_k} \bar{\boldsymbol{C}}-\boldsymbol{I}\right) \boldsymbol{P}_{k / k-1}\left(\hat{\boldsymbol{K}_k} \bar{\boldsymbol{C}}-\right. \\ \quad \boldsymbol{I})^{\mathrm{T}}+\gamma^2 \hat{\boldsymbol{K}}_k \boldsymbol{M} \boldsymbol{M}^{\mathrm{T}} \hat{\boldsymbol{K}}_k^{\mathrm{T}}+\hat{\boldsymbol{K}}_k \hat{\boldsymbol{R}}_k \hat{\boldsymbol{K}}_k^{\mathrm{T}}\end{array}$ | (60) |
Step 4 Repeat Step 1-3 to the next samples.
Step 5 The fault estimation of the actuator and sensor fault are obtained by Eq.(40).
Moreover, in Step 1-5,
In this section, a 5-car HST model is selected for simulation analysis. Parameters of model are shown in Table 1.
| Table 1 Parameters of HST |
Assume that all the speed and position information of the HST model can be effectively measured, then C can be regarded as C=I9. The measurement uncertainties ΔE=MFkN satisfies M= [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]T, and N=1, the sampling interval σ=0.01 s, the robust bound γ=1.05.
Three types of faults are considered, namely, a fault occurring in the third high-speed train drive, a fault occurring on the coupler between the last two cars, a fault appearing in the velocity sensor of the first car. The distribution matrices of the concerning three faults are given as follows:
| $\boldsymbol{F}_a=\left[\begin{array}{llllllllllll}0 & 0 & 0 & 0 & 0 & 0 & 0.85 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1.2 & 0 & 0 & 0\end{array}\right]^{\mathrm{T}}$ | (61) |
| $\boldsymbol{F}_s=\left[\begin{array}{llllllllllll}0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right]^{\mathrm{T}}$ | (62) |
and the fault signals are expressed as
| $f_a^c(t)= \begin{cases}0, & t \leqslant 5 \\ -0.04(-1+0.2 \operatorname{sawtooth}(t)), & 5<t \leqslant 15 \\ 0, & t>15\end{cases}$ | (63) |
| $\boldsymbol{f}_a^d(t)= \begin{cases}0, & t \leqslant 4 \\ 0.06\left(1+e^{(-t+7.5)}\right), & 4<t \leqslant 15 \\ 0, & t>15\end{cases}$ | (64) |
| $\boldsymbol{f}_{\mathrm{s}}(t)= \begin{cases}0, & t \leqslant 2.5 \\ 10^{-3}\left(-1+\sin \left(0.1 \boldsymbol{x}_4(t) \boldsymbol{x}_5(t)\right)\right), & 2.5<t \leqslant 15 \\ 0, & t>15\end{cases}$ | (65) |
where sawtooth (t) represents 0.16 Hz sawtooth signal. Actuator fault fac(t), coupler fault fad(t), and sensor fault fs(t) can be considered as loss efficacy of traction motor, variance of spring constant, and sensor drift, respectively.
The cruising speed of HST is given as follows:
| $\boldsymbol{v}_r= \begin{cases}200 \mathrm{~km} / \mathrm{h}, & t<50 \mathrm{~s} \\ (200+0.6(t-50)) \mathrm{km} / \mathrm{h}, & 50 \leqslant t<100 \mathrm{~s} \\ 230 \mathrm{~km} / \mathrm{h}, & 100 \leqslant t<300 \mathrm{~s} \\ (230-0.625(t-300)) \mathrm{km} / \mathrm{h}, & 300 \leqslant t<316 \mathrm{~s} \\ 20 \mathrm{~km} / \mathrm{h}, & t>316 \mathrm{~s}\end{cases}$ | (66) |
The true values of the process noise and measurement noise are given as
| $\boldsymbol{Q}_k=\operatorname{diag}\left(\boldsymbol{Q}_{1, k}, \cdots, \boldsymbol{Q}_{9, k}\right)=\boldsymbol{I}_9+0.5 \boldsymbol{I}_9 \sin (0.0003 \mathrm{k})$ | (67) |
| $\boldsymbol{R}_k=\operatorname{diag}\left(\boldsymbol{R}_{1, k}, \cdots, \boldsymbol{R}_{9, k}\right)=1.1 \boldsymbol{I}_9+0.08 \boldsymbol{I}_9 \cos (0.0002 \mathrm{k})$ | (68) |
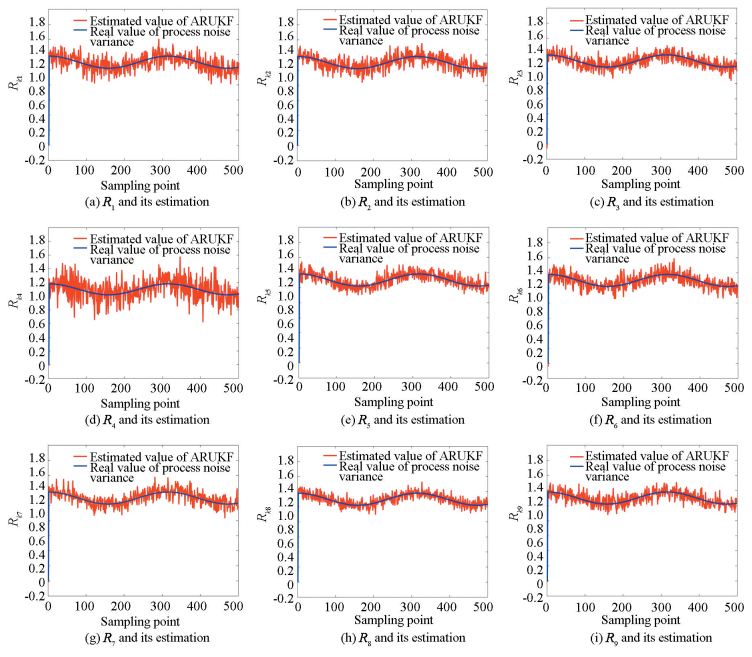
Fig. 2 is the state variable estimation, Fig. 3 is the fault estimation, Fig. 4 is the process noise estimation, and Fig. 5 is the measurement noise estimation. The root mean square error (RMSE) of the estimated values of state, fault, process noise and measurement noise are shown in Tables 2-5, respectively.

|
Fig.2 State estimation results of HST |

|
Fig.3 Fault estimation results |

|
Fig.4 Process noise estimation results |
|
Fig.5 Measurement noise estimation results |
| Table 2 RMSEs of state estimation |
| Table 3 RMSEs of fault estimation |
| Table 4 RMSEs of process noise estimation |
| Table 5 RMSEs of measurement noise estimation |
From Fig. 2 and Fig. 3, it is seen that ARUKF achieves better estimation accuracy than RUKF. Tables 2-5 further show the estimation accuracy of ARUKF. The average value of ARUKF algorithm for state and fault estimation error is 0.0329 and 0.005, respectively. The average value of RUKF algorithm for state and fault estimation error is 0.0731 and 0.0105, respectively. The estimation error of ARUKF is about 1/2 of RUKF. The results of Fig. 4 and Fig. 5 show that ARUKF implemented an effectiveness estimation for process noise and measurement noise. The average value of ARUKF's estimation error for process noise and measurement noise is 0.0779 and 0.0764, respectively. From the above analysis it is known that for ARUKF algorithm, as the introduced moving windows, this algorithm implemented an unbiased estimation for process noise so that better state estimation and fault estimation are implemented. The simulation results show the effectiveness of the proposed method.
5 ConclusionsThis paper proposes an adaptive filtering method based on robust UKF considering unknown noise and measurement uncertainty, establishes an augmented state space system, and introduces a robust lower bound to decrease the measurement uncertainties affecting on the estimation accuracy. In addition, an adaptive algorithm based on moving window is proposed to improve the performance of RUKF and implements an unbiased estimation of the unknown noise in order to estimate the concurrent faults accurately. Further, a five-car model of HST is introduced for simulation to show the effectiveness of this method. The results show that this method effectively improves the filtering accuracy for HST dynamic models with unknown noise and measurement uncertainty, and achieves accurate estimation of concurrent faults compared with the conventional UKF-based method. References
| [1] |
Zhang K P, Jiang B, Tao G, et al. MIMO evolution model-based coupled fault estimation and adaptive control with high-speed train applications. IEEE Transactions on Control Systems Technology, 2018, 26(5): 1552-1566. DOI:10.1109/TCST.2017.2735360 (  0) 0) |
| [2] |
Liu S K, Jiang B, Mao Z H, et al. Observer based fault estimation for inverter devices of traction systems with disturbance. 2017 Chinese Automation Congress (CAC). Piscataway: IEEE, 2017. 2006-2010. DOI: 10.1109/CAC.2017.8243100.
(  0) 0) |
| [3] |
Estima J O, Cardoso A J M. A new algorithm for real-time multiple open-circuit fault diagnosis in voltage-fed pwm motor drives by the reference current errors. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3496-3505. DOI:10.1109/TIE.2012.2188877 (  0) 0) |
| [4] |
Liu J, Li Y F, Zio E. A SVM framework for fault detection of the braking system in a high speed train. Mechanical Systems & Signal Processing, 2017, 87(A): 401-409. DOI:10.1016/j.ymssp.2016.10.034 (  0) 0) |
| [5] |
Cheng C, Wang W J, Luo H, et al. State-degradation-oriented fault diagnosis for high-speed train running gears system. Sensors, 2020, 20(4): 1017. DOI:10.3390/s20041017 (  0) 0) |
| [6] |
Jeong K, Choi S B, Choi H. Sensor fault detection and isolation using a support vector machine for vehicle suspension systems. IEEE Transactions on Vehicular Technology, 2020, 69(4): 3852-3863. DOI:10.1109/TVT.2020.2977353 (  0) 0) |
| [7] |
Liang K W, Qin N, Huang D Q, et al. 1D convolutional neural networks for fault diagnosis of high-speed train bogie. Proceedings of IEEE 23rd International Conference on Digital Signal Processing (DSP). Piscataway: IEEE, 2018. 1-5. DOI: 10.1109/ICDSP.2018.8631651.
(  0) 0) |
| [8] |
Liang K, Qin N, Huang D Q, et al. Convolutional recurrent neural network for fault diagnosis of high-speed train bogie. Complexity, 2018, 2018: 1-13. DOI:10.1155/2018/4501952 (  0) 0) |
| [9] |
Zhang Y J, Qin N, Huang D Q, et al. Fault diagnosis of high-speed train bogie based on deep neural network. IFAC-PapersOnLine, 2019, 52(24): 135-139. DOI:10.1016/j.ifacol.2019.12.395 (  0) 0) |
| [10] |
Mao Z H, Tao G, Jiang B, et al. Adaptive compensation of traction system actuator failures for high-speed trains. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(11): 2950-2963. DOI:10.1109/TITS.2017.2666428 (  0) 0) |
| [11] |
Wang Y J, Song Y D, Gao H, et al. Distributed fault-tolerant control of virtually and physically interconnected systems with application to high-speed trains under traction/braking failures. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(2): 535-545. DOI:10.1109/TITS.2015.2479922 (  0) 0) |
| [12] |
Gao R Z, Wang Y J, Lai J F, et al. Neuro-adaptive fault-tolerant control of high speed trains under traction-braking failures using self-structuring neural networks. Information Sciences, 2016, 367-368: 449-462. DOI:10.1016/j.ins.2016.05.033 (  0) 0) |
| [13] |
Li D Y, Li P, Cai W C, et al. Neural adaptive fault tolerant control for high speed trains considering actuation notches and antiskid constraints. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(5): 1706-1718. DOI:10.1109/TITS.2018.2832635 (  0) 0) |
| [14] |
Liu X Y, Alfi S, Bruni S. An efficient recursive least square-based condition monitoring approach for a rail vehicle suspension system. Vehicle System Dynamics, 2016, 54(6): 814-830. DOI:10.1080/00423114.2016.1164869 (  0) 0) |
| [15] |
Ameid T, Menacer A, Talhaoui H, et al. Rotor resistance estimation using extended Kalman filter and spectral analysis for rotor bar fault diagnosis of sensorless vector control induction motor. Measurement, 2017, 111: 243-259. DOI:10.1016/j.measurement.2017.07.039 (  0) 0) |
| [16] |
Ma J, Ni S H, Xie W J, et al. An improved strong tracking multiple-model adaptive estimation: a fast diagnosis algorithm for aircraft actuator fault. Transactions of the Institute of Measurement and Control, 2016, 38(7): 846-854. DOI:10.1177/0142331215589611 (  0) 0) |
| [17] |
Li X Y, Jin J, Shen Y. Modified unscented Kalman filter for X-ray pulsar-based navigation system in the presence of measurement outliers. Proceedings of the Institution of Mechanical Engineers. Part G: Journal of Aerospace Engineering, 2018, 232(2): 260-269. DOI:10.1177/0954410016679196 (  0) 0) |
| [18] |
Wang M, Liang T T. Adaptive Kalman filtering for sensor fault estimation and isolation of satellite attitude control based on descriptor systems. Transactions of the Institute of Measurement and Control, 2019, 41(6): 1686-1698. DOI:10.1177/0142331218787605 (  0) 0) |
| [19] |
Bai W Q, Dong H R, Yao X M, et al. Robust fault detection for the dynamics of high-speed train with multi-source finite frequency interference. ISA Transactions, 2018, 75: 76-87. DOI:10.1016/j.isatra.2018.01.032 (  0) 0) |
| [20] |
Chang J L. Applying discrete-time proportional integral observers for state and disturbance estimations. IEEE Transactions on Automatic Control, 2006, 51(5): 814-818. DOI:10.1109/TAC.2006.875019 (  0) 0) |
| [21] |
Gao Z W, Breikin T, Wang H. Discrete-time proportional and integral observer and observer-based controller for systems with both unknown input and output disturbances. Optimal Control Applications and Methods, 2008, 29(3): 171-189. DOI:10.1002/oca.819 (  0) 0) |
| [22] |
Wang M, Liang T T, Zhou Z H. Sensor fault diagnosis observer design for linear sampled-data descriptor system with time-vary delay. Journal of Harbin Institute of Technology (New Series), 2019, 26(6): 12-22. DOI:10.11916/j.issn.1005-9113.18046 (  0) 0) |
 2023, Vol. 30
2023, Vol. 30


