Rolling element bearings are established to reduce friction to a significantly low level. Cylindrical roller bearings have a superior radial load competence than ball bearings, whereas tapered roller bearings (TRBs) are able to transmit a blend of huge radial and thrust forces in contrast to cylindrical roller bearings. Due to this feature, TRBs are preferred in a variety of applications, for example, in the ground vehicles, locomotive and airplane axles, spindles of various machinery, steel mills, building and lifting equipment, printing machines, and various equipment. In such applications, critical requirements of the high consistency and the long life have given an impetus to the improvement in the design technology of TRBs.
In the past, rolling element bearing industries traditionally optimized their bearings based on experiences and feedback from users. A lot of research attempts have been performed and published in open literature in the field of synthesis and the study of a range of mechanical components. However, extremely less literature exists on the design of rolling bearings, particularly on TRBs. Moyer and Mckelvey[1] investigated the Timken roller bearing company's rating formula for determining basic TRB ratings. Karna[2] offered both theoretical and test analyses on the type of the coefficient of friction at the roller with rib end of a TRB. Andréason[3] proposed a method for calculating bearing forces in a double-row TRB configuration that considered the misalignment, starting preload, and shaft and housing deflections. Liu[4] offered an theoretical analysis of force dispersal in TRBs that were running at high speeds with collective loads and no friction loads. Based on information of EHL rolling resistance and EHL oil-film thickness, Aihara[5] developed an equation for determining the running torque of TRBs. Changsen[6] described gradient based optimization procedure, without illustrations, for the design of TRBs that included constraint factors, which were suggested to be chosen arbitrary. Harris[7] provided a broad study of antifriction bearings. It deals with the bearing types, geometry, and tolerances, and provides intricate study of the static and dynamic force pattern of a range of rolling bearings. Based on the quasi-static and dynamic equations, Bercea et al.[8] established a thorough analysis model for double-row TRBs.
Rolling element bearing design is a nonlinear optimization formulation with a set of constraints. Researchers have used evolutionary algorithms to optimize the synthesis of deep-groove ball bearings[9-10] and cylindrical roller bearings[11-13] using genetic algorithms[14-15]. Rolling bearings have been optimized by using various evolutionary algorithms[16-22]. TRBs were optimized by Verma and Tiwari[23] with the goal of maximizing dynamic capacity while minimizing variation due to manufacturing tolerance. Kalyan et al.[24] optimized a set of standard TRBs using multi-objective optimization through genetic algorithm that derived Pareto-optimal fronts and surfaces for a typical TRB. Tiwari and Chandran[25] proposed optimization of deep groove ball bearing using multiple objectives like dynamic capacity, minimum film-thickness and max temperature considered independently. A similar study of TRBs inspired from Ref. [21] is needed to be performed on the design of TRBs based on multitude of objectives from a more practical operating condition of bearings (which is due to axial load, preload, radial load, and torque).
All the above-mentioned optimizations of bearings deal with the enhancement of dynamic capacity as the objective function. However, hardly any comprehensive work is available on TRBs design with the maximization of the elasto-hydrodynamic (EHL) minimum film-thickness (Hmin) as an objective function. Moreover, all of the above cited optimum design are based on genetic algorithms, and using alternative evolutionary algorithms (for example, the Artificial Bee Colony (ABC) optimization algorithm) would have increased trust in optimized designs. Karaboga and Basturk[26-27] first proposed the ABC optimization algorithm, which is based on a population-based swarm intelligence algorithm. The ABC algorithm is a non-conventional method, which is appropriate for such complex non-linear optimization formulations, and they can usually find a near overall optimal solution with elevated likelihood.
In the present work, an optimized design of TRBs has been proposed innovatively for three basic objectives: dynamic capacity (Cd), minimum EHL film-thickness (Hmin), and greatest bearing temperature (Tmax). The optimization has been performed by the ABC algorithm sequentially. Thermal consideration has two aspects, one is the lubricant life, the other is bearing preload condition. Both affect the bearing life implicitly. Improvement in design procedures especially in the form of new objective functions based on the wear and thermal aspects, and incorporation of some new realistic constraints have been performed. A comparison of these optimum designs based on three different objectives with previously published works has been presented. A sensitivity analysis was conducted to examine the effects of production variations in design parameters on TRB objective functions.
1 Formulation of the Optimization Problem for TRB DesignA TRB consists of an internal race (or the cone), an external race (or the cup), and a series of rollers in the form of frustum of cones, as shown in Fig. 1. A cage on the cone contains a set of rollers as a single unit. A single-row TRB must additionally be applied to a longitudinal force or be preloaded or braced axially, or else it will disassemble due to the raceways' inclined position. The cone consists of two flanges, the smaller and larger flanges. The smaller flange, in combination with the cage, keeps rollers on the conical pathway, while the larger flange carries the longitudinal load component caused by the tapered form of the rollers. The 3-dimensional volume existing for the bearing determined by the typical peripheral geometries is a critical requirement for the design of TRB. These geometries are the information that can be used in the design formulation. Fig. 2 depicts the nomenclature of a single-row TRB with peripheral geometries specified according to bearing standard[28]. To select periphery geometries for the current study, the bearing standard and the SKF bearing general catalogues[29] have been consulted.

|
(A: front face of the cup; B: front face of the cone; C: back face of the cone; D: cone; E: roller; F: cup) Fig.1 Cross section of a tapered roller bearing |

|
Fig.2 Cross section of a tapered roller bearing with inner and outer race with roller |
1.1 Fitness Functions
As has been pointed out, three fitness functions have been considered for sequential optimization. They are dynamic capacity (Cd), the minimum EHL film-thickness (Hmin), and the bearing maximum temperature (Tmax). Fitness functions Cd and Hmin have to be maximized. However, Tmax has to be minimized. Hence, some of fitness functions might have contradiction with each other during optimization of the TRB design.
1.1.1 Dynamic capacity (Cd)The basic dynamic load capacity is a main decisive issue in obtaining the fatigue life of bearings. The formula for the fundamental dynamic load capacity is specified in Refs. [7], [19], and [30]. In the optimization formulation, the maximization of Cd of the bearing is one of fitness functions. Then, it is expressed as max{f1(X)} =max{Cd}, with f1(X) denoting the fitness function, and X representing design parameter vector that will be examined once all fitness functions have been discussed.
1.1.2 EHL minimum film-thickness (Hmin)An alternate key requirement is a longer bearing wear life. It is achieved by reducing direct metal interaction between rollers and ring raceways, and it is proportional to the lubricant's EHL minimum film thickness (Hmin)[7]. In consideration of prerequisite of low wear, it is aimed to boost up the EHL minimum film-thickness. For the internal and external raceways, Hmin is defined distinctly. Hence, the minimum of the two is maximized. The fitness function is written as
| $H_{\min }=\min \left(H_{\text {inner }}, H_{\text {outer }}\right)$ | (1) |
The expression for Hmin and Hmax are given in Refs. [7] and [21]. The maximization of Hmax is taken as the fitness function, which is given as max{f2(X)} = max{Hmin}, with f2{X} representing the fitness function.
1.1.3 Maximum bearing temperature (Tmax)Bearings are the main cause of heat. The kind and quantity of lubricant, and substance for the manufacturing of bearing parts is dictated by the operating temperature of a bearing. Often the highest temperature occurs at the roller and interior raceway interaction of the bearing[31]. Contact temperatures are found out by heat balance equations in two steps. By solving simultaneous heat balance equations (Fig. 3 and Table 1), the lubricant temperature is obtained. Then the temperature at the interior raceway-roller contact is obtained (Fig. 4 and Table 2). In the present formulation, all three heat transfer approaches (i.e., conduction, convection, and radiation) have been considered. In the current analysis, the minimization of Tmax (inner raceway roller contact temperature) is the fitness function. The fitness function is represented as min{f3(X)} =min{Tmax}.
|
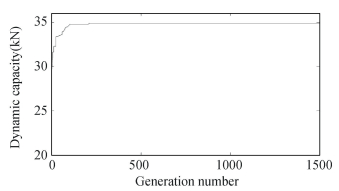
Fig.3 Variation of Cd with the number of generations |
| Table 1 Optimized design parameters, constraint factors, and obtained internal geometric variables of TRBs taking Cd as objective function by ABC algorithm |
|
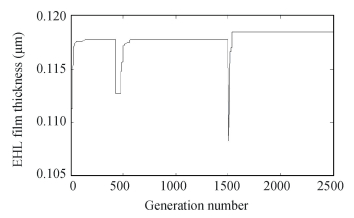
Fig.4 Variation of Hmin with the number of generations |
| Table 2 Optimized design parameters, constraint factors, and obtained internal geometric variables of TRBs taking Hmin as objective function by ABC algorithm |
1.2 Design Variable Vector
In the present paper, the word variables are used in conjunction with design variables. These are the variables designers have freedom to optimize based on certain constraints. Other bearing geometries are fixed and designer has no flexibility to change due to bearing standards. From the above three formulations and some of constraint equations to be discussed subsequently, the general objective function is expressed as
| $\begin{array}{l}\left(\max \left[C_d\right] \text { or } \max \left[H_{\min }\right] \text { or } \min \left[T_{\max }\right]\right) \equiv \\ \;\; f(\boldsymbol{X})=f\left(D_r, D_m, l_e, Z, K_{D \min }, K_{D \max }, \varepsilon, e, \xi, \alpha_o, \zeta\right)\end{array}$ | (2) |
where five independent geometric parameters, roller men diameter Dr, bearing pitch diameter Dm, roller effective length le, number of rollers Z, outer race cone angle αo, and six bearing constraint parameters (KDmin, KDmax, ε, ξ, e, and ζ) are both included as intended variables. Constraint factors (to be discussed in next section) have been treated as variables by providing certain feasible bounds to them.
1.3 Defining Bounds of Design Variable[20]A method of getting bounds of design parameters from group of constraints is briefly described as follows:
Constraints 1 & 2
The pitch diameter of the bearing is set to fall between the internal and external diameters of the bearing to ensure space for the chamfering of pointed corners of the cup and cone (Fig. 2).
Constraints 3 & 4
The range of Dr is obtained from the strength and geometric aspects. The upper limit is found from the bearing geometry and the lower limit of Dr is estimated from the contact stress equations. The smallest value of Dr should ensure that the contact stress generated owes to the exterior forces. The Hertzian contact stress expression for the roller contact[7] is given as
| $\sigma_{c_{\max }}^l=268.71 \sqrt{\frac{Q_{\max }}{D_r l_e}} \quad {\rm with} \quad D_r \approx 0.625 l_e$ | (3) |
where σcmaxl is the upper limit of the contact stress at interior raceway, and Qmax is contact force on the interior raceway at the heaviest loaded rolling element. An approximate relation for Dr and le given in Eq. (3) is used to obtain the minimal value of Dr. By using the highest contact stress as the secured contact stress (σcsafe= 4000 MPa) in Eq. (3), the lower limit of Dr can be calculated. Qmax is estimated with Stribeck's conventional expression[7]. The highest value of Dr is constrained by periphery dimensions, i.e., outer diameter D, and bore diameter d. This is calculated by assuming that the cup and cone's corners are chamfered.
Constraints 5 & 6
The diameter is never more than its length of roller in roller bearings. Similarly, both face widths of the cup should be more than the length of the roller.
Constraints 7 & 8
From least value of Dm and highest value of Dr, the least number of rollers is estimated. From higher limit of Dm and lower limit of Dr, the highest number of rollers is estimated in similar way.
1.4 Descriptions of ConstraintsIn total, 28 constraints have been considered, which are generally based on strength and geometric parameters and out of these 28 constraints, the first 27 are exactly the same as the constraints considered in Ref. [20].
Constraint 28
To avoid a sharp corner in the cup, the big-end, S2mino[32], should be greater than the cup's radius (r5min) and a minimum land of 1 mm should be added as
| $g_{28}(X)=S_{2_{\min }}^o \geqslant\left[r_{5_{\min }}+1.0+C_{2_{\min }} \tan \left(\alpha_o\right)\right]$ | (4) |
Now the objective functions and constraints have been defined completely. The next step is to apply evolutionary algorithm to obtain the optimum bearing design.
2 Computational Procedures for Evolutionary Algorithms[20]The constrained optimization problem is solved by the ABC algorithm. The algorithm implementation will be briefly discussed in the subsequent subsections.
The constraint violation task CV(X) estimates the total of the regularized constraint violation of the result (X) and is given as
| $C_V(X)=\sum\limits_{j=9}^{28}\left\langle g_j(X)\right\rangle$ | (5) |
The bracket operator 〈〉 represents the complete magnitude of the operand when the operand is negative. Despite the fact that the operand is non-negative, it produces a magnitude of zero. Because different constraints can result in data of varying magnitudes, it is required to regularize all constraints before applying Eq. (5). As an illustration, a constraint gj(X)≥bj is regularized with the succeeding alteration[33]:
| $g_j(X) \equiv \frac{g_j(X)}{b_j}-1 \geqslant 0$ | (6) |
where bj is a constraint limiter. Equality constraints are also normalized on identical steps. Because normalized constraint violations acquire the similar level of value, these could be merely summed as an overall constraint violation in Eq. (6). These chosen results are enhanced by ABC operators. Constrained optimization problems can be tackled by numerous ways. The parameter-less method[33] is applied to tackle constraints and the penalty parameter-less method is convenient for optimization algorithms running with the population. The penalty parameter-less approach[34] is commonly used to study constrained optimization problems by converting them to unconstrained formulations.
3 Numerical SimulationsA set of TRBs are chosen from TRB catalogue, which are related to a variety of size and tapered angles for getting optimum designs by the planned procedure. Table 7 of Ref. [20] lists the standard periphery, internal, and chamfering proportions. It also contains the standard Cd of TRB from the SKF general catalogue. 30% of Cd is treated as a comparable external transverse load exerted on the TRB for estimating two constraints based on the strength, i.e., Constraints 24 & 25 (Refer to Table 6 of Ref. [20]), for the optimum synthesis of bearing elements is based on the kinematics and stress aspect. The equivalent load is assumed to be a constant and in the actual bearing such extremely large forces will be hardly applied to it. Therefore, for optimization of Hmin and Tmax the applied force is taken as 10% of Cd. Material characteristics of the bearing steel are as follows. Secure contact stress, yield strength, Young's modulus, and Poisson's ratio are 4000 MPa, 600 MPa, 210 GPa, 0.3, respectively. Lubricant data and air characteristics are tabulated in Table 3 and Table 4 of Ref. [20], respectively. For the present case, the population size, quantity of generations and limit are chosen after observing several runs as 100, 1500, and 1000, respectively for Cd as objective function, for Tmax, they are 100, 1100, and 2500, respectively; and for Hmin, they are 100, 1000, and 2500, respectively.
| Table 3 Optimized design parameters, constraint factors, and obtained internal geometric variables of TRBs taking Tmax as objective function through ABC algorithm |
| Table 4 Parametric sensitivity analysis of the optimized design parameters for 30204 |
3.1 Implementation of the ABC Algorithm[20]
TRBs listed in Table 1 are optimized successively. First, the limits of basic design variables for a specific bearing number are obtained from Constraints 1 to 8. The bearing model 30204 has been taken for illustrating the convergence study. Bounds of basic design variables Dm, Dr, le, Z, KDmin, KDmax, ε, e, ξ, αo and ζ obtained from the procedure described above are 22.00 mm-37.14 mm, 5.541 mm - 6.926 mm, 5.541 mm-10.774 mm, 9-20, 0.3-0.4, 0.5-0.6, 0.4-0.5, 0.01-0.07, 0.80-0.95, 0-25.0 and 0.125-0.250, respectively. The flange height is considered to be a fraction of the roller bearing (ζ) and this fraction varies from 0.125 to 0.250. From the expression of Cd and Hmin, it is clear that they are independent of flange height. The design variable ζ has been taken as 0.125 on the basis of algebraic and safe stress issues. Using obtained bounds, basic design parameters are produced for inhabitants' quantity of 100 for all three objective functions. The simulation is executed for a definite quantity of generations. It is enlarged in progression pending the optimal summit in the synthesis constantly unaffected with added enhancement in generations. On the basis of the junction summit in the existing optimization formulation, the quantity of generations is considered as 2500 for Tmax and Hmin, and for Cd it is taken as 1500. It is very important to test various parameters of ABC algorithm for different objective functions and associated constraints and choose suitable values after thorough parametric study.
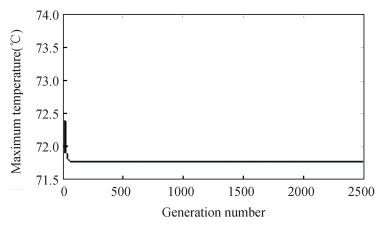
3.2 Convergence AnalysisThe deviation of dynamic capacity with the quantity of generations is depicted in Fig. 3. For early generations, the results converged to a lesser magnitude of fitness (i.e., 29.70 kN) up to the 8th generation. At 18th generation number, an abrupt alter in fitness function magnitude is attained. Subsequently, it is steady at 33.37 kN, then a swift enhancement in the fitness function magnitude is seen at the generation quantity of 181, and from the generation quantity of 616 onwards, it is steady at a fitness value of 34.82 kN. Fig. 4 depicts the change in EHL minimum film-thickness by generation quantity. The initial solution value is equal to 0.117 μm up to generation number 427. Beyond this, it shows fluctuation at generation number 428 and 1511 (0.112 μm and 0.108 μm, respectively). The solution is stable from generation number 1158 and converged to a value of 0.118 μm. Fig. 5 depicts the variation of utmost temperature versus the number of generations. At early stages, the value is equal to 73.63℃ up to the 7th generation, then it is equal to 71.77 ℃ in the 34th generation and from the generation 563 onwards it is stable at the value of 71.75 ℃.
|
Fig.5 Variation of Tmax with number of generations |
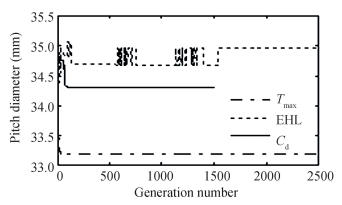
Fig. 6 depicts the deviation of pitch diameter (the finest solution in each generation) with generation number for all three objectives. They converged at the generation number of 1306, 578, and 1447 for Cd, Tmax, and Hmin, respectively; and converged values are 34.28 mm, 33.18 mm, and 34.96 mm, respectively.
|
Fig.6 Variation of pitch diameter with number of generations |
Fig. 7 depicts the deviation of roller diameter (the finest solution in each generation) with the quantity of generations. Final convergences of the roller diameter are observed beyond 1280, 715, and 1564 generations, respectively, for Cd, Tmax, and Hmin. With values of the roller diameter as 6.62 mm, 6.67 mm, and 5.98 mm, respectively. Fig. 8 depicts the deviation of effectual span of the tapered roller (the finest solution in each generation) for the generation number. From generations 503, 1221, and 1574 onwards for Cd, Tmax, and Hmin, the effective roller length remains the same with values of 10.85 mm, 9.6 mm, and 10.89 mm, respectively. Fig. 9 shows the relationship between the number of rollers (the best solution in each generation) and the generation number. Finally, at the generation number of 73, 1, and 1541 for Cd, Tmax, and Hmin, the number of rollers converges to 14, 16, and 18, respectively. Fig. 10 depicts the relationship between the contact angle (the best outcome in each generation) and the number of generations. At generation numbers of 666, 1306, and 1574 for Cd, Tmax, and Hmin, the contact angle converges to 15.41°, 11.58°, and 15.58°, respectively. According to the convergence study, the convergence of design variables is rather rapid.
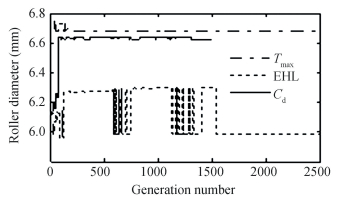
|
Fig.7 Variation of the roller diameter with generations |
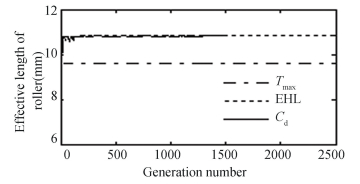
|
Fig.8 Variation of the effective length of roller with generations |

|
Fig.9 Variation of number of rollers with generations |

|
Fig.10 Variation of the contact angle with generations |
Based on optimum designs obtained from three objective functions, Fig. 11 shows the comparison of objective function values for individual optimum designs. Parameter 1 represents values of Hmin obtained from design variables for three optimized design objectives. From the plot, it is apparent that the value is a minimum for design variables optimized for Tmax. Parameter 2 represents values of Cd obtained from design variables for three optimized design objectives. It is evident that the value of Cd is a minimum for design variables optimized for Tmax (Cd is reduced by 16%). Parameter 3 represents the values of Tmax obtained from design variables for three optimized design objectives. From the plot it is observed that the value of Tmax is a minimum for design variables optimized for Tmax as objective function, and highest for Hmin as the objective function (Tmax is increased by 7%). Fig. 12 shows the comparison of design variables for three objective functions. It is observed that for Tmax as the objective function, the effective length, contact angle, number of rollers, and pitch diameter touch the lower limit and the roller diameter touches the upper limit. For Hmin as the objective function, the effective length, contact angle, number of rollers, and pitch diameter touch the upper bound and the roller diameter touches the lower bound. While for Cd as the objective function, the effective length, contact angle, number of rollers, roller diameter, and pitch diameter converge in between converged values for Tmax and Hmin. Highest duration of the computation method (for a single bearing design) is 15 min. Overall, it is very important to see how objective functions and design variables are taking its optimum values. As can be observed from present study, different objective function can have different convergence behavior. Herein, constraints play a very important role. For present case, the number of rollers has to be integer and it changes the optimization process significantly if its value changes suddenly during convergence.
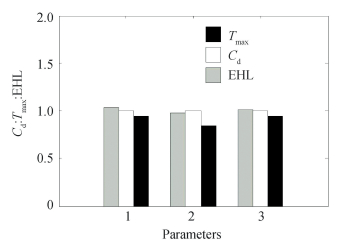
|
Fig.11 Comparison of the objective function |
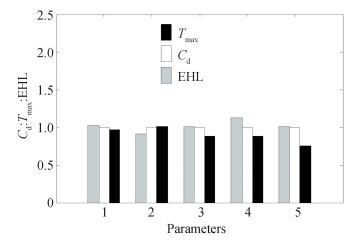
|
Fig.12 Comparison of the optimized design parameters |
3.3 Post-Processing of the Optimized Data and Its Analysis
Magnitudes of the highest contact force on the cone, the Hertzian contact stress on the cone, the location of highest dynamic shear inside the cone[7], the highest dynamic shear stress, and the highest principal stress in the flange for the typical bearing 30204 for the objective function Cd are 6633.77 N, 2815.69 MPa, 0.083 mm, 1407.84 MPa, and 600 N/mm2, respectively. For the objective function Tmax are 1002.53 N, 1188.73 MPa, 0.034 mm, 594.36 MPa, and 47.24 N/mm2, respectively; and for the objective function Hmin, the values are 7247.80 N, 3481.48 MPa, 0.102 mm, 1740.74 MPa, and 311.83 N/mm2, respectively.
Optimal interior dimensions of TRBs are given in Tables 1-3 that contain the optimized five essential geometrical design parameters and six design constraint factors. These also include eight subsequent analyzed interior geometric parameters of bearings through the optimized basic geometric design parameters. A sketch of a representative optimized TRB design signifying optimized magnitudes of intended variables for TRB numeral 30205 is depicted in Fig. 13. Table 1 shows comparison of optimized dynamic capacity available in standard catalogues. It can be seen appreciable amount of increase in the dynamic capacity of the optimized bearing. Application of the ABC algorithm for TRBs along with GA[16] results gives more confidence on the optimized results. The outcome of the present optimization is very significant since it gives overall idea of initial bearing geometry based on various criteria considered in present analysis, which is otherwise difficult to simulate in experimental test setup.
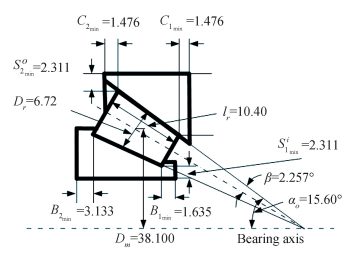
|
Fig.13 Optimum design of a typical tapered roller bearing 30205 (mm) |
3.4 Parametric Sensitivity Analyses Using Monte Carlo Simulation Techniques
During manufacturing, it is common to observe 0.5%-1.0% variation in the design variable data of various machine elements. To assess a bearing synthesis, it is essential to evaluate the deviation in the estimated fitness function concerning such small deviations in design variables. This concern is addressed here by the Monte Carlo simulation technique[35]. Among the design variables, the variables that have production deviations are Dm, Dr, αo, and le. Hence, the effect on fitness function of changing these variables is analyzed by an utmost of ±1% about a specified optimal position. The sensitivity of three objectives will be exhibited with reverence to all variables, individually and together. The investigation is imposed for the bearing number 30204 on the optimized design parameters. The data of optimized synthesized variables for 30204 are listed in Table 4. Constraint violations have been checked in each case and shown to be relatively less. In preceding analysis, deviations of the entire objectives due to deviations of synthesis variables are found to be extremely small. The objective function and/or constraint violations are likely to cause variations. The objective function has been observed to be well behaved. Despite the huge number of constraints, throughout the sensitivity analysis, none of them were found to be violated. It suggests that small variations occur in fitness function values on ±1% variations in optimal synthesized geometric parameters. It is because the current optimal synthesis formulation is nicely constrained through rational derivations. The outcome of the sensitivity analysis is definitely highly significant since it gives confidence in optimized design even with consideration of manufacturing tolerances.
From the present analysis, it is inferred that for TRBs, the majority of optimal parameters have modest consequence on the fitness function about its optimal value. It demonstrates that converged bearing designs are indifferent against minor deviations that are difficult to evade in the process of production.
4 ConclusionsA method for the optimal synthesis of TRBs has been suggested in the present work. Three objective functions were considered and are subjected to non-linear constraints. The optimal bearing synthesis was implemented using the ABC algorithm. Optimum designs from the ABC algorithm for three objectives were compared. It is concluded that the maximum temperature is contradictory to other two objectives, i.e., dynamic capacity and EHL film-thickness. An analysis has been performed to guarantee the closeness to comprehensive optimal location in the bearing synthesis. A sensitive study was also performed to obtain the cause of variation of synthesis parameters owing to production deviations, and the outcome indicates that hardly any synthesis variables have severe concern on fitness functions. From the present analysis, it is inferred that for TRBs, most of the optimal parameters have minor impact on the fitness function about its optimal value. It demonstrates that converged bearing designs are indifferent against minor deviations that are difficult to get away from the process of production. The suggested optimal synthesis procedure can be considered as a vital stride in the direction of more advance design necessity of the TRB that demands a greater number of factors, for example, as diametric deviations, compound static and dynamic forces along with related Hertzian stress investigation and profiling of surfaces in contact. This could be untaken by the optimization of multiple fitness functions of the TRBs for the user defined goal requirements. The non-dominating sets are analyzed on a particular bearing in the form of Pareto front, and based on application requirement of the user, one can choose trade-off among the objective functions for the optimum design of the bearing. Present work addresses three conflicting fitness functions, i.e., the dynamic capacity, minimum EHL thickness, and maximum temperature. We have not considered the static capacity as it does not conflict with dynamic capacity and results in similar optimized design as with the dynamic capacity. Moreover, the misalignment or slack that can occur in the TRB may be considered in designing when the preload value is reduced. References
| [1] |
Moyer C A, Mckelvey R E. A rating formula for tapered roller bearing. SAE Transactions, 1963, 71: 490-507. DOI:10.4271/630481 (  0) 0) |
| [2] |
Karna C L. Performance characteristics at the rib roller end contact in tapered roller bearings. ASLE Transactions, 1974, 17(1): 14-21. DOI:10.1080/05698197408981434 (  0) 0) |
| [3] |
Andréason S. Load distribution in a taper roller bearing arrangement considering misalignment. Tribology, 1973, 6(3): 84-92. DOI:10.1016/0041-2678(73)90241-8 (  0) 0) |
| [4] |
Liu J Y. Analysis of tapered roller bearings considering high speed and combined loading. Journal of Lubrication Technology, 1976, 98(4): 564-572. DOI:10.1115/1.3452933 (  0) 0) |
| [5] |
Aihara S. A new running torque formula for tapered roller bearings under axial load. Journal of Tribology, 1987, 109(3): 471-477. DOI:10.1115/1.3261475 (  0) 0) |
| [6] |
Changsen W. Analysis of Rolling Element Bearings. London: Mechanical Engineering Publications, 1991: 332-342.
(  0) 0) |
| [7] |
Harris T A. Rolling Bearings Analysis. New York: John Wiley and Sons, 1966.
(  0) 0) |
| [8] |
Bercea I, Cretu S, Nélias D. Analysis of double-row tapered roller bearings, Part I-Model. Tribology Transactions, 2003, 46(2): 228-239. DOI:10.1080/10402000308982622 (  0) 0) |
| [9] |
Chakraborty I, Kumar V, Nair S B, et al. Rolling element bearing design through genetic algorithms. Engineering Optimization, 2003, 35(6): 649-659. DOI:10.1080/03052150310001624403 (  0) 0) |
| [10] |
Gupta S, Tiwari R, Nair S B. Multi-objective design optimisation of rolling bearings using genetic algorithms. Mechanism and Machine Theory, 2007, 42(10): 1418-1443. DOI:10.1016/j.mechmachtheory.2006.10.002 (  0) 0) |
| [11] |
Rao B R, Tiwari R. Optimum design of rolling element bearings using genetic algorithms. Mechanism and Machine Theory, 2007, 42(2): 233-250. DOI:10.1016/j.mechmachtheory.2006.02.004 (  0) 0) |
| [12] |
Kumar K S, Tiwari R, Reddy R S. Development of an optimum design methodology of cylindrical roller bearings using genetic algorithms. International Journal for Computational Methods in Engineering Science and Mechanics, 2008, 9(6): 321-341. DOI:10.1080/15502280802362995 (  0) 0) |
| [13] |
Kumar K S, Tiwari R, Prasad P V V N. An optimum design of crowned cylindrical roller bearings using genetic algorithms. Journal of Mechanical Design, 2009, 131(5): 051011. DOI:10.1115/1.3116344 (  0) 0) |
| [14] |
Goldberg D E. Genetic Algorithms in Search, Optimization, and Machine Learning. Boston: Addison-Wesley Publishing Company, 1989.
(  0) 0) |
| [15] |
Deb K. Optimization for Engineering Design, Algorithms and Examples. New Delhi: Prentice-Hall of India Private Ltd., 1996.
(  0) 0) |
| [16] |
Chaturbhuj N, Nair S B, Tiwari R. Design optimization for tapered roller bearings using genetic algorithm. Proceedings of the International Conference on Artificial Intelligence, 2003, 1: 421-427. (  0) 0) |
| [17] |
Lin W Y. Optimum design of rolling element bearings using a genetic algorithm-differential evolution (GA-DE) hybrid algorithm. Proceedings of the Institution of Mechanical Engineers, Part C, Journal of Mechanical Engineering Science, 2011, 225(3): 714-721. DOI:10.1243/09544062JMES2389 (  0) 0) |
| [18] |
Wang Z W, Meng L Q, Hao W S, et al. Optimal design of parameters for four column tapered roller bearing. Applied Mechanics and Materials, 2011, 63. DOI:10.4028/www.scientific.net/AMM.63-64.201 (  0) 0) |
| [19] |
Tiwari R, Sunil K K, Reddy R S. An optimal design methodology of tapered roller bearings using genetic algorithms. International Journal for Computational Methods in Engineering Science and Mechanics, 2012, 13(2): 108-127. DOI:10.1080/15502287.2011.654375 (  0) 0) |
| [20] |
Tiwari R, Chandran R. Thermal based optimum design of tapered roller bearing through evolutionary algorithm. ASME 2013 Gas Turbine India Conference. Singapore: ASME, 2013. V001T05A021-V001T05A021. DOI: 10.1115/GTINDIA2013-3792.
(  0) 0) |
| [21] |
Tiwari R, Chandran R M P. Multitude of objectives based optimum designs of cylindrical roller bearings with evolutionary methods. Journal of Tribology, 2015, 137(4): 041504. DOI:10.1115/1.4030166 (  0) 0) |
| [22] |
Dandagwhal R D, Kalyankar V D. Design optimization of rolling element bearings using advanced optimization technique. Arabian Journal for Science and Engineering, 2019, 44: 7407-7422. DOI:10.1007/s13369-019-03767-0 (  0) 0) |
| [23] |
Verma S K, Tiwari R. Robust optimum design of tapered roller bearings based on maximization of fatigue life using evolutionary algorithm. Mechanism and Machine Theory, 2020, 152: 103894. DOI:10.1016/j.mechmachtheory.2020.103894 (  0) 0) |
| [24] |
Kalyan M, Tiwari R, Ahmad S. Multi-objective optimization in geometric design of tapered roller bearings based on fatigue, wear and thermal considerations through genetic algorithms. Sādhanā, 2020, 45: 142. DOI:10.1007/s12046-020-01385-3 (  0) 0) |
| [25] |
Tiwari R, Chandran R. Optimal design of deep-groove ball bearings based on multitude of objectives using evolutionary algorithms. Multidiscipline Modeling inMaterials and Structures, 2018, 14(3): 567-588. DOI:10.1108/MMMS-06-2017-0058 (  0) 0) |
| [26] |
Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x (  0) 0) |
| [27] |
Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm. Appllied Soft Computing, 2008, 8(1): 687-697. DOI:10.1016/j.asoc.2007.05.007 (  0) 0) |
| [28] |
Bureau of Indian Standards. IS 7461 (Part-1). General plan of boundary dimensions for tapered roller bearings. New Delih: Bureau of Indian Standards, 1993.
(  0) 0) |
| [29] |
SKF. SKF General Catalogue. Germany: Media Print, 2005.
(  0) 0) |
| [30] |
Bureau of Indian Standards. IS 3824. Rolling Bearings-Dynamic Load Ratings and Rating Life. New Delih: Bureau of Indian Standards, 2002.
(  0) 0) |
| [31] |
Harris T A, Barnsby R M. Tribological performance prediction of aircraft gas turbine mainshaft ball bearings. Tribology Transactions, 1998, 41(1): 60-68. DOI:10.1080/10402009808983722 (  0) 0) |
| [32] |
Jamison W E, Kauzlarich J J, Mochel E V. Geometric effects on the rib-roller contact in tapered roller bearings. ASLE Transactions, 1977, 20(1): 79-88. DOI:10.1080/05698197708982820 (  0) 0) |
| [33] |
Deb K. An efficient constraint handling method for genetic algorithms. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2-4): 311-338. DOI:10.1016/S0045-7825(99)00389-8 (  0) 0) |
| [34] |
Deb K. Multi-objective Optimization Using Evolutionary Algorithms. New York: John Wiley and Sons, 2001.
(  0) 0) |
| [35] |
Choi J, Harvey J W, Conklin M H. Use of multi-parameter sensitivity analysis to determine relative importance of factors influencing natural attenuation of mining contaminants. https://permanent.access.gpo.gov/lps39001/lps39001/toxics.usgs.gov/pubs/wri99-4018/Volume1/sectionC/1405_Choi/pdf/1405_Choi.pdf, 2022-03-27.
(  0) 0) |
 2023, Vol. 30
2023, Vol. 30


